Optimization of catheter placement for convection-enhanced delivery to brain tumors

Lisa H. Antoine; Roy P. Koomullil; Timothy M. Wick; Arie Nakhmani

doi:10.12688/f1000research.28247.1

Home Browse Optimization of catheter placement for convection-enhanced delivery...

ALL Metrics

-

Views

-

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Optimization of catheter placement for convection-enhanced delivery to brain tumors

[version 1; peer review: 2 approved with reservations]

Lisa H. Antoine ¹, Roy P. Koomullil², Timothy M. Wick¹, Arie Nakhmani³

PUBLISHED 12 Jan 2021

Author details Author details

¹ School of Engineering, University of Alabama at Birmingham, Birmingham, AL, 35294, USA
² Mechanical Engineering, University of Alabama at Birmingham, Birmingham, AL, 35294, USA
³ Electrical and Computer Engineering, University of Alabama at Birmingham, Birmingham, AL, 35294, USA

Lisa H. Antoine
Roles: Conceptualization, Data Curation, Formal Analysis, Funding Acquisition, Investigation, Methodology, Project Administration, Software, Validation, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Roy P. Koomullil
Roles: Conceptualization, Formal Analysis, Funding Acquisition, Investigation, Methodology, Project Administration, Software, Supervision, Validation, Visualization, Writing – Review & Editing

Timothy M. Wick
Roles: Formal Analysis, Funding Acquisition, Methodology, Project Administration, Supervision, Validation, Writing – Review & Editing

Arie Nakhmani
Roles: Validation, Visualization, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

Abstract

Background: Recent trends suggest that physicians will diagnose thousands of children in the United States with a brain or central nervous system tumor in 2020. Malignant brain tumors are difficult to treat, with low life expectancy rates in children and adults. Convection-enhanced delivery (CED) shows promise for the treatment of brain tumors, yet remains in clinical trials despite being developed more than 20 years ago. To advance CED to standard of care status and help improve survival rates, this study group developed a quantitative computer simulation model to determine and optimize therapy distribution in brain tumors based on the catheter infusion locations for CED.
Methods: The simulations resulted in the identification of four infusion reference locations, which were used to conduct an optimization study to identify the optimal locations for CED. Patient-specific T1-weighted images and diffusion-weighted images provided information regarding tumor shape and size and the approximate rate at which therapy distributes at spatial locations within the tumor. Using the images, the researchers in this study developed a model which allowed the calculation of therapy distribution within the tumor while considering its permeability, porosity, and interstitial fluid pressure characteristics. We divided the tumor into regions and calculated distribution for four infusion locations per region. Using the location from each region with the highest volume distribution allowed our study group to conduct the response surface optimization.
Results: Twelve optimal locations emerged from the optimization with volume percentage distributions ranging from 7.92% to 9.09%, compared to 2.87% to 6.32% coverage for non-optimal locations. This optimization method improved distribution from 27.80% to 45.95%, which may improve therapeutic value.
Conclusions: Catheter placement appears to influence volume therapy distribution percentages. The selection of the highest percentages per region may provide optimal therapy for the entire tumor region.

Keywords

brain tumor, convection-enhanced delivery, optimization

Corresponding author: Lisa H. Antoine

Competing interests: No competing interests were disclosed.

Grant information: The University of Alabama at Birmingham Blazer Graduate Research Fellowship and NIH grant number 5K12GM088010-12 funded this research.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2021 Antoine LH et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Antoine LH, Koomullil RP, Wick TM and Nakhmani A. Optimization of catheter placement for convection-enhanced delivery to brain tumors [version 1; peer review: 2 approved with reservations]. F1000Research 2021, 10:18 (https://doi.org/10.12688/f1000research.28247.1) First published: 12 Jan 2021, 10:18 (https://doi.org/10.12688/f1000research.28247.1) Latest published: 12 Jan 2021, 10:18 (https://doi.org/10.12688/f1000research.28247.1)

Introduction

Surgery, radiation therapy, and chemotherapy are the standard of care for brain tumors¹. Surgery or tumor resection removes all or part of the tumor; however, this method is invasive and risky. Radiation therapy seeks to remove the tumor using high-energy x-rays, while chemotherapy attacks the tumor using drugs taken either orally or intravenously. Radiation therapy and chemotherapy may cause side effects, which may include hair loss and decreased mental functionality¹.

Although therapy delivery methods, such as Ommaya reservoirs and convection-enhanced delivery (CED), are not standards of care, these methods are available in clinical trials, appear to be less invasive, and could offer effective treatment^2–5. Ommaya reservoirs use a catheter-reservoir system implanted under the scalp for therapy delivery, while CED uses a catheter-syringe-pump system for therapy delivery. In this study, researchers used a response surface optimization (RSO) technique for the selection of the ideal catheter placement locations, which may improve the effectiveness of CED.

In general, optimization techniques improve speed and accuracy during the search for the ideal solution for a given problem. Study groups used an array of these techniques to address the challenges associated with brain tumor treatments^6–10. Li et al. developed an optimization method using a genetic algorithm to determine catheter positions that would yield optimal therapy concentrations in the tumor and white matter, while limiting concentrations in the cortex⁶. The study demonstrated that a genetic algorithm can determine optimal catheter positions and suggests that it may be sufficient to determine the optimal locations for our study. Vidotto et al. used a neural network based algorithm to improve the accuracy and speed of axon diameter distribution within the brain⁷.

Zhang et al. used RSO to determine the optimal extrusion die design, which resulted in a more accurate extrudate shape and lower extrusion die production costs¹¹. Using a response surface methodology Sultana et al. predicted that jute fiber can improve compressive and tensile concrete strength¹². This group validated the predicted results against experimental results and concluded that the variation was only approximately 5%. Akhbar et al. used RSO to optimize rotational speed and feed to prevent heat damage during bone-drilling surgical procedures¹³. Albe et al. examined the effect of pH and salt concentration on the extraction of sunflower protein using the response surface to maximize the protein¹⁴. Silva et al. used RSO to achieve a mean recovery of 91% and overall precision of 5% when verified using fortified samples of pharmaceutical residues¹⁵. Each of these groups used RSO and improved the accuracy of their respective designs, which suggests that this technique will optimize the infusion locations in our study within 5% precision.

In this study RSO allowed an efficient determination of the optimal location for therapy distribution and includes design of experiments (DOE), response surface, and optimization. DOE uses input and output parameters as the major components and analyzes the input-output relationship generating design points that lie within boundaries in proximity of the baseline point. The response surface results from an algorithm that does not simulate a complete solution, but instead performs a quick analysis of the DOE sampling percentages using cross-validation to predict surface percentages. The fitness function associates DOE percentages to surface percentages, where alignment of the percentages on a diagonal line suggests that the response surface fits the DOE percentages. Using results from DOE and response surface, optimization determines the ideal locations for the maximum therapy distribution.

Methods

Tumor parameters

To conduct response surface optimization, the researchers derived the tumor geometry with x, y, z lengths of 12.86 mm, 30.4 mm, and 37.43 mm, respectively, and volume of 5031.35 mm³ from patient specific T1-weighted images (T1W)¹⁶. The anonymized T1W (approved for use by the University of Alabama Institutional Review Board as not human-subjects research) includes 135 dicom files for one subject were obtained from The University of Alabama at Birmingham Department of Radiology. Diffusion tensors inside the tumor resulted from the diffusion-weighted images (DWI) of the patient using the DSI Studio 2019_10 version¹⁷. Viscous resistance of the tumor is the transformation of the diffusion tensor as discussed by the Støverud group¹⁸. Because the tensors may not align to the center of the computational elements, it was necessary to interpolate these values using trilinear interpolation.

Therapy parameters

We expect the suspension of the oncolytic herpes simplex virus to be uniform in a fluid and use a transport equation to model fluid flow inside the tumor¹⁹. Velocity components in the transport equation are a function of the therapy infusion rate and thereby, calculated by solving the Navier-Stokes equation¹⁹ with an assumption of laminar flow inside the tumor. The virus density and viscosity information were unavailable. Therefore, we analyzed the flow using density and viscosity values for water of 1×10^-6 kg/mm³ and 1.003×10^-6 kg/mm-s, and a porosity value of 0.6 and pressure of 266.65 Pa from previous studies^20,21.

Optimization

The researchers selected six input parameters, which included x, y, and z coordinates along the tumor boundaries and fixed values for flow rate (0.1 mL/hr), minimum dose (1×10^-19 mL/mm³), and radius (1.5 mm). The radius of 1.5 mm ensures that the infusion location is larger than the catheter radius (0.5 mm). After the selection and analysis of 16 locations (x, y, z coordinates) within the tumor, four baseline locations were available for the response surface optimization. The baselines represent the locations that produced the highest therapy distribution percentages in the tumor.

DOE generated 28 sampling points using the input parameters of the baseline point as the reference point. Default lower and upper bounds for the coordinates reflect the baseline point as the midpoint. ANSYS (free student version download available) calculated therapy percentages for sampling points using default parameters – flow rate, infusion location radius, and minimum dose¹⁹. Based on the DOE, the response surface determines minimum and maximum percentages. The goodness of fit compared the predicted response surface to the observed surface for the design points and determined the surface quality and discrepancies between observed and predicted percentages.

Nonlinear Programming by Quadratic Lagrangian (NLPQL)¹⁹ provided a local optimization solution, which maximizes the therapy distribution percentages. Baseline point specification was necessary to define the exploration region and identify three candidate points per region. Number of evaluations varied by region and included several iterations. Tolerance for checking convergence was 0.0001.

Results

Volume distribution percentages from region one design points ranged from 3.01 % to 9.02%, region two ranged from 4.19% to 9.09%, region three ranged from 2.51% to 8.12%, and region four ranged from 3.17% to 8.18%.

Response surfaces in region one suggest that maximum therapy distribution percentage is approximately 9% (Figure 1). Location combinations of y and z (Figure 1c) appear to produce a larger region with percentages that are greater than 8% as opposed to combinations of locations x and y (Figure 1a) and locations x and z (Figure 1b). Maximum therapy distribution for region one occurred at location -13.28 mm, 23.80 mm, 39.77 mm and was approximately 9.02%.

Figure 1. Region one response surface for therapy distribution percentages.

(a) x axis represents input parameters along the x direction, y axis represents input parameters along the y direction; (b) z axis represents input parameters along the z direction; (c) y and z input combinations appear to include the highest number of locations with therapy distribution percentages greater than 8%.

Response surfaces in region two suggest that the therapy distribution percentage is approximately 9% (Figure 2). Location combinations of y and z (Figure 2c) appear to produce a larger region with percentages that are greater than 8% when compared to combinations of locations x and y (Figure 2a) and x and z (Figure 2b). Maximum therapy distribution for region two occurred at location -11.04 mm, 15.17 mm, 26.68 mm and was approximately 9.09%.

Figure 2. Region two response surface for therapy distribution percentages.

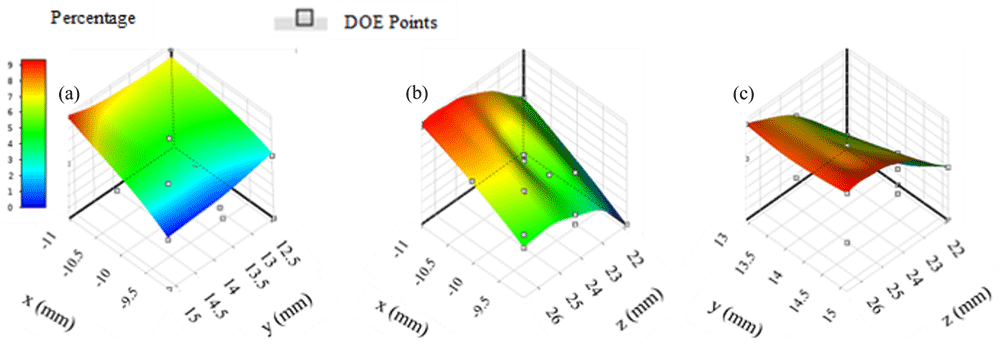
(a) x axis represents input parameters along the x direction, y axis represents input parameters along the y direction; (b) z axis represents input parameters along the z direction; (c) y and z input combinations appear to include the highest number of locations with therapy distribution percentages greater than 8%.

Response surfaces in region three suggest that maximum therapy distribution percentage is approximately 8% (Figure 3). Location combinations of y and z (Figure 3c) appear to produce a larger region with percentages that are greater than 7% as opposed to combinations of locations x and y (Figure 3a) and locations x and z (Figure 3b). Maximum therapy distribution for region three occurred at location -9.17 mm, 6.81 mm, 31.20 mm and was approximately 8.12%.

Figure 3. Region three response surface for therapy distribution percentages.

(a) x axis represents input parameters along the x direction, y axis represents input parameters along the y direction; (b) z axis represents input parameters along the z direction; (c) y and z input combinations appear to include the highest number of locations with therapy distribution percentages greater than 7%.

Response surfaces in region four suggest that maximum therapy distribution percentage is approximately 8% (Figure 4). Location combinations of x and z (Figure 4b) appear to produce a larger region with percentages that are greater than 7% as opposed to x and y (Figure 4a) or y and z (Figure 4c). Maximum therapy distribution for region four occurred at location -12.89 mm, 17.93 mm, 48.80 mm and was approximately 8.27%.

Figure 4. Region four response surface for therapy distribution percentages.

(a) x axis represents input parameters along the x direction, y axis represents input parameters along the y direction; (b) z axis represents input parameters along the z direction, x and z input combinations appear to include the highest number of locations with therapy distribution percentages greater than 7%; (c) y and z input combinations appear to include high numbers of locations with percentages greater than 7%.

During optimization the goal was to maximize the volume distribution percentage to a value greater than or equal to 8% based upon the observed percentages from the design points. The number of evaluations varied among the regions with region one and two requiring 22 and 47 evaluations, respectively. Regions three and four required 39 and 59 evaluations, respectively.

Optimization resulted in twelve optimal locations – three locations for each region. Maximum therapy distribution percentages throughout the regions ranged from 8.12% to 9.09% (Table 1). The location of the largest therapy distribution of 9.02% in region one was -13.28 mm, 23.80 mm, 39.77 mm, while the location in region two with a distribution of 9.09% was -11.04 mm, 15.17 mm, 26.68 mm. In regions three and four the largest distributions were 8.12% at location -9.17 mm, 6.81 mm, 31.20 mm and 8.27% at -12.89 mm, 17.94 mm, 48.80 mm, respectively. Optimal locations clustered together (Figure 5) and clustered closely to the baseline locations for region three.

Table 1. Optimal locations by region with corresponding xyz spatial coordinates and therapy distribution percentages.

	x (mm)	y (mm)	z (mm)	Therapy Distribution Percentage (%)
REGION ONE
Location 1	-13.28	23.80	39.77	9.02
Location 2	-13.28	24.10	39.77	8.78
Location 3	-13.28	23.80	40.24	8.67
REGION TWO
Location 1	-11.04	15.17	26.68	9.09
Location 2	-11.04	15.17	26.55	9.04
Location 3	-10.94	15.17	26.68	9.01
REGION THREE
Location 1	-9.17	6.81	31.20	8.12
Location 2	-9.61	7.13	30.97	8.09
Location 3	-9.61	6.50	31.31	8.08
REGION FOUR
Location 1	-12.89	17.94	48.80	8.27
Location 2	-12.89	17.78	48.80	8.18
Location 3	-12.89	18.10	48.80	7.92

Figure 5. Tumor infusion optimal locations with corresponding baseline locations by region.

Discussion

More than 25 years ago Bobo et al. introduced CED to deliver therapy to treat brain tumors; however, CED currently remains in clinical trials and appears to be mostly tested for safety and toxicity^22,23. Shi et al. reviewed CED clinical treatment methods from 1997 through 2018 and found that irrespective of therapeutic agents, survival rates during phase III clinical trials did not improve²⁴. Median survival times for the Carpenter et al., Weaver et al., Sampson et al., Hau et al., and Desjardins et al. trials were 7, 5.2, 7.5, 11, and 12.5 months, respectively^25–29. These survival times may correlate to the difficulty in reaching all tumor cells and in evaluating the movement of therapy within the tumor³⁰. Shi et al. suggested that catheter placement and corresponding therapy distribution may be the missing link.

In an effort to promote CED to standard of care, the current study aimed to quantitatively identify the optimal catheter locations for therapy delivery to brain tumors. The optimization technique requires one baseline location from each region with the highest therapy distribution. This group randomly selected 16 locations to determine the four baselines.

Response surfaces revealed 2D regions that show maximum therapy distribution. Both the predicted percentages from the response surface and observed percentages from the design of experiments aligned closely, which suggest that the response surface fits the design points. NLPQL approximated derivatives using the central differences scheme to refine the results and produce three locations per region with the maximum therapy percentages.

The mean percentage of the locations was 8.82% for region one with location -13.28 mm, 23.80 mm, 39.77 mm, yielding the highest percentage at 9.02%, while the baseline location (-12.07 mm, 26.45 mm, 44.19 mm) yielded therapy distribution of 6.26%, which varies from the mean distribution percentage by 29.05%. The mean Euclidean distance between the baseline and the three locations is 2.05 mm.

The mean percentage was 9.05% for region two with location -11.04 mm, 15.17 mm, 26.68 mm yielding the highest percentage at 9.09%, which contrasts with the baseline location (-10.03 mm, 13.79 mm, 24.25 mm) and its yield of 6.32%. Although the Euclidean distance between the two locations is 2.97 mm, the baseline provides 30.47% less therapy distribution than this location, which results from the optimization.

Location (-9.17 mm, 6.81 mm, 31.20 mm) for region three returned a distribution percentage of 8.12%, which varies by 34.73% from the baseline location (-8.73 mm, 6.48 mm, 29.71 mm) at 5.30%. The Euclidean distance between the locations is 1.59 mm. Location (-12.89 mm, 17.94 mm, 48.80 mm) for region four produced an optimal therapy distribution percentage of 8.27%, while the baseline location (-11.72 mm, 19.76 mm, 54.22 mm) returned therapy distribution of 4.47%, which varies by 45.95% from this location. Euclidean distance between the two locations is 5.84 mm.

Conclusions

In summary, CED as a brain tumor treatment method shows promise, but the treatment still remains in clinical trials despite being available for more than 20 years. The missing link for advancement to standard of care for CED may be the selection of catheter placement that yields the highest distribution percentage.

We developed an optimization method to determine the optimal catheter placement based on diffusion, viscous resistance, porosity, fluid pressure, and tumor geometry. Our results suggest that catheter placement does influence volume distribution percentages and that this optimization method improved distribution from 27.80% to 45.95%. The selection of the highest percentages per region may provide optimal therapy for the tumor.

In the future, investigators can verify this optimization method using patient-specific T1W and DWI data and therapy-specific density and viscosity information. Experimental validation using animal models is a critical step in determining the effectiveness of this quantitative tool^31–39.

Data availability

Harvard Dataverse: Catheter placement selection for convection-enhanced delivery of therapeutic agents to brain tumors. https://doi.org/10.7910/DVN/H7C6A2¹⁶.

- The dataset includes T1-weighted and diffusion-weighted images for the study subject.

Data are available under the terms of the Creative Commons Zero “No rights reserved” data waiver (CC0 1.0 Public domain dedication).

Faculty Opinions recommended

References

1. Brain Tumor - Types of Treatment 2020. Accessed June 9, 2020. Reference Source
2. Phase II Study of Intraventricular Methotrexate in Children With Recurrent or Progressive Malignant Brain Tumors. 2020. Accessed June 9, 2020. Reference Source
3. Methotrexate and Etoposide Infusions Into the Fourth Ventricle in Children With Recurrent Posterior Fossa Brain Tumors. Accessed June 9, 2020. Reference Source
4. Convection-Enhanced Delivery (CED) of MDNA55 in Adults With Recurrent or Progressive Glioblastoma. Accessed June 9, 2020. Reference Source
5. A Phase 1 Study of M032, a Genetically Engineered HSV-1 Expressing IL-12, in Patients with Recurrent/Progressive Glioblastoma Multiforme, Anaplastic Astrocytoma, or Gliosarcoma. Accessed June 9, 2020. Reference Source
6. Li D, Ivanchenko O, Sindhwani N, et al.: Optimal catheter placement for chemotherapy. 20th European symposium on computer aided process engineering. Comput Aided Chem Eng. 2010; 28: 223–228. Publisher Full Text
7. Vidotto M, De Momi E, Gazzara M, et al.: FCNN-based axon segmentation for convection-enhanced delivery optimization. Int J Comput Assist Radiol Surg. 2019; 14(3): 493–499. PubMed Abstract | Publisher Full Text
8. Hajishamsaei M, Pishevar A, Bavi O, et al.: A novel in silico platform for a fully automatic personalized brain tumor growth. Magn Reson Imaging. 2020; 68: 121–126. PubMed Abstract | Publisher Full Text
9. Girard A, Saint-Jalmes H, Chaboub N, et al.: Optimization of time frame binning for FDOPA uptake quantification in glioma. PLoS One. 2020; 15(4): e0232141. PubMed Abstract | Publisher Full Text | Free Full Text
10. Zade AE, Haghighi SS, Soltani M: Reinforcement learning for optimal scheduling of Glioblastoma treatment with Temozolomide. Comput Methods Programs Biomed. 2020; 193: 105443. PubMed Abstract | Publisher Full Text
11. Zhang G, Huang X, Li S, et al.: Optimized design method for profile extrusion die based on NURBS modeling. Fibers Polym. 2019; 20: 1733–1741. Publisher Full Text
12. Sultana N, Hossain SMZ, Alam MS, et al.: An experimental investigation and modeling approach of response surface methodology coupled with crow search algorithm for optimizing the properties of jute fiber reinforced concrete. Constr Build Mater. 2020; 243: 118216. Publisher Full Text
13. Akhbar MFA, Yusoff AR: Fast & Injurious: Reducing thermal osteonecrosis regions in the drilling of human bone with multi-objective optimization. Measurement. 2020; 152: 107385. Publisher Full Text
14. Albe Slabi S, Mathe C, Basselin M, et al.: Multi-objective optimization of solid/liquid extraction of total sunflower proteins from cold press meal. Food Chem. 2020; 317: 126423. PubMed Abstract | Publisher Full Text
15. Silva JM, Azcarate FJ, Knobel G, et al.: Multiple response optimization of a QuEChERS extraction and HPLC analysis of diclazuril, nicarbazin and lasalocid in chicken liver. Food Chem. 2020; 311: 126014. PubMed Abstract | Publisher Full Text
16. Antoine L: "Catheter placement selection for convection-enhanced delivery of therapeutic agents to brain tumors". Harvard Dataverse V1, 2020. http://www.doi.org/10.7910/DVN/H7C6A2
17. Yeh FC, Wedeen VJ, Tseng WYI: Generalized q-Sampling imaging. IEEE Trans Med Imaging. 2010; 29(9): 1626–1635. PubMed Abstract | Publisher Full Text
18. Stoverud KH, Darcis M, Helmig R, et al.: Modeling Concentration Distribution and Deformation During Convection-Enhanced Drug Delivery into Brain Tissue. Transp Porous Media. 2012; 92: 119–143. Publisher Full Text
19. ANSYS® [computer program] Version 19.1.
20. Jain R: Transport in Molecules in the Tumor Interstitium: A Review. Cancer Res. 1987; 47(12): 3039–3051. PubMed Abstract
21. Boucher Y, Salehi H, Witwer B, et al.: Interstitial fluid pressure in intracranial tumours in patients and in rodents. Br J Cancer. 1997; 75(6): 829–836. PubMed Abstract | Publisher Full Text | Free Full Text
22. Bobo R, Laske D, Akbasak A, et al.: Convection-enhanced delivery of macromolecules in the brain. Proc Natl Acad Sci U S A. 1994; 91(6): 2076–2080. PubMed Abstract | Publisher Full Text | Free Full Text
23. Bernstock JD, Wright Z, Bag AK, et al.: Stereotactic Placement of Intratumoral Catheters for Continuous Infusion Delivery of Herpes Simplex Virus -1 G207 in Pediatric Malignant Supratentorial Brain Tumors. World Neurosurg. 2019; 122: E1592–E1598. PubMed Abstract | Publisher Full Text | Free Full Text
24. Shi M, Sanche L: Convection-Enhanced Delivery in Malignant Gliomas: A Review of Toxicity and Efficacy. J Oncol. 2019; 2019: 1–13. PubMed Abstract | Publisher Full Text | Free Full Text
25. Carpentier A, Laigle-Donadey F, Zohar S, et al.: Phase 1 trial of a CpG oligodeoxynucleotide for patients with recurrent gliobastoma. Neuro Oncol. 2006; 8(1): 60–66. PubMed Abstract | Publisher Full Text | Free Full Text
26. Weaver M, Laske D: Transferrin receptor ligand-targeted toxin conjugate (Tf-CRM107) therapy of malignant gliomas. J Neurooncol. 2003; 65(1): 3–13. PubMed Abstract | Publisher Full Text
27. Sampson JH, Akabani G, Friedman AH, et al.: Comparison of intratumoral bolus injection and convection-enhanced delivery of radiolabeled antitenascin monoclonal antibodies. Neurosurg Focus. 2006; 20(4): E14. PubMed Abstract | Publisher Full Text
28. Hau P, Jachimczak P, Schlingensiepen R, et al.: Inhibition of TGF-beta2 with AP 12009 in recurrent malignant gliomas: from preclinical to phase I/II studies. Oligonucleotides. 2007; 17(2): 201–212. PubMed Abstract | Publisher Full Text
29. Desjardins A, Gromeier M, Herndon JE, et al.: Recurrent glioblastoma treated with recombinant poliovirus. N Engl J Med. 2018; 379(2): 150–161. PubMed Abstract | Publisher Full Text | Free Full Text
30. Warren K: Beyond the blood-brain barrier: the importance of central nervous system (CNS) pharmacokinetics for the treatment of CNS tumors, including diffuse intrinsic pontine glioma. Front Oncol. 2018; 8: 239. PubMed Abstract | Publisher Full Text | Free Full Text
31. Beffinger M, Schellhammer L, Pantelyushin S, et al.: Delivery of Antibodies into the Murine Brain via Convection-enhanced Delivery. J Vis Exp. 2019; (149): 1–7. PubMed Abstract | Publisher Full Text
32. Kanemitsu T, Kawabata S, Fukumura M, et al.: Folate receptor-targeted novel boron compound for boron neutron capture therapy on F98 glioma-bearing rats. Radiat Environ Biophys. 2019; 58(1): 59–67. PubMed Abstract | Publisher Full Text
33. Allen J, Wang J, Zolotarskaya OY, et al.: PEAMOtecan, a novel chronotherapeutic polymeric drug for brain cancer. J Control Release. 2020; 321: 36–48. PubMed Abstract | Publisher Full Text
34. Enríquez Pérez J, Kopecky J, Visse E, et al.: Convection-enhanced delivery of temozolomide and whole cell tumor immunizations in GL261 and KR158 experimental mouse gliomas. BMC Cancer. 2020; 20(1): 7. PubMed Abstract | Publisher Full Text | Free Full Text
35. Stephen ZR, Chiarelli PA, Revia RA, et al.: Time-Resolved MRI Assessment of Convection-Enhanced Delivery by Targeted and Nontargeted Nanoparticles in a Human Glioblastoma Mouse Model. Cancer Res. 2019; 79(18): 4776–4786. PubMed Abstract | Publisher Full Text | Free Full Text
36. Tosi U, Kommidi H, Bellat V, et al.: Real-Time, in Vivo Correlation of Molecular Structure with Drug Distribution in the Brain Striatum Following Convection Enhanced Delivery. ACS Chem Neurosci. 2019; 10(5): 2287–2298. PubMed Abstract | Publisher Full Text
37. Pang HH, Chen PY, Wei KC, et al.: Convection-Enhanced Delivery of a Virus-Like Nanotherapeutic Agent with Dual-Modal Imaging for Besiegement and Eradication of Brain Tumors. Theranostics. 2019; 9(6): 1752–1763. PubMed Abstract | Publisher Full Text | Free Full Text
38. Finbloom JA, Aanei IL, Bernard JM, et al.: Evaluation of Three Morphologically Distinct Virus-Like Particles as Nanocarriers for Convection-Enhanced Drug Delivery to Glioblastoma. Nanomaterials (Basel). 2018; 8(12): 1007. PubMed Abstract | Publisher Full Text | Free Full Text
39. Khateeb K, Griggs D, Sabes P, et al.: Convection Enhanced Delivery of Optogenetic Adeno-associated Viral Vector to the Cortex of Rhesus Macaque Under Guidance of Online MRI Images. J Vis Exp. 2019; (147): 1–8. PubMed Abstract | Publisher Full Text

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 12 Jan 2021

Author details Author details

¹ School of Engineering, University of Alabama at Birmingham, Birmingham, AL, 35294, USA
² Mechanical Engineering, University of Alabama at Birmingham, Birmingham, AL, 35294, USA
³ Electrical and Computer Engineering, University of Alabama at Birmingham, Birmingham, AL, 35294, USA

Lisa H. Antoine
Roles: Conceptualization, Data Curation, Formal Analysis, Funding Acquisition, Investigation, Methodology, Project Administration, Software, Validation, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Roy P. Koomullil
Roles: Conceptualization, Formal Analysis, Funding Acquisition, Investigation, Methodology, Project Administration, Software, Supervision, Validation, Visualization, Writing – Review & Editing

Timothy M. Wick
Roles: Formal Analysis, Funding Acquisition, Methodology, Project Administration, Supervision, Validation, Writing – Review & Editing

Arie Nakhmani
Roles: Validation, Visualization, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

The University of Alabama at Birmingham Blazer Graduate Research Fellowship and NIH grant number 5K12GM088010-12 funded this research.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (1)

version 1

Published: 12 Jan 2021, 10:18

https://doi.org/10.12688/f1000research.28247.1

Copyright

© 2021 Antoine LH et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

Antoine LH, Koomullil RP, Wick TM and Nakhmani A. Optimization of catheter placement for convection-enhanced delivery to brain tumors [version 1; peer review: 2 approved with reservations]. F1000Research 2021, 10:18 (https://doi.org/10.12688/f1000research.28247.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 1

VERSION 1

PUBLISHED 12 Jan 2021

Views

5

Reviewer Report 24 Sep 2021

Chengyue Wu, Oden Institute for Computational Engineering and Sciences, The University of Texas at Austin, Austin, TX, USA

Approved with Reservations

https://doi.org/10.5256/f1000research.31243.r93999

Summary and broad comments:

In this study, the authors investigated a response surface-based technique to assist optimization of catheter placement of convection-enhanced delivery (CED). As the main strength, this study presented a surrogate scheme to generate a ... Continue reading

Summary and broad comments:

In this study, the authors investigated a response surface-based technique to assist optimization of catheter placement of convection-enhanced delivery (CED). As the main strength, this study presented a surrogate scheme to generate a continuous surface of the therapy delivery outcome (measured by therapy distribution percentage within the tumor) from sparsely sampled candidates of catheter placement. If validated, this technique does have the potential to address the challenge of intensive time consumption of simulating all candidates to place CED catheter(s). Thus, I do appreciate the authors’ effort in this investigation and have a positive point of view on the potential significance of this study.

However, the current presentation of the aim, methods, and detailed implementation is not clear in the paper. It is hard to follow how the experiments (for both MRI data collection and in silico simulation) are performed and why they are designed as such. Many essential details of the mathematical justification and numerical implementation are missing, so the reported technique is not replicable in the present. I would suggest the authors rethink the presentation and the design, as well as provide more descriptions and, if applicable, more in silico validations for revision. Please see below for more specific suggestions.

Specific comments:

Introduction

The introduction described optimization techniques that have been used for CED catheter placement and the applications of RSO which was used for this study. However, it did not cover much information about the actual challenges in the field of optimization of catheter placement for CED. For example, a failed planning of the CED catheter could lead to a significant backflow along the catheter, a leakage into CSF, or a blockage of the catheter tube. The choice of CED catheter placement is a complex decision-making process and time-consuming because it needs to consider multiple factors including the distance of catheter tips to CSF volumes, the effect of catheter trajectory on white matter connectivity, and the heterogeneity of brain tissue. There has been commercial software assisting this process, and there are many studies aiming to improve the related techniques. The introduction would benefit from a brief review on the unmet needs or challenges in the field of computer-assisted optimization of CED catheter placement, and how this study might contribute to overcoming any of these challenges.
Please provide a reference to the response surface optimization technique. And, if “DOE” refers to a developed method or scheme, please also provide a reference.
This study investigated the oncolytic herpes simplex for the therapy, which could be considered large particles. However, small molecules and nanoparticles would have very different fluid dynamics. Was this factor considered when simulating the distribution of therapy?

Methods

Tumor parameters: How many patients were included in this study – I assume one? If so, basic information about this patient should be described. For example, what kind of brain cancer they had and did this patient actually go through the CED administration?
Tumor parameters: I would refer to the imaging technique to reconstruct diffusion tensors as “Diffusion Tensor Imaging (DTI)”, instead of “DWI” since the standard DWI does not provide a measurement of tensors. Also, please provide the basic information about the imaging protocol (e.g. imaging scanner, acquisition sequence, and parameters).
Therapy parameters: The actual model used for simulating CED in this study is unclear. What are the boundary conditions? How the infusion source term is defined? What numerical methods, solvers, and/or software were used? Was the simulation conducted within the tumor or within the whole brain?
It is mentioned in the “Tumor parameters” section that the map of viscous resistance is calculated from DTI, while in the section of “Therapy parameters”, it indicated that the flow was analyzed using the viscosity value for water (also, the unit of “1.003 * 10-6 kg/mm-s” is confusing. I assume the authors mean “kg/mm⋅s”). Which assignment was actually used for the experiments?
Optimization: radius = 1.5 mm for what? The point source for infusion?
Optimization: How were the 16 candidates for catheter placement chosen? And what do you mean by “four baseline locations”? It is indicated in the manuscript that “The baselines represent the locations that produced the highest therapy distribution percentages in the tumor”. How did you know this before performing the simulation? If it is a result of the simulation, it should not be mentioned in the Methods section to avoid confusion. If it is prior information, please indicate how it is determined. And is there any relationship between the “16 locations” and “28 DOE-generated sampling points”?
Optimization: If I understand correctly, the response surface is generated using sampling points obtained from DOE by some sort of interpolation. So what algorithm was used to generate this surface? Are there any theories indicating how many sampling points are sufficient to guarantee a unique (or at least robust) solution of the response surface? Are there any assumptions on the geometry of the target response surface for the solution to be realistic, and how these assumptions/conditions are justified for the application in this study? If there are related theories and the assumptions can be justified mathematically, please provide the references or derivations. If the theoretical justification is not available, I would suggest doing a denser sampling in the input parameter space (for example, 500 candidates of the catheter tip location), and then compare the response surfaces generated by dense sampling with that by the sparse sampling (as presented in the current study) to evaluate whether the sparse sampling is sufficient to represent the geometry of real response surface. These could be included in the main text or as a supplemental.
Optimization: How are the tumor regions defined? Why four and are they physiologically different?
Optimization: Why are only locations on the tumor boundaries considered as candidates? In real practice, the tip of CED would be inserted into the tumor (usually the center of the tumor, if surgically accessible), instead of putting on the tumor burden.

Discussion

It is claimed that the predicted percentages from the response surface and observed percentages from the DOE aligned closely. But the actual value of the goodness of fit is not given. This claim needs to be supported by a quantitative report in the Results section.

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

No
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Partly

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: MRI acquisition and analysis, medical image processing, computational fluid dynamics, image-based mathematical modeling for cancer.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Respond or Comment

Views

13

Reviewer Report 18 Jun 2021

Ryuta Saito, Department of Neurosurgery, Graduate School of Medicine, Nagoya University, Nagoya, Japan

Approved with Reservations

https://doi.org/10.5256/f1000research.31243.r86990

In this paper, the authors developed a quantitative computer simulation model to optimize the catheter infusion locations for convection-enhanced delivery (CED). The selection of catheter placement is one of the most important points to consider for successful therapeutic distribution.
... Continue reading

In this paper, the authors developed a quantitative computer simulation model to optimize the catheter infusion locations for convection-enhanced delivery (CED). The selection of catheter placement is one of the most important points to consider for successful therapeutic distribution.

Unfortunately, this study just contains mathematical calculations with lots of assumptions without any verification. However, the mathematical methods the authors demonstrated in this manuscript give some suggestions for optimal catheter locations.

I think solving the following issues will improve this study:

The authors selected suspension of the oncolytic HSV as an infusate. Density and viscosity vary among infusates. Does the optimal placement differ when the density and viscosity of infusate change?
How about changing the flow rate? The calculation is done at a constant rate of 0.1 mL/hr. A higher rate such as 0.2 mL/hr is also used in clinical trials. Does it give any difference in optimal catheter placement?

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Brain tumor surgery, CNS drug delivery.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Respond or Comment

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 12 Jan 2021

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 1 12 Jan 21	read	read

Ryuta Saito, Nagoya University, Nagoya, Japan
Chengyue Wu, The University of Texas at Austin, Austin, USA

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

Back to all reports

Reviewer Report

5 Views

24 Sep 2021 | for Version 1

Chengyue Wu, Oden Institute for Computational Engineering and Sciences, The University of Texas at Austin, Austin, TX, USA

5 Views Cite this report Responses(0)

Approved With Reservations

Summary and broad comments:

In this study, the authors investigated a response surface-based technique to assist optimization of catheter placement of convection-enhanced delivery (CED). As the main strength, this study presented a surrogate scheme to generate a continuous surface of the therapy delivery outcome (measured by therapy distribution percentage within the tumor) from sparsely sampled candidates of catheter placement. If validated, this technique does have the potential to address the challenge of intensive time consumption of simulating all candidates to place CED catheter(s). Thus, I do appreciate the authors’ effort in this investigation and have a positive point of view on the potential significance of this study.

However, the current presentation of the aim, methods, and detailed implementation is not clear in the paper. It is hard to follow how the experiments (for both MRI data collection and in silico simulation) are performed and why they are designed as such. Many essential details of the mathematical justification and numerical implementation are missing, so the reported technique is not replicable in the present. I would suggest the authors rethink the presentation and the design, as well as provide more descriptions and, if applicable, more in silico validations for revision. Please see below for more specific suggestions.

Specific comments:

Introduction

The introduction described optimization techniques that have been used for CED catheter placement and the applications of RSO which was used for this study. However, it did not cover much information about the actual challenges in the field of optimization of catheter placement for CED. For example, a failed planning of the CED catheter could lead to a significant backflow along the catheter, a leakage into CSF, or a blockage of the catheter tube. The choice of CED catheter placement is a complex decision-making process and time-consuming because it needs to consider multiple factors including the distance of catheter tips to CSF volumes, the effect of catheter trajectory on white matter connectivity, and the heterogeneity of brain tissue. There has been commercial software assisting this process, and there are many studies aiming to improve the related techniques. The introduction would benefit from a brief review on the unmet needs or challenges in the field of computer-assisted optimization of CED catheter placement, and how this study might contribute to overcoming any of these challenges.
Please provide a reference to the response surface optimization technique. And, if “DOE” refers to a developed method or scheme, please also provide a reference.
This study investigated the oncolytic herpes simplex for the therapy, which could be considered large particles. However, small molecules and nanoparticles would have very different fluid dynamics. Was this factor considered when simulating the distribution of therapy?

Methods

Tumor parameters: How many patients were included in this study – I assume one? If so, basic information about this patient should be described. For example, what kind of brain cancer they had and did this patient actually go through the CED administration?
Tumor parameters: I would refer to the imaging technique to reconstruct diffusion tensors as “Diffusion Tensor Imaging (DTI)”, instead of “DWI” since the standard DWI does not provide a measurement of tensors. Also, please provide the basic information about the imaging protocol (e.g. imaging scanner, acquisition sequence, and parameters).
Therapy parameters: The actual model used for simulating CED in this study is unclear. What are the boundary conditions? How the infusion source term is defined? What numerical methods, solvers, and/or software were used? Was the simulation conducted within the tumor or within the whole brain?
It is mentioned in the “Tumor parameters” section that the map of viscous resistance is calculated from DTI, while in the section of “Therapy parameters”, it indicated that the flow was analyzed using the viscosity value for water (also, the unit of “1.003 * 10-6 kg/mm-s” is confusing. I assume the authors mean “kg/mm⋅s”). Which assignment was actually used for the experiments?
Optimization: radius = 1.5 mm for what? The point source for infusion?
Optimization: How were the 16 candidates for catheter placement chosen? And what do you mean by “four baseline locations”? It is indicated in the manuscript that “The baselines represent the locations that produced the highest therapy distribution percentages in the tumor”. How did you know this before performing the simulation? If it is a result of the simulation, it should not be mentioned in the Methods section to avoid confusion. If it is prior information, please indicate how it is determined. And is there any relationship between the “16 locations” and “28 DOE-generated sampling points”?
Optimization: If I understand correctly, the response surface is generated using sampling points obtained from DOE by some sort of interpolation. So what algorithm was used to generate this surface? Are there any theories indicating how many sampling points are sufficient to guarantee a unique (or at least robust) solution of the response surface? Are there any assumptions on the geometry of the target response surface for the solution to be realistic, and how these assumptions/conditions are justified for the application in this study? If there are related theories and the assumptions can be justified mathematically, please provide the references or derivations. If the theoretical justification is not available, I would suggest doing a denser sampling in the input parameter space (for example, 500 candidates of the catheter tip location), and then compare the response surfaces generated by dense sampling with that by the sparse sampling (as presented in the current study) to evaluate whether the sparse sampling is sufficient to represent the geometry of real response surface. These could be included in the main text or as a supplemental.
Optimization: How are the tumor regions defined? Why four and are they physiologically different?
Optimization: Why are only locations on the tumor boundaries considered as candidates? In real practice, the tip of CED would be inserted into the tumor (usually the center of the tumor, if surgically accessible), instead of putting on the tumor burden.

Discussion

It is claimed that the predicted percentages from the response surface and observed percentages from the DOE aligned closely. But the actual value of the goodness of fit is not given. This claim needs to be supported by a quantitative report in the Results section.

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

No
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Partly

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

MRI acquisition and analysis, medical image processing, computational fluid dynamics, image-based mathematical modeling for cancer.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

13 Views

18 Jun 2021 | for Version 1

Ryuta Saito, Department of Neurosurgery, Graduate School of Medicine, Nagoya University, Nagoya, Japan

13 Views Cite this report Responses(0)

Approved With Reservations

In this paper, the authors developed a quantitative computer simulation model to optimize the catheter infusion locations for convection-enhanced delivery (CED). The selection of catheter placement is one of the most important points to consider for successful therapeutic distribution.

Unfortunately, this study just contains mathematical calculations with lots of assumptions without any verification. However, the mathematical methods the authors demonstrated in this manuscript give some suggestions for optimal catheter locations.

I think solving the following issues will improve this study:

The authors selected suspension of the oncolytic HSV as an infusate. Density and viscosity vary among infusates. Does the optimal placement differ when the density and viscosity of infusate change?
How about changing the flow rate? The calculation is done at a constant rate of 0.1 mL/hr. A higher rate such as 0.2 mL/hr is also used in clinical trials. Does it give any difference in optimal catheter placement?

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Brain tumor surgery, CNS drug delivery.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

Respond to this report

Responses (0)

[1] 1. Brain Tumor - Types of Treatment 2020. Accessed June 9, 2020. Reference Source

[2] 2. Phase II Study of Intraventricular Methotrexate in Children With Recurrent or Progressive Malignant Brain Tumors. 2020. Accessed June 9, 2020. Reference Source

[3] 3. Methotrexate and Etoposide Infusions Into the Fourth Ventricle in Children With Recurrent Posterior Fossa Brain Tumors. Accessed June 9, 2020. Reference Source

[4] 4. Convection-Enhanced Delivery (CED) of MDNA55 in Adults With Recurrent or Progressive Glioblastoma. Accessed June 9, 2020. Reference Source

[5] 5. A Phase 1 Study of M032, a Genetically Engineered HSV-1 Expressing IL-12, in Patients with Recurrent/Progressive Glioblastoma Multiforme, Anaplastic Astrocytoma, or Gliosarcoma. Accessed June 9, 2020. Reference Source

[6] 6. Li D, Ivanchenko O, Sindhwani N, et al.: Optimal catheter placement for chemotherapy. 20th European symposium on computer aided process engineering. Comput Aided Chem Eng. 2010; 28: 223–228. Publisher Full Text

[7] 7. Vidotto M, De Momi E, Gazzara M, et al.: FCNN-based axon segmentation for convection-enhanced delivery optimization. Int J Comput Assist Radiol Surg. 2019; 14(3): 493–499. PubMed Abstract | Publisher Full Text

[8] 8. Hajishamsaei M, Pishevar A, Bavi O, et al.: A novel in silico platform for a fully automatic personalized brain tumor growth. Magn Reson Imaging. 2020; 68: 121–126. PubMed Abstract | Publisher Full Text

[9] 9. Girard A, Saint-Jalmes H, Chaboub N, et al.: Optimization of time frame binning for FDOPA uptake quantification in glioma. PLoS One. 2020; 15(4): e0232141. PubMed Abstract | Publisher Full Text | Free Full Text

[10] 10. Zade AE, Haghighi SS, Soltani M: Reinforcement learning for optimal scheduling of Glioblastoma treatment with Temozolomide. Comput Methods Programs Biomed. 2020; 193: 105443. PubMed Abstract | Publisher Full Text

[11] 11. Zhang G, Huang X, Li S, et al.: Optimized design method for profile extrusion die based on NURBS modeling. Fibers Polym. 2019; 20: 1733–1741. Publisher Full Text

[12] 12. Sultana N, Hossain SMZ, Alam MS, et al.: An experimental investigation and modeling approach of response surface methodology coupled with crow search algorithm for optimizing the properties of jute fiber reinforced concrete. Constr Build Mater. 2020; 243: 118216. Publisher Full Text

[13] 13. Akhbar MFA, Yusoff AR: Fast & Injurious: Reducing thermal osteonecrosis regions in the drilling of human bone with multi-objective optimization. Measurement. 2020; 152: 107385. Publisher Full Text

[14] 14. Albe Slabi S, Mathe C, Basselin M, et al.: Multi-objective optimization of solid/liquid extraction of total sunflower proteins from cold press meal. Food Chem. 2020; 317: 126423. PubMed Abstract | Publisher Full Text

[15] 15. Silva JM, Azcarate FJ, Knobel G, et al.: Multiple response optimization of a QuEChERS extraction and HPLC analysis of diclazuril, nicarbazin and lasalocid in chicken liver. Food Chem. 2020; 311: 126014. PubMed Abstract | Publisher Full Text

[16] 16. Antoine L: "Catheter placement selection for convection-enhanced delivery of therapeutic agents to brain tumors". Harvard Dataverse V1, 2020. http://www.doi.org/10.7910/DVN/H7C6A2

[17] 17. Yeh FC, Wedeen VJ, Tseng WYI: Generalized q-Sampling imaging. IEEE Trans Med Imaging. 2010; 29(9): 1626–1635. PubMed Abstract | Publisher Full Text

[18] 18. Stoverud KH, Darcis M, Helmig R, et al.: Modeling Concentration Distribution and Deformation During Convection-Enhanced Drug Delivery into Brain Tissue. Transp Porous Media. 2012; 92: 119–143. Publisher Full Text

[19] 19. ANSYS® [computer program] Version 19.1.

[20] 20. Jain R: Transport in Molecules in the Tumor Interstitium: A Review. Cancer Res. 1987; 47(12): 3039–3051. PubMed Abstract

[21] 21. Boucher Y, Salehi H, Witwer B, et al.: Interstitial fluid pressure in intracranial tumours in patients and in rodents. Br J Cancer. 1997; 75(6): 829–836. PubMed Abstract | Publisher Full Text | Free Full Text

[22] 22. Bobo R, Laske D, Akbasak A, et al.: Convection-enhanced delivery of macromolecules in the brain. Proc Natl Acad Sci U S A. 1994; 91(6): 2076–2080. PubMed Abstract | Publisher Full Text | Free Full Text

[23] 23. Bernstock JD, Wright Z, Bag AK, et al.: Stereotactic Placement of Intratumoral Catheters for Continuous Infusion Delivery of Herpes Simplex Virus -1 G207 in Pediatric Malignant Supratentorial Brain Tumors. World Neurosurg. 2019; 122: E1592–E1598. PubMed Abstract | Publisher Full Text | Free Full Text

[24] 24. Shi M, Sanche L: Convection-Enhanced Delivery in Malignant Gliomas: A Review of Toxicity and Efficacy. J Oncol. 2019; 2019: 1–13. PubMed Abstract | Publisher Full Text | Free Full Text

[25] 25. Carpentier A, Laigle-Donadey F, Zohar S, et al.: Phase 1 trial of a CpG oligodeoxynucleotide for patients with recurrent gliobastoma. Neuro Oncol. 2006; 8(1): 60–66. PubMed Abstract | Publisher Full Text | Free Full Text

[26] 26. Weaver M, Laske D: Transferrin receptor ligand-targeted toxin conjugate (Tf-CRM107) therapy of malignant gliomas. J Neurooncol. 2003; 65(1): 3–13. PubMed Abstract | Publisher Full Text

[27] 27. Sampson JH, Akabani G, Friedman AH, et al.: Comparison of intratumoral bolus injection and convection-enhanced delivery of radiolabeled antitenascin monoclonal antibodies. Neurosurg Focus. 2006; 20(4): E14. PubMed Abstract | Publisher Full Text

[28] 28. Hau P, Jachimczak P, Schlingensiepen R, et al.: Inhibition of TGF-beta2 with AP 12009 in recurrent malignant gliomas: from preclinical to phase I/II studies. Oligonucleotides. 2007; 17(2): 201–212. PubMed Abstract | Publisher Full Text

[29] 29. Desjardins A, Gromeier M, Herndon JE, et al.: Recurrent glioblastoma treated with recombinant poliovirus. N Engl J Med. 2018; 379(2): 150–161. PubMed Abstract | Publisher Full Text | Free Full Text

[30] 30. Warren K: Beyond the blood-brain barrier: the importance of central nervous system (CNS) pharmacokinetics for the treatment of CNS tumors, including diffuse intrinsic pontine glioma. Front Oncol. 2018; 8: 239. PubMed Abstract | Publisher Full Text | Free Full Text

[31] 31. Beffinger M, Schellhammer L, Pantelyushin S, et al.: Delivery of Antibodies into the Murine Brain via Convection-enhanced Delivery. J Vis Exp. 2019; (149): 1–7. PubMed Abstract | Publisher Full Text

[32] 32. Kanemitsu T, Kawabata S, Fukumura M, et al.: Folate receptor-targeted novel boron compound for boron neutron capture therapy on F98 glioma-bearing rats. Radiat Environ Biophys. 2019; 58(1): 59–67. PubMed Abstract | Publisher Full Text

[33] 33. Allen J, Wang J, Zolotarskaya OY, et al.: PEAMOtecan, a novel chronotherapeutic polymeric drug for brain cancer. J Control Release. 2020; 321: 36–48. PubMed Abstract | Publisher Full Text

[34] 34. Enríquez Pérez J, Kopecky J, Visse E, et al.: Convection-enhanced delivery of temozolomide and whole cell tumor immunizations in GL261 and KR158 experimental mouse gliomas. BMC Cancer. 2020; 20(1): 7. PubMed Abstract | Publisher Full Text | Free Full Text

[35] 35. Stephen ZR, Chiarelli PA, Revia RA, et al.: Time-Resolved MRI Assessment of Convection-Enhanced Delivery by Targeted and Nontargeted Nanoparticles in a Human Glioblastoma Mouse Model. Cancer Res. 2019; 79(18): 4776–4786. PubMed Abstract | Publisher Full Text | Free Full Text

[36] 36. Tosi U, Kommidi H, Bellat V, et al.: Real-Time, in Vivo Correlation of Molecular Structure with Drug Distribution in the Brain Striatum Following Convection Enhanced Delivery. ACS Chem Neurosci. 2019; 10(5): 2287–2298. PubMed Abstract | Publisher Full Text

[37] 37. Pang HH, Chen PY, Wei KC, et al.: Convection-Enhanced Delivery of a Virus-Like Nanotherapeutic Agent with Dual-Modal Imaging for Besiegement and Eradication of Brain Tumors. Theranostics. 2019; 9(6): 1752–1763. PubMed Abstract | Publisher Full Text | Free Full Text

[38] 38. Finbloom JA, Aanei IL, Bernard JM, et al.: Evaluation of Three Morphologically Distinct Virus-Like Particles as Nanocarriers for Convection-Enhanced Drug Delivery to Glioblastoma. Nanomaterials (Basel). 2018; 8(12): 1007. PubMed Abstract | Publisher Full Text | Free Full Text

[39] 39. Khateeb K, Griggs D, Sabes P, et al.: Convection Enhanced Delivery of Optogenetic Adeno-associated Viral Vector to the Cortex of Rhesus Macaque Under Guidance of Online MRI Images. J Vis Exp. 2019; (147): 1–8. PubMed Abstract | Publisher Full Text

Optimization of catheter placement for convection-enhanced delivery to brain tumors

Abstract

Keywords

Introduction

Methods

Tumor parameters

Therapy parameters

Optimization

Results

Figure 1. Region one response surface for therapy distribution percentages.

Figure 2. Region two response surface for therapy distribution percentages.

Figure 3. Region three response surface for therapy distribution percentages.

Figure 4. Region four response surface for therapy distribution percentages.

Table 1. Optimal locations by region with corresponding xyz spatial coordinates and therapy distribution percentages.

Figure 5. Tumor infusion optimal locations with corresponding baseline locations by region.

Discussion

Conclusions

Data availability

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated