Impact of diagnostic accuracy on the estimation of excess mortality from incidence and prevalence: simulation study and application to diabetes in German men

Ralph Brinks; Thaddäus Tönnies; Annika Hoyer

doi:10.12688/f1000research.28023.1

Home Browse Impact of diagnostic accuracy on the estimation of excess mortality...

ALL Metrics

-

Views

-

Downloads

Get PDF

Get XML

Export

▬

✚

Method Article

Impact of diagnostic accuracy on the estimation of excess mortality from incidence and prevalence: simulation study and application to diabetes in German men

[version 1; peer review: 2 approved, 1 approved with reservations]

Ralph Brinks ^1-3, Thaddäus Tönnies¹, Annika Hoyer³

PUBLISHED 27 Jan 2021

Author details Author details

¹ Institute for Biometry and Epidemiology, German Diabetes Center, Duesseldorf, 40225, Germany
² Chair for Medical Biometry and Epidemiology, Faculty of Health/School of Medicine, University Hospital Duesseldorf, Witten, 58448, Germany
³ Department of Statistics, Ludwig Maximilian University of Munich, Munich, 80539, Germany

Ralph Brinks
Roles: Conceptualization, Formal Analysis, Methodology, Project Administration, Software, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Thaddäus Tönnies
Roles: Investigation, Methodology, Writing – Review & Editing

Annika Hoyer
Roles: Conceptualization, Investigation, Methodology, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

Abstract

Aggregated data about the prevalence and incidence of chronic conditions is becoming more and more available. We recently proposed a method to estimate the age-specific excess mortality in chronic conditions from aggregated age-specific prevalence and incidence data. Previous works showed that in age groups below 50 years, estimates from this method were unstable or implausible. In this article, we examine how limited diagnostic accuracy in terms of sensitivity and specificity affects the estimates. We use a simulation study with two settings, a low and a high prevalence setting, and assess the relative importance of sensitivity and specificity. It turns out that in both settings, specificity, especially in the younger age groups, dominates the quality of the estimated excess mortality. The findings are applied to aggregated claims data comprising the diagnoses of diabetes from about 35 million men in the German Statutory Health Insurance. Key finding is that specificity in the lower age groups (<50 years) can be derived without knowing the sensitivity. The false-positive ratio in the claims data increases linearly from 0.5 per mil at age 25 to 2 per mil at age 50.
As a conclusion, our findings stress the importance of considering diagnostic accuracy when estimating excess mortality from aggregated data using the method to estimate excess mortality. Especially the specificity in the younger age-groups should be carefully taken into account.

Keywords

Illness-death model, chronic conditions, diabetes, lupus, partial differential equations, epidemiology

Corresponding author: Ralph Brinks

Competing interests: No competing interests were disclosed.

Grant information: The author(s) declared that no grants were involved in supporting this work.

Copyright: © 2021 Brinks R et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Brinks R, Tönnies T and Hoyer A. Impact of diagnostic accuracy on the estimation of excess mortality from incidence and prevalence: simulation study and application to diabetes in German men [version 1; peer review: 2 approved, 1 approved with reservations]. F1000Research 2021, 10:49 (https://doi.org/10.12688/f1000research.28023.1) First published: 27 Jan 2021, 10:49 (https://doi.org/10.12688/f1000research.28023.1) Latest published: 27 Jan 2021, 10:49 (https://doi.org/10.12688/f1000research.28023.1)

Introduction

For research purposes, aggregated data about the prevalence and incidence of chronic conditions become more and more available. Examples range from data of huge public health surveys, such as the National Health Interview Study (NHIS) in the US [CDC 2020] or the Global Health Data Exchange (GHDx) catalog [GHD 2020], which covers up to three decades of international health data, to claims data from health service providers [CMS 2020].

Recently, we proposed a new method to estimate the age-specific excess mortality in chronic conditions from aggregated age-specific prevalence and incidence data based on a differential equation [Tönnies et al., 2018; Brinks et al., 2019]. The idea, in brief, is to relate the temporal change of the prevalence with the incidence and the excess mortality. If the incidence and prevalence are given, the excess mortality can be estimated. In age groups below 50 years of age, estimates from this method have been proven to be unstable or implausible [Brinks et al., 2020]. For example, we obtained estimates of the mortality rate ratio in type 2 diabetes with values greater than 100 in ages below 40 years [Brinks et al., 2020]. The typical range for type 2 diabetes in this age group is between 3 and 10 [Carstensen et al., 2020]. In [Brinks et al., 2020] it was hypothesized “that the diagnostic accuracy of the claims data plays a crucial role for the proposed methods of estimating excess mortality.”

Similar to diagnostic accuracy studies, we are interested in the sensitivity and specificity of the available diagnoses in the claims data. As “gold standard” we consider the presence or absence of the chronic condition in real life (as judged by an expert from the associated medical domain). Within the claims data, two types of error may occur: People with the condition in real life might not have the diagnosis coded in the claims data (false negative) or vice versa, people without the condition in real life might have a corresponding diagnosis (false positive). Finally, this leads to the concept of sensitivities and specificities of the aggregated prevalence and incidence data.

The aim of this article is twofold: First, we want to examine and quantify the impact of diagnostic accuracy on the estimates of excess mortality. For this, we use a simulation study comprising two settings, a low and high prevalence setting. Second, as a real-world application of the findings in the first part, we estimate the age-specific diagnostic accuracy of claims data about diabetes from about 35 million German men in the Statutory Health Insurance [Goffrier et al., 2017].

Methods

Before we start with the simulation and the real-world application, we briefly sketch the theoretical background. Detailed derivations are given in Extended Data [Brinks et al., 2021].

Based on the illness-death model for chronic diseases (Figure 1), it can be shown that the temporal change, $\partial p = (\partial_{t} + \partial_{a}) p$ , of the age-specific prevalence p is related to the incidence rate i, and the mortality rates m₀ and m₁ of the people with and without the chronic condition (disease), respectively. Instead of the rates m₀ and m₁, the general mortality m = pm₁ + (1 − p) m₀ and the mortality rate ratio R = m₁/m₀ can be used according to the following equations [Brinks et al., 2014; Brinks et al., 2016]:

(1)

\begin{array}{l} \partial p & = (1 - p) {i - p \times (m_{1} - m_{0})} \\ = (1 - p) {i - m \times p (R - 1) / [1 + p (R - 1)]} . \end{array}

Figure 1. Illness-death model.

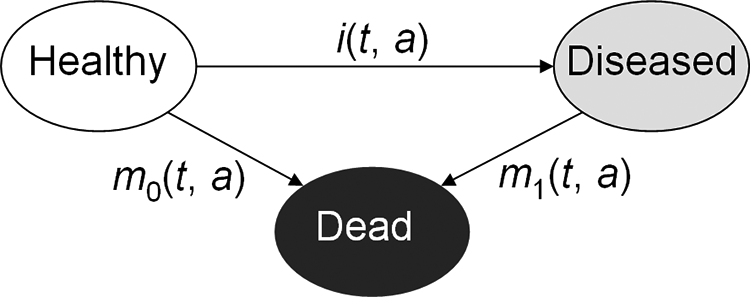
People aged a at time t in the population are in one of the three states: Healthy, Diseased, or Dead. Transitions between these states are described by the rates i, m₀, and m₁, which in general depend on t and a.

Given the age-specific prevalence p, the age-specific incidence rate i and the general mortality rate m, Equation (1) provides an estimator for the mortality rate ratio R:

(2)

R = 1 + 1 / p \times {i - \partial p / (1 - p)} / {m - i + \partial p / (1 - p)} .

Assuming that the sensitivity (se) and specificity (sp) in the age-specific prevalence and incidence are known, the prevalence p and incidence i in Equations (1) and (2) can be obtained from the observed (and possibly imperfect) prevalence p^(obs) and incidence i^(obs) by

(3a)

p = (p^{(obs)} - 1 + s p_{p}) / (s e_{p} + s p_{p} - 1)

and

(3b)

i = (i^{(obs)} - 1 + s p_{i}) / (s e_{i} + s p_{i} - 1) .

The derivations of these equations are shown in Extended Data Appendix 2 [Brinks et al., 2021]. The observed values p^(obs) and i^(obs) may have been prone to error by incomplete case-detection (i.e., se < 1) and/or false positive findings (sp < 1). If all sensitivities and specificities equal 1, we find p = p^(obs) and i = i^(obs). Note that in Equations (3a) and (3b) we distinguish between sensitivities and specificities in prevalence and incidence (indicated by the sub-indices p and i, respectively). To examine potential age effects, se and sp may depend on age a. Age dependency is taken into account, because diagnostic accuracy in many diseases is known to depend on age. For example, sensitivity of diagnosing type 2 diabetes in 80 years old people is higher than in 40 year old people, which is, for instance, reflected by the higher percentage of undiagnosed diabetes in younger age groups [Gregg et al., 2004].

Simulation studies

The steps for running the simulation studies in the low and high prevalence setting are as follows: We first solve Equation (1) with known i, m and R to obtain prevalence data p. Second, imperfect diagnostic accuracy is mimicked by using Equations (3a) and (3b) such that the quantities p^(obs) and i^(obs) are observed instead of the (true) quantities p and i. In the third step, Equation (2) is applied to p^(obs) and i^(obs) in order to obtain an estimate for the mortality rate ratio (R^(obs)). Finally, R^(obs) is compared to the true R underlying the simulation. This is done for a wide range of age-groups (Table 1).

Table 1.Description of the parameter settings in the simulations.

	Setting
	Low prevalence	High prevalence
Incidence i	Lupus in women [Brinks et al., 2016]	Type 2 diabetes in men [Tamayo et al., 2016]
Mortality rate ratio R	Lupus [Bernatsky et al., 2006]	Type 2 diabetes [Carstensen et al., 2020]
General mortality m	Federal Statistical Office of Germany [FSG 2020]	Federal Statistical Office of Germany [FSG 2020]
Considered age range	20-70 years	40-80 years
Sensitivity (base-case) younger age older age	99.5% at 20 years of age 99.5% at 70 years of age	95% at 40 years of age 95% at 80 years of age
Specificity (base-case) younger age older age	99.999% at 20 years of age 99.999% at 70 years of age	99.95% at 40 years of age 99.95% at 80 years of age

We use two figures for the comparisons: 1) The age-specific difference between R and R^(obs) and 2) the summed absolute relative errors (where the sum is taken over the whole considered age range). The later figure is used to assess the relative importance of the sensitivities and specificities in the form of a tornado plot. A tornado plot displays the change of the considered outcome compared to a base-case scenario, if exactly one input variable, say the sensitivity of the incidence in an age group, is changed while all the other input values (i.e., the remaining sensitivities and specificities) are kept fixed. This is done for all input variables. The changes in the output are presented as vertical bars, which are then ordered descendingly to indicate the importance of the associated input variables on the output. The descending order leads to the largest bar being presented on top and the smallest bar at the bottom, which visually appears as a half of a tornado (see Figure 3).

Table 1 shows the parameters for the two simulation settings in the low and the high prevalence scenarios. The low and the high prevalence scenarios are motivated by systemic lupus erythematosus (SLE) in women and type 2 diabetes in men, respectively. As SLE is more relevant in younger ages, we consider the age range from 20 to 70 years in this setting. Type 2 diabetes is especially important for ages greater then 40, which lead us to the choice of considering the range 40 to 80 years of age. Although the values for the sensitivity and specificity in Table 1 are the same in the younger and older ages, they are treated independently to allow exploration of the relative importance in the tornado plots. In any case, sensitivities and specificities are interpolated affine-linearly between the younger and the older age.

The source code for use with the free, open-source statistical software R (The R Foundation For Statistical Computing) can be found in [Brinks et al., 2020].

Real world data

Based on claims data of German men in the Statutory Health Insurance (SHI), Goffrier and colleagues report the age-specific prevalence p^(obs) of type 2 diabetes in the years 2009 and 2015 [Goffrier et al., 2017]. Furthermore, the age- and sex-specific incidence rate i^(obs) in middle of the period, i.e., in the year 2012, is given in the same report. In addition to the prevalence and incidence, the mortality rate ratios R of men with and without diabetes in the German SHI in the year 2014 have been reported in [Scheidt-Nave 2019]. Strictly speaking, the estimates of R from [Scheidt-Nave 2019] might have undergone diagnostic inaccuracies as well. However, the estimates are based on individual data (ID) and potential biases in ID analyses (e.g., by missing disease status at death [Binder et al., 2017]), are beyond the scope of this article. Thus, for simplicity we assume R = R^(obs).

We use these data about p^(obs), i^(obs) and R to obtain estimates about the age-specific sensitivity and specificity of the prevalence and incidence via Equations (3a) and (3b). For this, we make the following approach: for each age group (denoted a_k, k = 1, …, K) we assume that the sensitivity and specificity of prevalence and incidence are the same, i.e., se_p(a_k) = se_i(a_k) and sp_p(a_k) = sp_i(a_k), for all k = 1, …, K. The assumption of same sensitivity and specificity with respect to prevalence and incidence is justified because prevalent and incident cases are derived from reported diagnoses of all physicians treating the men in the SHI. If prevalence data suffer from incomplete case-detection or false positive findings, incidence data will suffer in the same way.

If we assume for the moment that the sensitivity se = se_p = se_i is known, we can combine Equations (3a) and (3b) with Equation (1) to estimate the specificity sp = sp_p = sp_i. This is possible, because with given general mortality m from the Federal Statistical Office of Germany [FSG 2020], all measures p^(obs), i^(obs), and R in Equation (1) are known from [Goffrier et al., 2017] and [Scheidt-Nave 2019] after applying the corrections in Equations (3a) and (3b). Hence for known sensitivity se, we can calculate sp from these data and the analytical findings in the previous section by a functional relation Φ

(4)

s p = Φ (s e, p^{(obs)}, i^{(obs)}, m, R)

The exact formula for the functional relation Φ between sp on the left hand side and se, p^(obs), i^(obs), m, and R on the right hand side of Equation (4), is lengthy and presented together with its derivation and an algorithm in Extended Data Appendix 3 [Brinks et al., 2021]. An implementation of the algorithm in the statistical software R can be found in [Brinks et al., 2020]. For now, it is sufficient to notice that the relation in Equation (4) follows from Equations (1), (3a) and (3b).

Unfortunately, we do not know the sensitivity of the diagnoses in the claims data. To overcome this problem, we use a probabilistic approach and randomly sample se from epidemiologically reasonable ranges between 70% and 99%. Then, we examine how the estimated specificity sp changes. For easier interpretation, we present the false positive ratio (FPR), FPR = 1 − sp.

The data and the source code for use with the free statistical software R (The R Foundation For Statistical Computing) can be found in [Brinks et al., 2020] (DOI: 10.5281/zenodo.4300684).

Results

Simulation studies

Figure 2 shows the estimated age-specific mortality rate ratios R in the simulation studies. The left and right panel in Figure 2 refers to the low and high prevalence settings, respectively. While in case of perfect diagnostic accuracy, i.e. sp = se = 100%, the input values of the simulation (blue lines) and the estimates by Equation (2) (solid black dots) do not (visually) differ. Imperfect sensitivity and specificity lead to estimates biased upwards (open circles). It becomes visible that with increasing age the difference between the true and estimated values decreases.

Figure 2. Age-specific mortality rate ratios (R) in the simulations.

The low prevalence and high prevalence setting are shown in the left and right panels, respectively. The input values are shown as blue lines. Mortality rate ratios R are estimated without any (visual) difference in case of perfect sensitivity se = 100% and perfect specificity sp = 100% (solid dots). In case of imperfect sensitivity and specificity, the estimates of R are biased upward (open circles).

In the assessment of the relative importance of the sensitivity and specificity in prevalence and incidence, we obtain the tornado plots as shown in Figure 3. Irrespective of the low (left panel in Figure 3) and high (right panel) prevalence setting, the specificity of the incidence (sp_i) in the lower age group has the greatest impact on the estimated mortality rate ratios. Specificity sp_i in the higher age group has the second strongest effect, followed by the specificities in prevalence (sp_p). The impact of the sensitivities is far weaker compared to the specificities. Note that the relative importance (abscissa) is given on the log scale.

Figure 3. Tornado plots for relative importance of the sensitivity and specificity.

In both settings, low (left panel) and high prevalence (right), the specificities (prefix sp) are the four dominant error factors in estimating the mortality rate ratio R. Compared to specificities, sensitivities (prefix se) have a low impact on the error in R.

By comparing the horizontal bars in the low and high prevalence settings, we see that the four specificities in the low prevalence settings have a greater effect than those in the high prevalence setting. The opposite is true in the sensitivities: in the high prevalence setting sensitivities have a larger impact than in the low prevalence setting.

Real world data

From Equation (4) we infer FPR = 1 - Φ(se, p^(obs), i^(obs), m, R). After uniformly sampling se(a_k), where a_k = 25, 32.5, 40, …, 85, represents the K = 9 age groups [a_k - 7.5/2, a_k + 7.5/2) of width 7.5 years, k = 1, …, 9, from the range 0.7 to 0.99 with N = 10000 samples, and calculating the associated FPR, we obtain the graph presented in Figure 4. Each dot in the grey area represents an FPR_n(a_k) based on a random se_n(a_k), n = 1, …, N. We see that irrespective of the randomly sampled values se_n(a_k) for a_k < 50, the FPR increases from 0.5 to 2 per mil. For example, at age 40 the FPR is about 1.5 per mil, which means that roughly 3 in 2000 diagnoses of type 2 diabetes at that age are false positive findings. For age groups > 50, we can see an upper bound for the FPR that continues linearly, while the lower bound can reach 0 at ages between 60 and 70 years. For higher ages, the lower bound of the FPR increases again.

Figure 4. Age-specific false-positive ratios (FPR) in the simulated sensitivity scenarios.

Each dot in the grey area represents the FPR generated by one of the scenarios about the age-specific sensitivities.

Discussion

In this work we have described the impact of diagnostic accuracy on the estimates of the excess mortality of a chronic condition from aggregated age-specific prevalence and incidence data. It turned out in simulation studies that the specificity in lower age groups had the greatest impact on the estimated mortality rate ratio. Compared to sensitivity, specificity has a greater impact across all age groups. The reason may be seen in the fact that the specificity has a direct additive effect on the true prevalence and incidence, while the sensitivity has an multiplicative impact only, cf. Equations (3a) and (3b).

In the simulation studies it turned out that estimation of the mortality rate ratio is accurately possible if the underlying sensitivity and specificities are known. In principle, these quantities are estimable in surveys. For example, in the claims data a cross-sectional comparison of the diagnoses with the gold standard (expert examination) could be conducted. These findings could be used to apply the corrections as in Equations (3a) and (3b) before using Equation (1) to estimate the mortality rate ratio.

By application of the theory to the claims data from 35 million German men, we were able to estimate the false positive ratio (FPR) in diabetes diagnoses. The most striking conclusion is the linearly increasing FPR in age groups between 20 and 50 years. In age groups older than 50 years of age, we could estimate upper and lower bounds for the FPR, which allows an assessment of diagnostic quality in the claims data.

Although most of our findings can be seen in the general theory of using the method of estimating excess mortality described in [Tönnies et al., 2018] and [Brinks et al., 2019], the application to real world data has two limitations that are important to mention. First, we assumed that the age-specific sensitivity and specificity are the same in both years 2009 and 2015. This might be an oversimplification, because it could, at least in principle, be that the diagnostic accuracy during this period of six years changed, for example, by implementation of screening programs, change of diagnostic criteria or by changes of reimbursement policies for diagnosing diabetes. However, we are not aware of such changes and refer studies about temporal changes in diagnostic accuracy to future analysis.

The second limitation lies in the assumption that the observed mortality rate ratio R^(obs) in 2014 as reported in [Scheidt-Nave 2019] equals the true rate ratio R in 2012. Since the mortality rate ratio is relatively stable [p. 59 in Breslow et al., 1980], the mismatch between the two years is unlikely to impose a problem. However, we cannot assess the difference between the observed and true rate ratio. The main reason is the brief and vague description of the methods to estimate R in [Scheidt-Nave 2019]. For example, it remains unclear how the possible problem of competing risks (contracting diabetes versus dying without diabetes) has been addressed. However, the findings in [Scheidt-Nave 2019] are consistent with epidemiological surveys in Germany [Röckl et al., 2017] and with observations from the Danish diabetes register [Carstensen et al., 2020]. Thus, we think that the assumption R^(obs) = R is justified.

Apart from these limitations, our findings stress the importance of considering diagnostic accuracy when estimating excess mortality from aggregated data using the method described in Equation (1). In particular the specificity in the younger age-groups should be taken care about.

Data Availability

Underlying data

Zenodo: Simulation to study impact of diagnostic accuracy on estimation of excess mortality, http://doi.org/10.5281/zenodo.4300684 [Brinks et al., 2020].

Zenodo: Estimation of excess mortality from incidence and prevalence: impact of the diagnostic accuracy, http://doi.org/10.5281/zenodo.4302183 [Brinks et al., 2020].

Extended data

Zenodo: Extended Data: Impact of diagnostic accuracy on the estimation of excess mortality from incidence and prevalence - simulation study and application to diabetes in German men, http://doi.org/10.5281/zenodo.4434806 [Brinks et al., 2021].

This project contains the following extended data:

- Detailed derivations of the Equations (1) to (4).

Data are available under the terms of the Creative Commons Attribution 4.0 International license (CC-BY 4.0).

Competing interests

No competing interests were disclosed.

References

Bernatsky S, Boivin JF, Joseph L, et al.: Mortality in systemic lupus erythematosus. Arthritis Rheum. 2006; 54: 2550–7. PubMed Abstract | Publisher Full Text
Binder N, Herrnböck AS, Schumacher M: Estimating hazard ratios in cohort data with missing disease information due to death. Biom J 2017; 59(2): 251–269. PubMed Abstract | Publisher Full Text
Breslow NE, Day NE: Statistical Methods in Cancer Research. In: The Analysis of Case-Control studies Lyon: IARC; 1980; Vol 1. .
Brinks R, Landwehr S: Age- and time-dependent model of the prevalence of non-communicable diseases and application to dementia in Germany. Theor Popul Biol. 2014; 92: 62–8. PubMed Abstract | Publisher Full Text
Brinks R, Hoyer A, Landwehr S: Surveillance of the incidence of non-communicable diseases (NCDs) with sparse resources: a simulation study using data from a National Diabetes Registry, Denmark, 1995-2004. PLoS One. 2016; 11(3): e0152046. PubMed Abstract | Publisher Full Text | Free Full Text
Brinks R, Hoyer A, Weber S, et al.: Age-specific and sex-specific incidence of systemic lupus erythematosus: an estimate from cross-sectional claims data of 2.3 million people in the German statutory health insurance 2002. Lupus Sci Med. 2016; 25;3(1): e000181. PubMed Abstract | Publisher Full Text | Free Full Text
Brinks R, Tönnies T, Hoyer A: New ways of estimating excess mortality of chronic diseases from aggregated data: insights from the illness-death model. BMC Public Health. 2019; 19(1): 844. PubMed Abstract | Publisher Full Text | Free Full Text
Brinks R, Tönnies T, Hoyer A: Assessing two methods for estimating excess mortality of chronic diseases from aggregated data. BMC Res Notes. 2020; 13: 216. PubMed Abstract | Publisher Full Text | Free Full Text
Brinks R, Tönnies T, Hoyer A: Simulation to study impact of diagnostic accuracy on estimation of excess mortality (Version 01).Zenodo; 2020. Publisher Full Text
Brinks R, Tönnies T, Hoyer A: Estimation of excess mortality from incidence and prevalence: impact of diagnostic accuracy (Version 01).Zenodo; 2020. Publisher Full Text
Brinks R, Tönnies T, Hoyer A: Estimation of excess mortality from incidence and prevalence: impact of diagnostic accuracy (Version 01).Zenodo; 2021. Publisher Full Text
Carstensen B, Rønn PF, Jørgensen ME: Prevalence, incidence and mortality of type 1 and type 2 diabetes in Denmark 1996-2016. BMJ Open Diabetes Res Care. 2020; 8: e001071. PubMed Abstract | Publisher Full Text | Free Full Text
Centers for Disease Control and PreventionNational Health Interview Survey (NHIS).Reference Source Last access, 2020-12-07.
Centers for Medicare & Medicaid ServicesChronic Conditions Public Use Files (PUF).Reference Source Last access, 2020-12-07
Federal Statistical Office of GermanyPeriod life table for 2011/13. Table code 12621-0001, GENESIS-Online database, Last access 2020-12-06.
Global Health Data Exchangedata catalog. by the Institute for Health Metrics and Evaluation (IHME), Seattle WAReference Source Last access, 2020-12-07.
Goffrier B, Schulz M, Bätzing-Feigenbaum J: Administrative Prävalenzen und Inzidenzen des diabetes mellitus von 2009 bis 2015. Versorgungsatlas. 2017. Publisher Full Text
Gregg EW, Cadwell BL, Cheng YJ, et al.: Trends in the Prevalence and Ratio of Diagnosed to Undiagnosed Diabetes According to Obesity Levels in the U.S. Diabetes Care 2004; 27(12): 2806–2812. PubMed Abstract | Publisher Full Text
Röckl S, Brinks R, Baumert J, et al.: All-cause mortality in adults with and without type 2 diabetes: findings from the national health monitoring in Germany. BMJ Open Diabetes Res Care. 2017; 5(1): e000451. PubMed Abstract | Publisher Full Text | Free Full Text
Scheidt-Nave C: Nationale Diabetes-Surveillance am Robert Koch-Institut Diabetes in Deutschland - Bericht der Nationalen Diabetes-Surveillance 2019.Robert-Koch-Institut Berlin2019. Publisher Full Text
Tönnies T, Hoyer A, Brinks R: Excess mortality for people diagnosed with type 2 diabetes in 2012 - estimates based on claims data from 70 million Germans. Nutr Metab Cardiovasc Dis. 2018; 28(9): 887–91. PubMed Abstract | Publisher Full Text
Tamayo T, Brinks R, Hoyer A, et al.: The Prevalence and Incidence of Diabetes in Germany. Dtsch Arztebl Int 2016; 113(11): 177–82. PubMed Abstract | Publisher Full Text | Free Full Text

Comments on this article Comments (1)

Version 1

VERSION 1 PUBLISHED 27 Jan 2021

Author Response 28 Jan 2021

Ralph Brinks, Institute for Biometry and Epidemiology, German Diabetes Center, Duesseldorf, 40225, Germany

28 Jan 2021

Author Response

Instead of Gregg et al., the reference below might be a better source for the age-dependency of undiagnosed and diagnosed diabetes (see top of Figure 3 in this article):

... Continue reading Instead of Gregg et al., the reference below might be a better source for the age-dependency of undiagnosed and diagnosed diabetes (see top of Figure 3 in this article):

Selvin E, Parrinello CM, Sacks DB, Coresh J. Trends in prevalence and control of diabetes in the United States, 1988-1994 and 1999-2010. Ann Intern Med. 2014 Apr 15;160(8):517-25. doi: 10.7326/M13-2411. PMID: 24733192; PMCID: PMC4442608. Link
Instead of Gregg et al., the reference below might be a better source for the age-dependency of undiagnosed and diagnosed diabetes (see top of Figure 3 in this article):

Selvin E, Parrinello CM, Sacks DB, Coresh J. Trends in prevalence and control of diabetes in the United States, 1988-1994 and 1999-2010. Ann Intern Med. 2014 Apr 15;160(8):517-25. doi: 10.7326/M13-2411. PMID: 24733192; PMCID: PMC4442608. Link
Competing Interests: No competing interests were disclosed. Close
Report a concern
Comment

Author details Author details

¹ Institute for Biometry and Epidemiology, German Diabetes Center, Duesseldorf, 40225, Germany
² Chair for Medical Biometry and Epidemiology, Faculty of Health/School of Medicine, University Hospital Duesseldorf, Witten, 58448, Germany
³ Department of Statistics, Ludwig Maximilian University of Munich, Munich, 80539, Germany

Ralph Brinks
Roles: Conceptualization, Formal Analysis, Methodology, Project Administration, Software, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Thaddäus Tönnies
Roles: Investigation, Methodology, Writing – Review & Editing

Annika Hoyer
Roles: Conceptualization, Investigation, Methodology, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Article Versions (1)

version 1

Published: 27 Jan 2021, 10:49

https://doi.org/10.12688/f1000research.28023.1

Copyright

© 2021 Brinks R et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

Brinks R, Tönnies T and Hoyer A. Impact of diagnostic accuracy on the estimation of excess mortality from incidence and prevalence: simulation study and application to diabetes in German men [version 1; peer review: 2 approved, 1 approved with reservations]. F1000Research 2021, 10:49 (https://doi.org/10.12688/f1000research.28023.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Current Reviewer Status: ?

Key to Reviewer Statuses VIEW HIDE

ApprovedThe paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approvedFundamental flaws in the paper seriously undermine the findings and conclusions

Version 1

VERSION 1

PUBLISHED 27 Jan 2021

Views

10

Reviewer Report 07 Jun 2021

Bruce Bartholow Duncan, Postgraduate Program in Epidemiology and Hospital de Clínicas de Porto Alegre, Universidade Federal do Rio Grande do Sul, Porto Alegre, Brazil

Approved with Reservations

https://doi.org/10.5256/f1000research.30994.r85843

This is an important evaluation of the use of secondary data from a claims database to estimate the sensitivity and specificity of the inclusion in the database of chronic diseases present in the covered population. Secondary data are increasingly being ... Continue reading

This is an important evaluation of the use of secondary data from a claims database to estimate the sensitivity and specificity of the inclusion in the database of chronic diseases present in the covered population. Secondary data are increasingly being used for disease surveillance, in this case for diabetes mellitus. As they come with error, corrections must frequently be made in analyses. These corrections must be derived and evaluated, as is done here. My comments do not include a verification of the equations presented, which I have no reason to doubt. However, such verification is a task for someone other than myself.

Major comments:

"false positive ratio", I believe, should be "false positive rate".
The authors have appropriately alerted that sensitivity and specificity, as used here, are not of a diagnostic test, but rather of the presence of a diagnosis in the claims data. As these terms are applied in a context different from the usual one, I believe that readers would benefit from a bit greater detail, noting that sensitivity is the capacity of the claims system to include in its database all cases of diabetes (whether detected or not) present in those covered by the system and specificity is the capacity to include only true cases of diabetes among those covered. Thus, for example, a covered individual who has diabetes but was never tested and thus never detected would be a false negative, detracting from sensitivity.
The horizontal axis of graphs in Figure 3 is the "Relative importance". Please define what this means.
At the end of the Results, the authors state: "...which means that roughly 3 in 2000 diagnoses of type 2 diabetes at that age are false positive findings...". As the FPR is being described, the denominator should not be diagnoses of type 2 diabetes, but rather covered individuals truly without diabetes.
A major issue for the diabetes epidemiology community is the relative frequency of undiagnosed diabetes, i.e., for every 100 true cases, how many are unknown cases). Some discussion of how to use the approach presented to achieve estimates of the prevalence of undiagnosed diabetes (1-positive predicted value) could increase the relevance of this report (or a future one).
Figure 4: Is it possible to trace not only the bounds of the estimated FPR, but also the FPR point estimate at each age?
Why are the base-case sensitivity and specificity so high? In terms of sensitivity, the IDF´s 2019 Diabetes Atlas (https://www.diabetesatlas.org/en/) estimates that 24% of those with diabetes in its European region are undiagnosed. A German investigation estimated that between 3 and 9% of adults had undiagnosed diabetes (Tamayo et al., 2014¹). In terms of specificity, the fact that several percent of those who report having diabetes, when tested, are found to have normoglycemia (1-positive predicted value), coupled with the known large within-individual (biologic) variability over time of available means of diagnosis, suggests that specificity is not 99.95%.
Is not the greater impact of specificity mainly due to the fact that many more individuals in the population do not have diabetes than do, and thus the specificity is acting on a larger (at younger ages far larger) fraction of the population?
The mortality rate ratio of diabetes has declined considerably over recent decades (see: Tables 3 and 4 of Gregg et al. (2018²). However, as you state, the impact of this decline over a 2 year period is likely to be sufficiently small as to not impose a problem.

Minor comments:

Keywords should be reviewed. My understanding is that they should be MeSH terms. Thus, for example, "lupus" should be "systemic lupus erythematosus".
1st sentence Introduction, better: "...of chronic conditions has become...".
Page 4, before "Simulation studies", better: "...For example, the sensitivity of a code for type 2 diabetes in the claims database in 80 years old...".
Last sentence page 4, better: "exemplified" than "motivated".
Discussion, second paragraph: I don´t understand what "accurately possible" means.

Additional comments related to specific review questions;

As I am not fluent in R, I cannot verify that the additional materials include the source data. I imagine not, as the source data must be huge, and initially with personal identifiers.

Is the rationale for developing the new method (or application) clearly explained?

Yes
Is the description of the method technically sound?

Yes
Are sufficient details provided to allow replication of the method development and its use by others?

Yes
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?

Partly
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?

Partly

References

1. Tamayo T, Schipf S, Meisinger C, Schunk M, et al.: Regional differences of undiagnosed type 2 diabetes and prediabetes prevalence are not explained by known risk factors.PLoS One. 2014; 9 (11): e113154 PubMed Abstract | Publisher Full Text
2. Gregg E, Cheng Y, Srinivasan M, Lin J, et al.: Trends in cause-specific mortality among adults with and without diagnosed diabetes in the USA: an epidemiological analysis of linked national survey and vital statistics data. The Lancet. 2018; 391 (10138): 2430-2440 Publisher Full Text

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: diabetes epidemiology

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Respond or Comment

Views

8

Reviewer Report 01 Jun 2021

Dianna J. Magliano, Department of Diabetes and Population Health, Baker Heart and Diabetes Institute, Melbourne, Vic, Australia; School of Public Health and Preventive Medicine, Monash University, Melbourne, Vic, Australia

Approved

https://doi.org/10.5256/f1000research.30994.r85844

This is a modelling analysis which aims to assess the impact of diagnostic accuracy on the estimation of excess mortality from incidence and prevalence using a simulation study. The stimulation study which is developed tests two scenarios: one with a ... Continue reading

This is a modelling analysis which aims to assess the impact of diagnostic accuracy on the estimation of excess mortality from incidence and prevalence using a simulation study. The stimulation study which is developed tests two scenarios: one with a high prevalence setting and the other with a low prevalence setting. The finding is then applied to real diabetes data from claims data from the German Statutory Health insurance. The modelling shows that when estimating excess mortality of diabetes, diagnostic accuracy is very important. Specificity is more important than sensitivity across all age groups, and in particular, specificity in younger people has the greatest impact on the estimated mortality rate ratios.

Overall, this is a clear and well-presented piece of work. One thing which may be useful is to have some idea of the size of the impact of specificity on the estimation of mortality ratio rate, in comparison to the effect of sensitivity. The authors state that there is a difference between the effect of sensitivity and specificity, but it may be useful for the reader to understand how much of an impact it has.

My other points are minor and relate to language:

The last line of the abstract should be re-written. Starting that sentence with ‘especially’ means the sentence is unclear. You could start with: ‘In particular…’.
The first sentence of the introduction could be re written to say: “…chronic diseases are becoming more available.”
The heading in the first row of table 1 could be more descriptive. Expand on “setting”. In the actual table heading: insert the word “used” between “settings “and “in”.
Table entries of “Lupus” should be written in full.
Significant figures in table 1 are not consistent. I do understand why though.
Figure 3 should have the panels labelled on figure. “low prevalence” and “high prevalence” or A and B.

Is the rationale for developing the new method (or application) clearly explained?

Yes
Is the description of the method technically sound?

Yes
Are sufficient details provided to allow replication of the method development and its use by others?

Partly
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Diabetes epidemiology

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Respond or Comment

Views

11

Reviewer Report 24 May 2021

Andreas Wienke, Institute of Medical Epidemiology, Biostatistics, and Informatics, Martin-Luther-University Halle-Wittenberg, Halle, Germany

Approved

https://doi.org/10.5256/f1000research.30994.r85845

First I would like to congratulate the authors for this excellent paper which examines how limited diagnostic accuracy in terms of sensitivity and specificity affects estimates of excess mortality based on prevalence and incidence data. In the first part relevant ... Continue reading

First I would like to congratulate the authors for this excellent paper which examines how limited diagnostic accuracy in terms of sensitivity and specificity affects estimates of excess mortality based on prevalence and incidence data. In the first part relevant formulas from previous work by the authors are given with respect to the relationship between prevalence and incidence on one side and on excess mortality on the other side. Then, based on assumptions about sensitivity and specificity of aggregated data the influence of sensitivity and specificity at different ages in a high and low prevalence situation are investigated by simulations. One key result is that specificity can be obtained without knowledge of the sensitivity in lower age groups. Furthermore, the false positive ratio is investigated and quantified. Finally, the methodology is applied to diabetes 2 data of 35 million men in the German Statutory Health Insurance.

The paper is written in a very clear and sound style, I have only very minor remarks:

At page 4 the authors state that sensitivity of diagnosing type 2 diabetes in 80 years old people is higher than in 40 years old people. Surprisingly, this is not taken into account in Table 1 where sensitivity is given as 95% for both age groups.
In Figure 2 there is no blue line to see because of the coincidence of the simulation and the perfect estimation. It is explained in the text, but should be solved for the figure.
Maybe it makes the discussion in the second last paragraph more clear when the authors add (again) that the estimates of R⁽^obs) considered there are based on individual data.

Is the rationale for developing the new method (or application) clearly explained?

Yes
Is the description of the method technically sound?

Yes
Are sufficient details provided to allow replication of the method development and its use by others?

Yes
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: biostatistics and epidemiology

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Respond or Comment

Comments on this article Comments (1)

Version 1

VERSION 1 PUBLISHED 27 Jan 2021

Author Response 28 Jan 2021

Ralph Brinks, Institute for Biometry and Epidemiology, German Diabetes Center, Duesseldorf, 40225, Germany

28 Jan 2021

Author Response

Instead of Gregg et al., the reference below might be a better source for the age-dependency of undiagnosed and diagnosed diabetes (see top of Figure 3 in this article):

... Continue reading Instead of Gregg et al., the reference below might be a better source for the age-dependency of undiagnosed and diagnosed diabetes (see top of Figure 3 in this article):

Selvin E, Parrinello CM, Sacks DB, Coresh J. Trends in prevalence and control of diabetes in the United States, 1988-1994 and 1999-2010. Ann Intern Med. 2014 Apr 15;160(8):517-25. doi: 10.7326/M13-2411. PMID: 24733192; PMCID: PMC4442608. Link
Instead of Gregg et al., the reference below might be a better source for the age-dependency of undiagnosed and diagnosed diabetes (see top of Figure 3 in this article):

Selvin E, Parrinello CM, Sacks DB, Coresh J. Trends in prevalence and control of diabetes in the United States, 1988-1994 and 1999-2010. Ann Intern Med. 2014 Apr 15;160(8):517-25. doi: 10.7326/M13-2411. PMID: 24733192; PMCID: PMC4442608. Link
Competing Interests: No competing interests were disclosed. Close
Report a concern
Comment

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2	3
Version 1 27 Jan 21	read	read	read

Andreas Wienke, Martin-Luther-University Halle-Wittenberg, Halle, Germany
Dianna J. Magliano, Baker Heart and Diabetes Institute, Melbourne, Australia; Monash University, Melbourne, Australia
Bruce Bartholow Duncan, Universidade Federal do Rio Grande do Sul, Porto Alegre, Brazil

Comments on this article

All Comments(1)

Add a comment

Sign up for content alerts

Browse by related subjects

Back to all reports

Reviewer Report

10 Views

07 Jun 2021 | for Version 1

Bruce Bartholow Duncan, Postgraduate Program in Epidemiology and Hospital de Clínicas de Porto Alegre, Universidade Federal do Rio Grande do Sul, Porto Alegre, Brazil

10 Views Cite this report Responses(0)

Approved With Reservations

This is an important evaluation of the use of secondary data from a claims database to estimate the sensitivity and specificity of the inclusion in the database of chronic diseases present in the covered population. Secondary data are increasingly being used for disease surveillance, in this case for diabetes mellitus. As they come with error, corrections must frequently be made in analyses. These corrections must be derived and evaluated, as is done here. My comments do not include a verification of the equations presented, which I have no reason to doubt. However, such verification is a task for someone other than myself.

Major comments:

"false positive ratio", I believe, should be "false positive rate".
The authors have appropriately alerted that sensitivity and specificity, as used here, are not of a diagnostic test, but rather of the presence of a diagnosis in the claims data. As these terms are applied in a context different from the usual one, I believe that readers would benefit from a bit greater detail, noting that sensitivity is the capacity of the claims system to include in its database all cases of diabetes (whether detected or not) present in those covered by the system and specificity is the capacity to include only true cases of diabetes among those covered. Thus, for example, a covered individual who has diabetes but was never tested and thus never detected would be a false negative, detracting from sensitivity.
The horizontal axis of graphs in Figure 3 is the "Relative importance". Please define what this means.
At the end of the Results, the authors state: "...which means that roughly 3 in 2000 diagnoses of type 2 diabetes at that age are false positive findings...". As the FPR is being described, the denominator should not be diagnoses of type 2 diabetes, but rather covered individuals truly without diabetes.
A major issue for the diabetes epidemiology community is the relative frequency of undiagnosed diabetes, i.e., for every 100 true cases, how many are unknown cases). Some discussion of how to use the approach presented to achieve estimates of the prevalence of undiagnosed diabetes (1-positive predicted value) could increase the relevance of this report (or a future one).
Figure 4: Is it possible to trace not only the bounds of the estimated FPR, but also the FPR point estimate at each age?
Why are the base-case sensitivity and specificity so high? In terms of sensitivity, the IDF´s 2019 Diabetes Atlas (https://www.diabetesatlas.org/en/) estimates that 24% of those with diabetes in its European region are undiagnosed. A German investigation estimated that between 3 and 9% of adults had undiagnosed diabetes (Tamayo et al., 2014¹). In terms of specificity, the fact that several percent of those who report having diabetes, when tested, are found to have normoglycemia (1-positive predicted value), coupled with the known large within-individual (biologic) variability over time of available means of diagnosis, suggests that specificity is not 99.95%.
Is not the greater impact of specificity mainly due to the fact that many more individuals in the population do not have diabetes than do, and thus the specificity is acting on a larger (at younger ages far larger) fraction of the population?
The mortality rate ratio of diabetes has declined considerably over recent decades (see: Tables 3 and 4 of Gregg et al. (2018²). However, as you state, the impact of this decline over a 2 year period is likely to be sufficiently small as to not impose a problem.

Minor comments:

Keywords should be reviewed. My understanding is that they should be MeSH terms. Thus, for example, "lupus" should be "systemic lupus erythematosus".
1st sentence Introduction, better: "...of chronic conditions has become...".
Page 4, before "Simulation studies", better: "...For example, the sensitivity of a code for type 2 diabetes in the claims database in 80 years old...".
Last sentence page 4, better: "exemplified" than "motivated".
Discussion, second paragraph: I don´t understand what "accurately possible" means.

Additional comments related to specific review questions;

As I am not fluent in R, I cannot verify that the additional materials include the source data. I imagine not, as the source data must be huge, and initially with personal identifiers.

Is the rationale for developing the new method (or application) clearly explained?

Yes
Is the description of the method technically sound?

Yes
Are sufficient details provided to allow replication of the method development and its use by others?

Yes
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?

Partly
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?

Partly

References

1. Tamayo T, Schipf S, Meisinger C, Schunk M, et al.: Regional differences of undiagnosed type 2 diabetes and prediabetes prevalence are not explained by known risk factors.PLoS One. 2014; 9 (11): e113154 PubMed Abstract | Publisher Full Text
2. Gregg E, Cheng Y, Srinivasan M, Lin J, et al.: Trends in cause-specific mortality among adults with and without diagnosed diabetes in the USA: an epidemiological analysis of linked national survey and vital statistics data. The Lancet. 2018; 391 (10138): 2430-2440 Publisher Full Text

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

diabetes epidemiology

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

8 Views

01 Jun 2021 | for Version 1

Dianna J. Magliano, Department of Diabetes and Population Health, Baker Heart and Diabetes Institute, Melbourne, Vic, Australia; School of Public Health and Preventive Medicine, Monash University, Melbourne, Vic, Australia

8 Views Cite this report Responses(0)

Approved

This is a modelling analysis which aims to assess the impact of diagnostic accuracy on the estimation of excess mortality from incidence and prevalence using a simulation study. The stimulation study which is developed tests two scenarios: one with a high prevalence setting and the other with a low prevalence setting. The finding is then applied to real diabetes data from claims data from the German Statutory Health insurance. The modelling shows that when estimating excess mortality of diabetes, diagnostic accuracy is very important. Specificity is more important than sensitivity across all age groups, and in particular, specificity in younger people has the greatest impact on the estimated mortality rate ratios.

Overall, this is a clear and well-presented piece of work. One thing which may be useful is to have some idea of the size of the impact of specificity on the estimation of mortality ratio rate, in comparison to the effect of sensitivity. The authors state that there is a difference between the effect of sensitivity and specificity, but it may be useful for the reader to understand how much of an impact it has.

My other points are minor and relate to language:

The last line of the abstract should be re-written. Starting that sentence with ‘especially’ means the sentence is unclear. You could start with: ‘In particular…’.
The first sentence of the introduction could be re written to say: “…chronic diseases are becoming more available.”
The heading in the first row of table 1 could be more descriptive. Expand on “setting”. In the actual table heading: insert the word “used” between “settings “and “in”.
Table entries of “Lupus” should be written in full.
Significant figures in table 1 are not consistent. I do understand why though.
Figure 3 should have the panels labelled on figure. “low prevalence” and “high prevalence” or A and B.

Is the rationale for developing the new method (or application) clearly explained?

Yes
Is the description of the method technically sound?

Yes
Are sufficient details provided to allow replication of the method development and its use by others?

Partly
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Diabetes epidemiology

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

11 Views

24 May 2021 | for Version 1

Andreas Wienke, Institute of Medical Epidemiology, Biostatistics, and Informatics, Martin-Luther-University Halle-Wittenberg, Halle, Germany

11 Views Cite this report Responses(0)

Approved

First I would like to congratulate the authors for this excellent paper which examines how limited diagnostic accuracy in terms of sensitivity and specificity affects estimates of excess mortality based on prevalence and incidence data. In the first part relevant formulas from previous work by the authors are given with respect to the relationship between prevalence and incidence on one side and on excess mortality on the other side. Then, based on assumptions about sensitivity and specificity of aggregated data the influence of sensitivity and specificity at different ages in a high and low prevalence situation are investigated by simulations. One key result is that specificity can be obtained without knowledge of the sensitivity in lower age groups. Furthermore, the false positive ratio is investigated and quantified. Finally, the methodology is applied to diabetes 2 data of 35 million men in the German Statutory Health Insurance.

The paper is written in a very clear and sound style, I have only very minor remarks:

At page 4 the authors state that sensitivity of diagnosing type 2 diabetes in 80 years old people is higher than in 40 years old people. Surprisingly, this is not taken into account in Table 1 where sensitivity is given as 95% for both age groups.
In Figure 2 there is no blue line to see because of the coincidence of the simulation and the perfect estimation. It is explained in the text, but should be solved for the figure.
Maybe it makes the discussion in the second last paragraph more clear when the authors add (again) that the estimates of R⁽^obs) considered there are based on individual data.

Is the rationale for developing the new method (or application) clearly explained?

Yes
Is the description of the method technically sound?

Yes
Are sufficient details provided to allow replication of the method development and its use by others?

Yes
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

biostatistics and epidemiology

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

[1] Bernatsky S, Boivin JF, Joseph L, et al.: Mortality in systemic lupus erythematosus. Arthritis Rheum. 2006; 54: 2550–7. PubMed Abstract | Publisher Full Text

[2] Binder N, Herrnböck AS, Schumacher M: Estimating hazard ratios in cohort data with missing disease information due to death. Biom J 2017; 59(2): 251–269. PubMed Abstract | Publisher Full Text

[3] Breslow NE, Day NE: Statistical Methods in Cancer Research. In: The Analysis of Case-Control studies Lyon: IARC; 1980; Vol 1. .

[4] Brinks R, Landwehr S: Age- and time-dependent model of the prevalence of non-communicable diseases and application to dementia in Germany. Theor Popul Biol. 2014; 92: 62–8. PubMed Abstract | Publisher Full Text

[5] Brinks R, Hoyer A, Landwehr S: Surveillance of the incidence of non-communicable diseases (NCDs) with sparse resources: a simulation study using data from a National Diabetes Registry, Denmark, 1995-2004. PLoS One. 2016; 11(3): e0152046. PubMed Abstract | Publisher Full Text | Free Full Text

[6] Brinks R, Hoyer A, Weber S, et al.: Age-specific and sex-specific incidence of systemic lupus erythematosus: an estimate from cross-sectional claims data of 2.3 million people in the German statutory health insurance 2002. Lupus Sci Med. 2016; 25;3(1): e000181. PubMed Abstract | Publisher Full Text | Free Full Text

[7] Brinks R, Tönnies T, Hoyer A: New ways of estimating excess mortality of chronic diseases from aggregated data: insights from the illness-death model. BMC Public Health. 2019; 19(1): 844. PubMed Abstract | Publisher Full Text | Free Full Text

[8] Brinks R, Tönnies T, Hoyer A: Assessing two methods for estimating excess mortality of chronic diseases from aggregated data. BMC Res Notes. 2020; 13: 216. PubMed Abstract | Publisher Full Text | Free Full Text

[9] Brinks R, Tönnies T, Hoyer A: Simulation to study impact of diagnostic accuracy on estimation of excess mortality (Version 01).Zenodo; 2020. Publisher Full Text

[10] Brinks R, Tönnies T, Hoyer A: Estimation of excess mortality from incidence and prevalence: impact of diagnostic accuracy (Version 01).Zenodo; 2020. Publisher Full Text

[11] Brinks R, Tönnies T, Hoyer A: Estimation of excess mortality from incidence and prevalence: impact of diagnostic accuracy (Version 01).Zenodo; 2021. Publisher Full Text

[12] Carstensen B, Rønn PF, Jørgensen ME: Prevalence, incidence and mortality of type 1 and type 2 diabetes in Denmark 1996-2016. BMJ Open Diabetes Res Care. 2020; 8: e001071. PubMed Abstract | Publisher Full Text | Free Full Text

[13] Centers for Disease Control and PreventionNational Health Interview Survey (NHIS).Reference Source Last access, 2020-12-07.

[14] Centers for Medicare & Medicaid ServicesChronic Conditions Public Use Files (PUF).Reference Source Last access, 2020-12-07

[15] Federal Statistical Office of GermanyPeriod life table for 2011/13. Table code 12621-0001, GENESIS-Online database, Last access 2020-12-06.

[16] Global Health Data Exchangedata catalog. by the Institute for Health Metrics and Evaluation (IHME), Seattle WAReference Source Last access, 2020-12-07.

[17] Goffrier B, Schulz M, Bätzing-Feigenbaum J: Administrative Prävalenzen und Inzidenzen des diabetes mellitus von 2009 bis 2015. Versorgungsatlas. 2017. Publisher Full Text

[18] Gregg EW, Cadwell BL, Cheng YJ, et al.: Trends in the Prevalence and Ratio of Diagnosed to Undiagnosed Diabetes According to Obesity Levels in the U.S. Diabetes Care 2004; 27(12): 2806–2812. PubMed Abstract | Publisher Full Text

[19] Röckl S, Brinks R, Baumert J, et al.: All-cause mortality in adults with and without type 2 diabetes: findings from the national health monitoring in Germany. BMJ Open Diabetes Res Care. 2017; 5(1): e000451. PubMed Abstract | Publisher Full Text | Free Full Text

[20] Scheidt-Nave C: Nationale Diabetes-Surveillance am Robert Koch-Institut Diabetes in Deutschland - Bericht der Nationalen Diabetes-Surveillance 2019.Robert-Koch-Institut Berlin2019. Publisher Full Text

[21] Tönnies T, Hoyer A, Brinks R: Excess mortality for people diagnosed with type 2 diabetes in 2012 - estimates based on claims data from 70 million Germans. Nutr Metab Cardiovasc Dis. 2018; 28(9): 887–91. PubMed Abstract | Publisher Full Text

[22] Tamayo T, Brinks R, Hoyer A, et al.: The Prevalence and Incidence of Diabetes in Germany. Dtsch Arztebl Int 2016; 113(11): 177–82. PubMed Abstract | Publisher Full Text | Free Full Text

Impact of diagnostic accuracy on the estimation of excess mortality from incidence and prevalence: simulation study and application to diabetes in German men

Abstract

Keywords

Introduction

Methods

(1)

Figure 1. Illness-death model.

(2)

(3a)

(3b)

Simulation studies

Table 1.Description of the parameter settings in the simulations.

Real world data

(4)

Results

Simulation studies

Figure 2. Age-specific mortality rate ratios (R) in the simulations.

Figure 3. Tornado plots for relative importance of the sensitivity and specificity.

Real world data

Figure 4. Age-specific false-positive ratios (FPR) in the simulated sensitivity scenarios.

Discussion

Data Availability

Underlying data

Extended data

Competing interests

References

Comments on this article Comments (1)

Open Peer Review

Comments on this article Comments (1)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated