A better approach to discuss medical science and engineering data with a modified Lehmann Type – II model

Muhammad Zafar Iqbal; Muhammad Zeshan Arshad; Gamze Özel; Oluwafemi Samson Balogun

doi:10.12688/f1000research.54305.1

Home Browse A better approach to discuss medical science and engineering data...

ALL Metrics

-

Views

-

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

A better approach to discuss medical science and engineering data with a modified Lehmann Type – II model

[version 1; peer review: 2 approved with reservations]

Muhammad Zafar Iqbal¹, Muhammad Zeshan Arshad ¹, Gamze Özel², Oluwafemi Samson Balogun³

PUBLISHED 17 Aug 2021

Author details Author details

¹ Department of Mathematics and Statistics, University of Agriculture, Faisalabad, Faisalabad, Punjab, 38000, Pakistan
² Department of Statistics, Hacettepe University, Ankara, Ankara, Turkey
³ School of Computing, University of Eastern Finland, Kuopio, 70211, Finland

Muhammad Zafar Iqbal
Roles: Conceptualization, Data Curation, Writing – Original Draft Preparation, Writing – Review & Editing

Muhammad Zeshan Arshad
Roles: Conceptualization, Data Curation, Methodology, Software, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Gamze Özel
Roles: Conceptualization, Investigation, Writing – Original Draft Preparation, Writing – Review & Editing

Oluwafemi Samson Balogun
Roles: Conceptualization, Funding Acquisition, Writing – Original Draft Preparation, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

Abstract

Background: Modeling with the complex random phenomena that are frequently observed in reliability engineering, hydrology, ecology, medical science, and agricultural sciences was once thought to be an enigma. Scientists and practitioners agree that an appropriate but simple model is the best choice for this investigation. To address these issues, scientists have previously discussed a variety of bounded and unbounded, simple to complex lifetime models.
Methods: We discussed a modified Lehmann type II (ML-II) model as a better approach to modeling bathtub-shaped and asymmetric random phenomena. A number of complementary mathematical and reliability measures were developed and discussed. Furthermore, explicit expressions for the moments, quantile function, and order statistics were developed. Then, we discussed the various shapes of the density and reliability functions over various model parameter choices. The maximum likelihood estimation (MLE) method was used to estimate the unknown model parameters, and a simulation study was carried out to evaluate the MLEs' asymptotic behavior.
Results: We demonstrated ML- II's dominance over well-known competitors by modeling anxiety in women and electronic data.

Keywords

Power Function Distribution; Lehmann Type I, II Distribution; Failure Rate Function; Moments; Maximum Likelihood; Order Statistics; Quantile; Rényi Entropy.

Corresponding author: Muhammad Zeshan Arshad

Competing interests: No competing interests were disclosed.

Grant information: This work was supported by Digiteknologian TKI-ymparisto project A74338 (ERDF, Regional Council of Pohjois-Savo).
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2021 Iqbal MZ et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Iqbal MZ, Arshad MZ, Özel G and Balogun OS. A better approach to discuss medical science and engineering data with a modified Lehmann Type – II model [version 1; peer review: 2 approved with reservations]. F1000Research 2021, 10:823 (https://doi.org/10.12688/f1000research.54305.1) First published: 17 Aug 2021, 10:823 (https://doi.org/10.12688/f1000research.54305.1) Latest published: 17 Aug 2021, 10:823 (https://doi.org/10.12688/f1000research.54305.1)

Introduction

Over the last two decades, researchers' increasing interest in the development of new models has explored the remarkable characteristics of the baseline model. As a result, new models open new avenues for theoretical and applied researchers to address real-world problems, allowing them to fit asymmetric and complex random phenomena more proficiently and adequately. As a result, several modifications, extensions, and generalizations have been developed and discussed in the literature, with the Lehmann¹ type – I (L – I) and Lehmann type – II (L – II) models being among the simplest and most useful. The simple exponentiation of any arbitrary baseline model is given by L – I.

F (x; α; ξ) = G^{α} (x; ξ)

where $0 < x < 1$ , and $α > 0$ is a shape parameter.

Gupta et al.² are credited with the use of L–I on exponential distributions. On the other hand, Cordeiro et al.³ established the L–II–G class of distributions and developed a dual transformation of L–I, which is given by

F (x; α; ξ) = 1 - {(1 - G (x; ξ))}^{α}

where $G (x; ξ)$ is cumulative distribution function (CDF) of the arbitrary baseline model, based on the parametric vector $ξ$ with $α > 0$ as a shape parameter.

The closed-form feature of L–II allows one to derive and study its numerous properties, and in the literature, both approaches (L–I and L–II) have been extensively used in favor of the power function (PF) model, to study the unexplored characteristics of the classical and modified models. Recently, Arshad et al.^4,5 developed bathtub-shaped failure rate and PF models followed by L–II and L–I families, respectively, and explored their applications in engineering data. Awodutire et al.⁶ generalized the half-logistic via L–II class, and Akilandeswari et al.⁷ proposed the Laplace L–I reliability growth model and discussed its application in the early detection of software failure based on time between failure observations.

The PF is a special case of the beta distribution in distribution theory, and its significance can be evaluated using statistical tests such as the likelihood ratio test. The PF's simplicity and utility has compelled researchers to investigate its further generalizations and applications in various fields of science. For this, we recommend that the reader look at Dallas's illustrious work.⁸ He discovered an intriguing relationship between PF and Pareto models when the inverse transformation of the Pareto variable explored the PF.⁸ Meanwhile, Meniconi and Barry⁹ discovered the PF as a best-fit model on electronic component data. Characterization is based on the independence of record values and order statistics, with lower record values attributed to Chang¹⁰ and Tavangar,¹¹ respectively. Cordeiro and Brito¹² created the beta version of the PF and discussed its use in petroleum reservoir and milk production data. The PF was characterized by Ahsanullah et al.¹³ using lower record values. Zaka et al.¹⁴ discussed techniques for estimating PF parameters such as least square (LS), relative least square (RLS), and ridge regression (RR). Tahir et al.¹⁵ generalized the PF via the Weibull-G class and applied it to bathtub-shaped data. Shahzad et al.¹⁶ used the techniques of L-, TL-, LL-, and LH moments to calculate the PF moments. Haq et al.¹⁷ generalized the PF via the QRTM-G class and investigated its application in two-lifetime data. Okorie et al.¹⁸ generalized the PF via the Marshall-Olkin-G class (Marshall and Olkin¹⁹) and investigated its application in data on anxiety in women and evaporation. Usman et al.²⁰ proposed an exponentiated version of transmuted PF and investigated its application in biological and engineering data. Hassan et al.²¹ generalized the PF by following the odd exponential-G class (Tahir et al.²²) and discussed its application in three-lifetime data. Zaka et al.²³ developed a new reflected PF and investigated its application in medical sciences data, while Al-Mutairi²⁴ discussed the weighted PF via the QRTM G-class and investigated its application in the engineering sector.

Modified Lehmann type II model

We developed a potentiated lifetime model known as the modified Lehmann type II (ML-II) model. It is constrained by the interval (0, 1). The ML-II is extremely well suited to modeling asymmetric and bathtub-shaped phenomena. By including a scale parameter ( $α > 0$ ), in the baseline model, it begins to outperform its competitors in terms of fit and robustness of the tail weight/skewness of the density function.

The ML-II is said to follow a random variable X if its associated CDF and corresponding probability density function (PDF) are given by

(1)

F_{ML - II} (x; α; β) = 1 - {(\frac{1 - x}{1 + αx})}^{β}

and

(2)

f_{ML - II} (x; α; β) = \frac{β (α + 1) {(1 - x)}^{β - 1}}{{(1 + αx)}^{β + 1}}

where $0 < x < 1$ , and $α > - 1, β > 0$ are the scale and shape parameters, respectively. For $α$ = 0, the ML-II reduces to the L–II (baseline model).

Balogun et al.,^25,26 has developed the generalized version and G-class of ML-II (Equation (1)), respectively, and explored their applications in multidisciplinary areas of science.

We had the following objectives:

(i) to develop a two-parameter model with an approach that had not been studied and discussed in the past;
(ii) For the new model to have attractive closed-form features for CDF, PDF, and a likelihood function that is simple to interpret,;
(iii) PDF and HRF to hold J, reversed-J, and bathtub shapes;
(iv) To provide comparative results and a better fit than competing models.

This article is divided into the following sections:’Linear representation’ presents a mixture representation as well as numerous structural and reliability measures. ‘Estimation’ includes the estimation of model parameters using the maximum likelihood estimation (MLE) method, as well as a simulation study. ‘Application’ discusses real-world applications, and the final section summarizes the conclusion.

Linear representation

The linear representations of CDF and PDF make the calculations much easier than the traditional integral computation for determining the mathematical properties. We consider the binomial expansion for this.

{(1 - z)}^{β} = \sum_{i = 0}^{\infty} {(- 1)}^{i} (\begin{matrix} β \\ i \end{matrix}) z^{i}, |z| < 1

F_{ML - II} (x; α; β) = 1 - {(1 - x)}^{β} {(1 + αx)}^{- β}

F_{ML - II} (x; α; β) = 1 - \sum_{i = 0}^{\infty} {(- 1)}^{i} (\begin{matrix} β \\ i \end{matrix}) x^{i} \sum_{j = 0}^{\infty} {(\begin{matrix} - β \\ j \end{matrix}) (αx)}^{j}

Hence, the mixture representation of CDF is given as

F_{ML - II} (x; α; β) = \sum_{i, j = 0}^{\infty} ϕ_{ij} x^{i + j}

PDF is given as follows

f_{ML - II} (x; α; β) = β (1 + α) \sum_{i = 0}^{\infty} {(- 1)}^{i} (\begin{matrix} β - 1 \\ i \end{matrix}) x^{i} \sum_{j = 0}^{\infty} {(\begin{matrix} β + 1 \\ j \end{matrix}) (αx)}^{j}

or

f_{ML - II} (x; α; β) = β (1 + α) \sum_{i, j = 0}^{\infty} η_{ij} x^{i + j}

where $ϕ_{ij} = (\begin{matrix} β \\ i \end{matrix}) (\begin{matrix} - β \\ j \end{matrix}) {(- 1)}^{i} α^{j}, α > - 1, β > 0, η_{ij} = α^{j} {(- 1)}^{i} (\begin{matrix} β - 1 \\ i \end{matrix}) (\begin{matrix} β + 1 \\ j \end{matrix}), α > - 1, β > 0$

Reliability characteristics

The probability model plays an important role in reliability engineering by analyzing and predicting the lifespan of a component. Notable contributions include the survival function S(x), hazard rate function h(x), cumulative hazard rate function h_c(x), reverse hazard rate function h_r(x), Mills ratio M(x), and odd function O(x)).

The reliability function can be defined as the probability that a component will survive at time x. It is defined analytically as $S (x) = 1 - F (x)$ . The survival/reliability function of X is denoted by

(3)

S_{ML - II} (x; α; β) = {(\frac{1 - x}{1 + αx})}^{β}

Terms such as “failure rate function”, “hazard rate function”, and “force of mortality” are frequently discussed in the literature. These terms are used to describe the failure rate of a component over a specific time period (say x). It is mathematically defined as $h (x) = f (x) / R (x)$ .

The failure rate function of X is denoted by

(4)

h_{ML - II} (x; α; β) = \frac{β (α + 1)}{(1 - x) (1 + αx)}

The mechanical components/parts of some systems are frequently assumed to follow the bathtub-shaped failure rate phenomenon. To discuss the significance of the MLII, several well-established and useful reliability measures are available in the literature. One of them is the cumulative hazard rate function, which is defined as $h_{c} (x) = - lo g (S (x)) .$ The cumulative hazard rate function of X is denoted by

h_{c - ML - II} (x; α; β) = - lo g ({(\frac{1 - x}{1 + αx})}^{β})

The reverse hazard rate function is defined by $h_{r} (x) = f (x) / F (x) .$ The reverse hazard rate function of X is given by

h_{r - ML - II} (x; α; β) = \frac{β (α + 1) {(1 - x)}^{β - 1}}{(1 + αx) ({(1 + αx)}^{β} - {(1 - x)}^{β})}

Mills ratio is defined by $M (x) = S (x) / f (x) .$ Mills ratio of X is given by

M_{ML - II} (x; α; β) = \frac{(1 + αx) {(1 - x)}^{β}}{β (α + 1) {(1 - x)}^{β - 1}}

The odd function is defined by $O (x) = F (x) / S (x) .$ The odd function of X is given by

O_{ML - II} (x; α; β) = \frac{{(1 + αx)}^{β} - {(1 - x)}^{β}}{{(1 - x)}^{β}}

As mentioned above, we can obtain the linear expression for reliability characteristics. In terms of linear expression, the reliability and failure rate functions of X are given by

{S^{*}}_{ML - II} (x; α; β) = \sum_{i = 0}^{\infty} {(- 1)}^{i} (\begin{matrix} β \\ i \end{matrix}) x^{i} \sum_{j = 0}^{\infty} {(\begin{matrix} - β \\ j \end{matrix}) (αx)}^{j}

and

{h^{*}}_{ML - II} (x; α; β) = \frac{β (1 + α) \sum_{i = 0}^{\infty} {(- 1)}^{i} (\begin{matrix} β - 1 \\ i \end{matrix}) x^{i} \sum_{j = 0}^{\infty} {(\begin{matrix} β + 1 \\ j \end{matrix}) (αx)}^{j}}{\sum_{i = 0}^{\infty} {(- 1)}^{i} (\begin{matrix} β \\ i \end{matrix}) x^{i} \sum_{j = 0}^{\infty} {(\begin{matrix} - β \\ j \end{matrix}) (αx)}^{j}}

Limiting behavior

Propositions 1 and 2 discuss the limiting behavior of the ML-II's cumulative distribution (CDF), density (PDF), reliability (S(x)), and failure rate (h(x)) functions for x $\to 0$ and x $\to 1 .$

Proposition-1. The limiting behavior of the CDF, PDF, S(x), and h(x) of the ML-II at x $\to 0$ is given below.

F_{ML - II} (0; α; β) \sim 0

f_{ML - II} (0; α; β) \sim β (1 + α)

S_{ML - II} (0; α; β) \sim 1

h_{ML - II} (0; α; β) \sim β (1 + α)

Proposition-2. The limiting behavior of CDF, PDF, S(x), and h(x) of the ML-II at x $\to 1$ is given as follows, respectively.

F_{ML - II} (1; α; β) = 1

f_{ML - II} (1; α; β) = 0

S_{ML - II} (1; α; β) = 1

h_{ML - II} (1; α; β) = 0

Shapes of density and failure rate functions

The possible shapes of the ML-II's density and failure rate functions are sketched over various model parameter choices shown in Figures 1 and 2. Figure 1 depicts the J, reverse-J, and bathtub shapes of the density function, while Figure 2 depicts the U, bathtub, and reverse-J shapes of the failure rate function.

Figure 1. Density function.

Figure 2. Failure rate function.

Quantile, mode, skewness, and kurtosis

The concept of quantile function was introduced by Hyndman and Fan.²⁷ Inverting the CDF yields the p^th quantile function of ML-II (Equation (1)). The quantile function is defined as follows: $p = F (x_{p}) = P (X \leq x_{p}), p \in (0, 1) .$ Then, the quantile function of X is given by

(5)

x_{p - ML - II} = \frac{1 - {(1 - p)}^{1 / β}}{1 + α {(1 - p)}^{1 / β}}, α > - 1, β > 0

Put p = 0.25, 0.50, and 0.75 in Equation (3) to get the first quartile, median, and third quartile of X. To generate random numbers in the future, we will assume that the CDF in Equation (1) follows a uniform distribution u = U. (0, 1).

The mode of X is calculated by taking the first derivative of PDF (Equation (2)) and equating it to zero, as shown by

{f^{/}}_{ML - II} (x; α; β) = \frac{β (α + 1) {(1 - x)}^{β} {(1 + αx)}^{- β - 2} (2 αx - (1 + α) β - α + 1)}{{(1 - x)}^{2}} = 0

As a result, a simplified form of the mode is given by

{Mode}_{ML - II} = \frac{(α + 1) (β + 1) - 1}{2 α}, α > - 1, β > 0

Measures of skewness and kurtosis based on quartiles and octiles are less sensitive to outliers and work well against models, but they are deficient in moments.

Bowley’s²⁸ measure of skewness

S_{B} = \frac{Q_{(\frac{3}{4})} + Q_{(\frac{1}{4})} - 2 Q_{(\frac{1}{2})}}{Q_{(\frac{3}{4})} - Q_{(\frac{1}{4})}}

Moor’s²⁹ measure of kurtosis

K_{M} = \frac{Q_{(\frac{3}{8})} - Q_{(\frac{1}{8})} - Q_{(\frac{5}{8})} + Q_{(\frac{7}{8})}}{Q_{(\frac{6}{8})} - Q_{(\frac{2}{8})}}

According to Figures 3 and 4, the skewness and kurtosis plots of the ML-II may be positively skewed.

Figure 3. Skewness.

Figure 4. Kurtosis.

Moments and associated measures

Moments play a significant role in distribution theory, where they are used to discuss the various characteristics and important features of the probability model.

Theorem 1. Let X $\sim$ ML-II ( $x; α, β$ ), with $α > - 1, β > 0$ , then the r-th ordinary moment (say $μ_{r}^{'}$ ) of X is given by

μ_{r - ML - II}^{'} = E \sum_{i = 0}^{\infty} D_{i} B (r + i + 1, β)

where E = $β (1 + α), D_{i} = α^{i} (\begin{matrix} - β - 1 \\ i \end{matrix})$

Proof: r-th ordinary moment can be written by following Equation (2) as

μ_{r - ML - II}^{'} = β (1 + α) \int_{o}^{1} x^{r} {(1 - x)}^{β - 1} {(1 + α x)}^{- (β + 1)} dx

μ_{r - ML - II}^{'} = αβγ (1 + α) \sum_{i = 0}^{\infty} D_{i} \int_{o}^{1} x^{r + i} {(1 - x)}^{β - 1} dx

As a result, the above integral reduces to the r-th moment, which is given by

(6)

μ_{r - ML - II}^{'} = E \sum_{i = 0}^{\infty} D_{i} B (r + i + 1, β)

where B( $x; α, β$ ) = $\int_{0}^{x} t^{α} {(1 - t)}^{β - 1} dt$ is the beta function, E = $β (1 + α), D_{i} = α^{i} (\begin{matrix} - β - 1 \\ i \end{matrix})$ and $α > - 1, β > 0$

The r-th moment is quite helpful in the development of several statistics. For instance, the mean of X can be obtained by setting r =1 in Equation (6) and is given by

μ_{1 - ML - II}^{'} = E \sum_{i = 0}^{\infty} D_{i} B (2 + i, β)

Moment generating function $M_{X} (t)$ is defined as $M_{X} (t) = \sum_{r = 0}^{\infty} \frac{t^{r}}{r!} μ_{r}^{'}$ . It is obtained by following Equation (6) and is given by

M_{X - ML - II} (t) = E \sum_{r = 0}^{\infty} \frac{t^{r}}{r!} \sum_{i = 0}^{\infty} D_{i} B (r + i + 1, β)

Characteristic function is defined as $\emptyset_{X} (t) = \sum_{r = 0}^{\infty} \frac{{(it)}^{r}}{r!} μ_{r}^{'}$ . It is obtained by following Equation (6) and is given by

\emptyset_{X - ML - II} (t) = E \sum_{r = 0}^{\infty} \frac{{(it)}^{r}}{r!} \sum_{i = 0}^{\infty} D_{i} B (r + i + 1, β)

The factorial generating function of X is defined as $F_{x} (t) = E {(1 + t)}^{x} = E (e^{xln (1 + t)}) = \sum_{r = 0}^{\infty} \frac{{(ln (1 + t))}^{r}}{r!} μ_{r}^{'} .$ It is obtained by following Equation (6) and is given by

F_{x - ML - II} (t) = E \sum_{r = 0}^{\infty} \frac{{(ln (1 + t))}^{r}}{r!} \sum_{i = 0}^{\infty} D_{i} B (r + i + 1, β)

The Fisher index $\frac{Var (X)}{E (X)}$ may play a supportive role in the discussion of variability in X and it is given by

{Fisher index}_{ML - II} = \frac{E \sum_{i = 0}^{\infty} D_{i} B (3 + i, β) - {(E \sum_{i = 0}^{\infty} D_{i} B (2 + i, β))}^{2}}{E \sum_{i = 0}^{\infty} D_{i} B (2 + i, β)}

For the negative moments of X, substitute r by – w in Equation (6) and it is given by

μ_{- w - ML - II}^{'} = E \sum_{i = 0}^{\infty} D_{i} B (- w + i + 1, β)

Furthermore, for fractional positive and fractional negative moments of X, substitute r by $(\frac{m}{n})$ and $(- \frac{m}{n})$ in Equation (6), respectively.

The Mellin transformation is well-known in statistics as a product distribution as well as a quotient for independent random variables. The Mellin transformation is presented by $M_{x} (m) = E (x^{m - 1}) = \int x^{m - 1} f (x) dx .$ The Mellin transformation of X is given by

M_{x - ML - II} (m) = E \sum_{i = 0}^{\infty} D_{i} B (m + i, β) .

where B( $x; α, β$ ) = $\int_{0}^{x} t^{α} {(1 - t)}^{β - 1} dt$ is the beta function, E = $β (1 + α), D_{i} = α^{i} (\begin{matrix} - β - 1 \\ i \end{matrix})$ and $α > - 1, β > 0$ .

One may perhaps further determine the well-established statistics such as skewness ( $τ_{1} = μ_{3}^{2} / μ_{2}^{3}$ ), and kurtosis ( $τ_{2} = μ_{4} / μ_{2}^{2}$ ), of X by integrating Equation (6). A well-established relationship between the central moments $(μ_{s})$ and cumulants ( $K_{s}$ ) of X may easily be defined by ordinary moments by $μ_{s} = \sum_{k = 0}^{s} {(\begin{matrix} s \\ k \end{matrix}) (- 1)}^{k} {(μ_{1}^{/})}^{s} μ_{s - k}^{/}$ . Hence, the first four cumulants can be calculated by $K_{1} = μ_{1}^{/}$ , $K_{2} = μ_{2}^{/} - μ_{1}^{/ 2}$ , $K_{3} = μ_{3}^{/} - 3 μ_{2}^{/} μ_{1}^{/} + 2 μ_{1}^{/ 3}$ , and $K_{4} = μ_{4}^{/} - 4 μ_{3}^{/} μ_{1}^{/} - 3 μ_{2}^{/ 2} + 12 μ_{2}^{/} μ_{1}^{/ 2} - 6 μ_{1}^{/ 4}$ .

Some numerical results of the first four ordinary moments ( $μ_{1}^{/}, μ_{2}^{/}, μ_{3}^{/}, μ_{4}^{/}$ ), mode (a value that appears frequently in data), $ε^{2}$ = variance (a measure of dispersion), $τ_{1} =$ skewness (measure of asymmetry), and $τ_{2} =$ kurtosis (a measure to discuss the heaviness of the distribution tails) for some chosen parameters are presented in Table 1 for S-I ( $α = 0.5, β = 0.9$ ), S-II ( $α = 0.9, β = 1.5$ ), S-III ( $α = 1.2, β = 1.9$ ), S-IV ( $α = 3.2, β = 0.9$ ), and S-V ( $α = 0.2, β = 3.9$ ). Note that the results of moments and variance decrease gradually, while skewness falls between 0 and 1, mode increases, and kurtosis can be negative subject to the model parameter combinations.

Table 1.

Numerical results of moments ( $μ_{s}^{/}$ ), variance ( $ε^{2}$ ), skewness ( $τ_{1}$ ), and kurtosis ( $τ_{2}$ ).

$μ_{s}^{/}$	S-I	S-II	S-III	S-IV	S-V
$μ_{1}^{/}$	0.460	0.295	0.224	0.302	0.181
$μ_{2}^{/}$	0.297	0.143	0.089	0.163	0.056
$μ_{3}^{/}$	0.221	0.086	0.046	0.110	0.023
$μ_{4}^{/}$	0.176	0.058	0.028	0.067	0.011
Mode	1.850	2.083	2.241	1.091	12.200
$ε^{2}$	0.029	0.044	0.025	0.067	0.002
$τ_{1}$	0.010	0.100	0.492	0.028	1.292
$τ_{2}$	0.119	0.598	0.981	0.483	−0.076

Incomplete moments

Lower incomplete (LI) and upper incomplete moments are the two types of incomplete moments. LI moments are defined by $Φ_{r} (t) = \int_{0}^{t} x^{r} f (x) dx$ . The LI moments of X are given as

(7)

Φ_{r - ML - II} (t) = E \sum_{i = 0}^{\infty} D_{i} B_{t} (r + i + 1, β)

The residual life function of random variable X, $R (t) = (X - t / X > t)$ , is the likelihood that a component whose life says x, survives in the different time intervals at $t \geq 0$ . Analytically, it can be written as follows:

S_{R (t) - ML - II} (x; α; β) = \frac{S (x + t)}{S (t)}

Residual life function of X

S_{R (t) - ML - II} (x; α; β) = \frac{{(1 - (x + t))}^{β} {(1 + α t)}^{β}}{{(1 + α (x + t))}^{β} {(1 - t)}^{β}}

with the associated CDF is given as follows

F_{R (t) - ML - II} (x; α; β) = \frac{{(1 + α (x + t))}^{β} {(1 - t)}^{β} - {(1 - (x + t))}^{β} {(1 + α t)}^{β}}{{(1 + α (x + t))}^{β} {(1 - t)}^{β}}

The mean residual life function of X is given by

E (S_{R - ML - II} (x; α; β)) = \frac{1}{S (t)} (μ_{1}^{/} - \int_{0}^{t} xf (x) dx) - t, t \geq 0

E (S_{R - ML - II} (x; α; β)) = \frac{{(1 + α t)}^{β}}{{(1 - t)}^{β}} (E \sum_{i = 0}^{\infty} D_{i} (B (2 + i, β) - B_{t} (2 + i, β))) - t

Further, the reverse residual life can be defined as $\bar{R} (t) = t - X / X \leq t$

S_{\bar{R} (t) - ML - II} (x; α; β) = \frac{F (t - x)}{F (t)}, t \geq 0

Reverse residual life function of X

S_{\bar{R} (t) - ML - II} (x; α; β) = \frac{{(1 - (t - x))}^{β} {(1 + α t)}^{β}}{{(1 + α (t - x))}^{β} {(1 - t)}^{β}}

with the associated CDF is given as follows

F_{\bar{R} (t) - ML - II} (x; α; β) = \frac{{(1 + α (t - x))}^{β} {(1 - t)}^{β} - {(1 - (t - x))}^{β} {(1 + α t)}^{β}}{{(1 + α (t - x))}^{β} {(1 - t)}^{β}}

The mean reversed residual life function/mean waiting time is given by

E (S_{\bar{R} - ML - II} (x; α; β)) = t - \frac{1}{F (t)} \int_{0}^{t} xf (x) dx, t \geq 0

E (S_{\bar{R} - ML - II} (x; α; β)) = t - \frac{{(1 + α x)}^{β}}{{(1 + α x)}^{β} - {(1 - x)}^{β}} E \sum_{i = 0}^{\infty} D_{i} B_{t} (2 + i, β)

where B( $x; α, β$ ) = $\int_{0}^{x} t^{α} {(1 - t)}^{β - 1} dt$ is the beta function, E = $β (1 + α), D_{i} = α^{i} (\begin{matrix} - β - 1 \\ i \end{matrix}),$ and $α > - 1, β > 0$

Order statistics

Order statistics and its moments play an important role in reliability analysis and life testing of a component in quality control. Let X₁, X₂, X₃ , ..., X_n be a random sample of size n following the ML-II model and {X₍₁₎ < X₍₂₎ < X₍₃₎ < ... < X_(n)} be the corresponding order statistics. The random variables X_(i) , X₍₁₎ , X_(n) are the i-th, minimum, and maximum order statistics of X, respectively.

The PDF of the i-th order statistics is given by

f_{(i : n)} (x) = \frac{1}{B (i, n - i + 1)!} {(F (x))}^{i - 1} {(1 - F (x))}^{n - i} f (x),

i = 1,2, 3, … , n.

By incorporating Equations (1) and (2), the PDF of the i-th order statistics is given by

(8)

f_{(i : n) - ML - II} (x; α; β) = \frac{β (α + 1)}{B (i, n - i + 1)!} {(1 - {(\frac{1 - x}{1 + αx})}^{β})}^{i - 1} {({(\frac{1 - x}{1 + αx})}^{β})}^{n - i} (\frac{{(1 - x)}^{β - 1}}{{(1 + αx)}^{β + 1}})

Equation (8) can be written as

(9)

f_{(i : n) - ML - II} (x; α; β) = \frac{1}{B (i, n - i + 1)!} (β (α + 1)) \sum_{i, j = 0}^{\infty} G_{ij} {(- 1)}^{i} α^{j} x^{j} {(1 - x)}^{2 β + i - 1}

Straightforward computation of Equation (9) leads to the w-th moment order statistics of X and it is given by

(10)

E (X^{w}) = μ_{w - OS - ML - II}^{/} = \frac{1}{B (i, n - i + 1)!} (β (α + 1)) \sum_{i, j = 0}^{\infty} G_{ij} {(- 1)}^{i} α^{j} B (j + 1, 2 β + i)

where $G_{ij} = (\begin{matrix} β \\ i \end{matrix}) (\begin{matrix} - (αβ + α + i) \\ j \end{matrix}), α > - 1, β > 0 .$ Further, the minimum and maximum order statistics of $X$ follow directly from Equation (8) with i = 1 and i = n, respectively.

Stress – strength reliability

Let X₁ and X₂ represent a component's strength and stress, respectively, following the same univariate distribution. The inadequacy or effectiveness of a component is dependent on whether $X_{2} > X_{1}$ and $X_{2} < X_{1}$ , respectively. Stress – strength reliability can be written as $R = P (X_{2} < X_{1}) .$

Theorem 2. Let $X_{1} \sim$ ML-II ( $x; α, β_{1}$ ) and $X_{2} \sim$ ML-II ( $x; α, β_{2}$ ) be independent ML-II distributed random variables; then the reliability R is defined as $\frac{β_{2}}{β_{1} + β_{2}}$

Proof: Reliability R is defined as

R = \int f_{1} (x) F_{2} (x) dx

Reliability of X is given by

R_{ML - II} = \int (\frac{β_{1} (α + 1) {(1 - x)}^{β_{1} - 1}}{{(1 + α x)}^{β_{1} + 1}}) (1 - {(\frac{1 - x}{1 + α x})}^{β_{2}}) dx .

Hence the above integral reduces R in terms of $β_{1}$ and $β_{2}$ , refers to the stress-strength reliability of the ML-II, and it is given by

R_{ML - II} = \frac{β_{2}}{β_{1} + β_{2}}, β_{1}, β_{2} > 0

Entropy

There are a number of schools of thought about defining entropy measures. Entropy can be the quantity of disorderedness, randomness, diversity, or sometimes an uncertainty in a system.

The Rényi³⁰ entropy of X is defined by

I_{δ} (X) = \frac{1}{1 - δ} lo g \int_{0}^{1} f^{δ} (x) dx, δ > 0 and δ \neq 1

First, we simplify $f (x)$ in terms of $f^{δ} (x)$ by considering Equation (2)

{f^{δ}}_{ML - II} (X; α; β; δ) = β^{δ} {(α + 1)}^{δ} {(1 - X)}^{δ (β - 1)} {(1 + α X)}^{- δ (β + 1)}

by applying the binomial expansion to this equation, we get

{f^{δ}}_{ML - II} (X; α; β; δ) = β^{δ} {(α + 1)}^{δ} \sum_{i = 0}^{\infty} (\begin{matrix} - δ (β + 1) \\ i \end{matrix}) α^{i} X^{i} {(1 - X)}^{δ (β - 1)}

and by placing this information in $I_{δ} (X)$ , we get

I_{δ - ML - II} (X; α; β; δ) = \frac{1}{1 - δ} lo g (β^{δ} {(α + 1)}^{δ} \int_{0}^{1} \sum_{i = 0}^{\infty} (\begin{matrix} - δ (β + 1) \\ i \end{matrix}) α^{i} x^{i} {(1 - x)}^{δ (β - 1)} dx)

hence, by integrating the last equation we obtain the reduced form of the Rényi entropy of X and it is given by

(11)

I_{δ - ML - II} (X; α; β; δ) = \frac{1}{1 - δ} lo g (β^{δ} {(α + 1)}^{δ} \sum_{i = 0}^{\infty} A_{i} B (δ (β - 1) + 1, i + 1))

where $A_{i} = (\begin{matrix} - δ (β + 1) \\ i \end{matrix}) α^{i}, α > - 1, β > 0 .$

A generalization of the Boltzmann-Gibbs entropy is the $η$ – entropy, although in physics, it is referred to as the Tsallis entropy. The Tsallis³¹ entropy/ $η$ – entropy is described by

H_{η} (X) = \frac{1}{η - 1} (1 - \int_{0}^{1} f^{η} (x) dx), η > 0 and η \neq 1 .

The Tsallis Entropy of X is given by

H_{η - ML - II} (X; α; β; η) = \frac{1}{η - 1} (1 - β^{η} {(α + 1)}^{η} \sum_{i = 0}^{\infty} C_{i} B (η (β - 1) + 1, i + 1))

where $C_{i} = (\begin{matrix} - η (β + 1) \\ i \end{matrix}) α^{i}, α > - 1, β > 0 .$

Havrda and Charvat³² introduced $ω -$ entropy measure. It is presented by

H_{ω} (X) = \frac{1}{2^{ω - 1} - 1} (\int_{0}^{1} f^{ω} (x) dx - 1), ω > 0 and ω \neq 1 .

The Havrda and Charvat entropy of X is given by

H_{ω - ML - II} (X; α; β; ω) = \frac{1}{2^{ω - 1} - 1} ((β^{ω} {(α + 1)}^{ω} \sum_{i = 0}^{\infty} F_{i} B (ω (β - 1) + 1, i + 1)) - 1)

where $F_{i} = (\begin{matrix} - ω (β + 1) \\ i \end{matrix}) α^{i}, α > - 1, β > 0 .$

Arimoto³³ generalized the work of³² by introducing $ε -$ entropy measure. It is presented by

H_{ε} (X) = \frac{1}{2^{ε - 1} - 1} ({(\int_{0}^{1} f^{\frac{1}{ε}} (x) dx)}^{ε} - 1), ε > 0 and ε \neq 1 .

The Arimoto entropy of X is given by

H_{ε - ML - II} (X; α; β; ε) = \frac{1}{2^{ε - 1} - 1} ({(\begin{matrix} β^{\frac{1}{ε}} {(α + 1)}^{\frac{1}{ε}} \\ \times \sum_{i = 0}^{\infty} G_{i} B (\frac{1}{ε} (β - 1) + 1, i + 1) \end{matrix})}^{ε} - 1)

where $G_{i} = (\begin{matrix} - \frac{1}{ε} (β + 1) \\ i \end{matrix}) α^{i}, α > - 1, β > 0 .$

Boekee and Lubba³⁴ developed the $τ -$ entropy measure. It is presented by

H_{τ} (X) = \frac{τ}{τ - 1} (1 - {(\int_{0}^{1} f^{τ - 1} (x) dx)}^{\frac{1}{τ}}), τ > 0 and τ \neq 1 .

Boekee and Lubba entropy of X is given by

H_{τ - ML - II} (X; α; β; τ) = \frac{τ}{τ - 1} (1 - {(\begin{matrix} β^{(τ - 1)} {(α + 1)}^{(τ - 1)} \\ \times \sum_{i = 0}^{\infty} I_{i} B ((τ - 1) (β - 1) + 1, i + 1) \end{matrix})}^{\frac{1}{τ}})

where $I_{i} = (\begin{matrix} - (τ - 1) (β + 1) \\ i \end{matrix}) α^{i}, α > - 1, β > 0 .$

Mathai and Haubold³⁵ generalized the classical Shannon entropy known as $ζ -$ entropy. It is presented by

H_{ζ} (X) = \frac{1}{ζ - 1} (\int_{0}^{1} f^{2 - ζ} (x) dx - 1), ζ > 0 and ζ \neq 1 .

The Mathai and Haubold entropy of X is given by

H_{ζ - ML - II} (X; α; β; ζ) = \frac{1}{ζ - 1} (\begin{matrix} (1 - β^{(2 - ζ)} {(α + 1)}^{(2 - ζ)} \sum_{i = 0}^{\infty} J_{i} B ((2 - ζ) (β - 1) + 1, i + 1)) \\ - 1 \end{matrix})

where $J_{i} = (\begin{matrix} - (2 - ζ) (β + 1) \\ i \end{matrix}) α^{i}, α > - 1, β > 0 .$

Table 2 presents the flexible behavior of the entropy measures for some chosen model parameters for S-VI ( $α = 1.1, β = 2.1$ ), S-VII ( $α = 1.1, β = 1.5$ ), and S-VIII ( $α = 2.1, β = 3.5$ ).

Table 2.

Numerical results of Rényi, Tsallis, Havrda and Charvat, Arimoto, Boekee and Lubba, and Mathai and Haubold entropy measures.

Entropy	Initial value	S-VI	S-VII	S-VIII	Status
Rényi	$δ = 1.1$	9.977	4.330	7.023	Decreasing
	$δ = 1.5$	2.721	1.181	1.915
	$δ = 1.7$	2.203	0.956	1.551
	$δ = 1.9$	1.915	0.831	1.348
Tsallis	$η = 1.1$	0.743	0.340	0.548	Decreasing
	$η = 1.5$	0.322	0.168	0.267
	$η = 1.7$	0.180	0.096	0.154
	$η = 1.9$	0.057	0.031	0.051
Havrda and Charvat	$ω = 1.1$	0.004	0.002	0.004	Increasing
	$ω = 1.5$	0.176	0.095	0.162
	$ω = 1.7$	0.433	0.232	0.405
	$ω = 1.9$	0.899	0.471	0.847
Arimoto	$ε = 1.1$	0.008	0.003	0.005	Increasing
	$ε = 1.5$	0.652	0.161	0.281
	$ε = 1.7$	3.329	0.454	0.824
	$ε = 1.9$	177.609	1.104	2.115
Boekee and Lubba	$τ = 1.1$	0.756	0.344	0.556	Increasing Decreasing
	$τ = 1.5$	0.466	0.233	0.371
	$τ = 1.7$	0.394	0.202	0.321
	$τ = 1.9$	0.343	0.177	0.282
Mathai and Haubold	$ζ = 1.1$	-0.517	-0.283	−0.455	Increasing Decreasing
	$ζ = 1.5$	−0.322	−0.167	−0.266
	$ζ = 1.7$	−0.214	−0.106	−0.169
	$ζ = 1.9$	−0.083	−0.037	−0.061

Estimation

In this section, we estimate the parameters of the ML-II by following the method of MLE as this method provides the maximum information about the unknown model parameters. Let $X_{1}, X_{2}, X_{3}, \dots, X_{n}$ be a random sample of size n from the ML-II, then the likelihood function $L (ϑ) = \prod_{i = 1}^{n} f (x; α; β)$ of X is given by

L_{ML - II} (ϑ) = {(β (α + 1))}^{n} \prod_{i = 1}^{n} \frac{{(1 - x_{i})}^{β - 1}}{{(1 + α x_{i})}^{β + 1}}

The log-likelihood function $Lo g L (ϑ) = l (ϑ)$ of X is

(12)

l_{ML - II} (ϑ) = n (lo g β + lo g (1 + α)) + (β - 1) \sum_{i = 0}^{n} lo g (1 - x_{i}) - (β + 1) \sum_{i = 0}^{n} lo g (1 + α x_{i})

Now, we are concerned about obtaining the MLEs of the ML-II. For this, first, we maximize the Equation (12) and second, we calculate the partial derivatives w.r.t., the unknown parameters ( $α, β$ ) and equate to zero, respectively. The score vector components are given by

U (ϑ) = \frac{\partial l}{∂ϑ} = {(\frac{\partial l}{\partial α}, \frac{\partial l}{\partial β})}^{T}

Partial derivatives w.r.t. $α, β$ are given as follows, respectively

\frac{\partial l_{ML - II}}{∂α} = \frac{n}{1 + α} - (β + 1) \sum_{i = o}^{n} (\frac{x_{i}}{1 + α x_{i}})

\frac{\partial l_{ML - II}}{\partial β} = \frac{n}{β} + \sum_{i = 0}^{n} lo g (1 - x_{i}) - \sum_{i = 0}^{n} lo g (1 + α x_{i})

The last two non-linear equations do not provide the analytical solution for the MLEs and the optimum value of $α$ , and $β$ . The Newton-Raphson (an appropriate) algorithm plays a supportive role in these kinds of ML estimates. Numerical solutions and estimates of the parameters are calculated using R version 3.6.2 (statistical software).

Simulation

In this sub-section, to observe the asymptotic performance of MLE's $\hat{φ} = (\hat{α}, \hat{β})$ , we discuss the following algorithm.

Step - 1: A random sample x₁, x₂, x₃ , ..., x_n of sizes n = 150, 200, 250, 300, 350, 400, 450, and 500 from Equation (5).

Step - 2: The required results are obtained based on the different combinations of the model parameters placed in S-IX ( $α$ = 3.2, $β$ = 2.5), S-X ( $α$ = 0.2, $β$ = 0.9), and S-XI ( $α$ = 0.2, $β$ = 1.5).

Step - 3: Results of mean, variance (Var.), bias, mean square error (MSE), coverage probability (CP), and average width (AW) are calculated via nlmib in R. These results are presented in Tables 3 to 8.

Table 3.

Mean, variance (Var.), bias, mean square error (MSE), coverage probability (CP), and average width (AW) of ( $α$ ) for S-IX.

Sample	Mean	Var.	Bias	MSE	CP	AW
150	3.126	2.822	−0.074	1.681	0.912	6.383
200	3.157	2.262	−0.043	1.505	0.915	5.527
250	3.163	1.823	−0.036	1.351	0.915	4.931
300	3.142	1.442	−0.058	1.202	0.919	4.469
350	3.155	1.211	−0.045	1.101	0.928	4.137
400	3.155	1.109	−0.046	1.054	0.922	3.867
450	3.155	0.956	−0.045	0.979	0.929	3.942
500	3.174	0.843	−0.026	0.919	0.929	3.463

Table 4.

Mean, variance (Var.), bias, mean square error (MSE), coverage probability (CP), and average width (AW) of ( $β$ ) for S-IX.

Sample	Mean	Var.	Bias	MSE	CP	AW
150	2.964	1.664	0.464	1.370	0.950	4.491
200	2.835	1.066	0.334	1.085	0.936	3.397
250	2.759	0.743	0.259	0.900	0.942	2.809
300	2.713	0.520	0.213	0.752	0.956	2.431
350	2.669	0.382	0.169	0.641	0.951	2.148
400	2.652	0.319	0.152	0.585	0.950	1.974
450	2.632	0.257	0.133	0.524	0.954	1.823
500	2.607	0.209	0.107	0.471	0.953	1.693

Table 5.

Mean, variance (Var.), bias, mean square error (MSE), coverage probability (CP), and average width (AW) of ( $α$ ) for S-X.

Sample	Mean	Var.	Bias	MSE	CP	AW
150	0.255	0.083	0.055	0.293	1.000	1.432
200	0.247	0.069	0.048	0.267	0.998	1.218
250	0.236	0.058	0.036	0.243	0.996	1.070
300	0.223	0.046	0.023	0.216	0.997	0.962
350	0.218	0.040	0.018	0.201	0.996	0.883
400	0.216	0.037	0.015	0.193	0.990	0.824
450	0.211	0.s033	0.011	0.182	0.994	0.772
500	0.211	0.031	0.011	0.175	0.992	0.730

Table 6.

Mean, variance (Var.), bias, mean square error (MSE), coverage probability (CP), and average width (AW) of ( $β$ ) for S-X.

Sample	Mean	Var.	Bias	RMSE	CP	AW
150	0.906	0.013	0.006	0.115	0.970	0.587
200	0.904	0.011	0.004	0.104	0.954	0.499
250	0.906	0.009	0.006	0.095	0.957	0.442
300	0.906	0.008	0.006	0.088	0.969	0.401
350	0.906	0.007	0.006	0.081	0.969	0.369
400	0.905	0.006	0.005	0.078	0.968	0.345
450	0.906	0.005	0.006	0.075	0.971	0.324
500	0.9050	0.005	0.005	0.072	0.960	0.306

Table 7.

Mean, variance (Var.), bias, mean square error (MSE), coverage probability (CP), and average width (AW) of ( $α$ ) for S-XI.

Sample	Mean	Var.	Bias	MSE	CP	AW
150	0.263	0.097	0.064	0.319	1.00	1.633
200	0.254	0.082	0.054	0.291	0.998	1.382
250	0.243	0.068	0.043	0.264	0.995	1.211
300	0.228	0.055	0.028	0.235	0.998	1.087
350	0.222	0.047	0.022	0.219	0.996	0.996
400	0.219	0.044	0.019	0.211	0.994	0.928
450	0.214	0.039	0.014	0.198	0.993	0.869
500	0.213	0.036	0.013	0.191	0.988	0.821

Table 8.

Mean, variance (Var.), bias, mean square error (MSE), coverage probability (CP), and average width (AW) of ( $β$ ) for S-XI.

Sample	Mean	Var.	Bias	MSE	CP	AW
150	1.509	0.052	0.009	0.227	0.957	1.335
200	1.508	0.045	0.008	0.208	0.945	1.125
250	1.511	0.037	0.011	0.194	0.954	0.992
300	1.513	0.032	0.013	0.180	0.963	0.898
350	1.513	0.028	0.013	0.168	0.965	0.824
400	1.512	0.026	0.013	0.163	0.960	0.768
450	1.514	0.024	0.015	0.156	0.966	0.722
500	1.512	0.022	0.012	0.149	0.958	0.680

Step - 4: Each sample is replicated 1000 times.

Step - 5: A gradual decrease with the increase in sample size is observed in mean, biases, MSEs, and Var.

Step - 6: CPs of all the parameters $φ = (α, β)$ are approximately 0.975, approaching the nominal value, and AW decreases when sample sizes increases.

Furthermore, the frequent use of the measures in the development of average estimate (AE), bias, MSE, CP, AW, are given as follows:

AE (\hat{φ}) = \frac{1}{N} \sum_{i = 1}^{N} \hat{φ}, Var (\hat{φ}) = \frac{1}{N} \sum_{i = 1}^{N} {(φ - {\bar{φ}}_{i})}^{2}, Bias (\hat{φ}) = \frac{1}{N} \sum_{i = 1}^{N} ({\hat{φ}}_{i} - φ)

MSE (\hat{φ}) = \frac{1}{N} \sum_{i = 1}^{N} {({\hat{φ}}_{i} - φ)}^{2}, CP (\hat{φ}) = \sum_{i = 1}^{N} I ({\hat{φ}}_{i} - 0.975 {se}_{{\hat{φ}}_{i}}, {\hat{φ}}_{i} + 0.975 {se}_{{\hat{φ}}_{i}}), and

AW (\hat{φ}) = \frac{1}{N} \sum_{i = 1}^{N} |({\hat{φ}}_{i} + 0.975) - ({\hat{φ}}_{i} - 0.975)|

Application

In this section, we explore the application of ML-II in medical science and engineering data. For this, we consider two lifetime datasets. The first dataset was originally reported by Smithson and Verkuilen.³⁶ They studied a group of 166 healthy women's anxiety performance, i.e., outside of a pathological clinical setting, from Townsville, Queensland, Australia; data points are 0.01, 0.17, 0.01, 0.05, 0.09, 0.41, 0.05, 0.01, 0.13, 0.01, 0.05, 0.17, 0.01, 0.09, 0.01, 0.05, 0.09, 0.09, 0.05, 0.01, 0.01, 0.01, 0.29, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.09, 0.37, 0.05, 0.01, 0.05, 0.29, 0.09, 0.01, 0.25, 0.01, 0.09, 0.01, 0.05, 0.21, 0.01, 0.01, 0.01, 0.13, 0.17, 0.37, 0.01, 0.01, 0.09, 0.57, 0.01, 0.01, 0.13, 0.05, 0.01, 0.01, 0.01, 0.01, 0.09, 0.13, 0.01, 0.01, 0.09, 0.09, 0.37, 0.01, 0.05, 0.01, 0.01, 0.13, 0.01, 0.57, 0.01, 0.01, 0.09, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.05, 0.01, 0.01, 0.01, 0.13, 0.01, 0.25, 0.01, 0.01, 0.09, 0.13, 0.01, 0.01, 0.05, 0.13, 0.01, 0.09, 0.01, 0.05, 0.01, 0.05, 0.01, 0.09, 0.01, 0.37, 0.25, 0.05, 0.05, 0.25, 0.05, 0.05, 0.01, 0.05, 0.01, 0.01, 0.01, 0.17, 0.29, 0.57, 0.01, 0.05, 0.01, 0.09, 0.01, 0.09, 0.49, 0.45, 0.01, 0.01, 0.01, 0.05, 0.01, 0.17, 0.01, 0.13, 0.01, 0.21, 0.13, 0.01, 0.01, 0.17, 0.01, 0.01, 0.21, 0.13, 0.69, 0.25, 0.01, 0.01, 0.09, 0.13, 0.01, 0.05, 0.01, 0.01, 0.29, 0.25, 0.49, 0.01,0.01.

The second dataset was recently reported by Rahman et al.³⁷ They studied the lifetime (in days) of 30 electronic devices and the dataset was as follows: 0.020, 0.029, 0.034, 0.044, 0.057, 0.096, 0.106, 0.139, 0.156, 0.164, 0.167, 0.177, 0.250, 0.326, 0.406, 0.607, 0.650, 0.672, 0.676, 0.736, 0.817, 0.838, 0.910, 0.931, 0.946, 0.953, 0.961, 0.981, 0.982, 0.990.

The ML-II is compared with its competing models (presented in Table 9) based on a series of criteria, namely, -Log-likelihood (-LL), Akaike information criterion (AIC), Bayesian information criterion (BIC), consistent Akaike information criterion (CAIC), and Kolmogorov Smirnov test (K-S) test statistics. Table 10 presents a set of descriptive statistics and Tables 11 and 12 present the parameter estimates and standard errors (in parenthesis) along the goodness-of-fit test. As seen in Tables 11 and 12, the performance of the ML-II abundantly satisfies the criteria of a better fit model. Consequently, we declare that the ML-II is a better fit among all competing models on the anxiety in women data. Moreover, Figures 5 and 6 present the empirically fitted plots comprising PDF (a), CDF (b), Kaplan-Meier Survival (c), Probability-Probability (P-P) (d), Box (e), and total test time (TTT) (f) plots (see Aarset³⁸), which confirm the close fit to the data as well.

Figure 5.

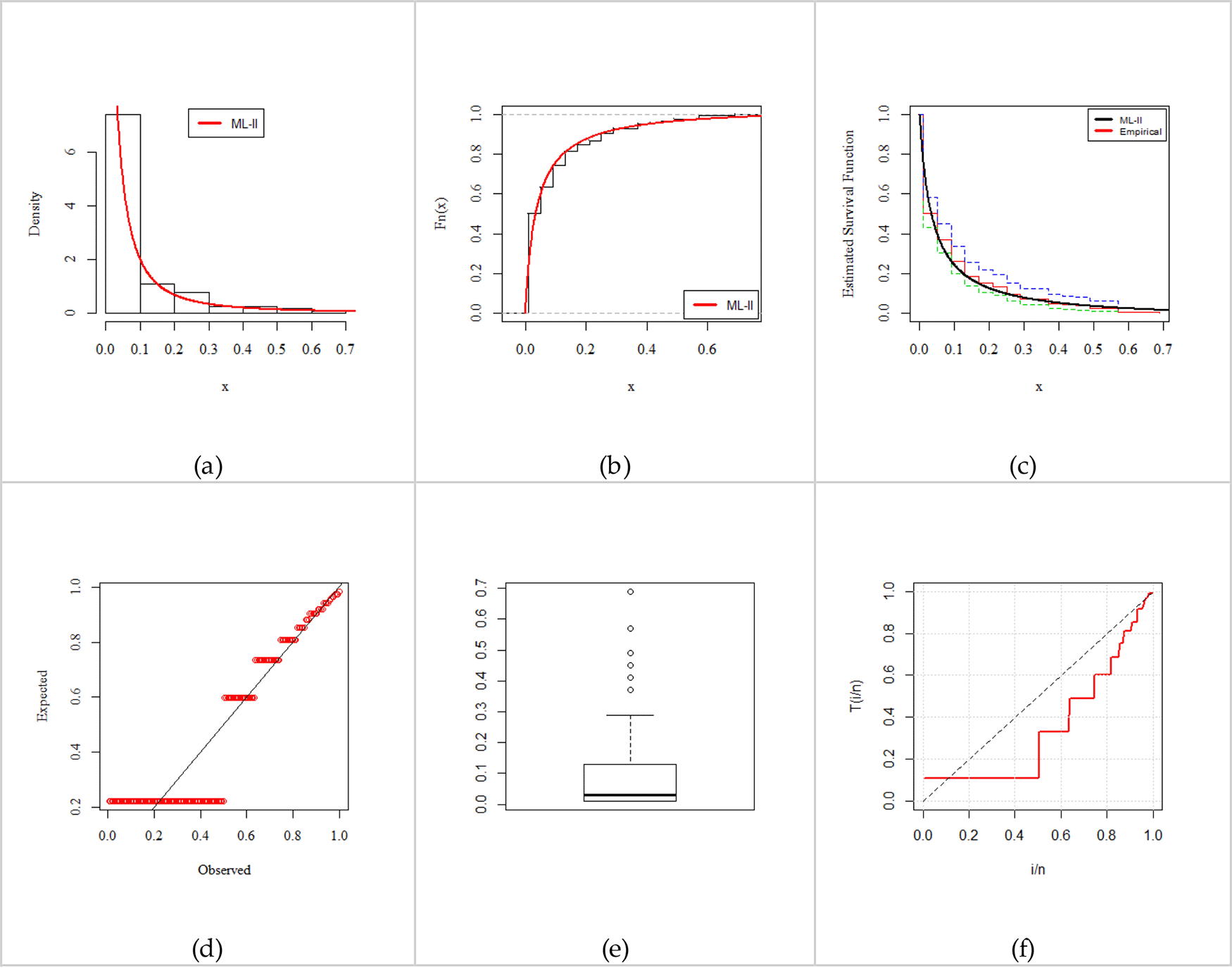
Fitted Probability density function (PDF) (a), Cumulative distribution function (CDF) (b), Kaplan-Meier survival (c), Probability – Probability (PP) (d), Box (e), and Total Test Time (TTT) (f) Plots for women’s anxiety data.

Figure 6.

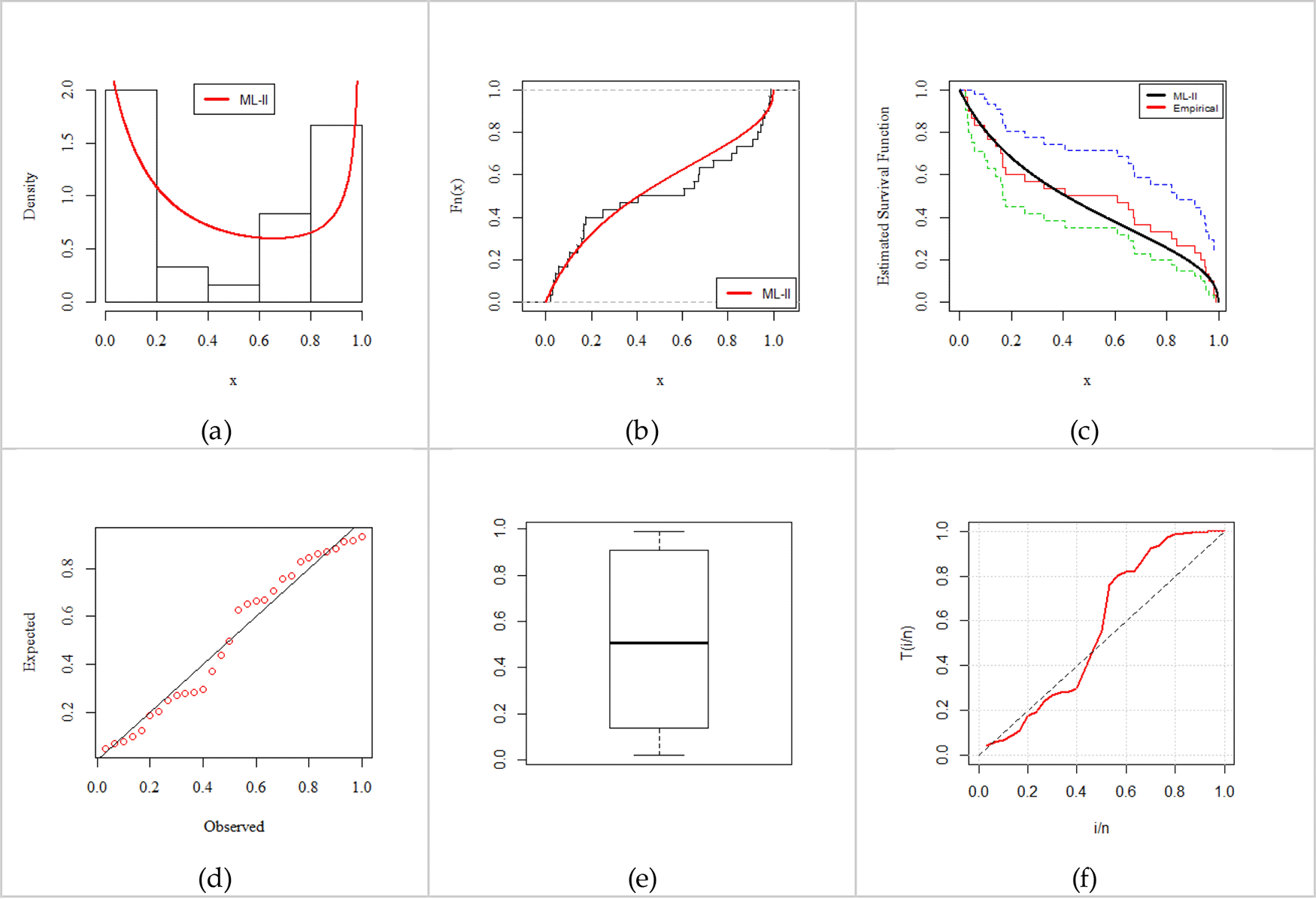
Fitted Probability density function (a), Cumulative distribution function (b), Kaplan-Meier survival (c), Probability-Probability (d), Box (e), and Total Test Time (f) Plots for 30 electronic devices data.

Table 9. Competitive models Cumulative distribution functions (cdfs).

Kum = Kumaraswamy distribution ; L–I = Lehmann type I distribution; L–II = Lehmann type II distribution ; T-Kum = transmuted Kumaraswamy distribution ; Mostafa type-II distribution ; T-GPW = transmuted generalized power Weibull distribution; T-Lin = transmuted Lindley distribution.

Abbreviations	Model	Parameter/variable range	Reference
Kum	$G_{I} (x; α; β) = 1 - {(1 - x^{α})}^{β}$	$α, β > 0,$ 0 < x < 1	Kumaraswamy³⁹
L-I	$G_{II} (x; α) = x^{α}$	$α > 0,$ 0 < x < 1	Lehmann¹
L-II	$G_{III} (x; α) = 1 - {(1 - x)}^{α}$	$α > 0,$ 0 < x < 1	Lehmann¹
T-Kum	$G_{IV} (x; α; β; ε) = (1 + ε) (1 - {(1 - x^{α})}^{β}) -$ $ε {(1 - {(1 - x^{α})}^{β})}^{2}$	$α, β > 0,$ $\|ε\| \leq 1$ x > 0	Khan et al.⁴⁰
MT-II	$G_{V} (x; α) = exp (x^{α} log 2) - 1$	$α > 0,$ 0 < x < 1	Muhammad⁴¹
T-GPW	$G_{VI} (x; α; β; ε) = (1 + ε) (1 - e^{{(1 - (1 + x^{α}))}^{β}}) -$ $ε {(1 - e^{{(1 - (1 + x^{α}))}^{β}})}^{2}$	$α, β > 0$ , $\|ε\| \leq 1$ , x > 0	Khan⁴²
T-Lin	$G_{VII} (x; α) = (1 + ε) (1 - \frac{1 + α + αx}{1 + α} e^{(- αx)}) - ε {(1 - \frac{1 + α + αx}{1 + α} e^{(- αx)})}^{2},$	$α > 0$ $\|ε\| \leq 1,$ x > 0	Khan et al.⁴³

Table 10. Descriptive statistics.

Data	Minimum	1^st Quart	Mean	3^rd Quart	Skewness	Kurtosis	95% C.I.	Maximum
Women’s anxiety	0.010	0.010	0.091	0.130	2.212	7.959	(0.071,0.112)	0.690
Electronic devices	0.020	0.143	0.494	0.892	0.062	1.312	(0.353,0.634)	0.990

Table 11. Maximum likelihood estimations with standard errors (in parenthesis) and goodness of fit for the women’s anxiety data.

Model	$\hat{α}$	$\hat{β}$	$\hat{ε}$	-LL	AIC	BIC	HQIC	K-S
ML-II	27.793 (7.857)	0.988 (0.154)	−	−258.657	−513.315	−507.091	−510.788	0.276
T-GPW	0.780 (0.046)	5.898 (1.005)	0.453 (0.213)	−250.605	−495.210	−485.874	−491.420	0.292
T-Kum	0.703 (0.048)	3.805 (0.688)	0.569 (0.178)	−247.915	−489.831	−480.495	−486.041	0.290
Kum	0.642 (0.045)	4.473 (0.582)	−	−244.314	−484.629	−478.405	−482.103	0.287
T-Lin	9.434 (0.960)	−	0.555 (0.124)	−239.783	−475.565	−469.341	−473.039	0.376
L-II	9.082 (0.705)	−	−	−218.538	−435.077	−431.965	−433.814	0.412
L-I	0.299 (0.023)	−	−	−187.727	−373.454	−370.342	−372.191	0.270

Table 12. Maximum likelihood estimations (MLEs) with standard errors (in parenthesis) and goodness of fit for the lifetime (in days) of 30 electronic devices data.

Model	$\hat{α}$	$\hat{β}$	$\hat{ε}$	-LL	AIC	BIC	HQIC	K-S
ML-II	4.852 (3.842)	0.428 (0.115)	−	−4.401	−4.802	−2.000	−3.906	0.128
T-Kum	0.609 (0.178)	0.585 (0.174)	0.125 (0.495)	−3.534	−1.069	3.134	0.276	0.409
Kum	0.587 (0.161)	0.611 (0.134)	−	−3.502	−3.005	−0.203	−2.108	0.385
L-II	0.780 (0.142)	−	−	−1.00	−0.007	1.393	0.440	0.029
L-I	0.816 (0.149)	−	−	−0.659	0.680	2.081	1.128	0.189
MT-II	0.700 (0.139)	−	−	−1.056	−0.113	1.287	0.334	0.253

Conclusion

We developed a potentiated lifetime model that exhibited the bathtub-shaped failure rate and addressed the most efficient and consistent results over complex random phenomena in this article. We called the proposed model a modified Lehmann type II (ML-II) model because it was a modified version of the Lehmann type II model. Several structural and reliability measures were developed and discussed. We used the maximum likelihood estimation method to estimate model parameters, and we also ran a simulation study to investigate the asymptotic performance of the MLEs. Data on anxiety in women from Smithson and Verkuilen³⁶ and data on 30 electronic devices from Rahman et al.,³⁷ were modeled to reveal the dominance ML-II over its competitors. It is hoped that in the future, the ML-II will be regarded as a superior alternative to the baseline model.

Data availability

Figshare: two_dataset.doc, https://doi.org/10.6084/m9.figshare.14903142.⁴⁵

This project contains the following extended data:

• Smithson and Verkuilen dataset: anxiety test scores from a group of 166 healthy women
• Rahman et al., dataset: lifetime (in days) of 30 electronic devices

The authors of this work sought and obtained consent to use the dataset from the respective authors. The dataset from Smithson and Verkuilen³⁷ was originally published on Smithson's website and saved under Example 2.text. Rahman et al.'s dataset is available in their publication.³⁸ The dataset was published in an open repository with the authors' permission.

Grant information

This work was supported by Digiteknologian TKI-ymparisto project A74338 (ERDF, Regional Council of Pohjois-Savo).

Competing interests

No competing interests were disclosed.

References

1. Lehmann EL: The power of rank tests. Ann. Math. Stat. 1953; 24: 23–43. Publisher Full Text
2. Gupta RC, Gupta P, Gupta RD: Modeling failure time data by Lehmann alternatives. Communications in Statistics-Theory and Methods. 1998; 27: 887–904. Publisher Full Text
3. Cordeiro GM, De Castro M: A new family of generalized distributions. J. Stat. Comput. Simul. 2011; 81: 883–893. Publisher Full Text
4. Arshad MZ, Iqbal MZ, Anees A, et al.: New Bathtub Shaped Failure Rate Model: Properties, and Applications to Engineering Sector. Pak. J. Statist. 2021; 37: 57–80.
5. Arshad MZ, Iqbal MZ, Ahmad M: Exponentiated Power Function Distribution: Properties and Applications. JSTA. 2020; 19: 297–313. Publisher Full Text
6. Awodutire PO, Nduka EC, Ijomah MA: Lehmann Type II Generalized Half Logistic Distribution: Properties and Application. Mathematical Theory and Modeling . 2020; 10: 103–115.
7. Akilandeswari VS, Poornima R, Saavithri V: Lehmann-Type Laplace distribution-Type I software reliability growth model. OPSEARCH . 2016; 54: 233–259.
8. Dallas AC: Characterization of Pareto and power function distribution. Ann. Math. Stat. 1976; 28: 491–497. Publisher Full Text
9. Meniconi M, Barry D: The power function distribution: A useful and simple distribution to assess electrical component reliability. Microelectron Reliab. 1996; 36: 1207–1212. Publisher Full Text
10. Chang SK: Characterizations of the power function distribution by the independence of record values. J. Chungcheong Math Soc. 2007; 20: 139–146.
11. Tavangar M: Power function distribution characterization by dual generalized order statistics. JIRSS. 2011; 10: 13–27.
12. Cordeiro GM, Brito RDS: The beta power distribution. Braz. J. Probab. 2012; 26: 88–112. Publisher Full Text
13. Ahsanullah M, Shakil M, Golam-Kibria BMG: A characterization of the power function distribution based on lower records. ProbStat. Forum. 2013; 6: 68–72.
14. Zaka A, Akhter AS, Farooqi N: Methods for estimating the parameters of the power function distribution. J. Stat. 2014; 21: 90–102. Publisher Full Text
15. Tahir MH, Alizadeh M, Mansoor M, et al.: The Weibull power function distribution with applications. Hacettepe J. Math. Stat. 2014; 45: 245–265. Publisher Full Text
16. Shahzad MN, Asghar Z, Shehzad F, et al.: Parameter estimation of power function distribution with TL-moments. Rev. Colomb. Estad. 2015; 38: 321–334. Publisher Full Text
17. Ahsan-ul-Haq M, Butt NS, Usman RM, et al.: Transmuted power function distribution. Gazi univ. j. sci. 2016; 29: 177–185.
18. Okorie IE, Akpanta AC, Ohakwe J: Marshall-Olkin extended power function distribution. EJPS. 2017; 5: 16–29. Publisher Full Text
19. Marshall AW, Olkin I: A new method for adding a parameter to a family of distributions with applications to the exponential and Weibull families. Biometrika . 1997; 84: 641–652. Publisher Full Text
20. Usman RM, Ahsan-ul-Haq M, Bursa N, et al.: Exponentiated Transmuted Power Function Distribution: Theory & Applications. Gazi Univ. J. Sci. 2018; 31: 660–675. Publisher Full Text
21. Hassan A, Elshrpieny E, Mohamed R: Odd generalized exponential power function distribution. Gazi Univ. J. Sci. 2019; 32: 351–370.
22. Tahir MH, Cordeiro GM, Alizadeh M, et al.: The odd generalized exponential family of distributions with applications. JSDA. 2015; 2: 1–28. Publisher Full Text
23. Zaka A, Akhter AS, Jabeen R: The new reflected power function distribution: Theory, simulation & application. AIMS Mathematics . 2020; 5: 5031–5054. Publisher Full Text
24. Al-Mutairi AO: Transmuted Weighted Power Function Distribution. Pak. J. Statist. 2017; 33: 491–498.
25. Balogun OS, Iqbal MZ, Arshad MZ, et al.: A new generalization of Lehmann type-II distribution: Theory, simulation, and applications to survival and failure rate data. Scientific African . 2021; 12: 1–13. Publisher Full Text
26. Balogun OS, Arshad MZ, Iqbal MZ, et al.: A new modified Lehmann type – II G class of distributions: exponential distribution with theory, simulation, and applications to engineering sector. F1000 Res. 2021. Publisher Full Text
27. Bowley AL: Elements of Statistics . 4th ed. New York, USA: Charles Scribner; 1920.
28. Moors JJA: A quantile alternative for kurtosis. J. R. Stat. Soc., Ser. D Stat. 1998; 37: 25–32. Publisher Full Text
29. Hyndman RJ, Fan Y: Sample quantile in statistical packages. Amer. Statist. 1996; 50: 361–365. Publisher Full Text
30. Rényi A: On measures of entropy and information, 4th Fourth Berkeley Symposium on Mathematical Statistics and Probability . Berkeley, USA: University of California Press; 1961; 547–561.
31. Tsallis C: Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988; 52: 479–487. Publisher Full Text
32. Havrda J, Charvat FS: Quantification method of classification processes: Concept of structural-entropy. Kybernetika . 1967; 3: 30–35.
33. Arimoto S: Information theoretical considerations on estimation theory. Inf. Control. 1971; 73: 181–190. Publisher Full Text
34. Boekee E, Van Der Lubbe JCA: The R-norm information measure. Inf. Control. 1980; 45: 136–155. Publisher Full Text
35. Mathai AM, Haubold HJ: On a Generalized Entropy Measure Leading to the Pathway Model with a Preliminary Application to Solar Neutrino Data. Entropy . 2013; 15: 4011–4025. Publisher Full Text
36. Smithson M, Verkuilen J: A better lemon-squeezer? Maximum likelihood regression with beta distributed dependent variables. Psycholog. Meth. 2006; 11: 54–71. PubMed Abstract | Publisher Full Text
37. Rahman MM, Al-Zahrani B, Shahbaz SH, et al.: Cubic Transmuted Uniform Distribution: An Alternative to Beta and Kumaraswamy Distributions. EJPAM . 2019; 12: 1106–1121. Publisher Full Text
38. Aarset MV: How to identify bathtub hazard rate. IEEE. Trans. Reliab. 1987; 36: 106–108. Publisher Full Text
39. Kumaraswamy P: A generalized probability density function for double-bounded random processes. J. Hydrol. 1980; 46: 79–88. Publisher Full Text
40. Khan MS, King R, Hudson IL: Transmuted Kumaraswamy distribution. SiT. 2016; 17: 1–28. Publisher Full Text
41. Muhammad M: A New Lifetime Model with a Bounded Support. Asian J. Math. 2017; 7: 1–11. Publisher Full Text
42. Khan MS: Transmuted Generalized Power Weibull Distribution. Thailand. Stat. 2018; 16: 156–172.
43. Khan MS, King R, Hudson IL: Some Structural Properties of the Transmuted Lindley Distribution with Application to Women's Anxiety Data. JPSS . 2018; 16: 69–80.
44. Iqbal MZ, et al.: Two_dataset.doc. figshare. Dataset. 2021. Publisher Full Text

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 17 Aug 2021

Author details Author details

¹ Department of Mathematics and Statistics, University of Agriculture, Faisalabad, Faisalabad, Punjab, 38000, Pakistan
² Department of Statistics, Hacettepe University, Ankara, Ankara, Turkey
³ School of Computing, University of Eastern Finland, Kuopio, 70211, Finland

Muhammad Zafar Iqbal
Roles: Conceptualization, Data Curation, Writing – Original Draft Preparation, Writing – Review & Editing

Muhammad Zeshan Arshad
Roles: Conceptualization, Data Curation, Methodology, Software, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Gamze Özel
Roles: Conceptualization, Investigation, Writing – Original Draft Preparation, Writing – Review & Editing

Oluwafemi Samson Balogun
Roles: Conceptualization, Funding Acquisition, Writing – Original Draft Preparation, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

This work was supported by Digiteknologian TKI-ymparisto project A74338 (ERDF, Regional Council of Pohjois-Savo).
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (1)

version 1

Published: 17 Aug 2021, 10:823

https://doi.org/10.12688/f1000research.54305.1

Copyright

© 2021 Iqbal MZ et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

Iqbal MZ, Arshad MZ, Özel G and Balogun OS. A better approach to discuss medical science and engineering data with a modified Lehmann Type – II model [version 1; peer review: 2 approved with reservations]. F1000Research 2021, 10:823 (https://doi.org/10.12688/f1000research.54305.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 1

VERSION 1

PUBLISHED 17 Aug 2021

Views

0

Reviewer Report 10 Sep 2024

Matthew Iwada Ekum, Lagos State University of Science and Technology, Ikorodu, Lagos, Nigeria

Approved with Reservations

https://doi.org/10.5256/f1000research.57782.r314601

Research Paper Review
The authors' work title is appropriate as “A better approach to discuss medical science and engineering data with a modified Lehmann Type – II model”. The work is well organized and follows a logical sequence as ... Continue reading

Research Paper Review
The authors' work title is appropriate as “A better approach to discuss medical science and engineering data with a modified Lehmann Type – II model”. The work is well organized and follows a logical sequence as expected. However, the following comments are very necessary and important before the paper can be indexed.

The literature review, especially the empirical review needs more work on Power Function distribution and its applications. So, it is advisable to include more empirical works in the study to strengthen the background of the study. See the following work.
Ref 1, Ref 2 , Ref 3, Ref 4
Write the objective in prose. Do not itemize it; it is not a seminar paper or project.
Explain who would benefit from this study, i.e. the significance of the Study. Include this after the objectives, before the last paragraph.
Major properties and characterization of the distributions have been established but to improve this work as a specific distribution from a new family, you are expected to show the stochastic ordering of the distribution. Also, show the relationship of this distribution with existing distributions or at least how it can be transformed to its parent distributions. See this work for a guide Ref 5
Also include areas of further study such as its regression model and inferences using the new distribution. See this distribution. See this paper as an example of a further study Ref 6
This present work developed a new distribution by combining Power Function (PF) distribution with Lehmann Type II. All the suggested references are based on combining PF with other distributions. So, they can have more arguments to support the usefulness of PF.The stochastic ordering is very important for a new distribution. I also referred the authors to a work where stochastic ordering was used as a guide. They may decide to use other materials as guide for the stochastic ordering. The stochastic ordering is very important.The essence of developing a model is to apply it in Statistical inferences like regression and hypothesis testing using real life data. So, even if this present work does not extend to regression model, suggestions can be given to extend it to regression in further studies. Normal-PF was also shown as an example.

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

References

1. A, Eno Adeleke, I.A, Matthew: Lambda Upper Bound Distribution: Some Properties and Applications. ResearchGate. 2020.
2. E, Matthew A, Muminu Adeleke, I.A., Eno A, et al.: Class of Generalized Power Function Distributions: Properties and Applications. ResearchGate. 2021. 48-27
3. Ekum M, Akarawak E, Adamu M: Optimization of Gamma–Power–Log–logistic distribution and its applications in modelling volume of oil spillage. Scientific African. 2023; 21. Publisher Full Text
4. E, Matthew K, Mundher O, Adeyinka. A, et al.: Normal-Power Function Distribution with Logistic Quantile Function: Properties and Application. ResearchGate. 2021. 90-101
5. Ekum M, Adamu M, Akarawak E: T-Dagum: A Way of Generalizing Dagum Distribution Using Lomax Quantile Function. Journal of Probability and Statistics. 2020; 2020: 1-17 Publisher Full Text
6. Ekum M, Adamu M, Akarawak E: Normal-Power-Logistic Distribution: Properties and Application in Generalized Linear Model. Journal of the Indian Society for Probability and Statistics. 2022; 24 (1): 23-54 Publisher Full Text

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Probability distributions and Linear model. Theory and applications.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Respond or Comment

Views

6

Reviewer Report 17 Jan 2022

Lazhar Benkhelifa, Department of Mathematics and Informatics, Larbi Ben M’Hidi University, Oum El Bouaghi, Algeria

Approved with Reservations

https://doi.org/10.5256/f1000research.57782.r119893

The linear representations of CDF and PDF are based on some infinite sums. The authors need to prove that these sums converge for all or some values of the parameters.
In page

The linear representations of CDF and PDF are based on some infinite sums. The authors need to prove that these sums converge for all or some values of the parameters.
In page 6, it is better to present the proofs of the propositions 1 and 2.
In page 6, is it possible to give mathematical proof about the shapes of the pdf and hazard rate function?
In pages 7-8, what are the ranges of the skewness and kurtosis for the new model?
In order to check the accuracy of the expressions of the rth moments, the authors need to compare the obtained results with the numerical results based on Monte Carlo approximations.
The authors need to show that the introduced distribution is identifiable with respect to parameter vector ϑ=(α,β)^{T}.
The authors discussed only one estimation methods. Can they attempt others estimation methods and compare their performances?
The description of the estimation procedure is a little bit too brief. It would be good to expand on the algorithm used to estimate the model parameters (are they using a Newton-Raphson algorithm with the exact Hessian matrix?).
The likelihood equations are given in page 15. Obviously, they have not got an explicit solution and the MLE must be numerically calculated. At this point, the authors should do a study (theoretical or at least numerical): have these equations always got a solution? if so, is it unique? In this context, the authors must give more details about this issue, considering some plots of the log-likelihood (profile log-likelihood) function.
Confidence intervals for the parameters were based on asymptotic normality. In page 15, the authors should add the asymptotic normality of ϑ=(α,β)^{T}. Also, the authors should add the interval estimates for ϑ in real data sets.
At the end of Section (Application), more information about the numerical computation will be useful. For example, does the procedure involve iteration and/or initialization? What statistical package was used to obtain the results in this paper?
The comparison between the AIC, BIC and CAIC are important but not sufficient to decide between one or another distribution. The authors should use the Cramer-von Mises and Anderson-Darling statistics with their p-values to decide which is the best distribution.
A standard tool to evaluate the fit of a distribution is the P-P plot. Add this plot, in the application section.
In practice, much lifetime data is subject to censoring, but there is no discussion of this.
At least a short discussion on the estimation under Bayesian paradigm would be really nice. This would really strengthen the content of the paper.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests: No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Respond or Comment

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 17 Aug 2021

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 1 17 Aug 21	read	read

Lazhar Benkhelifa, Larbi Ben M’Hidi University, Oum El Bouaghi, Algeria
Matthew Iwada Ekum, Lagos State University of Science and Technology, Ikorodu, Nigeria

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

Back to all reports

Reviewer Report

0 Views

10 Sep 2024 | for Version 1

Matthew Iwada Ekum, Lagos State University of Science and Technology, Ikorodu, Lagos, Nigeria

0 Views Cite this report Responses(0)

Approved With Reservations

Research Paper Review
The authors' work title is appropriate as “A better approach to discuss medical science and engineering data with a modified Lehmann Type – II model”. The work is well organized and follows a logical sequence as expected. However, the following comments are very necessary and important before the paper can be indexed.

The literature review, especially the empirical review needs more work on Power Function distribution and its applications. So, it is advisable to include more empirical works in the study to strengthen the background of the study. See the following work.
Ref 1, Ref 2 , Ref 3, Ref 4
Write the objective in prose. Do not itemize it; it is not a seminar paper or project.
Explain who would benefit from this study, i.e. the significance of the Study. Include this after the objectives, before the last paragraph.
Major properties and characterization of the distributions have been established but to improve this work as a specific distribution from a new family, you are expected to show the stochastic ordering of the distribution. Also, show the relationship of this distribution with existing distributions or at least how it can be transformed to its parent distributions. See this work for a guide Ref 5
Also include areas of further study such as its regression model and inferences using the new distribution. See this distribution. See this paper as an example of a further study Ref 6
This present work developed a new distribution by combining Power Function (PF) distribution with Lehmann Type II. All the suggested references are based on combining PF with other distributions. So, they can have more arguments to support the usefulness of PF.The stochastic ordering is very important for a new distribution. I also referred the authors to a work where stochastic ordering was used as a guide. They may decide to use other materials as guide for the stochastic ordering. The stochastic ordering is very important.The essence of developing a model is to apply it in Statistical inferences like regression and hypothesis testing using real life data. So, even if this present work does not extend to regression model, suggestions can be given to extend it to regression in further studies. Normal-PF was also shown as an example.

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

References

1. A, Eno Adeleke, I.A, Matthew: Lambda Upper Bound Distribution: Some Properties and Applications. ResearchGate. 2020.
2. E, Matthew A, Muminu Adeleke, I.A., Eno A, et al.: Class of Generalized Power Function Distributions: Properties and Applications. ResearchGate. 2021. 48-27
3. Ekum M, Akarawak E, Adamu M: Optimization of Gamma–Power–Log–logistic distribution and its applications in modelling volume of oil spillage. Scientific African. 2023; 21. Publisher Full Text
4. E, Matthew K, Mundher O, Adeyinka. A, et al.: Normal-Power Function Distribution with Logistic Quantile Function: Properties and Application. ResearchGate. 2021. 90-101
5. Ekum M, Adamu M, Akarawak E: T-Dagum: A Way of Generalizing Dagum Distribution Using Lomax Quantile Function. Journal of Probability and Statistics. 2020; 2020: 1-17 Publisher Full Text
6. Ekum M, Adamu M, Akarawak E: Normal-Power-Logistic Distribution: Properties and Application in Generalized Linear Model. Journal of the Indian Society for Probability and Statistics. 2022; 24 (1): 23-54 Publisher Full Text

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Probability distributions and Linear model. Theory and applications.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

6 Views

17 Jan 2022 | for Version 1

Lazhar Benkhelifa, Department of Mathematics and Informatics, Larbi Ben M’Hidi University, Oum El Bouaghi, Algeria

6 Views Cite this report Responses(0)

Approved With Reservations

The linear representations of CDF and PDF are based on some infinite sums. The authors need to prove that these sums converge for all or some values of the parameters.
In page 6, it is better to present the proofs of the propositions 1 and 2.
In page 6, is it possible to give mathematical proof about the shapes of the pdf and hazard rate function?
In pages 7-8, what are the ranges of the skewness and kurtosis for the new model?
In order to check the accuracy of the expressions of the rth moments, the authors need to compare the obtained results with the numerical results based on Monte Carlo approximations.
The authors need to show that the introduced distribution is identifiable with respect to parameter vector ϑ=(α,β)^{T}.
The authors discussed only one estimation methods. Can they attempt others estimation methods and compare their performances?
The description of the estimation procedure is a little bit too brief. It would be good to expand on the algorithm used to estimate the model parameters (are they using a Newton-Raphson algorithm with the exact Hessian matrix?).
The likelihood equations are given in page 15. Obviously, they have not got an explicit solution and the MLE must be numerically calculated. At this point, the authors should do a study (theoretical or at least numerical): have these equations always got a solution? if so, is it unique? In this context, the authors must give more details about this issue, considering some plots of the log-likelihood (profile log-likelihood) function.
Confidence intervals for the parameters were based on asymptotic normality. In page 15, the authors should add the asymptotic normality of ϑ=(α,β)^{T}. Also, the authors should add the interval estimates for ϑ in real data sets.
At the end of Section (Application), more information about the numerical computation will be useful. For example, does the procedure involve iteration and/or initialization? What statistical package was used to obtain the results in this paper?
The comparison between the AIC, BIC and CAIC are important but not sufficient to decide between one or another distribution. The authors should use the Cramer-von Mises and Anderson-Darling statistics with their p-values to decide which is the best distribution.
A standard tool to evaluate the fit of a distribution is the P-P plot. Add this plot, in the application section.
In practice, much lifetime data is subject to censoring, but there is no discussion of this.
At least a short discussion on the estimation under Bayesian paradigm would be really nice. This would really strengthen the content of the paper.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests

No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

Respond to this report

Responses (0)

[1] 1. Lehmann EL: The power of rank tests. Ann. Math. Stat. 1953; 24: 23–43. Publisher Full Text

[2] 2. Gupta RC, Gupta P, Gupta RD: Modeling failure time data by Lehmann alternatives. Communications in Statistics-Theory and Methods. 1998; 27: 887–904. Publisher Full Text

[3] 3. Cordeiro GM, De Castro M: A new family of generalized distributions. J. Stat. Comput. Simul. 2011; 81: 883–893. Publisher Full Text

[4] 4. Arshad MZ, Iqbal MZ, Anees A, et al.: New Bathtub Shaped Failure Rate Model: Properties, and Applications to Engineering Sector. Pak. J. Statist. 2021; 37: 57–80.

[5] 5. Arshad MZ, Iqbal MZ, Ahmad M: Exponentiated Power Function Distribution: Properties and Applications. JSTA. 2020; 19: 297–313. Publisher Full Text

[6] 6. Awodutire PO, Nduka EC, Ijomah MA: Lehmann Type II Generalized Half Logistic Distribution: Properties and Application. Mathematical Theory and Modeling . 2020; 10: 103–115.

[7] 7. Akilandeswari VS, Poornima R, Saavithri V: Lehmann-Type Laplace distribution-Type I software reliability growth model. OPSEARCH . 2016; 54: 233–259.

[8] 8. Dallas AC: Characterization of Pareto and power function distribution. Ann. Math. Stat. 1976; 28: 491–497. Publisher Full Text

[9] 9. Meniconi M, Barry D: The power function distribution: A useful and simple distribution to assess electrical component reliability. Microelectron Reliab. 1996; 36: 1207–1212. Publisher Full Text

[10] 10. Chang SK: Characterizations of the power function distribution by the independence of record values. J. Chungcheong Math Soc. 2007; 20: 139–146.

[11] 11. Tavangar M: Power function distribution characterization by dual generalized order statistics. JIRSS. 2011; 10: 13–27.

[12] 12. Cordeiro GM, Brito RDS: The beta power distribution. Braz. J. Probab. 2012; 26: 88–112. Publisher Full Text

[13] 13. Ahsanullah M, Shakil M, Golam-Kibria BMG: A characterization of the power function distribution based on lower records. ProbStat. Forum. 2013; 6: 68–72.

[14] 14. Zaka A, Akhter AS, Farooqi N: Methods for estimating the parameters of the power function distribution. J. Stat. 2014; 21: 90–102. Publisher Full Text

[15] 15. Tahir MH, Alizadeh M, Mansoor M, et al.: The Weibull power function distribution with applications. Hacettepe J. Math. Stat. 2014; 45: 245–265. Publisher Full Text

[16] 16. Shahzad MN, Asghar Z, Shehzad F, et al.: Parameter estimation of power function distribution with TL-moments. Rev. Colomb. Estad. 2015; 38: 321–334. Publisher Full Text

[17] 17. Ahsan-ul-Haq M, Butt NS, Usman RM, et al.: Transmuted power function distribution. Gazi univ. j. sci. 2016; 29: 177–185.

[18] 18. Okorie IE, Akpanta AC, Ohakwe J: Marshall-Olkin extended power function distribution. EJPS. 2017; 5: 16–29. Publisher Full Text

[19] 19. Marshall AW, Olkin I: A new method for adding a parameter to a family of distributions with applications to the exponential and Weibull families. Biometrika . 1997; 84: 641–652. Publisher Full Text

[20] 20. Usman RM, Ahsan-ul-Haq M, Bursa N, et al.: Exponentiated Transmuted Power Function Distribution: Theory & Applications. Gazi Univ. J. Sci. 2018; 31: 660–675. Publisher Full Text

[21] 21. Hassan A, Elshrpieny E, Mohamed R: Odd generalized exponential power function distribution. Gazi Univ. J. Sci. 2019; 32: 351–370.

[22] 22. Tahir MH, Cordeiro GM, Alizadeh M, et al.: The odd generalized exponential family of distributions with applications. JSDA. 2015; 2: 1–28. Publisher Full Text

[23] 23. Zaka A, Akhter AS, Jabeen R: The new reflected power function distribution: Theory, simulation & application. AIMS Mathematics . 2020; 5: 5031–5054. Publisher Full Text

[24] 24. Al-Mutairi AO: Transmuted Weighted Power Function Distribution. Pak. J. Statist. 2017; 33: 491–498.

[25] 25. Balogun OS, Iqbal MZ, Arshad MZ, et al.: A new generalization of Lehmann type-II distribution: Theory, simulation, and applications to survival and failure rate data. Scientific African . 2021; 12: 1–13. Publisher Full Text

[26] 26. Balogun OS, Arshad MZ, Iqbal MZ, et al.: A new modified Lehmann type – II G class of distributions: exponential distribution with theory, simulation, and applications to engineering sector. F1000 Res. 2021. Publisher Full Text

[27] 27. Bowley AL: Elements of Statistics . 4th ed. New York, USA: Charles Scribner; 1920.

[28] 28. Moors JJA: A quantile alternative for kurtosis. J. R. Stat. Soc., Ser. D Stat. 1998; 37: 25–32. Publisher Full Text

[29] 29. Hyndman RJ, Fan Y: Sample quantile in statistical packages. Amer. Statist. 1996; 50: 361–365. Publisher Full Text

[30] 30. Rényi A: On measures of entropy and information, 4th Fourth Berkeley Symposium on Mathematical Statistics and Probability . Berkeley, USA: University of California Press; 1961; 547–561.

[31] 31. Tsallis C: Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988; 52: 479–487. Publisher Full Text

[32] 32. Havrda J, Charvat FS: Quantification method of classification processes: Concept of structural-entropy. Kybernetika . 1967; 3: 30–35.

[33] 33. Arimoto S: Information theoretical considerations on estimation theory. Inf. Control. 1971; 73: 181–190. Publisher Full Text

[34] 34. Boekee E, Van Der Lubbe JCA: The R-norm information measure. Inf. Control. 1980; 45: 136–155. Publisher Full Text

[35] 35. Mathai AM, Haubold HJ: On a Generalized Entropy Measure Leading to the Pathway Model with a Preliminary Application to Solar Neutrino Data. Entropy . 2013; 15: 4011–4025. Publisher Full Text

[36] 36. Smithson M, Verkuilen J: A better lemon-squeezer? Maximum likelihood regression with beta distributed dependent variables. Psycholog. Meth. 2006; 11: 54–71. PubMed Abstract | Publisher Full Text

[37] 37. Rahman MM, Al-Zahrani B, Shahbaz SH, et al.: Cubic Transmuted Uniform Distribution: An Alternative to Beta and Kumaraswamy Distributions. EJPAM . 2019; 12: 1106–1121. Publisher Full Text

[38] 38. Aarset MV: How to identify bathtub hazard rate. IEEE. Trans. Reliab. 1987; 36: 106–108. Publisher Full Text

[39] 39. Kumaraswamy P: A generalized probability density function for double-bounded random processes. J. Hydrol. 1980; 46: 79–88. Publisher Full Text

[40] 40. Khan MS, King R, Hudson IL: Transmuted Kumaraswamy distribution. SiT. 2016; 17: 1–28. Publisher Full Text

[41] 41. Muhammad M: A New Lifetime Model with a Bounded Support. Asian J. Math. 2017; 7: 1–11. Publisher Full Text

[42] 42. Khan MS: Transmuted Generalized Power Weibull Distribution. Thailand. Stat. 2018; 16: 156–172.

[43] 43. Khan MS, King R, Hudson IL: Some Structural Properties of the Transmuted Lindley Distribution with Application to Women's Anxiety Data. JPSS . 2018; 16: 69–80.

[44] 44. Iqbal MZ, et al.: Two_dataset.doc. figshare. Dataset. 2021. Publisher Full Text

A better approach to discuss medical science and engineering data with a modified Lehmann Type – II model

Abstract

Keywords

Introduction

Modified Lehmann type II model

(1)

(2)

Linear representation

Reliability characteristics

(3)

(4)

Limiting behavior

Shapes of density and failure rate functions

Figure 1. Density function.

Figure 2. Failure rate function.

Quantile, mode, skewness, and kurtosis

(5)

Figure 3. Skewness.

Figure 4. Kurtosis.

Moments and associated measures

(6)

Table 1.

(7)

Order statistics

(8)

(9)

(10)

Stress – strength reliability

Entropy

(11)

Table 2.

Estimation

(12)

Simulation

Table 3.

Table 4.

Table 5.

Table 6.

Table 7.

Table 8.

Application

Figure 5.

Figure 6.

Table 9. Competitive models Cumulative distribution functions (cdfs).

Table 10. Descriptive statistics.

Table 11. Maximum likelihood estimations with standard errors (in parenthesis) and goodness of fit for the women’s anxiety data.

Table 12. Maximum likelihood estimations (MLEs) with standard errors (in parenthesis) and goodness of fit for the lifetime (in days) of 30 electronic devices data.

Conclusion

Data availability

Grant information

Competing interests

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated