The impact of testing and treatment on the dynamics of Hepatitis B virus

Olajumoke Oludoun; Olukayode Adebimpe; James Ndako; Michael Adeniyi; Oluwakemi E. Abiodun; Babatunde Gbadamosi

doi:10.12688/f1000research.72865.1

Home Browse The impact of testing and treatment on the dynamics of Hepatitis B...

ALL Metrics

-

Views

-

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

The impact of testing and treatment on the dynamics of Hepatitis B virus

[version 1; peer review: 2 approved]

Olajumoke Oludoun ¹, Olukayode Adebimpe², James Ndako³, Michael Adeniyi⁴, Oluwakemi E. Abiodun⁵, Babatunde Gbadamosi⁶

Olajumoke Oludoun ¹, Olukayode Adebimpe², [...] James Ndako³, Michael Adeniyi⁴, Oluwakemi E. Abiodun⁵, Babatunde Gbadamosi⁶

PUBLISHED 17 Sep 2021

Author details Author details

¹ Physical sciences, Landmark University, Omu Aran, Kwara State, Nigeria
² Physical Sciences, Landmark University, Omu Aran, Kwara, Nigeria
³ Biological Sciences, Landmark University, Omu Aran, Kwara, Nigeria
⁴ Mathematics, Lagos State Polytechnic, Lagos, Lagos, Nigeria
⁵ Physical Sciences (Mathematics Programme), Landmark University, Omu Aran, Kwara, Nigeria
⁶ Computer Science, Landmark University, Omu Aran, Kwara, Nigeria

Olajumoke Oludoun
Roles: Conceptualization, Methodology, Writing – Original Draft Preparation

Olukayode Adebimpe
Roles: Conceptualization, Writing – Review & Editing

James Ndako
Roles: Supervision, Writing – Review & Editing

Michael Adeniyi
Roles: Methodology

Oluwakemi E. Abiodun
Roles: Methodology, Writing – Original Draft Preparation

Babatunde Gbadamosi
Roles: Formal Analysis

OPEN PEER REVIEW

REVIEWER STATUS

Abstract

Despite the intervention of WHO on vaccination for reducing the spread of Hepatitis B Virus (HBV), there are records of the high prevalence of HBV in some regions. In this paper, a mathematical model was formulated to analyze the acquisition and transmission process of the virus with the view of identifying the possible way of reducing the menace and mitigating the risk of the virus. The models' positivity and boundedness were demonstrated using well-known theorems. Equating the differential equations to zero demonstrates the equilibria of the solutions i.e., the disease-free and endemic equilibrium. The next Generation Matrix method was used to compute the basic reproduction number for the models. Local and global stabilities of the models were shown via linearization and Lyapunov function methods respectively. The importance of testing and treatment on the dynamics of HBV were fully discussed in this paper. It was discovered that testing at the acute stage of the virus and chronic unaware state helps in better management of the virus.

Keywords

: Positivity and boundedness of solutions, Equilibria of solutions, Next generation matrix, Linearization, Lyapunov functions, local and global stabilities.

Corresponding author: Olajumoke Oludoun

Competing interests: No competing interests were disclosed.

Grant information: The author(s) declared that no grants were involved in supporting this work.

Copyright: © 2021 Oludoun O et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Oludoun O, Adebimpe O, Ndako J et al. The impact of testing and treatment on the dynamics of Hepatitis B virus [version 1; peer review: 2 approved]. F1000Research 2021, 10:936 (https://doi.org/10.12688/f1000research.72865.1) First published: 17 Sep 2021, 10:936 (https://doi.org/10.12688/f1000research.72865.1) Latest published: 17 Sep 2021, 10:936 (https://doi.org/10.12688/f1000research.72865.1)

1. Introduction

Hepatitis is an inflammation/scarring of the liver that contributes to various health complications, including death. It occurs due to an immune system attack by the virus in the liver and damages this vital organ of the body in the process (Ciupe et al., 2014). The hepatitis B virus (HBV) can survive outside the body for at least seven days. If the virus enters the body of someone who is not protected by vaccination during this time, it can still cause infection. The average incubation time for HBV is 75 days, but it can range from 30 to 180 days. Within 30 to 60 days of infection, the virus may be detected, persist, and grow into chronic hepatitis B (CDC, 2019). Hepatitis B is most common in the Western Pacific region with prevalence rate 6.2% and Africa with prevalence rate of 6.1%, with the Americas region (0.7%) having the lowest prevalence (WHO, 2019).

In highly endemic areas, the most common form of transmission of hepatitis B is from mother to child at birth (vertical transmission) or through horizontal route (contact with infected blood), particularly from infected children to uninfected children during the first five years of life. Chronic infection develops in infants infected by their mothers or before the age of five. It is often transmitted through transdermal or mucosal contact of infected persons to infected blood and different body fluids, such as spittle, catamenial, vaginal and spermatic fluids and, to a lesser degree, perspiration, breast milk, tears, and urine. In particular, hepatitis B can be transmitted through sexual contact in unvaccinated men who have sex with men (MSM) and heterosexual people who have multiple sexual partners or have contact with sex workers. However, adult infection contributes to chronic hepatitis in less than 5% of cases. This transmission may similarly ensue when needles and syringes are reused, whether in healthcare settings or among drug users. Furthermore, an infection can occur during medical, surgical, and dental procedures, such as tattooing or using razors and other similar objects contaminated with infected blood (Mpeshe and Nyerere, 2019).

2. Mathematical formulation

Some chronic carriers are unaware of their status and as such transmit the virus unknowingly and also at higher risk of cirrhosis and makes treatment less effective (Niederau, 2014, Mcpherson et al., 2013, Cohen et al., 2011, Piorkowsky, 2009, Lin et al., 2009, Meffre et al., 2004).

In view of this, this model is developed to factor the aforementioned set of people. In the model, the population is divided into the following different groups: the susceptible, the acute, the chronic unaware carriers, the chronic aware carriers, the treated chronic aware and the recovered individuals.

The total population at time $t,$ denoted by $N (t)$ is divided into the six subgroups corresponding to different epidemiological status: susceptible individuals $S (t)$ , acute $A (t)$ , unaware chronically infected $C_{u} (t)$ , aware chronically infected $C_{a} (t)$ , treated $T_{c} (t)$ , and removed/recovered class $R (t)$ . The model equation is subject to the initial conditions,

(1)

S (t) \geq 0, A (t) \geq 0, C_{u} (t) \geq 0, C_{a} (t) \geq 0, T_{c} (t) \geq 0, R (t) \geq 0

Figure 1 represents schematically the epidemiology of HBV infected model. The different disease stages are reproduced by the different circle and the arrows indicate the way individual progress from one stage to the other. It is assumed that at time, $t,$ susceptible individuals, $S,$ enter the population at a constant rate, $Π .$ For all classes, individuals die at a constant natural mortality rate, $μ .$ HBV chronically infected individuals $(C_{u} (t)$ , $C_{a} (t))$ have an additional death rate due to HBV, $ⅆ_{c}$ (Zhang and Zhang (2018)). It is assumed that HBV infected individuals on treatment, $T_{c} (t)$ do not transmit HBV infection. Susceptible individuals, $S (t),$ may acquire HBV infection when in contact with individuals in A $, C_{u},$ and $C_{a},$ populace at a rate, $λ$ (force of infection associated with HBV), where

(2)

λ = \frac{β (A + α_{1} C_{u} + α_{2} C_{a})}{N}

Figure 1. Compartmental flow diagram of HBV model.

Parameter $β$ represents the probability that a contact will result in an HBV infection while $α_{1}, α_{2} > 1$ respectively account for modification parameter of chronic HBV-infected individuals.

A proportion of the acute HBV-infected individuals, $σ,$ spontaneously clear the virus, then return to being susceptible. The HBV acutely infected individuals develop to chronic without been aware if no testing at a rate, $γ .$ The acutely infected and chronic unaware individual progress to chronic aware stage with a testing $ν_{1}, ν_{2}$ respectively and moved to treatment stage after testing at the rate $δ$ . $ω$ is the recovery rate of treated infected individual with full immunity.

These assumptions lead to the system of equations in (3)

(3)

\frac{d S}{d t} = Π - λ S + σ A - μ S \frac{d A}{d t} = λ S - (σ + γ + ν_{1}) A \frac{d C_{u}}{d t} = γ A - (ν_{2} + μ + d_{c}) C_{u} \frac{d C_{a}}{d t} = ν_{2} C_{u} + ν_{1} A - (δ + μ + d_{c}) C_{a} \frac{d T_{c}}{d t} = δ C_{a} - (ω + μ) T_{c} \frac{d R}{d t} = ω T_{c} - μ R

where $λ = \frac{β (A + α_{1} C_{u} + α_{2} C_{a})}{N}$

2.1 Positivity and boundedness of solutions

For the system of equations (3) to be epidemiologically meaningful, it is important to prove that all solution with non-negative initial conditions will remain non-negative.

Lemma 1: The initial values of the parameters are

\{S (0) \geq 0, A (0) \geq 0, C_{u} (0) \geq 0, C_{a} (0) \geq 0, T_{c} (0) \geq 0, R (0) \geq, 0 and N (0) \geq 0\} \in Φ

Then the solution of the model $\{S (t), A (t), C_{u} (t), C_{a} (t), T_{c} (t), R (t), N (t)\}$ is positive for all $t \geq 0 .$

Proof

Considering the first equation in (3),

\frac{dS}{dt} = Π - λS + σA - μS

\frac{dS}{dt} \geq - (λ + μ) S \int \frac{1}{S} dS \geq \int - (λ + μ) dt

S \geq S_{0} e^{- (λ + μ) t} \geq 0

Hence, $S \geq 0$

with respect to the second equation in (3);

\frac{dA}{dt} = λS - (σ + γ + ν_{1}) A

\frac{dA}{dt} \geq - (σ + γ + ν_{1}) A

\int \frac{1}{A} dA \geq \int - (σ + γ + ν_{1}) dt

A \geq A_{0} e^{- (σ + γ + ν_{1}) t} \geq 0

Hence, $A \geq 0$ . Same goes for the other compartments

Clearly, the above state variables are positive on bounding plane $ℝ_{+}^{6}$ .

For the boundedness the following calculation follows:

N (t) = S (t) + A (t) + C_{u} (t) + C_{a} (t) + T_{c} (t) + R (t)

N^{'} = S' + A' + C_{u}' + C_{a}' + T_{c}' + R'

(4)

N^{'} = Π - λS + σA - μS + λS - (σ + γ + ν_{1}) A + γA - (ν_{2} + μ + d_{c}) C_{u} + ν_{2} C_{u} + ν_{1} A - (δ + μ + d_{c}) C_{a} + δ C_{a} - (ω + μ) T_{c} + ω T_{c} - μR

Simplifying:

(5)

N^{'} + μN = Π - d_{c} C_{u}

(6)

N^{'} + μN \leq Π

Integrating gives:

N^{'} \leq \frac{Π}{μ} + k e^{- μt}

max_{lim_{n \to \infty}} N \leq lim_{n \to \infty} (\frac{Π}{μ} + k e^{- μt}) \leq \frac{Π}{μ}

It follows that the solutions of the model system (3) are positive and bounded in the region

T = \{(S + A + C_{u} + C_{a} + T_{c} + R)\} \in ℝ_{+}^{6} : S + A + C_{u} + C_{a} + T_{c} + R \leq \frac{Π}{μ}

It follows from Lemma 1 that it is sufficient to consider the dynamics of system (3) and the model can be considered to be epidemiologically well-posed.

2.2 Equilibrium points

The disease-free equilibrium of the equation (3) exists and is given by:

(7)

(E_{0}) = [\frac{Π}{μ}, 0, 0, 0, 0, 0]

The endemic steady states are calculated here which is done by setting system of equation in (3.3.3) to zero and setting $S = S^{*}, A = A^{*}, C_{u} = {C_{u}}^{*}, C_{a} = {C_{a}}^{*}, T_{c} = {T_{c}}^{*}, R = R^{*}$ so that

(8)

S^{*} = (\frac{\begin{array}{l} Π (μ^{3} + (δ + γ + 2 d_{c} + υ_{1} + υ_{2}) μ^{2} + ({d_{c}}^{2} + (υ_{1} + υ_{2} + δ + γ) d_{c} + (υ_{2} + δ) γ + (υ_{2} + δ) υ_{1} + δ υ_{2}) μ) \\ + δ (υ_{1} d_{c} + υ_{2} (υ_{1} + γ)) (υ_{1} + σ + γ) \end{array}}{L})

(9)

A^{*} = - (\frac{\begin{matrix} (υ_{1} - β + γ + σ) {d_{c}}^{2} + ((2 υ_{1} - 2 β + 2 γ + 2 σ) μ + (υ_{2} + δ - β α_{1}) γ + (υ_{2} + δ - β α_{2}) υ_{1} - (β - σ) (υ_{2} + δ)) d_{c} \\ + (υ_{1} - β + γ + σ) μ^{2} + ((υ_{2} + δ - β α_{1}) γ + (υ_{2} + δ - β α_{2}) υ_{1} - (β - σ) (υ_{2} + δ)) μ + ((- {δα}_{1} - α_{2} υ_{2}) β) Π \end{matrix}}{L})

(10)

{C_{u}}^{*} = A^{*} γ

(11)

{C_{a}}^{*} = \frac{{C_{u}}^{*} ((υ_{1} + υ_{1} μ) + υ_{2} (υ_{1} + γ))}{γ}

(12)

{T_{c}}^{*} = - ({C_{a}}^{*} (\frac{μ^{2}}{{d_{c}}^{2}} + \frac{μ}{d_{c}} + \frac{υ_{2}}{μ^{2}} + \frac{1}{υ_{1} + υ_{2}}) δ)

(13)

R^{*} = ω {T_{c}}^{*}

where

L = ((υ_{2} + μ + d_{c}) (υ_{1} + γ + σ) μ^{3} + ((2 υ_{1} + 2 γ + 2 σ) d_{c}) + (υ_{1} + γ + σ) υ_{2} + (β + δ) γ + (β + δ) υ_{1} + δσ) μ^{2} + ((υ_{1} + γ + σ) {d_{c}}^{2} + ((υ_{1} + γ + σ) υ_{2} - γ^{2} + (2 β + δ - σ - 2 υ_{1}) γ - υ_{1}^{2} + (2 β + δ - σ) υ_{1} + δσ) d_{c} + ((β + δ) γ + (β + δ) υ_{1} + δσ) υ_{2} + β (υ_{1} + γ) (γ α_{1} + α_{2} υ_{1} + δ)) μ - (υ_{1} + γ) (υ_{1} - β + γ + σ) {d_{c}}^{2} + (- (υ_{1} + γ) (υ_{1} - β + γ + σ) υ_{2} + (β α_{1} - δ) γ^{2} + ((- δ + (α_{1} + α_{2}) β) υ_{1} + δ (β - σ)) γ + (δ + α_{2} υ_{1}) β υ_{1}) d_{c} + β (γ α_{1} + α_{2} υ_{1} + δ) υ_{2} + δγ α_{1}) (υ_{1} + γ) (δ + μ + d_{c}) (μ + ω)

2.3 Basic reproduction number

The basic reproduction number ( $R_{o}$ ) which is the number of secondary infections caused by an infectious individual is determined by the next generation matrix which is given by $ρ (F V^{- 1})$

where:

F = [\begin{matrix} β & β α_{1} & β α_{2} \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix}]

V = [\begin{matrix} σ + γ + υ_{1} & 0 & 0 \\ - γ & d_{c} + μ + υ_{2} & 0 \\ - υ_{1} & - υ_{2} & d_{c} + μ + δ \end{matrix}]

V^{- 1} = [\begin{matrix} \frac{1}{σ + γ + υ_{1}} & 0 & 0 \\ \frac{γ}{(σ + γ + υ_{1}) (d_{c} + μ + υ_{2})} & \frac{1}{d_{c} + μ + υ_{2}} & 0 \\ \frac{γ υ_{2} + υ_{1} μ + υ_{1} d_{c} + υ_{1} υ_{2}}{(σ + γ + υ_{1}) (d_{c} + μ + υ_{2}) (d_{c} + μ + δ)} & \frac{υ_{2}}{(d_{c} + μ + υ_{2}) (d_{c} + μ + δ)} & \frac{1}{(d_{c} + μ + δ)} \end{matrix}]

(14)

R_{o} = \frac{β}{σ + γ + υ_{1}} + \frac{β α_{1} γ}{(σ + γ + υ_{1}) (d_{c} + μ + υ_{2})} + \frac{β α_{2} (γ υ_{2} + υ_{1} μ + υ_{1} d_{c} + υ_{1} υ_{2})}{(σ + γ + υ_{1}) (d_{c} + μ + υ_{2}) (d_{c} + μ + δ)}

2.4 Local stability analysis of the disease-free equilibrium $E_{0}$

Theorem 1: $E_{0}$ is locally asymptotically stable if $R_{0}$ < 1 and unstable if $R_{0}$ > 1.

Proof: The resulting matrix from the linearized model is $\frac{dX}{dt} = AX$

X = {(x_{1}, x_{2}, x_{3}, x_{4}, x_{5,} x_{6})}^{T}, (x_{1}, x_{2}, x_{3}, x_{4}, x_{5,} x_{6}) \in R_{+}^{6}, and

The resulting Jacobian matrix at $E_{0}$ is

(15)

J (E_{0}) = [\begin{array}{l} - μ - λ & - β + σ & - β α_{1} & - β α_{2} & 0 & 0 \\ 0 & β - σ - γ - ν_{1} - λ & β α_{1} & β α_{2} & 0 & 0 \\ 0 & γ & - d_{c} - μ - ν_{2} - λ & 0 & 0 & 0 \\ 0 & ν_{1} & ν_{2} & - d_{c} - μ - δ - λ & 0 & 0 \\ 0 & 0 & 0 & δ & - ω - μ - λ & 0 \\ 0 & 0 & 0 & 0 & ω & - μ - λ \end{array}]

From (15), $λ_{1} = - μ, λ_{2} = - ω - μ, λ_{3} = - μ$

and the resulting quadratic equation is:

(16)

(β - σ - γ - ν_{1} - λ) (- d_{c} - μ - ν_{2} - λ) (- d_{c} - μ - δ - λ) - β α_{1} (- d_{c} - μ - δ - λ) γ + β α_{2} ((- d_{c} - μ - ν_{2} - λ) ν_{1} - γ ν_{2})

(17)

f (λ) = λ^{3} + (2 μ + ν_{1} + ν_{2} - β + δ + γ + σ + 2 d_{c}) λ^{2} + (β α_{2} ν_{1} - βδ - 2 βμ - 2 β d_{c} - β ν_{2} + δγ + δμ + δσ + δ d_{c} + δ ν_{1} + δ ν_{2} + 2 γμ + 2 γ d_{c} + γ ν_{2} + μ^{2} + 2 μσ + 2 μ d_{c} + 2 μ ν_{1} + μ ν_{2} + 2 σ d_{c} + σ ν_{2} + {d_{c}}^{2} + 2 d_{c} ν_{1} + d_{c} ν_{2} + ν_{1} ν_{2} - γβ α_{1}) λ + γ μ^{2} + γ {d_{c}}^{2} + μ^{2} σ + μ^{2} ν_{1} + σ {d_{c}}^{2} + {d_{c}}^{2} ν_{1} + μσ ν_{2} + 2 μ d_{c} ν_{1} + μ ν_{1} ν_{2} + σ d_{c} ν_{2} + d_{c} ν_{1} ν_{2} - βδμ - βδ d_{c} - βδ ν_{2} - 2 βμ d_{c} - βμ ν_{2} - β d_{c} ν_{2} - β μ^{2} - β {d_{c}}^{2} + δγμ + δγ d_{c} + δγ ν_{2} + δμσ + δμ ν_{1} + δσ d_{c} + δσ ν_{2} + δ d_{c} ν_{1} + δ ν_{1} ν_{2} + 2 γμ d_{c} + γμ ν_{2} + γ d_{c} ν_{2} + 2 μσ d_{c} - βδγ α_{1} - βγμ α_{1} - βγ α_{1} d_{c} + ν_{2} γβ α_{2} + ν_{1} β α_{2} d_{c} + ν_{1} β α_{2} μ + ν_{1} β α_{2} ν_{2}

Now, $λ_{1}$ , $λ_{2}, λ_{3}$ < 0 since the values are assumed positive. If $R_{0}$ < 1, $E_{0}$ is stable and unstable when $R_{0}$ < 1.

2.5 Global stability of the disease-free equilibrium

The global behavior of the equilibrium system (3) is analyzed here in this section.

Theorem 2: For system (3), the disease-free equilibrium $E_{0}$ is asymptotically stable globally if $R_{0} < 1$ .

Proof: Considering the Lyapunov function defined as:

(18)

G (A, C_{u}, C_{a}) = (\frac{1}{B_{0}}) A + (\frac{β α_{1}}{B_{0} B_{1}} + \frac{β α_{2} υ_{2}}{B_{0} B_{1} B_{2}}) C_{u} + (\frac{β α_{2}}{B_{0} B_{2}}) C_{a}

(19)

G' (A, C_{u}, C_{a}) = (\frac{1}{B_{0}}) A' + (\frac{β α_{1}}{B_{0} B_{1}} + \frac{β α_{2} υ_{2}}{B_{0} B_{1} B_{2}}) C_{u}' + (\frac{β α_{2}}{B_{0} B_{2}}) C_{a}'

(20)

G' (A, C_{u}, C_{a}) = (\frac{1}{B_{0}}) ((\frac{β (A + α_{1} C_{u} + α_{2} C_{a})}{N}) S - (σ + γ + ν_{1}) A) + (\frac{β α_{1}}{B_{0} B_{1}} + \frac{β α_{2} υ_{2}}{B_{0} B_{1} B_{2}}) (γA - (ν_{2} + μ + d_{c}) C_{u}) + (\frac{β α_{2}}{B_{0} B_{2}}) (ν_{2} C_{u} + ν_{1} A - (δ + μ + d_{c}) C_{a})

At DFE, S=N so that (20) becomes:

(21)

G' (A, C_{u}, C_{a}) = (\frac{1}{B_{0}}) (β (A + α_{1} C_{u} + α_{2} C_{a}) - (σ + γ + ν_{1}) A) + (\frac{β α_{1}}{B_{0} B_{1}} + \frac{β α_{2} υ_{2}}{B_{0} B_{1} B_{2}}) (γA - (ν_{2} + μ + d_{c}) C_{u}) + (\frac{β α_{2}}{B_{0} B_{2}}) (ν_{2} C_{u} + ν_{1} A - (δ + μ + d_{c}) C_{a})

Expanding and simplifying (21) gives:

(22)

G' = [\frac{β}{B_{0}} + \frac{β α_{1} γ}{B_{0} B_{1}} + \frac{β α_{2} υ_{2} γ}{B_{0} B_{1} B_{2}} + \frac{β α_{2} ν_{1}}{B_{0} B_{2}} - 1] A + [\frac{β α_{1}}{B_{0}} - \frac{β α_{1} B_{1}}{B_{0} B_{1}} - \frac{β α_{2} υ_{2} B_{1}}{B_{0} B_{1} B_{2}} + \frac{β α_{2} ν_{2}}{B_{0} B_{2}}] C_{u} + [\frac{β α_{2}}{B_{0}} - \frac{β α_{2} B_{2}}{B_{0} B_{2}}] C_{a}

(23)

G' = [R_{0} - 1] A \leq 0

From Equation (23), it can be deduced that the DFE is globally stable since $R_{0}$ < 1.

2.6 Local stability of endemic equilibrium

Theorem 3: If $R_{0} > 1$ , then the endemic equilibrium is locally asymptotically stable.

Proof:

The endemic equilibria of system (3), denoted by $(S^{*}, A^{*}, {C_{u}}^{*}, {C_{a}}^{*}, {T_{c}}^{*}, R^{*}),$ can be rewritten as:

Let S = x + S^{*}, A = y + A^{*}, C_{u} = z + {C_{u}}^{*}, C_{a} = h + {C_{a}}^{*}, T_{c} = p + {T_{c}}^{*}, R = j + R^{*}

(25)

J = [\begin{array}{l} B_{0} - μ - λ & - B_{1} + σ & - B_{2} & - B_{3} & B_{4} & B_{5} \\ - B_{6} & B_{7} - σ - γ - ν_{1} - λ & B_{8} & B_{9} & - B_{11} & - B_{12} \\ 0 & γ & - d_{c} - μ - ν_{2} - λ & 0 & 0 & 0 \\ 0 & ν_{1} & ν_{2} & - d_{c} - μ - δ - λ & 0 & 0 \\ 0 & 0 & 0 & δ & - ω - μ - λ & 0 \\ 0 & 0 & 0 & 0 & ω & - μ - λ \end{array}]

From (25), $λ_{1} = - μ, λ_{2} = - (ω + μ), λ_{3} = - (d_{c} + μ + ν_{2})$ , then;

(26)

J = [\begin{array}{l} B_{0} - μ - λ & - B_{1} + σ & - B_{2} \\ - B_{6} & B_{7} - σ - γ - ν_{1} - λ & B_{8} \\ 0 & γ & - d_{c} - μ - ν_{2} - λ \end{array}]

from (26);

λ^{3} + (γ + 2 μ + σ - B_{0} - B_{4} + d_{c} + ν_{1} + ν_{2}) λ^{2} + (2 γμ - B_{0} γ + γ d_{c} + γ ν_{2} + μ^{2} + 2 μσ - {μB}_{0} - 2 μ B_{4} + μ d_{c} + 2 μ ν_{1} + {μν}_{2} - σ B_{0} + σ B_{3} + σ d_{c} + σ ν_{2} + B_{0} B_{4} - B_{0} d_{c} - B_{0} ν_{1} - B_{0} ν_{2} - B_{3} B_{1} - B_{4} d_{c} - B_{4} ν_{2} + d_{c} ν_{1} + ν_{1} ν_{2}) λ + B_{5} γ + γμ ν_{2} + {μσν}_{2} + μ ν_{1} ν_{2} + B_{3} B_{2} γ + γ μ^{2} + μ^{2} σ + μ^{2} ν_{1} + μ d_{c} ν_{1} + γμ d_{c} + μσ d_{c} - μ^{2} B_{4} - γμ B_{0} - γ B_{0} d_{c} - γ B_{0} ν_{2} - μ {σB}_{0} + μ {σB}_{3} + μ B_{0} B_{4} - μ B_{0} ν_{1} - μ B_{3} B_{1} - μ B_{4} d_{c} - μ B_{4} ν_{2} - σ B_{0} d_{c} - σ B_{0} ν_{2} + σ B_{3} d_{c} + σ B_{3} ν_{2} + B_{0} B_{4} d_{c} + B_{0} B_{4} ν_{2} - B_{0} d_{c} ν_{1} - B_{0} ν_{1} ν_{2} - B_{3} B_{1} d_{c} - B_{3} B_{1} ν_{2}

The result of the determinant of the Jacobian matrix is of the form:

(27)

a_{0} λ^{3} + a_{1} λ^{2} + a_{2} λ + a_{3}

where

a_{0} = 1

a_{1} = γ + 2 μ + σ - B_{0} - B_{4} + d_{c} + ν_{1} + ν_{2}

a_{2} = 2 γμ - B_{0} γ + γ d_{c} + γ ν_{2} + μ^{2} + 2 μσ - {μB}_{0} - 2 μ B_{4} + μ d_{c} + 2 μ ν_{1} + {μν}_{2} - σ B_{0} + σ B_{3} + σ d_{c} + σ ν_{2} + B_{0} B_{4} - B_{0} d_{c} - B_{0} ν_{1} - B_{0} ν_{2} - B_{3} B_{1} - B_{4} d_{c} - B_{4} ν_{2} + d_{c} ν_{1} + ν_{1} ν_{2}

a_{3} = B_{5} γ + γμ ν_{2} + {μσν}_{2} + μ ν_{1} ν_{2} + B_{3} B_{2} γ + γ μ^{2} + μ^{2} σ + μ^{2} ν_{1} + μ d_{c} ν_{1} + γμ d_{c} + μσ d_{c} - μ^{2} B_{4} - γμ B_{0} - γ B_{0} d_{c} - γ B_{0} ν_{2} - μ {σB}_{0} + μ {σB}_{3} + μ B_{0} B_{4} - μ B_{0} ν_{1} - μ B_{3} B_{1} - μ B_{4} d_{c} - μ B_{4} ν_{2} - σ B_{0} d_{c} - σ B_{0} ν_{2} + σ B_{3} d_{c} + σ B_{3} ν_{2} + B_{0} B_{4} d_{c} + B_{0} B_{4} ν_{2} - B_{0} d_{c} ν_{1} - B_{0} ν_{1} ν_{2} - B_{3} B_{1} d_{c} - B_{3} B_{1} ν_{2}

By the Routh–Hurwitz criterion governing the polynomials of order 3, we have the following:

1. $a_{2} . a_{3}$ are positive
2. $a_{1} a_{2} > a_{3}$

From equation (27), 1 and 2 are satisfied.

Therefore, endemic equilibrium is locally asymptotically stable.

2.7 Global stability of the endemic equilibrium

Theorem 4: The equations of the model have a positive distinctive endemic equilibrium whenever $R_{0}$ > 1, which is said to be globally asymptotically stable.

Proof: Considering the Lyapunov function defined as:

(28)

L (S^{*}, A^{*}, {C_{u}}^{*}, {C_{a}}^{*}, {T_{c}}^{*}, R^{*}) = (S - S^{*} ln (\frac{S}{S^{*}})) + (A - A^{*} ln (\frac{A}{A^{*}})) + (C_{u} - {C_{u}}^{*} ln (\frac{C_{u}}{{C_{u}}^{*}})) + (C_{a} - {C_{a}}^{*} ln (\frac{C_{a}}{{C_{a}}^{*}})) + (T_{c} - {T_{c}}^{*} ln (\frac{T_{c}}{{T_{c}}^{*}})) + (R - R^{*} ln (\frac{R}{R^{*}}))

where L takes it derivative along the system directly as:

(29)

\frac{dL}{dt} = (1 - \frac{S^{*}}{S}) \frac{dS}{dt} + (1 - \frac{A^{*}}{A}) \frac{dA}{dt} + (1 - \frac{{C_{u}}^{*}}{C_{u}}) \frac{d C_{u}}{dt} + (1 - \frac{{C_{a}}^{*}}{C_{a}}) \frac{d C_{a}}{dt} + (1 - \frac{{T_{c}}^{*}}{T_{c}}) \frac{d T_{c}}{dt} + (1 - \frac{R^{*}}{R}) \frac{dR}{dt}

(30)

\frac{dL}{dt} = (1 - \frac{S^{*}}{S}) [Π - (\frac{β (A + α_{1} C_{u} + α_{2} C_{a})}{N}) S + σA - μS] + (1 - \frac{A^{*}}{A}) [(\frac{β (A + α_{1} C_{u} + α_{2} C_{a})}{N}) S - (σ + γ + ν_{1}) A] + (1 - \frac{{C_{u}}^{*}}{C_{u}}) [γA - (ν_{2} + μ + d_{c}) C_{u}] + (1 - \frac{{C_{a}}^{*}}{C_{a}}) [ν_{2} C_{u} + ν_{1} A - (δ + μ + d_{c}) C_{a}] + (1 - \frac{{T_{c}}^{*}}{T_{c}}) [δ C_{a} - (ω + μ) T_{c}] + (1 - \frac{R^{*}}{R}) [ω T_{c} - μR]

At equilibrium,

(31)

Π = (\frac{β (A * + α_{1} C_{u} * + α_{2} C_{a} *)}{N *}) S * - σ A * + μ S * (σ + γ + ν_{1}) = (\frac{β (A * + α_{1} C_{u} * + α_{2} C_{a} *)}{A N *}) S * (ν_{2} + μ + d_{c}) = \frac{γ A *}{C_{u} *} (δ + μ + d_{c}) = \frac{ν_{2} C_{u} *}{C_{a} *} + \frac{ν_{1} A *}{C_{a} *} (ω + μ) = \frac{δ C_{a} *}{T_{c} *} ω = \frac{μ R *}{T_{c} *}

(32)

\frac{dL}{dt} = (1 - \frac{S^{*}}{S}) [(\frac{β (A * + α_{1} C_{u} * + α_{2} C_{a} *)}{N *}) S * - σA * + μS * - (\frac{β (A + α_{1} C_{u} + α_{2} C_{a})}{N}) S + σA - μS] + (1 - \frac{A^{*}}{A}) [(\frac{β (A + α_{1} C_{u} + α_{2} C_{a})}{N}) S - (\frac{β (A * + α_{1} C_{u} * + α_{2} C_{a} *)}{AN *}) S * A] + (1 - \frac{{C_{u}}^{*}}{C_{u}}) [γA - \frac{γA *}{C_{u} *} C_{u}] + (1 - \frac{{C_{a}}^{*}}{C_{a}}) [ν_{2} C_{u} + ν_{1} A - \frac{ν_{2} C_{u} *}{C_{a} *} + \frac{ν_{1} A *}{C_{a} *} C_{a}] + (1 - \frac{{T_{c}}^{*}}{T_{c}}) [δ C_{a} - \frac{δ C_{a} *}{T_{c} *} T_{c}] + (1 - \frac{R^{*}}{R}) [\frac{μR *}{T_{c} *} T_{c} - μR] = (1 - \frac{S^{*}}{S}) [\frac{βA * S *}{N *} + \frac{β α_{1} C_{u} * S *}{N *} + \frac{β α_{2} C_{a} * S *}{N *} - σA * + μS * - \frac{βAS}{N} - \frac{β α_{1} C_{u} S}{N} - \frac{β α_{2} C_{a} S}{N} + σA - μS] + (1 - \frac{A^{*}}{A}) [\frac{βAS}{N} - \frac{βAS *}{N *} + \frac{β α_{1} C_{u} S}{N} - \frac{β α_{1} C_{u} * S * A}{A * N *} + \frac{β α_{2} C_{a} S}{N} - \frac{β α_{2} C_{a} * S * A}{A * N *}] + (1 - \frac{{C_{u}}^{*}}{C_{u}}) γA [1 - \frac{A * C_{u}}{A C_{u} *}] + (1 - \frac{{C_{a}}^{*}}{C_{a}}) [ν_{2} C_{u} (1 - \frac{{C_{u}}^{*} C_{a}}{C_{u} C_{a} *}) + ν_{1} A (1 - \frac{A^{*} C_{a}}{A C_{a} *})] + δ C_{a} (1 - \frac{{T_{c}}^{*}}{T_{c}}) [1 - \frac{C_{a} * T_{c}}{C_{a} T_{c} *}] - μR (1 - \frac{R^{*}}{R}) [1 - \frac{R * T_{c}}{{RT}_{c} *}]

(33)

= (1 - \frac{S^{*}}{S}) [- \frac{βAS}{N} (1 - \frac{A * S * N}{ASN *}) - \frac{β α_{1} C_{u} S}{N} (1 - \frac{C_{u *} S * N}{C_{u} SN *}) + \frac{β α_{2} C_{a} S}{N} (1 - \frac{C_{a *} S * N}{C_{a} SN *}) - σA (1 - \frac{A^{*}}{A}) - μS - (1 - \frac{S^{*}}{S})] + (1 - \frac{A^{*}}{A}) [\frac{βAS}{N} (1 - \frac{A * S * N}{ASN *}) - \frac{β α_{1} C_{u} S}{N} (1 - \frac{C_{u *} S * AN}{C_{u} SA * N *}) + \frac{β α_{2} C_{a} S}{N} (1 - \frac{C_{a *} S * AN}{C_{a} SA * N *})] + (1 - \frac{{C_{u}}^{*}}{C_{u}}) γA [1 - \frac{A * C_{u}}{A C_{u} *}] + (1 - \frac{{C_{a}}^{*}}{C_{a}}) [ν_{2} C_{u} (1 - \frac{{C_{u}}^{*} C_{a}}{C_{u} C_{a} *}) + ν_{1} A (1 - \frac{A^{*} C_{a}}{A C_{a} *})] + δ C_{a} (1 - \frac{{T_{c}}^{*}}{T_{c}}) [1 - \frac{C_{a} * T_{c}}{C_{a} T_{c} *}] - μR (1 - \frac{R^{*}}{R}) [1 - \frac{R * T_{c}}{{RT}_{c} *}]

= - μS {(1 - \frac{S^{*}}{S})}^{2} - \frac{βAS}{N} (1 - \frac{S^{*}}{S}) (1 - \frac{A^{*} S^{*} N}{ASN *}) - \frac{β α_{1} C_{u} S}{N} (1 - \frac{S^{*}}{S}) (1 - \frac{C_{u *} S * N}{C_{u} SN *}) - \frac{β α_{2} C_{a} S}{N} (1 - \frac{S^{*}}{S}) (1 - \frac{C_{a *} S * N}{C_{a} SN *}) - σA (1 - \frac{S^{*}}{S}) (1 - \frac{A^{*}}{A}) + \frac{βAS}{N} (1 - \frac{A^{*}}{A}) (1 - \frac{S^{*} N}{SN *}) + \frac{β α_{1} C_{u} S}{N} (1 - \frac{A^{*}}{A}) (1 - \frac{C_{u *} S * AN}{C_{u} SA * N *}) + \frac{β α_{2} C_{a} S}{N} (1 - \frac{A^{*}}{A}) (1 - \frac{C_{a *} S * AN}{C_{a} SA * N *}) + σA (1 - \frac{{C_{u}}^{*}}{C_{u}}) (1 - \frac{A^{*} C_{u}}{A C_{u} *}) + ν_{2} C_{u} (1 - \frac{{C_{a}}^{*}}{C_{a}}) (1 - \frac{{C_{u}}^{*} C_{a}}{C_{u} C_{a} *}) + ν_{1} A (1 - \frac{{C_{a}}^{*}}{C_{a}}) (1 - \frac{A^{*} C_{a}}{A C_{a} *}) + δ C_{a} (1 - \frac{{T_{c}}^{*}}{T_{c}}) (1 - \frac{C_{a} * T_{c}}{C_{a} T_{c} *}) - μR (1 - \frac{R^{*}}{R}) (1 - \frac{R * T_{c}}{{RT}_{c} *})

(34)

= - μS {(1 - \frac{S^{*}}{S})}^{2} + P_{1} (S, A, C_{a}, C_{u}, T_{c}, R) + P_{2} (S, A, C_{a}, C_{u}, T_{c}, R)

where,

P_{1} (S, A, C_{a}, C_{u}, T_{c}, R) = - \frac{βAS}{N} (1 - \frac{S^{*}}{S}) (1 - \frac{A^{*} S^{*} N}{ASN *}) - \frac{β α_{1} C_{u} S}{N} (1 - \frac{S^{*}}{S}) (1 - \frac{C_{u *} S * N}{C_{u} SN *}) - \frac{β α_{2} C_{a} S}{N} (1 - \frac{S^{*}}{S}) (1 - \frac{C_{a *} S * N}{C_{a} SN *}) - σA (1 - \frac{S^{*}}{S}) (1 - \frac{A^{*}}{A}) - μR (1 - \frac{R^{*}}{R}) (1 - \frac{R * T_{c}}{{RT}_{c} *})

P_{2} (S, A, C_{a}, C_{u}, T_{c}, R) = \frac{βAS}{N} (1 - \frac{A^{*}}{A}) (1 - \frac{S^{*} N}{SN *}) + \frac{β α_{1} C_{u} S}{N} (1 - \frac{A^{*}}{A}) (1 - \frac{C_{u *} S * AN}{C_{u} SA * N *}) + \frac{β α_{2} C_{a} S}{N} (1 - \frac{A^{*}}{A}) (1 - \frac{C_{a *} S * AN}{C_{a} SA * N *}) + σA (1 - \frac{{C_{u}}^{*}}{C_{u}}) (1 - \frac{A^{*} C_{u}}{A C_{u} *}) + ν_{2} C_{u} (1 - \frac{{C_{a}}^{*}}{C_{a}}) (1 - \frac{{C_{u}}^{*} C_{a}}{C_{u} C_{a} *}) + ν_{1} A (1 - \frac{{C_{a}}^{*}}{C_{a}}) (1 - \frac{A^{*} C_{a}}{A C_{a} *}) + δ C_{a} (1 - \frac{{T_{c}}^{*}}{T_{c}}) (1 - \frac{C_{a} * T_{c}}{C_{a} T_{c} *})

$P_{1} \leq 0$ whenever

(35)

ASN * \geq A^{*} S^{*} N, C_{u} SN * \geq {C_{u}}^{*} S^{*} N, C_{a} SN * \geq {C_{a}}^{*} S^{*} N, R T_{c} * \geq R * T_{c}

and $P_{2} \leq 0$ whenever

(36)

S^{*} N \geq SN *, C_{u} * S * AN \geq C_{u} SA * N *, {C_{a}}^{*} S^{*} AN \geq C_{a} SA * N *, A * C_{u} \geq A C_{u} *, C_{u} * C_{a} \geq C_{u} {C_{a}}^{*}, A * C_{a} \geq A {C_{a}}^{*}, {C_{a}}^{*} T_{c} \geq C_{a} T_{c} *

Thus, $\frac{dL}{dt} \leq 0$ if the condition in (35) and (36) holds.

therefore, by LaSalle asymptotic stability theorem (LaSalle, 1976), and Oke et al. (2020) the positive equilibrium state $\frac{dL}{dt}$ is globally asymptotically stable in the positive region $R_{+}^{6}$ .

3. Numerical computation

The numerical study is carried out using maple software embedded code for the Runge-Kutta of fourth order. Here, the subsequent default values are assumed for the embedded parameters taken from theoretical studies in literatures $γ = 0.9, β = 0.008, σ = 0.59, d (c) = 0.00693, μ = 0.00693, ω = 0.1, ν_{1} = 0.002, ν_{2} = 0.002, α_{1} = 0.0016, α_{2} = 0.0016, δ = 0.0085, Π = 0.07$ . The values remain unchanged throughout* the computations except otherwise indicated.

The effects of varying the testing rate of the acute individuals $(υ_{1}),$ testing rate of chronic individuals ( $υ_{2}$ ) and treatment rate of chronic individuals ( $δ$ ) on the population dynamics are shown in Figures 2 to 7. From Figures 2 and 3, an increase in the parameters values reduces susceptible and acute populations thereby reducing the spread HBV due to low interaction between the host immune system and the virus. Therefore, the appearance of HBV and the pathogenesis reduces, which in so doing, lessens the potential injury on the liver. Hence, the liver is shielded from hepatocellular carcinoma over time. The rate of chronic unaware and chronically aware individuals is examined in Figures 4 and 5. The parameter variations show a significant decrease in the chronic unaware population which implies that testing at that stage is a great tool for reducing the disease transmission. The transmission process dies down as the time progresses; this discourages liver inflammation as a result of lowering the infected individuals. Meanwhile, the chronic population in Figure 5, depicts a high significant influence of the acutely infected and chronically unaware infected individuals over time. A chronic infection phase is found at the time range $10 < t < 20,$ as such, the individuals are exposed to liver carcinoma or cirrhosis. Hence, the chronic population diminishes as the parameters are increased.

Figure 2.

Behavioral dynamics of susceptible population when varying testing rate for acute and chronic individuals and treatment for chronic individuals.

Figure 3.

Behavioral dynamics of acute population when varying testing rate for acute and chronic individuals and treatment for chronic individuals.

Figure 4.

Behavioral dynamics of chronic unaware population when varying testing rate for acute and chronic individuals and treatment for chronic individuals.

Figure 5.

Behavioral dynamics of chronic aware population when varying testing rate for acute and chronic individuals and treatment for chronic individuals.

Figure 6.

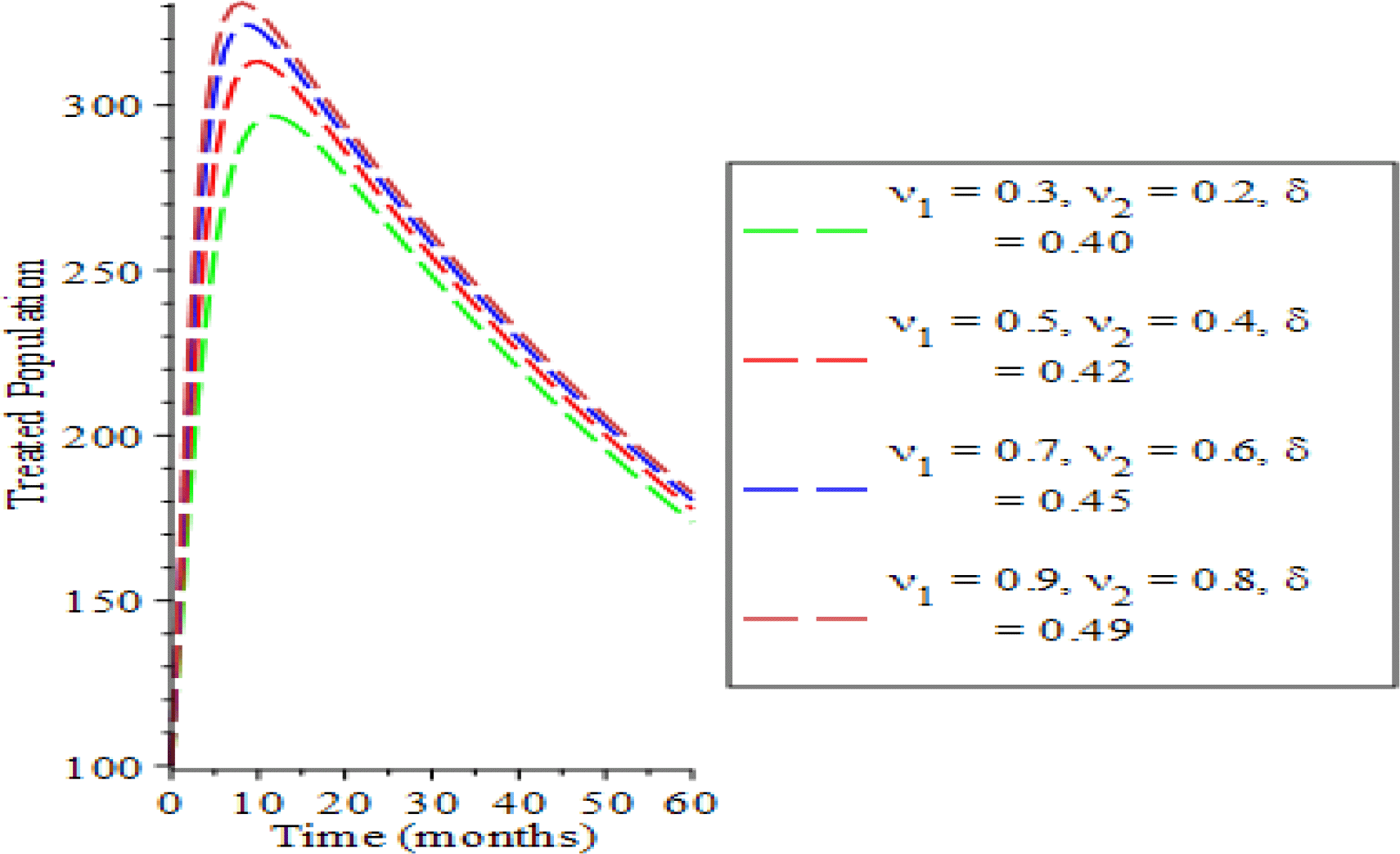
Behavioral dynamics of treated population when varying testing rate for acute and chronic individuals and treatment for chronic individuals.

Figure 7.

Behavioral dynamics of recovered population when varying testing rate for acute and chronic individuals and treatment for chronic individuals.

In Figures 6 and 7, the impact of varying the testing rate of the acute individuals $(υ_{1}),$ testing rate of chronic individuals ( $υ_{2}$ ) and treatment rate of chronic individuals ( $δ$ ) on the treated and the recovered population are presented. The treated population increases with parameters variation along the rising time (t) as a result of long time effect of parameter values. The recovery rate is enhanced as observed in Figure 7 due to significant simulation of surface antibodies of Hepatitis B. This is in conformity with the works of Pang et al. (2010) and Ullah et al. (2019). This result implies that an intensification in testing at all infectious states and rise in treatment of chronic individual will bring about a reduction in the HBV transmission process which is a response to the WHO goal for 2030 that concentrating efforts on awareness program and campaign will sure bring about a decrease or eradication in the transmission process of the virus (WHO, 2020).

4. Conclusion

A deterministic model of hepatitis B testing was developed and investigated, which included testing in the chronic unaware state as well as testing in all infectious states. The model has disease-free and endemic equilibria. The basic reproduction number was calculated using the next generation matrix method. The equilibria's local and global stability were discussed and shown to be asymptotically stable. The testing and treatment rate effects were thoroughly discussed.

Data availability

No data are associated with this article.

Grant information

None declared.

Competing interests

None declared.

References

Ciupe SM, Ribeiro RM, Perelson AS: Antibody Responses during Hepatitis B Viral Infection. PLoS Comput Biol. 2014; 10(7): e1003730. PubMed Abstract | Publisher Full Text | Free Full Text
Cohen C, Holmberg SD, McMahon BJ, et al.: Is chronic hepatitis B being undertreated in the United States? J Viral Hepatol. 2011; 18(1):377–383. PubMed Abstract | Publisher Full Text
LaSalle JP: The Stability of Dynamical Systems, Regional Conference Series in Applied Mathematics Philadelphia, Pa,USA: SIAM; 1976.
Lin SY, Chang ET, So SK: Stopping a silent killer in the underserved Asian and pacific islander community: a chronic hepatitis B and liver cancer prevention clinic by medical students. Asian Pac J Cancer Prev. 2009; 10(9):383–386. PubMed Abstract
McPherson S, Valappil M, Moses SE, et al.: Targeted case finding for hepatitis B using dry blood spot testing in the British-Chinese and South Asian populations of the North-East of England. J Viral Hepatol. 2013; 20(1):638–644. PubMed Abstract | Publisher Full Text
Meffre C, Le Strat Y, Delarocque-Astagneau E, et al.: Prevalence of hepatitis B and hepatitis C virus infections in France in 2004: social factors are important predictors after adjusting for known risk factors. J Med Virol. 2010; 82(2), 546–555. PubMed Abstract | Publisher Full Text
Mpeshe SC, Nyerere N: Modeling approach to assess the transmission dynamics of Hepatitis B infection in Africa. Int J Advance App Math Mechanic. 2019; 6(3): 51–61.
Niederau C: Chronic hepatitis B in 2014: great therapeutic progress, large diagnostic deficit. World J Gastroenterol. 2014; 20(33):11595–11617. PubMed Abstract | Publisher Full Text | Free Full Text
Oke IS, Ojo MM, Adeniyi OM, et al.: Mathematical modeling of malaria disease with control strategy. Comm Math Biol Neurosci. 2020; 43(1), 180–188. Publisher Full Text
Pang J, Cui JA, Zhou X: Dynamical behavior of a hepatitis B virus transmission model with vaccination. J Theoretical Biol. 2010; 265(4):572–578. PubMed Abstract | Publisher Full Text
Piorkowsky NY: Europe’s hepatitis challenge: defusing the “viral time bomb”. J Hepatol. 2009; 51(1):1068–1073. PubMed Abstract | Publisher Full Text
Ullah S, Khan MA, Gómez-Aguilar JF: Mathematical formulation of hepatitis B virus with optimal control analysis. Optim Control Appl Methods. 2019; 40(3):529–544. Publisher Full Text
Zhang J, Zhang S: Application and Optimal Control for an HBV Model with Vaccination and Treatment. Discrete Dyn Nat Soc. 2018; 20(7):69–73. Publisher Full Text

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 17 Sep 2021

Author details Author details

¹ Physical sciences, Landmark University, Omu Aran, Kwara State, Nigeria
² Physical Sciences, Landmark University, Omu Aran, Kwara, Nigeria
³ Biological Sciences, Landmark University, Omu Aran, Kwara, Nigeria
⁴ Mathematics, Lagos State Polytechnic, Lagos, Lagos, Nigeria
⁵ Physical Sciences (Mathematics Programme), Landmark University, Omu Aran, Kwara, Nigeria
⁶ Computer Science, Landmark University, Omu Aran, Kwara, Nigeria

Olajumoke Oludoun
Roles: Conceptualization, Methodology, Writing – Original Draft Preparation

Olukayode Adebimpe
Roles: Conceptualization, Writing – Review & Editing

James Ndako
Roles: Supervision, Writing – Review & Editing

Michael Adeniyi
Roles: Methodology

Oluwakemi E. Abiodun
Roles: Methodology, Writing – Original Draft Preparation

Babatunde Gbadamosi
Roles: Formal Analysis

Competing interests

No competing interests were disclosed.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Article Versions (1)

version 1

Published: 17 Sep 2021, 10:936

https://doi.org/10.12688/f1000research.72865.1

Copyright

© 2021 Oludoun O et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

Oludoun O, Adebimpe O, Ndako J et al. The impact of testing and treatment on the dynamics of Hepatitis B virus [version 1; peer review: 2 approved]. F1000Research 2021, 10:936 (https://doi.org/10.12688/f1000research.72865.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 1

VERSION 1

PUBLISHED 17 Sep 2021

Views

4

Reviewer Report 17 Dec 2021

Segun oke, Department of Mathematical and Applied Mathematics, University of Pretoria, Pretoria, South Africa

Approved

https://doi.org/10.5256/f1000research.76473.r94650

The authors worked on the impact of testing and treatment on the dynamics of Hepatitis B virus. Although the manuscript is well presented and gives new insight into the Hepatitis B virus, especially for unvaccinated men who have sex with ... Continue reading

The authors worked on the impact of testing and treatment on the dynamics of Hepatitis B virus. Although the manuscript is well presented and gives new insight into the Hepatitis B virus, especially for unvaccinated men who have sex with men (MSM) and heterosexual people who have multiple sexual partners or have contact with sex workers.

In their paper, a mathematical model was formulated to analyse the acquisition and transmission process of the virus with the view of identifying the possible way of reducing the menace and mitigating the risk of the virus. The models’ positivity and boundedness were demonstrated using well-known theorems. Equating the differential equations to zero demonstrates the equilibria of the solutions i.e., the disease-free and endemic equilibrium. The next Generation Matrix method was used to compute the basic reproduction number for the models. Local and global stabilities of the models were shown via linearization and contrition of Lyapunov function methods respectively. The authors concluded by showing disease-free, endemic equilibria. The basic reproduction number was calculated using the next-generation matrix method. The equilibria's local and global stability were discussed and shown to be asymptotically stable. The testing and treatment rate effects were thoroughly discussed. I believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Some minor comments:

The authors need to review more literature to back up their claims.
The introduction is too short and is not well cited. For example:

"In highly endemic areas, the most common form of transmission of hepatitis B is from mother to child at birth (vertical transmission) or through horizontal route (contact with infected blood), particularly from infected children to uninfected children during the first five years of life. vaginal and spermatic fluids and, to a lesser degree, perspiration, breast milk, tears, and urine. In particular, hepatitis B can be transmitted through sexual contact in unvaccinated men who have sex with men (MSM) and heterosexual people who have multiple sexual partners or have contact with sex workers" there is no citation here.
The authors need to add epidemiological interpretation and recommendations to the manuscript.
The conclusion needs to be rewritten.

Is the work clearly and accurately presented and does it cite the current literature?

No
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

No

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Mathematical modelling, Mathematical Oncology, Optimal control, Epidemiology, etc

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Respond or Comment

Views

12

Reviewer Report 06 Oct 2021

Sulyman Olakunle Salawu, Department of Mathematics, Landmark University, Omu-aran, Nigeria

Approved

https://doi.org/10.5256/f1000research.76473.r94651

Reviewer Reports on the impact of testing and treatment on the dynamics of Hepatitis B virus.
The impacts of different parameters were examined. The manuscript is well written and presented logically. The abstract captures accurately the whole work and ... Continue reading

Reviewer Reports on the impact of testing and treatment on the dynamics of Hepatitis B virus.
The impacts of different parameters were examined. The manuscript is well written and presented logically. The abstract captures accurately the whole work and the introduction is sound. However, I have the following comments and queries for the authors:

The authors should explain what prompted the choice of method of solution used over other techniques.
The significance and motivation of the study are not clear. The authors should clarify these.
There is a need to reference equation (3) to establish its correctness and source.
Some grammatical mistakes should be checked through.
Why have the authors chosen to engage in this study?
A likely extension of the study should be stated or recommended.

The manuscript should be indexed subject to minor correction.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

No source data required
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Mathematical Modeling and flow dynamic

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Respond or Comment

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 17 Sep 2021

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 1 17 Sep 21	read	read

Sulyman Olakunle Salawu, Landmark University, Omu-aran, Nigeria
Segun oke, University of Pretoria, Pretoria, South Africa

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

Back to all reports

Reviewer Report

4 Views

17 Dec 2021 | for Version 1

Segun oke, Department of Mathematical and Applied Mathematics, University of Pretoria, Pretoria, South Africa

4 Views Cite this report Responses(0)

Approved

The authors worked on the impact of testing and treatment on the dynamics of Hepatitis B virus. Although the manuscript is well presented and gives new insight into the Hepatitis B virus, especially for unvaccinated men who have sex with men (MSM) and heterosexual people who have multiple sexual partners or have contact with sex workers.

In their paper, a mathematical model was formulated to analyse the acquisition and transmission process of the virus with the view of identifying the possible way of reducing the menace and mitigating the risk of the virus. The models’ positivity and boundedness were demonstrated using well-known theorems. Equating the differential equations to zero demonstrates the equilibria of the solutions i.e., the disease-free and endemic equilibrium. The next Generation Matrix method was used to compute the basic reproduction number for the models. Local and global stabilities of the models were shown via linearization and contrition of Lyapunov function methods respectively. The authors concluded by showing disease-free, endemic equilibria. The basic reproduction number was calculated using the next-generation matrix method. The equilibria's local and global stability were discussed and shown to be asymptotically stable. The testing and treatment rate effects were thoroughly discussed. I believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Some minor comments:

The authors need to review more literature to back up their claims.
The introduction is too short and is not well cited. For example:

"In highly endemic areas, the most common form of transmission of hepatitis B is from mother to child at birth (vertical transmission) or through horizontal route (contact with infected blood), particularly from infected children to uninfected children during the first five years of life. vaginal and spermatic fluids and, to a lesser degree, perspiration, breast milk, tears, and urine. In particular, hepatitis B can be transmitted through sexual contact in unvaccinated men who have sex with men (MSM) and heterosexual people who have multiple sexual partners or have contact with sex workers" there is no citation here.
The authors need to add epidemiological interpretation and recommendations to the manuscript.
The conclusion needs to be rewritten.

Is the work clearly and accurately presented and does it cite the current literature?

No
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

No

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Mathematical modelling, Mathematical Oncology, Optimal control, Epidemiology, etc

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

12 Views

06 Oct 2021 | for Version 1

Sulyman Olakunle Salawu, Department of Mathematics, Landmark University, Omu-aran, Nigeria

12 Views Cite this report Responses(0)

Approved

Reviewer Reports on the impact of testing and treatment on the dynamics of Hepatitis B virus.
The impacts of different parameters were examined. The manuscript is well written and presented logically. The abstract captures accurately the whole work and the introduction is sound. However, I have the following comments and queries for the authors:

The authors should explain what prompted the choice of method of solution used over other techniques.
The significance and motivation of the study are not clear. The authors should clarify these.
There is a need to reference equation (3) to establish its correctness and source.
Some grammatical mistakes should be checked through.
Why have the authors chosen to engage in this study?
A likely extension of the study should be stated or recommended.

The manuscript should be indexed subject to minor correction.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

No source data required
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Mathematical Modeling and flow dynamic

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

[1] Ciupe SM, Ribeiro RM, Perelson AS: Antibody Responses during Hepatitis B Viral Infection. PLoS Comput Biol. 2014; 10(7): e1003730. PubMed Abstract | Publisher Full Text | Free Full Text

[2] Cohen C, Holmberg SD, McMahon BJ, et al.: Is chronic hepatitis B being undertreated in the United States? J Viral Hepatol. 2011; 18(1):377–383. PubMed Abstract | Publisher Full Text

[3] LaSalle JP: The Stability of Dynamical Systems, Regional Conference Series in Applied Mathematics Philadelphia, Pa,USA: SIAM; 1976.

[4] Lin SY, Chang ET, So SK: Stopping a silent killer in the underserved Asian and pacific islander community: a chronic hepatitis B and liver cancer prevention clinic by medical students. Asian Pac J Cancer Prev. 2009; 10(9):383–386. PubMed Abstract

[5] McPherson S, Valappil M, Moses SE, et al.: Targeted case finding for hepatitis B using dry blood spot testing in the British-Chinese and South Asian populations of the North-East of England. J Viral Hepatol. 2013; 20(1):638–644. PubMed Abstract | Publisher Full Text

[6] Meffre C, Le Strat Y, Delarocque-Astagneau E, et al.: Prevalence of hepatitis B and hepatitis C virus infections in France in 2004: social factors are important predictors after adjusting for known risk factors. J Med Virol. 2010; 82(2), 546–555. PubMed Abstract | Publisher Full Text

[7] Mpeshe SC, Nyerere N: Modeling approach to assess the transmission dynamics of Hepatitis B infection in Africa. Int J Advance App Math Mechanic. 2019; 6(3): 51–61.

[8] Niederau C: Chronic hepatitis B in 2014: great therapeutic progress, large diagnostic deficit. World J Gastroenterol. 2014; 20(33):11595–11617. PubMed Abstract | Publisher Full Text | Free Full Text

[9] Oke IS, Ojo MM, Adeniyi OM, et al.: Mathematical modeling of malaria disease with control strategy. Comm Math Biol Neurosci. 2020; 43(1), 180–188. Publisher Full Text

[10] Pang J, Cui JA, Zhou X: Dynamical behavior of a hepatitis B virus transmission model with vaccination. J Theoretical Biol. 2010; 265(4):572–578. PubMed Abstract | Publisher Full Text

[11] Piorkowsky NY: Europe’s hepatitis challenge: defusing the “viral time bomb”. J Hepatol. 2009; 51(1):1068–1073. PubMed Abstract | Publisher Full Text

[12] Ullah S, Khan MA, Gómez-Aguilar JF: Mathematical formulation of hepatitis B virus with optimal control analysis. Optim Control Appl Methods. 2019; 40(3):529–544. Publisher Full Text

[13] Zhang J, Zhang S: Application and Optimal Control for an HBV Model with Vaccination and Treatment. Discrete Dyn Nat Soc. 2018; 20(7):69–73. Publisher Full Text

The impact of testing and treatment on the dynamics of Hepatitis B virus

Abstract

Keywords

1. Introduction

2. Mathematical formulation

(1)

(2)

Figure 1. Compartmental flow diagram of HBV model.

(3)

2.1 Positivity and boundedness of solutions

(4)

(5)

(6)

2.2 Equilibrium points

(7)

(8)

(9)

(10)

(11)

(12)

(13)

2.3 Basic reproduction number

(14)

2.4 Local stability analysis of the disease-free equilibrium E0

(15)

(16)

(17)

2.5 Global stability of the disease-free equilibrium

(18)

(19)

(20)

(21)

(22)

(23)

2.6 Local stability of endemic equilibrium

(25)

(26)

(27)

2.7 Global stability of the endemic equilibrium

(28)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

(36)

3. Numerical computation

Figure 2.

Figure 3.

Figure 4.

Figure 5.

Figure 6.

Figure 7.

4. Conclusion

Data availability

Grant information

Competing interests

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated

2.4 Local stability analysis of the disease-free equilibrium $E_{0}$