Introduction
The evolutionary mechanism of conservation during embryogenesis, and its connection to the gene regulatory networks that control development, are fundamental questions in systems biology1–3. Several models have been presented in the context of morphological, molecular, and genetic developmental patterns. The most widely discussed model is the “developmental hourglass”, which places the strongest conservation across species in the “phylotypic stage”. The first observations supporting the hourglass model go back to von Baer when he noticed that there exists a mid-developmental stage in which embryos of different animals look similar4. On the other hand, the “developmental funnel” model of conservation predicts increasing diversification as development progresses5,6.
Recently, the hourglass model has come under new light. Multiple studies have observed the hourglass pattern across diverse biological processes, including transcriptome divergence7–12, transcriptome age7,13,14, molecular interaction15, and evolutionary selective constraints10,15,16. Despite these observations the genomic basis and even the existence of the developmental hourglass effect have been the subject of an intense debate1,6,14,17–22. More importantly, the underlying mechanism that can shape the developmental process in the hourglass or funnel forms is still unknown.
We aim to understand the conditions under which the hourglass effect can emerge in a general setting, based on an abstract model for the evolution of embryonic development. The model focuses on a hierarchical network that represents the temporal “execution” of the underlying Gene Regulatory Network (GRN) during development. Each layer of the network corresponds to a developmental stage. The nodes at each layer represent regulatory genes (i.e., genes encoding transcription factors or signaling molecules) that undergo significant activity change at that corresponding stage. The edges from genes at one layer to genes at the next layer represent regulatory interactions that cause those activity changes. We refer to this hierarchical network as Developmental Gene Execution Network (DGEN) to distinguish it from the corresponding GRN. A DGEN is subject to evolutionary perturbations (e.g., gene deletions, rewiring, duplication) that may be lethal, or that may impede development, for the corresponding organism.
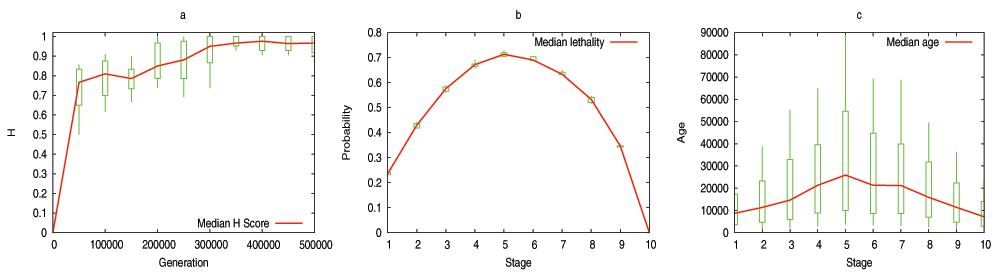
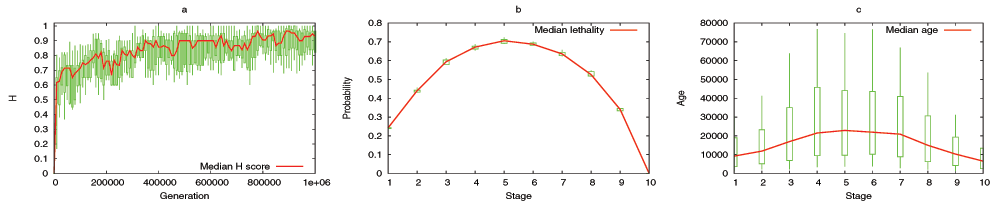
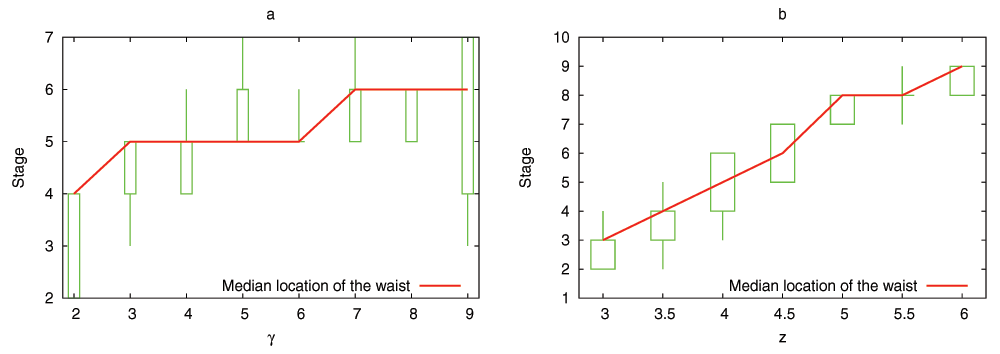
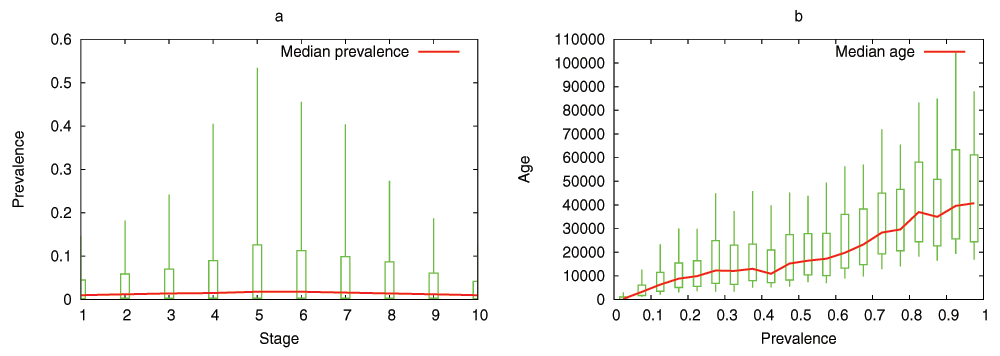
The model predicts that the evolutionary process shapes the DGENs of a population in the form of an hourglass, under fairly general assumptions. Specifically, the number of genes at each developmental stage follows an hourglass pattern, with the smallest number at the “waist” of the hourglass. The main condition for the appearance of the hourglass pattern is that the DGEN should gradually get sparser as development progresses, with general-purpose regulatory genes at the earlier developmental stages and highly specialized regulatory genes at the later stages. This assumption is motivated from the well established patterns of increasing modularity as the embryo develops23. Under the previous condition, the model predicts that gene regulatory changes or rewiring in mid-development are more likely to cause cascades of removing non-essential genes from the DGEN, compared to early or late developmental stages. Another model prediction is that the evolutionary age of DGEN genes also follows an hourglass pattern, with the oldest genes concentrated at the waist.
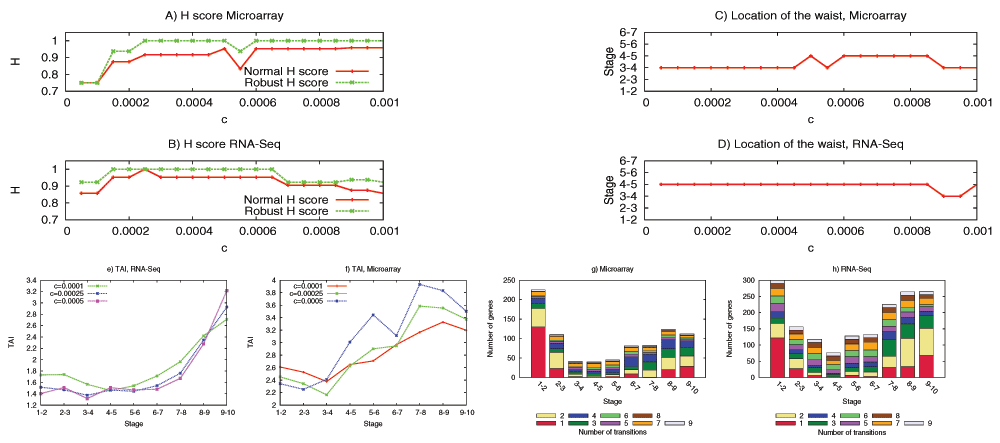
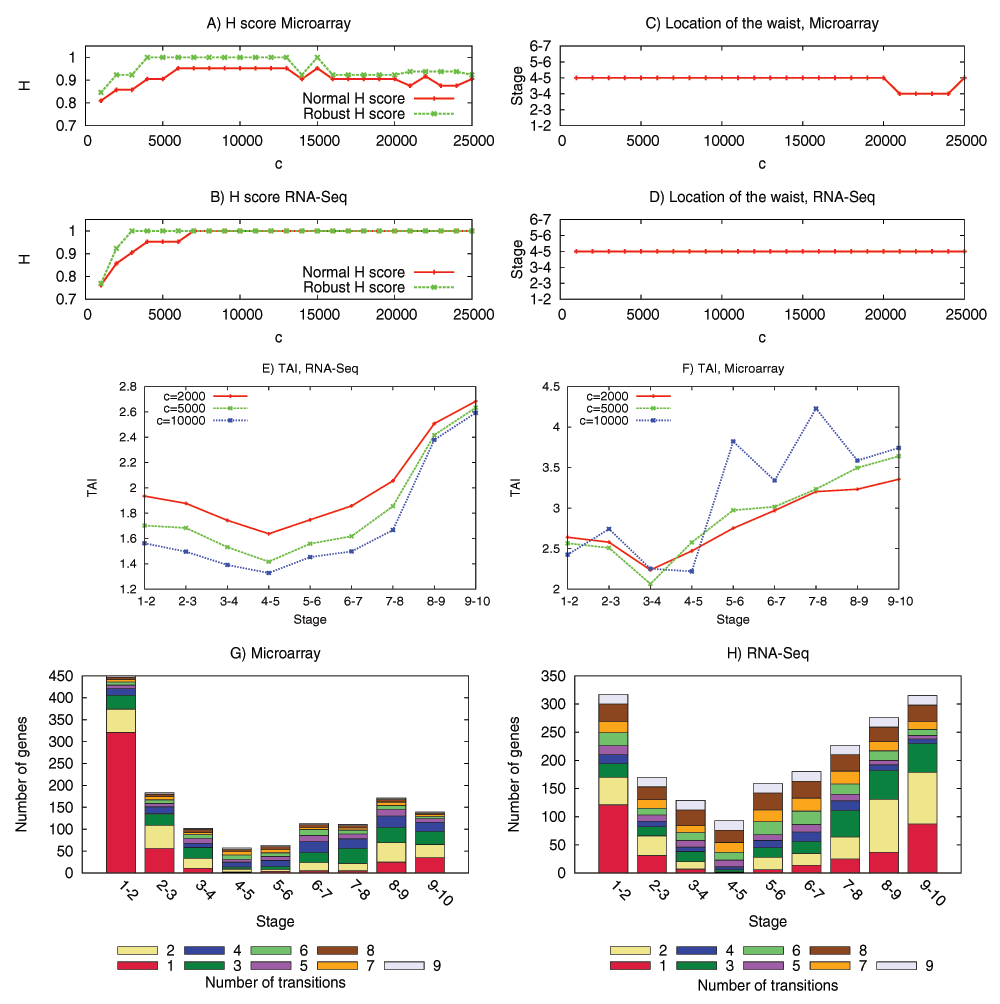
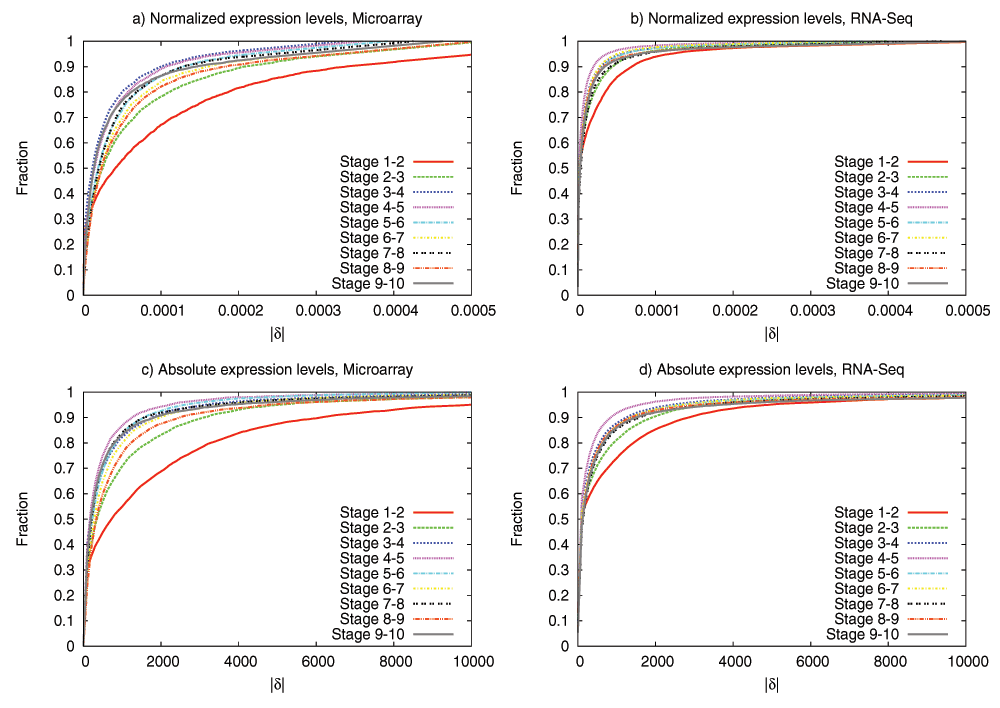
We have examined the aforementioned predictions using transcriptome data from the development of Drosophila melanogaster and Arabidopsis thaliana. This data is insufficient to reconstruct the complete DGEN of these species but it allows to estimate the number of genes at each developmental stage, given an activity variation threshold. Under a wide range of this threshold, the inferred DGEN shape follows an hourglass pattern, the waist of that hourglass roughly coincides with the previously reported phylotypic stage for these species, and the age of the corresponding genes follows the predicted hourglass pattern.
Developmental gene execution networks
As a first-order approximation, a regulatory gene can be modeled in one of several discrete functional states24. In the simplest case, a regulatory gene can act as a binary switch (“on” and “off”) but in general a gene may have more than two functional states. The transition of a regulatory gene X from one functional state to another is often (but not always) caused by one or more upstream regulators of X that go through a functional state transition before X. We use the term transitioning gene to refer to a regulatory gene that goes through a functional state transition at a given developmental time anywhere at the developing embryo.
A DGEN is a directed and acyclic network; see Figure 1a for an abstract example. The vertical direction refers to developmental time, from the zygote at the top to the developed organism at the bottom. In the horizontal direction we can represent different spatial domains, even though this is not necessary and it is not done in our model. For instance, the zygote at the top of the DGEN would be a single domain, while the organism at the bottom of the DGEN would have the largest number of spatial domains.
Development is often approximated (conceptually and experimentally) as a succession of discrete developmental stages. The duration of a developmental stage can be thought of as the typical time that is required for a gene’s functional state transition, and it does not need to be the same for all stages. Each layer of a DGEN refers to a developmental stage, and it includes only the transitioning genes during that stage anywhere in the embryo. The same gene can appear in more than one stage if it goes through several functional state transitions during development. Additionally, a DGEN edge from a gene X at stage l to a gene Y at stage l + 1 implies that the functional transition of X caused the functional transition of Y at the next stage. If gene Y has more than one incoming edge, its functional state transition was caused by the coupled effect of more than one transitioning genes at the earlier stage. Any upstream regulators of Y that remained at the same functional state at stage l are not included in that stage of the DGEN.
The sequence of developmental stages is denoted by l = 1 . . . L. The set of transitioning genes at stage l is G(l). A gene g at stage l<L regulates a set of downstream genes at stage l+1 denoted by D(g) (outgoing edges from g). Similarly, a gene g at stage l>1 is regulated by a set of upstream genes U(g) at stage l-1 (incoming edges to g). The functional transitions at the first stage are assumed to be caused by regulatory maternal genes that initiate the developmental process.
Model description
The model captures certain aspects of both the developmental process, in the form of a given DGEN for each embryo, and of the evolutionary process, as random perturbations in the structure of individual DGENs in a population. The model does not need to capture the actual functional state transitions or the regulatory input function of each gene. It does capture however the dynamic and stochastic effect of structural network perturbations (gene deletion, rewiring and duplication) on the success of the developmental process, as explained in the following.
Similar to the Wright-Fisher model25, we consider a population of N individuals, each represented by a DGEN. In each generation, individuals reproduce asexually, inheriting the DGEN of their parent. Various evolutionary events can cause structural changes in the DGEN of an individual that may result in “developmental failure”. Such individuals (and their DGENs) are replaced with developmentally successful individuals so that the population size remains constant.
The model is meant to be as general as possible and so the regulatory interactions between genes of successive stages are determined probabilistically, as follows. Each stage l is assigned a regulatory specificity, or simply specificity s(l) with 0 ≤ s(l) ≤ 1. A gene g at stage l acts as upstream regulator for a gene g′ at stage l + 1 with probability s′(l) = 1 − s(l). So, the specificity of a developmental stage determines how likely it is for regulatory genes of that stage to cause a state transition of the genes at the next stage; a higher specificity decreases that likelihood.
Our major assumption is that the regulatory specificity increases substantially as development progresses. In other words, the DGEN becomes gradually sparser along the developmental time axis, with s(1) << s(L). This assumption is plausible for the following reasons. First, as development progresses the embryo grows in size forming distinct spatial domains. So, extracellular gene regulation becomes more difficult, especially across different domains. Additionally, as development progresses the transitioning genes become more organ- or tissue-specific, implying that their downstream interactions become sparser. Unfortunately, a direct and empirical investigation of the increasing specificity assumption requires knowledge of the complete DGEN for a given species; this is currently not feasible for even the most well-studied model organisms. However, this assumption is plausible if we consider the well established patterns of increasing modularity as the embryo develops at the morphological, signaling, and genomic levels23.
The DGEN structural changes we consider are gene deletions, gene duplications, and gene rewiring:
Deletions (DL): This event removes a gene from the DGEN, including its incoming and outgoing edges. There are many genetic mechanisms that may cause such events. A DL event deletes each gene of an individual and at each generation with probability PDL.
Duplication (DP): This event creates an identical copy of a gene g with the same downstream and upstream regulators and at the same developmental stage as g. The two genes may have different fates if one of them is subject later to deletion or rewiring. Otherwise, the two genes are considered identical. A DP event duplicates each gene of an individual and at each generation with probability PDP.
Rewiring (RW): This event changes the upstream and/or downstream regulators of a gene. Changes in the upstream versus downstream regulators may have different biological basis. The former occur, for instance, as a result of mutations in the transcription factor binding sites in a gene’s promoter or mutations in distal regulatory elements such as enhancers, while the latter may be mostly caused by coding sequence mutations. The details of the rewiring process do not affect the results qualitatively as long as the average density of edges in each stage remains consistent with the specificity of that stage. The specific rewiring mechanisms we use are presented next.
Suppose that a RW event affects gene g at stage l. The upstream regulators of g are recomputed based on the specificity of the previous stage, i.e., by choosing each distinct gene of stage l −1 with probability s′(l −1). For the downstream regulators of g, we randomly remove N– existing outgoing edges of g, and then add N+ outgoing edges to randomly chosen genes of stage l + 1 that g is not already connected to. If B(N, p) denotes a Binomial random variable with N trials and success probability p, the random variables N− and N+ are independent and they both follow the B(|D(g)|, s′(l)) distribution (|X| denotes the cardinality of set X). Thus, the number of downstream edges of gene g after a Rewiring event becomes:
|Dnew(g)| = |D(g)| − N–+ N+,
which is at least 0 and at most 2 × |D(g)|. This captures that the downstream regulators of g are derived by incremental changes in D(g), instead of giving g a completely new network configuration (thereby, new regulatory function). The higher the regulatory specificity of a stage, the less likely these incremental changes are. An RW event rewires each gene of an individual and at each generation with probability PRW.
A gene deletion or rewiring event at stage l can remove an upstream regulator from genes at stage l + 1. A loss of incoming edges may trigger the regulatory failure of a gene, as described next.
Regulatory failures (RF): A gene g may not be able to change functional state if some of its upstream regulators U(g) are lost due to DL or RW events (see Figure 1b). Even though regulatory networks are often robust to structural perturbations, even a partial gene loss in U(g) may disable g causing a regulatory failure. It is plausible that the probability of a regulatory failure increases with the fraction of lost upstream regulators. So, if U′(g) is the new set of upstream regulators and |U(g)| > |U′(g)| > 0, gene g is removed with probability:
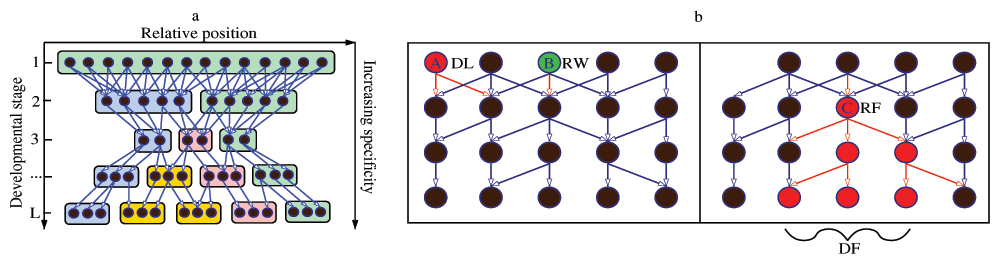
Figure 1. An abstract DGEN.
(A) The circles denote state-transitioning genes, edges represent directed regulatory interactions, and colored boxes refer to spatial domains that form during development. If regulatory genes become increasingly function-specific as development progresses, the network gradually becomes sparser in that direction. (B) Evolutionary perturbations on a DGEN’s structure: Gene A is deleted (DL), while gene B is rewired (RW) losing an outgoing edge. This RW event causes the regulatory failure (RF) of gene C, which then causes a cascade of five more RF events. This cascade causes developmental failure (DF). Note that the removal of some upstream regulators does not always cause an RF event (e.g., genes regulated by A).
while if |U′(g)| = 0 we set PRF (1) = 1. z is the RF parameter and it depends on the robustness of regulatory interactions to gene loss (see Figure 2).
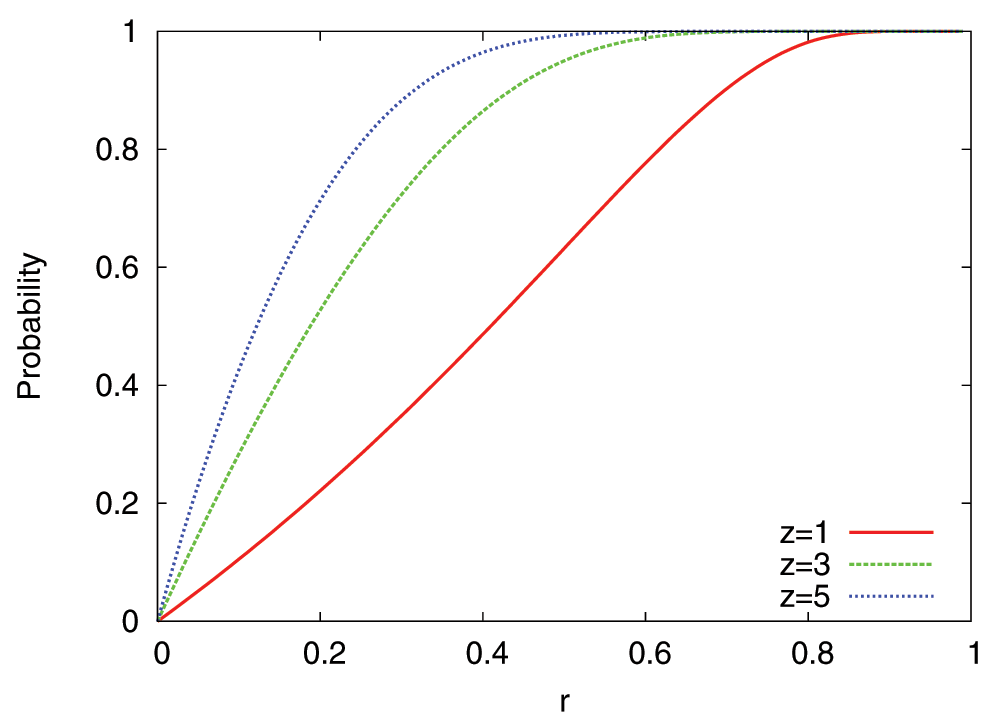
Figure 2. Probability of Regulatory Failure (RF) for three values of the parameter z.
r is the fraction of upstream regulating edges that are lost due to a DL or RW event.
When a DL or RW event causes one or more RF events, the latter can trigger additional RF events in subsequent developmental stages, leading to cascades of regulatory failures. Such RF cascades may cause developmental failure, meaning that the developed embryo is unable to survive or reproduce.
Developmental failure (DF): The last stage of a DGEN represents the fully developed embryo. If that stage includes Γ transitioning genes at a successfully developed embryo, the simplest assumption is that an individual with less than Γ genes at stage-L has failed to develop properly. Such DGENs are removed from the population and they are replaced with randomly chosen but successfully developed DGENs. We have also experimented with two variations of the DF event: first, the individual is removed if its last stage has less than Γ − γ genes, where γ is small relative to Γ, and second, the probability of a DF event increases as the number of genes at stage-L decreases below Γ. The qualitative results, as described next, do not change with these two model variations.






Comments on this article Comments (0)