Effect of microfluidic rectangular microelectrode geometry on bioparticles manipulation in dielectrophoretic application

Introduction

Dielectrophoresis (DEP) has been proven as a versatile manipulation technique commonly used in a microfluidic platform¹. DEP technique is commonly used to manipulate dielectric particles in a non-uniform electric field by the induction of DEP force (F_DEP)². Dielectrophoresis is an electrokinetic motion phenomenal occurring when a polarizable particle is put in nonuniform electric fields, and the particle mobility is influenced by the ambient electric field, as well as the characteristics of the dielectric particles or solutions³. Its versatility has provided various benefits for clinical application, laboratory diagnostics and research application⁴.

In the case of a DEP setting where target bioparticle (particle) such proteins and cells are in the submicro to nano size, the DEP force applied onto the particles will be extreme small. It is because according to the DEP equation (1), the key influence in particle motion by DEP force was determined by the electric field gradient and the particle volume, which was defined by its radius. Therefore, smaller particle will experience smaller DEP force for particle trapping or separation⁵. In order to compensate for this unchangeable particle radius variable, the microelectrodes geometry design must be optimized to provide an effective and higher performance of DEP response. To achieve of this, according to the equation (1), one of the optimizations of the microelectrodes geometry design that can be done is to design an electrode that can provide a higher electric field gradient to compensate the small particle radius⁶. Moreover, the optimization may lead to require lower voltage that can circumvent for joule heating effect, while having high throughput performance for higher particle DEP manipulation ability⁷.

For the case a homogeneous spherical particle in the suspension medium, the general time-averaged DEP force amplitude can be expressed by the classical DEP force as equation (1). ε_m denoted as the absolute relative permittivity of suspension medium, while ε₀= 8.854×10^-12 F/mis the permittivity of the vacuum, the spherical particle’s radius is denoted as r or r_ext,. E_RMS is the root-mean-square of the applied electric field in AC, and Re[f_CM] is the real part of Clausius-Mossotti (CM) factor². The equation of the real part of Clausius-Mossotti factor Re[f_CM] is given in equation (2).

The subscripts “p” and “m” are referred to particle and medium respectively. inline math and inline math are the complex permittivity with respect to particle and medium which can be defined as in equation (3)⁸

σ_p and σ_m is the electric conductivity of a particle and medium respectively. ω is angular frequency of the applied electric field defined as ω = πƒ, where ƒ is the frequency of the electric field and $j=\sqrt{-1}$.

In order to optimizing the electrode geometry and design, there are several geometrical parameters that will be affecting the electric field gradient ∇E² which are the width of the electrodes and the spacing between the two electrodes^9,10.

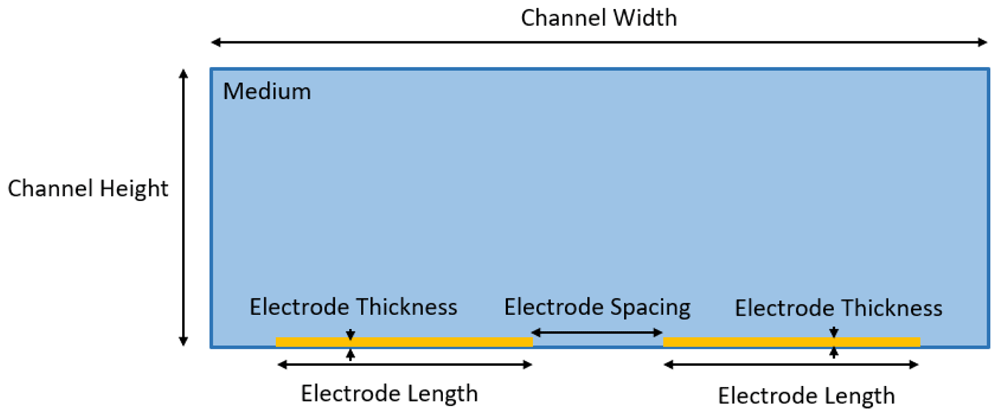
To further study on this, a rectangular geometry shape electrode has been designed as shown in Figure 1 which is an interdigitated castellated type design which consist of two same-sized electrodes, and these two electrodes are made up of gold material with the thickness of 0.15 µm. The two electrodes were positioned with a spacing gap between them and placed at the bottom of the microfluidic channel, the microelectrode dimension has been shown in Table 1. For 3 main variables with each parameter used to study the optimization of electric field gradient were: 1. the microfluidic channel height (20 µm, 30 µm, 40 µm, 50 µm), 2. the electrode width (20 µm, 40 µm, 60 µm, 80 µm, 100 µm) and 3. the electrode gap spacing (5 µm, 10 µm, 15 µm, 20 µm, 25 µm, 30 µm, 35 µm, 40 µm, 45 µm, 50 µm).

Figure 1. Top section view of the microfluidic channel and the rectangular microelectrode design.

Simulation study

A Finite Element Method (FEM) simulation study was performed by using COMSOL Multiphysics version 5.5 software (RRID: RRID:SCR_014767; URL: https://www.comsol.com/comsol-multiphysics). A 2D space dimension FEM simulation analysis has been carried for this study with only considering the cross-section view of the microfluidic change. Electric currents (ec) physics module was added to defines the electrical potential in the fluid domain and the electric field current was governed by the Ohm’s law continuity equation. The simulation study was carried out in the settings of frequency domain (AC). The governing equations for this frequency domain, electric current, electrical conductivity and relative permittivity are expressed as below:

J denoted as electric current density, σ is electrical conductivity, V electrical voltage, E electrical field, D electric displacement field, ε₀ is the relative permittivity of air and ε_r is the relative permittivity of the fluid respected to the air. By solving these equations, the electric field E in the microfluidic system is calculated and the electric field E is in direct relation to the amount of DEP force according to equation (1).

The cross-section microfluidic and its rectangular geometry electrodes have been created according to the dimension in the Figure 2. Gold material were assigned for both the electrodes with the electrical conductivity, σ = 44.2x10⁶ S/m and relative permittivity, ε = 1, for the medium within the microchannel was a deionized water with its electrical conductivity, σ = 0.0002 S/m and relative permittivity, ε = 78. Under the electric currents (ec) physics module, 10 V peak to peak AC electric potential was set to be applied to the electrodes. The boundaries of one electrode have been input an electric potential V₀ = 10V, while the other electrode with its boundaries were input with electric potential V₀ = -10 V. The remaining boundaries of the channel were set to be insulated. Extremely fine mesh was generated for this created model. Lastly, a study was generated with electric current model that defines the electrical potential and it is conducted in a frequency domain (AC).

Figure 2. Cross-section view of the microfluidic channel filled with suspending medium and both rectangular microelectrodes at the bottom.

The numerical results such as electrical potential distribution Vpp, electric field distribution V/m and electric field gradient ∇E² were generated from this model. This numerical study was performed with 5 different channel height (20µm, 30µm, 40µm, 50µm) and with the input of different combination parameters of electrode width and electrode spacing as according to the Table 2.

Results and Discussions

A parametric study on the geometrical parameters of rectangular shape microelectrode for DEP microfluidic platform has been conducted to identify its optimization microfluidic and electrode design for DEP manipulation of micro to nano particles. In this numerical study, an electric field gradient was generated in the model as shown in Figure 3, by further input of different design variables into the study model such channel height, electrode width and electrode spacing and its parameters to study the optimization of the rectangular microelectrode and identify its optimum design parameters. Electric field gradient $\nabla E_x^2$ is the key identifier for an effective DEP microfluidic platform, therefore in the generation of the electric field gradient result in this cross-section microfluidic model, only the horizontal component of the electric field gradient $\nabla E_x^2$ is considered.

Figure 3. Microfluidic channel and the microelectrodes model that created in the COMSOL simulation software.

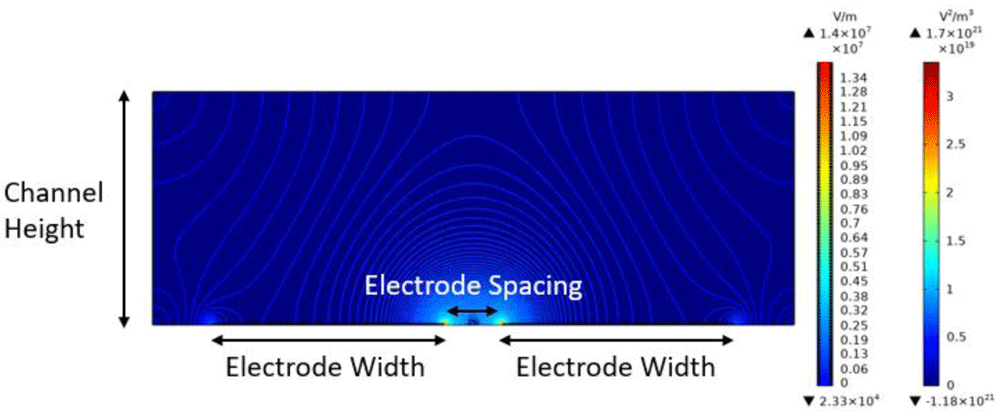
The result shows the electric field gradient distribution and the electric field contour.

According to the 3D plot result from Figure 4 has shown that the electric field gradient $\nabla E_x^2$ is exponentially increased when the applied peak-to-peak voltage is increased. However, the electric field gradient remained unchanged to the increase of applied frequency. Although the frequency has not contributed to the electric field gradient but note that it is still an important factor that influence the particle, as the particle DEP response is highly dependent on applied frequency and which is governed by the equation (2) and equation (3)¹¹. This result has shown that the applied voltage has a substantial influence on the electric field gradient, however the applied frequency will have no effect on the electric field gradient. From the generated 3D plot of all the 4 different channel heights as shown in Figure 5, it has been shown in all the graph that the electric field gradient is gradually decreasing when the electrode spacing is increased and the electric field gradient had a drop at certain point when the electrode width increased beyond 40µm and 80µm.

Figure 4. The influence on electric field gradient by the peak-to-peak voltage and frequency.

Figure 5. The 3D plots of the simulation results with the combination of the variables with its parameters.

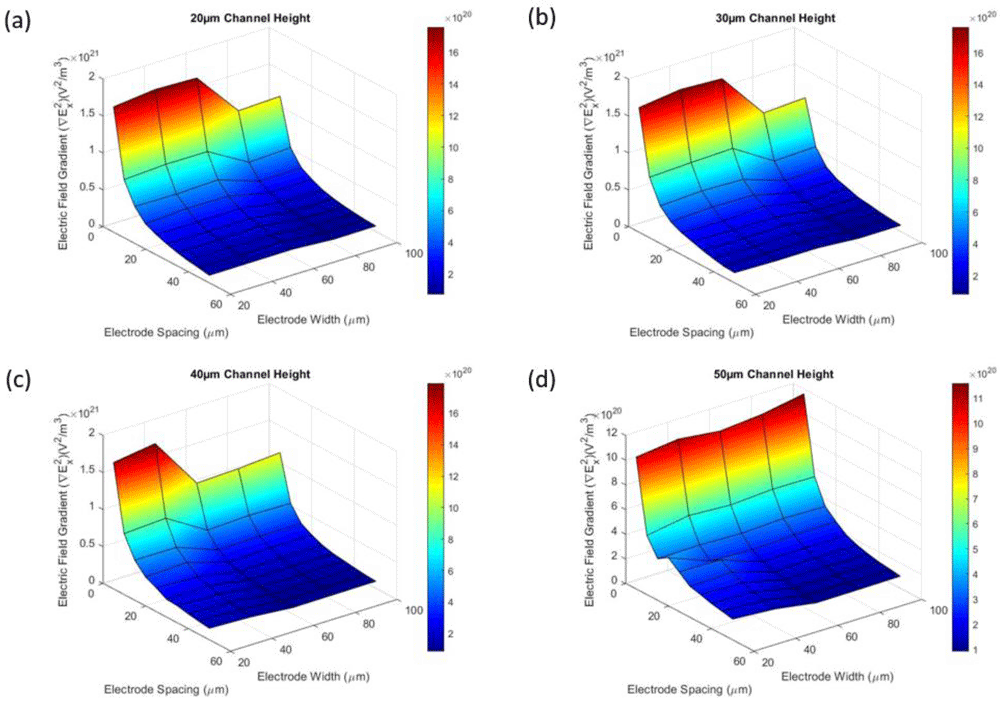
The 3D plots generated with MATLAB R2019b.

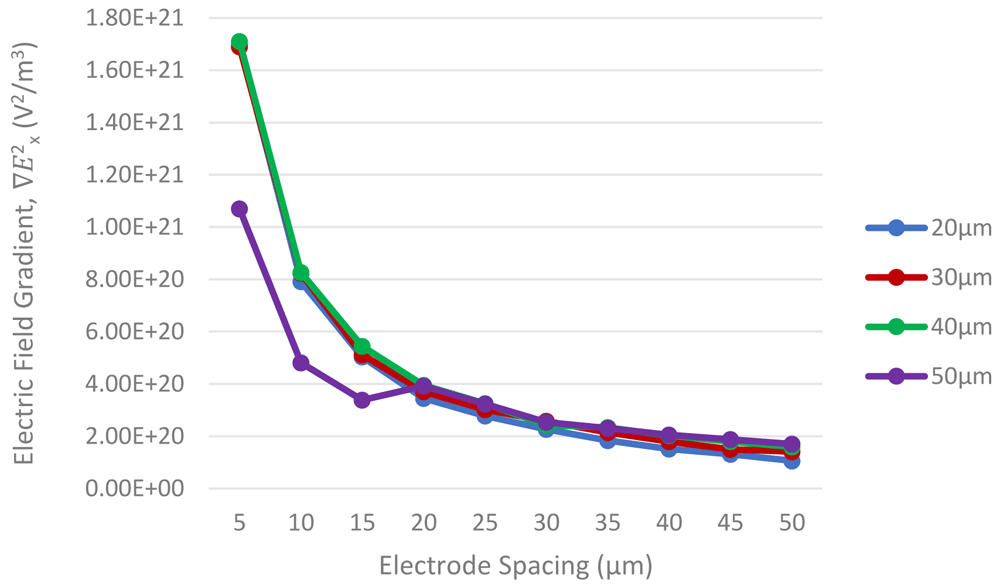
Firstly, for channel height influencing on ∇E²_x values are as shown in Figure 6. As observed from the graph, the difference in channel heights (20 µm, 30 µm, 40 µm) have similar pattern and have very little difference on the electrode’s ∇E²_x values. The ∇E²_x values gradually increased when the electrode spacing increased. Only the channel height of 50µm showed lowest ∇E²_x values at the beginning range of electrode spacing from 5 µm to 15 µm. Further to investigate, extend on channel height from 5 µm to 100 µm, with width of electrode 20 µm and electrode spacing 5 µm kept constant as shown in Figure 8. The ∇E²_x values have observed a fall between 40 µm to 70 µm channel height. Therefore, the optimum channel height design should be 40 µm.

Figure 6. Graph result of electrode spacing influence on the electric field gradient with respect to 20µm electrode width for different channel height.

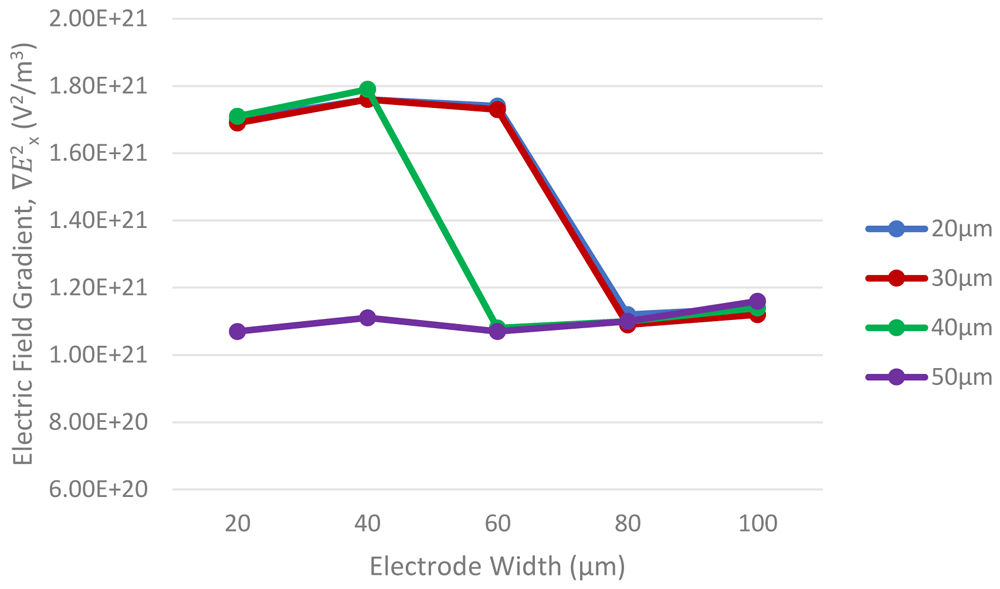
For the electrode widths results as shown in Figure 7, when the channel height is 20µm and 30µm, the ∇E²_x values for different range of electrode widths are in the same pattern. It has been shown that when the electrode width exceeded 60µm, the ∇E²_x values have dwindled about 64% drop in ∇E²_x value. For channel height 40µm the drop in ∇E²_x values have started early at 40µm electrode width. However, the electrode widths were not much influence on the ∇E²_x values when the channel height reached 50µm, but it has been the least amount of ∇E²_x values, it has about 63% less ∇E²_x values compared to other channel, since then the ∇E²_x values were not much fluctuated and constantly stayed within its ∇E²_x range. The optimum design for the electrode width is within 60µm and channel height within 30µm.

Figure 7. Graph result of electrode width influencing on electric field gradient for different channel height with respect to 5µm electrode spacing.

Figure 8. The graph of different channel height influencing on the electric field gradient ∇E2x with respect to constant electrode width 20 µm and electrode spacing 5 µm.

Conclusion

Based on the simulation results, the optimum geometrical parameters for rectangular shape electrode design for the strongest DEP force was identified. In this simulation and parametric studies were only focused on the DEP force and did not include other factors such as hydrodynamic forces, joule heating effects, particles Brownian motion in the microfluidic device. As according to this study, 1. The applied voltage has significant influence on electric field gradient, ∇E²_x, however the frequency will not have effect on electric field gradient, nonetheless it is strongly responsible to the DEP response of the particle based on the polarizability between the medium and particle, 2. For the optimum design considerations for rectangular shape microelectrode, the electrode width is advised to fall below 60µm and 3. the channel height should below 30µm to obtain the strongest DEP force for particle manipulation in this microfluidic design.