Analysis of the replanting of banana hills with infection by the bacterium <i>Ralstonia solanacearum</i> philotype II race 2 and economic losses

Marly Grajales-Amorocho; Cesar Acosta-Minoli; Dalia Muñoz-Pizza; Oscar Manrique-Arias; Anibal Muñoz Loaiza

doi:10.12688/f1000research.55456.1

Home Browse Analysis of the replanting of banana hills with infection by the bacterium...

ALL Metrics

-

Views

-

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Analysis of the replanting of banana hills with infection by the bacterium Ralstonia solanacearum philotype II race 2 and economic losses

[version 1; peer review: awaiting peer review]

Marly Grajales-Amorocho ¹, Cesar Acosta-Minoli², Dalia Muñoz-Pizza³, Oscar Manrique-Arias⁴, Anibal Muñoz Loaiza⁴

Marly Grajales-Amorocho ¹, Cesar Acosta-Minoli², [...] Dalia Muñoz-Pizza³, Oscar Manrique-Arias⁴, Anibal Muñoz Loaiza⁴

PUBLISHED 21 Apr 2022

Author details Author details

¹ Research group on Biodiversity and Biotechnology, University of Quindío, Armenia, Quindío, 630001, Colombia
² Software Study and Development Group, University of Quindío, Armenia, Quindío, Colombia
³ Oceanographic Research Institute, Autonomous University of Baja California, Ensenada, Baja California, Mexico
⁴ Group of Mathematical Modeling in Epidemiology, University of Quindío, Armenia, Quindío, Colombia

Marly Grajales-Amorocho
Roles: Conceptualization, Investigation, Methodology, Writing – Original Draft Preparation, Writing – Review & Editing

Cesar Acosta-Minoli
Roles: Conceptualization, Data Curation, Supervision

Dalia Muñoz-Pizza
Roles: Conceptualization, Writing – Review & Editing

Oscar Manrique-Arias
Roles: Data Curation, Formal Analysis, Investigation, Validation

Anibal Muñoz Loaiza
Roles: Data Curation, Formal Analysis, Investigation, Methodology, Supervision, Validation

OPEN PEER REVIEW

REVIEWER STATUS AWAITING PEER REVIEW

Abstract

Background: Moko is a disease caused by the bacterium Ralstonia solanacearum philotype II race 2, which has caused great economic losses and continues without proper management. So far there is no treatment to control the disease and the best solution is to avoid the arrival of the bacteria. This is done through strategies for managing the cultivation and eradication of infected plants, since the bacteria have the ability to spread through water, wind, and animals, among others. However, the main form of dispersal is infected planting material (hills). Methods: For this reason, to investigate the dynamics of Moko disease in plantain, a population simulation model with nonlinear ordinary differential equations was presented, with disease prevention and population of susceptible and infected plants and associated economic losses over time. Results: We found that replanting infected hills has a large effect on increasing the incidence of the disease and on production costs, in addition to generating greater economic losses. Both prevention strategies should be implemented in a medium proportion ( f=60% ; g=70%), in order to sustain a reasonable amount of susceptible plants over time. With this, the infected plants tend to be controlled, as well as leading to lower economic losses in general. Conclusion: cultural control strategies in banana Moko disease, such as disinfestation of tools, footwear, weed pruning, among others, are important agronomic practices for disease control, however the identification of infected hills plays an essential role in preventing the spread of the disease.

Keywords

Mathematical model, Moko, plantain, Ralstonia solanacearum.

Corresponding author: Marly Grajales-Amorocho

Competing interests: No competing interests were disclosed.

Grant information: This work was supported by the University of Quindío with the vice-rector for research and the group of mathematical modeling in epidemiology GMME - Colombia.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2022 Grajales-Amorocho M et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Grajales-Amorocho M, Acosta-Minoli C, Muñoz-Pizza D et al. Analysis of the replanting of banana hills with infection by the bacterium Ralstonia solanacearum philotype II race 2 and economic losses [version 1; peer review: awaiting peer review]. F1000Research 2022, 11:447 (https://doi.org/10.12688/f1000research.55456.1) First published: 21 Apr 2022, 11:447 (https://doi.org/10.12688/f1000research.55456.1) Latest published: 21 Apr 2022, 11:447 (https://doi.org/10.12688/f1000research.55456.1)

Introduction

The banana is a fruit of particular economic importance in the department of Quindío, Columbia. It is a ubiquitous part of the Colombian family shopping basket, and for this reason it is cultivated throughout the country. This cultivation has also provided the economic support for many households for many years. However, currently its cultivation worldwide continues to be affected by a phytosanitary problem caused by the bacterium Ralstonia solanacearum philotype II race 2 (Fegan & Prior, 2006), which produces the disease known as Moko, threatening the food security of thousands of people (Garćia et al., 2019).

This bacterium, after entering the plant, causes obstruction in the xylem, limiting the flow of water towards the aerial part of the plant, leading to symptoms such as wilting and yellowing of the youngest leaves It is found in high cell densities and infected tissues, a typical symptom is a white, milky liquid that accumulates on the surface of freshly cut stems, rhizomes or tubers (Agudelo Valencia & Florez Mogollon, 2019; Denny, 2006), as well as rot or non-uniform maturation of fruits. Infected plants will eventually die from the disease.

The forms of transmission are many, such as through infested soil, by root contact, by insect vectors (the flower cluster being the site of primary infection), by domestic animals, and by water. In infected plants the bacterium acts systematically in the tissues, being found both in the leaf, in the pseudostem, in the corm and even in the hill (the planting material). Infected hills is the main form of dispersion among the different banana-producing regions in most countries where the disease occurs (Álvarez et al., 2013). Infected hills that have not been identified are known to facilitate long-distance dispersal of bacterial wilt pathogens, and the spread of Moko disease from Central America to the Philippines has been attributed to infected planting material (Álvarez et al., 2013; Blomme et al., 2017).

Currently, the control of moko disease is limited to preventive measures (Figure 1), excessive use of pesticides, and eradication of diseased plants (Grajales-Amorocho & Muñoz-Loaiza, 2021). There is no clear plan to eliminate the bacteria by 100%, however, through comprehensive management measures, the application of the ICA plan and the management of plant material, it is possible to reduce the source of infection (Agudelo Valencia & Florez Mogollon, 2019). For this reason, in different regions, strategies are being implemented to obtain disease-free planting material through thermal chambers and in vitro culture among other tools (Álvarez et al., 2013). Likewise there is an urgent need to prioritize the application of the prevention and control strategies of the disease, to avoid an increase in the foci of infection, which would have consequences for the crops of those who do not implement them and for neighboring crops (Grajales-Amorocho & Muñoz-Loaiza, 2021). This is where mathematical modeling becomes a tool that serves to demonstrate the importance of these prevention strategies and to make decisions in possible future scenarios of increased incidence of the disease.

Figure 1. Plantain crop that implements prevention strategies in a farm of Armenia, Quindío, Colombia.

Vector-borne diseases have caused the devastation of many important crops around the world (Bokil et al., 2019). These authors modeled vector-borne diseases caused by viruses, but this time they included a constant reseeding rate that expanded existing models to include replanting frequency and replanting abundance. In overseeding frequency, when this is done with infected material dependent on the selection frequency parameter, while in overseeding in abundance, overseeding depends on abundance through a selection rate parameter represented $ε$ . The authors recognized different thresholds for disease elimination showing how the equilibrium densities of healthy plants and infected plants tolerance with the parameter values. They used the theory of optimal control to investigate the effects of the rogue and the use of insecticides in order to maximize the healthy plants that are harvested, finding differences in the control strategies in the two models for large values of $ε$ . Also, the combination of dishonest strategies and the use of insecticides work better than a single control.

Zhao and Smith (2019) established two impulsive models of diseases in plants with periodic and state-dependent non-linear cultural control, with the aim of eradicating disease and keeping the number of infected plants below an economic threshold. They focused on saturated non-linear weeding (rogué) (identification and removal of infected plants), with three scenarios for healthy plants: constant reseeding rate, proportional reseeding rate, and proportional incidental elimination. They determined the conditions for the existence and stability of the disease-free periodic solution, the existence of a positive periodic solution, and permanence. They found that extinction of the disease will be a consequence of the increase in the harvesting rate, the increase in the intervention period or the decrease in the number of replanting. These authors determined that control methods have an important effect on the development of the disease, and the density-dependent parameters can slow down extinction and promote the growth of healthy plants. These results suggest that the disease can be successfully eradicated or that the infection can be kept below the level with adequate control measures. The analysis methodology they developed provides a broad vision to explore plant disease models with non-linear impulsive control strategies.

Munar-Vivas et al. (2010) relied on information provided in field on maps integrated into the geographic information system (GIS) with the objective of evaluating the presence of Moko disease in the Colombian region of Urabá, in three periods of time. They were able to show that 76% of Moko found during the three time periods were linked to carts used to transport fruits and field consumables. The spread of the disease depends largely on the vulnerability or susceptibility of the host, as well as environmental conditions, proximity to sources of contaminated water, and management practices. Incubation times may change depending on the maturity stage of the infected plant, the route or mechanism of infection, and environmental conditions.

With all this in mind, a dynamic system was formulated based on ordinary differential equations that interpret the dynamics of the incidence of banana Moko disease, including prevention and analysis of production costs.

Methods

The model

Previously, mathematical models were used only for health problems in humans with epidemic models SI, SIS, SIR, SIRS among others; currently, they are a useful tool in various areas. With these models the representation of biological systems can be achieved and thus knowledge of the behavior and the dynamics of certain diseases are facilitated, helping to predict and make future decisions that facilitate control (Jeger et al., 2018).

A population model with nonlinear ordinary differential equations is proposed, which interprets the dynamics of the Moko of plantain, with the following assumptions:

• A fraction $h$ of reseeding with the disease is included.
• A constant reseeding rate is considered γ.
• A disease prevention fraction is included in the susceptible plant population over time.
• A variable population of plants is assumed.
• The maximum capacity of plants in the study region is included.
• A plant removal rate is considered with Moko.

The variables and parameters of the model are: $x (t)$ the average number of susceptible banana plants, and $y (t)$ the average number of infected banana plants and $P (t) = x (t) + y (t)$ total number of banana plants at time $t$ , respectively.

The model parameters are γ: constant replanting rate; $k$ : carrying capacity (maximum population) of banana plants in the study region; and β: probability of infection transmission. The preventive controls are $g$ : fraction of infected banana plants eliminated and $f$ : fraction of susceptible banana plants that receive prevention of contagion of the bacteria.

The dynamic system that interprets the infectious process including prevention and elimination (Figure 2), is formed by the following two non-linear differential equations:

(1)

\frac{dx (t)}{dt} = (1 - h) γ (1 - \frac{x (t) + y (t)}{k}) x (t) - β \frac{y (t)}{x (t) + y (t)} (1 - f) x (t)

(2)

\frac{dy (t)}{dt} = h γ (1 - \frac{x (t) + y (t)}{k}) x (t) + β \frac{y (t)}{x (t) + y (t)} (1 - f) x (t) - gy (t)

Figure 2. Banana Moko's disease diagram with prevention.

With initial conditions $x (0) = x_{0}$ , $y (0) = y_{0}$ , $P (0) = x (0) + y (0)$ , $γ$ , $k > 0$ , $0 < f$ , $g,$ $β < 1$ , $P \leq k$ .

The region of eco-epidemiological sense is defined where the trajectories of the plant infection dynamics make sense,

(3)

Ω = \{(x, y) \in R_{+}^{2} : 0 \leq x \leq k, 0 \leq y \leq k\} .

And the variation of the population of diseased plants eliminated in time, is given by the following equation,

(4)

\frac{dω (t)}{dt} = gy (t)

Results and conclusion

In this section the equations of economic losses and simulations of the populations and of these losses are derived.

Economic losses due to Moko

Is defined $r (t)$ as the load (incidence) of banana plants by infected hills in replanting and $\frac{dr}{dt}$ the variation of this population with respect to time,

(5)

\frac{dr (t)}{dt} = h γ (1 - \frac{x (t) + y (t)}{k}) x (t)

We define $P_{r} (t)$ the economic loss due to overseeding with infected hills, such that

(6)

P_{r} (t) = P_{r} r (t)

where

P_{r}

is the cost per hill planted and treated.

Deriving equation (6) with respect to $t$ and substituting the derivative $\frac{dr}{dt}$ , we obtain the differential equation for the economic loss due to replanting of infected hills

(7)

\frac{d P_{r} (t)}{dt} = P_{r} h γ (1 - \frac{x (t) + y (t)}{k}) x (t)

Similarly, we defined the economic loss by infected banana plants eliminated $P_{ω} (t),$

(8)

P_{ω} (t) = p_{ω} ω (t)

Where $P_{ω}$ is the cost of removing each plant with Moko.

Deriving with respect to $t$ and substituting the derivative $\frac{dω}{dt}$ , we obtain

(9)

\frac{Pω (t)}{dt} = p_{ω} gy (t)

The total loss by replanting and by elimination of infected plants in time is $P_{e} (t) = P_{ω} (t) + P_{r} (t)$ , and its variation in time is given by the differential equation,

(10)

\frac{P_{e} (t)}{dt} = p_{r} h γ (1 - \frac{x (t) + y (t)}{k}) x (t) + p_{ω} gy (t)

Population simulations and economic losses

The model simulations were made with Maple software version 18 (Maple, RRID:SCR_014449) using the values of the populations and initial losses, as the values of the parameters indicated in Table 1. An open-source alternative software that can perform equivalent functions is RStudio version 1.4 (RRID:SCR_000432).

Table 1. Variables, parameters, parameter values, and initial populations at $t = 0$ .

Variables, Parameters	Description	value	Reference
$x (t)$	Susceptible plants	800	-
$y (t)$	Infected plants	8	-
$P (t) = x (t) + y (t)$	Total plants	808	-
$ω (t)$	Eliminated infected plants	0	-
$P_{r} (t)$	Losses due to overseeding	0	-
$Pω (t)$	Elimination losses	0	-
$P_{e} (t)$	Total losses	0	-
$k$	Carrying capacity	1300	Per hectare
$h$	Overseeding percentage	0,1-0,3	Per hectare
$β$	Transmission coefficient	0,7	-
$γ$	Overseeding rate	3	-
$f$	Prevention percentage	0-0,1-0,8-0,6	-
$g$	Percentage Elimination of plants	0,1-0,8-0,7	-
$p_{ω}$	Costs for each $y$	10.200	Farmer
$p_{r}$	Costs for overseeding	1.500	Farmer

Evaluating different scenarios in the conditions of the strategies of prevention and elimination of infected plants, we can observe (as shown in Figure 3a) that implementing 10% of prevention strategies, eliminating 80% of the infected plants and doing a reseeding with 10 % of infected hills, the population of susceptible plants is sustained over time. This would be a good agronomic management for the sustainability of the crop, of the harvest and would avoid greater economic losses, associating only with losses of approximately 100 or 200,000 thousand pesos with a trend to stabilize at that value. However, the losses due to the elimination of infected plants would be greater when implementing this strategy in a greater proportion, highlighting that it is a methodology that must be implemented in large proportions to avoid the spread of the disease. On the contrary, in the reseeding of 30% infected hills with the same prevention conditions (Figure 3b), the economic losses associated with the elimination of infected plants tend to an exponential increase in costs week after week and replanting in week 50, with an approximate value of 2,000,000 pesos and a tendency to increase in the following weeks.

Figure 3. Behavior of economic losses due to overseeding (black line), by elimination of infected plants (red line) and total losses (blue line) in a time t with f=0,1 and g=0,8; for a) h=0,1 and d) h=0,3.

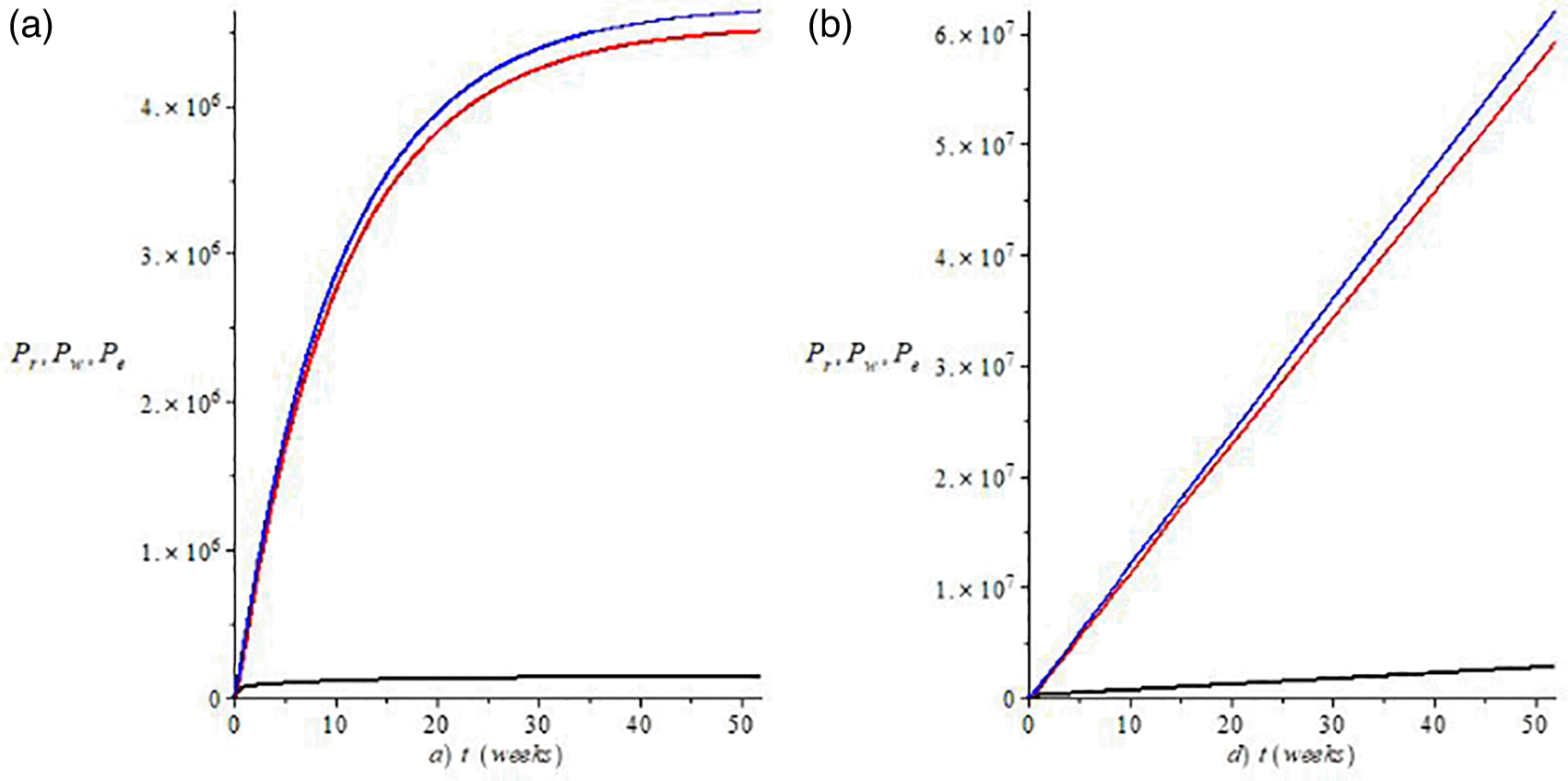
By evaluating different scenarios, we can demonstrate the importance of early elimination of infected plants, showing when the prevention strategies are implemented by 80% and only 10% of the infected plants are eliminated, the susceptible population tends over time to decrease. In terms of economic losses in these scenarios, in week 50 it can be observed that they are greater by approximately 1,000,000 pesos for reseeding by 30% (Figure 4b) compared to reseeding of 10%, which causes losses of approximately 200,000 pesos (Figure 4a). We can also see that the losses associated with infected plants and their elimination, in both cases will have an exponential increase week after week.

Figure 4. Behavior of economic losses due to overseeding (black line), by elimination of infected plants (red line) and total losses (blue line) in a time t with f=0,8 and g=0,1, for b) h=0,1 and e) h=0,3.

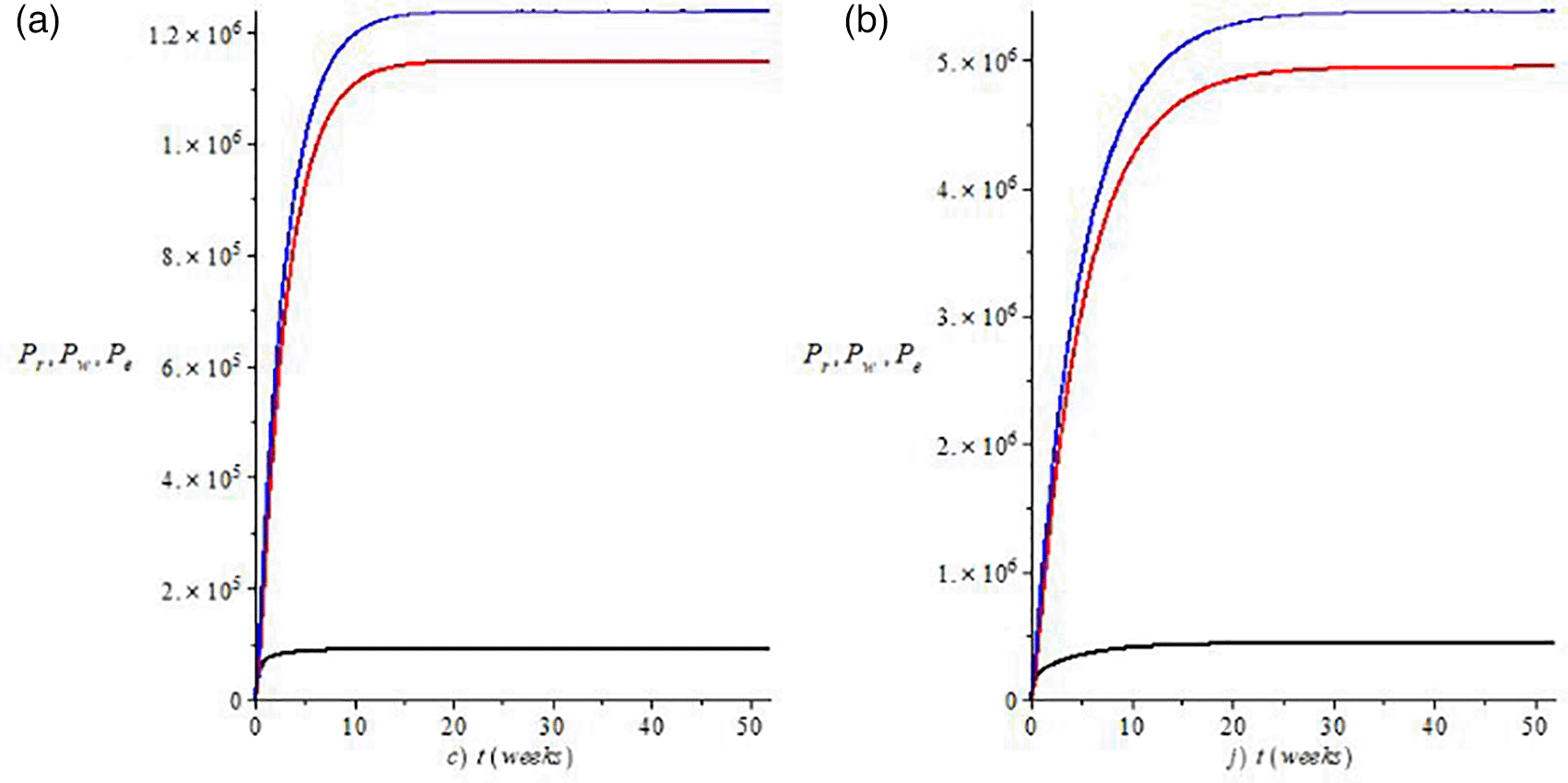
Finally, in the best of cases it is observed that by using both strategies in a medium proportion $(f 60 % - g 70 %),$ susceptible plants tend to be sustained over time and infected plants tend to be controlled. In this scenario it is observed that economic losses are generally lower; for example, in the reseeding of infected plants by 10% (Figure 5a), after week 50, approximately 100,000 pesos would be lost, while for the reseeding by 30% (Figure 5b) approximately 1,000,000 pesos would be lost. Additionally, the losses associated with infected plants and their elimination in week 50 will no longer have an exponential increase but tend to stabilize at 1,200,000 pesos and 5,000,000 pesos respectively.

Figure 5. Behavior of economic losses due to overseeding (black line), by elimination of infected plants (red line) and total losses (blue line) in a time t with f=0,6 and g=0,7 for c) h=0,1 and j) h=0,3.

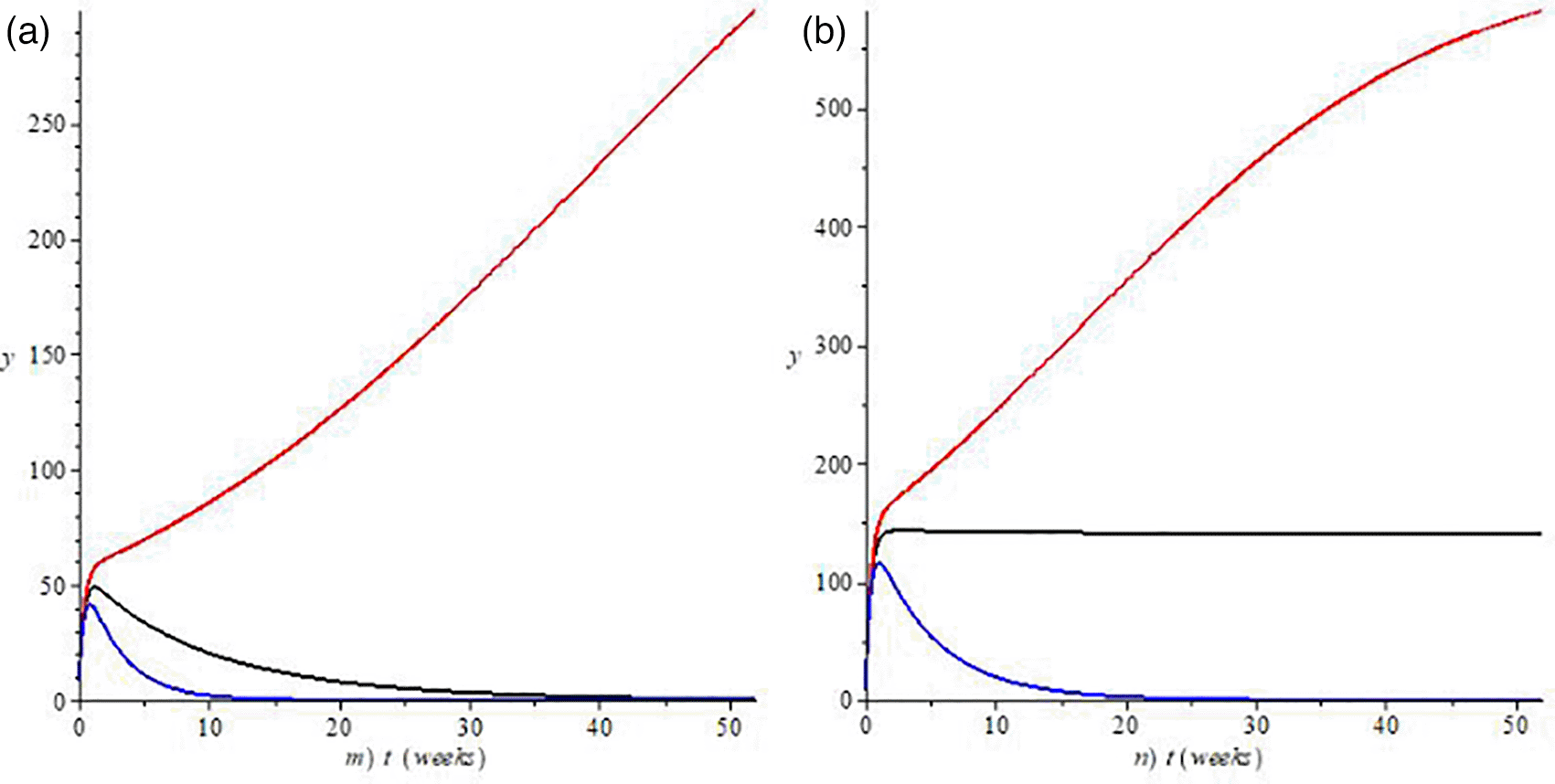
In Figures 6a, we show the behaviour of the infected plant population over time with reseeding by 10% and in figure and 6b with reseeding by 30% in different scenarios, demonstrating the importance of early elimination of infected plants to prevent the spread of the illness. In Figure 6a the red line corresponds to the low elimination of infected plants (f 80% -g 10%) showing an increase in time of the exponential type of the population, while in the black line in both scenarios it is shown that the population of infected plants tends to be controlled, in the 10% replanting it tends to be controlled, while in the 30% replanting the population tends to stabilize at approximately 150 infected plants over time. Finally, the blue line shows that when both strategies are applied in a medium proportion, the population of infected plants tends to be controlled and disappear in time either at 10 and 30% overseeding, associating this with good agronomic management and sustainability of the crop, avoiding greater economic losses and reduction of production costs.

Figure 6. Behaviour of infected plants (black line) f=0,1 and g=0,8; (red line) f=0,8 and g=0,1; (blue line) f=0,6 and g=0,7, corresponding to m) h=0,1 and n) h=0,3.

In conclusion, cultural control strategies in banana Moko disease, such as disinfestation of tools, footwear, and weed pruning are important agronomic practices for disease control. However the identification of planting infected hills plays an essential role in preventing the spread of the disease and stopping the increase of foci infection, as well as in the early elimination of infected plants, thus leading to a decrease in production costs.

The analysis shows that to reduce production costs, both prevention strategies can be implemented to a lesser extent, thereby reducing labour, etc., but still keeping the disease in a controlled state.

Data availability

All data underlying the results are available as part of the article and no additional source data are required.

Acknowledgements

The authors thank the Vice-rector for Research of the University of Quindío, the Ph.D. in Sciences and the Mathematical Modeling in Epidemiology Group GMME for supporting us in this study.

References

Agudelo Valencia JY, Florez Mogollon VC: EL MOKO (Ralstonia solanacearum) En Plátano y Banano: Incidencia y Medidas Alternativas de Control en el Contexto Colombiano. Univ. Nac. abierta y a distancia –UNAD; 2019.
Álvarez E, Ceballos G, Gañán L, et al.: Producción de material de ‘siembra’ limpio en el manejo de las enfermedades limitantes del plátano. Cent. Int. Agric. Trop. CIAT. 2013; 1–23.
Blomme G, Dita M, Jacobsen KS, et al.: Bacterial diseases of bananas and enset: Current state of knowledge and integrated approaches toward sustainable management. Front. Plant Sci. 2017; 8: 1–25. PubMed Abstract | Publisher Full Text
Bokil VA, Allen LJS, Jeger MJ, et al.: Optimal control of a vectored plant disease model for a crop with continuous replanting. J. Biol. Dyn. 2019; 13: 325–353. PubMed Abstract | Publisher Full Text
Denny TP: Plant pathogenic, Group.2006. Publisher Full Text
Fegan M, Prior P: Diverse members of the Ralstonia solanacearum species complex cause bacterial wilts of banana. Australas. Plant Pathol. 2006; 35: 93–101. Publisher Full Text
Garćia RO, Kerns JP, Thiessen L: Ralstonia solanacearum species complex: A quick diagnostic guide. Plant Heal. Prog. 2019; 20: 7–13. Publisher Full Text
Grajales-Amorocho M, Muñoz-Loaiza A: A theoretical model for optimal control of banana Moko (Musa AAB Simmonds). F1000Res. 2021a; 9: 1443. PubMed Abstract | Publisher Full Text
Grajales-Amorocho M, Muñoz-Loaiza A: Prevention strategies of Moko Ralstonia solanacearum philotype II race 2 in plántain (Musa AAB Simmonds), using a simulation model. Acta Agric. Scand. Sect. B Soil Plant Sci. 2021b; 71: 208–214. Publisher Full Text
Jeger MJ, Madden LV, Van Den Bosch F: Plant virus epidemiology: Applications and prospects for mathematical modeling and analysis to improve understanding and disease control. Plant Dis. 2018; 102: 837–854. PubMed Abstract | Publisher Full Text
Munar-Vivas O, Morales-Osorio JG, Castañeda-Sánchez DA: Use of field-integrated information in GIS-based maps to evaluate Moko disease (Ralstonia solanacearum) in banana growing farms in Colombia. Crop Prot. 2010; 29: 936–941. Publisher Full Text
Zhao T, Smith RJ: Global dynamical analysis of plant-disease models with nonlinear impulsive cultural control strategy. Math. Biosci. Eng. 2019; 16: 7022–7056. PubMed Abstract | Publisher Full Text

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 21 Apr 2022

Author details Author details

¹ Research group on Biodiversity and Biotechnology, University of Quindío, Armenia, Quindío, 630001, Colombia
² Software Study and Development Group, University of Quindío, Armenia, Quindío, Colombia
³ Oceanographic Research Institute, Autonomous University of Baja California, Ensenada, Baja California, Mexico
⁴ Group of Mathematical Modeling in Epidemiology, University of Quindío, Armenia, Quindío, Colombia

Marly Grajales-Amorocho
Roles: Conceptualization, Investigation, Methodology, Writing – Original Draft Preparation, Writing – Review & Editing

Cesar Acosta-Minoli
Roles: Conceptualization, Data Curation, Supervision

Dalia Muñoz-Pizza
Roles: Conceptualization, Writing – Review & Editing

Oscar Manrique-Arias
Roles: Data Curation, Formal Analysis, Investigation, Validation

Anibal Muñoz Loaiza
Roles: Data Curation, Formal Analysis, Investigation, Methodology, Supervision, Validation

Competing interests

No competing interests were disclosed.

Grant information

This work was supported by the University of Quindío with the vice-rector for research and the group of mathematical modeling in epidemiology GMME - Colombia.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (1)

version 1

Published: 21 Apr 2022, 11:447

https://doi.org/10.12688/f1000research.55456.1

Copyright

© 2022 Grajales-Amorocho M et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

Grajales-Amorocho M, Acosta-Minoli C, Muñoz-Pizza D et al. Analysis of the replanting of banana hills with infection by the bacterium Ralstonia solanacearum philotype II race 2 and economic losses [version 1; peer review: awaiting peer review]. F1000Research 2022, 11:447 (https://doi.org/10.12688/f1000research.55456.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 21 Apr 2022

Open Peer Review

Reviewer Status

AWAITING PEER REVIEW

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

[1] Agudelo Valencia JY, Florez Mogollon VC: EL MOKO (Ralstonia solanacearum) En Plátano y Banano: Incidencia y Medidas Alternativas de Control en el Contexto Colombiano. Univ. Nac. abierta y a distancia –UNAD; 2019.

[2] Álvarez E, Ceballos G, Gañán L, et al.: Producción de material de ‘siembra’ limpio en el manejo de las enfermedades limitantes del plátano. Cent. Int. Agric. Trop. CIAT. 2013; 1–23.

[3] Blomme G, Dita M, Jacobsen KS, et al.: Bacterial diseases of bananas and enset: Current state of knowledge and integrated approaches toward sustainable management. Front. Plant Sci. 2017; 8: 1–25. PubMed Abstract | Publisher Full Text

[4] Bokil VA, Allen LJS, Jeger MJ, et al.: Optimal control of a vectored plant disease model for a crop with continuous replanting. J. Biol. Dyn. 2019; 13: 325–353. PubMed Abstract | Publisher Full Text

[5] Denny TP: Plant pathogenic, Group.2006. Publisher Full Text

[6] Fegan M, Prior P: Diverse members of the Ralstonia solanacearum species complex cause bacterial wilts of banana. Australas. Plant Pathol. 2006; 35: 93–101. Publisher Full Text

[7] Garćia RO, Kerns JP, Thiessen L: Ralstonia solanacearum species complex: A quick diagnostic guide. Plant Heal. Prog. 2019; 20: 7–13. Publisher Full Text

[8] Grajales-Amorocho M, Muñoz-Loaiza A: A theoretical model for optimal control of banana Moko (Musa AAB Simmonds). F1000Res. 2021a; 9: 1443. PubMed Abstract | Publisher Full Text

[9] Grajales-Amorocho M, Muñoz-Loaiza A: Prevention strategies of Moko Ralstonia solanacearum philotype II race 2 in plántain (Musa AAB Simmonds), using a simulation model. Acta Agric. Scand. Sect. B Soil Plant Sci. 2021b; 71: 208–214. Publisher Full Text

[10] Jeger MJ, Madden LV, Van Den Bosch F: Plant virus epidemiology: Applications and prospects for mathematical modeling and analysis to improve understanding and disease control. Plant Dis. 2018; 102: 837–854. PubMed Abstract | Publisher Full Text

[11] Munar-Vivas O, Morales-Osorio JG, Castañeda-Sánchez DA: Use of field-integrated information in GIS-based maps to evaluate Moko disease (Ralstonia solanacearum) in banana growing farms in Colombia. Crop Prot. 2010; 29: 936–941. Publisher Full Text

[12] Zhao T, Smith RJ: Global dynamical analysis of plant-disease models with nonlinear impulsive cultural control strategy. Math. Biosci. Eng. 2019; 16: 7022–7056. PubMed Abstract | Publisher Full Text

Analysis of the replanting of banana hills with infection by the bacterium Ralstonia solanacearum philotype II race 2 and economic losses

Abstract

Keywords

Introduction

Figure 1. Plantain crop that implements prevention strategies in a farm of Armenia, Quindío, Colombia.

Methods

The model

(1)

(2)

Figure 2. Banana Moko's disease diagram with prevention.

(3)

(4)

Results and conclusion

Economic losses due to Moko

(5)

(6)

(7)

(8)

(9)

(10)

Population simulations and economic losses

Table 1. Variables, parameters, parameter values, and initial populations at t=0.

Figure 3. Behavior of economic losses due to overseeding (black line), by elimination of infected plants (red line) and total losses (blue line) in a time t with f=0,1 and g=0,8; for a) h=0,1 and d) h=0,3.

Figure 4. Behavior of economic losses due to overseeding (black line), by elimination of infected plants (red line) and total losses (blue line) in a time t with f=0,8 and g=0,1, for b) h=0,1 and e) h=0,3.

Figure 5. Behavior of economic losses due to overseeding (black line), by elimination of infected plants (red line) and total losses (blue line) in a time t with f=0,6 and g=0,7 for c) h=0,1 and j) h=0,3.

Figure 6. Behaviour of infected plants (black line) f=0,1 and g=0,8; (red line) f=0,8 and g=0,1; (blue line) f=0,6 and g=0,7, corresponding to m) h=0,1 and n) h=0,3.

Data availability

Acknowledgements

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated

Table 1. Variables, parameters, parameter values, and initial populations at $t = 0$ .