The recursive-adaptive rental subscription model (R-ARSM) in the new normal: an application to the housing sector

Friday Zinzendoff Okwonu; Nor Aishah Ahad; Joshua Sarduana Apanapudor; Festus Irimisose Arunaye; Innocent Ejiro Okoloko

doi:10.12688/f1000research.75360.1

Home Browse The recursive-adaptive rental subscription model (R-ARSM) in the new...

ALL Metrics

-

Views

-

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

The recursive-adaptive rental subscription model (R-ARSM) in the new normal: an application to the housing sector

[version 1; peer review: awaiting peer review]

Friday Zinzendoff Okwonu^1-3, Nor Aishah Ahad¹, Joshua Sarduana Apanapudor², Festus Irimisose Arunaye², Innocent Ejiro Okoloko⁴

Friday Zinzendoff Okwonu^1-3, Nor Aishah Ahad¹, [...] Joshua Sarduana Apanapudor², Festus Irimisose Arunaye², Innocent Ejiro Okoloko⁴

PUBLISHED 25 Jan 2022

Author details Author details

¹ School of Quantitative Sciences, College of Arts and Sciences, UNIVERSITI UTARA MALAYSIA, Sintok, Kedah, 06010, Malaysia
² Department of Mathematics, DELTA STATE UNIVERSITY, Abraka, Delta, P.M.B.1, Nigeria
³ Institute of Strategic Industrial Decision Modeling, School of Quantitative Sciences, College of Arts and Sciences, UNIVERSITI UTARA MALAYSIA, Sintok, Kedah, 06010, Malaysia
⁴ Faculty of Computing, Dennis Osadebay University, Anwai Rd, Asaba, Nigeria

Friday Zinzendoff Okwonu
Roles: Conceptualization, Methodology, Software, Validation

Nor Aishah Ahad
Roles: Data Curation, Supervision, Writing – Original Draft Preparation

Joshua Sarduana Apanapudor
Roles: Data Curation

Festus Irimisose Arunaye
Roles: Writing – Review & Editing

Innocent Ejiro Okoloko
Roles: Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS AWAITING PEER REVIEW

Abstract

Background: The last three decades have witnessed a remarkable transformation from a traditional billing system to a subscription model. Many organizations have adopted the subscription models especially in the service sectors like telecommunication, internet service providers, and satellite television operators. During the lockdown occasioned by the coronavirus disease (COVID-19) pandemic, people were forced to subscribe for their daily needs, and their lifestyle was altered, and people must reset to cope with the new normal. The new normal era has exposed many people to subscribe to what they could afford based on length of time and limited resources. Unexpected daily economic challenges emerged, and people relocated to affordable places which led to rent default, rent arrears, and refund requests. This paper focused on how to solve rent default, rent arrears, and refund request problems in the public and private housing sector.
Methods: Relying on this, we proposed recursive-adaptive rental subscription models (R-ARSM) that could allow tenants options to subscribe for house rent with available resources. The R-ARSM concept mimics the internet subscription, mobile phone subscription, and satellite television subscription models whereby services to customers on annually, monthly, weekly, daily, and hourly rates are terminated when the subscribed amount elapses.
Results: The model based on the penalty constant showed that it is a balanced model for both landlords and tenants in the housing sector. The R-ARSM showed promising results, it is time-dependent and indicates the tenant's available balance per period.
Conclusions: The analysis revealed that the R-ARSM concept would solve refund requests and rent default problems if implemented.

Keywords

Landlord, House, Tenant, Rent, Recursive, Adaptive, Subscription, Refund

Corresponding author: Nor Aishah Ahad

Competing interests: No competing interests were disclosed.

Grant information: The author(s) declared that no grants were involved in supporting this work.

Copyright: © 2022 Okwonu FZ et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Okwonu FZ, Ahad NA, Apanapudor JS et al. The recursive-adaptive rental subscription model (R-ARSM) in the new normal: an application to the housing sector [version 1; peer review: awaiting peer review]. F1000Research 2022, 11:89 (https://doi.org/10.12688/f1000research.75360.1) First published: 25 Jan 2022, 11:89 (https://doi.org/10.12688/f1000research.75360.1) Latest published: 25 Jan 2022, 11:89 (https://doi.org/10.12688/f1000research.75360.1)

1. Introduction

The past three decades has witnessed a transformation from the traditional billing system to a service subscription model in which customers subscribe for services in advance. This innovation was based on the concepts devised by the business executives that initiated the service subscription model, which allows customers to subscribe according to their needs based on available options and resources. The past two decades have resulted in a rapid adoption of this model. Service providers such as the telecom sector, satellite network providers and electricity corporations have adopted this model. In this paper, we investigate the problems which arise between landlords and tenants based on the traditional rental model. We consider robust and efficient rental models that would solve the existing rental problems in the housing sector. Before we proceed, let us briefly discuss some of the existing problems between landlords and tenants in general.

1.1 Background of the study

The house is an integral part of man's daily life and, without it, many factors would be hampered. Different researchers have discussed housing, its classifications, and its importance to man (Vale et al. 2014; Wahi et al. 2018). It is a global problem, and the government alone cannot provide affordable housing for all its citizens. As such, many housing developers and planners have been actively involved in this sector (Gayinu et al. 2014; Mohd Noor 2017; Bakhtyar et al. 2013). Many people across the globe suffer from the effect of a lack of better and more affordable sources of accommodation. Different studies have discussed housing shortages in urban and semi-urban areas (Bhide et al. 2019; Gayinu et al. 2014; Mohd Noor 2017; Bakhtyar et al. 2013; Wahi et al. 2018) and unaffordability due to the high cost of building materials and loans (Djebarni & Al-Abed 2000). Bhide et al. (2019) argued that housing problems should not be limited to affordable housing, but a robust approach should be adopted to tackle the housing problem. Notable scholars have discussed the difficulties to access affordable houses and the number of occupants that reside in small apartments (Abiodun 1976).

In some countries, the federal and state government collaborate to provide affordable houses for low-income earners. In recent times, the private sector has played a significant role to complement the efforts of different tiers of government to ensure their citizens have good shelter. In addition, individuals also rent their houses to tenants to complement the housing deficit. The problem with the above is the mode of renting and rent payment. It is often the case that landlords or estate managers require annual or monthly rent payment. In many instances the potential tenants are willing to rent the property, but the rent conditions, such as annual or monthly rent payments or security deposits and the lump-sum payments involved, become major hurdles. These conditions have led many people to be homeless, especially daily income earners.

During the early days of the global system of mobile communication (GSM) in Nigeria, many people were willing to subscribe to a GSM network, but the network carriers configured their system to per-minutes billing, which was very expensive to many intending users and as a result GSM users were relatively few in number. After some time, people began to clamour for per-second billing, which was eventually granted by an indigenous network carrier. With this per-second billing, many people started subscribing for any amount they desired. In several cities, there are numerous unoccupied public and private buildings or houses, and many homeless people are willing to rent but because of the lump-sum payment and high cost of renting they cannot afford decent accommodation. Could this be related to the per-minute billing of GSM networks in Nigeria, in which many wanted to subscribe but because of the high cost of per-minute billing they decided to forgo their intention? For the Nigerian case, the rate of subscription drastically increased when network providers converted to the per-second billing system. The number of sim card registrations for different GSM network providers skyrocketed and many people of different classifications had access to mobile telephones. So, this model can be replicated in the housing sector to accommodate the daily income earners. However, the implementation of this model in the existing conventional public and private housing system may be a herculean task in terms of monitoring tenants' exit times. However, with the technological advancement and transformation of traditional cities into smart cities, it will be possible in the future.

Smart cities and their components have been discussed extensively (Mohanty, Choppali & Kougianos 2016; Eremia, Toma & Sanduleac 2017; Georgiadis, Christodoulou & Zinonos 2021; Praharaj & Han 2019; Ahvenniemi et al. 2017; Ross & Maynard 2021). We define a smart city as a digitally connected city where all infrastructure is digitally bounded with digital entry permission. With the rapid growth in technological advancement and emergence of smart cities, the existing rent default problem could easily be resolved by the rent subscription model. Smart house concepts are about digitalization, whereby every activity is connected to a digital platform. The smart house implies that everything has a digital relationship with access permission. We define a smart house as a connected platform whereby every facility is connected to a digital framework that requires digital permission. The entry access point requires digital permission, as such subscription for smart houses can be done in a similar way to internet subscriptions. In this case, the subscribed amount is the access key to the house and when this subscription elapses, access to the house is deactivated automatically, thereby denying the tenants/occupants access to the house. An alternative to smart houses is to modify the doors of conventional houses to smart doors, to serve the purpose of the proposed models and thereby solving rental default problems.

1.2 Problem statement

In some countries, poor locals, foreigners, and migrant workers with low financial status constitute a large chunk of people with housing difficulties and rental default. Over the years, there have been arguments between landlords and tenants over rent default or rent arrears. This problem also extends to overstay in service apartments or hotels. The problem of rent defaults and refunds has generated many litigations globally. Sometimes the exact amount, based on the length of stay and under-stay, has generated a refund crisis between landlords and tenants.

Certain conditions may alter the plans of either party; the landlord may decide to sell the house, or the tenant may decide to quit the house halfway thereby leading to a refund request. Refund requests are not an easy task for both parties. In some cases, either party will default which may lead to court action, or the case of long-term rental default which the house owner would want to recoup.

Private individuals have resorted to renting part of their houses for economic reasons, while others build for business concerns. The rental policy of such privately owned houses is exclusively decided by the landlords or caretakers. The mode of payments, maintenance, and periodic rental increase is the exclusive preserve of the landlords. These policies, in the form of a tenancy agreement, have been breached by the landlords and tenants due to circumstances that may be beyond their control. The landlord often requests annual or monthly rental. In many instances, rent default and refund have been the subject of discussion and litigation between landlords and tenants. Different studies have discussed rent default in public and private housing management (Salleh, Johari & Yusof 2008). Salleh et al. (2008) observed that rent default has multiple implications to the parties involved, such as rent refund and rent arrears.

The concept of advance rental payment is a recognized practice and an accepted norm in the society. Rental default and refund are as old as this norm. One difficulty inherent to this concept is the possibility of the tenant requesting a refund midway through the tenancy agreement. In all of these cases, the basic problem is the refund request, which in many situations may not be suitable for the landlord or the tenant. Previous studies have not discussed refund requests, the prevention of rental default problems, or weekly, daily, and hourly housing rent schemes, but have instead focused mainly on affordable houses for low-income earners and rental default. In this paper, we propose rental subscription models whereby rental default is impossible and renting is subscription based. The main contribution of this paper is to solve the rent default problem, thereby making rent arrears impossible in the public and private housing sector and allowing prospective tenants the option to subscribe for house rent based on available resources. Another objective of the study is to provide opportunities for people to have access to a shelter by subscribing weekly or daily, to solve the housing needs of low-income earners and daily income earners.

The rest of this paper is organized as follows. Section 2 describes the recursive annual rental subscription model (R-ARSM). It gives details about the rent subscription models and discussed possible refund request computations based on time. The R-ARSM computes the tenant's annual, monthly, weekly, daily, and hourly subscription balance. Section 3 discusses the adaptive rental subscription model (ARSM) whereby rental default and rental arrears is impossible. Section 4 contains different problems and applications to annual, monthly, daily, and hourly subscription problems, refund requests, discussions, and recommendations. Conclusions follow in Section 5.

2. Methods

In some countries, the rental policy is well structured while others allow landlords or caretakers, or associations to determine the rental policies. The landlords in some cases may request two years, a year, six months, or monthly rent from prospective tenants. The landlords also draft the tenancy agreements on their terms which both parties sign to commence the mutual understanding. In the following subsections, we elaborate on different types of subscription models with refund requests as a key factor.

2.1 R-ARSM

The R-ARSM is very flexible and would allow tenants to subscribe annually and provide a flexible refund request framework. The model computes tenancy per month, weeks, days, hours, minutes, and second balance. The five-step R-ARSM is described as follows:

(1)

\sum_{i = 1}^{n} x_{i} = \prod \hat{α} n,

where

\hat{α}

is per month rental rate,

n

denotes the number of months per year and

β

is a user’s defined boundary constant which accounts for the depreciation of the house and furniture for the period of individual tenancy. Therefore, Equation (1) can be written as

(2)

∆ = \prod \hat{α} n

Equation (2) denotes annual rental. Then Equation (3) computes per month rate

(3)

X = [\frac{∆}{M}] + M^{- 1} β = [\frac{\prod \hat{α} n}{M}] + M^{- 1} β,

Step 1

From Equation (3), $M$ implies the number of months per year and $U$ is the monthly rate

(4)

U = \prod_{i = 1}^{M} (X R_{i}), R = 1, 2, . ., M

(5)

φ = \prod_{i = 1}^{M} ∆ (ϑ_{i}),

where

ϑ

is a unit constant. Based on the definitions of Equation (4) and Equation (5), we applied the concept of residual discussed in Sharpe (2015), Delucchi (1976), Neter et l. (1996) and Barnett et al. (1975) in a reversed form, and defined the modified residual using Equation (4-5) to obtain Equation (6)

(6)

∆_{\nabla} = \prod_{i = 1}^{M} ∆ (ϑ_{i}) - \prod_{i = 1}^{M} (X R_{i}) = φ - U

where

φ

is the observed annual rental value and

U

is the expected sum of monthly rental value. In general,

∆_{\nabla}

denotes per month balance, which is zero at the end of the last month if both landlords and tenants keep to the tenancy agreement and a specified value if the tenancy agreement is breached. Individual occupancy value for multiple occupants can be computed based on Equation (7)

(7)

ε_{t} = \frac{∆_{\nabla}}{α}

where

α

denotes the number of occupants per rental period. Equation (7) is a modification of the standardized residual discussed in Haberman (1973) which describes individual cell contribution. The last expression describes multiple occupants’ situations where each occupant contributes to pay for the rent. Equation (6) can be written as

(8)

∆_{\nabla} = \{\begin{matrix} 0 if φ = U \\ γ_{n} if φ \neq U \end{matrix},

from Equation (8)

∆_{\nabla} = 0

means that all parties complied with the agreement while

∆_{\nabla} = γ_{n}

implies a breach of agreement and refund

(γ_{n})

is required. For the multiple occupant’s application, we have

ɯ_{ɯ} = 0, if φ = \sum ε_{t}

and

ɯ_{ɯ} = γ_{n} ifφ \neq \sum ε_{t},

that is

(9)

ɯ_{ɯ} = \{\begin{matrix} 0 if φ = \sum ε_{t} \\ γ_{n} if φ \neq \sum ε_{t} \end{matrix},

If all occupants comply with the tenancy agreement $φ - \sum ε_{t} = 0$ no refund is required while $φ \neq \sum ε_{t}$ implies a breach of agreement, hence a refund request would be required.

Step 2

Let $X$ be as defined in step (1) and $N$ denotes the number of days in the given month, then the daily rate $X_{1}$ is defined as

(10)

X_{1} = \frac{X}{N}

(11)

γ = \prod_{i = 1}^{N} (X_{1} J_{i}), J = 1, 2, \dots, N

(12)

w = \prod_{i = 1}^{N} X (ϑ_{i})

(13)

∆_{1} = \prod_{i = 1}^{N} X (ϑ_{i}) - \prod_{i = 1}^{N} (X_{1} J_{i}) = w - γ

Where $∆_{1}$ denotes per month balance which is zero at the end of the last day and individual occupancy value for multiple occupants can be defined as

(14)

ε_{q} = \frac{∆_{1}}{α}

where

α

denotes the number of tenants per rental period. A similar discussion as in Equations (8-9) is applicable.

Step 3

Let $X_{1}$ be as defined in step 2 and $K$ the number of hours per day, then the hourly rate $Y_{1}$ is computed as follows

(15)

Y_{1} = \frac{X_{1}}{K}

(16)

γk = \prod_{i = 1}^{K} (Y_{1} e_{i}), e = 1, 2, \dots, K

(17)

wh = \prod_{i = 1}^{K} X_{1} (ϑ_{i})

(18)

DH = \prod_{i = 1}^{K} X_{1} (ϑ_{i}) - \prod_{i = 1}^{K} (Y_{1} e_{i}) = wh - γk

Where $DH$ denotes per day balance which is zero at the end of the last hours and Equation (19) explain per individual rental for multiple occupants

(19)

ε_{s} = \frac{DH}{α}

where

α

denotes the number of occupants per rental period. A similar explanation as in Equations (8-9) is applied.

Step 4

Let $Y_{1}$ be as defined in step 3 and $g$ is the number of minutes per hour, then per minutes rate $Y_{2}$ is defined as

(20)

Y_{2} = \frac{Y_{1}}{g}

(21)

Td = \prod_{i = 1}^{g} (Y_{2} v_{i}), v = 1, 2, \dots, g

(22)

sx = \prod_{i = 1}^{g} Y_{1} (ϑ_{i})

(23)

D_{Uk} = \prod_{i = 1}^{g} Y_{1} (ϑ_{i}) - \prod_{i = 1}^{g} (Y_{2} v_{i}) = sx - Td

Where $D_{Uk}$ denotes per minute balance which is zero at the end of the last minutes and the individual rate for the period is defined as

(24)

ε_{p} = \frac{D_{Uk}}{α}

where

α

denotes the number of users per rental period. A similar explanation as in Equations (8-9) is applied.

Step 5

Let $Y_{2}$ be as defined in step 4 and $l$ denotes the number of seconds per minute, then per second rate $Y_{3}$ is defined as

(25)

Y_{3} = \frac{Y_{2}}{l}

(26)

rw = \prod_{i = 1}^{l} (Y_{3} h_{i}), h = 1, 2, \dots, l

(27)

zs = \prod_{i = 1}^{l} Y_{2} (ϑ_{i})

(28)

D_{U} = \prod_{i = 1}^{l} Y_{2} (ϑ_{i}) - \prod_{i = 1}^{l} (Y_{3} h_{i}) = rw - zs

Where $D_{U}$ denotes per second balance which is zero at the end of the last second and the individual rate for multiple occupants for the period is defined as

(29)

ε_{w} = \frac{D_{U}}{α}

where

α

denotes the number of users per rental period. A similar description based on Equations (8-9) is applied. Therefore, the refund request by either party is based on the following expression

(*)

Ʊ = ∆ - ɸ,

where

ɸ = ∆_{\nabla} + ∆_{1} + D_{H} + D_{UK} + D_{U}

and

∆

is the total annual rental

, ɸ

denote the total amount of rental for the period, which comprises of the following:

∆_{\nabla}

denotes monthly rent,

∆_{1}

number of days (or weekly rental),

D_{H}

hourly,

D_{UK}

minute and

D_{U}

per second rates for the period and

Ʊ

denotes the total amount to be refunded if the agreement is breached. The description of (*) can be expressed as follows

(30)

Ʊ = \{\begin{matrix} 0 if ∆ = ɸ \\ c if ∆ \neq ɸ \end{matrix}

$Ʊ = 0$ implies that all parties complied with the tenancy agreement and $Ʊ = c$ implies that a breach of agreement has occurred, therefore the tenant can request for refund.

2.2 Recursive monthly rental subscription model (RMRSM)

This subsection discusses the RMRSM. The RMRSM accounts for a period of one month for the tenant, which comprises the number of weeks, days, hours, minutes, and seconds. This model adopts the same process discussed in subsection 2.1. The monthly recursive model is described as follows.

Step 1

For the RMRSM, the penalty constant Ƹ is defined as in subsection 2.1. Let $X$ denote the monthly rate and $N$ number of days per the specific month, therefore the daily rate is defined as

(31)

X_{1} = \frac{X}{N} + N^{- 1} Ƹ,

Hence, we invoke the process discussed in Equations (11-14) and Equations (7-9), respectively.

Step 2

Let $X_{1}$ denote the definition in step 1 in Equation (31), then

(32)

Y_{1} = \frac{X_{1}}{K}

Based on Equation (32), Equations (16-19) and Equations (7-9) follows.

Step 3

Let $Y_{1}$ denote the definition in step 2, Equation (32), and $K_{1}$ denotes the number of minutes per hour, then

(33)

Y_{2} = \frac{Y_{1}}{K_{1}}

Based on the definition of $Y_{1}$ in Equation (32), the computational procedure described in Equations (20-24) and Equations (7-9) is adopted.

Step 4

Let $Y_{2}$ be as defined in Equation (33), then

(34)

Y_{3} = \frac{Y_{2}}{l}

Relying on $Y_{3}$ in Equation (34), the computational steps in Equation (23-26) and Equation (7-9) follow, respectively.

Therefore,

(**)

Ʈ = X - ɸɰ

where

ɸ ɰ = ∆_{1} + D_{H} + D_{UK} + D_{U}

and

X

is the monthly rate,

ɸɰ

denote the total rate for the tenancy period which include the following:

∆_{1}

number of days (or weeks),

D_{H}

hourly,

D_{UK}

minute and

D_{U}

per second rates and

Ʈ

denotes the total amount to be refunded. Therefore, the analysis expressed in Equation (30) follows.

2.3 Recursive daily rental subscription model (RDRSM)

The RDRSM finds applications in such areas as hotels, homestays, service apartments, and short rest accommodations. This approach can alleviate some of the associated problems in this sector. This procedure is described as follows.

Step 1

Let $X_{1}$ denote daily rate, $K$ corresponds to the number of hours per day and ʠ denotes penalty function, which is user-defined, therefore we have

(35)

Y_{1} = \frac{X_{1}}{K} + K^{- 1} ʠ

Using Equation (35) as input, the computation of this procedure follows from Equation (16-19) and Equations (7-9), respectively.

Step 2

Let $Y_{1}$ be as defined in step 1, Equation (35), and let $K_{1}$ denote the number of minutes per hour, then we have

(36)

Y_{2} = \frac{Y_{1}}{K_{1}}

Relying on Equation (36), this procedure follows a similar computational framework in Equations (20-24) and Equation (7-9), respectively.

Step 3

Let $Y_{2}$ be as defined in step 2, Equation (36), and $K_{2}$ denotes the number of seconds per minutes, then

(37)

Y_{3} = \frac{Y_{2}}{K_{2}}

Using Equation (37), Equations (26-29) and Equations (7-9) follow immediately.

Therefore,

(***)

Ʈɼ = X_{1} - ɸ ɱɰ

where

ɸ ɱɰ = D_{H} + D_{U K} + D_{U}

and $X_{1}$ is the daily rate, $ɸɱɰ$ total occupancy rate for the period which includes $D_{H}$ hourly, $D_{UK}$ minute and $D_{U}$ per second rates. Therefore $Ʈɼ$ can be defined as in Equation (30) and the discussions follow immediately. The recursive rental subscription model recursively computes the period of tenancy corresponding to the defined rates and allows for an equitable refund if the need arises. This model may not completely solve the problem of rental default, but it affords tenants and landlords a unique opportunity to solve rental refund requests. The discussion in the next section will completely eradicate the rental default problem in the housing sector.

3. ARSM

In the last section, we discussed different types of recursive subscription models and refund requests for the conventional housing rental system. In this section, we focus on the adaptive rental subscription model for smart houses. We assumed that in the adaptive concept, intended tenants could access the smart house if they subscribed for a period. The adaptive access card (AAC) will allow the intending tenants to access the smart door into the house and once the subscription elapsed the tenant would not be able to access the house. If the subscription is extended, the AAC will be activated, and the tenant can have access to the house. The ARSM would solve the problem of rental default and prevent rental arrears in the future. The ARSM does not require a refund request and is described as follows.

Let $X$ denotes the annual subscription rate, ɯ be user-defined penalty value, $N$ number of months per year and let ʍ be the resources at hand, then

(38)

W = \frac{X}{N} + N^{- 1} ɯ

(39)

Q = \frac{ʍ}{W}

Equation (38) determines the average rent value per month and $Q$ denote the duration or period for the subscribed amount. Let $\partial_{i} = 1, 2, 3, \dots ., N$ and $∆_{j} = 1, M \leq N,$ then

(40)

ʧ = \prod_{i = 1}^{N} W (\partial_{i}),

Equation (40) is the subscription rate and Equation (41) below define an individual optional subscription for a specific period

(41)

ɸ = \prod_{j = 1}^{M} ʍ (∆_{j}) .

Therefore, Equation (42) defines the subscription and deactivation period

(42)

∆ = \prod_{j = 1}^{M} ʍ (∆_{j}) - \prod_{i = 1}^{N} W (\partial_{i}) = ɸ - ʧ, j \leq i

Equation (42) can be expressed as follows

(43)

∆ = \{\begin{matrix} 0, if ɸ = ʧ \\ - ε if ɸ < ʧ \end{matrix}

From Equation (43), if $∆ = 0$ implies that the tenant subscribed for the full duration or period $Q$ and will elapse after $Q$ period. On the other hand, if $∆ = - ε$ indicates that the tenant subscription period has elapsed. A negative balance $(- ε)$ indicates that the AAC would be automatically deactivated. The ARSM model is suitable for annual, monthly, weekly, daily, and hourly concepts. This model will always update the tenant's account after subscribing for a specific period.

3.1 Adaptive daily rental subscription model (ADRSM)

Let $W_{∆}$ be the daily subscription rate, $K$ denote the number of hours per day, $α$ be the penalty constant, and $β$ the amount an individual has, then Equation (38-39) can be written as follows

(44)

V = \frac{W_{∆}}{K} + K^{- 1} α

(45)

Z = \frac{β}{V}

where Equation (44) gives the average rate per hour and Equation (45) determines the number of hours the available resources can sustain. A similar procedure to Equations (40-42) is applied for this model. We redefined variables in Equations (44-45) and apply the explanation in Equations (40-42) to justify the number of minutes the available amount could subscribe. The ADRSM is suitable for daily rental and can be applied to hotels, service apartments, homestay, guest houses, and transit lodges. The uniqueness of the adaptive model is that it can be used for any house with smart doors.

4. Applications

We will apply the rent data set to the recursive and adaptive models described above to determine the annual, monthly, and daily rental (Okwonu 2022).

4.1 Problem 1

A landlord in a particular city in Nigeria owned an estate of four flats and two self-contained apartments. Over the last four years, he has been managing the estate with little stress due to poor estate conditions or tenant mobility. However, tenant mobility seems to be on the increase due to the coronavirus disease (COVID-19) pandemic. A tenant rented a two-bedroom apartment and paid annual rental of #360,000 and a maintenance fee of #30,000. After six months, two weeks, and four days, the tenant informed the landlord of his intention to relocate to his hometown due to the economic situation occasioned by COVID-19 and his retrenchment from his job. He appealed to the landlord for a refund of the balance of the rent paid, since he is seriously seeking funds to relocate his family to his hometown. Unfortunately, the landlord disagreed, saying the contractual agreement is one year. On compassionate grounds the landlord said he will refund the balance if another tenant is ready to rent the apartment and that is the only option, he could make any refund.

The recursive model can be applied to this problem because it involves periodic refund requests associated with the annual rent paid. To avoid this type of problem in the future, recursive model 2.1 can be incorporated in the future tenancy agreements to enhance smooth refund requests. Let us apply the model to this problem to determine the rental period and refund request. To solve this problem, we input the annual rental rate in the model, the number of months, weeks, days, and if possible, the last hour and minutes of stay so that the refund request would be fair to both parties. The R-ARSM is time-dependent, therefore tenancy period and refund are bounded by time. Table 1 gives the model breakdown of the rate per month, day, hour, minute, and second, respectively.

Table 1. Breakdown analysis of #390,000 annual rent for recursive models.

Monthly rental	Daily rental	Per-hour rental	Per-minute rental	Per-second rental
#32,500	#1048.3871	#43.682796	0.7280466k	0.0121341k

Table 2 below gives the recursive model breakdown balance for annual rental, per month, per day, hours, minutes, and seconds based on problem 1. For the period of renting, that is, six months, two weeks, four days, and 8 hours 30 minutes. Based on the situation, the landlord decided to compute the total amount for the duration of the tenancy. In this case, we will use Equations (6,13,18,23) and Equations (*, 30), respectively. Applying the above, the tenant refund request would be #175,757.73 (45.1%). This analysis is shown in Table 3 and Figure 1, respectively.

Table 2. Breakdown analysis of annual rent balance based on recursive models.

Months	MB(6)	Days	DB(13)	Hours	HB(18)	Mins	MB(23)	Secs	SB(28)
1	357500	1	31451.613	1	1004.7043	1	42.954749	1	0.7159125
2	325000	2	30403.226	2	961.02151	2	42.226703	2	0.7037784
3	292500	3	29354.839	3	917.33871	3	41.498656	3	0.6916443
4	260000	4	28306.452	4	873.65591	4	40.770609	4	0.6795102
5	227500	5	27258.065	5	829.97312	5	40.042563	5	0.667376
6	195000	6	26209.677	6	786.29032	6	39.314516	6	0.6552419
7	162500	7	25161.29	7	742.60753	7	38.58647	7	0.6431078
8	130000	8	24112.903	8	698.92473	8	37.858423	8	0.6309737
9	97500	9	23064.516	9	655.24194	9	37.130376	9	0.6188396
10	65000	10	22016.129	10	611.55914	10	36.40233	10	0.6067055
11	32500	11	20967.742	11	567.87634	11	35.674283	11	0.5945714
12	0	12	19919.355	12	524.19355	12	34.946237	12	0.5824373
		13	18870.968	13	480.51075	13	34.21819	13	0.5703032
		14	17822.581	14	436.82796	14	33.490143	14	0.5581691
		15	16774.194	15	393.14516	15	32.762097	15	0.5460349
		16	15725.806	16	349.46237	16	32.03405	16	0.5339008
		17	14677.419	17	305.77957	17	31.306004	17	0.5217667
		18	13629.032	18	262.09677	18	30.577957	18	0.5096326
		19	12580.645	19	218.41398	19	29.84991	19	0.4974985
		20	11532.258	20	174.73118	20	29.121864	20	0.4853644
		21	10483.871	21	131.04839	21	28.393817	21	0.4732303
		22	9435.4839	22	87.365591	22	27.665771	22	0.4610962
		23	8387.0968	23	43.682796	23	26.937724	23	0.4489621
		24	7338.7097	24	0	24	26.209677	24	0.436828
		25	6290.3226			25	25.481631	25	0.4246938
		26	5241.9355			26	24.753584	26	0.4125597
		27	4193.5484			27	24.025538	27	0.4004256
		28	3145.1613			28	23.297491	28	0.3882915
		29	2096.7742			29	22.569444	29	0.3761574
		30	1048.3871			30	21.841398	30	0.3640233
		31	-3.64E-12			31	21.113351	31	0.3518892
						32	20.385305	32	0.3397551
						33	19.657258	33	0.327621
						34	18.929211	34	0.3154869
						35	18.201165	35	0.3033527
						36	17.473118	36	0.2912186
						37	16.745072	37	0.2790845
						38	16.017025	38	0.2669504
						39	15.288978	39	0.2548163
						40	14.560932	40	0.2426822
						41	13.832885	41	0.2305481
						42	13.104839	42	0.218414
						43	12.376792	43	0.2062799
						44	11.648746	44	0.1941458
						45	10.920699	45	0.1820116
						46	10.192652	46	0.1698775
						47	9.4646057	47	0.1577434
						48	8.7365591	48	0.1456093
						49	8.0085125	49	0.1334752
						50	7.2804659	50	0.1213411
						51	6.5524194	51	0.109207
						52	5.8243728	52	0.0970729
						53	5.0963262	53	0.0849388
						54	4.3682796	54	0.0728047
						55	3.640233	55	0.0606705
						56	2.9121864	56	0.0485364
						57	2.1841398	57	0.0364023
						58	1.4560932	58	0.0242682
						59	0.7280466	59	0.0121341
						60	0	60	0

Table 3. Recursive annual rental subscription model refund request.

6 Months	18 days	8 Hours	30 Minutes	Seconds	Total rental	Refund request
#195,000	#18,870.97	349.46	21.84	0	#214242.27(54.9%)	#175757.73(45.1%)

Figure 1. Refund request analysis using recursive annual rental subscription model.

In Table 2, assuming the tenant complied with the tenancy agreement the balance at the end of the last month would be zero and every other computation would be zero. Consider that the tenants breached the tenancy agreement at the end of the 5^th month from Table 2, it implies that the tenant balance is #227,500 (58.33%), based on Equations (6,8). Assume that a tenant that pays monthly rental complies with the terms of the agreement, the balance at the end of the month is zero. On the other hand, if the tenant decides to quit after spending 19 days in the house, the tenant’s balance would be #12,580.645 (38.7%), based on Equation (13). Suppose the tenant paid for one day as in the hotel system and after six hours decided to vacate the room, the balance from the payment would be #786.29 (75%), based on Equation (18). Figure 2 to Figure 4 show the computational framework of the R-ARSM based on Equations (6,13,18,23,28). These figures imply that the models are time dependent.

Figure 2. Recursive annual rental subscription model for annual rental.

Figure 3. Recursive monthly rental subscription model for monthly rental.

Figure 4. Recursive daily rental subscription model for hourly rental.

Figure 3 and Figure 4 indicate the RMRSM and RDRSM based on Table 1.

Figure 2 to Figure 4 revealed periodic deduction based on the recursive models. So far these illustrations only solve refund requests. How do we solve the rental default and rent arrears problem? Once we solve the rental default problem, we would have also solved the arrears problem.

4.2. Problem 2. application of adaptive model

Assume that Mr. X wanted to rent an apartment in a smart city and the cost of renting is #3,500,000 per annum and he is expected to pay an additional #1,900,000 for utilities and depreciation. At present, he has #3,150,000 and he is not certain that he will complete the annual subscription for the next two months. He is determined to rent the smart house. He approached the smart city manager and explained to him his intention to rent the house and his financial status. He promised to complete the rental at the end of the fourth month. The manager advised him to subscribe with the available resources and that he can resubscribe before the existing subscription elapses, otherwise he may not have access to the house when his subscription elapses. Mr. X agreed and subscribed with the available money. A week before the expiration of the subscribed amount he resubscribed with #305,000 and further subscribed with #10,000. How long would he reside in the house? Table 4 below contains the details.

Table 4. Adaptive rate and duration breakdown analysis.

Monthly rental	Q months	daily rental	Q days	Hour rental	Q hours
#450,000	7	#14,516.1290	21	#604.8387	16.5

The adaptive Q in Table 5 indicates that if Mr. X could not continue his subscription based on the available subscriptions in Table 4 his tenancy would elapse. The breakdown analysis of Mr. X’s subscription is shown in Figure 5. The analysis in Table 5 showed that rent arrears and rental default problems could be solved in the future if an adaptive subscription model is adopted for the housing sector by installing smart doors.

Table 5. Adaptive model Q analysis.

Months	Q months	Days	Q days	Hours	Q hours
1	2700000	1	290483.87	1	9395.1613
2	2250000	2	275967.74	2	8790.3226
3	1800000	3	261451.61	3	8185.4839
4	1350000	4	246935.48	4	7580.6452
5	900000	5	232419.35	5	6975.8065
6	450000	6	217903.23	6	6370.9677
7	0*	7	203387.1	7	5766.129
8	-450000	8	188870.97	8	5161.2903
9	-900000	9	174354.84	9	4556.4516
10	-1350000	10	159838.71	10	3951.6129
11	-1800000	11	145322.58	11	3346.7742
12	-2250000	12	130806.45	12	2741.9355
		13	116290.32	13	2137.0968
		14	101774.19	14	1532.2581
		15	87258.065	15	927.41935
		16	72741.935	16	322.58065*
		17	58225.806	17	-282.2581
		18	43709.677	18	-887.0968
		19	29193.548	19	-1491.935
		20	14677.419	20	-2096.774
		21	161.29032*	21	-2701.613
		22	-14354.84	22	-3306.452
		23	-28870.97	23	-3911.29
		24	-43387.1	24	-4516.129
		25	-57903.23
		26	-72419.35
		27	-86935.48
		28	-101451.6
		29	-115967.7
		30	-130483.9
		31	-145000

* Mean quit.

Figure 5. Mr. X subscription breakdown based on the adaptive rental subscription model.

Based on Figure 6, if Mr. X does not subscribe after the last day of the 7^th month, his tenancy would automatically elapse which implies that the AAC would have been deactivated, but if he immediately resubscribed as in Figure 7 and Figure 8, the AAC will activate and hence his tenancy would be renewed. This process would continue depending on his subscription status. This is summarized in Figure 5.

Figure 6. Adaptive rental subscription model for Q period in months.

Figure 7. Adaptive daily rental subscription model for Q period in days.

Figure 8. Adaptive hourly rental subscription model/adaptive minute rental subscription model Q period in hours/minutes.

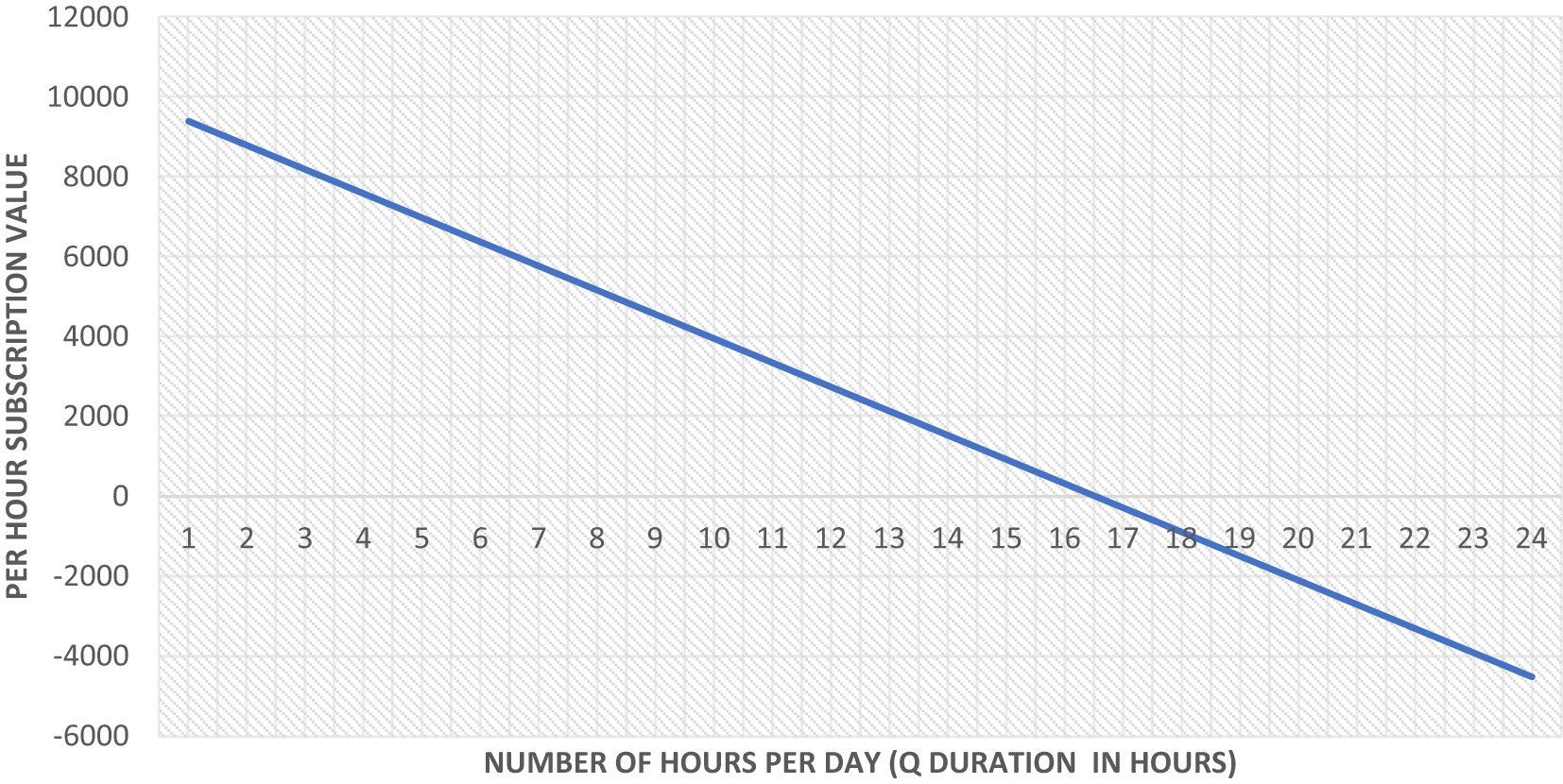
In Figure 7, he subscribed for 21 days, and in Figure 8 for 16 hours 30 minutes (0.68 day). He is expected to vacate the house at the end of the Q period.

4.3 Extension of problem 2

Let assume that Mr. X paid the complete annual rent. Figure 9 is the ARSM for an annual payment and Q duration. After the last day of the last month, Mr. X cannot access the house unless he subscribes again. The adaptive concept is unique in many ways because it can easily be implemented by installing smart doors in existing houses.

Figure 9. Adaptive rental subscription model for Q period per year.

5. Discussion

The recursive model in section 2 would provide the tenant the opportunity to pay rent annually, monthly, or weekly based on the available resources. It gives an equal opportunity to source the monthly rental. In case of the annual rent payment as in problem 1, the tenant may decide to quit the house and request a refund. The tenant can also pay rent for three months and two weeks and quit the house when the rental elapses or continue to stay until they can afford to pay another rental. The recursive model would provide opportunities for all classes of people to rent a house but would enhance rent default and rent arrears. The recursive model aligns with the robust housing plans enunciated by Bhide et al. (2019) and provides solutions to the problems enumerated by Ehrenpreis (2006). The recursive model embedded the concept enunciated by Parashar et al. (2020) and Tiwari and Rao (2016) to solve homelessness. The adaptive (ARS) model would make rental default impossible, and hence provide solutions to the problem of rental arrears discussed by Salleh, Johari and Yusof (2008) and Sufian (2015). However, the recursive model would allow tenants to retain the house and would continuously update the rent arrears. Part of the recursive model could be associated with the generosity of the COVID Act in Malaysia (Zul Rafique & Partners, 2020) whereby landlords could not evict tenants due to the proclamation of Movement Control Order (MCO) in Malaysia during the outbreak of COVID-19. In the absence of the COVID Act, the recursive model mimics the conventional renting method. On the other hand, the adaptive model is a business model which drastically adopts the internet and satellite television subscription model. The shortfall of the adaptive model is that a housing scheme which would be suitable for it would be very expensive. The adaptive model can be initiated now to catch up with the rapid technological advancement in the establishment of smart cities. At present, the adaptive model can be implemented by installing smart doors in existing houses or buildings. In general, the adaptive model is suitable for smart houses while the recursive model can be considered as the traditional renting model. The recursive model is very interactive and flexible whereas the adaptive model is rigid in concept. The recursive model can be used for housing for all citizens, but the adaptive model requires a periodic subscription which may not be affordable by all. Though both shared the subscription concept, their respective flexibility and rigidity differentiated their operational concepts.

5.1 Recommendation

With the high rate of rental arrears in the public and private housing sectors, the adaptive model would be the preferred model to solve rental default. On the other hand, the recursive model could be used for the low income and daily income earners since it is very flexible and it updates the rent arrears. In general, the adaptive model is very suitable for the private sector housing developer. The adaptive model is also suitable for shopping mall and other large scale housing developers. These models are recommended to the government for action.

5.2 Conclusion

This paper has advanced flexible and rigid rental subscription models. The recursive model can be adopted for ‘traditional’ renting, as they allow for interaction and flexibility with regards to rental default. It also allows for a rent refund. It can be described as a model that could allow housing for people with limited resources. The recursive model is flexible in the sense that the tenant would default and still reside in the house. It is a good model for low-income and daily income earners because it provides space for them to source their rent. The adaptive model is a purely business-concern based model that allows access when subscribed. It is a non-interactive model that helps to solve corporate and high-profile rental default problems. The analysis showed that the application of the recursive model is easy and cheap, however the adaptive model is expensive. The analysis in the tables and figures showed the operational framework of the models. Therefore, the analysis showed that the recursive and adaptive models are suitable to solve rental refund and rental default problems.

Data availability

Harvard Dataverse: Replication Data for: RENT CHARGES. https://doi.org/10.7910/DVN/U081B1 (Okwonu 2022)

This project contains the following underlying data:

• AccoDataset 2.tab (This data set contains information on rent charges per annum in five major cities in Nigeria)

Data are available under the terms of the Creative Commons Zero “No rights reserved” data waiver (CC0 1.0 Public domain dedication).

Acknowledgements

The authors would like to thank Universiti Utara Malaysia and Delta State University, Abraka for their support upon the completion of this research. This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

References

Abiodun JO: Housing Problems in Nigerian Cities. Town Plan. Rev. 1976; 47(4): 339–347
Ahvenniemi H, Huovila A, Pinto-Seppä I, et al.: What are the differences between sustainable and smart cities?. Cities. 2017; 60: 234–245. Publisher Full Text
Bakhtyar B, Zaharim A, Sopian K, et al.: Housing for Poor People: A Review on Low Cost Housing Process in Malaysia. WSEAS Trans. Environ. Dev. 2013; 9(2).
Barnett V, Neter J, Wasserman W: Applied Linear Statistical Models. Journal of the Royal Statistical Society. Series A (General). 1975; 138(2): 258.
Bhide A, Crenshaw K, Shaban A, et al.: Housing Poverty in Urban India: The Failures of Past and Current Strategies and the Need for a New Blueprint. Econ. Polit. Wkly. 2019; 10.
Delucchi KL: On the Use and Misuse of Chi-Square. A Handbook for Data Analysis in the Behavioral Sciences: Statistical Issues. 1976.
Djebarni R, Al-Abed A: Satisfaction Level with Neighbourhoods in Low-Income Public Housing in Yemen. Prop. Manag. 2000; 18(4) Publisher Full Text
Ehrenpreis D: What is poverty? Concepts and measures. International Policy Centre for Inclusive Growth; 2006; No. 9.
Eremia M, Toma L, Sanduleac M: The Smart City Concept in the 21st Century. Procedia Engineering. 2017; 181: 12–19. Publisher Full Text
Gayinu B, Fapohunda J, Haldenwang R, et al.: A Conceptual Framework For Sustainable – Affordable Housing For The Rural Poor In Less Developed Economies 2. Housing Issues: A Framework for Conceptualization. New England Journal of Public Policy. 2014; 6(1).
Georgiadis A, Christodoulou P, Zinonos Z: Citizens’ Perception of Smart Cities: A Case Study. Applied Sciences (Switzerland). 2021; 11(6): 2517. Publisher Full Text
Haberman SJ: The Analysis of Residuals in Cross-Classified Tables. Biometrics. 1973; 29(1): 205–220. Publisher Full Text
Neter J, Kutner MH, Nachtsheim CJ, et al.: Applied Linear Statistical Models. Fourth Edition. J. Educ. 1996; 36(3).
Mohanty SP, Choppali U, Kougianos E: Everything You Wanted to Know about Smart Cities. IEEE Consumer Electronics Magazine. 2016; 5(3): 60–70. Publisher Full Text
Mohd Noor MZ: FlexZhouse: New Business Model for Affordable Housing in Malaysia. A+BE Architecture and the Built Environment. 2017; 2: 1–318
Okwonu F: Replication Data for: RENT CHARGES. Harvard Dataverse, V1. 2022. Publisher Full Text
Salleh NA, Johari N, Yusof N: Rent Arrears and Their Implications in Public Housing. 2nd International Conference on Built Environment in Developing Countries (ICBEDC 2008), no. Icbedc. 2008.
Parashar D, Thakur N, Dharwal D, et al.: Impact Of Land Policies On Housing Markets: Case of Noida, India. Int. J. Manag. 2020; 11(6).
Praharaj S, Han H: Cutting through the Clutter of Smart City Definitions: A Reading into the Smart City Perceptions in India. City Cult. Soc. 2019; 18: 100289. Publisher Full Text
Ross P, Maynard K: Towards a 4th Industrial Revolution. Intelligent Buildings International. 2021; 13. Publisher Full Text
Sharpe D: Your Chi-Square Test Is Statistically Significant: Now What?. Pract. Assess. Res. Eval. 2015; 20(1): 8.
Sufian A: A Conceptual Study on Landlord and Tenant Law in Peninsular Malaysia: A Focus on Private Residential Tenancy. Proceedings of the 26th International Business Information Management Association Conference - Innovation Management and Sustainable Economic Competitive Advantage: From Regional Development to Global Growth, IBIMA 2015. 2015.
Tiwari P, Rao J: Housing Markets and Housing Policies in India. SSRN Electron. J. 2016. Publisher Full Text
Vale LJ, Shamsuddin S, Gray A, et al.: What Affordable Housing Should Afford: Housing for Resilient Cities. Cityscape: A Journal of Policy Development and Research. 2014; 16(2): 21–50
Wahi N, Zin RM, Munikanan V, et al.: Problems and Issues of High Rise Low Cost Housing in Malaysia. IOP Conference Series: Materials Science and Engineering. 2018; 341(1): 012027. Publisher Full Text
Rafique Z; Partners. Landlord’s Rights and Remedies under Temporary Measures for Reducing the Impact of Coronavirus Disease 2019 (Covid-19) ACT 2020-A Right Denied?.2020.

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 25 Jan 2022

Author details Author details

¹ School of Quantitative Sciences, College of Arts and Sciences, UNIVERSITI UTARA MALAYSIA, Sintok, Kedah, 06010, Malaysia
² Department of Mathematics, DELTA STATE UNIVERSITY, Abraka, Delta, P.M.B.1, Nigeria
³ Institute of Strategic Industrial Decision Modeling, School of Quantitative Sciences, College of Arts and Sciences, UNIVERSITI UTARA MALAYSIA, Sintok, Kedah, 06010, Malaysia
⁴ Faculty of Computing, Dennis Osadebay University, Anwai Rd, Asaba, Nigeria

Friday Zinzendoff Okwonu
Roles: Conceptualization, Methodology, Software, Validation

Nor Aishah Ahad
Roles: Data Curation, Supervision, Writing – Original Draft Preparation

Joshua Sarduana Apanapudor
Roles: Data Curation

Festus Irimisose Arunaye
Roles: Writing – Review & Editing

Innocent Ejiro Okoloko
Roles: Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Article Versions (1)

version 1

Published: 25 Jan 2022, 11:89

https://doi.org/10.12688/f1000research.75360.1

Copyright

© 2022 Okwonu FZ et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

Okwonu FZ, Ahad NA, Apanapudor JS et al. The recursive-adaptive rental subscription model (R-ARSM) in the new normal: an application to the housing sector [version 1; peer review: awaiting peer review]. F1000Research 2022, 11:89 (https://doi.org/10.12688/f1000research.75360.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 25 Jan 2022

Open Peer Review

Reviewer Status

AWAITING PEER REVIEW

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

[1] Abiodun JO: Housing Problems in Nigerian Cities. Town Plan. Rev. 1976; 47(4): 339–347

[2] Ahvenniemi H, Huovila A, Pinto-Seppä I, et al.: What are the differences between sustainable and smart cities?. Cities. 2017; 60: 234–245. Publisher Full Text

[3] Bakhtyar B, Zaharim A, Sopian K, et al.: Housing for Poor People: A Review on Low Cost Housing Process in Malaysia. WSEAS Trans. Environ. Dev. 2013; 9(2).

[4] Barnett V, Neter J, Wasserman W: Applied Linear Statistical Models. Journal of the Royal Statistical Society. Series A (General). 1975; 138(2): 258.

[5] Bhide A, Crenshaw K, Shaban A, et al.: Housing Poverty in Urban India: The Failures of Past and Current Strategies and the Need for a New Blueprint. Econ. Polit. Wkly. 2019; 10.

[6] Delucchi KL: On the Use and Misuse of Chi-Square. A Handbook for Data Analysis in the Behavioral Sciences: Statistical Issues. 1976.

[7] Djebarni R, Al-Abed A: Satisfaction Level with Neighbourhoods in Low-Income Public Housing in Yemen. Prop. Manag. 2000; 18(4) Publisher Full Text

[8] Ehrenpreis D: What is poverty? Concepts and measures. International Policy Centre for Inclusive Growth; 2006; No. 9.

[9] Eremia M, Toma L, Sanduleac M: The Smart City Concept in the 21st Century. Procedia Engineering. 2017; 181: 12–19. Publisher Full Text

[10] Gayinu B, Fapohunda J, Haldenwang R, et al.: A Conceptual Framework For Sustainable – Affordable Housing For The Rural Poor In Less Developed Economies 2. Housing Issues: A Framework for Conceptualization. New England Journal of Public Policy. 2014; 6(1).

[11] Georgiadis A, Christodoulou P, Zinonos Z: Citizens’ Perception of Smart Cities: A Case Study. Applied Sciences (Switzerland). 2021; 11(6): 2517. Publisher Full Text

[12] Haberman SJ: The Analysis of Residuals in Cross-Classified Tables. Biometrics. 1973; 29(1): 205–220. Publisher Full Text

[13] Neter J, Kutner MH, Nachtsheim CJ, et al.: Applied Linear Statistical Models. Fourth Edition. J. Educ. 1996; 36(3).

[14] Mohanty SP, Choppali U, Kougianos E: Everything You Wanted to Know about Smart Cities. IEEE Consumer Electronics Magazine. 2016; 5(3): 60–70. Publisher Full Text

[15] Mohd Noor MZ: FlexZhouse: New Business Model for Affordable Housing in Malaysia. A+BE Architecture and the Built Environment. 2017; 2: 1–318

[16] Okwonu F: Replication Data for: RENT CHARGES. Harvard Dataverse, V1. 2022. Publisher Full Text

[17] Salleh NA, Johari N, Yusof N: Rent Arrears and Their Implications in Public Housing. 2nd International Conference on Built Environment in Developing Countries (ICBEDC 2008), no. Icbedc. 2008.

[18] Parashar D, Thakur N, Dharwal D, et al.: Impact Of Land Policies On Housing Markets: Case of Noida, India. Int. J. Manag. 2020; 11(6).

[19] Praharaj S, Han H: Cutting through the Clutter of Smart City Definitions: A Reading into the Smart City Perceptions in India. City Cult. Soc. 2019; 18: 100289. Publisher Full Text

[20] Ross P, Maynard K: Towards a 4th Industrial Revolution. Intelligent Buildings International. 2021; 13. Publisher Full Text

[21] Sharpe D: Your Chi-Square Test Is Statistically Significant: Now What?. Pract. Assess. Res. Eval. 2015; 20(1): 8.

[22] Sufian A: A Conceptual Study on Landlord and Tenant Law in Peninsular Malaysia: A Focus on Private Residential Tenancy. Proceedings of the 26th International Business Information Management Association Conference - Innovation Management and Sustainable Economic Competitive Advantage: From Regional Development to Global Growth, IBIMA 2015. 2015.

[23] Tiwari P, Rao J: Housing Markets and Housing Policies in India. SSRN Electron. J. 2016. Publisher Full Text

[24] Vale LJ, Shamsuddin S, Gray A, et al.: What Affordable Housing Should Afford: Housing for Resilient Cities. Cityscape: A Journal of Policy Development and Research. 2014; 16(2): 21–50

[25] Wahi N, Zin RM, Munikanan V, et al.: Problems and Issues of High Rise Low Cost Housing in Malaysia. IOP Conference Series: Materials Science and Engineering. 2018; 341(1): 012027. Publisher Full Text

[26] Rafique Z; Partners. Landlord’s Rights and Remedies under Temporary Measures for Reducing the Impact of Coronavirus Disease 2019 (Covid-19) ACT 2020-A Right Denied?.2020.