Keywords
Perovskite material, DFT calculation, SOC effect, Strain, Optoelectronic properties,
This article is included in the Energy gateway.
This article is included in the Perovskite Solar Cells collection.
Perovskite material, DFT calculation, SOC effect, Strain, Optoelectronic properties,
Photovoltaic (PV) technology is a notable participant in the energy industry due to its significant ability to lower oil consumption, ameliorate greenhouse gas (GHG) emissions, and lessen environmental deterioration.1 The potential for developing conventional solar cells such as Si is limited due to their indirect, suboptimal bandgaps and costly fabrication processes.2 In 2009, halide perovskite was initially introduced.3 The solar technology field has been showing increased attraction in organic-inorganic perovskites because of their remarkable properties, including a significant bandgap, universal accessibility, exceptional optical absorption capabilities, low reflectivity, and cost-effectiveness.4–9 The power conversion efficiency (PCE) rapidly increased over the last thirteen years, from 3.8% to 25.8%.10 The PCE of CsPbI3 perovskite solar cells can achieve 17.9%11 without hole transport layer (HTL) in 2022 and 19.06%12 with HTL in 2023. The improvement of perovskite materials’ properties during the last 10 years has expedited this progression. Metal halide-based inorganic perovskites are attracting a lot of interest. The organic-inorganic perovskites’ difficulty with long-term longevity is a significant concern because of its susceptibility to moisture, wind, sunlight, and temperature when utilized in a natural environment.13,14 However, because of the low stability of lead (Pb) implemented in the perovskite materials, which causes rapid breakdown when exposed to specific circumstances like heat and moisture, the general use and improvement of perovskite solar cells are hampered. Another issue that restricts their employment is the device hysteresis effect, which results in instability and inconsistent outcomes under various measurement circumstances.15 Furthermore, lead toxicity is a significant concern during the production and disposal of perovskite solar cells, which impedes their sustainability and poses health and environmental risks.16 Zhu et al.17 revealed that inorganic halide perovskites had almost equal band edge carrier properties. Inorganic cubic perovskites have recently attracted interest as prospective options for LED, semiconductor, and solar technologies due to their straight bandgap nature and remarkable optical absorption characteristics.18–20 In addition, L. Zhang et al. discovered that inorganic perovskite solar cells may generate high open-circuit voltages in a consistent and long-lasting way.21 Perovskites with an A3BX3 type structure attract a lot of attention because of their extraordinary qualities, including the absence of lead, mechanical stability, superior electrical characteristics, and direct bandgap material. There have been no extensive studies on Sr3NI3 yet. The future applications of electronic and optoelectronic devices can greatly benefit from a thorough and comprehensive study of the inorganic perovskite Sr3NI3.
The bandgap of a solar cell significantly influences its PCE as it determines the generation of charge carriers and absorption of light. As per the Shockley-Queisser theory, a perovskite solar cell with a bandgap between 1.2 to 1.4 eV can achieve a PCE of up to 33%.22,23 Although inorganic halide perovskites are well-suited for optoelectronic and photovoltaic systems, they have a slight disadvantage of having a relatively higher bandgap.24,25 The ability to adjust the electronic bandgap using multiple methods is critical for achieving maximum PCE in inorganic halide perovskite solar cells. In recent times, there have been several types of research that have utilized strain engineering as a method to improve specific properties of a material.26–30 Strain engineering is an effective method for modifying perovskite materials’ atomic structure and physical characteristics, allowing them to be employed in solar applications. Recent investigations on the properties of materials resulting from strain have revealed an essential link between the material’s properties and its structural features.31–37 Applying a minor amount of pressure (less than 0.3 GPa) reduces the bandgap and improves the carrier lifetime by 70% to 100% in organic-inorganic tri-iodide perovskite materials.38 Rasidul Islam15 accomplished a thorough investigation on the characteristics of perovskites APbBr3 (where A represents Rb and Cs) and made notable conclusions regarding the impact of strain within the -6% to 6% range. Jing et al.39 conducted an extensive study on CsPbI3 and observed that by applying strain in the range of -5% to 5%, the bandgap of CsPbI3 may be adjusted to fall between 1.03 and 2.14 eV. Similarly, A. K. Hossain40 found that applying compressive strain on the inorganic perovskite CsSnCl3 can transform it from a semiconductor to a metallic substance, which possesses remarkable optical and electronic properties. By applying pressure to CH3NH3GeI3, it is possible to optimize the material’s potential for utilization in solar cells by attaining a more significant band gap energy, improved carrier mobility, and optimized absorption coefficients.41 Compressive and tensile strain can be used to successfully change some properties of CsGeI3, such as the bandgap and dielectric coefficient.42 Compressive and tensile strain considerably influence the structural, electrical, and optical properties of Sr3NI3 perovskite. Because of their larger atomic sizes, larger cations contain more nucleons than smaller ones, resulting in a modification in terms of the electronic band structure. The manipulation of electronic characteristics in various materials can typically be accomplished utilizing the spin-orbit coupling (SOC) phenomenon.43–45 When considering the SOC effect, the bandgap of halide perovskites may drop by approximately one electron volt (eV) and experience band splitting.45 Therefore, it is crucial to conduct a meticulous and systematic investigation of the SOC effect and biaxial strain variations in Sr3NI3 perovskite. Hence, performing a comprehensive analysis of the influence of strain and SOC effect on Sr3NI3 perovskite holds great significance.
This research aimed to execute FP-DFT computations to investigate how varying amounts of strain and SOC impact the structural, electrical, and optical characteristics of cubic Sr3NI3. Our investigation focused on a thorough analysis of the band structure and bandgap modification mechanism of Sr3NI3. Our primary focus was determining how the SOC phenomenon influences the electronic properties of the Sr3NI3 perovskite. We utilized two distinct methodologies to investigate the band structure of Sr3NI3 in our research. Our analysis specifically focused on the impact of strain and SOC changes on the bandgap, including both expansion and compression. According to our findings, Sr3NI3 has remarkable features that make it suitable for various semiconductor materials, including high-temperature superconducting materials, energy storage devices, and future solar cells.
The DFT computations were executed employing the Quantum Espresso simulation application package.46–50 The FP-DFT analysis of the Sr3NI3 perovskite structure was performed using a norm-conserving (NC) pseudopotential51–53 and the Perdew-Burke-Ernzerhof (PBE)54 exchange-correlation mechanism. The input data contained vital initial configurations, including the specification of the Brillouin zone grid, crystal structure arrangements, lattice constants, and the specified kinetic cut-off energy. To improve the performance and optimize the structure, adjustments were made to the kinetic energy cut-off and charge density cut-off parameters, setting them at 30 Rydberg (Ry) (approximately 410 eV) and 220 Rydberg (Ry) (approximately 2990 eV), respectively. The optimization of the lattice via vc-relax computation was carried out using a k-point (kx, ky, kz) dimension of (6×6×6). For the Self-consistent field (SCF) calculations, a convergence threshold of 10-6 atomic units and a maximum force tolerance of < 0.01 eV/was specified.15 A force convergence threshold of nearly 10-3 a.u was considered during the relaxation studies of ionic and structural adjustments. The use of modified PBE for metals was not implemented in our present study, despite the availability of approaches to control this inaccuracy.55,56 The biaxial compressive and tensile strain was reproduced by varying the astrained lattice parameter. To determine strain, we implemented a formula57:
In the formula, the unstrained lattice constant is denoted by the term “astrained.” The ε range is presented in 2% increments and spans -4% to +4%, whereas negative values indicate compressive strains, while positive values indicate tensile strains. Once the perovskite structure was dynamically stabilized, its optical properties were analyzed by calculating its complex dielectric functions, which are photon energy-dependent. We analyzed the optical properties of the material structures using the first-order time-dependent perturbation theory and verified their dynamical stability.58 The complex dielectric component was analyzed to determine the energy spectrum (measured in eV) at which it displays absorption peaks for photons. To calculate optical properties, a Monkhorst-Pack k-point grid with a 10 × 10 × 10 Gamma center was applied to sample the Brillouin zone. While determining the optical absorption coefficients, the complex dielectric function, represented by ε(ω) = ε1(ω) + jε2(ω), is considered the primary relationship.
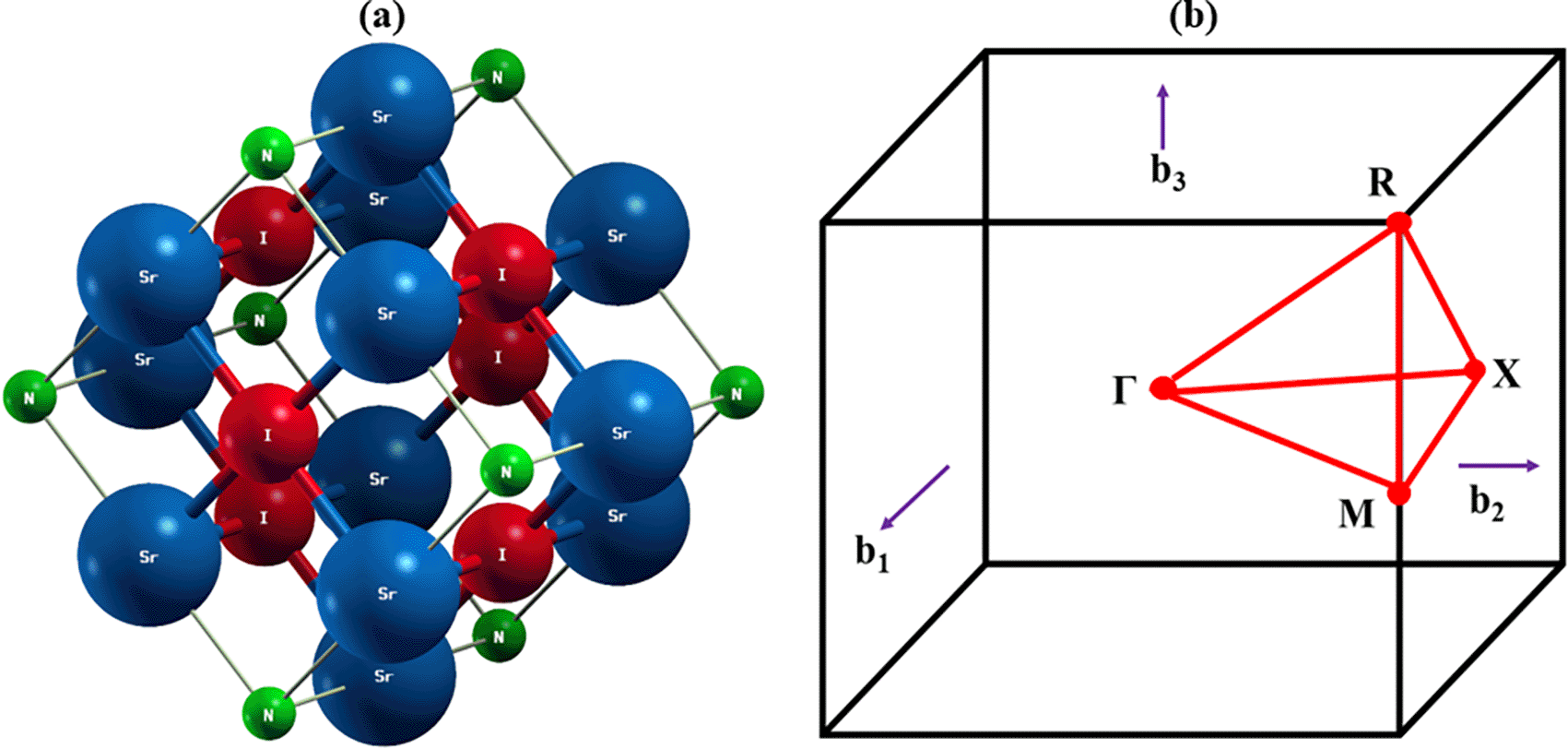
The optimum structure of the inorganic perovskite of Sr3NI3 is shown in Figure 1(a) and the k-path of the first Brillouin zone in order to identify their electronic band structure is shown in Figure 1(b). Sr3NI3 is a metal halide perovskite compound that crystallizes in a cubic structure with a high degree of symmetry. Specifically, its crystal structure is associated with the space group Pm-3m, a highly symmetric space group corresponding to a simple cubic lattice.59,60 The strontium (Sr) and nitrogen (N) atoms in the SrN4 tetrahedra are bound together by covalent bonds with varying bond lengths ranging from around 2.23 to 2.51. Iodine (I) atoms generate weak van der Waals interactions with the surrounding atoms rather than being directly bound to strontium or nitrogen atoms. The average bond lengths in Sr3NI3 have been calculated to be 2.46Å for Sr-N bonds and 3.00Å for I-Sr bonds. The Wyckoff notation, which describes the symmetry-equivalent locations inside the unit cell, may be used to represent the fractional coordinates of nitrogen (N), iodine (I), and strontium (Sr) atoms in Sr3NI3. The Wyckoff locations for Sr3NI3 in the cubic space group Pm-3m are: (i) The Sr atom occupies a single place at the 1a site, with fractional coordinates of (0,0,0), (ii) The 3c site is defined by three places filled by an I atom, with fractional coordinates of (0.5,0.5,0), (iii) The 3d site corresponds to three N atom-occupied sites with fractional coordinates of (0,0.5,0). First, the structural characteristics of Sr3NI3 perovskite must be computed before analyzing its various features. PBE was used to obtain the structural properties, identical to the lattice constant a(Å) value shown in Table 1. The greatest sustainable lattice constant for Sr3NI3 has been identified by calculating the total amount of energy while considering the lattice parameter. The Sr3NI3 compound’s lattice constant has been reported to be a = 6.33 Å.
Moreover, Cohesive and formation energy are valuable measurements for determining a structure’s stability. By calculating these energies for a given system, we can decide if the form is stable and use this information to validate its stability.61,62 The following formula may be used to compute these energies15:
| Structure | Lattice constant (Å) | Bandgap energy (eV) | ||
|---|---|---|---|---|
| This work | Previous work | This work | Previous work | |
| Sr3NI3 | 6.33 | 6.3363 | 0.733 (PBE) | 1.48 (HSE)63 |
Table 1 shows the lattice constant and energy bandgap of Sr3NI3 were determined through a comprehensive analysis that included experimental data and earlier DFT computations. The findings of our investigation demonstrate that the formation energy of Sr3NI3 is approximately -12.6 meV per atom, which is a negative value. It indicates that Sr3NI3 has negative conjunctive and formation energies, suggesting that the perovskite structure is stable.
Studying the electronic charge density of a component is a crucial aspect of analyzing its electronic characteristics. It involves creating a map of the charge density structure of the valence electrons in the unit cell, reflecting the overall charge concentration. By examining the total electronic charge density map, researchers can investigate the chemical bonding nature of the molecule. This charge density curve is composed of structural atoms that demonstrate how orbital electrons contribute to the electrical properties of atoms by accumulating charges.
Subsequently, a color density map that highlights differences in charge is used to link electronic DOS spectra from individual elements. The mapping of the charge density in the Sr3NI3 compound is displayed in Figure 2(a) 2D view, Figure 2(b) bird’s eye view, and Figure 2(c) 3D view, respectively. The electron density analysis indicates that the N and Sr atoms interact weakly, which plays a role in stabilizing the crystal lattice. Or, to put it another way, the crossing of the outer electrons between these two components suggests the presence of a covalent link.64,65 Furthermore, the charge density distribution reveals that the I atoms possess low electron density due to their poor electronegativity and tendency to form weak covalent bonds.66,67 The charge distribution analysis provides strong evidence for the covalent bonding features of the Sr-N atoms. The researchers observed that the charge density surrounding the atoms has an almost spherical shape, a characteristic of ionic bonding similar to that seen in previously published perovskites.66,67 The bonding between the Sr and I atoms is consistent with an ionic bond, while the N-I bond exhibits negative population values, indicating an antibonding property.
After structural optimization, we calculated the design of electronic bands and the highly symmetric point direction of Sr3NI3. A direct bandgap is usually necessary for a system to be an acceptable contender for optoelectronics device applications.68,69 The electronic properties of a substance are essentially dependent on its band structure, charge density, and density of states (DOS).70 The band configuration of the unstrained Sr3NI3 perovskite formation is shown in Figure 3(a). The Fermi levels have been zeroed out to evaluate the bandgap value conveniently. The crystal structure of the cubic Sr3NI3 is analyzed by considering the path Γ-X-M-R-Γ along the k-axis. Figure 3(a) illustrates the placements of the conduction band minimum (CBM) and valence band maximum (VBM) of Sr3NI3, both of which are situated near the Γ (Gamma) point. Based on the PBE calculations, it has been predicted that Sr3NI3 perovskite exhibits a direct bandgap structure with a bandgap value of approximately 0.733 eV. This result appears consistent with previously published values.71,72 When the bandgap of Sr3NI3 was calculated using the GGA method, it was significantly underestimated, which is a frequent disadvantage of the GGA method. Similarly, it was found that both the (LDA)+U and LDA techniques for local density approximation also underestimated the bandgap value of Sr3NI3.73 Several specialists have given several types of solutions to prevent this type of bandgap computing, including the GW methodology hybrid functional.74,75 Furthermore, a direct bandgap is necessary for crystalline substances to be suitable for advanced photothermal and sustainable energy applications. Because of their high direct bandgap value, these compounds are considered suitable for efficient solar cells and cells used in photovoltaic applications.

The partial density of states (PDOS) analysis explains how the distinct atoms and their various configurations in the structure impact the bandgap energy of Sr3NI3. Figure 3(b) illustrates the PDOS dispersion in Sr3NI3 for the -4 to 3 eV range. The PDOS analysis demonstrates that the forms of Sr and N, hybridized with I in the Sr3NI3 structure, extend throughout the entire energy range while maintaining the bandgap energy. It shows that the primary bond between Sr-I and N-I is covalent. Additionally, it was noticed in Sr3NI3 that there was electron charge transfer from Sr and N to I (illustrated in Figure 3b) due to the substantial difference in atomic states. According to the cubic phase analysis, the I-5p orbitals are essential in referring to the valence band of any perovskite structure. The investigation of the DOS in the vicinity of the valence band of Sr3NI3 in our work indicated that the I-2p orbital was the crucial factor. On the other hand, the N-2p orbital and a minor contribution from the Sr-3s orbitals significantly influenced the conduction band.
The SOC effect has been considered during the computation to precisely forecast the band structure because of the existence of nitrogen ions in the perovskite structure. The modification of CBM and VBM levels is significantly affected by the SOC effect, as illustrated in Figure 4(a) for both the conduction and valence band sections. The electronic features of Sr3NI3 perovskite were studied by factoring in the Hamiltonian equation that includes the SOC effect.76 The Hamiltonian equation is given by:
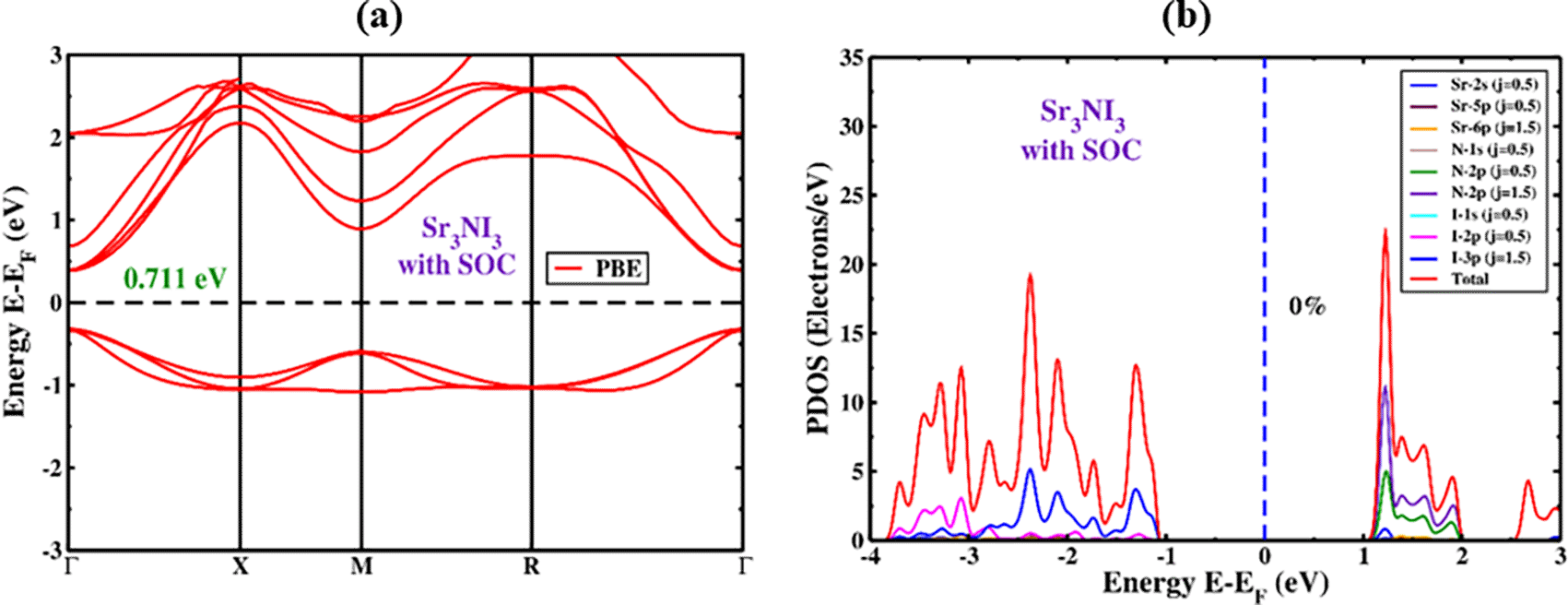
With regard to the SOC, HSOC represents the Hamiltonian operator that includes the effects of orbital angular momentum , potential energy or force , the mass of free electrons m0, and spin angular momentum , with ℏ representing the reduced Plank’s constant. The CBM shifted towards the Fermi level, whereas the VBM shifted upwards. Additionally, the only point in the crystal structure where the spin-degeneracy criterion is not satisfied is at the equally spaced point due to a band separation caused by inorganic perovskite crystals’ absence of inversion symmetry. The total angular momentum resulting from ls coupling can explain the band separation. The angular momentum of spin (s) and the angular momentum of orbital (l), where J is a value that falls between the absolute difference of l and s (|l-s|) and the sum of l and s (|l+s|). The values of l and j in s orbitals are 0 and 1/2 based on the molecular orbital theory, while the p orbitals have values of 1 and (1/2,3/2), and the d orbitals have values of 2 and (3/2,5/2). For each orbital, S equals +1/2 and -1/2. We saw the bandgap reducing when considering the SOC impact. The Sr3NI3 material has an energy band gap of 0.711 eV, which drives the valance and conduction bands closer to the Fermi level (Figure 4a). Table 2 displays the calculation of bandgap values for the Sr3NI3 perovskite both under and over SOC.
To better understand the band diagram of cubic Sr3NI3, we analyzed the PDOS in the presence of SOC. The PDOS revealed that the impact of the Sr atom is not limited by any predetermined rules when SOC is present, as demonstrated in Figure 4(b). The band edge remains unseparated at the high symmetry regions, even though the SOC effect divides I-2p and I-3p into p (j = 1/2) and p (j = 3/2). As depicted in Figure 4(b), the I-2p (j = 1/2) and I-3p (j = 3/2), atoms contribute the most significant portion of energy to the valence band (VB) within the range of -3.8 to -1.1 eV. The energy contribution to the CB side between 1 and 2 is mainly from N-2p (j = 1/2) and N-3p (j = 3/2).
We analyzed how the structures of Sr3NI3 are affected by applied strain (%), both under compressive and tensile stresses, while also considering the potential impact of the spin-orbit coupling (SOC) effect. We varied the amount of strain applied from compressive to tensile in steps of 1%, ranging from -4% to +4%. Throughout the compressive phase (-4% to 0%), we observed a displacement towards the Fermi level in the valence band maximum (VBM) and conduction band minimum (CBM) of perovskites, which is demonstrated in Figure 5(a). Similarly, as we applied tensile strain (+4% to 0%), we found that the VBM and CBM underwent a shift towards the Fermi level, while both VBM and CBM continued to remain at the Γ (Gamma)-point. Figure 6(a) shows the band configurations under compressive strain while considering the SOC impact of the Sr3NI3 compound. When considering compressive strain and including or excluding the SOC effect, the bond length of Sr, N, and I became shorter due to the clash between orbitals. Thus, the straight bandgap is established at the Γ (Gamma)-point whether or not the SOC effect is considered. Additionally, our observations revealed that higher levels of compressive strain lead to a decrease in the bandgap, both with and without accounting for the SOC effect.

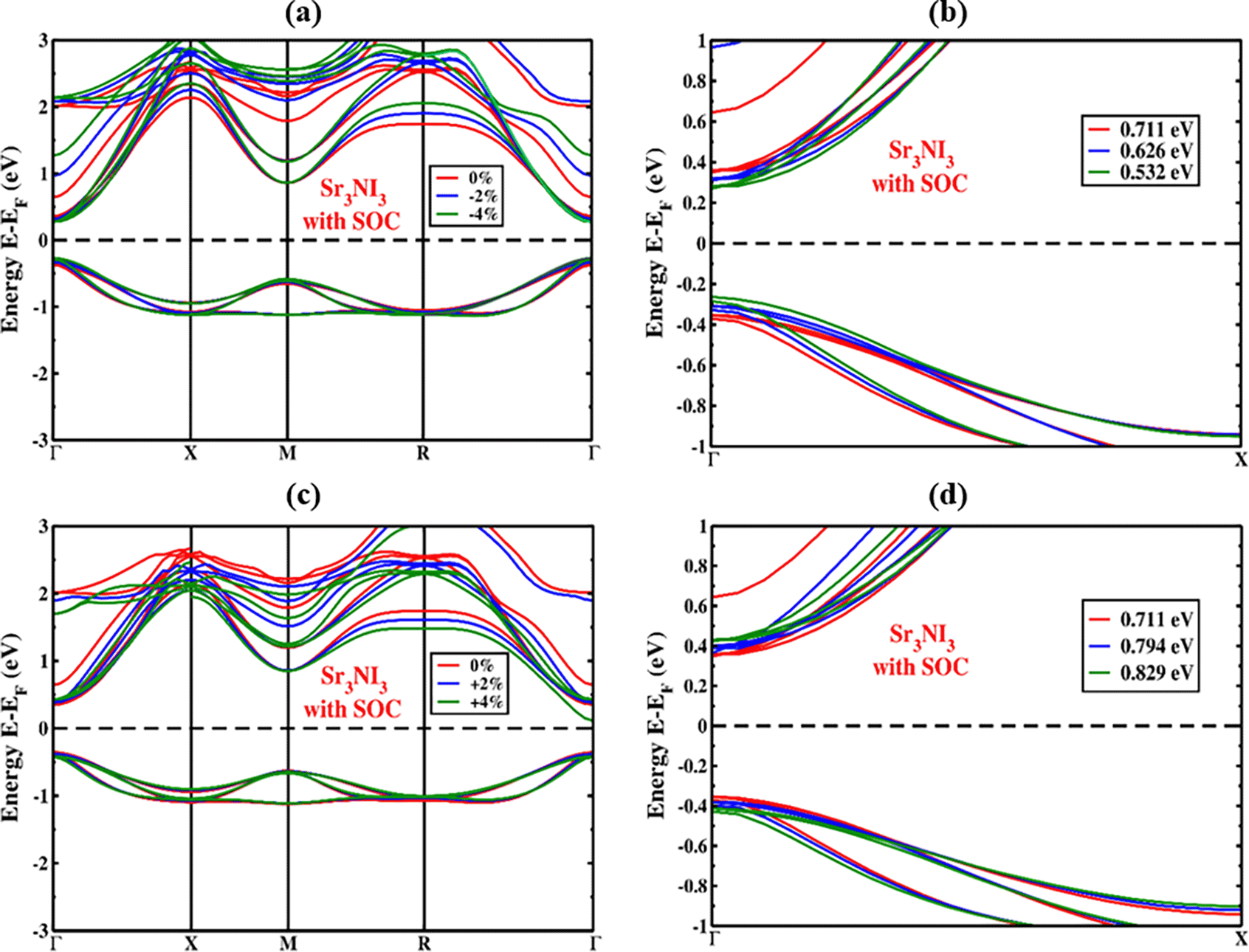
As shown in Figure 5(c), we also investigated the effects of tensile strain application (0% to +4%) on the electrical band structure of Sr3NI3 perovskite. The band configuration of the Sr3NI3 structure under tensile strain, considering the SOC effect, is displayed in Figure 6(c). We found an increase in the bandgap as an impact of the applied tensile strain, which is indicated by the deviation of the CBM and VBM from the Fermi energy level. Figures 5(b), 5(d), 6(b), and 6(d) provide a closer view of the Γ (Gamma)-point when both the compressive and tensile strains are considered, both with and without taking into consideration the SOC effect. The increase in bond length due to tensile strain resulted in a decrease in the force between the atoms of Sr, N, and I and an increase in atomic distance. We observed that the straight bandgap is formed at the Γ (Gamma)-point, regardless of whether the SOC effect is comprised. Furthermore, we noticed that higher tensile strain levels lead to an increase in the bandgap, irrespective of whether the SOC effect is considered or not.
The energy bandgap of the Sr3NI3 structure with respect to the strain being applied, whether or not the SOC effect show in Figure 7. Compressive and tensile strain applied to the Sr3NI3 structure results in a direct bandgap in the electronic band structure. The bandgap variations of the Sr3NI3 structure during compressive and tensile strain are presented in Table 2 like previous study.15 We observed a shift in the bandgaps of Sr3NI3, from 0.582 eV to 0.879 eV (without SOC) and from 0.532 eV to 0.829 eV (with SOC) when the applied strain varied from -4% to +4%. Sr3NI3 maintains its direct bandgap characteristic across the whole range of applied strains is a remarkable observation. The Shockley-Queisser hypothesis suggests that this particular structure can potentially improve a solar cell’s efficiency.23

The PDOS of Sr3NI3 under compressive and tensile strains are illustrated in Figure (8a, 8b) and Figure (8c, 8d), respectively. As the applied strain changes from -4% to +4%, the 2p orbital of the I atom becomes active towards the VBM side, slightly lower than the Fermi energy level. The 2p orbital of N atoms controls the significant portion of the entire DOS in the conduction band region. The stable position and arrangement of the DOS represented by the 2p orbital of N are not significantly affected by the induced strain on the CBM section. However, the total DOS performance improves as the strain varies from -4% to +4%. The total DOS for the Sr3NI3 structure is estimated to be 18 electrons/eV under -4% strain and 23 electrons/eV under +4% strain in Figure 8. The hybridized N-I and Sr-I orbitals are visible across the entire energy spectrum, but they are not visible within the bandgap zone.
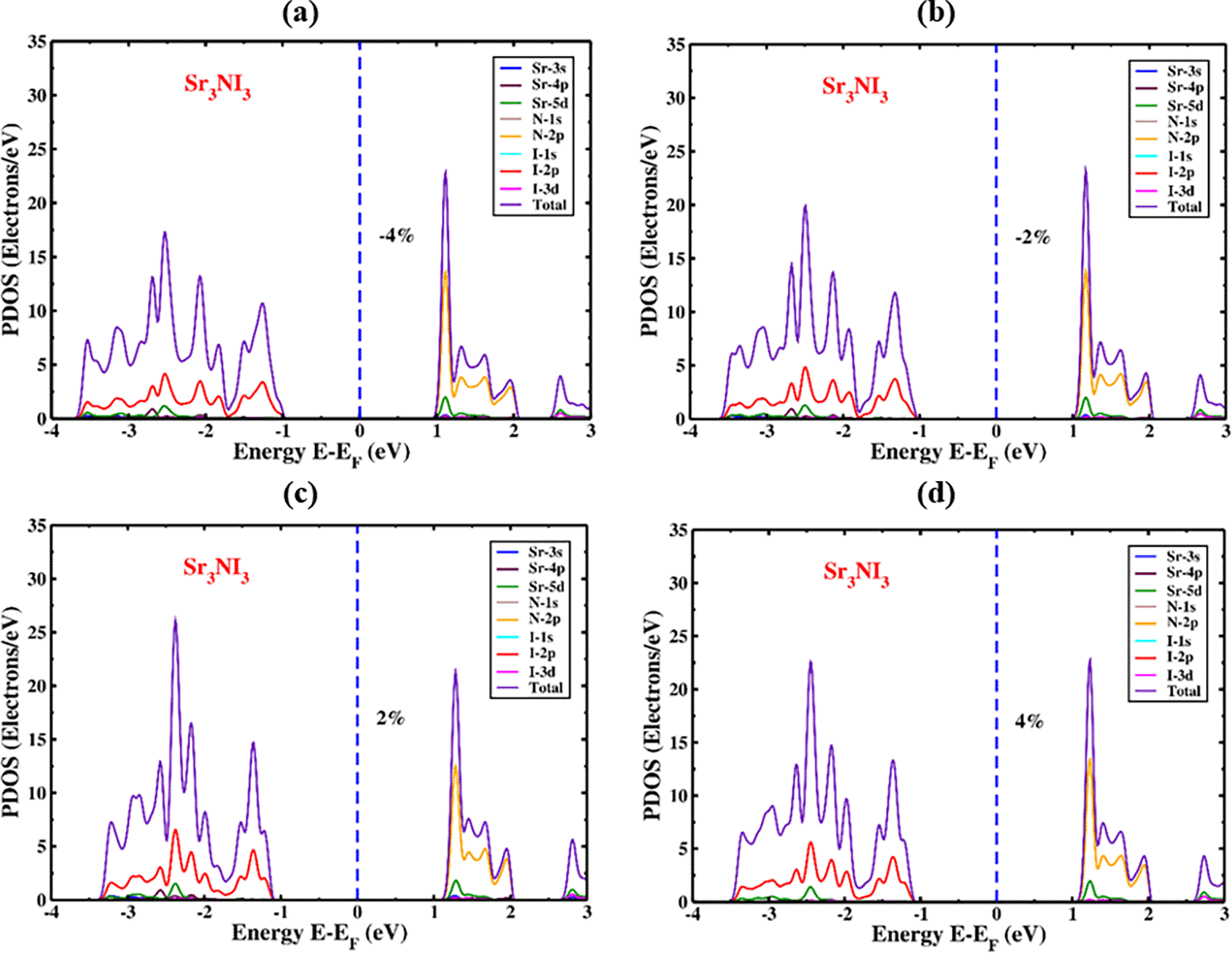
The PDOS of Sr3NI3 under both compressive and tensile strain is illustrated in Figure 9(a) and 9(b), and Figure 9(c) and 9(d), respectively, with the inclusion of the SOC effect. As the applied strain increases from -4% to +4% with the SOC effect, the 2p and 3p orbitals of the I atom become active towards the VBM side, appearing just below the Fermi energy level. Therefore, the 2p and 3p orbitals of the N atom control the majority of the TDOS in the region of CBM. The TDOS performance increases as the strain changes from -4% to +4%, with the SOC impact in consideration. Including the SOC effect leads to a change in the TDOS of the Sr3NI3 structure, as shown in Figure 9. Specifically, the TDOS is 17 electrons/eV at a strain of -4% and increases to 23 electrons/eV at a strain of +4%.
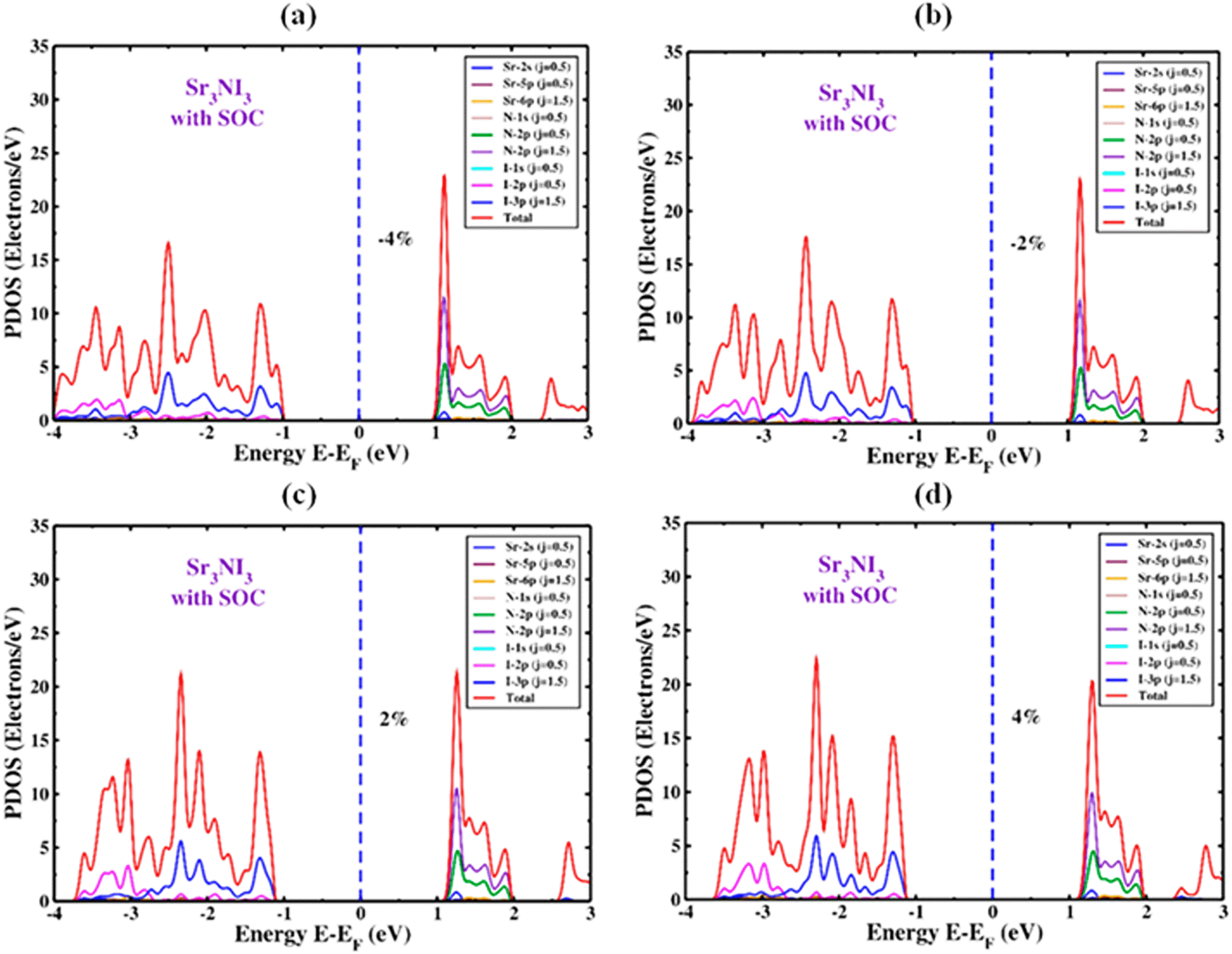
Figure 10 illustrates the total density of states (TDOS) for Sr3NI3 under different compressive and tensile strains, both with and without the SOC effect. Specifically, Figure 10(a) shows the TDOS without SOC impact, while Figure 10(b) shows the TDOS with SOC impact. The electronic band structure of Sr3NI3 can be accurately understood by analyzing the Total Density of States (TDOS). When analyzing unstrained Sr3NI3, it becomes apparent that the orbitals of the iodine (I) atoms play a significant role in the TDOS of the valence band below the Fermi level (EF). In contrast, the Sr-5d and N-2p (j=1.5) orbitals have a negligible impact, whether the SOC effect is present or not. Compared to the valence band, the orbitals of the nitrogen (N) atoms have a significant contribution to the TDOS of the conduction band above the Fermi level (EF), while the Sr-5d and I-2p orbitals have a negligible impact regardless of the presence or absence of SOC effect. Under compressive strains (0% to -4%), the TDOS line shifts towards the Fermi level, with or without the presence of the SOC effect. This shift causes the conductive properties of Sr3NI3 materials to improve. Conversely, under tensile strains (0% to +4%), the TDOS line deviates from the Fermi level, both with and without considering the SOC effect. The conductivity of Sr3NI3 is reduced as a result of this divergence.
An investigation of the optical properties of a material involves analyzing complex dielectric functions, electron loss function, absorption coefficient, and reflectivity. Studying these properties makes it possible to determine whether the material is appropriate for photovoltaic and optoelectronic applications. The optical performance of a substance can be improved by using a thermodynamic method known as biaxial strain. This method involves adjusting the lattice parameter of the material, which can effectively modulate its optical properties and improve its performance. The stretch-ability of different optical properties of Sr3NI3 under compressive (0% to -4%) and tensile (0% to +4%) stresses were investigated in this work. The study demonstrated how the material’s optical characteristics could be improved under different strains to better its performance. The dielectric function of a material is represented by the symbol ε(ω) and is calculated as the sum of two components. The first component is the real component, denoted by ε1(ω), and the second component is the imaginary component, represented by ε2(ω).
The Kramers-Kronig transformation is applied to calculate the real component of the dielectric function, whereas the imaginary part is calculated by evaluating the momentum matrix components.77,78 The real part of the dielectric constant can be used to investigate polarization and dispersion effects in Sr3NI3.79,80 Figure 11a and 11b illustrate the real and strain-induced components of the dielectric permittivity of unstrained Sr3NI3. The graphs show the real dielectric function values of up to 7.5 eV for photon energy. The dielectric constant’s real component offers valuable insights into a material’s polarization and dispersion effects. The maximum frequency of zero, denoted as ε1(0), is an essential parameter in the real component of the dielectric function. This parameter represents the electronic contribution to the dielectric constant’s real part and is a fundamental factor in the ε1(ω) component. The calculated value of ε1(0) for cubic Sr3NI3 is 6.95, as shown in Figure 11(a). Under optical excitation, the value of ε1(ω) in the material starts increase from ε1(0) to its maximum value, after which it suddenly drops. This response indicates that the material has a high absorption capacity for light in this spectral region. The positive values of ε1(ω) for unstrained Sr3NI3 indicate that the material is highly refractive and exhibits semiconductor-like properties. The maxima of the real component of the dielectric constant in the Sr3NI3 perovskite have been shifted by applying biaxial strain. Typically, materials with higher bandgap have less intense peaks in their dielectric constant compared to materials with narrow bandgap. Therefore, due to the reduction in bandgap under increasing compressive strain, the Sr3NI3 perovskite structure exhibits a higher dielectric constant peak and experiences a shift towards lower photon energies (redshift). The Sr3NI3 perovskite structure displays a lower dielectric constant peak and a shift towards higher photon energy (blueshift) when tensile strain increases.
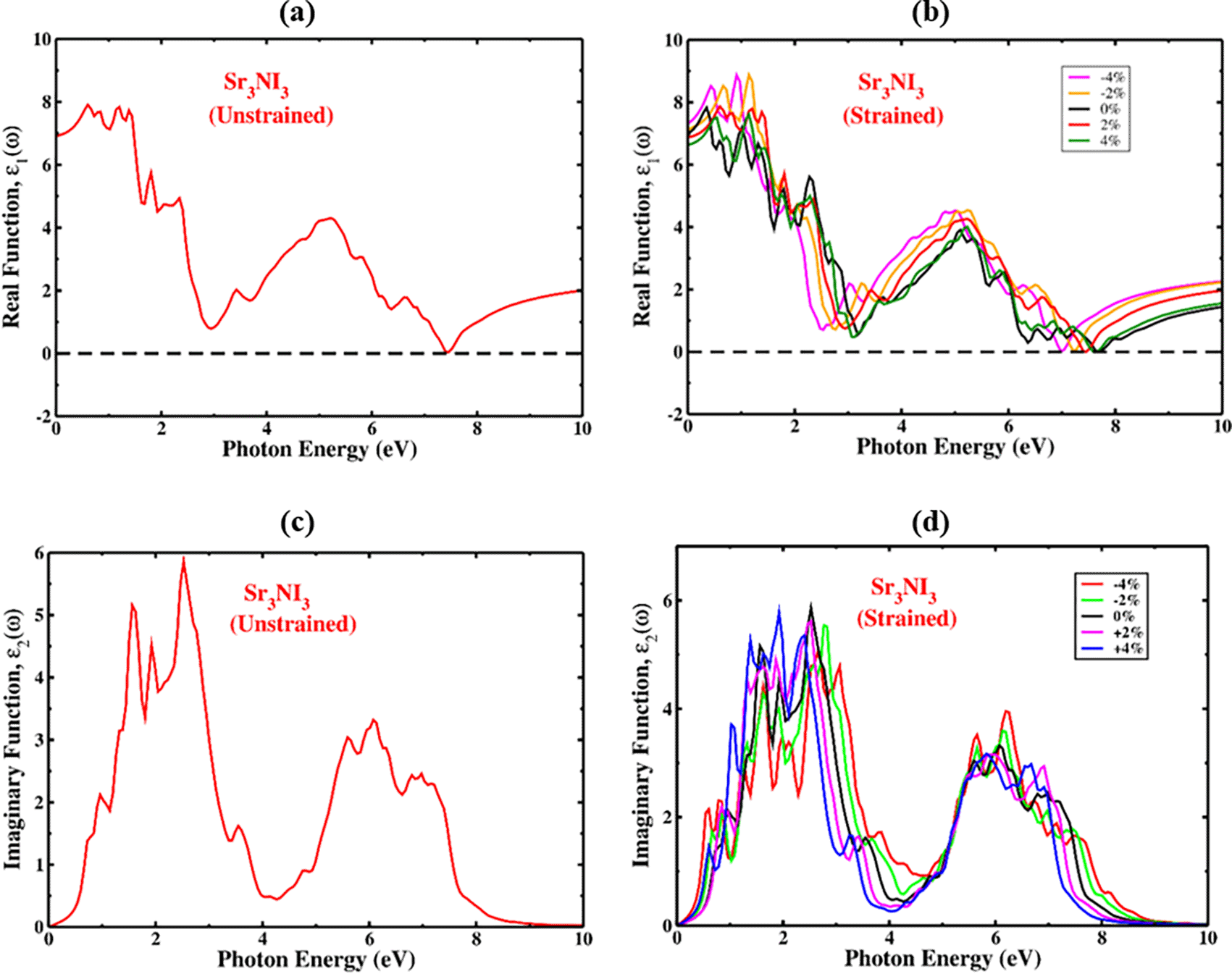
The behavior of the imaginary part of the dielectric function, ε2(ω), under unstrained and strained conditions, is illustrated in Figure 11(c) and 11(d), respectively. The dielectric function’s imaginary component is crucial for understanding optical absorption and the crystal structure’s capacity for storing energy caused by unbiased charge excitations. The imaginary dielectric function ε2(ω) provides information on the electronic bandgap and the energy of inter-band transitions near the Fermi level. This information can determine a material’s optical characteristics, such as its absorption and reflectivity. The absorption zone was mostly taken up of the values off ε2(ω) for Sr3NI3. Figure 11(c) shows that the most significant peaks of ε2(ω) for Sr3NI3 appear at an optical position of 6, indicating an energy of approximately 2.5 eV for absorption photons. As shown in Figure 11(d), when strain is applied, the imaginary portion of the dielectric function expands and moves toward longer wavelengths. The imaginary absorption peaks determine the movement of carriers from the valence band to the conduction band. The displacement of the peaks is attributed to fluctuations in the bandgap and lattice constant. Under compressive strain, the imaginary peaks show a red-shift, indicating a decrease in energy. Conversely, under tensile strain, the peaks exhibit a blue-shift, indicating an increase in energy, as depicted in Figure 11(d). The observed phenomenon implies that by applying either tensile or compressive strain to the Sr3NI3 compound, it may be possible to adjust the absorption spectral region, providing a means of tuning its properties.
Furthermore, we found that the imaginary dielectric portion is zero when photon energy exceeds 10 eV. The absence of ε2(ω) at high photon energies (above 10 eV) implies that the material has low optical absorption and higher optical transparency.
The “electron loss function” refers to the amount of energy that electrons dissipate while traversing a dielectric substrate. The “electron loss function” refers to the amount of energy that electrons dissipate while traversing a dielectric substrate. In Sr3NI3, the peak observed in the plot of L(ω) in Figure 12(a) indicates the dissipation of energy when photons with energy higher than the material’s bandgap are emitted. The electron loss function, L(ω), can be calculated using the formula . Figure 12(a) illustrates that the L(ω) peaks for the cubic structure of Sr3NI3 improve within the energy range of 8.5 to 9.18 eV. The highest peak of the loss function was observed at 8.8 eV, while the lowest peak was found at 2.5 eV in the case of Sr3NI3. The negligible presence of L(ω) peaks below 2 eV in Sr3NI3 indicates that it could be an efficient optical absorption layer for optical photon spectra and IR. The strain-applied Sr3NI3 displays a loss function for up to 10 eV of photon energies. According to Figure 12(b), the energy losses of Sr3NI3 can be predicted under different biaxial compressive and tensile strain conditions. According to the findings, increased compressive strain causes a large redshift, suggesting decreased photon energy and optical loss for all structures. Conversely, increasing tensile strain leads to a blueshift, indicating an increase in photon energy and optical loss. The loss function of Sr3NI3 plays a crucial role in its overall performance and should be carefully considered during the design and fine-tuning of these materials for specific applications.
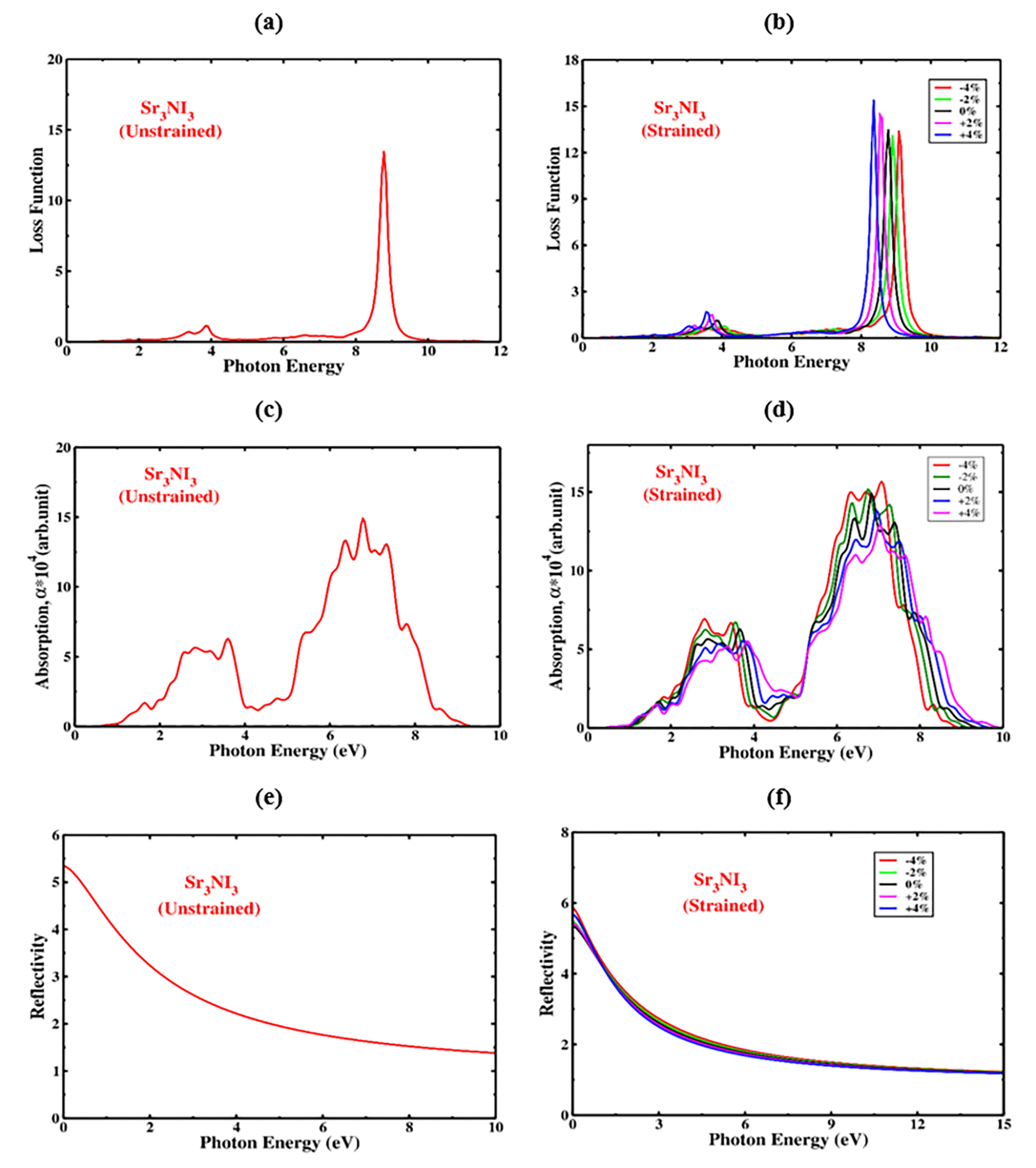
The absorption coefficient is an essential attribute of Sr3NI3 since it determines how much light the material absorbs at different wavelengths. The absorption coefficient of Sr3NI3 is impacted by various factors such as crystal structure, purity, and thickness of the material. The structure of the optical absorption coefficient for Sr3NI3 exhibits similar characteristics to that of the imaginary part of the dielectric constant for any given configuration. The visible region of the electromagnetic spectrum often contains the majority of the sun’s radiation, making it a region with a higher absorption coefficient. Figure 12(c) and 12(d) display the absorption coefficient of Sr3NI3 perovskite material as a function of photon energy, with and without biaxial strain, respectively. Under tensile strain, the absorption peak of Sr3NI3 exhibits a significant blueshift, while it displays a large redshift under compressive strain.
The compressed structure of Sr3NI3 has a more substantial absorption capacity in the visible spectrum, while the tensile structure has a lower absorption capacity than the unstrained material. Increasing compressive strain improves the absorption coefficient of Sr3NI3 in the visible range, which is crucial for solar cell applications. Conversely, increasing tensile strain causes the absorption coefficient of Sr3NI3 to decrease in the visible region. Optimizing the absorption coefficient of Sr3NI3 perovskite is essential in the design of photovoltaic devices based on this material. It can potentially improve the efficiency of these devices, making them more competitive with other types of solar cells.
Reflectivity refers to the amount of light reflected by Sr3NI3 perovskite when exposed to electromagnetic radiation, particularly visible light. The overall reflectivity of perovskite materials can vary significantly depending on factors such as composition, crystal structure, and surface shape. Additionally, the incident light’s wavelength and angle of incidence can also impact the reflectivity of Sr3NI3 perovskite. Figure 12(e) and 12(f) illustrate the reflectivity of Sr3NI3 perovskite as a function of photon energy in the absence and presence of biaxial strain, respectively. The reflectivity of Sr3NI3 perovskite shows the most variation between photon energies of 0 and 3.7 eV, with the peak reflectivity occurring at 0 eV. With increasing compressive strain, the reflectivity of the Sr3NI3 framework in the visible region increases, which is significant for the development of solar cells. Conversely, when tensile strain is applied, the reflectivity of the Sr3NI3 structure decreases in the visible region. These observations on the optical properties of Sr3NI3 are consistent with previous research. It is generally understood that materials with bandgaps lower than 3.1 eV tend to exhibit better performance in applications involving visible light.
Sr3NI3 has been researched for its possible use in optoelectronics and photovoltaics because of its good optoelectronic and electrical characteristics, such as a high absorption coefficient, high carrier mobility, and extended carrier lifetime. We thoroughly investigated the properties of Sr3NI3, an inorganic perovskite, using the first-principles DFT approach. We also studied the optical characteristics under various strains and found that the material displayed absorption peaks in the UV to visible range, which were either red-shifted or blue-shifted, depending on the type of strain applied. The analysis revealed that the direct bandgap of Sr3NI3’s structure was measured to be 0.733 eV. However, when considering the SOC effect, the electronic bandgap of Sr3NI3 decreased to 0.711 eV. The results clarify that with and without considering the SOC effect, the bandgap of Sr3NI3 rises as compressive strain increases, while it increases with induced tensile strain. Furthermore, it was observed that the peak value of the dielectric constant of Sr3NI3 changes towards higher photon energy (blueshift) when exposed to more significant tensile strain, while it shifts towards lower photon energy (redshift) when placed under tremendous compressive strain. These findings may open up possibilities for further exploration into the development of optoelectronic and photovoltaic devices based on Sr3NI3.
Zenodo: Data and code for Sr3NI3. https://doi.org/10.5281/zenodo.7958201 81
This project contains the following underlying data:
• With SOC (code that is used to generate the data files for the SOC effect)
• Without SOC (Code that is that are used to generate the data files without SOC effect)
• Data (In this folder, I included all the raw files that are used to generate all the figures)
Data are available under the terms of the Creative Commons Attribution 4.0 International license (CC-BY 4.0).
This research was funded by the Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R29), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the work clearly and accurately presented and does it cite the current literature?
Partly
Is the study design appropriate and is the work technically sound?
Yes
Are sufficient details of methods and analysis provided to allow replication by others?
Yes
If applicable, is the statistical analysis and its interpretation appropriate?
Partly
Are all the source data underlying the results available to ensure full reproducibility?
Partly
Are the conclusions drawn adequately supported by the results?
Yes
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Functional thin film materials
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | |
|---|---|
| 1 | |
|
Version 1 21 Aug 23 |
read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)