Analysis of the stationarity and correlation of the global temperature and carbon dioxide time series

Introduction

Since the years 1850–1900, the rapid and relentless phenomenon of global warming has severely and negatively altered Earth’s environment and its inhabitants. NASA describes global warming as “the long-term heating of Earth’s surface observed since the pre-industrial period (between 1850 and 1900) due to human activities, primarily fossil fuel burning, which increases heat-trapping greenhouse gas levels in Earth’s atmosphere” (NASA 2023). Carbon dioxide (CO₂) is naturally present in the atmosphere as part of the Earth’s carbon cycle (the natural circulation of carbon among the atmosphere, oceans, soil, plants, and animals) (EPA 2023). Unlike oxygen or nitrogen (which make up most of our atmosphere), greenhouse gases absorb heat radiating from the Earth’s surface and re-release it in all directions–including back toward the surface (Lindsey 2022). In order to preserve Earth’s future, action must be taken now. The first step is tracking how atmospheric carbon dioxide emissions affect global warming rates.

The correlation between global temperature and carbon dioxide levels has been investigated by many researchers in the literature (Florides and Christodoulides 2009; Macedo and Madaleno 2023; Hereher 2016; Palmer et al. 2007; Woodward and Gray 1993).

In the article, Global warming and carbon dioxide through science, (Florides and Christodoulides 2009) revealed that there is no way to definitively say whether or not CO₂ directly impacts global warming and temperature increases. This study used three independent sets of data (collected from ice cores and chemistry) to perform an analysis. Through a specific regression analysis of their data, they found that the data stating that there is a correlation between CO₂ concentration and temperature relies heavily on specific choices of data. From this conclusion, they found that for both chemistry data and ice core data, “one cannot be positive that indeed such a correlation exists”. Through further research into the topic, there is evidence that CO₂ is not inherently harmful to the environment, in addition to the fact that there is very little evidence linking CO₂ levels and temperature. In the end, they concluded, “It is our view that it is not yet sufficient, let alone rigorous, evidence that anthropogenic CO₂ increase is indeed the main factor contributing towards the global warming of the ${20}^{\mathrm{th}}$ century”.

Evidence from a Maximum Entropy Approach (Macedo and Madaleno 2023) uses a statistical approach based on maximum entropy to conduct a study that supports the results from different techniques that found that CO₂ does, in fact, impact the increase in global temperature. This study, along with a recent review of emerging literature, led them to the conclusion that the impact of CO₂ on our atmosphere is trending toward a detrimental conclusion. They further state that if people continue emitting CO₂ into the atmosphere, it will have a detrimental impact on human, plant, and animal health in the long run.

A time series-related analysis was used in Hereher (2016) to study the global temperature trends of land surface temperatures and climate changes based on the temperature data in Egypt. This study reports serious climate change in Egypt by detecting variability of land surface temperature (LST) over the last decade at selected locations, with varied geomorphological characteristics and human stressors. The time series for the land surface temperatures were acquired from satellite images from 2003 to 2014, totaling 276 images. The analysis suggests that the LST in Egypt increases by 1.54 °C/decade. The variation of LST depends on latitude, geology, topography, and surface albedo. The dataset used in this analysis is named MODIS, from the NASA Land Processes Distributed Active Archive Center website. This analysis found that the time-series MODIS LST data proved sufficient for the short-term monitoring of land surface temperature variations in Egypt. It is noted that geology, topography, and surface albedo have significant impacts on the LST of Egypt. Further, it was revealed that between the years of 2003-2014, the LST of Egypt increased by 0.3–1.06 °C/decade, and for urban areas, the excess LST is higher at 1.54 °C/decade.

According to a new isothermal analysis by Palmer et al. (2007) in order to produce a more accurate depiction of the underlying warming. They proposed a new analysis of millions of ocean temperature profiles intended to filter out local dynamical changes. According to the authors’ comments, it was a difficult analysis since oceans do not warm uniformly across the globe. They present decadal-scale analyses of the ocean’s thermal state relative to a fixed isotherm. This new diagnostic is less prone to the influence of dynamical processes at both high and low frequencies, and the results present a more globally uniform picture of ocean warming. The limitation of the isothermal analysis is that high-latitude oceans were not included.

Using the Autoregressive Moving Average (ARMA) model, a study of time series data on global warming and trends is presented in Woodward and Gray (1993). They concluded that atmospheric greenhouse gases will affect the continued projection of the warming trend of global temperatures. Further, they stated that there is no conclusive evidence that this trend will continue. This is due to the difference between data on long-term trends and data on random trends with the length of the temperature series.

Data sources

Global temperature anomalies and carbon dioxide data were obtained from (NASA 2023) global climate change website. The temperature anomalies (in Celsius) and carbon dioxide (parts per million) were used from 1960 to 2022. The temperature anomalies are used instead of the absolute temperature data, as they accurately represent the temperature variability over larger areas. Further, they give a frame of reference that allows more meaningful comparisons between locations and more accurate calculations of temperature trends (NOAA 2023).

Statistical time series review

This section provides an overview of the definitions and test formulas that we use in this article to examine the time series models. Time series analysis can be used to examine the outcomes of either a planned or unplanned intervention as well as to better understand the underlying naturalistic process and the pattern of change over time (Velicer and Molenaar 2012). In time series analysis, regularity is essential, and if time series data exhibits irregular behavior over time, establishing meaningful conclusions about the underlying causes will be challenging. This regular behavior is explained by the concept of stationarity. In general, to satisfy the conditions of stationarity, the time series must satisfy some strong conditions, and those conditions are too strong for most of the applications. Therefore, most time series seen in real life are analyzed using a weaker version of stationarity.

The weakly stationary time series should satisfy the following conditions (Shumway and Stoffer 2017).

If two time series are taken into account simultaneously, such as $x_t$ and $y_t$, they are said to be jointly stationary if the individual time series are stationary and the cross-covariance function solely depends on the lag value.

To evaluate the model’s goodness of fit, we utilize Akaike’s Information Criterion (AIC), the bias-corrected Akaike’s Information Criterion (AICc), and Bayesian Information Criterion (BIC). Those criteria measure the goodness of fit of the models by balancing the number of parameters of the model and the error of the fit. If $k$ is the number of parameters of the model, $n$ is the number of observations, and SSE is the sum squared error of the fit, then AIC is given by

The AICc is given by

With the Bayesian corrected term, the BIC takes the form

More details about those information criteria can be found in Akaike (1974, 1973, 1969) and Schwarz (1978).

Detrending and differencing are the two fundamental methods for transforming a non-stationary time series into a stationary one. The independence of the residuals can be visually demonstrated by using the residual plots. The autocorrelation plots and cross-correlation plots can be used the explain the nature of the correlation at different lag values. If ${\mu }_{x,t}$ and ${\mu }_{y,t}$ are the means of the time series $x_t$ and $y_t$ respectively, the autocovariance function of $x_t$ is defined by

The autocorrelation and cross-correlation functions are normalized versions of the above formulas. For a given time series $x_t$, and $y_t$ the autocorrelation (ACF) and cross-correlation (CCF) functions are given by

Because they depend on the locations of time points $s$ and $t$, the autocovariance and cross-covariance functions can change during the course of the series. If the autocovariance function depends on the separation $h=|t-s|$ rather than the points where the time series are situated, we are able to analyze sample time series data when there is only one series available.

Analysis of the global temperature and carbon dioxide time series

We use the global temperature anomalies from 1960 to 2022, obtained from NASA (2023). As demonstrated in Figure 1 most of the planet is warming (yellow, orange, and red). Only a few locations, most of them in the southern hemisphere oceans, cooled over this time period. According to the fact highlighted in Lindsey and Dahlman (2023) earth’s temperature has risen by an average of 0.14° Fahrenheit per decade since 1880. The temperature anomaly variability (in Celsius), including pre-industrial time, is shown in Figure 2. The trend is shown by the red dashed line while smoothing splines with the smoothing parameter value spar is 0.5, is demonstrated by the blue spline.

Figure 1. Recent temperature trend (1993-2022).

Climate.gov Media: https://www.climate.gov/media/15022.

Figure 2. Temperature anomaly from 1960 to 2022.

The red dashed line shows the trend and the blue line shows the temperature variability with smoothing spline (spar = 0.5).

The trend and irregular behavior of the temperature series require a modification to make it stationary before additional analysis can be done to uncover its other properties. The stationary time series are easy to study using established principles created in the time series literature because of their predictable long-term behavior.

We investigate detrending and differencing techniques to transform the original time series into stationary time series.

Stationarity in the temperature time series

The trend stationary model is the form of non-stationary series that is easiest to work with. As seen in Figure 2, the temperature series exhibits stationary behavior around the trend line (trend stationary). The stationary component of the time series might thus be filtered by just removing the trend. This trend stationary model can be written as

(8)

$$T_t={\mu }_t+T_t^s$$

where ${\mu }_t$ is the trend and $T_t^s$ is the stationary component. The equation for the trend line can be used to detrend the data, and it can be estimated by ordinary least squares regression.

(9)

$${\widehat{\mu }}_t=-33.82+0.02t$$

Using global temperature anomaly data from 1960 to 2022, the estimated trend line equation can be obtained as follows:

Figure 2 shows the superimposed estimated trend line (red). To get the detrended series, we simply subtract ${\widehat{\mu }}_t$ from $T_t$,

(10)

$${\widehat{T}}_t^s=T_t+33.82-0.02t$$

Because of the error of the estimated model in Eq. 10, ${\widehat{T}}_t^s$ may not be independent and identically distributed. In fact, our main goal is investigating the behavior of this stationary component ${\widehat{T}}_t^s$. According to the graphical representation in Figure 3a, detrending eliminates the original temperature time series trend. One of the main requirements of a stationary time series is the maintenance of a constant mean across the specified time period, which the elimination of trends helps to achieve. Figure 4a and Figure 4b show the autocorrelation function for the original and detrended global temperature anomaly time series respectively. The majority of the autocorrelation values for the detrended series are inside the 95% confidence band, indicating a significant improvement in the independence of lag-related correlation.

Figure 3. Detrended and differenced global temperature series from 1960 to 2022.

Figure 4. ACF for a) Global temperature anomaly, b) Detrended, and c) Differenced time series.

Differencing is the other technique we are utilizing here and in time series literature this is known as integrating. Differencing simply means subtracting past values from the current value. Figure 3b shows the differenced global temperature anomaly time series. This series also shows a similar pattern to that observed in the detrended series.

However, instead of treating drift as a fixed model, it can be modeled using a stochastic component. We define the stochastic drift model

(11)

$${\mu }_t=\alpha +{\mu }_{t-1}+w_t$$

where $w_t$ is the independent identically distributed random variable (called white noise or Gaussian process), which follows the normal distribution with mean 0 and fixed variance (say) ${\sigma }^2$. If $w_t$ is independent of $T_t^s$, differencing the model in Eq. 8 and substituting Eq. 11, we get

(12)

$$T_t-T_{t-1}=\alpha +w_t+T_t^s-T_{t-1}^s$$

Since $T_t^s$ is the stationary component of the global temperature time series $T_t$, we can show that the difference $T_t^s-T_{t-1}^s$ is also stationary. For that define, $Z_t=T_t^s-T_{t-1}^s$. Then $E\left(Z_t\right)$ does not depend on time $t$ since $T_t^s$ is stationary for $1960\le t<2022$.

Another key requirement of a stationary time series is the independence of the autocovariance from the time. It can depend on the time difference, but not on the actual time value. If $h$ represents the lag or shift value, the autocorrelation can be found as

(13)

$$cov\left(Z_{t+h},Z_t\right)=2cov\left(T_{t+h}^s,T_t^s\right)-cov\left(T_{t+h+1}^s,T_t^s\right)-cov\left(T_{t+h-1}^s,T_t^s\right)$$

Therefore, the autocorrelation of the differenced temperature time series does not depend on the actual time value, $t$ rather on the time lag or time difference. In addition to the computation results, this can be further verified by the ACF plots for differenced temperature data. Figure 4a displays the autocorrelation for the initial temperature anomaly. The ACF value decreases as the lag value increases, providing strong evidence for the temporal reliance of the covariance. On the other hand, Figure 4b and Figure 4c show, the autocorrelation for detrended and differenced data respectively. In comparison to the original time series ACF plot, both graphs demonstrate a significant reduction in the time-dependent correlation. The blue horizontal lines represent the 95% confidence level.

Stationarity of the carbon dioxide time series

The atmospheric carbon dioxide level, measured in parts per million (ppm) during the period from 1960 to 2022 is shown in Figure 5. We use detrending and referencing techniques to analyze the stationarity behavior of the CO₂ time series. Figure 6a shows the detrended carbon dioxide series. Unlike in the temperature series, the detrending does not remove the trend of the original CO₂ series. Also, according to Figure 6b the first differenced series either does not show stationary behavior in terms of the trend component or it still shows some sort of trend. But the second differenced series in Figure 6c shows a significant improvement toward the stationarity. Therefore, although the first differencing does not work here, the second differencing transforms the CO₂ series into a stationary time series. There are different transformations available in the time series literature to transform non-stationary time series into stationary form. In this article, we are not going to analyze other transformations, but one can try log or Box-Cox (Sakia 1992) family transformations.

Figure 5. Carbon dioxide level (ppm) from 1960 to 2022.

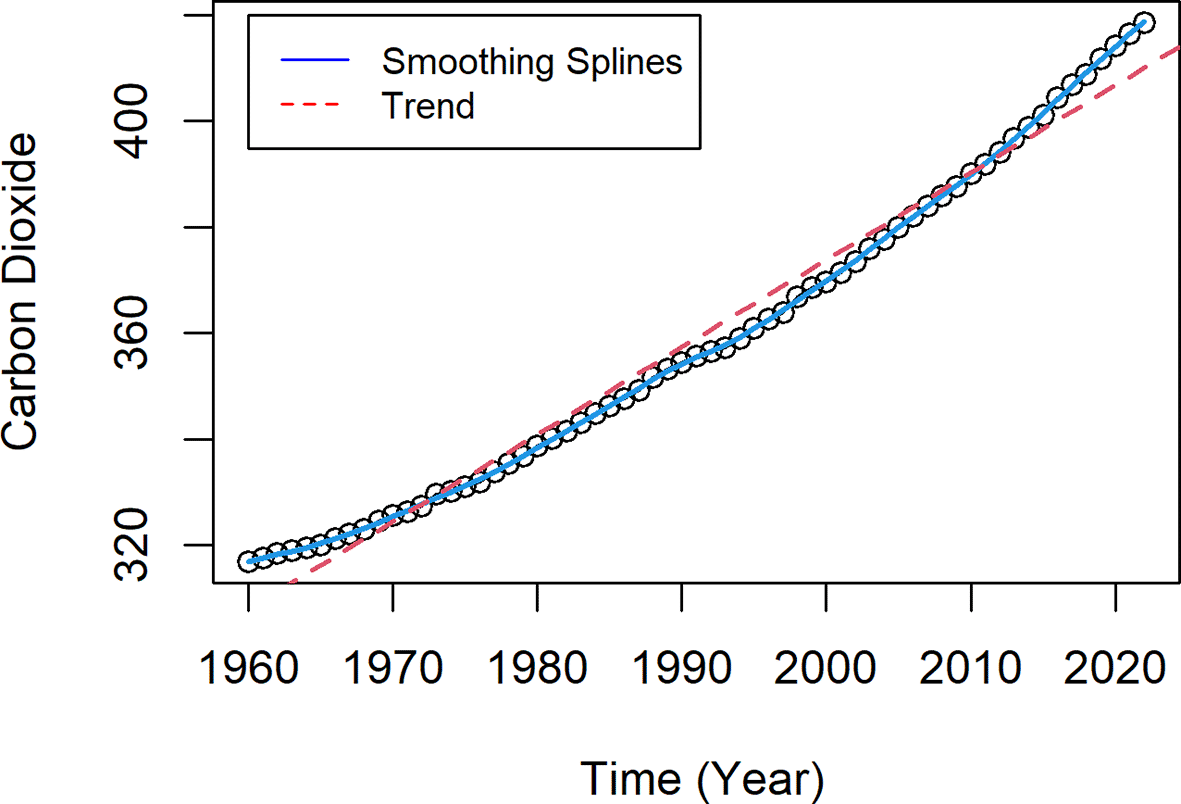
The red dashed line shows the trend (spar = 1) and the blue line shows the CO₂ variability with smoothing spline (spar = 0.5).

Figure 6. Detrended and Differenced CO₂ time series.

Figure 7a shows the ACF of the original carbon dioxide series. Detrending and differencing (first difference) are unable to eliminate the autocorrelation of the CO₂ time series as they did in the temperature series. Figure 7b-c illustrates this by demonstrating how the height of the vertical lines decreases as the lag increases. It is clear that autocorrelation breaks a stationarity rule by leaning on the actual time value.

Figure 7. ACF vs Lag: a) CO₂ (original) time series, b) CO₂ detrended time series, and c) CO₂ differenced (first differenced) time series.

Higher order differencing

When first-order differencing fails to convert the original data into a stationary form, higher-order differencing may be necessary for the majority of time series applications. If a quadratic trend is present, second-order differencing is the optimal order to apply. In general, if the trend is linear, first-order differencing might be sufficient. If a non-stationary time series needs to be differenced d times in order to become stationary, it is said to be of order d integrated. The generalized form of higher-order differencing can be described by the backshift operator, say $B$. According to the exposition in Shumway and Stoffer (2017), this operator can be defined as

(14)

$${\mathit{Bx}}_t=x_{t-1}$$

where $x_t$ is any time series. Extending to the power $k$, we can get the generalized form of the Backshift operator

(15)

$$B^k{x}_t=x_{t-k}$$

If the difference is defined by

(16)

$${\mathit{Dx}}_t=x_t-x_{t-1}$$

Then we can write,

(17)

$${\mathit{Dx}}_t=\left(1-B\right)x_t,$$

and further extending this iteration into the $k^{\mathrm{th}}$ power

(18)

$$D^k={\left(1-B\right)}^k.$$

Various differencing orders are used to decrease the time series’ unwanted deviations. These techniques are frequently used in ARIMA time series models.

Although $d=1$ works for global temperature anomalies, the CO₂ time series required higher-order differencing. The milder quadratic pattern suggests second-order differencing, and the corresponding figure after the second difference is shown in Figure 6c. As demonstrated in the autocorrelation plot for the second differenced time series in Figure 8, progress toward stationarity can be seen as the correlation values at different lags decline in contrast to the first differenced auto-correlation plot.

Figure 8. ACF plot: Carbon dioxide differenced series (d = 2).

Along with the graphical evidence of stationarity, the Augmented DickeyFuller (ADF) test (Dickey and Fuller 1981) can be utilized to determine whether or not the given time series is stationary. The ADF test results are shown in Table 1. The p-value for the detrended and differenced time series of the global temperature is less than 0.01. This allows us to reject the null hypothesis of the ADF test and accept the resulting time series as stationary within the corresponding significance level $\alpha =0.05$. The hypothesis tests for detrended and first differenced CO₂ time series are not statistically significant at $\alpha =0.05$, but the integrated order 2 series is stationary.

Table 1. Dickey - Fuller test’s p - values for detrended and differenced time series.

Time series/Transformation	Detrended	Differenced (d = 1)	Differenced (d = 2)
Global temperature anomaly	$<0.01$	$<0.01$	$<0.01$
Carbon dioxide	0.99	0.07	$<0.01$

Models for correlation analysis

We analyze the basic global temperature trend model and temperature and carbon dioxide models. We compare two models using AIC, AICc, BIC, R-squared value, and sum squared error (SSE). The main objective of these models is to further analyze the effect of carbon dioxide on global temperatures. The basic trend model for temperature (model 1):

The trend model (model 1) in Eq. 19 can be improved by introducing CO₂ as an explanatory variable.

Figure 9 shows the autocorrelation values for the carbon dioxide series at different lag values. Due to the considerable strength of the lag-related correlation in the second model, we adjust the carbon dioxide data for its mean, $\overline{C}=358.9675$ (ppm). If $C_t$ is the carbon dioxide level at time $t$, then we have model 2:

Figure 9. Scatter-plot matrix relating current CO₂ values ($C_t$), to past CO₂ values ($C_{t-h}$) for $h=\mathrm{1,2,3,4}.$ The values at the upper right corner are the sample autocorrelation at the corresponding lag values.

The value $k$ yielding the minimum AIC, AICc, and BIC specifies the best model. We note that the second model is substantially better than the first model. Model 2, which includes CO₂ accounting for 92.4% of the variability ($R^2$ value of model 2), which was 90.5% ($R^2$ value of model 1) without that. Also, it gives the best value for AIC and BIC. In addition, we can notice that AIC and AICc are nearly equal. To calculate those values, we used the formulas given in the equations 1, 2, and 3. Without using the aforementioned formulas, one can utilize the regression model summaries to obtain these values, although there might be a few minor variations from the corresponding values shown in Table 2.

Further, the trend model (model 1) can be compared to the model with carbon dioxide (model 2) with the null hypothesis, $H_0:{\beta }_3=0$. The corresponding $F$ statistic:

Further for the purpose of predicting the global temperature the prediction model can be given by,

Model assumption

This section examines the validity of model 2 that we previously presented. Here, we go into further detail about the regression model’s primary assumptions, such as linearity, residual normalcy, homoscedasticity, and independence of the residual errors.

As shown in Figure 10 “Residual vs. Fitted” subplot, the horizontal line without any obvious patterns is a sign of a solid linear relationship. In Figure 10, the “Normal Q-Q plot” is used to determine whether the residuals are distributed normally. It’s ideal if the residual points fall along the dashed straight line, which is not perfectly satisfied in this case. A “Scale Location” subplot is utilized to verify the homoscedasticity (homogeneity of variance) of the residuals. Homoscedasticity can be detected by a horizontal line with evenly spaced points, which is satisfied except for a few outliers as shown in Figure 10, “Scale-Location” subplot. A few influential observations can be identified according to Figure 10, “Residual vs. Leverage” subplot. According to the model diagnostic analysis, since model 2 satisfies the fundamental assumptions, it can be considered a viable model to explain the relationship between temperature anomaly and CO₂ across time.

Figure 10. Residual vs Fitted, Normal Q-Q plot, Scale Location plot, and Residual vs Leverage plot.

Cross correlation: Global temperature anomaly vs carbon dioxide

Analyzing the potential leading and lagging relationships between the global temperature and carbon dioxide series is another intriguing investigation. Leading and lagging relationships might be helpful when one time series is used to predict another. Let $T_t$ and $C_t$ represent the global temperature and CO₂ time series respectively. Consider the model of the form

According to the graphical demonstration of the cross-correlation function in Figure 11a for the original data, no time series leads or lags other series since peak shows occur at $l=0$. When viewed in relation to the zero-lag value, the cross-correlation is approximately symmetric. However, those original series are not stationary. We take integration order 2 into consideration when we analyze the behavior of the cross-correlation functions of the (weakly) stationary CO₂ and global temperature anomaly series. Although the first integrated temperature series is stationary, we use the differencing order 2 ($d=2$) to transform both series in order to tackle the dimension issues. According to Figure 11b most dominant cross-correlation for stationary series occurs at $l=0$ and $l=1$. Those integrated series are jointly stationary if the cross-correlation or cross-covariance function is a function only on the lag value.

Figure 11. Cross correlation of global temperature anomaly and carbon dioxide time series from 1960 to 2022: a) Original, b) Stationary (d = 2).

Discussion

According to the summary statistics criterion in Table 2, the impact of CO₂ on the global temperature cannot be negligible. The models we’ve examined can be improved by adding additional greenhouse gases and other factors that could have an impact on the global temperature. Although carbon dioxide is not the only greenhouse gas that can affect the temperature, it occupies a significant amount of space compared to other greenhouse gases.