Extracting ridge and valley lines in mountainous areas from airborne lidar data by utilizing line feature strength

Rey-Jer You; Chao-Liang Lee

doi:10.12688/f1000research.151861.1

Home Browse Extracting ridge and valley lines in mountainous areas from airborne...

ALL Metrics

-

Views

-

Downloads

Get PDF

Get XML

Export

▬

✚

Method Article

Extracting ridge and valley lines in mountainous areas from airborne lidar data by utilizing line feature strength

[version 1; peer review: 1 not approved]

Rey-Jer You¹, Chao-Liang Lee ²

PUBLISHED 05 Sep 2024

Author details Author details

¹ Department of Geomatics, National Cheng-Kung University, Tainan, 70101, Taiwan
² Department of Geomatics, National Cheng-Kung University, Tainan, 70101, Taiwan

Rey-Jer You
Roles: Methodology

Chao-Liang Lee
Roles: Methodology

OPEN PEER REVIEW

REVIEWER STATUS

Abstract

Background

Digital elevation models (DEMs) are important in many fields, such as geomatics and water conservation in mountainous areas. Geomorphic feature lines are necessary for topography interpolation and computation from DEMs.

Methods

Instead of a parameter space, we propose a novel automatic extraction of geomorphic feature lines in the feature space from discrete airborne light detection and ranging (LiDAR) data by the tensor voting method (TVM), which was originally developed for image data. A tensor field for discrete airborne LiDAR points was first established, and then, utilizing the TVM, a new geometric feature metric of data, the line feature strength, was captured. A practical line-growing method based on the local maxima line feature strength is proposed in this study.

Results

Compared with general line growing, which is based on a certain threshold, our line growing method is quite effective, particularly for the extraction of primary and minor ridge and valley lines in mountainous areas.

Conclusions

The method presented in this paper is fast and automated, and can furnish operators with a wealth of detailed information about minor line features. This enables the extraction of ridge and valley lines that are tailored to specific requirements. Undoubtedly, the method developed here can be generalized to a large amount of LiDAR data.

Keywords

LiDAR, feature extraction, ridge and valley.

Corresponding author: Chao-Liang Lee

Competing interests: No competing interests were disclosed.

Grant information: This work was funded by Institute for Information Industry, Ministry of Science and Technology, Taiwan- MOST 105-2119-M-006-034
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2024 You RJ and Lee CL. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: You RJ and Lee CL. Extracting ridge and valley lines in mountainous areas from airborne lidar data by utilizing line feature strength [version 1; peer review: 1 not approved]. F1000Research 2024, 13:1011 (https://doi.org/10.12688/f1000research.151861.1) First published: 05 Sep 2024, 13:1011 (https://doi.org/10.12688/f1000research.151861.1) Latest published: 05 Sep 2024, 13:1011 (https://doi.org/10.12688/f1000research.151861.1)

Introduction

Light detection and ranging (LiDAR) technology has gained increasing prominence because of its capacity to rapidly generate voluminous amounts of three-dimensional (3D) point clouds, enabling expedient characterization of Earth’s topography.

LiDAR can quickly provide a large amount of terrain data that is useful for building reconstruction, extraction of road paths, construction of topography, and terrain change monitoring etc.¹^–⁷ LiDAR is also employed for environmental protection, soil and water conservation, and the hydrological structure of mountainous areas, which are important issues.⁸^–¹⁰ Furthermore, LiDAR is a very useful tool for monitoring forest growth and forest area changes, especially for estimating vegetation height, canopy cover, and tree species in mountainous areas.¹¹^–¹³

Compared with photogrammetric data, LiDAR data offer a more straightforward approach for understanding changes in 3D topography. However, the irregular distribution of LiDAR point clouds can pose a challenge, particularly when shaping complex terrain within topological data. This paper introduces a method for extracting ridge and valley lines from low-density point clouds in mountainous regions.

Edge detection is an established technique in computer vision. Various algorithms, such as Sobel, Prewitt, and Laplacian algorithms, have been developed to identify line features.¹⁴ Image data are stored in pixel format, and moving masks can easily navigate this regular grid to extract line features. Conversely, the data storage format for irregularly discrete LiDAR data consists of the point coordinates. If image extraction techniques are employed, the point coordinates must be interpolated into a pixel format, which can influence the accuracy depending on the interpolation method used.

Scholars have proposed various methods for extracting line features from LiDAR data. Zhao and You⁴ focused on extracting road networks. Their approach entails the removal of points associated with buildings and trees by applying the elevation criteria. Subsequently, they employed the intensity data and variance between the tangent vectors to define the line segments. Given that roads possess a certain non-negligible width, a sufficient number of point clouds are usually present on road surfaces to enable line segment extraction. To deal with narrower features, such as power lines, McLaughlin¹⁵ proposed a method that uses covariance to calculate the eigenvalues. These eigenvalues can be employed to categorize the point clouds into three groups: vegetation, surfaces, and power lines. Cable-specific formulas are applied to the point clouds allocated to the power line category to yield complete power-line representations. Guan¹⁶ used ground-based LiDAR scanning to obtain point cloud data of street views and extracted individual power lines using Hough transformation and Euclidean distance clustering.

Line features that do not correspond to existing lines typically exist at points of change, such as turns and junction areas. Both sharp and gradual turns affect the position of the final extracted line segment. Bailly et al.¹⁷ used wavelet transformation and a flooding algorithm to identify the ditch lines in artificial drainage networks. In their study on mountainous settings, Chang et al.¹⁸ proposed a profile recognition and polygon-breaking algorithm (PPA) that performs target recognition, target connection, segment verification, and line smoothing. In the PPA approach, elevation grids from digital terrain models (DTMs) were used, and moving masks were employed to extend the ridge and valley lines. Gülgen and Gökgöz¹⁹ modified PPA to reduce the computational time required for the DTM generation process. However, PPA is easily influenced by noise, which may lead to redundant lines and non-matched results. A pre-processing procedure is necessary to obtain reliable valley and ridge lines.

A new type of data, termed feature strength, was introduced to aid feature extraction. Medioni et al.²⁰ applied the tensor voting method (TVM) to image data to obtain the eigenvalues and eigenvectors. This method enables the classification of image pixels into various features based on their strengths. TVM has also been demonstrated to be applicable to point-cloud data. You and Lin¹ utilized feature strength to extract surfaces and lines from data in urban settings. Furthermore, in the context of urban regions, feature strength data can serve as raw data for calibrating biases between LiDAR strips during the preprocessing stage.²¹ In urban environments, where buildings and roofs exhibit regular patterns, point clouds on surfaces are readily distinguishable from others owing to their high surface feature strength. Lines can be identified at the intersections of two adjacent surfaces. However, because of the irregular nature of mountainous regions, this approach may result in more fragmented surfaces, making it challenging to intersect ridge and valley lines. The aim of this study is to analyze and discuss the feature strength of point clouds in mountainous regions, particularly the line feature strength extracted by TVM.

Methods

Geometric feature strength

TVM encompasses three stages: tensor representation, tensor communication, and tensor decomposition/encoding.²⁰^,²² First, a tensor field was established by setting up a disk tensor for each LiDAR point, as proposed by You and Lin,¹ and the geometric character of each LiDAR point was represented by a second symmetric tensor. Using tensor communication, each point collects the tensors of neighboring LiDAR points to form its final tensor. Consequently, each point has a strong geometric relationship with its neighboring points based on the final tensor, which is helpful for the extraction of ridge and valley lines in mountainous areas. After tensor communication, the final tensor of each point was decomposed into surface features, line features, and noise point features by tensor encoding.²⁰ You and Lin¹^,² used a normal vector field to obtain the surface feature strengths using the TVM and applied the region-growing method to extract surface features from LiDAR point clouds for urban regions. For our purpose, the line feature strength (denoted as C here) is more suitable for extracting valley and river lines in mountainous regions than the other types of feature strength. This aspect is elaborated in the subsequent section.

Line feature strength

C data can be obtained using the TVM. This section describes the characteristics of C data. Figure 1 shows the same mountainous region from various perspectives and data modes. In Figure 1(a), the ridge and valley regions appear in the 2.5D view, with an elevation range of approximately 1,400 meters. Figure 1(b) shows the elevation data from a 2D view. Figure 1(c) presents the C data from a 2D view.

Figure 1. LiDAR data for a river and valley region, displayed in various views and data modes.

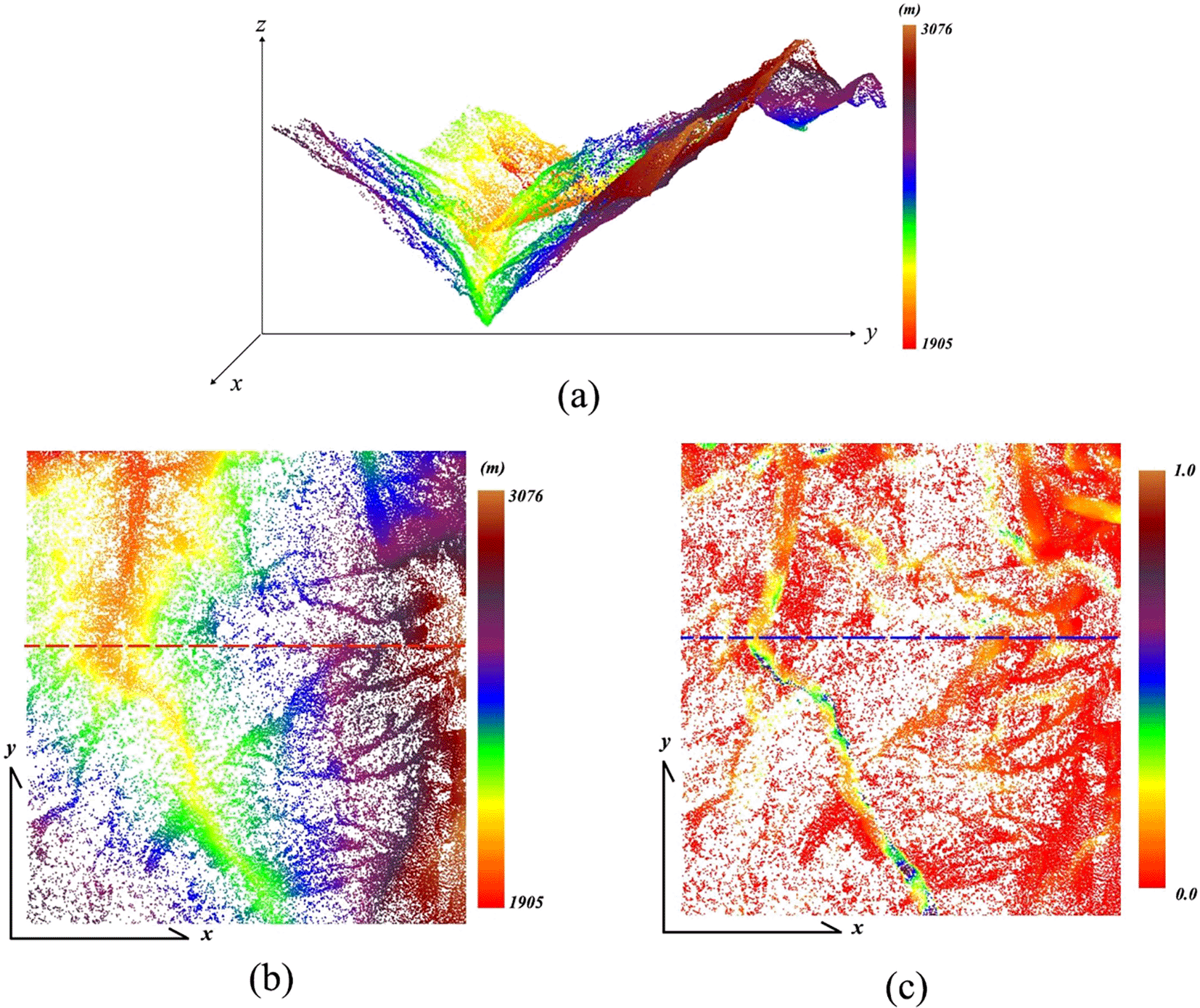
NOTE: (a) Point clouds illustrated in 2.5D view; (b) Elevation data illustrated in 2D view; (c) C data illustrated in 2D view. Own work.

To analyze the characteristics of the C data in relation to variations in elevation, this study established a section line. In Figure 2, the red line represents the elevation data and the blue line represents C data from the section lines shown in Figure 1(b) and (c). As depicted in Figure 2, C was higher in regions with large elevation gradients, and its magnitude was influenced by the extent of the elevation gradient. In areas with smaller elevation gradients, C was relatively stable. Hence, establishing a single threshold for identifying all points in the valley versus ridge regions is infeasible. In Figure 2, points near the ridge and valley regions display local maxima in the C data curves, confirming that C data can effectively assist in the identification of nodes of line features.

Figure 2. Section lines corresponding to C data in Figure 1.

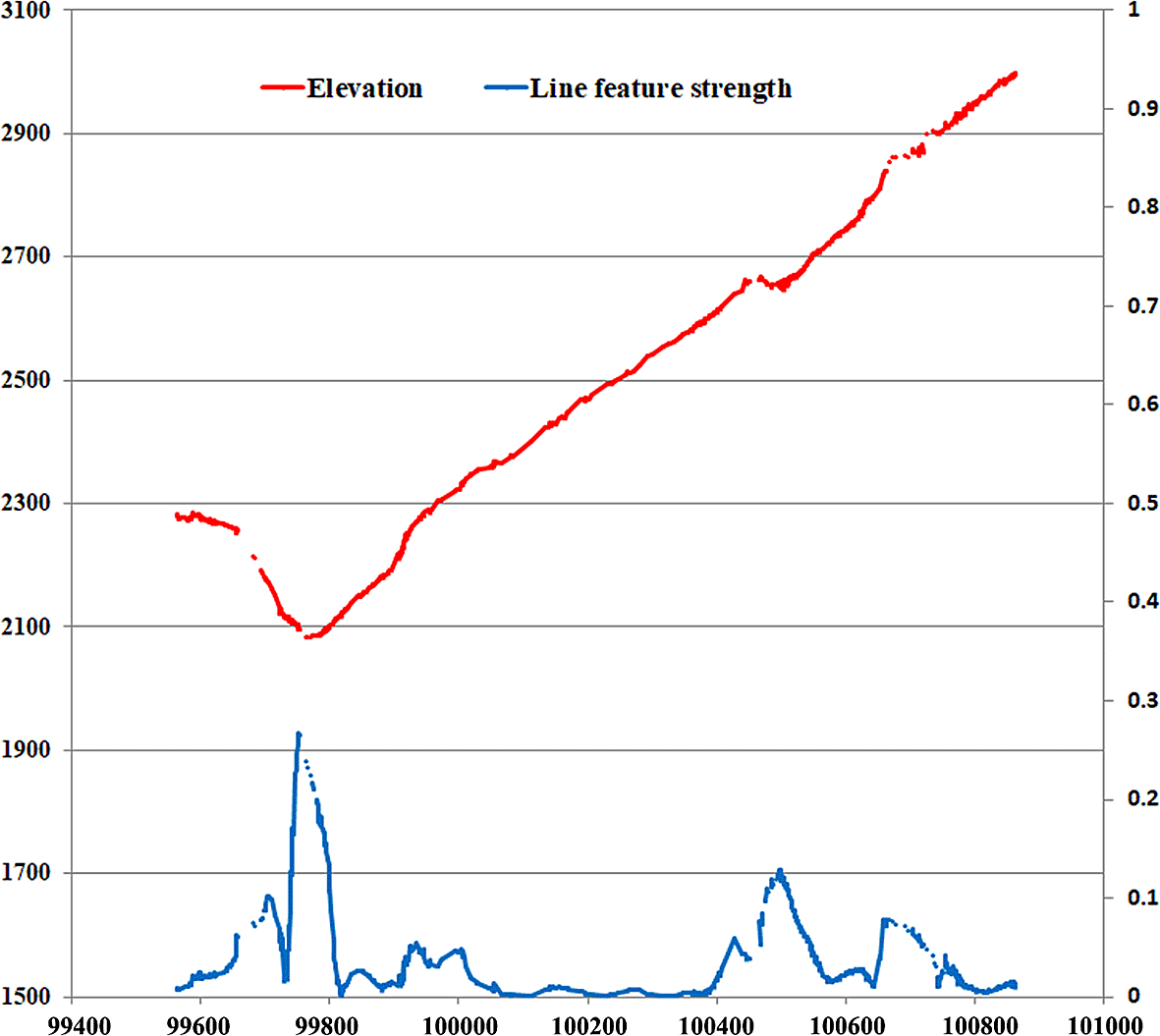
NOTE: Red line, elevation data; blue line, line feature strength data in section line of Figure 1(b) and (c). Own work.

Tangent vector of point clouds

The eigenvectors for LiDAR point clouds can be derived using the TVM. Each point cloud possessed three associated eigenvectors, each with a distinct interpretation. For points located on a surface, the first eigenvector is the vector that is normal to the surface. Conversely, for points situated on a line, the third eigenvector is the tangent vector along the direction of the line, as shown by Medioni et al.²⁰ and You and Lin.¹^,² Given that this study focuses on the extraction of ridge and valley lines, the tangent vector v for each point is considered. This vector is derived using the TVM and is crucial for eliminating extraneous point clouds.

Line growth

Drawing inspiration from the region-growing method, this study established line growth criteria by choosing seed points and setting item thresholds. According to the next section, points located on the ridge or valley regions have higher C values than their surrounding points. Hence, points with local maxima C values serve as seeds for initiating line growth. Second, the v vectors of adjacent points located in the same valley or ridge line are similar. These two considerations guide the line-growth process, the specifics of which are explained in the following section.

Choosing seeds with local maxima of line feature strength

This study establishes that such local maxima are directional in nature to provide a detailed explanation of how they are identified in 3D point cloud data. Vector v, derived from the TVM, is a critical factor. Points (i = 1, 2, …, k) considered centers within a specified search radius are divided into right (a = 1, …, m) and left (b = 1, …, n) subsets based on v, which serves as a divide. A center point cloud is deemed to be a local maxima in terms of C when the average C values on the two sides are lower than the C value of the center point. This is formalized in the following equations:

(1)

If (\frac{\sum_{a = 1}^{m} (C_{a})}{m} - C_{i}) < 0 and (\frac{\sum_{b = 1}^{n} (C_{b})}{n} - C_{i}) < 0

Subscript i indicates point i located on a line. $C_{a}$ represents the C value in point cloud a on the right-hand side of v (a = 1, …, m). $C_{b}$ represents the C value in point cloud b on the left-hand side of v (b = 1, …, n).

As depicted in Figure 3, points within the search radius are divided into right (R1, R2, R3, and R4) and left (L1 and L2) subsets based on v of P1. Point P1 is classified as the local maxima of C when it satisfies Equation (1). This criterion was employed to eliminate redundant points in the line growth process. Points satisfying Eq. (1) serve as candidate seeds for line growth.

Figure 3. Defining a local maxima in 3D space.

NOTE: points within the search radius are divided into right (R1, R2, R3, and R4) and left (L1 and L2) subsets based on v of P1. Point P1 is classified as the local maxima of C when it satisfies Equation (1). Own work.

When employing a large search radius, numerous point clouds not located on the line were included in the calculations. Conversely, when the search radius is small, many point clouds near the line segment are excluded, leading to incomplete line segments, particularly in the case of low-density point clouds. In this study, the radius used to identify point clouds with local maxima was consistent with the radius employed in TVM applications.

Setting an angle threshold between two tangent vectors

A threshold of C value may be chosen to determine all candidate seeds whose C values are larger than that threshold, as in the conventional growing method. The result would lead to the extraction of the primary ridge and valley lines only, but might filter out other minor lines. Different from the conventional method, candidate seeds are identified by seeking local C maxima for the line-growing in this article. Using this line-growing method, more details of the ridge and valley lines can be obtained. Points with higher C values are more likely to be located on lines and are therefore prioritized for line growth. According to empirical observations, neighboring points on a line should have similar tangent vectors. The threshold angle between the two v vectors can then be defined.

To meet the criteria of the angle threshold, the five points with the largest C value are regarded as the center of the ball in the TV’s searching radius, and the tangent vectors of points that meet the local maxima C value within the range are the calculated angles between the center points. The average angle value of the five groups was used as the basic threshold (ω), and three times the average value (3ω) was used as the threshold value in this study. An excessively large threshold can introduce inaccuracies by leading to the inclusion of numerous point clouds that are not actually part of the line segment, skewing the final calculations. Conversely, a too-small threshold can lead to the omission of relevant clouds and fragmentation of lines; the procedure cuts off branch lines to multiple single lines.

To preserve the detailed line features, the proposed approach adopts a moving mask algorithm from computer vision and employs an overlapping mechanism. The size of the moving ball matches that of the search ball used in the TVM, and its moving distance equals the radius of the ball. Points that satisfy both the angle threshold and Equation (1) are considered, with their C values serving as weights because a higher C value implies a higher likelihood that the point is part of a line. The node of a line and its associated tangent vector were then calculated using the following equations:

(2)

(V_{i}) = \frac{\sum (C_{j} ∙ V_{j})}{\sum C_{j}} when i = 1 \dots . n, j = 1 \dots . m

(3)

{(\begin{matrix} x \\ y \\ z \end{matrix})}_{i} = \frac{\sum (C_{j} ∙ {(\begin{matrix} x \\ y \\ z \end{matrix})}_{j})}{\sum C_{j}} when i = 1 \dots . n, j = 1 \dots . m

i: node i of a line. j: point j within the search ball.

n the number of nodes in a line. m: number of points within the search ball.

${(x y z)}_{i}^{T}$ and tangent vector $(V_{i})$ . The subsequent node of the line was determined using the following equation:

(4)

{(\begin{matrix} x \\ y \\ z \end{matrix})}_{i + 1} = {(\begin{matrix} x \\ y \\ z \end{matrix})}_{i} + Radius ∙ (\frac{V_{i}}{| V_{i} |})

In line with the techniques used in computer vision for line extraction, overlapping regions were maintained between the moving masks. In this study, approximately half of the search balls were designed to overlap adjacent balls.

P0 [Figure 4(a)] was selected as the initial seed. Points that satisfy both Equation (1) and the angle threshold within searching ball O1 are evaluated using Equations (2) and (3), which yield new values for P1 and v1, respectively. Search ball O2 is generated through Equation (4), and the procedure is repeated to obtain P2, v2, and so on until no points within the search ball meet the criteria. At this juncture, P1, P2, and P3 become the nodes of the line, as illustrated in Figure 4(b), and new seeds are selected for the growth of additional lines until all the points satisfying Equation (1) are used.

Figure 4. Line-growing procedure.

NOTE: (a) Move the searching ball to grow nodes and vectors on the basis of multiple criteria. (b) Connect the nodes to obtain a complete line. Own work.

Theoretical accuracy and interpolated accuracy

Node-point coordinates were calculated by weighting them in accordance with their C values. Equation (4) describes the method used to determine the node coordinates. To ascertain the theoretical accuracy, error propagation calculations were conducted for each point i, as outlined in Equation (5). For simplicity, any correlations among x_i, y_i, and z_i were disregarded.

(5)

σ_{x}^{2} = \sum {(\frac{σ_{x_{i}}}{(\sum C_{i})})}^{2} σ_{y}^{2} = \sum {(\frac{σ_{y_{i}}}{(\sum C_{i})})}^{2} σ_{z}^{2} = \sum {(\frac{σ_{z_{i}}}{(\sum C_{i})})}^{2}

Another quality indicator of a node point is interpolated accuracy using contour data obtained by Delauney triangulation. The formula is as follows:

(6)

z_{contour}^{i} = \sqrt{\frac{\sum (d_{i} ∙ d_{i})}{n}}

i: node i of a line. n the number of nodes in a line.

$d_{i}$ : elevation from point D to plane ABC in Figure 5.

Figure 5. Elevation d is obtained from point D to surface ABC in delauney triangulation.

NOTE: Interpolated accuracy using contour data is obtained by Delauney triangulation. Elevation d is applied in Equation (6). Own work.

Contour data were used to produce a Delauney triangulation network. The nodes of the line are interpolated to obtain the difference in the elevation data and calculate the interpolated accuracy for each line. Once the theoretical and interpolated accuracies of each node of a line segment have been determined, the error propagation technique can be used to obtain the error band of the segment (Figure 6). Here, x and y are treated as independent uncorrelated random variables, as indicated by the following formula:

(7)

σ_{x'}^{2} = σ_{x}^{2} . {cos}^{2} θ + σ_{y}^{2} . {sin}^{2} θ σ_{y'}^{2} = σ_{x}^{2} . {sin}^{2} θ + σ_{y}^{2} . {cos}^{2} θ

Figure 6. Confidence interval between two nodes with known standard deviations.

(a) Angle θ between two coordinate systems. (b) The confidence interval established between two known nodes on the basis of the selected significance level. From “a stochastic process-based model for the positional error of line segments in GIS.” by Shi, W., Liu, W., 2000, International Journal of Geographical Information Science, 14(1), 51-66.

When ( $x_{A}, y_{A}$ ) and ( $x_{B}, y_{B}$ ) follow a normal distribution, the transformed coordinates (x,y) and (x’,y’) also have a normal distribution. Given a significance level of α, the confidence interval for the line on the y’-axis can be calculated as ( $- Z_{\frac{α}{2}} . σ_{y'}$ $Z_{\frac{α}{2}}$ . $σ_{y'}$ ). Plotting and connecting all points within this confidence level yields Figure 6, which is similar to the GIS result.²³

Results

The LiDAR data employed in this study were collected in a mountainous region using an Optech Galaxy ALTM™ 30/70 scanner provided by Chung-Hsing Surveying, Taichung, Taiwan. The flight altitude was set at 4,400 m. Non-terrain LiDAR point clouds were filtered out of the data. The LiDAR system captured data at a density of 0.05 points/m² and had horizontal and vertical accuracies of approximately 2.2 and 0.35 m, respectively. The authors have provided flow diagram of line growin to benefit readers and peers to replicate our work in Figure 10. The mountainous region investigated in this study is shown in Figure 1(a). Given the low density of LiDAR data, a search radius of 50 m was selected to capture a sufficient number of point clouds for depicting ridge and valley lines.

Identifying local maxima in C values is critical for designating seed points to initiate the growth of ridge and valley lines. In Figure 7, the point clouds are classified into two types using Equation (1).

Figure 7. LiDAR point clouds in the mountainous region.

NOTE: Candidate seeds are indicated in orange, and other points are in green. Own work.

Following the initial phase, the line growth was executed using Equations (2)–(4). In this step, redundant point clouds were eliminated, and points were connected to form ridges or valley lines. Figure 8 illustrates the results with different colors demarcating the various line segments. The search radius was 50 m. The basic threshold (ω) is approximately 5°, and three times the average value (3ω) is 15°applied as the threshold value in this study. Although some fragmented ridge and valley lines were obtained, the line growth algorithm effectively extracted both prominent and subtle line features, despite the low point cloud density.

Figure 8. Ridge and valley lines after line growth.

NOTE: Each with a unique color. The most crucial lines were successfully extracted. Own work.

Ridges and valley lines were obtained following the line-growing procedure, although these lines consisted of fragmented segments (Figure 8). The theoretical accuracies of the ridge and valley lines were calculated and the corresponding data are listed in Table 1. The lowest horizontal and vertical theoretical accuracies are approximately 2.5 and 0.40 m. These values closely match the accuracies reported in LiDAR instrument documentation. In some instances, the theoretical accuracy surpassed the reported instrument accuracy. Notably, applying the line-growing method resulted in considerably greater line accuracy, as indicated by a 90% enhancement in both horizontal and vertical measurements (2.508 vs. 0.253 m and 0.398 vs. 0.040 m, respectively; Table 1).

Table 1. Theoretical accuracies of the results in the vertical and horizontal dimensions.

Theory accuracy	Horizontal (m)	Vertical (m)
Min	0.253	0.04
Max	2.508	0.398
Avg	1.239	0.197

In this region, a contour map was drawn by experienced survey workers using stereo plotters. The interval height of the contour lines was 20 m, and the nodes of the contour lines were applied to produce a Delauney triangulation network. The extracted nodes of the line in Figure 8 were interpolated using Equation (6), and the interpolated accuracy is displayed in Table 2. The worst interpolated accuracy (approximately 16.102 m) is still less than the interval height of contour lines (20m), therefore the method is effective in enhancing the accuracy, even at 98% (16.102 vs. 0.205 m).

Table 2. Interpolated accuracy in the experimental region.

Interpolation accuracy	Vertical (m)
Min	0.205
Max	16.102
Avg	3.403

Figure 9 shows the contour lines together with the results, and indicates the favorable accuracy and reliability of the results. Automated processes can reduce the required time and effort by eliminating redundant tasks.

Figure 9. Relationship between extracted lines and contour lines.

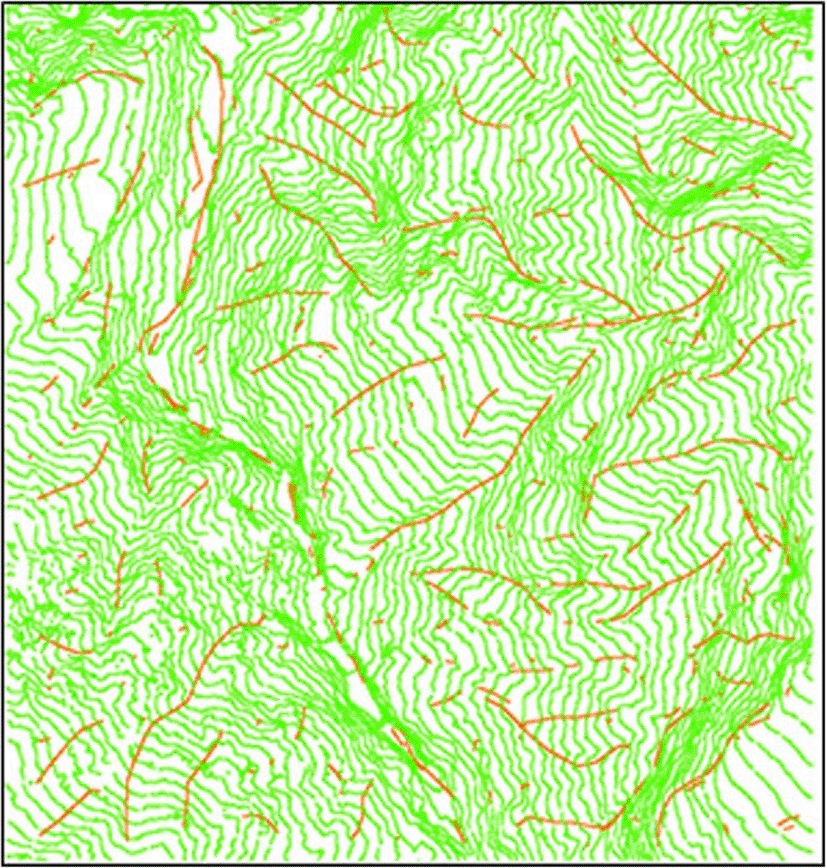
NOTE: Lines extracted through line growth (red) and contour lines (green). Own work.

Figure 10. Flow diagram.

Discussion

This study employed the TVM to obtain the line feature strength C and its corresponding eigenvector v of discrete LiDAR point clouds, which are helpful parameters for extracting valley and ridge lines from LiDAR datasets on mountainous terrain. By utilizing the local C maxima, redundant data points can be effectively eliminated, and the computational efficiency can be enhanced. Furthermore, the angles between successive v vectors serve as crucial metrics for refining the alignment of adjacent points along the lines. C and v values contribute substantially to the line-growing technique applied to mountainous regions in this study. The concept of a moving mask was adopted to maintain intricate line details. Employing the line-growing technique enables the extraction of primary and minor ridge and valley lines contingent upon specific project requirements. The method can be applied to any terrain to extract line features, which is different from setting thresholds to affect the final results.

The line-growing technique developed in this study can yield highly accurate line nodes for the extraction of ridge and valley lines in mountainous regions. The proposed approach is effective in capturing both primary and minor ridges but tends to produce lines that are short and fragmented. One avenue for improvement lies in connecting these fragmented ridge or valley lines when they belong to the same topographical features that will be studied in the future. The method presented in this paper is fast and automated and can furnish operators with a wealth of detailed information about minor line features. This enables the extraction of ridge and valley lines that are tailored to specific requirements. Undoubtedly, the method developed here can be generalized to a large amount of LiDAR data.

Ethical approval and consent

Ethical approval and consent were not required.

Data availability

Underlying data

Zenodo: Extracting Ridge and Valley Lines in Mountainous Areas from Airborne Lidar Data by Utilizing Line Feature Strength, https://doi.org/10.5281/zenodo.12771247.²⁴

This project contains the following underlying data:

• Contour.ods
• LidarData.ods

Data are available under the terms of the Creative Commons Zero “No rights reserved” data waiver (CC0 1.0 Public domain dedication).

Acknowledgements

The authors are grateful to Chung-Hsing Surveying Co., Ltd., Taichung, Taiwan, for providing LiDAR datasets.

References

1. You RJ, Lin BC: Building feature extraction from airborne Lidar data based on tensor voting algorithm. Photogramm. Eng. Remote. Sens. 2011; 77(12): 1221–1231. Publisher Full Text
2. You RJ, Lin BC: A quality prediction method for building model reconstruction using LiDAR data and topographic map. IEEE Trans. Geosci. Remote Sens. 2011; 49(9): 3471–3480. Publisher Full Text
3. Dey EK, Awrangjeb M, Tarsha Kurdi F, et al.: Machine learning-based segmentation of aerial LiDAR point cloud data on building roof. Eur. J. Remote Sens. 2023; 56(1): 2210745. Publisher Full Text
4. Zhao J, You S: Road network extraction from airborne LiDAR data using scene context. In 2012 IEEE Computer Society Con-ference on Computer Vision and Pattern Recognition Workshops. 2012; pp. 9–16. Publisher Full Text
5. Kraus K, Pfeifer N: Advanced DTM generation from LIDAR data. International Archives of Photogrammetry Remote Sensing And Spatial Inf. Sci. 2001; 34(3/W4): 23–30.
6. Štroner M, Urban R, Křemen T, et al.: UAV DTM acquisition in a forested area–comparison of low-cost photogrammetry (DJI Zenmuse P1) and LiDAR solutions (DJI Zenmuse L1). Eur. J. Remote Sens. 2023; 56(1): 2179942. Publisher Full Text
7. Okyay U, Telling J, Glennie CL, et al.: Airborne lidar change detection: An overview of Earth sciences applications. Earth Sci. Rev. 2019; 198: 102929. Publisher Full Text
8. Al-Kakey O, Othman AA, Al-Mukhtar M, et al.: Proposing Optimal Locations for Runoff Harvesting and Water Management Structures in the Hami Qeshan Watershed, Iraq. ISPRS Int. J. Geo Inf. 2023; 12(8): 312. Publisher Full Text
9. Vernon J, St. Peter J, Crandall C, et al.: Spatial Application of Southern US Pine Water Yield for Prioritizing Forest Management Activities. ISPRS Int. J. Geo Inf. 2023; 12(2): 34. Publisher Full Text
10. Soycan M, Tunalıoğlu N, Öcalan T, et al.: Three dimensional modeling of a forested area using an airborne light detection and ranging method. Arab. J. Sci. Eng. 2011; 36: 581–595. Publisher Full Text
11. Streutker DR, Glenn NF: LiDAR measurement of sagebrush steppe vegetation heights. Remote Sens. Environ. 2006; 102(1-2): 135–145. Publisher Full Text
12. Kushwaha SKP, Singh A, Jain K, et al.: Qualitative Analysis of Tree Canopy Top Points Extraction from Different Terrestrial Laser Scanner Combinations in Forest Plots. ISPRS Int. J. Geo Inf. 2023; 12(6): 250. Publisher Full Text
13. Michałowska M, Rapiński J, Janicka J: Tree species classification on images from airborne mobile mapping using ML. NET. Eur. J. Remote Sens. 2023; 56(1): 2271651. Publisher Full Text
14. Gonzales RC, Paul W: Digital image processing. Addison-Wesley Longman Publishing Co., Inc.; 1987.
15. McLaughlin RA: Extracting transmission lines from airborne LIDAR data. IEEE Geosci. Remote Sens. Lett. 2006; 3(2): 222–226. Publisher Full Text
16. Guan H, Yu Y, Li J, et al.: Extraction of power-transmission lines from vehicle-borne lidar data. Int. J. Remote Sens. 2016; 37(1): 229–247. Publisher Full Text
17. Bailly JS, Lagacherie P, Millier C, et al.: Agrarian landscapes linear features detection from LiDAR: application to artificial drainage networks. Int. J. Remote Sens. 2008; 29(12): 3489–3508. Publisher Full Text
18. Chang YC, Song GS, Hsu SK: Automatic extraction of ridge and valley axes using the profile recognition and polygon-breaking algorithm. Comput. Geosci. 2008; 24(1): 83–93. Publisher Full Text
19. Gülgen F, Gökgöz T: Automatic extraction of terrain skeleton lines from digital elevation models. International Archives of Photogrammetry, Remote Sensing and Spatial Inf. Sci. 2004; 35(B3).
20. Medioni G, Lee MS, Tang CK: A Computational framework for segmentation and grouping. Elsevier Science B.V; 2000.
21. You RJ, Lee CL: Accuracy improvement of airborne Lidar strip adjustment by using height data and surface Feature strength information derived from the tensor voting algorithm. ISPRS Int. J. Geo Inf. 2020; 9: 50. Publisher Full Text
22. Schuster HF: Segmentation of lidar data using the tensor voting framework. Proceedings of the XXth ISPRS Congress: Geo-Imagery Bridging Continents, Commission III, 12–23 July, Istanbul, Turkey, 12–23 July. 2004; pp. 1073–1078.
23. Shi W, Liu W: A stochastic process-based model for the positional error of line segments in GIS. Int. J. Geogr. Inf. Sci. 2000; 14(1): 51–66. Publisher Full Text
24. You R, Lee C: Extracting Ridge and Valley Lines in Mountainous Areas from Airborne Lidar Data by Utilizing Line Feature Strength. [Data set]. 2024. Publisher Full Text

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 05 Sep 2024

Author details Author details

¹ Department of Geomatics, National Cheng-Kung University, Tainan, 70101, Taiwan
² Department of Geomatics, National Cheng-Kung University, Tainan, 70101, Taiwan

Rey-Jer You
Roles: Methodology

Chao-Liang Lee
Roles: Methodology

Competing interests

No competing interests were disclosed.

Grant information

This work was funded by Institute for Information Industry, Ministry of Science and Technology, Taiwan- MOST 105-2119-M-006-034
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (1)

version 1

Published: 05 Sep 2024, 13:1011

https://doi.org/10.12688/f1000research.151861.1

Copyright

© 2024 You RJ and Lee CL. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

You RJ and Lee CL. Extracting ridge and valley lines in mountainous areas from airborne lidar data by utilizing line feature strength [version 1; peer review: 1 not approved]. F1000Research 2024, 13:1011 (https://doi.org/10.12688/f1000research.151861.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Peer review discontinued

Version 1

VERSION 1

PUBLISHED 05 Sep 2024

Views

12

Reviewer Report 26 Sep 2024

Fayez Tarsha Kurdi, University of Southern Queensland, Springfield Campus, Springfield, Australia

Not Approved

https://doi.org/10.5256/f1000research.166549.r324632

Introduction
large amount of terrain data that: remove “terrain”
please don’t use “etc”, please check the text.
If image extraction techniques are employed, please cite a suitable reference such as: [ ref 1 ]
Please replace ... Continue reading

Introduction
large amount of terrain data that: remove “terrain”
please don’t use “etc”, please check the text.
If image extraction techniques are employed, please cite a suitable reference such as: [ ref 1 ]
Please replace “Scholars” with “authors”.
In urban environments, where buildings and roofs exhibit regular patterns, point clouds
on surfaces are readily distinguishable from others owing to their high surface feature strength. Lines can be identified at the intersections of two adjacent surfaces. Please cite a suitable reference such as: [ ref 2 ]
Please highlight the contribution and novelty of this study.

Methods
Please don’t put two section titles consecutively, you must add a transition paragraph between them, please check the paper.

Please add an organigram that describes the suggested approach.

Geometric feature strength

You don’t discuss how you extracted the ground class from the measured point cloud.
Please detailed “tensor communication” approach and mention the used equations.
Please explain how you got Figure 2.

Please cite a reference about the calculation of eigenvectors such as: [ ref 3 ]

Please cite a reference for the region growing algorithm.
How did you select the threshold values?
Please cite a reference for the local maxima algorithm.
Please add a new section to detail all used thresholds.
Please cite the source of all used equations in the paper, if you develop an equation, please explain how you got it. Please define all parameters used in all used Equations.
Please define all equation elements under them.
Please add a datasets section to present the used data.
Figure 10 should be in the method section.
Please add a conclusion section and do not forget to present future work.

Is the rationale for developing the new method (or application) clearly explained?

Partly
Is the description of the method technically sound?

Partly
Are sufficient details provided to allow replication of the method development and its use by others?

Partly
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?

No

References

1. Tarsha-Kurdi F, Landes t, Grussenmeyer P: Joint combination of point cloud and DSM for 3D building reconstruction using airborne laser scanner data. ResearchGate. 2007. Reference Source
2. Tarsha Kurdi F, Awrangjeb M, Munir N: Automatic filtering and 2D modeling of airborne laser scanning building point cloud. Transactions in GIS. 2021; 25 (1): 164-188 Publisher Full Text
3. Dey E, Tarsha Kurdi F, Awrangjeb M, Stantic B: Effective Selection of Variable Point Neighbourhood for Feature Point Extraction from Aerial Building Point Cloud Data. Remote Sensing. 2021; 13 (8). Publisher Full Text

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Extraction and modeling of LiDAR data

I confirm that I have read this submission and believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

CITE

Report a concern

Respond or Comment

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 05 Sep 2024

Peer review discontinued

At the request of the author(s), this article is no longer under peer review.

What does this mean?

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1
Version 1 05 Sep 24	read

Fayez Tarsha Kurdi, University of Southern Queensland, Springfield Campus, Australia

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

Back to all reports

Reviewer Report

12 Views

26 Sep 2024 | for Version 1

Fayez Tarsha Kurdi, University of Southern Queensland, Springfield Campus, Springfield, Australia

12 Views Cite this report Responses(0)

Not Approved

Introduction
large amount of terrain data that: remove “terrain”
please don’t use “etc”, please check the text.
If image extraction techniques are employed, please cite a suitable reference such as: [ ref 1 ]
Please replace “Scholars” with “authors”.
In urban environments, where buildings and roofs exhibit regular patterns, point clouds
on surfaces are readily distinguishable from others owing to their high surface feature strength. Lines can be identified at the intersections of two adjacent surfaces. Please cite a suitable reference such as: [ ref 2 ]
Please highlight the contribution and novelty of this study.

Methods
Please don’t put two section titles consecutively, you must add a transition paragraph between them, please check the paper.

Please add an organigram that describes the suggested approach.

Geometric feature strength

You don’t discuss how you extracted the ground class from the measured point cloud.
Please detailed “tensor communication” approach and mention the used equations.
Please explain how you got Figure 2.

Please cite a reference about the calculation of eigenvectors such as: [ ref 3 ]

Please cite a reference for the region growing algorithm.
How did you select the threshold values?
Please cite a reference for the local maxima algorithm.
Please add a new section to detail all used thresholds.
Please cite the source of all used equations in the paper, if you develop an equation, please explain how you got it. Please define all parameters used in all used Equations.
Please define all equation elements under them.
Please add a datasets section to present the used data.
Figure 10 should be in the method section.
Please add a conclusion section and do not forget to present future work.

Is the rationale for developing the new method (or application) clearly explained?

Partly
Is the description of the method technically sound?

Partly
Are sufficient details provided to allow replication of the method development and its use by others?

Partly
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?

No

References

1. Tarsha-Kurdi F, Landes t, Grussenmeyer P: Joint combination of point cloud and DSM for 3D building reconstruction using airborne laser scanner data. ResearchGate. 2007. Reference Source
2. Tarsha Kurdi F, Awrangjeb M, Munir N: Automatic filtering and 2D modeling of airborne laser scanning building point cloud. Transactions in GIS. 2021; 25 (1): 164-188 Publisher Full Text
3. Dey E, Tarsha Kurdi F, Awrangjeb M, Stantic B: Effective Selection of Variable Point Neighbourhood for Feature Point Extraction from Aerial Building Point Cloud Data. Remote Sensing. 2021; 13 (8). Publisher Full Text

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Extraction and modeling of LiDAR data

I confirm that I have read this submission and believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

Respond to this report

Responses (0)

[1] 1. You RJ, Lin BC: Building feature extraction from airborne Lidar data based on tensor voting algorithm. Photogramm. Eng. Remote. Sens. 2011; 77(12): 1221–1231. Publisher Full Text

[2] 2. You RJ, Lin BC: A quality prediction method for building model reconstruction using LiDAR data and topographic map. IEEE Trans. Geosci. Remote Sens. 2011; 49(9): 3471–3480. Publisher Full Text

[3] 3. Dey EK, Awrangjeb M, Tarsha Kurdi F, et al.: Machine learning-based segmentation of aerial LiDAR point cloud data on building roof. Eur. J. Remote Sens. 2023; 56(1): 2210745. Publisher Full Text

[4] 4. Zhao J, You S: Road network extraction from airborne LiDAR data using scene context. In 2012 IEEE Computer Society Con-ference on Computer Vision and Pattern Recognition Workshops. 2012; pp. 9–16. Publisher Full Text

[5] 5. Kraus K, Pfeifer N: Advanced DTM generation from LIDAR data. International Archives of Photogrammetry Remote Sensing And Spatial Inf. Sci. 2001; 34(3/W4): 23–30.

[6] 6. Štroner M, Urban R, Křemen T, et al.: UAV DTM acquisition in a forested area–comparison of low-cost photogrammetry (DJI Zenmuse P1) and LiDAR solutions (DJI Zenmuse L1). Eur. J. Remote Sens. 2023; 56(1): 2179942. Publisher Full Text

[7] 7. Okyay U, Telling J, Glennie CL, et al.: Airborne lidar change detection: An overview of Earth sciences applications. Earth Sci. Rev. 2019; 198: 102929. Publisher Full Text

[8] 8. Al-Kakey O, Othman AA, Al-Mukhtar M, et al.: Proposing Optimal Locations for Runoff Harvesting and Water Management Structures in the Hami Qeshan Watershed, Iraq. ISPRS Int. J. Geo Inf. 2023; 12(8): 312. Publisher Full Text

[9] 9. Vernon J, St. Peter J, Crandall C, et al.: Spatial Application of Southern US Pine Water Yield for Prioritizing Forest Management Activities. ISPRS Int. J. Geo Inf. 2023; 12(2): 34. Publisher Full Text

[10] 10. Soycan M, Tunalıoğlu N, Öcalan T, et al.: Three dimensional modeling of a forested area using an airborne light detection and ranging method. Arab. J. Sci. Eng. 2011; 36: 581–595. Publisher Full Text

[11] 11. Streutker DR, Glenn NF: LiDAR measurement of sagebrush steppe vegetation heights. Remote Sens. Environ. 2006; 102(1-2): 135–145. Publisher Full Text

[12] 12. Kushwaha SKP, Singh A, Jain K, et al.: Qualitative Analysis of Tree Canopy Top Points Extraction from Different Terrestrial Laser Scanner Combinations in Forest Plots. ISPRS Int. J. Geo Inf. 2023; 12(6): 250. Publisher Full Text

[13] 13. Michałowska M, Rapiński J, Janicka J: Tree species classification on images from airborne mobile mapping using ML. NET. Eur. J. Remote Sens. 2023; 56(1): 2271651. Publisher Full Text

[14] 14. Gonzales RC, Paul W: Digital image processing. Addison-Wesley Longman Publishing Co., Inc.; 1987.

[15] 15. McLaughlin RA: Extracting transmission lines from airborne LIDAR data. IEEE Geosci. Remote Sens. Lett. 2006; 3(2): 222–226. Publisher Full Text

[16] 16. Guan H, Yu Y, Li J, et al.: Extraction of power-transmission lines from vehicle-borne lidar data. Int. J. Remote Sens. 2016; 37(1): 229–247. Publisher Full Text

[17] 17. Bailly JS, Lagacherie P, Millier C, et al.: Agrarian landscapes linear features detection from LiDAR: application to artificial drainage networks. Int. J. Remote Sens. 2008; 29(12): 3489–3508. Publisher Full Text

[18] 18. Chang YC, Song GS, Hsu SK: Automatic extraction of ridge and valley axes using the profile recognition and polygon-breaking algorithm. Comput. Geosci. 2008; 24(1): 83–93. Publisher Full Text

[19] 19. Gülgen F, Gökgöz T: Automatic extraction of terrain skeleton lines from digital elevation models. International Archives of Photogrammetry, Remote Sensing and Spatial Inf. Sci. 2004; 35(B3).

[20] 20. Medioni G, Lee MS, Tang CK: A Computational framework for segmentation and grouping. Elsevier Science B.V; 2000.

[21] 21. You RJ, Lee CL: Accuracy improvement of airborne Lidar strip adjustment by using height data and surface Feature strength information derived from the tensor voting algorithm. ISPRS Int. J. Geo Inf. 2020; 9: 50. Publisher Full Text

[22] 22. Schuster HF: Segmentation of lidar data using the tensor voting framework. Proceedings of the XXth ISPRS Congress: Geo-Imagery Bridging Continents, Commission III, 12–23 July, Istanbul, Turkey, 12–23 July. 2004; pp. 1073–1078.

[23] 23. Shi W, Liu W: A stochastic process-based model for the positional error of line segments in GIS. Int. J. Geogr. Inf. Sci. 2000; 14(1): 51–66. Publisher Full Text

[24] 24. You R, Lee C: Extracting Ridge and Valley Lines in Mountainous Areas from Airborne Lidar Data by Utilizing Line Feature Strength. [Data set]. 2024. Publisher Full Text

Extracting ridge and valley lines in mountainous areas from airborne lidar data by utilizing line feature strength

Abstract

Background

Methods

Results

Conclusions

Keywords

Introduction

Methods

Geometric feature strength

Line feature strength

Figure 1. LiDAR data for a river and valley region, displayed in various views and data modes.

Figure 2. Section lines corresponding to C data in Figure 1.

Tangent vector of point clouds

Line growth

Choosing seeds with local maxima of line feature strength

(1)

Figure 3. Defining a local maxima in 3D space.

Setting an angle threshold between two tangent vectors

(2)

(3)

(4)

Figure 4. Line-growing procedure.

Theoretical accuracy and interpolated accuracy

(5)

(6)

Figure 5. Elevation d is obtained from point D to surface ABC in delauney triangulation.

(7)

Figure 6. Confidence interval between two nodes with known standard deviations.

Results

Figure 7. LiDAR point clouds in the mountainous region.

Figure 8. Ridge and valley lines after line growth.

Table 1. Theoretical accuracies of the results in the vertical and horizontal dimensions.

Table 2. Interpolated accuracy in the experimental region.

Figure 9. Relationship between extracted lines and contour lines.

Figure 10. Flow diagram.

Discussion

Ethical approval and consent

Data availability

Underlying data

Acknowledgements

References

Comments on this article Comments (0)

Peer review discontinued

Comments on this article Comments (0)

Peer review discontinued

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated