Keywords
Kidney transplant, Linear mixed model, missing at random, Dropout Model, Sensitivity Analysis, Weighted generalized estimating Equation, and Multiple imputation.
Kidney transplant, Linear mixed model, missing at random, Dropout Model, Sensitivity Analysis, Weighted generalized estimating Equation, and Multiple imputation.
Chronic Kidney Disease (CKD) or renal failure is a public global health problem with an estimated prevalence of as 8 to 16% worldwide.1 The disease can develop at any age, but it becomes more common with increasing age and in women as compared to men.2 Currently, there are four treatments for patients diagnosed with renal failure namely, peritoneal dialysis, hemodialysis, transplantation and conservative management. Renal transplantation is considered the best among the four treatments since it has a significant effect on the length and quality of life of the patients. However, renal transplantation is also associated with some complications such as chronic rejection, severe side effects, and increased infection and blood disorders just to mention a few.2 Haematocrit levels is defined as the proportion, by volume, of the blood that consists of red blood cells. Normal range for haematocrit differs in gender, it is approximately 40% to 54% for males and 36% to 48% for females.3 Kidney failure is associated with the decrease in haematocrit level. Haematocrit levels in renal patients after transplant increases however, a persistent increase of haematocrit level greater than 51% after renal transplantation leads to blood disorder called post-transplant erythrocytosis (PTE). This usually occurs in two years after transplantation and it is very common in males than females.1
Missing values are a problem in many statistical analyses. Most software statistical procedures exclude the observations with missing values from the analysis.4 These observations are called incomplete cases. Although using only complete cases is simpler, we lose the in- formation that is in the incomplete cases. Excluding observations that have missing values also ignores the possibility of systematic differences between complete cases and incomplete cases, so the resulting inference might not apply to the entire population, especially when we have a small number of complete cases.4 Whenever there are missing data, there is loss of information, which causes a reduction in efficiency of the statistical inference on the parameters. The data of this study, which have been collected for some of the patients with incomplete measurements during the 10 years study period. Hence, the data contains missing observations. This study was conducted in order to investigate the evolution of haematocrit levels over time in renal patients after their transplant and to determine how the evolution depends on the age and gender of the patient accounting for the missingness in the data. In addition, to determine if this evolution also depends on the experience of cardiovascular problems during the years preceding the transplantation and rejection symptoms during the first three months after the transplantation took place.
To investigate evolution of Haematocrit levels (continuous and binary response) in renal trans plant patients over time after the transplant and how the evolution depends on gender, age, cardiovascular problems preceding the transplantation and rejection symptoms after the transplantation accounting for the missingness in the data.
Researchers have taken this data from secondary source (taken already collected data) of data, and it consists of 1160 (666 males and 494 females) patients who received a renal Trans plant and were followed up for a period of 10 years at most. In this analysis both the continuous and the discrete outcome were considered. The continuous Haematocrit level of the patients at each time point of measurement was discretized to obtain dichotomized outcome (normal and abnormal) on the log scale. The measurements were taken at fixed time points on a yearly basis except the first two measurements that were taken after 6 months in between after the transplant. The patient’s age, gender (males = 1 and females = 0), experience of cardiovascular problem during the years preceding the transplantation (Cardio: yes = 1 and no = 0) and rejection symptoms during the first three months after the transplantation took place (Reject: yes = 1 and no = 0) were considered as predictors. In addition, the variable time was considered on a log scale (log (Years+1)) in the analysis for continuous outcome in order to improve linearity and for discrete outcome the original time (year) was considered. The haematocrit measures the volume of red blood cells compared to the total blood volume (red blood cells and plasma). Thus, the dichotomization was based on the literature that the normal hematocrit levels for males is 40 to 54% and for females it is 36 to 48%.1 These values can be determined directly by micro-hematocrit centrifugation or calculated indirectly.1 Using the above mentioned cutoff points, haematocrit levels for males and females were dichotomized into normal and abnormal categories as follows:
Where Yij is the binary response value for patient i at j time, HCo is the baseline haematocrit level, and HCT is the other haematecrotic level measurements.
In this section, we describe various statistical techniques take into account the correlation among the response measurements and the missingness in the data set. To explore the data and get some idea different graphical methods as well as frequency table were employed. In addition, marginal model (Generalized Estimating Equations (GEE)) and random effect model (linear mixed model (LMM)) under different missingness assumptions were fitted.
This is to confirm that the researchers have ethical approval from the research ethics approval committee which is called Institutional Review Board (IRB) of Hasselt University, and we obtained verbal full consent from the participants, why verbal consent is that the data was collected immediate by asking their consent for each participant, but having written consent were not that much important.
Were performed to get insight of the data. We used both frequency tables and graphical techniques.
There are two patterns of missing data, namely, monotone or non-monotone. Monotone patterns, often called as dropout occur if a subject misses a measurement occasion never observed again and on the other hand, non-monotone, often called as intermittent occur if at least some subject values are observed again after a missing value occurs. There are 3 different missingness mechanisms which consist of missing completely at random (MCAR), missing at random (MAR) and missing not at random (MNAR). Data is said to be missing completely at random (MCAR) when the probability that responses are missing are unrelated to either the specific values that, in principle, should have been obtained or the set of observed responses. The essential feature of MCAR is that the observed data can be thought of as a random sample of the complete data.5 Data is said to be missing at random (MAR) when the probability that the responses are missing depends on the set of observed responses but is conditionally unrelated to the specific values that in principle, should have been obtained. When both assumptions of MCAR and MAR do not hold, the missingness is assumed to be missing not at random (MNAR). The probability of a measurement being missing depends on unobserved data and no simplification of the joint distribution of the full data is possible.6
The missing mechanism that occurs in the renal data set was explored using graphical techniques and fitting a logistic regression to the probability of dropouts. After exploring the possible missing mechanism, appropriate techniques of handling missing measurements were applied. Dealing with the problem of missing observation in a data set, different methods have been proposed. The major frameworks formulated to develop missing data models are selection models, pattern mixture models and shared parameter models. In this report we used selection models and pattern mixture models for sensitivity analysis. Selection model is a model that factors the joint distribution of the measurement and the nonresponse mechanism into the marginal measurement distribution and the non-response distribution, conditional on the measurements. That is, where, are the design matrices for fixed effects, random effects and the missing process and are vectors that parameterize the joint distribution. The pattern mixture model allows for a different response model for each pattern of missing values, the observed data being a mixture of these weighted by the probability of each missing value or dropout patterns. The shared-parameter models include random effects shared between both factors and it is assumed that the observations and missingness indicator are independent given the random effect. The nature of the missingness mechanism can affect the analysis of incomplete data and result of statistical inference. Methods for Handling Missing data were presented as follow.
The commonly used methods to analyze missing data are the Complete Case Analysis (CC) and Last Observation Carried Forward (LOCF). For the CC method, part of the data are removed, whereas for the latter the data are filled in. When using CC, only those subjects which have a complete profile are included in the analysis, resulting in a loss of information, and thus low efficiency. Moreover, this method relies on the strong (and often unrealistic) assumption of MCAR. If the missingness mechanism is not MCAR, it introduces biased results. LOCF can be regarded as an imputation method, where any missing value is substituted with the last observed one. For LOCF analysis to be valid, the MCAR assumption is necessary but not sufficient. In addition, it must be assumed that the patients’ outcomes remain constant after dropout. If these assumptions do not hold, the results may be severely biased.5 Because of the limitation of these methods were not used in the analysis of this report.
The direct likelihood method leads to valid inference under MAR assumption.7 Likelihood based-method MAR assumption uses all available data without deletion or imputation. The direct likelihood consists in applying likelihood-based models like linear, generalized linear and non-linear mixed models to longitudinal data without modeling the missingness process. A Linear mixed model was considered in this study with the continuous outcome variable. Linear mixed models are a random effects model useful when drawing inferences with respect to subject specific, including subject specific parameters.6 The estimates of random effects are useful in detecting between subject variability and, therefore, important in detecting special profiles (subjects evolving differently over time). Drawbacks are that LMM has increased complexity in estimation of parameters within a maximum likelihood context. Also it is difficult to check distributional assumptions of random effects.
Generalized Estimating Equation is a marginal model useful when the interest is on population average interpretation. GEE was proposed by Ref. 8 in order to avoid the computational complexity of full likelihood, and which can be considered whenever interest is restricted to the mean parameters. GEE was used in this study to fit a binary logistic regression model, for the binary response variable. Hence the GEE approach is limited to valid only under the strong assumption that the data are missing completely at random (MCAR). To allow the data to be missing at random (MAR), Robins, Rotnitzky, and Zhao (1995) proposed a class of weighted estimating equations. These can be viewed as an extension of GEE.6 The idea of weighted generalized estimating equations (WGEE) is to weight each subject’s measurements in the GEEs by the inverse probability that a subject drops out at that particular measurement occasion.6 This provides an analysis suitable under the MAR assumption. Weighted GEE alone is not able to handle intermittent missingness. Thus, it was applied in combination with multiple imputation to create monotone missingness in the data that was later used to fit WGEE.
Multiple imputation procedure replaces each missing value with a set of M plausible values, i.e., values’drawn’ from the distribution of a dataset, that represent the uncertainty about the right value to impute. The imputed datasets are then analyzed by using standard procedures for complete data and combining the results from these analyses. Multiple imputation, at least in its basic form, requires the missingness mechanism to be MAR.6
When fitting models to incomplete longitudinal data, it is important to assess the sensitivity of the conclusions to unverifiable assumptions. There are different ways of assessing sensitivity, in this study, sensitivity analysis based on multiple imputation was conducted where by the imputed data was adjusted by shifting by some values. This method was used to check if MAR assumptions are plausible. The missing values were imputed under a plausible scenario assuming the missing data are missing not at random (MNAR). If inference in this scenario leads to a conclusion different from that of inference under MAR, then the MAR assumption is questionable.4 SAS version 9.4 was used for statistical analysis and graphics. For statistical tests, 5% level of significance was used.
The summary statistics Table 1 below shows the frequencies and percentages for the baseline characteristics of the patients included in the study according to gender, cardio and reject. It was observed that out of 1160 patients, 43% of the patients were females while 57% were males and among these patients 18% of the patients experienced cardio-vascular problems during the years preceding the transplantation while 82% of the patients did not experience these problems. 32% of the patients showed symptoms of graft rejection during the first three months after the transplantation took place while 68% of the patients did not. In addition, it was observed that of the 1160 patients, then mean age for the patients at baseline was 46.43 years with a standard deviation of 13.31 years.
Figure 1 depicts the evolution of haematocrit levels for the first 30 selected patients over time. From these profiles, it was observed that there seems much between and within variability. It was also revealed that patients have different starting haematocrit levels at six months and the evolution for each patient varies over time. This suggests that random intercept and random slopes might be required for the analysis. In addition, the overall mean structure of evolution of haematocrit levels for the continuous and binary response are depicted in Figure 2. It was observed that the evolution of haematocrit levels varies (with some increases and decreases) over time. Thus, it was revealed that the proportions of patients having normal haematocrit levels seems to follow a high order polynomial for the time trend effect.
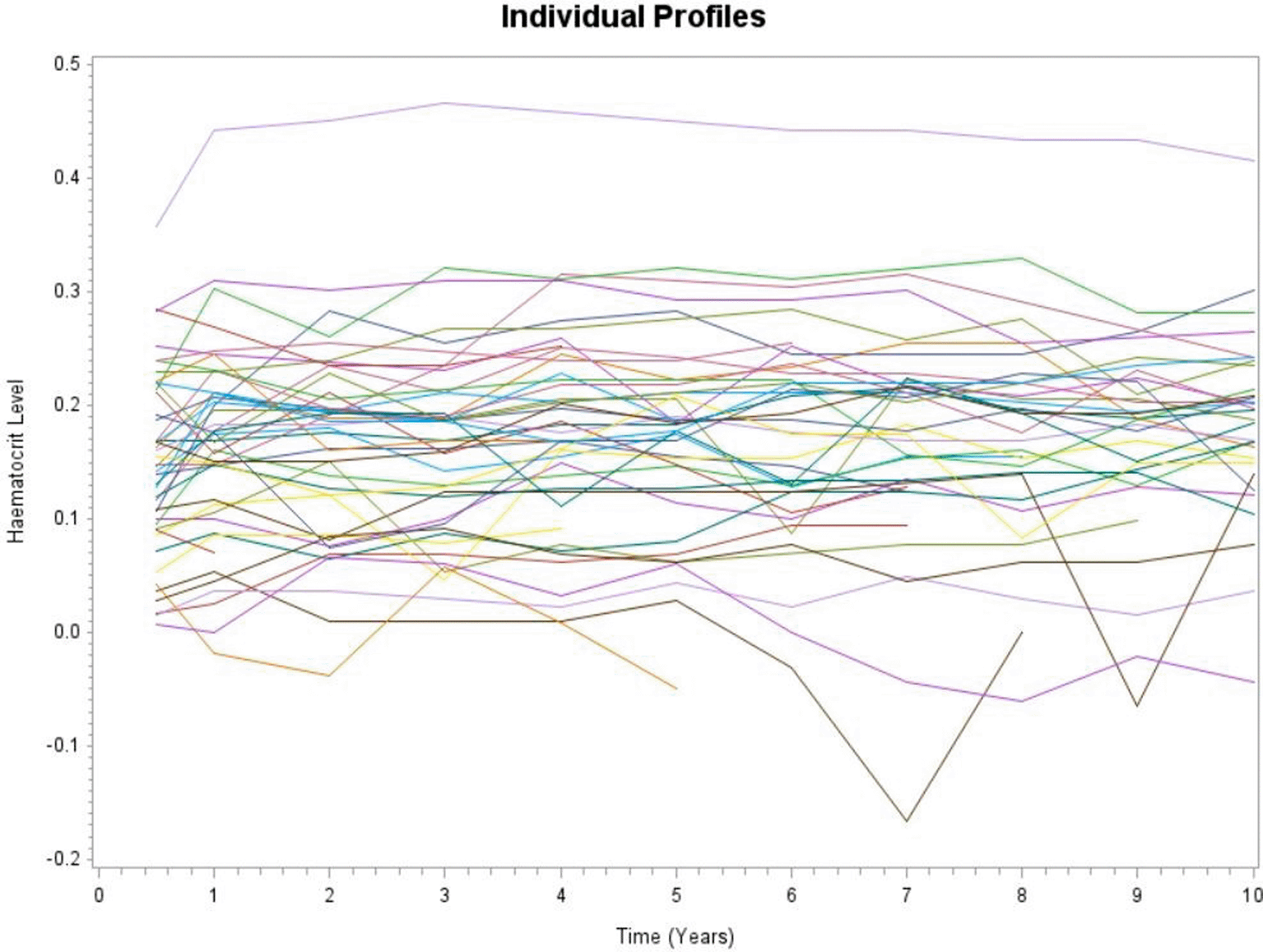
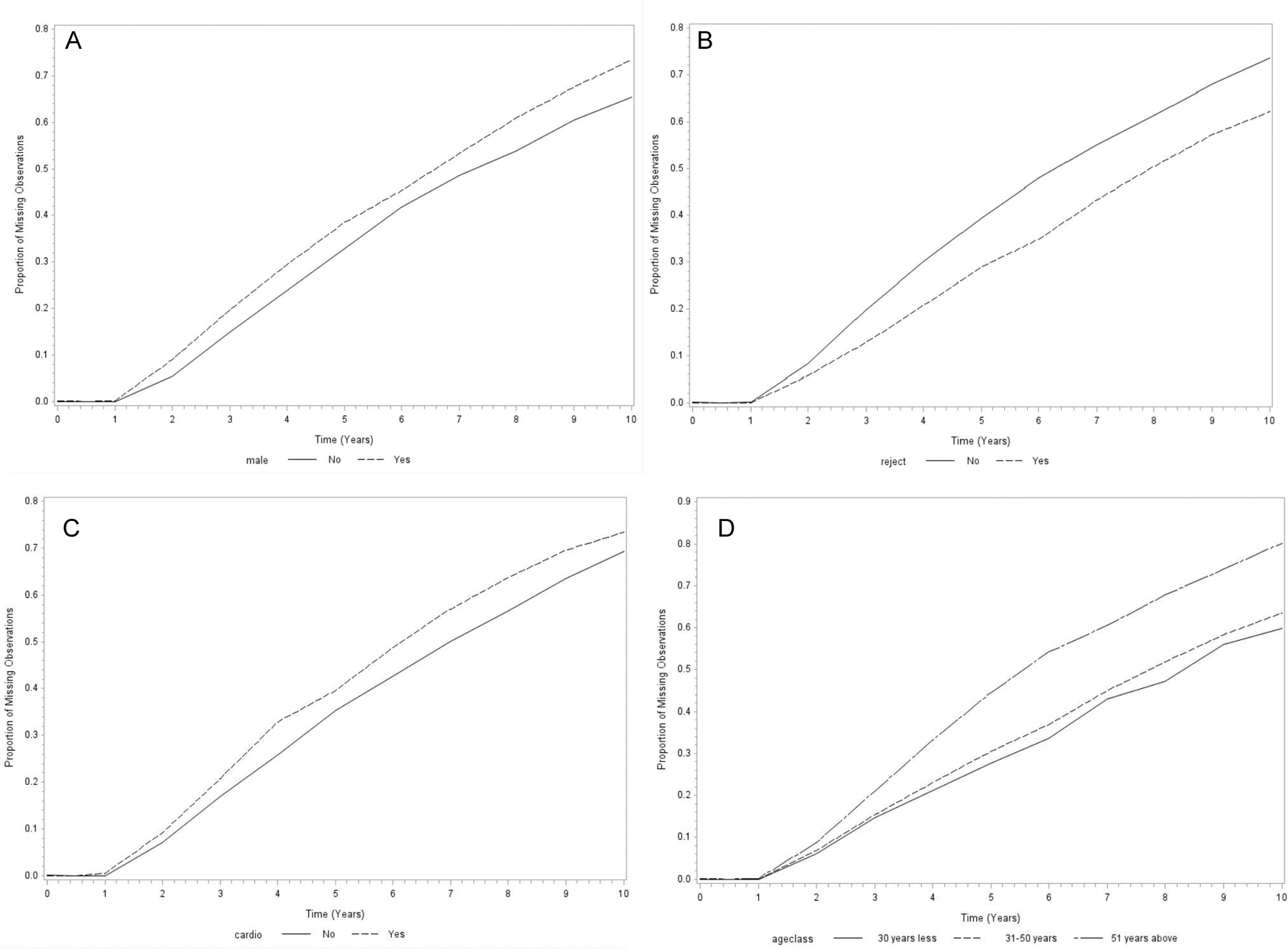
Table 2 shows the frequencies and percentages of missingness over time. It was observed that the number of missing observations increases over time with 1 (0.09%) observation missing at baseline, 418(36.03%) missing on the 6th measurement and 812(70%) missing on the last measurement. Furthermore, it was also observed that the proportion of missingness seems to vary with the covariates (Figure 3). Overall, for all the covariates from Figure 1, there seems to be no difference between or among the categories from baseline up to year 1 of follow-up which later starts to vary over time. The proportion of missingness seems to be higher for males than females and for patients without reject symptoms than those with reject symptoms over time. In addition, the proportion of missing over time seems to be higher for patients who experienced cardio problems than those that did not. With regards to age, it seems patients in the higher age group (above 50 years) seem to have a higher proportion of missingness over time compared to patients less than 50 years. However, patients in between 31 years to 50 years tend to have a slightly higher proportion of missingness compared to patients that are 30 years or less. Therefore, Figure 3 suggests that gender, age, experience of reject symptoms and cardiovascular problems might be the possible factors associated with dropout. However, these results cannot be conclusive based on the plots thus, a formal test was conducted in the following section by fitting a dropout model. Furthermore, missingness was explored in terms of the missingness patterns which involved obtaining frequencies and percentages of completers, dropouts and non-monotone missingness. It was 29.22% of the observations were completers, 69.57% dropouts and 1.23% of the observations were revealed to have a non-monotone missingness pattern (Table 3).
| Time (Years) | 0 | 0.5 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Frequency | 1 | 0 | 1 | 87 | 205 | 314 | 418 | 508 | 595 | 672 | 749 | 812 |
| Percentage | 0.09 | 0 | 0.09 | 7.50 | 17.67 | 27.07 | 36.03 | 43.79 | 51.29 | 57.93 | 64.57 | 70 |
In order to get an insight on which factors may influence the missingness of response variable, an ordinary logistic regression on the binary dropout indicator was fitted for the covariates gender, age, cardio, reject and previous outcome, and hematocrit level at baseline.
Where, Di indicating whether the patients observed or dropout at a particular visit. The above model applies for potential dropout only, and therefore is not suitable for the 14 patients with non-monotone missingness, therefore they were excluded for the model fitting. All of the covariates were significant except cardio and gender (Table 4). This implies that age and reject have a significant effect on dropout unlike cardio and gender. In addition, it was observed that the variable for the previous measurement was significant which revealed the evidence against MCAR in favor of MAR.
| Effect | Par. | Estimate (s.e) |
|---|---|---|
| Intercept | ψ0 | -8.2385 (0.711)* |
| Previous HC (HC-1) | ψ1 | -0.256 (0.0766)* |
| Baseline (HC0) | ψ2 | 1.536 (0.2046)* |
| Gender | ψ3 | -0.114 (0.077) |
| Cardio | ψ4 | 0.055 (0.100) |
| Reject | ψ5 | 0.225 (0.084)* |
| Age | ψ6 | 0.0162 (0.003)* |
The dropout model has several advantages as it enables to test whether the assumption of MCAR can be deemed plausible against MAR. In addition, awareness on the potential factors that lead to dropout provides useful information on monitoring in the study, focus can be on the group which is likely to have missing data and intensify procedures to mitigate it thus, reduce number of dropouts. On the other hand, the analysis has some drawbacks; it does not include all the subjects in the study since it excludes the intermittent missingness subjects. Thus, it leads to loss of information on accessing the potential factors affecting dropout. In addition, dropout in the study might be caused by other factors besides the factors considered in the study. Thus, it might not be possible to determine all the potential factors that lead to dropout of the patients in the study.
To end up with good model a mean structure that explains best the observed average trend and variance structure is required and the mean structure was tested using the subject specific model extension test (Fmeta). From the Fmeta results, it was observed that quartic time effect is sufficient to explain the total within subject variability for each subject in the data. Different models were fitted and tested using the likelihood ratio test to determine which covariates and the possible interactions between covariates that had an effect on the outcome. Thus, the covariates cardio, reject and some interactions were removed from the model. To account for the variability between measurements the random effect was considered and to know which random effect was sufficient to explain between measurements variability, the random effects were tested using the mixture chi-square test (direct likelihood linear mixed model). From this test the quartic time random effect was revealed to be sufficient to take into account the between measurement variability. However, due to convergence problem in multiple imputation the cubic time random effect was considered for both the direct likelihood and multiple imputation linear mixed model (LMM) analysis. Thus, the final model that was fitted was as follows;
Where HCij: Hematocrits level measurement for the ith patient at time point j, (i = 1… 1160 and j = 1…, ni). β1 to β11: Parameter estimates of the fixed effects. b0i to b3i: Parameter estimates of random effects. ei ∼ N (0, P): are vector of error components. The result for direct likelihood and multiple imputation based approach of LMM is given in Table 5. It was observed that time (quartic time trend evolution), gender and age have a significant effect on haematocrit levels. However, the effect of age and gender varies with time. Furthermore, the standard errors of parameter estimate for multiple imputation (MI) are slightly larger than direct likelihood since MI method gain efficiency. The significance of the covariates was remaining same in both method this is from the fact that as the number of multiple imputation increase both method tend to asymptotically the same and both are valid under MAR.
To find a plausible model, GEE was initially fitted with all covariates; including linear, quadratic, and other higher polynomial time effects as it was observed in the exploratory data analysis, as well as their interactions with other covariates in the model under the binary response. Insignificant variables based on 5% significance level were excluded from the model. Then the models were compared using QIC goodness of fit statistic and the model with smallest QIC was selected as the final model. Thus, the final GEE model was fitted as follows;
The final model was then fitted using different working correlation structures and the models were compared based on the closeness of the model-based and empirical corrected standard errors to obtain the best working correlation structure. From all the possible correlation structures that were considered (i.e. independence, exchangeable, unstructured and the auto-regressive of order 1 AR(1)), the unstructured correlation structure was revealed as the best working correlation structure since the standard errors of the model-based parameter are close to empirical estimates. Thus, the final model was fitted using the unstructured correlation structure.
The WGEE and GEE after multiple imputation models were fitted to account for the missingness in the data using the binary response (normal versus abnormal HC levels) which was later compared to standard GEE. When fitting the WGEE, the weights were applied at observational level while for GEE after multiple imputation, 20 imputations were applied. From the WGEE and GEE after multiple imputation results (Table 6), it was observed that time, age, gender, reject and the interaction between reject and time have a significant effect on having normal haematocrit levels in renal patients. In addition, it was observed that the log of odds for males having normal haematocrit levels are lower compared to females. It was also revealed that the odds of having normal haematocrit levels increases with increasing age. On the other hand, it was observed that the effect of reject symptoms on having normal haematocrit levels varies with time. It was also revealed that the evolution of normal versus abnormal haematocrit levels follows a 5th power time trend in GEE after multiple imputation while it significant quadratic time trend was observed in weighted GEE. This might be attributed to the fact that weighted GEE corrects for the bias due the missing or incomplete data which is not the case for standard GEE and GEE after multiple imputation. This was further observed from the standard errors of the parameter estimates of which they were higher in weighted GEE compared to the other results.
| Parameter | Std. GEE | WGEE | MI GEE | Sensitivity Analysis GEE | ||
|---|---|---|---|---|---|---|
| Est. (s.e) | Est. (s.e) | Est. (s.e) | Shift1: Est. (s.e) | Shift2: Est. (s.e) | Shift3: Est. (s.e) | |
| Intercept | -0.2943 (0.2093) | -0.6153 (0.2629) | -0.4899 (0.1827)* | -0.2288 (0.1921) | -0.6649 (0.2008)* | -0.6142 (0.2004)* |
| Age | 0.0111 (0.0030)* | 0.0146 (0.0039)* | 0.0152 (0.0019)* | 0.0108 (0.0018)* | 0.0119 (0.0021)* | 0.0125 (0.0020)* |
| Gender (M) | -0.6690 (0.0786)* | -0.3100 (0.1014)* | -0.4661 (0.0468)* | -0.5048 (0.0680)* | -0.2239 (0.0560)* | -0.2856 (0.0593)* |
| Reject (Yes) | -0.3557 (0.1050)* | -0.4437 (0.1400)* | -0.2851 (0.0815)* | -0.3342 (0.0789)* | -0.3066 (0.0805)* | -0.3106 (0.0805)* |
| Time | 0.8291 (0.2657)* | 1.0705 (0.3333)* | 0.9172 (0.3159)* | 0.8574 (0.3248)* | 1.4085 (0.3159)* | 1.3088 (0.3190)* |
| Time2 | -0.4045 (0.1555)* | -0.5773 (0.2015)* | -0.4700 (0.1839)* | -0.4141 (0.1924)* | -0.8268 (0.1844)* | -0.7508 (0.1866)* |
| Time3 | 0.0869 (0.0377)* | 0.1317 (0.0507) | 0.1011 (0.0443)* | 0.0785 (0.0472) | 0.2011 (0.0444)* | 0.1769 (0.0451)* |
| Time4 | -0.0087 (0.0040)* | -0.0136 (0.0056) | -0.0100 (0.0047)* | -0.0061 (0.0051) | -0.0217 (0.0047)* | -0.0184 (0.0048)* |
| Time5 | 0.0003 (0.0002)* | 0.0005 (0.0002) | 0.0004 (0.0002)* | 0.0002 (0.0002) | 0.0008 (0.0002)* | 0.0007 (0.0002)* |
| Reject (Yes)*Time | 0.0457 (0.0194)* | 0.0476 (0.0295)* | 0.0423 (0.0157)* | 0.0438 (0.0153)* | 0.0531 (0.0156)* | 0.0531 (0.0156)* |
The previous analysis which involved fitting GEE using different approaches (weighted GEE and GEE after multiple imputation), assumed that the missingness in the data was missing at random (MAR). However, the MAR assumption cannot be verified, because the missing values are not observed. Therefore, a sensitivity analysis was carried out using the pattern- mixture model under the missing not at random (MNAR) assumption to determine if the assumption of MAR can be deemed to be plausible.5 The sensitivity analysis involved fitting 3 standard GEE models after multiple imputation which involved imputing the missing values under the MNAR assumption. Three different data sets of imputations were obtained for the 3 models that were fitted. This was achieved by adjusting the shift of the imputed missing values of the last 3 measurements in the data set by gender. The first adjustment was applied on the males (Shift1 HC8 = 5, HC9 = 10 and HC10 = 15), the second (Shift2 HC8 = 10, HC9 = 10 and HC10 = 10) and third (Shift3 HC8 = 5, HC9 = 10 and HC10 = 15) adjustments were applied on the females. Thus, inference was conducted on the inputted data sets using GEE and results were compared to the weighted GEE and GEE after multiple imputation results.
From the sensitivity analysis inference results (Table 6), the results coincide with what was observed by fitting weighted GEE and GEE after multiple imputation thus, similar conclusions were arrived at. Therefore, it was observed that gender, reject, time, age and the interaction between time and reject had significant on renal patients having normal haematocrit levels over time. However, the evolution followed the 5th power time trend for shift 2 and 3 which coincide with the GEE results after multiple imputation which implies that the assumption of MAR was plausible. On the other hand, from shift 1 results, a quadratic time trend was observed which imply the MAR assumption might be questionable, however the same conclusion was obtained under WGEE. Therefore, it was observed that the assumption of MAR was plausible considering that both WGEE and GEE after multiple imputation are valid under MAR.
A kidney transplant is a surgical procedure to replace a healthy kidney from a donor into a person whose kidneys no longer function properly. The data set used for this analysis were from 1160 patients who received renal graft (kidney transplantation) which have been followed for at most 10 years. The continuous version haematocrit level and dichotomized version was used in this study. The hematocrit level dichotomized into binary response for males and females based on normal level cut-off points. Other patient characteristics such as gender, age, cardio-vascular problem during the years preceding the transplantation and graft rejection during the first 3 months after transplantation as a covariate. The aim of this study was to investigate the evolution of haematocrit levels in renal transplant patients over time after the transplant and how the evolution depends on gender, age, cardio-vascular problems preceding the transplantation and rejection symptoms after the transplantation accounting for the missingness in the data.
From the exploratory data analysis, the individual profile plots depict that there seems much within and between variability and the mean structures and average proportion structures using the continuous and binary response respectively revealed that haematocrit levels seems to follow a high order polynomial for the time trend effect. Furthermore, missingness was explored using the missingness patterns and graphical techniques. It was revealed that the proportion of missingness seems to increase over time and varies according to different levels of the covariates. In addition, majority of the subjects were revealed to be dropouts followed by completers while a few followed a non-monotone missing pattern.
Different statistical methods were employed in order to address the scientific question, this which involved fitting the dropout model, direct likelihood by fitting a linear mixed model, MI based approach, WGEE and MI GEE were fitted. From the dropout model, it was observed that the potential factors that are associated with dropout were reject and age. In addition, evidence against MCAR in favor of MAR was revealed.
Furthermore, after accounting for the missingness in the data set, in continuous response setting, both direct likelihood and MI based approach of Linear Mixed Model revealed that all the covariates included in the final models were significant. It was observed that the evolution of haematocrit levels follows a quartic time trend and the effect of time on the evolution varies according to gender and age. On the other hand, in the binary response setting, age, gender and reject had a significant effect on haematocrit levels however, the effect of reject varies with time. In addition, the effect of time followed a significant 5th power time trend under MI GEE and quadratic time trend under WGEE. However, both models are valid under MAR. In addition, similar conclusions were arrived at comparing MI GEE and standard GEE in terms of significance.
Sensitivity analysis under the MNAR assumption was done using pattern-mixture model in order to examine whether the MAR assumption is reasonable. The sensitivity analysis in evolved fitting three standard GEE models with three different data imputations by adjusting the shift of the missing values were used. The result from shift 1 has the same conclusion with the result from WGEE whereas the results from shift 2 and 3 have the same conclusion with MI GEE. This conclusion showed that the MAR assumption is reasonable and both WGEE and MI GEE are valid under MAR.
In conclusion, time has a significant effect on the evolution of haematocrit levels in renal transplant patients. The evolution of haematocrit levels follows a quartic time trend considering a continuous response setting and a 5th power time trend in the binary response setting. In addition, age, gender and rejection symptoms have a significant effect on the evolution of haematocrit levels in renal patients, however their effect varies with time. It was also observed that experiencing cardiovascular problems before the renal transplant does not have a significant effect on the evolution of haematocrit levels over time in renal patients.
Zenodo. Handling missingness and specify the dropout models in haematocrit levels over time in patients who received renal graft. DOI: https://doi.org/10.5281/zenodo.7866538.
Data are available under the terms of the Creative Commons Attribution 4.0 International license (CC-BY 4.0).
The authors would like to thank Hasselt University for funding this study. We would also like to thanks for all study participants, and advisors for their unreserved efforts and willingness to take part in this study.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)