Computational simulation of the effects of blood flow velocity on atherosclerosis progression in a human carotid artery

Vessel model and properties

Two domains (the arterial wall and lumen domains) were considered in the carotid artery 2-D straight model. It was assumed that the arterial wall was homogeneous, isotropic, and linear-elastic.¹⁹ The boundary conditions taken for the flow are described in Figure 1 and Table 1. Modified vessel dimensions on the carotid artery from previous work were adapted⁸ as indicated in Figure 1. The vessel and carotid model characteristics are presented in Table 1.

Figure 1. The geometry of the idealized carotid artery.

The diameter, length and thickness of the artery were taken as 6, 10 and 0.5 mm, respectively.

Blood properties

The assumption is that blood is Newtonian, incompressible, and viscous in carrying out Wall Shear Stress, and WSS (frictional forces exerted by the moving blood in the artery) studies in nature under the arterial conditions under investigation.^23,24 Laminar flow was also assumed for the blood rheology for the conditions under investigation. That is, Reynolds number values are less than 2300. This completely rules out the turbulent considerations. In the absence of underlying risks, constant blood parameters are presumed throughout the flow process. The rheological properties and density of blood are assumed to be 0.0035 Pa.s and 1050 kg/m³ respectively.²²

Boundary conditions

Since arteries undergo constant deformation, a linearly elastic arterial wall was assumed during the cardiac cycle of blood flow.⁸ The linear elastic model has been observed to yield results that closely align with experimental data.²⁵ The area under examination was the common carotid artery, with edge constraints implemented to ensure model stability during blood flow.²⁶ For fluid-structure interaction between the domains, the remaining nodes were designated as free.^19,27,28 The inlet velocity and traction boundary pressure were fully developed. Boundary conditions were applied at the artery’s inlet and outlet, respectively.^11,20,29 A constant mean (inlet) velocity of exposure was assumed throughout time. A no-slip condition at the arterial wall was also assumed during the cardiac cycle. The distribution of velocity along the cross-section of the vessel is as defined in the work of Alagbe et al. (2022).⁸

Model equation and computational set-up

A fluid-solid interaction (FSI) system was taken as the arterial flow model – with a simultaneous interaction between the solid and liquid domains. Blood flow in the artery was simulated using Navier-Stokes equation, incorporating model equations of Alagbe et al. (2022)⁸ were used for the simulation.

Plaque growth modelling

The plaque’s geometry was simplified and simulated starting at the artery’s central length (5 mm). Plaque growth, forming an asymmetric blockage, extended from the arterial wall as it progressed.

The model equations by Alagbe et al. (2022)⁸ and Tang et al. (2008)³⁰ for plaque initiation and development were adopted. This model gives a linear function expressed as;

σ represents principal shear stress (Plaque Wall Stress, PWS) in KPa, and τ denotes flow shear stress (WSS) in Dyne/cm². WTI measures the increase in plaque wall thickness in cm, reflecting the difference from the initial height. This model predicts the achievable plaque height relative to the initial height every 304 days, corresponding to one cycle of geometry update.

Simulation steps

From the modified work of Liu and Tang (2010),³¹ the two major stages of initiation and progression were adopted.

Initiation Stage: A plaque-free artery is assumed before plaque formation. The blood flow in the plaque-free vessel is taken as the initial condition. Values of WSS and PWS are taken at plaque initiation. These values are used to obtain the WTI value. With this WTI, the plaque is now freshly initiated in a new domain.

Progression Stage: Plaque growth is considered in relation to the initial plaque condition’s memory. The values for WSS and PWS are obtained from the fluid-solid interaction (FSI) model. By adding the WTI, the next plaque height was obtained. The steps are repeated and stopped at the expected time of exposure.

The stenosis severity is expected to increase with every geometry update, leading to an increase in plaque height. Stenosis severity quantifies the degree of arterial lumen blockage by the plaque, expressed in terms of luminal diameter. This obstruction limits blood flow in the axial direction.

Mesh independent study and validation of results

Navier-Stokes equation was solved with finite elements, quadratic velocity, linear pressure, and GMRES iteration, using COMSOL Multiphysics. The meshing used for the simulations were fine meshes as shown in Figure 2 because it guarantees an optimum between computational cost and result accuracy. For the developed carotid vessel geometry before the plaque is initiated, after implementing boundary conditions and selection of meshing protocol, the finalized geometry had 3 domains, 10 boundaries, and 8 vertices. The complete mesh consisted of 3078and 246 domain elements and 246 boundary elements respectively.

Figure 2. Tetrahedral fine mesh used for the simulation.

The meshing was done such that, they are more intricate around the boundaries and the wall/blood interface to ensure that the interactions between both domains are accurately computed.

Plaque initiation with inlet velocity

From Figure 3, it can be observed that there is a general decline in the rate of initiation of the plaque as the velocity of blood in the artery is increased from a minimum of 40 cm/s to 125 cm/s from its initial dimensions where there is no plaque (Figure 8). The variation of plaque initiation height with velocity shows a very strong linear relationship. On comparison of the change in plaque initiation height with velocity change, a 40 cm/s to 80 cm/s change in velocity (100% change) shows an approximate difference of -8.8% in plaque height, although this may seem like a small change, accumulated changes over the years could be significant in the determination of the period in time when the patient is at a high risk of stroke. Minimum and maximum stenosis within the velocity range occurred at 125 cm/s and 40 cm/s, respectively, with plaque heights 1.02 and 0.83 mm, indicating degrees of stenosis of 17 % and 13.8 %, respectively, indicating that persons with lower blood velocities would experience stroke earlier in life. The reason for this could be a result of the higher residence time usually associated with low velocities in plug flow systems; this leads to higher recirculation of blood within the region as well as more significant leaching of LDL into the permeable arterial wall within the region, at the end of this processes, the result is more stagnation and accumulation of biochemical cells.³² This buttresses the results of Liu & Tang (2010),³³ where a higher flow rate was associated with lower plaque heights.

Figure 3. Initiation stage of plaque growth at different inlet blood velocity after 304 days.

Lower inlet blood velocity favours a higher initiation of plaque growth.

Plaque height changes over time

Figure 4 shows that as time progressed, the differential increase in plaque height reduced. The work of Liu & Tang (2010)³³ buttresses this observation when a similar model was implemented in the coronary artery. It is also generally observed that lower blood velocity causes a higher differential increase in plaque deposition in the vessel over the years; the highest blood velocity of 45 cm/s studied produced the least amount of plaque deposition over the period. Figure 4 buttresses the initial study of Figure 3 that higher inlet velocities correspond to lower plaque growth, so also the plaque is observed to grow at a decreasing rate over the years; this is in line with the study of Stone et al. (1993)³⁴ which showed that higher degrees of stenosis retards the rate of growth. The velocity at the neck of the stenosis is much higher compared to other parts, as indicated in the velocity band plots. This observation aligns with the earlier statement that higher velocities around the plaque do not favor plaque progression.^33,35 A maximum differential plaque increase of 0.17 mm was recorded for an inlet velocity of 30 cm/s after the time-2 (604 days), and a minimum differential plaque height increase of 0.1 mm was observed for a velocity of 45 cm/s after the second year (608 days).

Figure 4. The effect of blood flow on plaque height for every 304 days in 5 years.

The plaque height is steadily higher for lower blood flow velocity over the period investigated.

Figure 5 shows how the overall plaque height increases with time, causing more obstruction of the blood vessel termed “stenosis,” which is measured as the amount of the arterial lumen domain (measured as a function of diameter) the plaque has blocked. Initially, at the initiation of the plaque, there is a sharp increase in plaque height from 0 mm to around 1.0 mm (Figure 9) for all cases of inlet velocity; this is a result of the associated low WSS effect on the initiation of plaque; However, as the plaque continued to develop, as a result of diminishing differential plaque deposit (as indicated by the plaque progression curve getting dampened), the changes in height became significantly less compared to the initiation stage. After about five years, the carotid vessel that was exposed to the 30 cm/s blood velocity had the highest degree of stenosis of about 30% (Figure 10), as indicated by the overall plaque height of 1.78 mm, and the artery exposed to the 45 cm/s inlet velocity experienced the least plaque height of 1.32 mm equivalent to a stenosis degree of 22% (Figure 11). These values may not seem significant at this early stage. Still, as indicated by the curve trend, the plaque height of the 30 cm/s and 45 cm/s inlet velocities, the divergence between the two curves seems to widen as time elapsed (in this case, after each geometric update); this indicates that after a long period in time, the significance of overall plaque height would be too massive to overlook (Figures 10 and 11).

Figure 5. After 5 years (for every 304 days), the plaque height increased steadily but highest plaque peaks were observed at the lowest blood velocity of 30 m/s.

Severity of stenosis versus WSS and PWS distribution

From Figure 6, it can be observed that, on a general note, the peak WSS values are localized at the peak of the plaque. This observation is in tandem with that made by Razavi et al. (2011)²² in the study of the inlet velocity cycle in the carotid artery. It can also be observed that WSS values are relatively lower and flattened before and after the region of the plaque location. As indicated in Figures 8 to 11, velocity contour plots indicate that areas of high velocity are localized just above the stenosis neck (peak), which could have been responsible for high WSS values around that region of plaque growth. This corroborates the fact that high wall stress is caused by high flow velocity. A high difference of about 500 dyne/cm² was observed between the far-developed stenosis of 80% and initial stenosis of 17%. Since high WSS values tend to retard plaque growth, this study gives a better insight into how high WSS values can go, depending on the level of stenosis and the probability or magnitude of plaque growth associated with these values. Taking a closer look at how WSS is distributed around the plaque, it can be seen that the lower region of the plaque tends to grow at a faster rate from lower WSS regions compared to the neck of the plaque.

Figure 6. The distribution of the wall shear stress (WSS) at 30m/s inlet blood velocity.

Figure 7 shows that the plaque height (measured in terms of the degree of stenosis) plays a significant role in PWS and its distribution around the plaque and the entire arterial wall. The higher the degree of stenosis, the more influential the PWS; 80% stenosis plaque neck experienced the maximum tensile stress of 0.3 kPa, while the initiation stage plaque neck experienced the minimum tensile stress of 0.09 kPa. Taking a holistic look at Figure 7 concerning Figures 8–11, higher plaque heights experience higher velocity distribution around the plaque, causing a higher force associated with blood flow around the plaque, resulting in higher compression stress. From the growth perspective, higher tensile stresses lead to a lower growth rate of the plaque and higher compression stresses lead to faster growth rates as indicated by the growth model in equation 1, this automatically implies that since higher plaque heights lead to higher tensile stresses around the plaque, hence, lower growths rates would be observed. However, as the plaque geometry increases in size, more compressional stresses are localized around the root, which would encourage growth as well as possible rupture at higher velocities. The PWS shock wave seen in Figure 7 at the region of arterial length 4 and 6 mm for 17.3% stenosis and 2 and 8 mm for 50% stenosis, could be a result of reflective backflow caused by the plaque obstruction.

Figure 7. The plaque wall stress (PWS) distribution at 30 m/s inlet blood velocity.

Figure 8. Velocity contour plot for a plaque-free artery at 30 m/s inlet blood velocity.

Figure 9. Velocity contour plot for at the plaque institution stage (17% stenosis) at 30 m/s inlet blood velocity.

At the plaque initiation stage, there is a sharp increase in plaque height from 0mm to 1.0 mm.

Figure 10. Velocity contour plot for 50 stenosis cycles at 30m/s inlet blood velocity.

Simulation for 5 years gives a 30% stenosed carotid artery at a blood velocity of 30 m/s.

Figure 11. Velocity contour plot for 50 stenosis cycles at 30m/s inlet blood velocity.

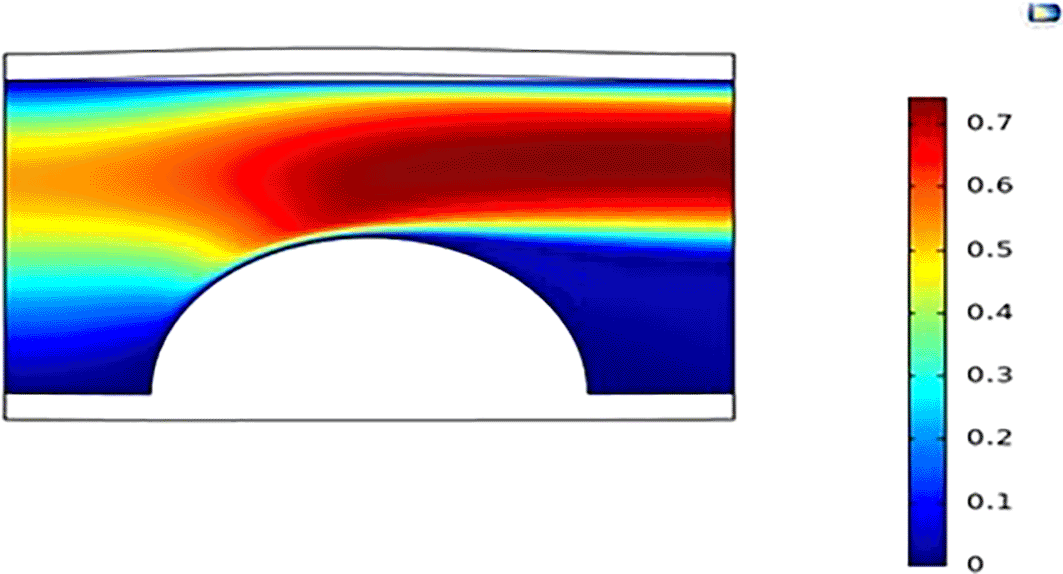
Simulation for 5 years gives a 22% stenosed carotid artery at a blood velocity of 45 m/s.

Figure 12. Wall shear stress (WSS) distribution at 80% stenosis.

WSS is seen to increase with plaque height.

Figure 13. PWS distribution at 80% stenosis.

It can be observed that blood velocity constitutes more force within the plaque as the plaque tends to resist the flow.

Inlet velocity and WSS and PWS distribution

Figure 12, shows the WSS distribution in the carotid artery model at plaque heights of 4.8 mm representing 80% of stenosis in the artery. Studies have shown that at this degree of stenosis, the plaque is usually in a very vulnerable state of rupture.³⁴ This study gives insight into the WSS and PWS distribution at the stage of plaque development, insights for further growth of plaque would also be drawn. It can be observed that WSS values are generally extremely high with 125 cm/s inlet blood velocity showing the highest WSS of about 2800 Dyne/cm² and 30 cm/s inlet velocity showing the lowest WSS value of about 500 Dyne/cm². The implication for these high WSS values is that; WSS-associated growth would be unlikely around this region, WSS WSS-associated plaque growth is more likely at lower shear stress values below 400 Dyne/cm².^12,30

As earlier seen in Figure 7, which shows how PWS increases as stenosis height increases, Figure 13 also exhibits these characteristics between inlet blood velocity and the PWS. It can be conveniently inferred that blood velocity constitutes more force within the plaque as the plaque tends to resist the flow. At this 80% degree stenosis, the maximum tensile stress was experienced at the neck of the plaque with the value of about 4 kPa for a velocity inlet of 125 cm/s. This plot gives a revelation that at the root of the stenosis at vessel length 1 mm to about 4 mm for 125 cm/s to 30 cm/s respectively, relatively high compressive force is observed for 125 cm/s inlet velocity with the value of -10 kPa. This gives an insight as to how this compressive force could cause a possible rupture of the plaque at the root and also how blood flow with higher velocities in fully-developed plaques has a higher probability of rupture, hence leading to stroke. The maximum compressive PWS was higher than the maximum tensile PWS.