Intestelligence: A pharmacological neural network using intestine data

Animal ethics

The intestinal tissues used in this study were surplus samples in a university student practical course that would otherwise have been discarded. Specifically, retired male breeder guinea pigs weighing 300–400 g (n = 14; SLC, Shizuoka, Japan) were used in our experiments. Consequently, the sample size was dictated by the enrollment of students in the course. The animals were housed in a temperature-controlled room (22 ± 1°C) with a 12-hour light-dark cycle (light from 07:00 to 19:00) and given ad libitum access to food and water. All animal experiments were performed with the approval of the Animal Experiment Ethics Committee of the University of Tokyo (approval number: P24-1) and in accordance with the University of Tokyo guidelines for the care and use of laboratory animals. Our experimental protocols adhered to the Fundamental Guidelines for Proper Conduct of Animal Experiments and Related Activities in Academic Research Institutions (Ministry of Education, Culture, Sports, Science and Technology, Notice No. 71 of 2006), the Standards for Breeding and Housing of and Pain Alleviation for Experimental Animals (Ministry of the Environment, Notice No. 88 of 2006), and the Guidelines on the Method of Animal Disposal (Prime Minister’s Office, Notice No. 40 of 1995). The primary outcome measure was the variation in ileum tissue length when subjected to different concentrations of acetylcholine (ACh) in a controlled bath setting. Animal identifiers were not identifiable to data analysts. All efforts were made to ameliorate the suffering of animals. Euthanasia methods involved intraperitoneal injection of sodium pentobarbital at a lethal dose of 100 mg/kg body weight to ensure a humane termination of life. Additionally, pre-established criteria for euthanizing animals displaying severe distress or declining health included indicators such as unexplained weight loss of over 20%, labored breathing, and other signs of suffering; however, none of the animals met these criteria. At the conclusion of the educational pharmacology course, all surviving animals were humanely euthanized, adhering to the same ethical standards, and were not used for subsequent experiments or educational activities.

Drugs

Acetylcholine chloride (C₇H₁₆ClNO₂; Wako, Japan) was dissolved in double distilled water at concentrations of 2×10⁻⁷, 2×10⁻⁶, 2×10⁻⁵, 2×10⁻⁴, 2×10⁻³, 2×10⁻², and 2×10⁻² M.

Intestinal contraction data acquisition

To isolate ileum tissue, guinea pigs were deeply anesthetized with 100 mg/kg pentobarbital (i.p.). The chest was opened, and the ileum was removed and washed with nutrient solution (in mM: NaCl 137, KCl 2.7, NaHCO₃ 11.9, CaCl₂ 1.8, MgCl₂ 1.0, D-glucose 5.5) that was bubbled with 5% CO₂/95% O₂. The tissue was cut to a length of approximately 3 cm, and mesenteric arteries were removed. Two hooks were used to mount the tissue; one hook was inserted at one end of the tissue and fixed to the tip of an aeration tube, while the other was connected to an isotonic displacement transducer (45347, NEC San-ei Instrument, Tokyo, Japan). The transducer was connected to an amplifier (AS1202, NEC San-ei Instruments) and a flatbed recorder (FBR-251A, TOA Electronics, Tokyo, Japan), which was used to record the ileum tissue responses (Figure 1A). Before starting the experiments, the ileum tissue strips were equilibrated, and a stable baseline recording was obtained at a resting tension of 0.5 g. Acetylcholine (ACh) solutions were then sequentially bath-applied to the organ bath at the following concentrations (in M): 1×10⁻⁹, 3×10⁻⁹, 1×10⁻⁸, 3×10⁻⁸, 1×10⁻⁷, 3×10⁻⁷, 1×10⁻⁶, 3×10⁻⁶, 1×10⁻⁵, 3×10⁻⁵, 1×10⁻⁴, 3×10⁻⁴, 1×10⁻³, and 3×10⁻³. Bath application was performed when a local maximum of the contraction reaction at the previous ACh concentration was confirmed. The ACh concentration [M] and intestine length [cm] were recorded, and these steps were repeated 2–3 times. The intestinal contraction rate [%] was calculated by averaging the contraction lengths over different trials and dividing the mean values by the maximum value. We collected the data for the dose–response curves from 512 ileum samples.

Sigmoid-curve fitting for the intestine contraction data at different acetylcholine concentrations

For each of the 512 data pairs, the ACh concentration was natural-log-transformed:

Thus, ${\overline{\mathrm{\beta }}}_0$ = ${\overline{\mathrm{\alpha }}}_0$ and ${\overline{\mathrm{\beta }}}_1$ = 0 (Figure 1C).

The mean square error (MSE) between the fitted sigmoid curve and the corresponding sample was calculated. Samples that fell outside the range of the mean ± 3 standard deviations (SDs) in the |${\mathrm{\beta }}_{0_{\mathrm{i}}}$|, |${\mathrm{\beta }}_{1_{\mathrm{i}}}$|, or MSE value for the i^th intestine sample were excluded from further analyses, leaving 503 intestine samples. It is important to emphasize that these criteria were not predetermined.

Forward passes of neural networks

The three-layer perceptron (control) and INN model had the same structure except for their activation functions. The common structure is written as follows:

$\mathbf{x}\in {ℝ}^{{\mathrm{D}}_{\mathrm{x}}}$: input vector (${\mathrm{D}}_{\mathrm{x}}$: dimension of the input vector)

${\mathrm{w}}_{\mathrm{ji}}^{\left(\mathrm{h}\right)}$: the weight between the i^th unit in the input layer and the j^th unit in the hidden layer (j = 1, 2, …, 100)

${\mathrm{b}}_{\mathrm{j}0}^{\left(\mathrm{h}\right)}$: 1, the bias of the j^th unit in the hidden layer

${\mathrm{\phi }}_{\mathrm{j}}^{\left(\mathrm{h}\right)}(·)$: the activation function of the j^th unit in the hidden layer

${\mathrm{w}}_{\mathrm{kj}}^{\left(\mathrm{h}\right)}$: the weight between the j^th unit in the hidden layer and the k^th unit in the output layer (k = 1, 2, …, ${\mathrm{D}}_{\mathrm{y}};{\mathrm{D}}_{\mathrm{y}}$ is dimension of the output vector)

${\mathrm{b}}_{\mathrm{k}0}^{\left(\mathrm{h}\right)}$: 1, the bias of the k^th unit in the hidden layer

${\mathrm{\phi }}_{\mathrm{k}}^{\left(\mathrm{o}\right)}(·)$: the activation function of the k^th unit in the output layer

$\widehat{\mathbf{y}}\in {ℝ}^{{\mathrm{D}}_{\mathrm{y}}}$: output vector.

On the other hand, the activation functions of the INN model, ${\mathrm{\phi }}_{\mathrm{j}}^{\left(\mathrm{h}\right)}\left({\mathrm{a}}_{\mathrm{j}}\right)$and ${\mathrm{\phi }}_{\mathrm{k}}^{\left(\mathrm{o}\right)}\left({\mathrm{a}}_{\mathrm{k}}\right)$, included two random variables ${\mathrm{B}}_0$and ${\mathrm{B}}_1$as parameters:

Note that Eq. 13 and Eq. 14 are identical when (${\mathrm{B}}_0$, ${\mathrm{B}}_1$) = (1, 0). For each INN activation function, namely, ${\mathrm{\phi }}_{\mathrm{j}\_\mathrm{INN}}^{\left(\mathrm{h}\right)}(·)$ (j = 1, 2, …, $100$) and ${\mathrm{\phi }}_{\mathrm{k}\_\mathrm{INN}}^{\left(\mathrm{o}\right)}(·)$ (k = 1, 2, …, ${\mathrm{D}}_{\mathrm{y}}$), the random variables $({\mathrm{B}}_{0,\mathrm{j}}$, ${\mathrm{B}}_{1,\mathrm{j}}$) and $({\mathrm{B}}_{0,\mathrm{k}}$, ${\mathrm{B}}_{1,\mathrm{k}}$) were sampled from 503 sets of experimentally obtained parameters {(${\mathrm{\beta }}_{0\_1},{\mathrm{\beta }}_{1\_1}$), (${\mathrm{\beta }}_{0\_2},{\mathrm{\beta }}_{1\_2}$), …, (${\mathrm{\beta }}_{0\_503},{\mathrm{\beta }}_{1\_503}$)} (Eqs. 1–6). The source code for the three-layer perceptron and INN is available on our GitHub repository: https://github.com/ywatanabe1989/intestelligence.

Cost function

The cross-entropy loss was adopted as the cost function, which was calculated as follows:

Backpropagation

The backpropagation method (Rumelhart et al., 1986) was adopted to efficiently calculate the gradient of the cost function, $\nabla {\mathrm{J}}_{\mathrm{m}}\left(\mathbf{\theta }\right)$.

The following notation was introduced:

According to Eq. 10, we have

Substituting Eqs. 17 and 20 into Eq. 16, we obtain

For the $\mathrm{\delta }$s of the hidden units, the chain rule for partial derivatives is applied to obtain:

By substituting Eq. 17 into Eq. 22 and using Eqs. 9 and 10, the following backpropagation formula is obtained:

Thus, the gradient of the cost function $\nabla {\mathrm{J}}_{\mathrm{m}}\left(\mathbf{\theta }\right)$ can be calculated using the backpropagation method.

Weight update

The model was trained using the stochastic gradient descent (SGD) algorithm.

If the error function consists of a sum over data points, $\mathrm{J}\left(\mathbf{\theta }\right)={\sum }_{\mathrm{n}}{\mathrm{J}}_{\mathrm{n}}\left(\mathbf{\theta }\right)$, after the presentation of pattern n, the SGD algorithm updates the parameter vector $\mathbf{\theta }$ using the following formula:

Here, τ denotes the iteration number, and η is the learning rate parameter.

Classification of handwritten digits

The MNIST database of handwritten digits (LeCun et al., 1998) was used for the experiments in this study. The control and INN models were trained based on 60,000 training data points and evaluated based on 10,000 test data points. Each image was 784 pixels (= 28 columns×28 rows), and the images were fed into models after being flattened into a vector. The mini-batch size was set to 100, and the learning rate was set to 0.05.

Simulations of INNs

The INN models were simulated by sampling the fitting parameters ${\mathrm{\beta }}_0$ and ${\mathrm{\beta }}_1$. Dummy fitting parameters ${\mathrm{\beta }}_{\text{dummy}}$ = (${\mathrm{\beta }}_{0\_\text{dummy}}$, ${\mathrm{\beta }}_{1\_\text{dummy}}$)^T were sampled from a bimodal Gaussian distribution, as described below.

When the slope at the inflection point $\left({(\frac{{\mathrm{\beta }}_{1\_\text{dummy}}}{{\mathrm{\beta }}_{0\_\text{dummy}}},\frac{1}{2})}^{\mathrm{T}}\right)$ of the simulated sigmoid function $(\text{slope:}-\frac{{\mathrm{\beta }}_{0\_\text{dummy}}}{4})$ was negative (${\mathrm{\beta }}_{0\_\text{dummy}}$ > 0), ${\mathbf{\beta }}_{\mathbf{\text{dummy}}}$ was resampled. A total of 140 (= 8 × 15) experiments were performed.

Classification of edible/inedible images

A total of 1,200 images of edible objects and 1,200 images of inedible objects were randomly sampled from https://www.sozaijiten.com. Then, 1,000 images from each class (edible/inedible) were used as training data, and the remaining 200 images from each class were used as test data.

The edible images included images of cooked meals and raw foods such as fruits, vegetables, and fish. The inedible images included images of tools, parts, coins, and other objects.

The images were converted into feature vectors using a pretrained convolutional neural network model (AlexNet; Krizhevsky et al., 2012) based on the Caffe deep learning framework (Jia et al., 2014). Specifically, for every input image, the output of the activation of the fc6 layer (4,096-dimension vector) was extracted.

These feature vectors were fed into the INN model instead of the original images to perform the 2-class classification task. The model consists of three layers: an input layer, a hidden layer, and an output layer. The input layer contains 4,097 nodes, including a bias unit. The hidden layer has 101 nodes, also inclusive of a bias unit. The output layer consists of 2 nodes corresponding to two classes: edible or inedible. The learning rate was set to 0.6.

Statistical methods

To compare classification accuracies of INN and Control, we employed the Mann-Whitney U test due to the absence of any specific parametric hypotheses. The test was conducted using the Python package SciPy (https://scipy.org/). The rank-biserial correlation was used as the effect size measure.

Ileal sample contraction during acetylcholine bath application

After different concentrations of Ach were sequentially applied, the lengths of the isolated ileum tissues decreased. We used an experimental device to measure the isotonic contraction of the intestinal tract (Figure 1A) and recorded the dose–response curves of the ilea during bath application of ACh at concentrations ranging from 10⁻⁹ to 10⁻³ M (Figure 1B, n = 512 tissues from 14 guinea pigs). Each dose–response curve was obtained from a single tissue and was normalized and fitted to a sigmoid function (Figure 1C) using two fitting parameters, ${\mathrm{\beta }}_0$ and ${\mathrm{\beta }}_1$ (Eqs. 1–6). The MSE between the experimentally recorded data and the fitted sigmoid curve was calculated for all 512 samples. Data samples for which the |${\mathrm{\beta }}_0$|, |${\mathrm{\beta }}_1$| or MSE values exceeded the mean ± 3SD were omitted from the following analysis, and the remaining 503 data points were used to construct the INN model. The distributions of ${\mathrm{\beta }}_0$ and ${\mathrm{\beta }}_1$ are plotted in Figure 1D and 1E. For ${\mathrm{\beta }}_0$, the sample mean $\overline{{\mathrm{\beta }}_0}$ was 3.06, and the sample variance ${{\mathrm{s}}^2}_{{\mathrm{\beta }}_0}$ was 1.38; for ${\mathrm{\beta }}_1$, the sample mean $\overline{{\mathrm{\beta }}_1}$ was 0.00 (due to the adjustment), and the sample variance ${{\mathrm{s}}^2}_{{\mathrm{\beta }}_1}$ was 3.23).

Figure 1. Dose–response curves of ACh-induced contractions of the ileum.

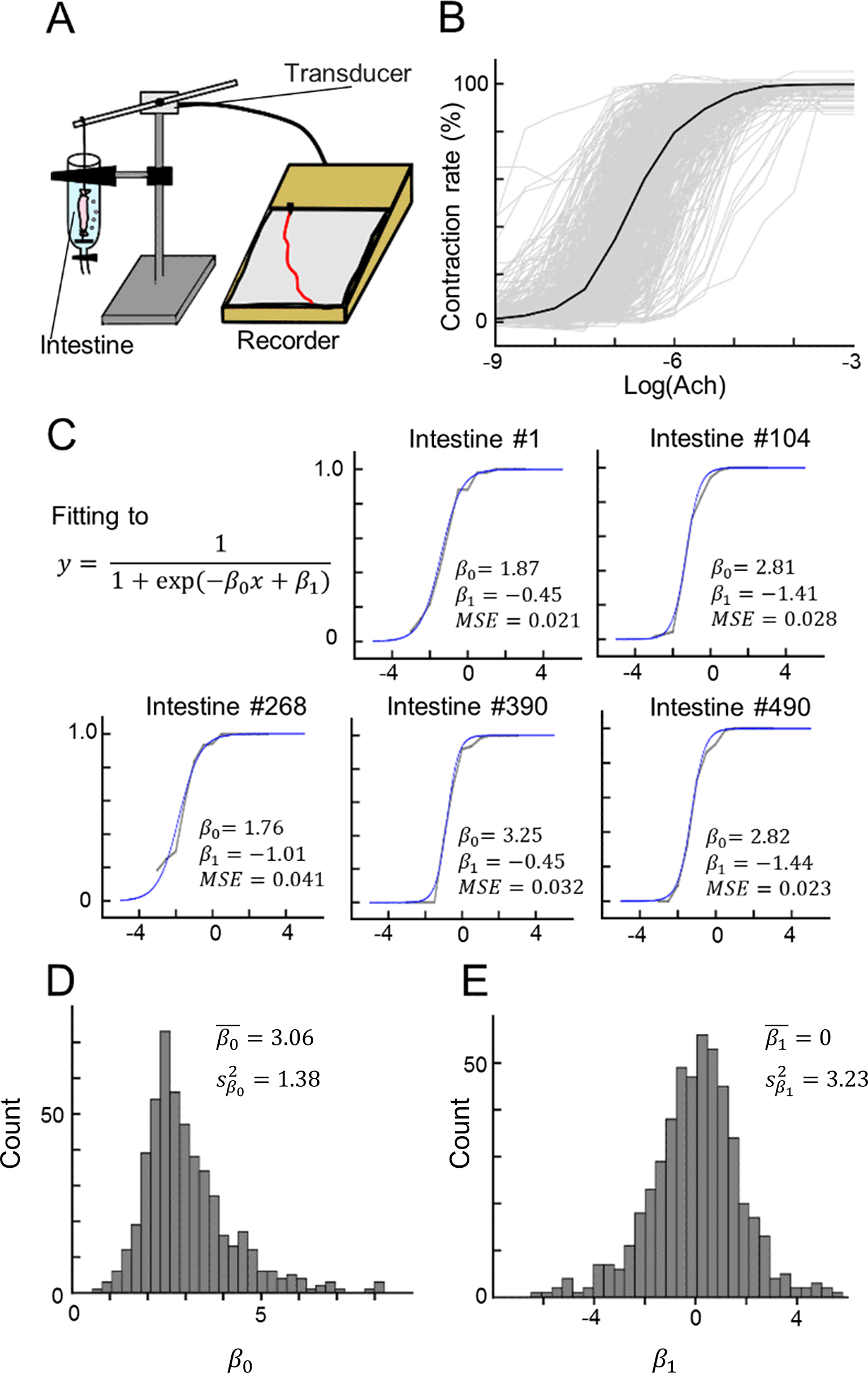
(A) Illustration of our experimental devices for measuring ileum contraction.

(B) The dose–response curves of 512 data points for contractions in response to bath application of ACh. Each gray line indicates a single data point, whereas the black line indicates the mean.

(C) Five examples of sigmoid fitting of the dose–response curves of ACh-induced ileum contraction. Note that ${\mathrm{\beta }}_0$ and ${\mathrm{\beta }}_1$ are fitting parameters.

(D, E) Distributions of the fitting parameters ${\mathrm{\beta }}_0$ (D) and ${\mathrm{\beta }}_1$ (E).

Classification of handwritten digits by the INN model

We constructed a three-layer perceptron (Control) and an INN, both with the same structure as illustrated in Figure 2A. These models were used for a 10-class classification task using handwritten digits from the MNIST database (LeCun et al., 1998). During 6,000 rounds of training, the cost of the Control model was lower than that of the INN model (Figure 2B; at Loop #6,000, Control: 0.558 ± 0.097; INN: 0.923 ± 0.188; p < 0.001; ns = 40; U = 1,556; Mann–Whitney U test; the rank-biserial correlation = - 0.945). Both models converged, but the sum of the absolute weight update of the Control model was lower than that of the INN model (Figure 2C; at Loop #6,000, Control: 1.83 ± 0.86; INN: 2.58 ± 0.94; p < 0.001; ns = 40; U = 1,182; Mann–Whitney U test; the rank-biserial correlation = - 0.478). The accuracy of the Control model was higher than that of the INN model (Figure 2D; at Loop #6,000, Control: 92.3 ± 0.4; INN: 85.7 ± 0.6; Chance: 10%; p < 0.001; ns = 40; U = 0; Mann–Whitney U test; the rank-biserial correlation = 1.000).

Figure 2. Handwritten number identification using the INN model.

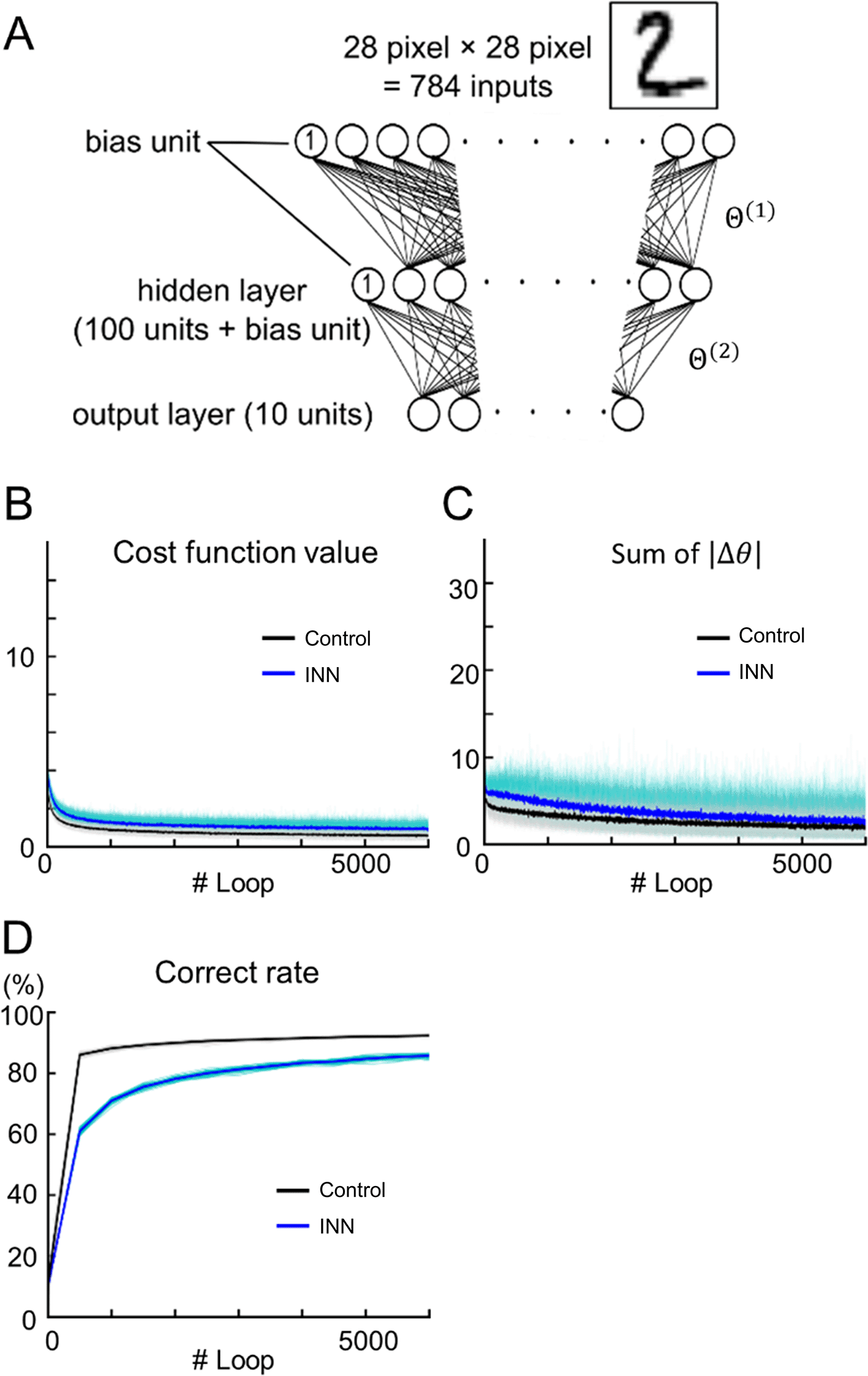
(A) A schematic diagram of the three-layer INN model. A conventional perceptron with the same structure was used as the control.

(B–D) Output values of test data during training. B, cost function; C, sum of the absolute weight updates; D, classification accuracy. The blue and black lines represent the INN and control model results, respectively. Each line indicates a single data point (n = 32 tuning trials), whereas the thick line indicates the mean.

We also observed the sample variance in the fitting parameters ${\mathrm{\beta }}_0$ and ${\mathrm{\beta }}_1$ (Figure 1D and 1E). These fluctuations might originate from (i) biological noise and (ii) differences in the experimental conditions. We hypothesized that the variations in ${\mathrm{\beta }}_0$ and ${\mathrm{\beta }}_1$ (${{\mathrm{\sigma }}^2}_{{\mathrm{\beta }}_0}$, ${{\mathrm{\sigma }}^2}_{{\mathrm{\beta }}_0}$) affect the classification accuracy of the model based on the MNIST dataset. To test this hypothesis, we simulated INNs using various values of ${{\mathrm{\sigma }}^2}_{{\mathrm{\beta }}_0}$ and ${{\mathrm{\sigma }}^2}_{{\mathrm{\beta }}_0}$. Figure 3 shows the accuracies of the virtually generated INNs in a pseudocolor map. The highest mean accuracy was 92.3% ± 0.3% for ${{\mathrm{\sigma }}^2}_{{\mathrm{\beta }}_0}$ = 0.0 and ${{\mathrm{\sigma }}^2}_{{\mathrm{\beta }}_1}$ = 0.0, and the lowest mean accuracy was 57.3% ± 5.5% for ${{\mathrm{\sigma }}^2}_{{\mathrm{\beta }}_0}$ = 3.0 and ${{\mathrm{\sigma }}^2}_{{\mathrm{\beta }}_1}$ = 50.

Figure 3. Relationship between INN performance in number identification tasks and parameter variation.

Accuracies of INNs as a function of the variance in the hyperparameters ${\mathrm{\beta }}_0$ and ${\mathrm{\beta }}_1$ (${{\mathrm{\sigma }}^2}_{{\mathrm{\beta }}_0}$ and ${{\mathrm{\sigma }}^2}_{{\mathrm{\beta }}_0}$). The experimentally obtained sample variance (${{\mathrm{s}}^2}_{{\mathrm{\beta }}_0}$ = 1.38; ${{\mathrm{s}}^2}_{{\mathrm{\beta }}_1}$ = 3.23) is indicated by the black dot.

Edible/inedible image classification by the INN model

A total of 1,200 images of edible and inedible objects were randomly chosen from the dataset and split into training/test datasets at a ratio of 5:1 (Figure 4A). The accuracies of the model based on the test data were evaluated during training. At loop #6,000, the accuracy was 88.5% ± 0.9% (Figure 4; n = 32 cross-validations).

Figure 4. Image classification using the INN model.

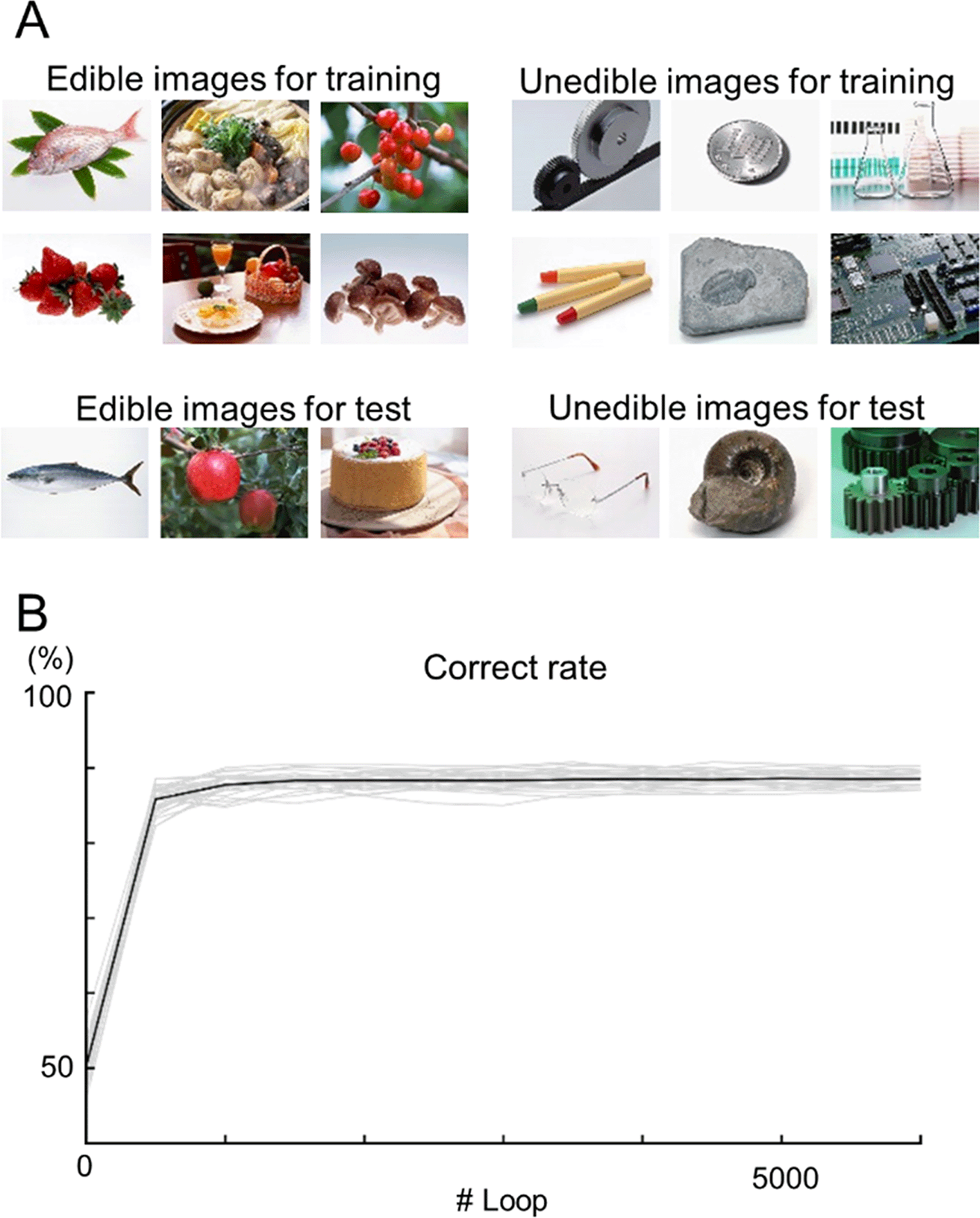
(A) Examples of edible (left) and inedible (right) images in the dataset. The top images were used for training, and the bottom images were used for testing. (B) The learning curves of the INN prediction results for the test data. Each gray line indicates a single data point (n = 32 cross-validation), whereas the black line indicates the mean.