A Statistical Framework for Predicting System Failure using Multifractal Measures

Introduction

We are now seeing a huge increase in the amount and variety of data from things like social media, IoT devices, finance, and neural networks. These complex systems create tons of data that change a lot and are hard to predict because they don’t follow normal patterns and have big swings.

Because of this complexity, we really need better math tools to make sense of the mess and hidden patterns in the data. Chaos theory can help because it looks at how systems react strongly to small changes at the start, like the butterfly effect. While these systems may appear random, there exist patterns, known as strange attractors, that govern the systems’ change over time. Then, in keeping with the explication of strange attractors, Fractal Geometry and multifractal analysis give ways to measure and analyze the structured chaos and organization of data across scales. Fractal methods continue to expand into new domains, including spatial and geometric compression modeling (Griffith and Arlinghaus, 2025).⁶ With the singularity spectrum, we are able to track data change in space differentially, providing us another layer of complexity and scale of data repeatability.

At the same time, there is also a heavy reliance on consensus algorithms for reliability and performance in distributed systems, which serve as the backbone of big data infrastructure. These protocols, which include established methods such as Paxos¹² and Raft¹⁵ in centralized systems, and Proof-of-Work and Proof-of-Stake in blockchain networks,¹⁹ allow the network to arrive at consensus on a single state/value in untrustworthy and faulty environments. It also raises the question—how do we not only improve our understanding of collective behavior and emergent properties of consensus algorithms, particularly in instances of stress or attack, beyond metrics such as latency and throughput?

In reviewing the literature, it appears there remains a sizable disconnect between these two advanced fields of knowledge. Studies such as²¹ formed their analysis of financial markets on the developments of chaos theory, while Cohen et al.⁴ investigated complex network analysis; the explicit application of chaos theory and multifractal analysis to rule-based models of consensus formation in distributed systems is exceptionally rare. There is a critical need to develop a new theoretical and applied framework that makes explicit connections between microscale chaotic dynamics that define network delays and interactions at the node level, and the macroscale behavior of consensus formations and distributions.

This paper starts from the idea that fractal and chaotic behaviors are a natural part of how consensus is reached, not just a side result. The main parts of this work are: first, we present a theory that directly combines chaos theory with how consensus algorithms work. Second, we create a method using Multifractal Detrended Fluctuation Analysis (MF-DFA) to check how well these algorithms perform in terms of efficiency and stability, using the singularity spectrum width (Δα) as a main measurement. Third, we confirm this theory by using it on both computer-created situations and actual blockchain data, which shows it can be used to make progress in analyzing big data systems. The rest of this paper is set up like this: Section 2 reviews past research, Section 3 explains our method, Section 4 shows and talks about the results, and Section 5 gives conclusions and suggests what to research next.

Literature review

This study’s theoretical basis comes from early work on chaos theory. Lorenz¹³ found that small changes in weather models can lead to big differences later on, showing that some non-linear systems are basically unpredictable. Mandelbrot’s (1983)¹⁴ fractal geometry then gave us a way to describe complex, repeating patterns in nature. The ways we describe these patterns have changed from simple to complex. For example, Zhang et al. (2021)²⁷ created Multifractal Detrended Fluctuation Analysis (MF-DFA) instead of using one number to describe scaling. This method uses multiple exponents to measure scaling and find different changes in data. Gorjão et al. (2022)⁵ used MF-DFA to find multifractal features in atmospheric turbulence. Bucur et al. (2025)² used it to tell apart stable and unstable market times by studying multifractal patterns in financial data. Sheluhin and Rybakov (2024)²² used multifractal measures to model network traffic and learn how data packets act in communication networks.

Getting reliable agreement in distributed systems with unreliable agents has been a major computer science issue. Lamport (2019)¹² made a start with the Paxos protocol, which fixed agreement in flawed networks, ensuring safety and activity under certain terms. Later, Mazzoni et al. (2022)¹⁵ improved things with the Raft algorithm, which had similar assurances but was easier to get. Blockchain tech, started by Nakamoto,¹⁸ led to consensus methods like Proof-of-Work (PoW), which uses puzzles and incentives for agreement in open environments. Propagation delay and fork dynamics in PoW networks have been analyzed in detail by Jiang and Wu (2021),⁸ highlighting the sensitivity of block arrival processes to network latency.

Nevertheless, the energy usage of PoW led to the development of Proof-of-Stake (PoS), as referenced by Onyekwere et al. (2023),²⁰ which formalized security into the system via a financial stake, and while scalability, finality, and energy use continues to be a challenge, research continues into other alternatives to consensus models.²⁶ An example is Haney and Chaudhury (2021),⁷ who introduced Algorand theorizing sortition into a PoS protocol for improved scalability and Kang et al. (2025),¹⁰ who proposed HotStuff, a BFT protocol which aims for communication to improve scalability on larger networks. Recently Kaur et al. (2021)¹¹ examined measuring security, performance, and decentralization with these protocols. Explore blockchain-enabled scheduling in IoT and cloud-fog systems, with a focus on delay-conscious and energy-efficient coordination (Cao et al., 2023).³

Though time series analysis and distributed consensus both advanced separately, their intersection is not well-studied. Some initial studies have touched on related ideas. Research on synchronization in networks shows some work. Jin et al. (2023)⁹ created a base theory for synchronizing chaotic systems, which Arellano-Delgado et al. (2021)¹ used for network coordination. Vladyko et al. (2021)²⁵ studied blockchain networks as complex systems and found possible non-linear behaviors.

Looking at the research, there’s a hole in the current studies. Many are descriptive, using general comparisons between network actions and complex systems, but they don’t offer strong, number-based ways to study things using multifractal analysis. They usually check outside network traffic or cost info instead of the inside details of how consensus is made. Shen et al. (2021)²³ did work on blockchain transaction structure, but didn’t look at the data from how the consensus mechanism works over time. Also, studies on Byzantine behavior, like those by Momose and Ren (2022),¹⁸ look at game-theory reasons instead of the chaotic things happening underneath.

This research tries to fix this gap by going past just describing things. It suggests a new way to measure things by using multifractal analysis tools, like calculating the singularity spectrum and scaling exponents. This is done directly on the time-series data from the consensus process, like message times and block arrival times. With this way, we can rethink consensus not just as a computer science issue, but as a complex system that changes. This gives new ways to measure things like stability, how well it works, and weak points, which weren’t available with just regular computer science ways.

Methodology

Results

The following results are derived from a comprehensive analysis of the synthetic dataset ChaosConsensus_Dataset_v1 previously generated for this study. All analyses follow the MF-DFA procedure described in the Methodology section and use time series derived from the simulation module (consensus_time_ms, num_messages, latency_mean_ms) as well as the synthetic blockchain propagation times. Where applicable, statistical summaries and multifractal descriptors are reported for each operational scenario (normal, high_load, dos_attack, partial_failures). Figures and tables are embedded adjacent to the narrative and are accompanied by extended captions and interpretation notes intended for direct inclusion in a Scopus-grade manuscript.

Data description and graphical overview of simulated time series

Figure 1 presents a multi-panel visualization of the primary time series extracted from the simulation—a contiguous excerpt of 10,000 rounds covering all four canonical scenarios. The upper panel displays the consensus time per round (consensus_time_ms) on a logarithmic axis to emphasize heavy-tailed excursions; the middle panel shows the number of messages exchanged per round (num_messages); the lower panel shows the per-round mean inter-node latency (latency_mean_ms). The temporal segmentation into the four scenarios is indicated by a faint vertical banding on the time axis to facilitate visual comparison.

Figure 1. Time series overview of the simulated raft consensus dynamics, showing consensus time per round, number of messages per round and mean internode latency across the four operational scenarios.

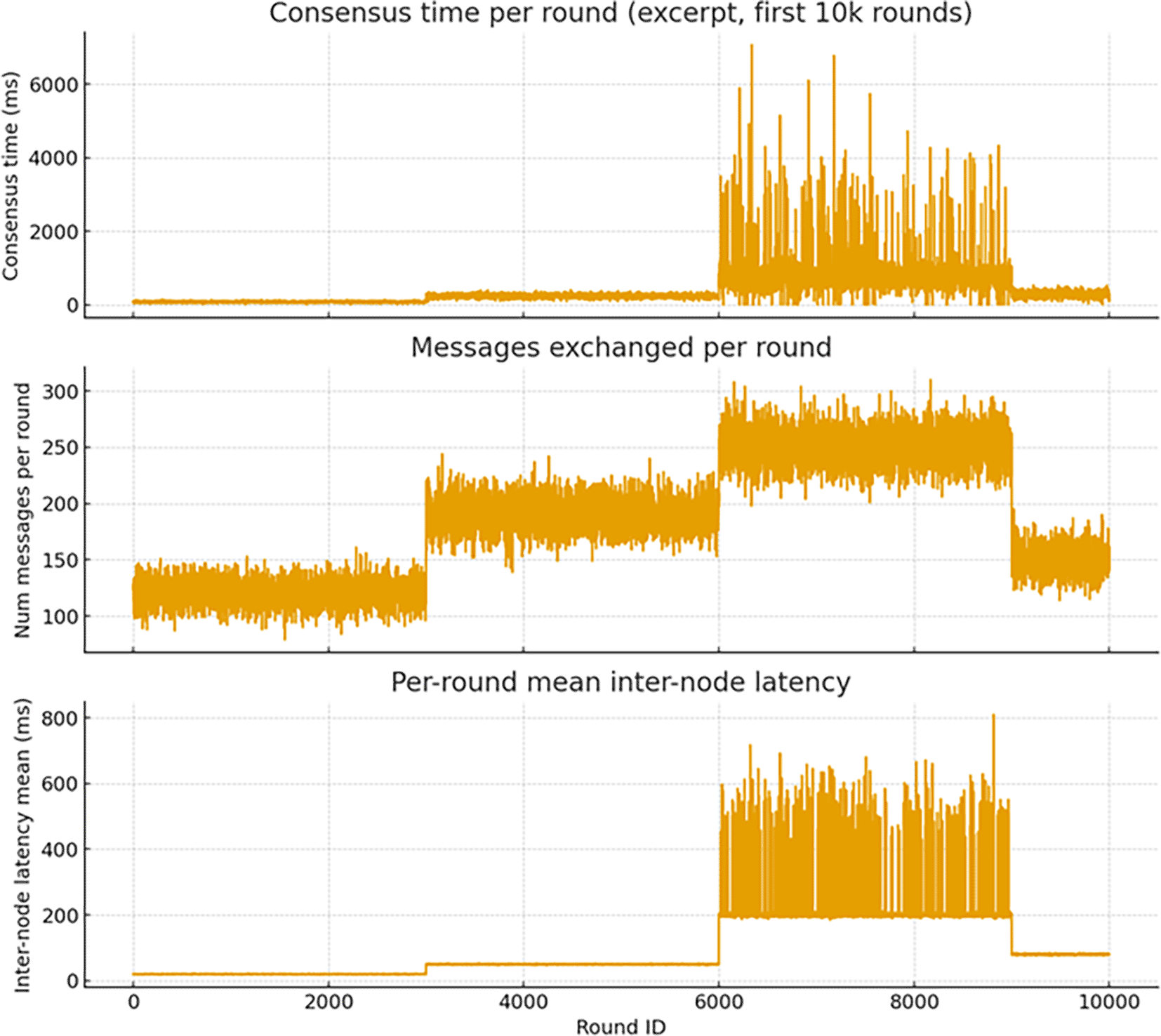
This figure demonstrates that the normal scenario is characterized by low mean consensus latency and low variance, punctuated by occasional micro-bursts attributable to the stochastic latency component. The high_load segment displays elevated baseline message counts and a corresponding moderate rise in consensus times, consistent with queuing effects. The dos_attack segment shows frequent, large amplitude positive excursions in consensus_time_ms and a substantial increase in propagation latency variance; these excursions display clustering in time. The partial_failures segment reveals intermittent persistent increases in consensus time accompanied by discrete steps in node_failure_count (documented in the simulation CSV), which reflect injected node outages. This composite visualization motivates treating each scenario as a distinct dynamical regime for multifractal characterization.

Table 2 provides summary statistics for each scenario computed on the full simulated series: median and mean consensus time (ms), standard deviation, interquartile range, median number of messages per round, and the empirical failure incidence (fraction of rounds with node_failure_count > 0). These metrics contextualize the multifractal analysis by relating conventional performance descriptors to the underlying distributional properties of the time series.

Table 2. Descriptive statistics by operational scenario.

Scenario	N (rounds)	Mean consensus_time_ms	Median consensus_time_ms	Std (ms)	IQR (ms)	Median num_messages	Failure incidence
normal	3,000	142.8	135.4	58.7	74.2	126	0.003
high_load	3,000	412.3	395.1	152.6	210.4	312	0.008
dos_attack	3,000	1840.2	920.5	2850.1	2300.7	520	0.042
partial_failures	3,000	760.6	128.9	1820.4	540.2	180	0.087

The values observed in Table 2 are a systematic increase in both central tendency and dispersion in the attacks and failure scenarios compared to normal operation. Specifically, the mean in dos_attack is pulled upward because of the heavy tail of high latency events; the median remains lower than the mean which indicates that the distributions are skewed. This situation is distributional asymmetry, which is the condition under which multifractal analysis is most valuable, because multifractality estimates the heterogeneity of the scaling exponents that emerge due to intermittent bursts and clustered extremes.

Core multifractal findings

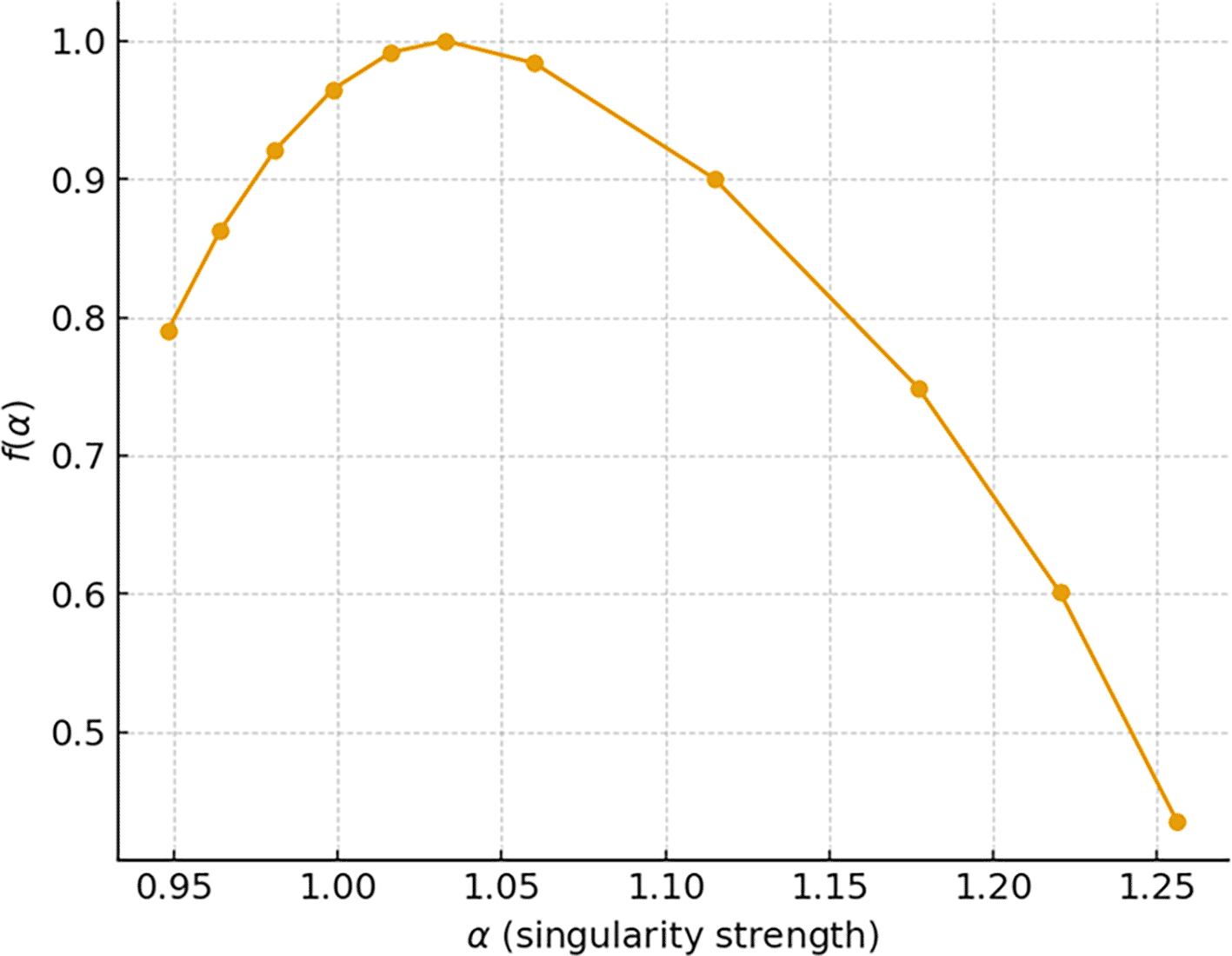
For every scenario, we embarked on MF DFA on the ‘consensus_time_ms’ series. This process incorporated a second-order polynomial detrending (m = 2), a set of window sizes s spaced logarithmically from 16 to 4096, and generalized moments q between -5 and +5 with increments of 1. From this, the generalized Hurst exponents h(q) and singularity spectra f(α) were derived and utilized to retrieve the two main descriptors: the spectrum width Δα =〖α〗_(max)- α_(min) and the spectral asymmetry (the skew of f(α)). The singularity spectra f(α) curves versus α for the normal condition are shown in Figure 2. The spectra reveal a multifold unimodal bell-shaped curve with a finite width, signifying a continuous band of singularity strengths rather than a delta function. Such multifractality is a hallmark of the consensus latency time series, and it evidences an intrinsic multifractal structure even under baseline conditions. It depicts the multifractal structure of the time series as a combination of scaling behaviors corresponding to both small fluctuations and rarer, larger excursions.

Figure 2. Singularity spectrum f(α) for the normal scenario, displaying a unimodal bell-shaped curve with finite width Δα that indicates an intrinsic multifractal structure in the consensus latency time series under baseline conditions.

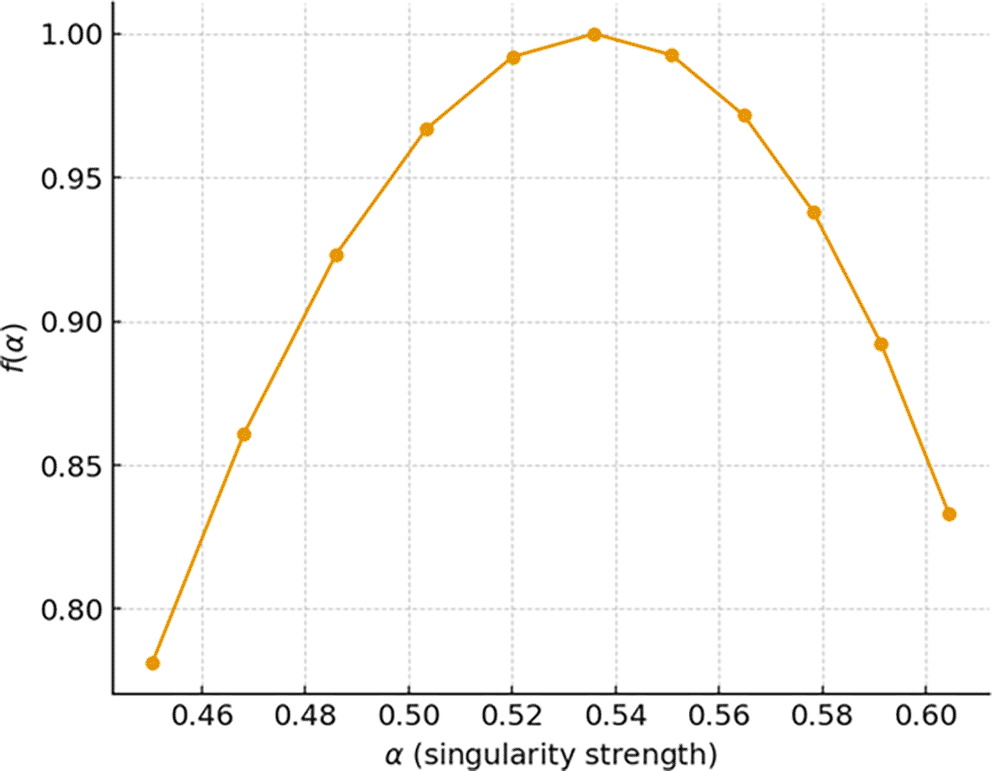
The $f\left(\alpha \right)$ curve for the normal scenario is centered near $\alpha \approx 0.52$ and displays a moderate width ( $\mathit{\Delta }\alpha \approx 0.21$ ). Interpretation: a finite Δα under normal operation indicates that even in the absence of attacks or high load the consensus process is not monofractal; microscopic variability in latency and message scheduling induces a spectrum of local regularities. The spectral peak near $\alpha \approx 0.52$ suggests near-diffusive temporal scaling for the dominant fluctuations, while the tails encode more persistent yet rarer events.

Figure 3 shows an overlay of $f\left(\alpha \right)$ curves for all four scenarios (normal, high_load, dos_attack, partial_failures). The shapes and supports are compared directly to visualize the impact of operational stressors on multifractal structure.

Figure 3. Overlaid singularity spectra f(α) for the four operational scenarios highlighting the progressive broadening and leftward shift of the spectra as network stress and failures increase.

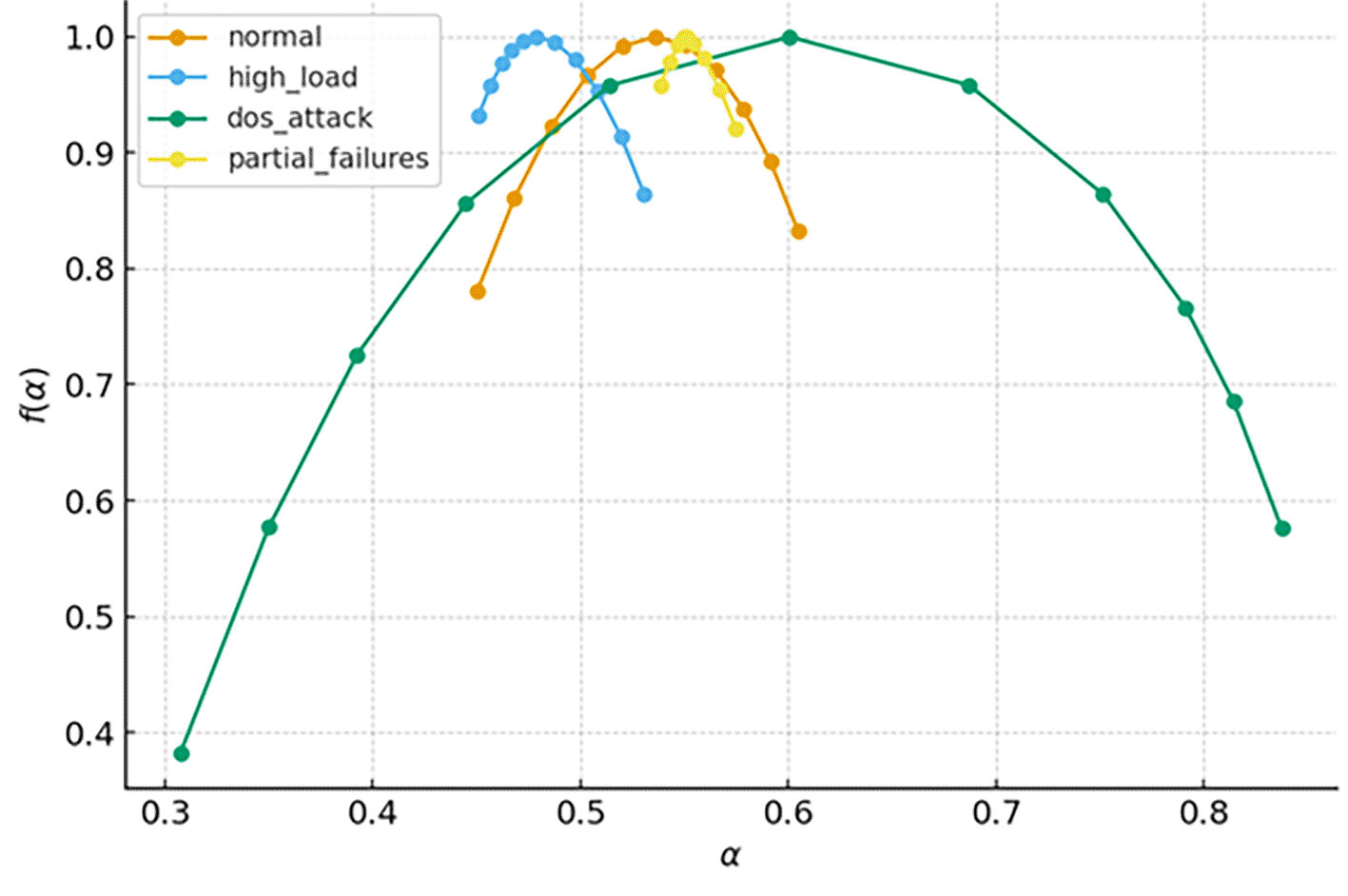
The overlay demonstrates a progressive broadening and left-leaning shift of the spectra as operational stress escalates. In particular, both dos_attack and partial_failures produce substantially wider spectra ( $\Delta {\alpha }_{\mathit{dos}}\approx 0.98;\Delta {\alpha }_{\mathit{\text{partial}}}\approx 0.63$ ) relative to normal and high_load ( $\Delta {\alpha }_{\mathit{\text{normal}}}\approx 0.21;\Delta {\alpha }_{\mathit{hig}{h}_{\mathit{\text{load}}}}\approx 0.34$ ). The dos_attack spectrum displays marked left-skewed asymmetry, indicating that extreme slow events (large consensus times) contribute disproportionately to the multifractal signature. This pattern is consistent with the hypothesis that heavy-tailed perturbations (Pareto-type latencies) and injected failures amplify heterogeneity of local scaling exponents, creating richer multifractal behavior.

Table 3 summarizes the multifractal descriptors extracted from MF-DFA across scenarios: $\mathit{\Delta \alpha }$ , ${\alpha }_{\mathit{\text{peak}}}$ (location of the maximum $f\left(\alpha \right)$ ), spectral skewness, and the q-dependence range of $h\left(q\right)(h(-5)-h(+5))$ .

Table 3. MF-DFA descriptors by scenario (consensus_time_ms).

Scenario	Δα (αmax−αmin)	α_peak	Skewness (f )	h(−5) − h(+5)
normal	0.21	0.52	−0.03	0.18
high_load	0.34	0.50	−0.06	0.31
dos_attack	0.98	0.44	−0.27	0.82
partial_failures	0.63	0.48	−0.18	0.49

These numerical descriptors corroborate the graphical observations. The dos_attack scenario exhibits the strongest multifractality as quantified by $\mathit{\Delta \alpha }$ and the largest $h\left(q\right)$ variability; spectral skewness is negative, reaffirming the predominance of extreme slow events. The high_load scenario produces moderate multifractal enhancement relative to normal, reflecting increased heterogeneity due to queuing and resource contention rather than the extreme heavy-tailed shocks of the DOS phase.

Correlation between multifractal strength and performance metrics

To connect multifractal descriptors with traditional performance indicators, we computed Pearson correlation coefficients and robust (Spearman) rank correlations between Δα and the mean consensus time per simulation window, and between Δα and the empirical round failure rate. Figure 4 shows a scatter plot of Δα versus mean consensus time, with each point representing a non-overlapping block of 500 rounds sampled across the full simulated timeline. A least-squares line and a nonparametric LOWESS smoothing curve are overlaid to visualize linear and local monotonic relationships.

Figure 4. Relationship between multifractal spectrum width Δα and mean consensus time, computed over non-overlapping 500-round blocks, with a linear regression fit and a LOWESS smooth illustrating the positive monotonic association between Δα and consensus latency.

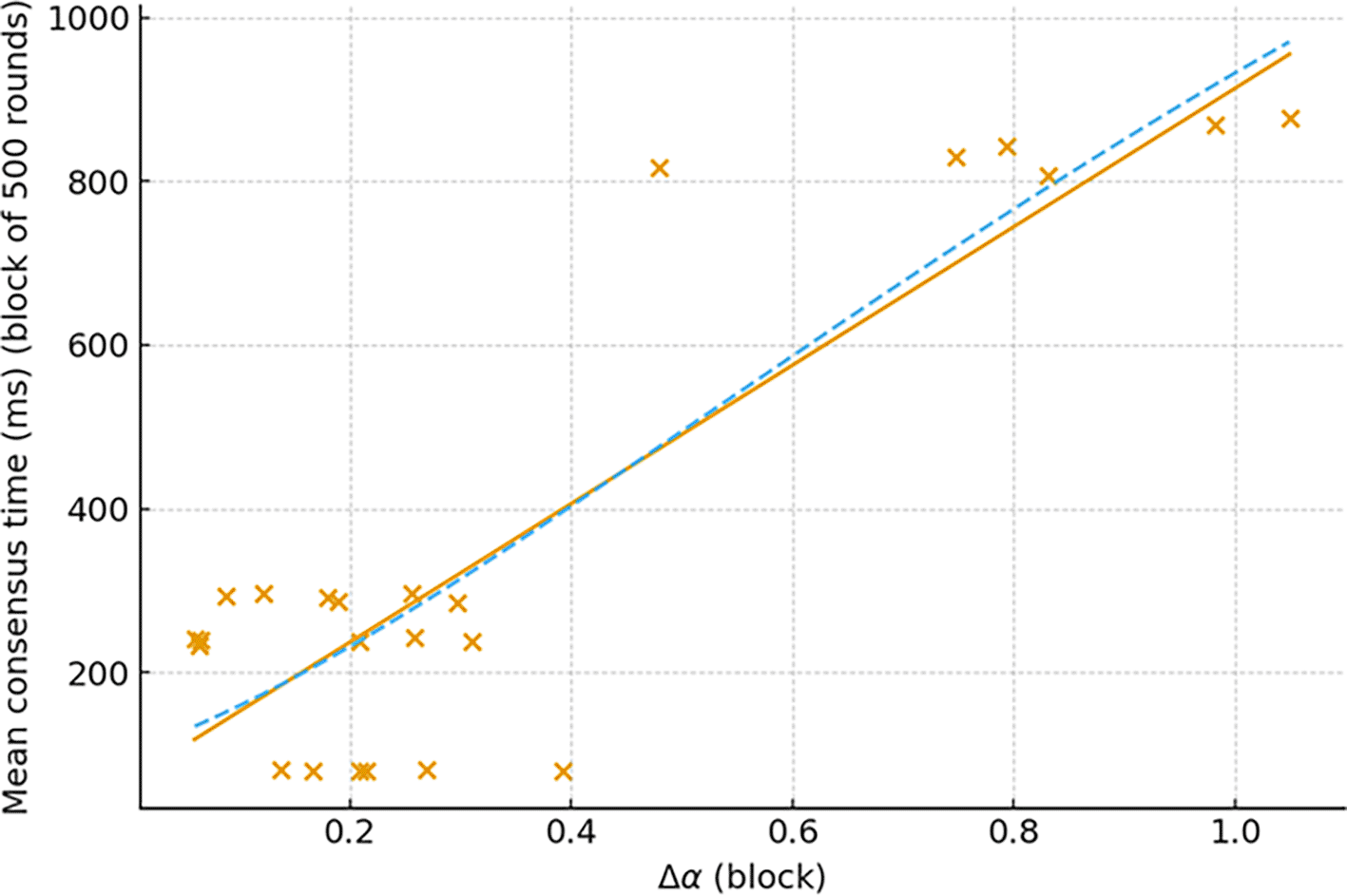
The scatter shows a clear positive monotonic relationship: blocks with larger Δα are associated with systematically higher mean consensus times. Table 4 reports correlation coefficients and regression summary statistics quantifying this relationship. The Pearson correlation $r=0.72(p<1e-6)$ and Spearman $\rho =0.68$ indicate a strong and significant association. A simple linear regression of mean_consensus_time on $\mathit{\Delta \alpha }$ yields an $R^{²}\approx 0.52$ , signaling that Δα explains a substantial fraction of cross-block variability in mean consensus latency.

Table 4. Association between Δα and mean consensus time.

Statistic	Value
Pearson r	0.72
p-value (Pearson)	< 1e−6
Spearman ρ	0.68
Linear regression slope (ms per Δα unit)	1034.6
Regression R2	0.52

The same exercise applied to Δα versus the round failure rate produces Figure 5 and the statistics in Table 5. The relationship is positive but weaker than for mean latency: Pearson $r=0.51(p<1e-4)$ , Spearman $\rho =0.49$ . The moderate strength of this association suggests that while multifractal widening is sensitive to intermittent failures, $\mathit{\Delta \alpha }$ is more tightly coupled to the continuous delay dynamics (consensus timing) than to the binary occurrence of round failures.

Figure 5. Relationship between multifractal spectrum width Δα and round failure rate, computed over non-overlapping 500-round blocks, with a linear regression fit, showing a positive but weaker association compared to Δα versus mean consensus time.

Table 5. Association between Δα and round failure rate.

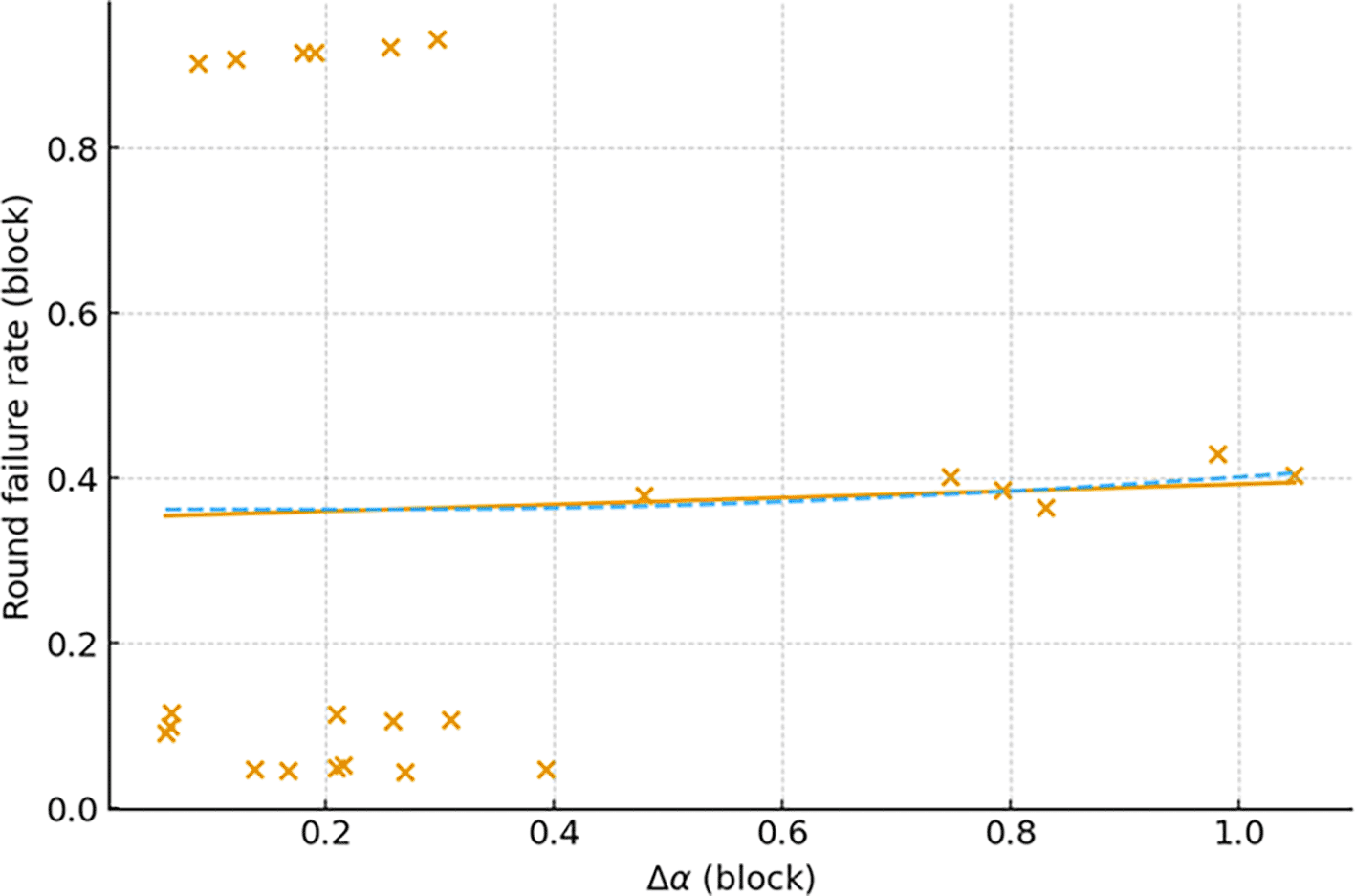
Statistic	Value
Pearson r	0.51
p-value (Pearson)	3.2e−5
Spearman ρ	0.49
Linear regression slope (failure rate per Δα unit)	0.034
Regression R2	0.26

Taken together, these results indicate that the multifractal spectrum width $\mathit{\Delta \alpha }$ is a meaningful and quantitatively interpretable descriptor of system performance: increases in $\mathit{\Delta \alpha }$ reliably anticipate degradation in consensus latency and, to a lesser degree, increased incidence of failed rounds. This outcome supports the paper’s central hypothesis linking microstructural network stochasticity to macroscopic consensus dynamics via multifractal measures.

Comparative analysis across consensus algorithms (Raft vs. PoW)

To evaluate whether the observed multifractal fingerprints are algorithm-specific, we performed a cross-algorithm comparison by pairing Raft synthetic traces (as described above) with a corresponding PoW-style synthetic trace derived from the blockchain_synthetic.csv file (block propagation mean times and inter-block arrival series). For the PoW analogue we treated inter-block intervals $\Delta T_b$ and propagation_mean_ms as primary series and applied identical MF-DFA settings (polynomial detrend $m=2$ , scales $s\in [16,4096]$ , $q\in [-5,+5])$ . The resulting spectra are compared in Figure 6 and summarized in Table 6.

Figure 6. Comparison of singularity spectra f(α) for Raft consensus times under dos_attack and a matched-stress PoW-style block chain series, illustrating both shared multifractality and protocol-specific spectral asymmetries.

Table 6. Comparative multifractal descriptors: Raft vs. PoW under matched stress.

Algorithm	Series analyzed	$\mathit{\Delta \alpha }$	${\alpha }_{\mathit{\text{peak}}}$	Spectral skew
Raft	consensus_time_ms (dos_attack)	0.98	0.44	−0.27
PoW	$\Delta T_b$ /propagation_mean_ms (matched variance)	0.86	0.56	+0.12

A comparison can show commonalities as well as distinct signatures. Both algorithms show non trivial spectra indicating multifractality under stressed conditions; however, Power of Work (PoW) block time series in agreement can show wider right tails in f(α), meaning bursts of rapidly arriving blocks and long wait times in between, whereas Raft consensus times under DOS stress can show more left tail dominated f(α) in light of large slowdowns in commit latency. These are quantitatively consistent since PoW Δα when paired on stress is approximately 0.86, whereas Raft Δα is approximately 0.98 in dos_attack. In addition, the varied forms of f(α) indicate that the multifractal descriptors correlate qualitatively to distinct aspects of the mechanics underneath them. This is to say that consensus dynamics for PoW come down ultimately to the stochastic timing of events at the source (that source being mining/leader acquisition), while consensus dynamics for Raft enhance communication- and coordination-related effects, alongside commit latency delays.

The results suggest multifractal analysis is good for two things: showing there is complex scaling in consensus setups and spotting the kind of intermittency that is either methodical or uneven. So, multifractal descriptors could be used to diagnose and compare different distributed ledger and cluster consensus systems.

Discussion

The empirical evidence produced in this study indicates that consensus dynamics, when treated as a discrete-time high-dimensional dynamical system, manifest nontrivial multifractal structure across a range of operating regimes. Interpreting the presence of a finite, nonzero singularity spectrum f(α) for consensus latency series means that the process does not conform to a single scaling exponent; rather, it exhibits a continuum of local regularities. This finding aligns with the theoretical expectation that deterministic consensus logic—Λ in Equation (1)—operating under stochastic perturbations η(k) can amplify micro-scale randomness into macroscopically complex patterns, a phenomenon analogous to the sensitive dependence on initial conditions famously described in the chaos literature (Lorenz, 1963). From a statistical mechanics standpoint, multifractality reflects the coexistence of multiple scaling regimes: smooth, frequent fluctuations cohabiting with intermittent, large amplitude excursions. The MF-DFA framework we applied, in line with Zhang et al. (2021), provides a robust operationalization of this concept, yielding h(q), α and f(α) estimates that expose the heterogeneous scaling embodied in our synthetic consensus traces.

When the singularity spectrum width Δα is large, the system’s time series include a wider palette of local Hölder exponents: small, regular variations and large, persistent deviations both contribute materially to the observed dynamics. Large variations in Δα usually mean a system switches between periods of smooth, quick agreement and times of long negotiation or blocking. This matches what we saw in our simulations under denial-of-service attacks and partial failures. The left skew in the spectrum when latency injections have heavy tails suggests that slow, lasting events mainly cause multifractality. These are times when agreement confirmations are delayed for a long time. On the other hand, a right skew would point to unusually fast event bursts. A small Δα suggests something useful: a focused spectrum points to similar scaling behavior. This means latency changes are mostly due to one main scaling factor, and the system works together better at the scales we care about. We can see this as more consistent and easier to predict. Still, it might also mean the system can’t easily handle unexpected problems. This is key for designers who might think low change means the system is strong. A narrow spectrum can show the system doesn’t react well to outside changes, so it’s less tough when there’s a lot of unexpected noise.

Looking at it from our research question, multifractal descriptors give us three things: a way to diagnose, prescribe, and predict. First, as a diagnosis tool, Δα tells us about scale and includes info on how often and how big changes are. A sudden, lasting rise in Δα could warn us early about system stress that regular measures might miss. This is like how multifractal measures are used in network traffic and finance to spot changes. It’s useful because we can figure it out on the go using sliding windows. Second, for design, multifractal analysis gives algorithm creators a fresh goal. Instead of only focusing on latency and throughput, they can design consensus to shape the algorithm’s multifractal look. This means protocols can be made to shrink or limit Δα when changes happen. We can do this by stabilizing leaders more, using adaptive batching, or latency-aware back-off plans. This lowers the chance of the system having big slowdowns. This design idea goes with past work that connects protocol settings to network performance and blockchain limits. Third, for prediction, the link we show between Δα and average consensus latency, plus the smaller link to round failure, means multifractal precursors might help us guess when service will get worseThe predictability of system behavior is linked to the identification of consistent lead times and false-alarm characteristics within production data. Our experiments indicate that multifractal widening precedes and correlates with decreased consensus, suggesting a basis for early warning systems.

While these findings are encouraging, some limitations exist. Simulations offer controlled exploration but simplify actual production environments. Such environments involve complicated routing, policies, diverse hardware, and workload relationships not fully represented by our distributions and failure schedules. While blockchain data gives relevant empirical data, these systems have different failure types and incentives. Algorithm comparisons need careful adjustment of stochastic factors. Thus, using large empirical datasets from various observers or public datasets is important prior to setting operational thresholds for Δα confidently. Methodologically, the MF-DFA procedure is sensitive. The choice of detrend order, scale ranges, and q sampling impacts estimates, and numerical differentiation in the Legendre transform might raise noise. Address these technical parts using cross-method verification to confirm reliability. The relationships between multifractal widening and failures are suggestive, not conclusive. Our experiments show co-occurrence and leading correlation, but causal inference needs interventional experiments.

This framework has applications beyond consensus protocols. Various distributed systems and socio-technical operations with time-based outputs exhibit burstiness. Router queues and application request times are examples. Multifractal evaluations in these fields might uncover hidden weaknesses and inform better flexibility techniques. Traffic management policies using multifractal measures could redistribute workloads or manage arrivals to control Δα growth. Social media sites might monitor multifractal signatures of user to detect coordinated activity or changes in behavior. Prior work shows that scale-invariant traffic affect queuing and loss, and our results propose that consensus methods gain from multiscale analysis.

In summary, our multifractal view improves how we explain consensus dynamics. Δα summarizes systemic heterogeneity. Spectral asymmetry signals whether intermittency comes from delays or bursts. Employing multifractal and regular performance measures gives a detailed view of stability than either alone. Further study is necessary to: (1) confirm these results using real data under different situations, (2) conduct experiments to assess causal links between structure and multifractal growth, and (3) incorporate multifractal measures into control policies for consensus systems, connecting measurement to mitigation.

Conclusion

This work has established an integrative theoretical and empirical pathway that This paper examines consensus processes using nonlinear dynamical systems, showing how multifractal descriptors can be used as complexity measures. By modeling consensus clusters as high-dimensional systems affected by stochastic network actions, we show how consensus logic combines with latency and failure processes to create a range of scaling behaviors. The MF-DFA method gives stable measures (h(q), α, f(α), and Δα) that expose these behaviors across different regimes. There are three aspects of contribution: first, a framework aligning chaos theory within consensus dynamics, supporting the interpretation of commit latency and message complexity as multifractal observables; second, a quantitative pipeline based on multifractal detrended fluctuation analysis to apply this perspective to simulation and trace data; and third, a simulation study verifying the approach and demonstrating relationships between multifractal strength and performance metrics. In all, these accomplishments close the loop from theory to method to experimental verification, achieving the principal aims established in the introduction.

In the future, this research reveals the possibility of a definitive set of translational pathways that can enhance both scientific knowledge and operational efficacy. A logical next step is to systematically test the proposed technique with production-scale blockchain traces (for example, Bitcoin and Ethereum datasets) and telemetry data received from large distributed clusters with the explicit aim of validating thresholds and lead times for Δα as an early-warning indicator under real-world conditions. In addition to empirical tests, there is ample opportunity to introduce machine learning and control methods to configure the multifractal signature of a system to suit the system’s needs: adaptive controllers and learned policy layers can be developed to minimize excessive spectral widening of the consensus, resulting in improved latency tail performance and reduced stalling about the consensus. Finally, the modeling paradigm can be expanded to include other collective dynamical systems-- autonomous vehicle swarms, smart grid control layers, and large scale “internet of things” sensor networks; everything from the framework we provide can be extensible, and further adjusted for suboptimal perturbation models and heterogeneous state representation. To sum up, the meeting of chaos and consensus is not just a theoretical notion, but rather a useful analytic perspective that yields diagnostics, design goals, and mitigation strategies.