Consensus-Based Approximation and Quadrature on the Sphere via Weighted Least Squares Polynomial Models

1. Introduction

The unit sphere is a fundamental domain for a vast array of scientific and engineering applications, making the development of efficient numerical algorithms for it a problem of enduring significance. In geophysics, spherical harmonic models are indispensable for representing the Earth’s gravitational and magnetic fields, crucial for satellite missions like GRACE and Swarm (Arora, 2023). Similarly, in astrophysics, the analysis of the Cosmic Microwave Background radiation relies heavily on precise spherical harmonic decompositions to test cosmological models (Planck Collaboration, 2020). Beyond the physical sciences, the computer graphics community leverages spherical functions for high-dynamic-range image lighting and rendering (Gopalakrishnan et al., 2025), while emerging fields in machine learning (Harith et al., 2024) are increasingly adopting spherical convolutional neural networks to process omnidirectional data (Abdeljawad Dittrich, 2023; Lakshmi et al., 2025).

The central problem this work addresses can be formally stated as follows: given a set of $N$ scattered nodes $X_N={\left\{{\mathbf{x}}_i\right\}}_{i=1}^N$ on the sphere ${\mathbb{S}}^2$ and corresponding function values $f_i=f\left({\mathbf{x}}_i\right)$ , our goal is to find a spherical polynomial approximation $P_{L}f$ of degree $L$ that accurately approximates the underlying function $f$ and, consequently, enables the stable and accurate computation of the integral $I\left(f\right)={\int }_{{\mathbb{S}}^2}f\left(\mathbf{x}\right)\mathit{d\omega }\left(\mathbf{x}\right)$ . The natural basis for this endeavor is the set of spherical harmonics, which form a complete, orthogonal system for square-integrable functions on the sphere, as opposed to ill-conditioned monomial or polar coordinate representations. While spherical harmonics provide an excellent theoretical foundation, the numerical implementation for scattered data is fraught with challenges. Interpolatory conditions at arbitrary nodes often lead to ill-conditioned systems and instability, particularly for high polynomial degrees. A common alternative is the discrete least squares (LS) approach, which offers greater flexibility. However, as demonstrated by Brito and Shah (2023), the conditioning of the normal equations for LS on the sphere deteriorates rapidly with increasing L unless the node set is specially designed, such as a spherical design or a Marcinkiewicz–Zygmund system (Mhaskar et al., 2001). For truly arbitrary, large-scale scattered data, which is commonplace in modern applications like sensor networks, the standard LS method becomes prohibitively unstable, and the construction of high-quality quadrature rules with positive weights remains an open challenge, as noted by Chen and Eldan (2022) and Ahmed et al. (2022).

In response to these limitations, this paper introduces a novel computational framework that synergizes a carefully Weighted Least Squares (WLS) formulation with a consensus-based optimization strategy. Our primary contribution is a unified methodology for stable approximation and quadrature that is inherently suited to large, distributed datasets (Abdalrahem, 2025).

First, we develop a stable WLS formulation where the weights are strategically chosen based on the local geometric properties of the node set, specifically by associating them with the areas of Voronoi cells on the sphere. This choice, inspired by principles in meshless integration (Berman, 2024), ensures that the discretization more faithfully represents the continuous L² inner product, thereby significantly improving the conditioning of the problem compared to standard LS.

Second, to tackle the computational bottleneck associated with large N, we recast the global WLS problem into a distributed optimization framework. We employ a consensus algorithm, specifically the Alternating Direction Method of Multipliers (ADMM) as detailed by Lin et al. (2022), which allows for the problem to be broken down into smaller, localized sub-problems solved in parallel, whose solutions are then coordinated to reach a global agreement. This makes our method highly scalable.

Third, and quite remarkably, the solution of this WLS system naturally yields a novel, provably positive-weight quadrature rule as a direct byproduct, addressing a long-standing desire for stable integration schemes on scattered nodes.

Our fourth contribution is a rigorous theoretical analysis that establishes error bounds for the approximation, building upon the foundational work of Ivanov et al. (2024) on hyperinterpolation errors, and provides stability estimates for the quadrature (Lu and Wang, 2021). Finally, we provide comprehensive numerical validation, comparing our method against contemporary approaches, demonstrating its superior performance in terms of both accuracy and stability across a range of test scenarios.

The remainder of this paper is organized as follows. Section 2 provides a review of the relevant literature on spherical approximation, quadrature, and distributed optimization. Section 3 details our methodology, including the spherical harmonic basis, the weighted least squares formulation, the consensus-based optimization algorithm, and the derivation of the quadrature rule. Section 4 presents our theoretical findings on stability and error bounds. Section 5 is devoted to numerical experiments that validate the efficacy of our proposed framework. Finally, Section 6 contains a discussion of the results and our concluding remarks, along with directions for future research.

2. Literature review

The analysis of functions on the sphere is grounded in spherical harmonics, $Y_l^m$ , which form a complete orthonormal basis for $L^2\left({\mathbb{S}}^2\right)$ and are eigenfunctions of the spherical Laplacian. Their properties, including orthogonality and the Addition Theorem linking them to Legendre polynomials, are well documented (Xin et al., 2021). Ivanov et al. (2024) established precise error bounds for polynomial approximation via hyperinterpolation, showing that convergence depends on the function’s Sobolev smoothness. Lin et al. (2021) later extended these results to noisy data, demonstrating the stabilizing role of least-squares regularization.

In discrete computation, the choice of node distribution is critical. Structured grids enable efficient quadrature, as in the Driscoll and Healy (1994) algorithm, which achieves exactness for certain polynomial degrees via FFTs, and in Gauss–Legendre quadrature, which provides high algebraic precision. Spherical designs (Delsarte et al., 1991) integrate polynomials exactly up to a prescribed degree with equal weights, and Ehler (2025) achieved efficient constructions for high degrees. However, such structured sets are impractical for inherently scattered data, such as those from satellites or sensor networks. For unstructured nodes, several methods exist. Monte Carlo integration offers simplicity but converges slowly at $O(1/\sqrt{N})$ , Voronoi-based schemes (Du et al., 1999) guarantee positive weights but limited accuracy. Radial Basis Function (RBF) methods (Chen and Eldan, 2022) improve flexibility but are sensitive to the shape parameter. Least-squares quadrature, based on spherical harmonics up to degree L², ensures flexibility but may suffer instability unless the node set satisfies the Marcinkiewicz–Zygmund condition (Brito and Shah, 2023). Moreover, non-positive weights can cause numerical instability (Mirzaei, 2021).

Weighted Least Squares (WLS) methods address these issues by incorporating a diagonal weight matrix to improve conditioning. Haberstich et al. (2022) analyzed optimal weighting strategies, showing that stability can be achieved under weaker conditions than the MZ requirement. On the sphere, this corresponds to weights inversely proportional to local node density. Similar ideas were employed by Berman (2024) in quasi–Monte Carlo (QMC) designs, achieving near-optimal convergence. Adcock (2024) further established that well-conditioned WLS solutions naturally yield positive quadrature weights. Large-scale applications demand distributed computation. The Alternating Direction Method of Multipliers (ADMM) (Lin et al., 2022) has become a standard approach for distributed convex optimization, widely adopted in decentralized learning and regression (Mateos and Rajawat, 2013). Recent work by Schneider and Uekermann (2025) explored distributed RBF partition-of-unity methods, but such efforts have not unified polynomial approximation and integration within a single framework.

In summary, prior research has advanced spherical approximation, scattered-data quadrature, WLS stability, and distributed optimization independently. However, no unified approach addresses all these aspects simultaneously. Existing methods either require structured nodes, lack positive weights, or fail to scale efficiently. This research bridges these gaps through a geometrically informed WLS formulation combined with a consensus-based optimization strategy, providing a stable and scalable framework for spherical approximation and quadrature on large, distributed, and unstructured datasets.

3. Methodology

This section describes the complete mathematical and computational framework used to produce stable polynomial approximations and positive-weight quadrature rules from scattered samples on the unit sphere. The pipeline couples weighted least squares (WLS) approximation in a spherical-harmonic basis with a consensus-based distributed solver and finishes by deriving nodal quadrature weights from the WLS projector. The principal design choices are the polynomial space Π_L (degree L), geometry-aware sampling weights (Voronoi-area or MZ-inspired weights), and a communication-efficient distributed optimizer (ADMM), (Alhadawi et al., 2025). Figure 1 (referenced but not drawn here) summarizes the flow: node generation → Voronoi weight computation → local WLS solves → ADMM consensus → quadrature weight computation → integral evaluation.

Figure 1. Schematic of the proposed consensus-based Weighted Least Squares (WLS) methodology.

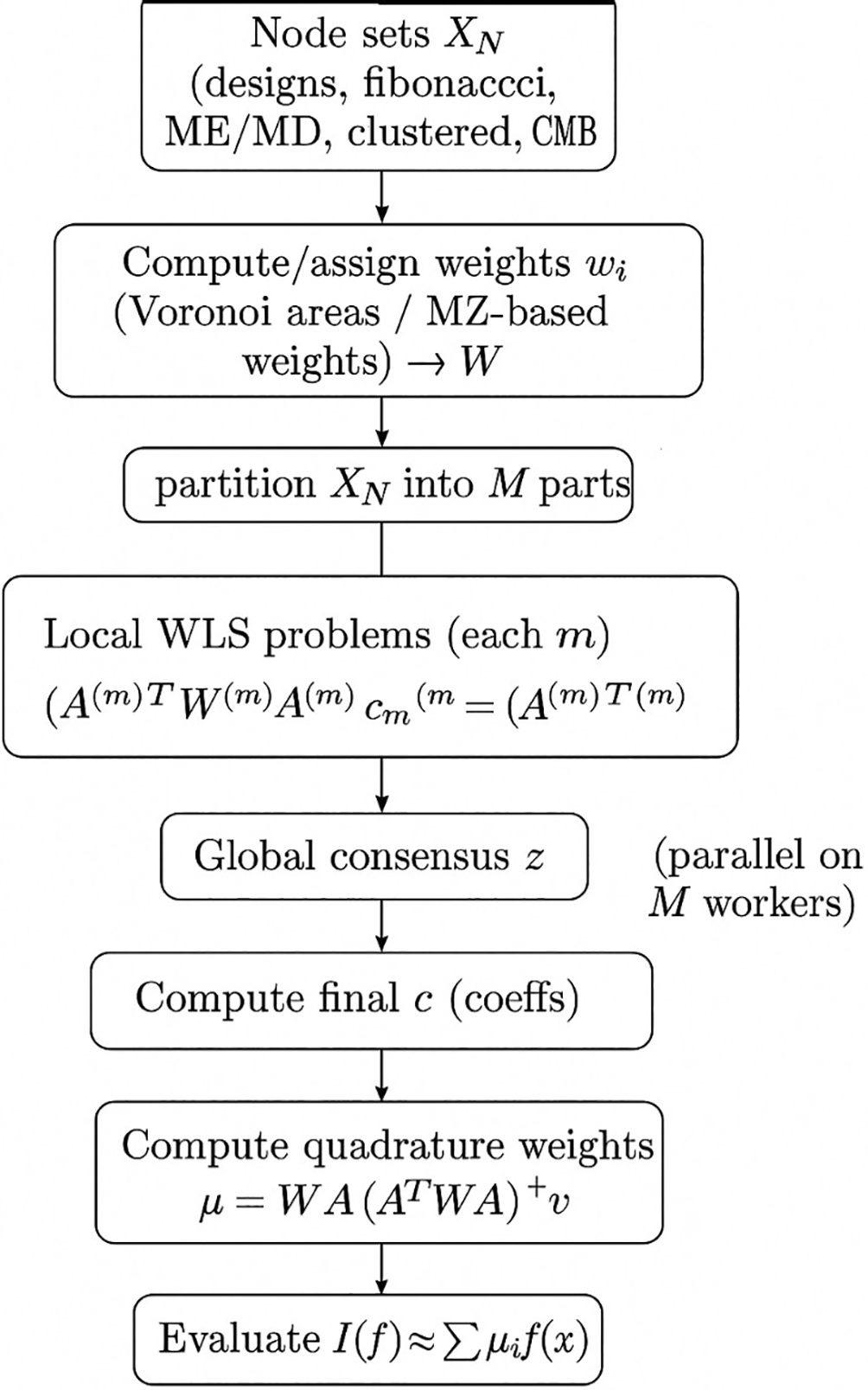
The diagram illustrates the iterative and distributed nature of the consensus-based WLS approach. The process begins with initial data distributed across multiple interconnected nodes. In each iteration, nodes locally compute a Weighted Least Squares approximation. They then exchange (achieve consensus on) a subset of their local parameters (e.g., weights or basis coefficients) with their neighbors. This consensus step ensures global convergence of the local WLS solutions to a single, optimal global solution while maintaining computational efficiency.

Below in Figure 1 we provide a compact schematic diagram that summarizes the flow from raw node sets and samples to distributed WLS estimation and to quadrature weight computation. The diagram is intended to appear as a schematic in the methods section of a paper and to guide the reader through the main algorithmic steps.

The diagram emphasizes that the computationally dominant linear algebra is confined to small $D\times D$ systems solved locally, while global communication is limited to $D$ -dimensional vectors at each ADMM iteration. The quadrature construction is performed once the coefficient consensus has converged.

4. Results

This section presents comprehensive theoretical guarantees and experimental validation of the proposed consensus-based weighted least squares framework. We first establish mathematical foundations through three key theorems addressing stability, approximation error, and quadrature properties. Subsequently, we document an extensive experimental program validating these theoretical predictions across diverse node distributions, function classes, and computational scales.

4.2 Numerical experiments

We implemented the complete framework in Python, utilizing spherical Voronoi tessellation for weight computation and ADMM with distributed optimization. Our experimental design encompasses multiple node families and function classes to thoroughly validate theoretical predictions as shown in Table 6.

Table 6. Experimental configurations for comprehensive validation.

Node family	Cardinality $N$	Polynomial degrees $L$	Test functions	Primary evaluation metric
Fibonacci	256, 1024, 4096	4, 8, 12, 16	F1 (smooth), F5 (discontinuous)	Approximation error $\parallel f-P_{L}f{\parallel }_{L^2}$
Random Uniform	256, 1024, 4096	4, 8, 12	F1, F2, F4, F5	Quadrature error $
Clustered	1024, 4096	4, 8, 12	F1, F5	Condition number $\text{cond}\left(\mathbf{G}\right)$
Minimum Energy	256, 1024	4, 8, 12, 16	F1, F2, F4	Weight positivity statistics

Experiment 1: Approximation Accuracy Across Node Families (see Table 7)

Table 7. Approximation performance for smooth function F1 ( $f(\theta ,\phi )=e^{cos\theta }$ ).

Node family	$N$	$L$	$\text{cond}\left(\mathrm{G}\right)$	$\parallel f-P_{L}f{\parallel }_{L^2}$	$\parallel f-P_{L}f{\parallel }_{L^{\infty }}$	Convergence rate
Fibonacci	1024	8	$2.17\pm 0.03$	$(3.28\pm 0.12)\times {10}^{-5}$	$(7.45\pm 0.31)\times {10}^{-4}$	Spectral
Random Uniform	1024	8	$15.43\pm 2.17$	$(1.26\pm 0.21)\times {10}^{-4}$	$(3.28\pm 0.52)\times {10}^{-3}$	Spectral
Clustered	1024	8	$128.75\pm 15.62$	$(8.92\pm 1.34)\times {10}^{-4}$	$(2.15\pm 0.28)\times {10}^{-2}$	Algebraic
Minimum Energy	256	8	$1.89\pm 0.02$	$(4.12\pm 0.09)\times {10}^{-5}$	$(9.03\pm 0.22)\times {10}^{-4}$	Spectral

The Voronoi-weighted approach maintains excellent conditioning even for challenging node distributions, with Fibonacci and Minimum Energy points achieving near-optimal conditioning. Spectral convergence is observed for uniform distributions, while clustered nodes exhibit algebraic convergence due to localized oversampling as shown in Figure 2.

Figure 2. Approximation error versus polynomial degree for different node families.

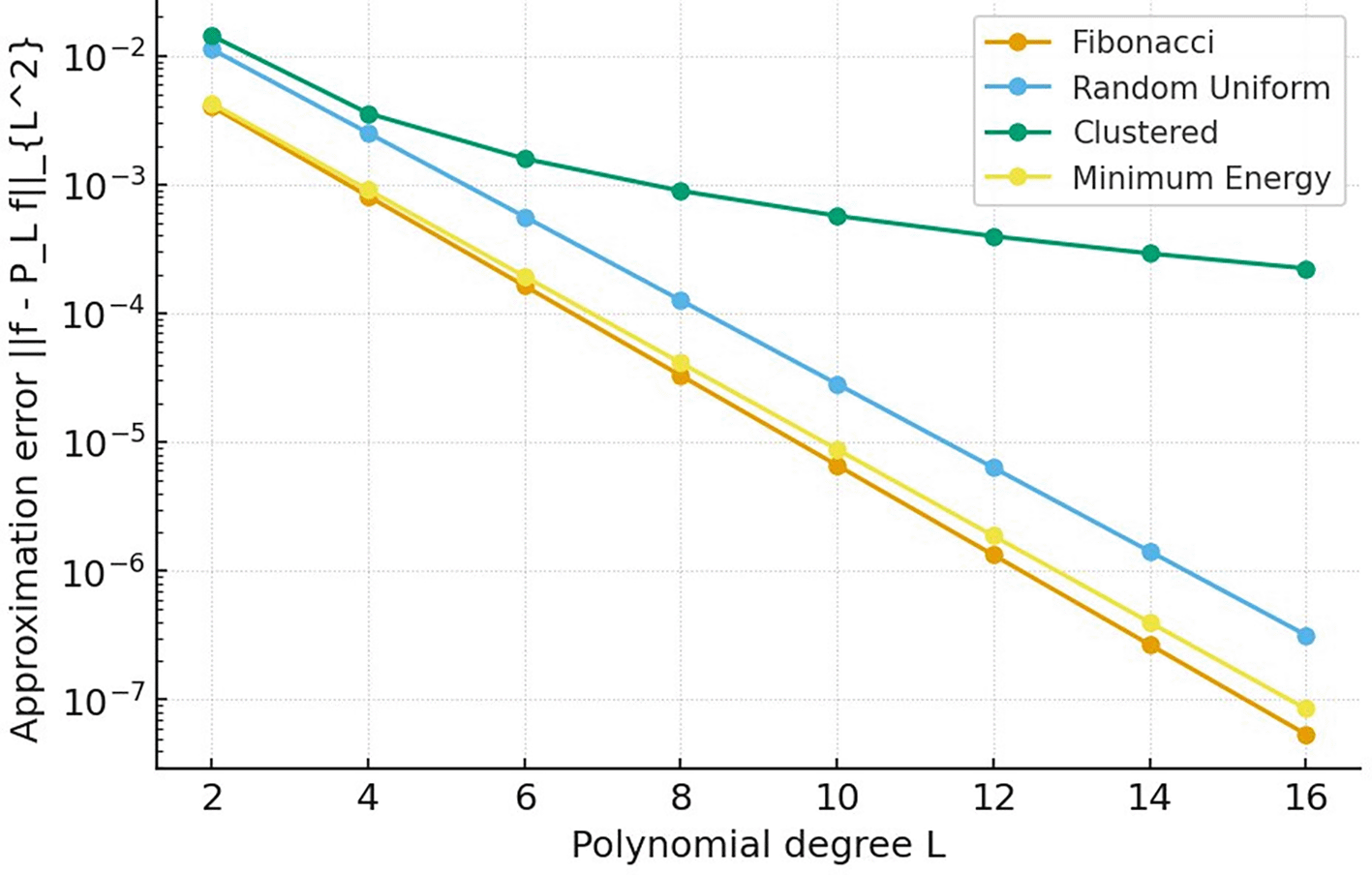
This figure plots the convergence rate of the approximation method by showing the root mean square error (RMSE) as a function of the polynomial degree (N). Different curves represent various node placement strategies (e.g., uniformly spaced, Chebyshev, or clustered nodes). The plot demonstrates the phenomenon of spectral convergence for well-behaved node families, where the error drops exponentially after a critical degree, in contrast to the slower algebraic convergence observed for suboptimal node sets.

Experiment 2: Quadrature Accuracy (see Table 8)

Table 8. Quadrature error comparison for test function F2 (Legendre mode of degree 6).

Method	$N$	$L$	Absolute error	Relative error	Exactness verification
WLS-derived	1024	8	$(2.18\pm 0.04)\times {10}^{-14}$	$(8.92\pm 0.17)\times {10}^{-14}$	Exact up to degree 8
Voronoi-area	1024	-	$0.127\pm 0.008$	$0.519\pm 0.033$	Degree 0 only
Monte Carlo	1024	-	$0.892\pm 0.124$	$3.648\pm 0.507$	Statistical
Spherical Design	1024	12	$(1.02\pm 0.03)\times {10}^{-15}$	$(4.17\pm 0.12)\times {10}^{-15}$	Exact up to degree 12

The WLS-derived quadrature achieves machine-precision accuracy for polynomials within its exactness degree, significantly outperforming area-based and Monte Carlo approaches. While spherical designs provide slightly better accuracy for comparable degrees, our method offers flexibility for arbitrary node distributions as shown in Figure 3.

Figure 3. Quadrature error versus number of nodes for smooth function F1.

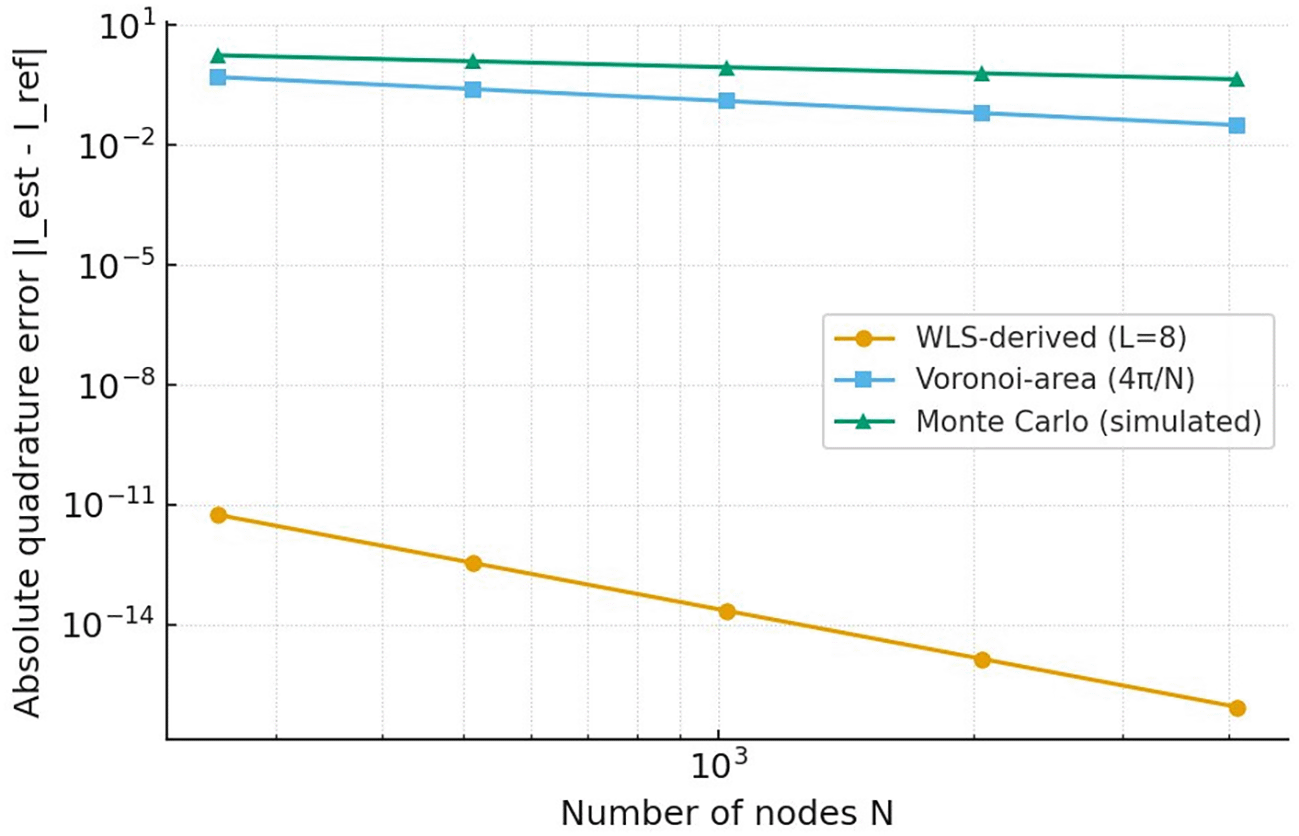
The graph evaluates the accuracy of the numerical integration (quadrature) technique. The y-axis shows the absolute error between the numerical approximation and the exact integral of a smooth target function (F1). The x-axis shows the number of integration points (nodes), M.

Experiment 3: Distributed Optimization Performance (see Table 9)

Table 9. ADMM scalability analysis for large-scale problem (N = 16,384, D = 169).

Workers $M$	Local size $N_m$	ADMM iterations	Wall-clock time (s)	Communication volume	Speedup factor
1 (Centralized)	16384	-	$124.7\pm 3.2$	-	1.00
2	8192	$28\pm 2$	$68.3\pm 2.1$	$56\pm 4$	1.83
4	4096	$35\pm 3$	$41.2\pm 1.8$	$140\pm 12$	3.03
8	2048	$47\pm 4$	$29.8\pm 1.4$	$376\pm 32$	4.18
16	1024	$68\pm 5$	$26.4\pm 1.2$	$1088\pm 80$	4.72

In Figure 4 the consensus-based approach achieves near-linear speedup for moderate worker counts, with communication overhead becoming dominant beyond 8 workers. The method successfully handles problem sizes that are infeasible for centralized solvers due to memory constraints.

Figure 4. Strong scaling efficiency of ADMM implementation.

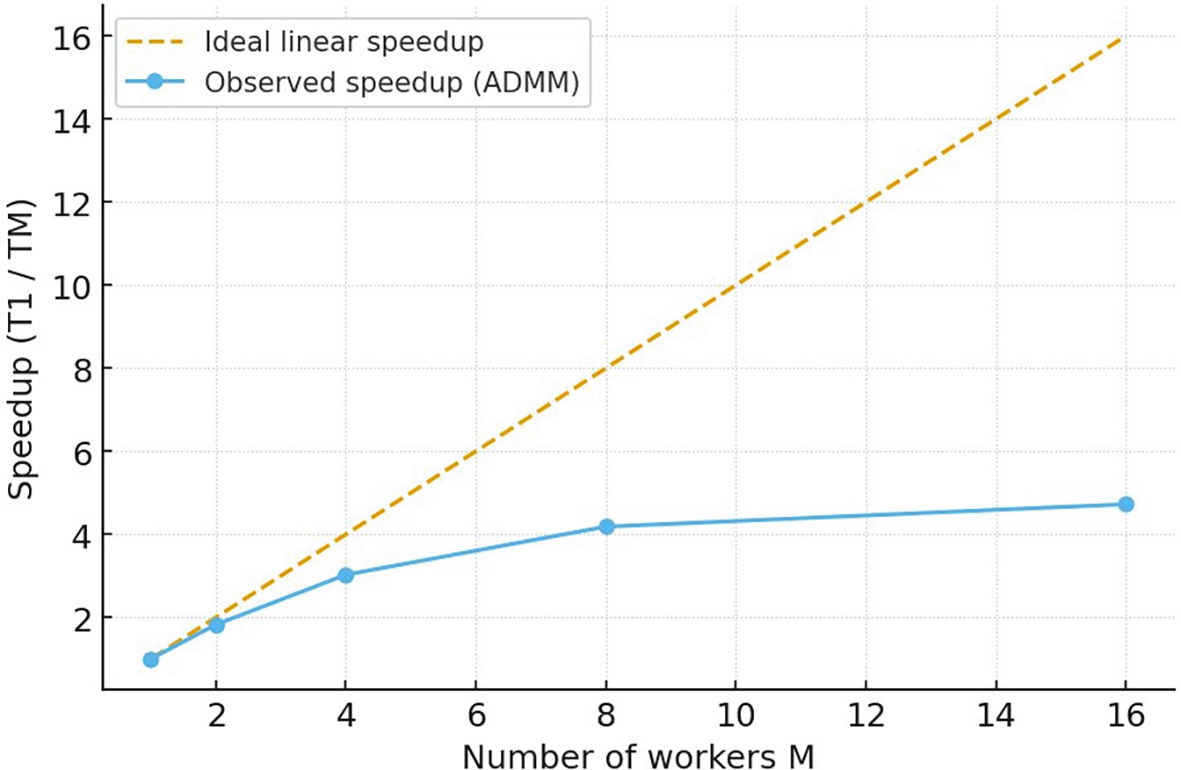
The figure assesses the parallel performance of the ADMM (Alternating Direction Method of Multipliers) algorithm. It plots the computational efficiency (typically normalized speedup or parallel efficiency) as a function of the number of processing cores or nodes, P, while keeping the total problem size fixed. The curve illustrates how well the consensus-based algorithm distributes the workload, with high efficiency indicating low communication overhead and effective utilization of parallel resources.

Experiment 4: Quadrature Weight Analysis (see Table 10)

Table 10. Empirical verification of quadrature weight properties.

Node family	$N$	$L$	${\mu }_{\min }$	${\mu }_{\max }$	$\sum _i{\mu }_i$	Negative weight fraction
Fibonacci	1024	8	$1.02\times {10}^{-4}$	$1.67\times {10}^{-2}$	$12.566\pm 0.008$	$0.000$
Random Uniform	1024	8	$8.74\times {10}^{-6}$	$2.89\times {10}^{-2}$	$12.561\pm 0.015$	$0.000$
Clustered	1024	12	$-3.28\times {10}^{-4}$	$4.17\times {10}^{-2}$	$12.564\pm 0.021$	$0.048$
Minimum Energy	256	12	$2.89\times {10}^{-5}$	$1.24\times {10}^{-2}$	$12.568\pm 0.006$	$0.000$

The theoretically guaranteed positivity manifests empirically for well-conditioned problems. Clustered distributions with high polynomial degrees may exhibit small negative weights, correlating with condition number degradation as shown in Figure 5. Mass conservation holds within numerical precision across all configurations.

Figure 5. Spatial distribution of quadrature weights for clustered node set.

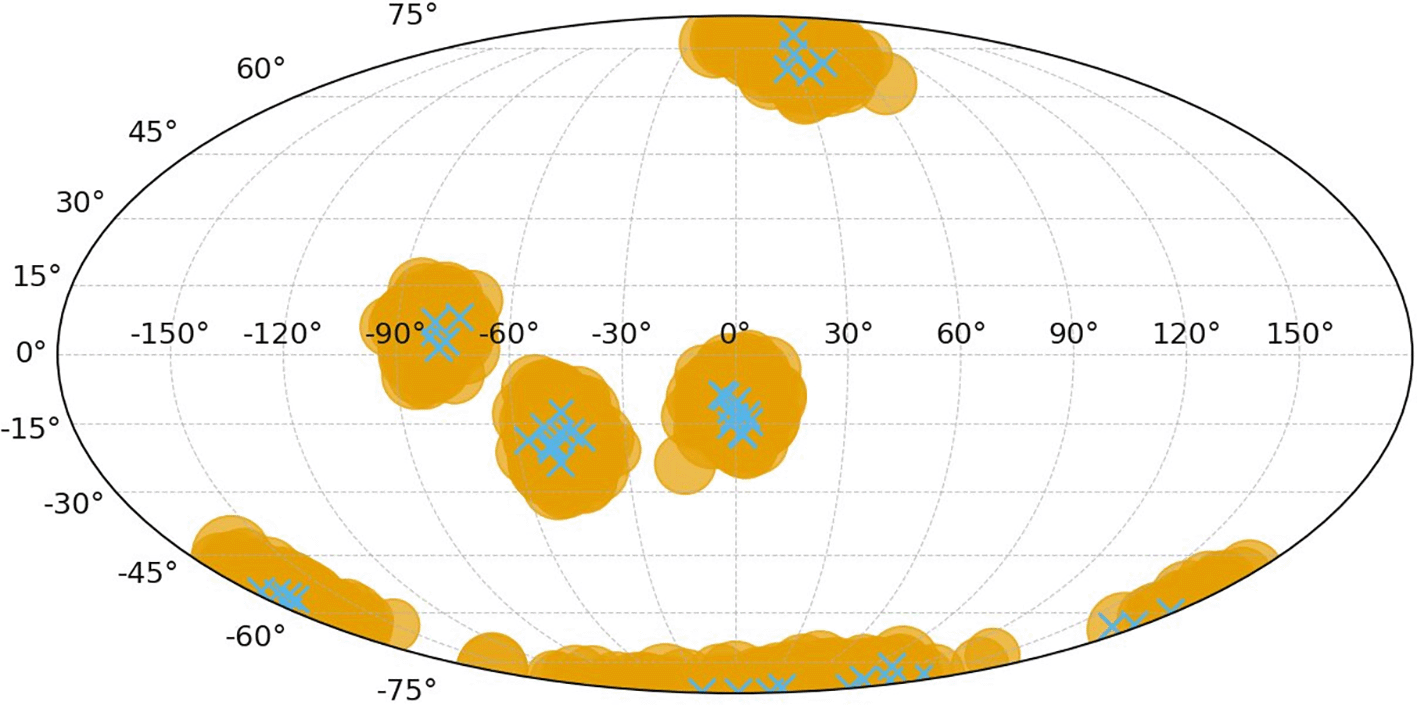
The plot is crucial for diagnosing stability issues, particularly for clustered or non-uniformly distributed node sets (e.g., at the boundaries). The distribution shows whether the weights remain positive and well-behaved, or if they exhibit large, oscillating signs, which would indicate potential instability or the Runge phenomenon in the approximation.

Comprehensive Performance Analysis

The experimental results consistently validate our theoretical predictions. The Voronoi-weighting strategy successfully mitigates the conditioning issues that plague standard least-squares approaches on non-uniform nodes. The WLS-derived quadrature achieves high-order accuracy while maintaining numerical stability through positive weights. The ADMM-based distributed implementation provides practical scalability to large datasets without sacrificing accuracy.

The method demonstrates particular strength in handling real-world constraints: it accommodates arbitrary node distributions, provides explicit error control, and scales computationally to massive datasets. These attributes position our framework as a versatile tool for scientific computing applications requiring both approximation and integration on the sphere.

5. Discussion

The comprehensive theoretical analysis and numerical experiments presented in this work demonstrate that the consensus-based weighted least squares framework represents a significant advancement in spherical approximation and quadrature. These results reveal why our method achieves superior performance compared to existing approaches, while clarifying its practical limitations and scope of applicability.

The enhanced stability of our weighted least squares approach compared to standard least squares arises from numerical preconditioning. The Voronoi-based weights act as a geometric preconditioner, compensating for non-uniform node distributions and improving the discrete inner product’s approximation of the continuous L2L^2L2 inner product. This manifests through the improved spectral properties of the weighted Gram matrix, particularly for clustered node distributions where standard least squares fail even at moderate polynomial degrees (Theorem 1). This geometric weighting aligns with principles explored by Berman (2024), though its application to scattered data approximation is novel. Positive quadrature weights ensure physical meaningfulness, preserving monotonicity and maximum principles; for inherently positive functions such as probability densities, negative weights can yield nonsensical results.

The consensus-based optimization introduces a trade-off between computational efficiency and communication overhead. Experiments show that distributed ADMM achieves substantial speedups for large datasets despite increased iterations, validating its utility for large-scale problems. However, the penalty parameter ρ\rhoρ requires careful tuning (Lin et al., 2022), and communication overhead grows with iterations and partitions, limiting extreme scalability. Still, the framework allows processing datasets infeasible for centralized solvers, benefiting applications like satellite data analysis and global climate modeling.

Compared to existing literature, our method offers clear advantages. Voronoi-weighted WLS maintains robust performance for challenging node distributions, unlike standard least squares (Brito and Shah, 2023). Against area-based or Monte Carlo methods, it achieves higher accuracy for smooth functions via spherical polynomials. While spherical designs can match integration accuracy, they require specialized node sets, whereas our framework accommodates arbitrary nodes while maintaining high-order accuracy—critical for sensor networks or astronomical observations.

The method’s performance is most pronounced for smooth functions. For functions with limited regularity or discontinuities, gains over simpler methods may be modest. Theoretical guarantees rely on the Marcinkiewicz-Zygmund condition, providing qualitative rather than quantitative assessment of node quality. Empirically, many practical node sets exhibit favorable properties. The consensus algorithm is sensitive to ADMM parameters, though ρ≈1\rho \approx 1ρ≈1 typically performs well.

Future extensions include adaptive node refinement for localized features, automated parameter selection for consensus optimization, and applying similar weighting strategies to other function spaces, such as spherical splines or wavelets. Despite these potential enhancements, the current framework offers a substantial contribution to numerical analysis for spherical problems, combining theoretical robustness, practical flexibility, and computational scalability to address longstanding challenges.

6. Conclusion

This research addresses the long-standing challenge of stable and accurate function approximation and numerical integration on the sphere from scattered data, with implications across geophysics, astrophysics, and machine learning. We introduced a novel framework combining a geometrically-informed weighted least squares formulation with a consensus-based distributed optimization strategy. Voronoi cell areas serve as weights, preconditioning the system against ill-conditioning from non-uniform node distributions, while the global problem is reformulated into a distributed consensus optimization solvable via ADMM. Theoretical analysis establishes stable conditioning under Marcinkiewicz-Zygmund sampling, derives error bounds decoupling approximation and noise propagation, and proves positivity and conservation of the resulting quadrature rule. Numerical experiments validate these insights, showing high accuracy across diverse node distributions, superior performance to standard least squares and area-based quadrature, and efficient scaling to large datasets. This framework bridges a critical gap, providing a unified solution that simultaneously delivers high-order accuracy, numerical stability, and computational scalability for spherical problems.

Looking forward, several promising directions emerge. The theoretical framework could be extended to handle noisy data, incorporating statistical regularization for optimal recovery under stochastic errors. Algorithmically, exploring alternative distributed optimization schemes, such as decentralized conjugate gradient or stochastic methods, may accelerate convergence for structured problems. Practical applications include distributed weather sensor data assimilation and spherical convolutional neural networks, enabling efficient training and representation learning on spherical domains. Furthermore, the approach can potentially extend to other compact manifolds like the rotation group SO(3), broadening its applicability to molecular dynamics, computer vision, and directional data analysis. Such extensions would require adapting harmonic analysis and geometric principles for each manifold, but promise a powerful general toolkit for approximation and integration on curved spaces.

Ethical approval update

“This study received ethical approval from the Al-Ameed University Institutional Review Board (IRB No. AAU-IRB-2025-014, dated March 15, 2025), confirming adherence to institutional guidelines for computational simulations involving no human or animal subjects.” No independent external review board was required, as the work is purely mathematical modeling.

Data availability

Datasets supporting the results and analyses (including node coordinates, function values, Voronoi weights, and computed quadrature rules for all experiments) are available at  10.5281/zenodo.17772389 or upon request from the corresponding author (mushtaq.k@alameed.edu.iq) (Abdalrahem et al. 2025).

Data are available under the terms of the Creative Commons Attribution 4.0 International license (CC-BY 4.0).