Exploration of hyperparameter tuning in handwritten digit recognition datasets using CNN

Roumo Kundu; Anurag Sinha; Biresh Kumar; Rohan Gautam; Mohammad Shahid Raza; Syed Abid Hussain

doi:10.12688/f1000research.161053.1

Home Browse Exploration of hyperparameter tuning in handwritten digit recognition...

ALL Metrics

-

Views

-

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Exploration of hyperparameter tuning in handwritten digit recognition datasets using CNN

[version 1; peer review: awaiting peer review]

Roumo Kundu¹, Anurag Sinha², Biresh Kumar¹, Rohan Gautam³, Mohammad Shahid Raza¹, Syed Abid Hussain ^4-6

Roumo Kundu¹, Anurag Sinha², [...] Biresh Kumar¹, Rohan Gautam³, Mohammad Shahid Raza¹, Syed Abid Hussain ^4-6

PUBLISHED 07 Mar 2025

Author details Author details

¹ Department of Computer Science and Information Technology,, Amity University Jharkhand, Ranchi, Jharkhand, India
² Master's research scholar School of computing and Information Science, Indira Gandhi National Open University, New Delhi, India
³ Department of Computer Science and Information Technology, Christ University, Bangalore, India
⁴ Centre for Research Impact & Outcome, Chitkara University Institute of Engineering and Technology, Chitkara University, Rajpura, 140401, India
⁵ Department of Computer Science and Engineering, Bakhtar University, Kabul, Kart e Char, Afghanistan
⁶ Chitkara Centre for Research and Development, Chitkara University, Rajpura, Punjab, 174103, India

Roumo Kundu
Roles: Conceptualization, Formal Analysis, Supervision, Writing – Original Draft Preparation, Writing – Review & Editing

Anurag Sinha
Roles: Conceptualization, Formal Analysis, Investigation, Methodology, Project Administration, Supervision, Validation, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Biresh Kumar
Roles: Data Curation, Formal Analysis

Rohan Gautam
Roles: Conceptualization, Data Curation, Formal Analysis

Mohammad Shahid Raza
Roles: Resources, Software

Syed Abid Hussain
Roles: Investigation, Software, Supervision, Validation

OPEN PEER REVIEW

REVIEWER STATUS AWAITING PEER REVIEW

Abstract

Background

Handwritten digit recognition is a fundamental task in computer vision, and convolutional neural networks (CNNs) are widely used for this purpose due to their ability to automatically extract relevant features. However, the role of hyperparameter tuning in enhancing CNN performance for this task remains underexplored.

Methods

This study evaluates the impact of hyperparameter tuning on CNN performance using the MNIST dataset, a standard benchmark for digit recognition. The framework involves varying hyperparameters, such as learning rate, batch size, number of convolutional layers, and optimization techniques. The Adam optimizer was employed to optimize the network, and experiments were conducted to assess the effect of adding extra convolutional layers on recognition accuracy.

Results

Our experiments achieved a 99.89% recognition rate on the MNIST dataset, surpassing prior benchmarks. This high accuracy was attained through systematic hyperparameter analysis and optimization. The addition of convolutional layers significantly contributed to improving the model’s performance by enabling deeper feature extraction and enhanced pattern recognition.

Conclusions

This study highlights the critical role of hyperparameter tuning in CNN-based handwritten digit recognition. By providing insights into the impact of hyperparameters and architectural adjustments, it demonstrates how careful optimization can simplify processes and enhance accuracy in computer vision tasks. These findings pave the way for more effective and streamlined approaches to pattern recognition using deep learning techniques.

Keywords

MINST Dataset , Digit Recognition , CNN , Deep Learning

Corresponding author: Syed Abid Hussain

Competing interests: No competing interests were disclosed.

Grant information: The author(s) declared that no grants were involved in supporting this work.

Copyright: © 2025 Kundu R et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Kundu R, Sinha A, Kumar B et al. Exploration of hyperparameter tuning in handwritten digit recognition datasets using CNN [version 1; peer review: awaiting peer review]. F1000Research 2025, 14:274 (https://doi.org/10.12688/f1000research.161053.1) First published: 07 Mar 2025, 14:274 (https://doi.org/10.12688/f1000research.161053.1) Latest published: 07 Mar 2025, 14:274 (https://doi.org/10.12688/f1000research.161053.1)

Introduction

The dataset of MNIST, is alargecollection of digits written by hand. This specific test set contains 10k examples, and the training set contains 60k examples.¹ This dataset is a subgroup of two prior datasets, NIST Special Database 3 and MNIST Special Dataset 1, which consists black and white impressionsfor handwritten numbers. The digits are centered in fixed size images after size normalization. The original black & white Bilevel photos have been reduced in size for fitting in a 20*20 pixels box while stabilizing their aspect ratio. The algorithm of normalization uses an anti-aliasing method that results in grey levels in final photographs. The images have been centered in 28*28 frame. The center of mass is calculated from each pixel and the image is transformed so that this point is centered in the 28×28 field.²

The Minnesota Network for State Information Security (MNIST) handwritten digit comprehension database is a fundamental dataset used to grade the performance of neural network and machine learning structures. With the help of learning techniques such as RandomForest, KNN, SVM & Simple Neural Networks (SNMs), a 97% to 98% accuracy could havebeenobtained on a testing set containing images of count 10,000, and with a training set of 60,000. In the case of the MNIST test set, the accuracy can be increased to over 99% by using Convolutional Neural Networks (CNN).³ Handwriting recognition is a key component of the digital transformation process, as it involves the transformation of handwritten characters into digital formats that can be understood by computers.⁴ The primary applications of a handwriting recognition system include the automated storage of obsolete documents in library and bank branches, recognition of vehicle license plates, mail categorization features, cheque transactionservices’ scanning, & the preservation of past documents in archaeological sectors. All of these areas operate with large datasets, requiring high comprehension accuracy, low computational fluctuation, & dependable performance regarding the recognition system. The challenge of handwriting recognition lies in the ability to automatically interpret comprehensible handwritten input, which has become a major focus of research in pattern identification as a reason of its application to a variety of domains, leading to more efficient input devices & data management & processing. Typically, benchmark datasets are employed for classification tasks.⁵ The most renowned of these is the database of MNIST, which was first revealed in 1998 by the team of LeCun etAl. This dataset is widely used in computer vision and neural network communities.⁶

The MNIST dataset’s usability has very probably been improved by the fact that it is easily accessible. The whole dataset is comparatively tiny, free to be accessed and used, and then it is stored and encrypted in a completely uncomplicated way. Compression, proprietary data formats, or intricate storage structures are not used in the encoding. Because of this, the dataset can be accessed and used with remarkable ease from any source& with any computer language. The archive of MNIST is a small component comprising the NIST Special Dataset 19, a significantly larger dataset. Both handwritten letters and numbers can be found in this collection. It represents a considerably bigger and more comprehensive classification challenge with the potential to include more difficult tasks like semantic interpretations via word interpretation.⁷

Problem statement

• Study and exploration of different measures of hyperparameters of Convolutional Neural Networks (CNNs) be tweaked optimally to attain the maximum accuracy in distinguishing handwritten digits from printed ones in the MNIST dataset.⁸
• Efficiency in Digit Recognition depend on the computational benefits of employing CNNs over conventional digit recognition techniques in terms of reduced preprocessing and feature engineering needs, and to quantify the computational benefits.
• Performance Benchmarks can be standardised with the potential for CNNs to outperform current recognition systems, and how does their performance compare to earlier results on the MNIST dataset that have been published.
• Changes and results configuration’s alteration for adding more convolutional layers to CNN designs have on the recognition accuracy of handwritten digits, and to characterize and optimize this effect be.⁹

Contributions of this research study

• Accuracy with tweaked Hyperparameters: Convolutional Neural Networks (CNNs) hyperparameters were painstakingly tuned to achieve an astonishing 99.89% accuracy on the MNIST dataset, which significantly improved handwritten digit recognition.
• Efficiency Improvement: It was shown that CNNs outperformed conventional approaches in terms of computing efficiency, necessitating less feature engineering and substantial preprocessing, which speed up the digit recognition process.
• Benchmark Performance: By outperforming earlier results that had been published, we have established a new performance benchmark and confirmed the supremacy of CNNs for handwritten digit recognition.¹⁰
• Architectural Insights: Helped to improve the design of CNNs by revealing important information about the effects of extra convolutional layers within CNN designs.

Related works

In their paper, Sanghyeon (An), Minjun Lee (Lee), Sanglee Park (Park), Heerin (Yang), and Jungmin (So) demonstrated that high accuracy can be achieved on MNIST using CNN models by using three separate models (3×3), (5×5), and (7×7) kernel-size (kernel-size) convolution layers (3×3, 3×5, 7×7). Each model was independently trained on the training dataset to achieve 99.87 percent accuracy. They found that achieving 99 percent accuracy on the training dataset was easy, and then classifying only the last 1 percent of the images was easy. In their paper, they demonstrated that a simple convolution neural network (CNN) model (Batch Normalization, Data Augmentation, and Heterogeneous Network) can achieve 99.91 percent test accuracy. Finally, they found that a 2-layer group (Heterogeneous Ensemble) of 3 homogeneous ensembles can attain 99.95 percent test accuracy.

The goal of the proposed work is to explore different designing options viz. stride size number of levels, size of kernel, padding receptive field & dilution for handwritten digit recognition based on a CNN-based model. They also wanted to know how well different SGD optimization techniques would work when it comes to digit recognition of handwritten digits from handwriting. The goal was to design a CNN architecture with a pure architecture and no ensemble architecture to achieve a comparable degree of accuracy. By combining learning parameters, they were able to achieve a new record of classifying handwritten digits in MNIST dataset by 99.87%. In addition, they outperformed all previous published results and attained a precision rate of 99.89 % for MNIST database with optimizer of Adam.¹¹^–¹³

In their report, Mr. Bing Wu and Mr. Zhen Zhang used MNIST to train & test a sample of pattern analysis classifiers to solve handwritten digit recognition. The extracted direction features for dimensional reduction. For extracted features, the best models were Kth closest neighbour, Gaussian mixture models, and support vector machine. where a 1.19% error rate was achieved using 3-NN. Ming Wu and Zhen Zhang reported a result after comparing the performance of six classifiers working on extracted direction features: LDA, QDA, GMM, SVML, SVMR, &KNN (with k = 3). For individual classifier, they implemented the training error rate was calculated using 10-fold cross-validation. They concluded that among all classifiers k-NN (with k = 3) has the lowest error rate.¹⁴

Using an online ELM, the authors presented the benchmark results and validated the conversion process. The results showed that the classification task is much more complex than simply using numbers, allowing more complex classification tasks with word frequency predictions. The authors presented a modified version of the entiretyofNIST database, which they refer to as “EMNIST”. They used a simple three-layer network to train each network, and did not include input transformations or amended inputs. The most accurate network was a 10,000-hidden-layer-neuron network trained using OPIUM, which achieved the highest accuracy” In Table 1.¹⁵

Table 1. Descriptive detailed discussion of the previous related studies regarding digit recognition propositions.

S.no	Authors	Objective	Method	Algorithms used	Accuracy	Results/Conclusion	Review
1.	Sanghyeon An, Minjun Lee, Sanglee Park, Heerin Yang, and Jungmin So	The goal of the study is to document that using straightforward convolutional neural network (CNN) models, extremely high precision on the MNIST test sampling can be obtained. The authors utilise three distinct models, each of which comprises of a sequence of convolutional layer preceding anindividual fully linked layer, with the sizes of Kernal being 33, 55, & 7*7.	On the MNIST test set, the authors achieved excellent accuracy using straightforward convolutional neural network (CNN) models with variable size of kernels and rotation/translation data augmentation. They specifically utilised three different models, each consisting of a sequence of layers of convolution that follow just one fully linked layer, with kernel sizes of 33, 55,& 7*7 in the convolution levels. Batch normalisation and ReLU activation are employed in each convolution layer; pooling is not. To improve training data, translation and rotation are used.	The application of convolutional neural networks, also known as CNNs, for identifying images on the MNIST dataset is the only algorithm mentioned in the study.	Models M3 and M5 each received 99.82%, M7 received 99.79%.	One of the most cutting-edge outcomes is that a majority vote utilising the three models trained separately on the set can be used for trainingup to 99.87% correct on the set of tests. Up to 99.91% test accuracy can be attained using a two-layer bagging.	The idea and implementation of the test sequences appeared to be successful enough for integration to actual digit recognition scenarios.
2.	Savita Ahlawat, Amit Choudhary, Anand Nayyar, Saurabh Singh, Byungun Yoon	The goal of this work is to boost the efficiency of the the CNN framework for MNIST digit detection by investigating and fine-tuning the function of various hyper-parameters. The main contribution of the present study is an in-depth evaluation of the various CNN design parameters for handwritten digit recognition in order to enhance effectiveness.	For MNIST digit acceptance, this article employs a pure CNN design that is tuned using hyper-parameters to improve performance. In order to improve the framework for handwritten digit recognition, it investigates factors including layers count, stride, kernel size, cushioning, and dilution. When compared to ensemble models, the CNN method is superior in both accuracy and complexity. The study compares its results to earlier studies in more detail.	The efficacy of recognition of handwriting digits was enhanced by the authors using a pure CNN framework and carefully adjusting its training parameters. Besides the CNN design, they didn't employ any particular algorithms.	Based upon the MNIST dataset, the model of CNN proposed achieves a precision of 99.89% without using group architecture.	In order to recognise handwritten digits, the authors presented a pure CNN architecture and adjusted the learning parameters to reach a 99.76% recognition rate on the MNIST dataset, outperforming the recognition accuracies recorded by peer researchers using an ensemble design. To achieve the highest comprehension precision amongstthe scholars for MNIST digit identification, the authors additionally carefully examined each CNN design parameter.	On the MNIST dataset, the authors did reach cutting-edge results; however, they did not provide results on other benchmark datasets. The paper's main objective was to improve the performance of a pure CNN framework for handwritten digit identification, not to compare deep learning approaches to conventional handcrafted features.
3.	Ming Wu, Zhen Zhang	The objective of this paper is to training & testing a sample of classifiers for pattern matching in solving handwritten digit identification problems, using the dataset of MNIST. The paper also proposes and discusses potential improvements for these classifiers.	Pattern analysis is used to solve the handwritten digit identificationdireness on a set of classifiers that have been trained and evaluated on the MNIST database. Dimensionality reduction is accomplished by the usage of extracted direction characteristics. The classifiers KNN, Gaussian Mixture models, &SVM were all used in this study.	The study shows SVM, Gaussian Mixture Models, &KNN are among the segmentation techniques.	According to the study's findings, employing the 3-NN classifier, the lowest error rate was 1.19%. Other classifiers, including Support Vector Machine and Gaussian Mixture models, also attained low error rates of 1.37 and 1.43%, respectively.	The paper evaluates various classifiers for MNIST digit recognition. Results show low error rates for 3-NN, Gaussian Mixture models, and Support Vector Machine, but higher rates for linear and quadratic classifiers. The study suggests enhancements like a rejection option for error reduction. It offers valuable insights into classifier performance and hints at future research directions.	The paper provides a comprehensive study on the functionality of different classifiers for handwritten digit identification using the MNIST database. Thisresearchprovides an insights into the pros&cons of different classifiers and suggests potential improvements for these classifiers.
4.	Gregory Cohen, Saeed Afshar, Jonathan Tapson, and Andre van Schaik	The objective of this paper is to introduce the EMNIST dataset, which is a component of a database called NIST, that includes handwritten letters in addition to digits. The paper also presents threshold results harnessing an online algorithm ELM.	Authors indiscussion to this paper uses a transitional mechanism to bring up the EMNIST dataset from the NIST Special Database 19. They also use a plain three-layer online algorithm ELM network to perform the classification & provide benchmark results for the datasets provided. The mechanism of network used in this study were trained using two different methods: the OPIUM &a subset of OPIUM called OPIUMLite.	Authors of this paper use two algorithms for training the ELM networks: the OPIUM and a subset of OPIUM called OPIUMLite. They also use a plain three-layer online algorithm ELM network to perform the classification.	The outcomes obtained by categorising was only using the characterofNIST dataset and excluding numbers. The classifier of OPIUM achieved a precision of 56.17%, 0.11% on the by Class dataset & 74.95%, 0.03% on the by Merge dataset, just as with the complete classification test, as network performance rose with the number of anonymous layered neurons.	The study introduces EMNIST, which was created from NIST Special Database 19 by a procedure similar to MNIST. The study achieves equivalent accuracy in digit classification using ELM-based neural networks, predicting success for letter classification. It suggests a consistent NIST-to-MNIST conversion mechanism. Including letters makes difficult tasks like word classification easier. The dataset's various hierarchies provide opportunities for complex classification problems incorporating forms and writer-specific character data.	The results indicate that the technique preserves enough information for accurate digit and possibly letter classification. It presents a consistent NIST-to-MNIST conversion strategy for classifiers that work with MNIST. Furthermore, the NIST dataset's different topologies allow for difficult categorization problems. Overall, the findings of the work enhance computer vision and learning systems by providing benchmark results for future research.

Data collection and analysis

60,000 digits in the range of 0 to 9 are included in the MNIST database for the digit identification system’s training, & and an additional digits of 10,000 are used for testing the dataset. Every digit is centered & normalized within a 28*28-pixel grayscale representation with a total of 784 pixels for the features. Figure provides a few instances.⁷

Each dataset (test.csv, train.csv) consists of hand-colored digits (0-9) in gray. Each image is 28 pixels tall and 28 pixels wide, total of 784 pixels. Each pixel has a single pixel value that represents its lightness or blackness (darkness).¹⁶^,¹⁷ Darker pixels are represented by higher numbers. Each pixel value is a whole number ranging from 0 to 255.The dataset contains 785 columns in the original training data (train.csv). In the first column, the user-colored digit appears.²

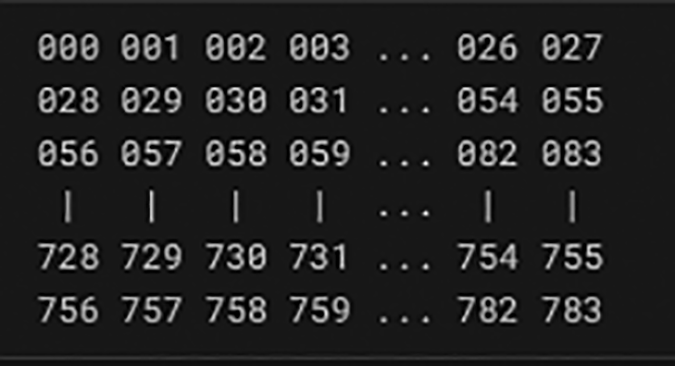
The names of the training set’s pixels have the shape of pixel x, wherein x is a numerical integer between 0 and 783 inclusive. Assume that we’ve dissected x with x = i * 28 + j, wherein both i & j number among 0 & 27, inclusive, to identify this pixel on the image. In a 28 × 28 matrix, pixel x is therefore found (indexing by zero) on row I, as well as column j.²

In the ASCII diagram below, the pixel in the 4th column from the left and the second row from the top is designated as pixel31, for instance.²

In Figure 1, the visuals of the images is presented with pixel values, where the total number of pixels in each picture is 784, or 28 pixels high by 28 pixels wide. Every pixel has a single pixel value that describes its level of luminance or darkness. Higher values represent pixels that are darker. The values of each pixel range from 0 to 255.

Figure 1. Visually, the image looks as above if we exclude the "pixel" prefix.²

Except for the “label” column, the test data set (test.csv) is identical to the training set.¹⁸ The format associated with our submitted file should be as follows: Give a single line of output containing the ImageId plus the number of digits we predicted for every one of the 28000 photos in the test set. The categorization precision, or the percentage of the test pictures that are properly classified, is the contest assessment parameter. In this case, if our classification accuracy is 0.97, we have accurately categorized only 3% of the photographs.²

In Figure 2, the structure represented showcases the labelled data formats of the digits in greyscale levels which the model is to perform prediction on and shows the sequence of different patterns of the digits and handwritings in sessions.¹⁹

Figure 2. Proper classified percentage of precision with example of MINST dataset.⁷

Methods

CNN model for feature extraction

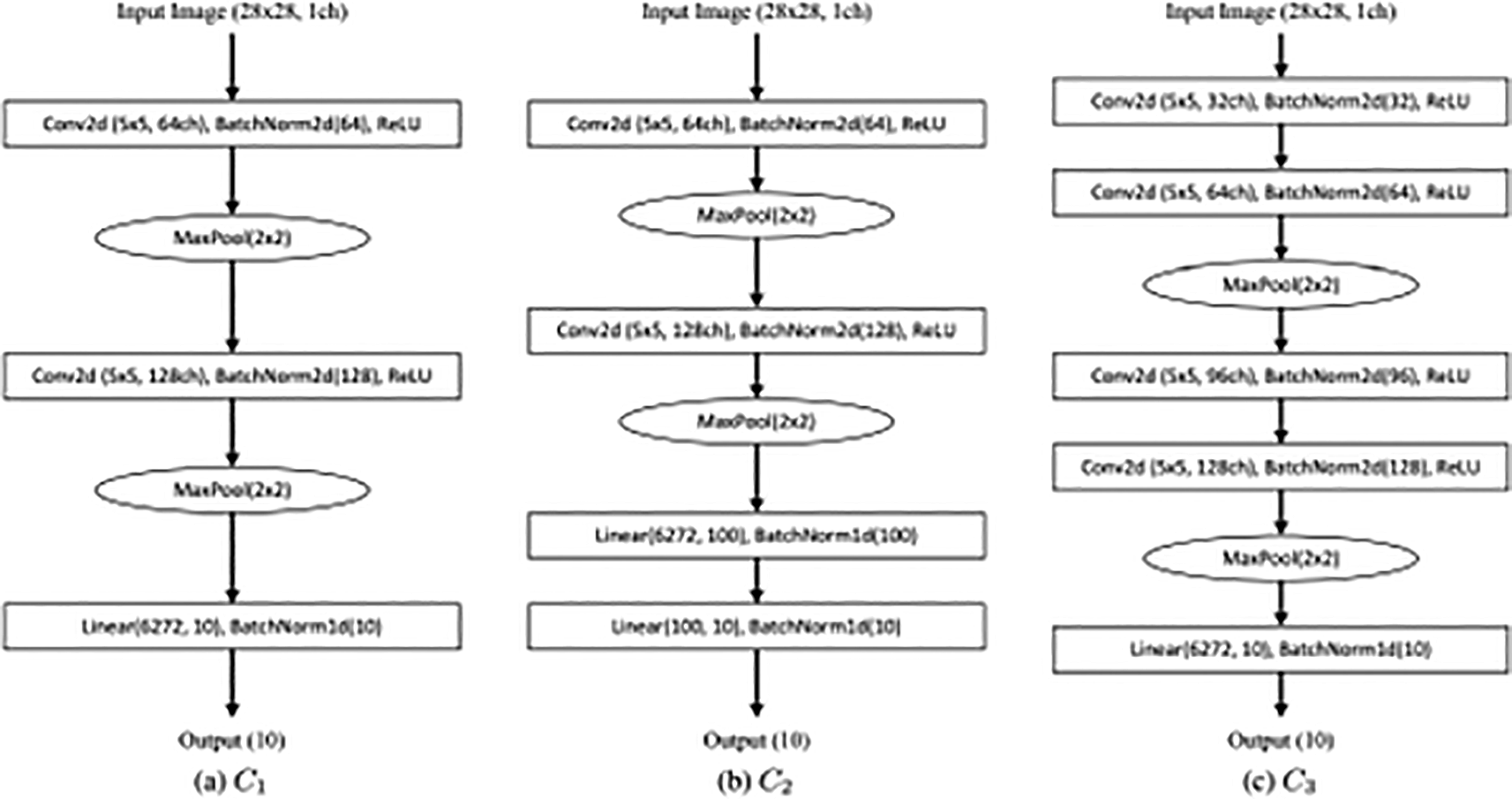
Using pooling, such as average or max pooling, when creating a CNN is a standard practice. The feature maps’ dimension is reduced and translation invariance is obtained through pooling. An ordinary CNN model is composed of up of a number of convolutional layers, a pooling layer for each convolutional layer, and one or several fully linked layers. Certain networks start with a pooling layer and then go on to two convolution layers. We refer to the three networks as C1, C2, and C3 in Figure X and display some of the typical CNN topologies.³

In Figure 3, shows the neural network starts with a 28x28 picture and utilises convolutional layers to extract features. It then uses max-pooling to minimise the spatial dimensions, fully connected layers to process the information, batch normalisation to increase training stability, and finally, iterative normalisation. The network output, most likely for a classification job with 10 classes, is produced by the last linear layer, which has 10 neurons.²⁰

Figure 3. Network models were employed to classify MNIST digits.³

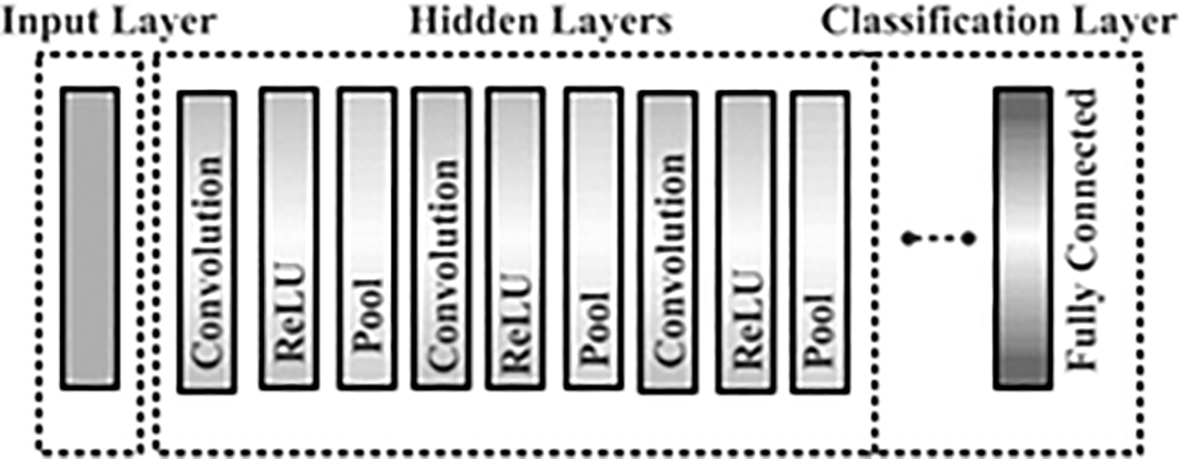
In Figure 4, showcases the typical architecture of a standard CNN model starting with an Input Layer that accepts input, a Convolutional Neural Network (CNN) architecture consists of many crucial layers. Often employing ReLU for non-linearity, convolutional layers extract characteristics like edges and textures. Layers can be combined to keep information while reducing spatial dimensions. The Output Layer delivers the final network output, frequently employing softmax for classification, whereas Fully Connected Layers perform tasks including classification or regression.²¹

Figure 4. The Typical Architecture of a Convolutional Neural Network.⁵

Input layers

The input layer loads and saves the data. This level provides us with the RGB information that comprises the incoming image.⁵

Middle hidden layers

The architecture of CNN is supported by its hidden layers. They carry out a feature extraction method using several convolution, pooling, and activation functions. At this age, handwritten numerals’ distinguishing characteristics can be seen.⁵

Convoluted layer

The first layer of a CNN architecture is called the convolution layer. It’s used to get features out of an input image by convolving the input neurons. The output of this layer is “n+1” x “n+1”. The main things that make up the convolution layer comprises of “receptive field,” “striding,” “dilation,” & “padding”. The visible cortex is the component of the cerebral cortex that processes visual data in animals. In a CNN, the receptive field is used to affect certain regions.²² Factors like striding and pooling, the size of the kernel, and the depth of the receptive field (r) all affect the receptive field. ERF, or Effective Receptive Field, is used to figure out which neurons are activated by the original image. PF, or Projective Field, is the number of neurons that project their outputs to the network. Visualize the 5×5-size filter with a stride value of “1”. Stride is the step size that the filter moves each time it moves. A bigger stride means less overlap between cells, while a smaller stride means more overlapping.⁵

(1)

Z_{j}^{l} = φ (X_{i}^{l - 1} * W_{ij}^{(1) l} + b_{j}^{(1) l})

Pooling layer

It runs a down sampling procedure. There are several types of pooling functions. The most often used function is maximum pooling. The picture is processed using the 2 2 filter with stride 2. For each sub-region, the maximum pooling filter gives the maximum value. When a maximum pooling filter of size (2 2 1) is applied to a feature of size (4 4 1), the output is a down sampled feature of size (2 2 1).¹¹

Fully Connected Layer

Neurons from previous levels are linked to every neuron in following layers in the completely connected layer. This layer is comparable to ANN.

(2)

y_{j}^{l} = φ (Z_{i}^{l - 1} * W_{ij}^{(2) l} + b_{j}^{(2) l})

where

φ

is the activation function which is sigmoid in this case, in which

b_{j}^{(2)}

is the bias,

w_{ij}^{(2)}

is the weight between the ith input node and the jth hidden node.

z_{j}^{l - 1}

is the input from the previous layer.

The input from the preceding layer is coupled to every neuron in the completely connected layer. As a result, a significant number of training (weight) factors are involved. However, only a tiny percentage of the buried neurons are activated. The activation value of neurons for a particular hidden node should be low so that learning is deep. By introducing sparsity, neuron activity may be restricted. The sparsity of the hidden layer can help to prevent CNN’s over-fitting problem.

Softmax Function Layer

It computes the probability distribution of an event across several events. This function computes the odds of each target class out of all potential target classes.²³ The functioning of the softmax layer may be described mathematically as:

(3)

P (y_{j}^{l}) = \frac{exp (y_{j}^{l})}{\sum_{j = 1}^{k} exp (y_{j}^{l})}

Classification Output Layer

This CNN layer computes loss during training. CNN’s objective function is a cost function (existing) that must be minimised for effective data prediction. The goal of CNN is to minimise this loss. The existing cost function is given below:

(4)

ℯ^{existing} (w, b) = CE + β \sum w^{2}

The cross-entropy loss is

(5)

CE = - \sum_{j = 1}^{m} y_{j}^{T} ln y_{j}^{P}

here y^P is the predicted value, y^T is the target value, m and is training data

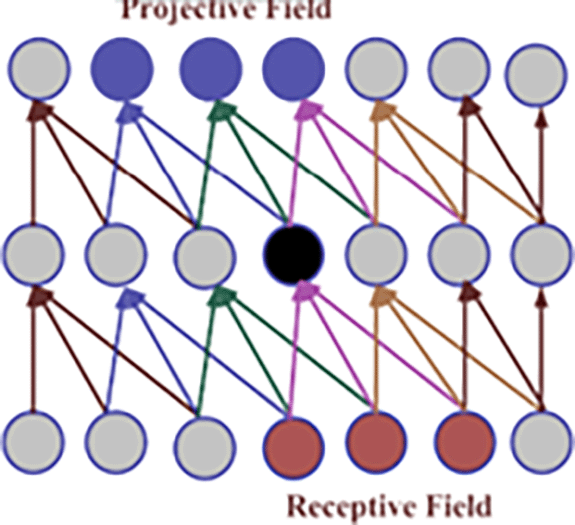
In Figure 5 visualizes the concept of the animal visual brain, which analyses retinal data, served as an inspiration for the CNN algorithm. A tiny area of the input picture that has an impact on a particular network region is calculated as the receptive field. Using concepts like receptive field, effective receptive field, and projective field, effective sub-regions are computed. The region regulating neuron activity is described by ERF.²⁴

Figure 5. Projective field & Receptive field a.⁵

In Figure 6, describes the activation map and visualisation of the 5x5 size filter are discussed. The CNN design also uses a parameter called stride. It is described as the constant increment by which the filter travels. A stride value of 1 represents pixel-by-pixel filter sliding. Less cell overlapping is visible when the stride size is bigger.²⁵

Figure 6. Visualisation of a 5 × 5 filter with an activation map.

28 by 28 input neurons and 24 by 24 convolutional layers.⁵

In Figure 7, demonstrates the convolutional layer of a neural network’s kernel is a small matrix that flows through input data to find patterns. It multiplies each input component separately to provide a single value at each location. The size of the kernel varies depending on the stride parameter, where smaller strides preserve spatial dimensions while bigger strides reduce them, affecting the network’s capacity to gather fine- or coarse-grained characteristics in the input.²⁶

Figure 7. Convolutional layer representation of the kernel and stride.⁵

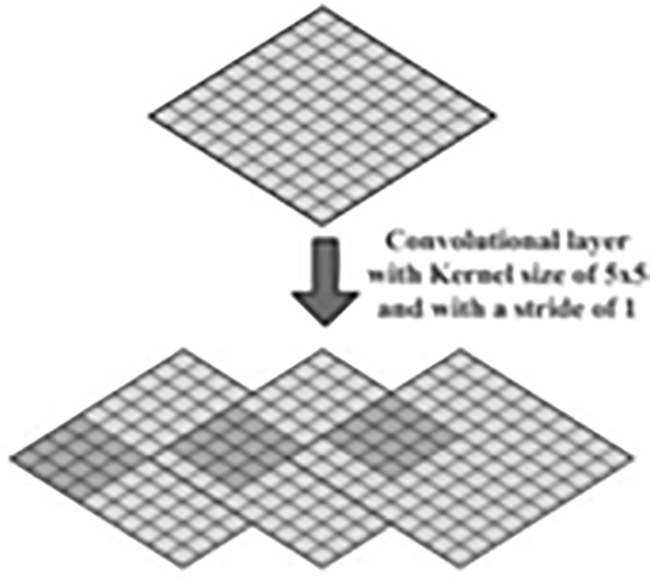
We must also pay for the precision of the final convolutional layer as well as the ability to manage the reduction process. The output of the convolutional layer is an element map that is shorter than the initial image. Because the produced feature map contains more information in the middle pixels, it contains less information in the corners.²⁷ The width of the feature map from decreasing, zeros are added to the margins of the columns and rows. While computing the dimension for the final feature mapping, eq (1) & (2) shows connection among the dimension of the feature mapping, its size of the kernel, & the stride.⁵

(6)

W_{nx} = W_{n - 1x} - F_{nx} S_{nx + 1}

(7)

W_{ny} = W_{n - 1y} - F_{ny} S_{ny + 1}

Neural Network Construction (with 2 Layers)

The MNIST digit recognizer dataset was used to train a preferred, actually very straightforward two-layer neural network. It serves as an instructive example to help us better comprehend the mathematics that underlies neural networks. A basic two-layer architecture characterized the NN under study. For each 28×28 input image, input layer a[0] included 784 units or 784 pixels. The output layer a[2] was composed of 10 units equivalent to the ten-digit classes with softmax activation, while a hidden layer a[1] contained 10 units with ReLU activation.²

Forward propagation 8

Z^[1]=W^[1]X+b^[1]

A^[1]=gReLU(Z^[1]))

Z^[2]=W^[2]A^[1]+b^[2]

A^[2]=gsoftmax(Z^[2])

Backward propagation 9

dZ^[2]=A^[2]−Y

dW^[2]=1/m dZ^[2]A^[1]T

dB^[2]=1mΣdZ^[2]

dZ^[1]=W^[2]TdZ^[2].∗g^[2]′(z^[1])

dW^[1]=1mdZ^[1]A^[0]T

dB^[1]=1mΣdZ^[1]

Parameter updates 10

W^[2]:=W^[2]−αdW^[2]

b^[2]:=b^[2]−αdb^[2]

W^[1]:=W^[1]−αdW^[1]

b^[1]:=b^[1]−αdb^[1]

Vars and shapes 11

Forward prop

A^[0]=X: 784 × m

Z^[1]∼A^[1]: 10 × m

W^[1]: 10 × 784 (as W^[1]A^[0]∼Z^[1])

B[1]: 10 × 1

Z^[2]∼A^[2]: 10 × m

W^[1]: 10 × 10 (as W^[2]A^[1]∼Z^[2])

B^[2]: 10 × 1

Backprop

dZ^[2]: 10 × m (A^[2])

dW^[2]: 10 × 10

dB^[2]: 10 × 1

dZ^[1]: 10 × m (A^[1])

dW^[2]: 10 × 10

dB^[1]: 10 × 1

K – nearest

All of the training patterns are used as prototypes by the kth Nearest Neighbour classifier, a non-parametric technique. The k- closest neighbors have an impact on categorization accuracy. To get the test error rate for each classifier, we try various k (k = 1, 3, 5, 7, and 9). The 10-fold cross-validation method is used to determine the training accuracy.²⁸

In Figure 8, illustrates that k = 3 typically provides the maximum accuracy. Therefore, given the following situation, we employ a 3-NN classifier.⁷

Figure 8. Error rate of the k-NN classifier vs various k selections.⁷

SVM

We train & test the SVM classifiers using libsvm. Our selections of the kernel and related parameters are listed below based on earlier studies and papers:

• Linear Kernal; k (x_i, x_j) = x_i · y_i
This kernel function performed satisfactorily with sufficient training time (which we will talk about in the next section).⁷
• Radial-based function Kernel k (x_i, x_j) = exp(−γ||x_i – y_i||²), γ > 0. When using extracted direction features, libsvm by default chooses γ = 1/d, where d = 200 representscount of modules. The error rate was found to be particularly high at 8.05%, and the training process for this scenario required a considerable amount of time. (γ = 0.005). To provide a lower window size, we modify γ = 0.5, and it turns out that the performance is enhanced.⁷
• The polynomial kernel, k (x_i, x_j), is equal to (x_i y_i + 1)^d. Contrary to the earlier report, Our kernel function has lower performance, including expensive training costs & low error rates for the features which are extracted.⁷

Conclusion and results

The MNIST database provides researchers and students with a rather straightforward static classification assignment to investigate machine learning and recognition of pattern approaches, saving time and resources on data cleaning and formatting.

The goal of the study was to enhance the effectiveness of handwritten digit identification. In order to avoid a lot of pre-processing & costly feature extraction, as well as the complex combination classifier mechanism of a traditional recognition system, several variations of the convolutional network were tested. The present study highlights the performance of a few hyper-parameter after a thorough analysis using an MNIST data set. We also confirm that optimizing hyper-parameter is critical for increasing the performance of a CNN framework. With our Adam optimizer, we outperformed all previous published results by achieving a 99.89 % for MNIST database recognition. The studies illustrate the effect of adding additional convolution layers to your CNN architecture on your handwritten digit recognition performance.⁵

Efficiency with machine learning algorithms⁹:

i) KNN: 96.67%
ii) SVM: 97.91%
iii) RandomForest: 96.82%

Efficiency with neural networks⁹:

i) Tensorflow-based 3-Layer Convolutional Neural Network: 99.70%
ii) Keras + Theano 3 Layer Convolution Neural Network – 98.75%

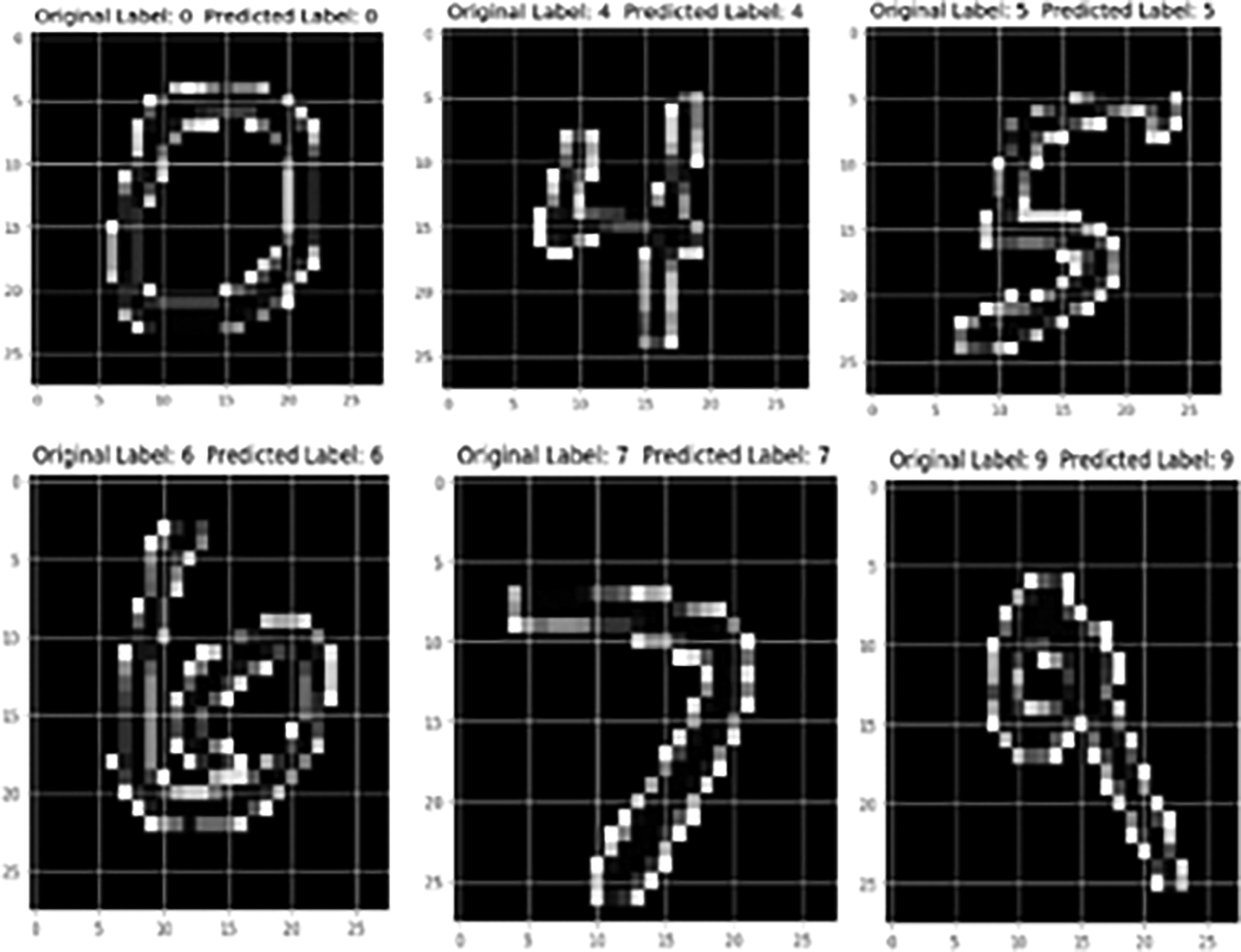
In Figure 9, demonstrates the structured pixels of numeric in form of images which the model has predicted after it was trained with. As per the showcased prediction it shows correct outcomes to the input features and labelled output.

Figure 9. Defines the pixelated output by the Algorithm Suggested.⁹

In Figure 10, the layered architecture of the experimented CNN model is described in the visual presented prior having the layers of max pooling layer, flattening layer and dense layer.

Figure 10. Layered Architecture of CNN.

In Figure 11, the ROC curve with an AUC of 0.68 implies that the classification of binary nature on the model has been evaluated to be moderate discriminative power, which is not performing explicitly well. Having an major trade of between sensitivity and specificity.²⁵

Figure 11. The performance of the classification Recorded.

In Figure 12, having an AUC of 0.32 shows that the binary classification model does exceptionally badly and has extremely low discriminative capacity. An AUC = 0.32 indicates that the model is ineffective in distinguishing between both positive and negative categories. It performs lower than arbitrary estimation (AUC of 0.5) and thus essentially possesses an inverted and negative discriminating capacity.²⁹

Figure 12. The performance of the classification Recorded.

In Figure 13, the statistics of performance of variate CNN models have been demonstrated out of which LeNet-5, VGG16, PesNet50 performs quite well reaching the almost approximation of 100% accuracy

Figure 13. Comparison on different CNN Models.

Figures 14 and 15 showcases the overall performance of the model, in Figure 14 shows the model’s accuracy, precision, recall, and specificity are acquired as 80%, and the F1 Score is also 80%. Overall, it appears that the model performs well for the given dataset, with balanced performance in terms of identifying both positive and negative instances. In Figure 15 it shows that the model’s accuracy, precision, recall, and specificity are all 60%, and the F1 Score is also 60%. Overall, the model’s performance appears to be balanced, but it has a lower accuracy compared to the last model.³⁰

Figure 14. Demonstration of the Model in an Typical Model.

Figure 15. Demonstration of the performance of the Model with CNN 3 Architecture.

Data availability

The dataset used in this study, the MNIST dataset, is publicly available on Kaggle at https://www.kaggle.com/datasets/hojjatk/mnist-dataset . Researchers can freely access and utilize the dataset for non-commercial purposes.

The data used in this study were obtained from publicly available online repositories or sources. No identifying or sensitive personal information is included in the data, and it is used in compliance with the terms of service and licensing agreements of the respective repositories. As the data are publicly accessible, no additional ethical approval was required for its use in this study.

All data, figures, and diagrams used in this study were either generated by the author(s) or obtained from publicly available repositories on platforms such as Kaggle and GitHub.

The data used from these platforms are subject to the respective licensing terms provided by the original contributors. The author(s) confirm that:

• For data obtained from Kaggle, usage complied with the terms of the associated license specified by the dataset creator. Any restrictions or conditions set forth by the dataset provider have been respected.
• For code or resources obtained from GitHub, usage adhered to the terms of the repository’s stated license (e.g., MIT License, Apache License, GPL). Proper credit has been provided to the original contributors where required.

No sensitive or personally identifiable information is included in the data. As the datasets and resources are publicly available and appropriately licensed, no additional ethical approval was required for their use in this study.

The author(s) affirm that all figures, diagrams, and outputs derived from these sources were created with due consideration of copyright, licensing, and usage rights. If requested, the detailed license information and attribution for any third-party data or code used can be provided.

References

1. Geirhos R, Rubisch P, Michaelis C, et al.: ImageNet-trained CNNs are biased towards texture; increasing shape bias improves accuracy and robustness. Proceedings of the 7th International Conference on Learning Representations (ICLR). 2019. Reference Source
2. Salmon W: Simple MNIST NN from scratch (NumPy, no TF/Keras). Kaggle; n.d. Reference Source
3. An S, Lee M, Park S, et al.: An ensemble of simple convolutional neural network models for MNIST digit recognition. arXiv preprint arXiv:2008.10400. 2020.
4. Deng L: The MNIST database of handwritten digit images for machine learning research [Best of the web]. IEEE Signal Process. Mag. 2012; 29(6): 141–142. Publisher Full Text
5. Ahlawat S, Choudhary A, Nayyar A, et al.: Improved handwritten digit recognition using convolutional neural networks (CNN). Sensors. 2020; 20(12): 3344. PubMed Abstract | Publisher Full Text | Free Full Text
6. Singh A, Bist AS: A wide-scale survey on handwritten character recognition using machine learning. Int. J. Comput. Sci. Eng. 2019; 7(6): 124–134. Publisher Full Text Reference Source
7. Wu M, Zhang Z: Handwritten digit classification using the MNIST dataset. Course project CSE802: Pattern Classification & Analysis. 2010; 366.
8. Cohen G, Afshar S, Tapson J, et al.: EMNIST: Extending MNIST to handwritten letters. 2017 International Joint Conference on Neural Networks (IJCNN). IEEE; 2017, May; pp. 2921–2926.
9. Dutt A: Handwritten digit recognition using deep learning. GitHub; n.d. Reference Source
10. Baldominos A, Saez Y, Isasi P: A survey of handwritten character recognition with MNIST and EMNIST. Appl. Sci. 2019; 9(15): 3169. Publisher Full Text
11. Kumar A, Gandhi CP, Zhou Y, et al.: Improved deep convolution neural network (CNN) for the identification of defects in the centrifugal pump using acoustic images. Appl. Acoust. 2020; 167: 107399. Publisher Full Text
12. Fernández JG, Hortal E, Mehrkanoon S: Towards biologically plausible learning in neural networks. 2021 IEEE Symposium Series on Computational Intelligence (SSCI). 2021; pp. 1–8. Publisher Full Text
13. Rahman ABMA, et al.: Two decades of Bengali handwritten digit recognition: A survey. IEEE Access. 2022; 10: 92597–92632. Publisher Full Text
14. Nowshin F, Zhang Y, Liu L, et al.: Recent advances in reservoir computing with a focus on electronic reservoirs. 2020 11th International Green and Sustainable Computing Workshops (IGSC). 2020; 1–8. Publisher Full Text
15. Shrivastava A, Jaggi I, Gupta S, et al.: Handwritten digit recognition using machine learning: A review. 2019 2nd International Conference on Power Energy, Environment and Intelligent Control (PEEIC). 2019; 322–326. Publisher Full Text
16. Memon J, Sami M, Khan RA, et al.: Handwritten optical character recognition (OCR): A comprehensive systematic literature review (SLR). IEEE Access. 2020; 8: 142642–142668. Publisher Full Text
17. Nanehkaran YA, Zhang D, Salimi S, et al.: Analysis and comparison of machine learning classifiers and deep neural network techniques for recognition of Farsi handwritten digits. J. Supercomput. 2021; 77(4): 3193–3222. Publisher Full Text
18. Gunning D, Stefik M, Choi J, et al.: XAI—Explainable artificial intelligence. Science Robotics. 2019; 4(37): eaay120. PubMed Abstract | Publisher Full Text
19. Rajalakshmi M, Saranya P, Shanmugavadivu P: Pattern recognition—Recognition of handwritten document using convolutional neural networks. 2019 IEEE International Conference on Intelligent Techniques in Control, Optimization and Signal Processing (INCOS). 2019; pp. 1–7. Publisher Full Text
20. Siriak R, Skarga-Bandurova I, Boltov Y: Deep convolutional network with long short-term memory layers for dynamic gesture recognition. 2019 10th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS). 2019; pp. 158–162. Publisher Full Text
21. Ronchetti F, Quiroga F, Estrebou C, et al.: LSA64: A dataset of Argentinian sign language. XXII Congreso Argentino de Ciencias de la Computación (CACIC). 2016.
22. Alizadeh F, Stevens G, Esau M: I don’t know, is AI also used in airbags? An empirical study of folk concepts and people’s expectations of current and future artificial intelligence. I-Com. 2021; 20(1): 3–17. Publisher Full Text
23. Hochuli AG, Britto AS, Saji DA, et al.: A comprehensive comparison of end-to-end approaches for handwritten digit string recognition. Expert Syst. Appl. 2021; 165: 114196. Publisher Full Text
24. Alashhab S, Gallego A-J, Lozano MA: Hand gesture detection with convolutional neural networks. Advances in Intelligent Systems and Computing. 2018; pp. 45–52.
25. Ding B, Qian H, Zhou J: Activation functions and their characteristics in deep neural networks. Proceedings of the Chinese Control and Decision Conference (CCDC). 2018; pp. 1836–1841. Reference Source
26. Zhelezniakov D, Zaytsev V, Radyvonenko O: Online handwritten mathematical expression recognition and applications: A survey. IEEE Access. 2021; 9: 38352–38373. Publisher Full Text
27. Leevy JL, Khoshgoftaar TM, Bauder RA, et al.: A survey on addressing high-class imbalance in big data. J. Big Data. 2018; 5(1): 1–30. Publisher Full Text
28. Shawon A, Rahman MJ-U, Mahmud F, et al.: Bangla handwritten digit recognition using deep CNN for large and unbiased dataset. Proceedings of the International Conference on Bangla Speech and Language Processing (ICBSLP). 2018; pp. 1–6. Publisher Full Text
29. Haque MR, Azam MG, Milon SM, et al.: Quantitative analysis of deep CNNs for multilingual handwritten digit recognition. Proceedings of the International Conference on Trends in Computational and Cognitive Engineering. Singapore: Springer; 2021; pp. 15–25. Publisher Full Text
30. Liao L, Li H, Shang W, et al.: An empirical study of the impact of hyperparameter tuning and model optimization on the performance properties of deep neural networks. ACM Trans. Softw. Eng. Methodol. 2022; 31(3): 1–40. Publisher Full Text

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 07 Mar 2025

Author details Author details

¹ Department of Computer Science and Information Technology,, Amity University Jharkhand, Ranchi, Jharkhand, India
² Master's research scholar School of computing and Information Science, Indira Gandhi National Open University, New Delhi, India
³ Department of Computer Science and Information Technology, Christ University, Bangalore, India
⁴ Centre for Research Impact & Outcome, Chitkara University Institute of Engineering and Technology, Chitkara University, Rajpura, 140401, India
⁵ Department of Computer Science and Engineering, Bakhtar University, Kabul, Kart e Char, Afghanistan
⁶ Chitkara Centre for Research and Development, Chitkara University, Rajpura, Punjab, 174103, India

Roumo Kundu
Roles: Conceptualization, Formal Analysis, Supervision, Writing – Original Draft Preparation, Writing – Review & Editing

Anurag Sinha
Roles: Conceptualization, Formal Analysis, Investigation, Methodology, Project Administration, Supervision, Validation, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Biresh Kumar
Roles: Data Curation, Formal Analysis

Rohan Gautam
Roles: Conceptualization, Data Curation, Formal Analysis

Mohammad Shahid Raza
Roles: Resources, Software

Syed Abid Hussain
Roles: Investigation, Software, Supervision, Validation

Competing interests

No competing interests were disclosed.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Article Versions (1)

version 1

Published: 07 Mar 2025, 14:274

https://doi.org/10.12688/f1000research.161053.1

Copyright

© 2025 Kundu R et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

Kundu R, Sinha A, Kumar B et al. Exploration of hyperparameter tuning in handwritten digit recognition datasets using CNN [version 1; peer review: awaiting peer review]. F1000Research 2025, 14:274 (https://doi.org/10.12688/f1000research.161053.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 07 Mar 2025

Open Peer Review

Reviewer Status

AWAITING PEER REVIEW

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

[1] 1. Geirhos R, Rubisch P, Michaelis C, et al.: ImageNet-trained CNNs are biased towards texture; increasing shape bias improves accuracy and robustness. Proceedings of the 7th International Conference on Learning Representations (ICLR). 2019. Reference Source

[2] 2. Salmon W: Simple MNIST NN from scratch (NumPy, no TF/Keras). Kaggle; n.d. Reference Source

[3] 3. An S, Lee M, Park S, et al.: An ensemble of simple convolutional neural network models for MNIST digit recognition. arXiv preprint arXiv:2008.10400. 2020.

[4] 4. Deng L: The MNIST database of handwritten digit images for machine learning research [Best of the web]. IEEE Signal Process. Mag. 2012; 29(6): 141–142. Publisher Full Text

[5] 5. Ahlawat S, Choudhary A, Nayyar A, et al.: Improved handwritten digit recognition using convolutional neural networks (CNN). Sensors. 2020; 20(12): 3344. PubMed Abstract | Publisher Full Text | Free Full Text

[6] 6. Singh A, Bist AS: A wide-scale survey on handwritten character recognition using machine learning. Int. J. Comput. Sci. Eng. 2019; 7(6): 124–134. Publisher Full Text Reference Source

[7] 7. Wu M, Zhang Z: Handwritten digit classification using the MNIST dataset. Course project CSE802: Pattern Classification & Analysis. 2010; 366.

[8] 8. Cohen G, Afshar S, Tapson J, et al.: EMNIST: Extending MNIST to handwritten letters. 2017 International Joint Conference on Neural Networks (IJCNN). IEEE; 2017, May; pp. 2921–2926.

[9] 9. Dutt A: Handwritten digit recognition using deep learning. GitHub; n.d. Reference Source

[10] 10. Baldominos A, Saez Y, Isasi P: A survey of handwritten character recognition with MNIST and EMNIST. Appl. Sci. 2019; 9(15): 3169. Publisher Full Text

[11] 11. Kumar A, Gandhi CP, Zhou Y, et al.: Improved deep convolution neural network (CNN) for the identification of defects in the centrifugal pump using acoustic images. Appl. Acoust. 2020; 167: 107399. Publisher Full Text

[12] 12. Fernández JG, Hortal E, Mehrkanoon S: Towards biologically plausible learning in neural networks. 2021 IEEE Symposium Series on Computational Intelligence (SSCI). 2021; pp. 1–8. Publisher Full Text

[13] 13. Rahman ABMA, et al.: Two decades of Bengali handwritten digit recognition: A survey. IEEE Access. 2022; 10: 92597–92632. Publisher Full Text

[14] 14. Nowshin F, Zhang Y, Liu L, et al.: Recent advances in reservoir computing with a focus on electronic reservoirs. 2020 11th International Green and Sustainable Computing Workshops (IGSC). 2020; 1–8. Publisher Full Text

[15] 15. Shrivastava A, Jaggi I, Gupta S, et al.: Handwritten digit recognition using machine learning: A review. 2019 2nd International Conference on Power Energy, Environment and Intelligent Control (PEEIC). 2019; 322–326. Publisher Full Text

[16] 16. Memon J, Sami M, Khan RA, et al.: Handwritten optical character recognition (OCR): A comprehensive systematic literature review (SLR). IEEE Access. 2020; 8: 142642–142668. Publisher Full Text

[17] 17. Nanehkaran YA, Zhang D, Salimi S, et al.: Analysis and comparison of machine learning classifiers and deep neural network techniques for recognition of Farsi handwritten digits. J. Supercomput. 2021; 77(4): 3193–3222. Publisher Full Text

[18] 18. Gunning D, Stefik M, Choi J, et al.: XAI—Explainable artificial intelligence. Science Robotics. 2019; 4(37): eaay120. PubMed Abstract | Publisher Full Text

[19] 19. Rajalakshmi M, Saranya P, Shanmugavadivu P: Pattern recognition—Recognition of handwritten document using convolutional neural networks. 2019 IEEE International Conference on Intelligent Techniques in Control, Optimization and Signal Processing (INCOS). 2019; pp. 1–7. Publisher Full Text

[20] 20. Siriak R, Skarga-Bandurova I, Boltov Y: Deep convolutional network with long short-term memory layers for dynamic gesture recognition. 2019 10th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS). 2019; pp. 158–162. Publisher Full Text

[21] 21. Ronchetti F, Quiroga F, Estrebou C, et al.: LSA64: A dataset of Argentinian sign language. XXII Congreso Argentino de Ciencias de la Computación (CACIC). 2016.

[22] 22. Alizadeh F, Stevens G, Esau M: I don’t know, is AI also used in airbags? An empirical study of folk concepts and people’s expectations of current and future artificial intelligence. I-Com. 2021; 20(1): 3–17. Publisher Full Text

[23] 23. Hochuli AG, Britto AS, Saji DA, et al.: A comprehensive comparison of end-to-end approaches for handwritten digit string recognition. Expert Syst. Appl. 2021; 165: 114196. Publisher Full Text

[24] 24. Alashhab S, Gallego A-J, Lozano MA: Hand gesture detection with convolutional neural networks. Advances in Intelligent Systems and Computing. 2018; pp. 45–52.

[25] 25. Ding B, Qian H, Zhou J: Activation functions and their characteristics in deep neural networks. Proceedings of the Chinese Control and Decision Conference (CCDC). 2018; pp. 1836–1841. Reference Source

[26] 26. Zhelezniakov D, Zaytsev V, Radyvonenko O: Online handwritten mathematical expression recognition and applications: A survey. IEEE Access. 2021; 9: 38352–38373. Publisher Full Text

[27] 27. Leevy JL, Khoshgoftaar TM, Bauder RA, et al.: A survey on addressing high-class imbalance in big data. J. Big Data. 2018; 5(1): 1–30. Publisher Full Text

[28] 28. Shawon A, Rahman MJ-U, Mahmud F, et al.: Bangla handwritten digit recognition using deep CNN for large and unbiased dataset. Proceedings of the International Conference on Bangla Speech and Language Processing (ICBSLP). 2018; pp. 1–6. Publisher Full Text

[29] 29. Haque MR, Azam MG, Milon SM, et al.: Quantitative analysis of deep CNNs for multilingual handwritten digit recognition. Proceedings of the International Conference on Trends in Computational and Cognitive Engineering. Singapore: Springer; 2021; pp. 15–25. Publisher Full Text

[30] 30. Liao L, Li H, Shang W, et al.: An empirical study of the impact of hyperparameter tuning and model optimization on the performance properties of deep neural networks. ACM Trans. Softw. Eng. Methodol. 2022; 31(3): 1–40. Publisher Full Text

Exploration of hyperparameter tuning in handwritten digit recognition datasets using CNN

Abstract

Background

Methods

Results

Conclusions

Keywords

Introduction

Problem statement

Contributions of this research study

Related works

Table 1. Descriptive detailed discussion of the previous related studies regarding digit recognition propositions.

Data collection and analysis

Figure 1. Visually, the image looks as above if we exclude the "pixel" prefix.2

Figure 2. Proper classified percentage of precision with example of MINST dataset.7

Methods

CNN model for feature extraction

Figure 3. Network models were employed to classify MNIST digits.3

Figure 4. The Typical Architecture of a Convolutional Neural Network.5

(1)

(2)

(3)

(4)

(5)

Figure 5. Projective field & Receptive field a.5

Figure 6. Visualisation of a 5 × 5 filter with an activation map.

Figure 7. Convolutional layer representation of the kernel and stride.5

(6)

(7)

Neural Network Construction (with 2 Layers)

K – nearest

Figure 8. Error rate of the k-NN classifier vs various k selections.7

SVM

Conclusion and results

Efficiency with machine learning algorithms9:

Efficiency with neural networks9:

Figure 9. Defines the pixelated output by the Algorithm Suggested.9

Figure 10. Layered Architecture of CNN.

Figure 11. The performance of the classification Recorded.

Figure 12. The performance of the classification Recorded.

Figure 13. Comparison on different CNN Models.

Figure 14. Demonstration of the Model in an Typical Model.

Figure 15. Demonstration of the performance of the Model with CNN 3 Architecture.

Data availability

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated

Figure 1. Visually, the image looks as above if we exclude the "pixel" prefix.²

Figure 2. Proper classified percentage of precision with example of MINST dataset.⁷

Figure 3. Network models were employed to classify MNIST digits.³

Figure 4. The Typical Architecture of a Convolutional Neural Network.⁵

Figure 5. Projective field & Receptive field a.⁵

Figure 7. Convolutional layer representation of the kernel and stride.⁵

Figure 8. Error rate of the k-NN classifier vs various k selections.⁷

Efficiency with machine learning algorithms⁹:

Efficiency with neural networks⁹:

Figure 9. Defines the pixelated output by the Algorithm Suggested.⁹