Keywords
R/Bioconductor Package, Conjunctive Bayesian Networks, CT-CBN, H-CBN, B-CBN, R-CBN, Cancer Progression Pathways, Fitness Landscapes
This article is included in the RPackage gateway.
This article is included in the Bioconductor gateway.
Conjunctive Bayesian Networks (CBN) are probabilistic graphical models used to describe mutation accumulation processes such as tumorigenesis. Several CBN models exist, which have enabled the analysis and modeling of cancer progression pathways using cross-sectional genomic data. However, these models are implemented in different languages with heterogeneous input and output formats. Moreover, the recent developments towards robust inference of cancer progression pathways (i.e., the R-CBN and B-CBN models), highlight the need for departure from the maximum-likelihood-based frameworks (i.e., the CT-CBN and H-CBN models), which requires substantial implementational adjustments. Thus, we introduce the CBN2Path R/Bioconductor package that not only provides a unifying interface to accommodate all CBN models, but it also offers the necessary functionalities to facilitate robust inference, analysis and visualization of cancer progression pathways.
R/Bioconductor Package, Conjunctive Bayesian Networks, CT-CBN, H-CBN, B-CBN, R-CBN, Cancer Progression Pathways, Fitness Landscapes
Tumorigenesis is a stepwise process driven by a sequence of molecular changes that are described as pathways of cancer progression. Conjunctive Bayesian Networks (CBN) are probabilistic graphical models designed for the analysis and modeling of these pathways.1 CBN models have evolved into different varieties such as CT-CBN,2 H-CBN,3 B-CBN,4 and R-CBN,5 each addressing different aspects of this task. However, the software corresponding to these methods is not well integrated because they are implemented in different languages with heterogeneous input and output formats. This necessitates a unifying platform that integrates these models and enables the standardization of input and output formats. Evam-tools6 is an R package that takes the initial steps towards this end. However, it does not include the B-CBN model or the recently developed R-CBN algorithm, which focuses on robust inference of cancer progression pathways.5 Importantly, the B-CBN and R-CBN algorithms for pathway quantification necessitate exhaustive consideration and weighting of all potential dependency structures (posets) within the mutational quartets. This requires reimplementation of the CBN models and adjustment of downstream pathway analysis and modeling functions. Therefore, here we introduce the CBN2Path R package that not only includes the original implementation of the CBN models (e.g., CT-CBN and H-CBN) in a unifying interface but also accommodates the necessary modifications to support robust CBN algorithms (e.g., B-CBN and R-CBN). Importantly, CBN2Path includes a collection of functions required to quantify predictability,7 analyze robustness,5 and visualize mutational pathways from pre-processed cross-sectional genomic data. It is important to note that the R-CBN method has great potential for wide application in future predictive models because of its unique ability to offer an optimal balance between robustness and predictability.5 Thus, we anticipate that CBN2Path will be a commonly used package in the field, particularly by providing a platform to facilitate future applications of the R-CBN model.
CBN2Path is implemented as a standard R package and hosted in the Bioconductor repository. Furthermore, the developed version of CBN2Path is available on GitHub. All functions were documented, and examples were included. The main functions included in CBN2Path are listed in Table 1, and their features and capabilities are described in detail in the tutorial (vignette) accompanied by the package. CBN2Path can be installed and used mainly on Unix platforms.
if (!require("BiocManager", quietly = TRUE)) install.packages("BiocManager") BiocManager::install("CBN2Path")
The main functions are listed and categorized into five parts: i) input preparation, ii) CBN models, iii) pathway quantification, iv) fitness landscape analysis, and v) the downstream analysis. For each function, the name (the first column), description (the second column) and the returned value (the third column) are provided.
During the installation of CBN2Path, other packages that it depends on are automatically installed, including coda, cowplot, doMC, foreach, ggplot2, ggraph, grDevices, graphics, igraph, magrittr, patchwork, rlang, R6, stats, and tidygraph.
CBN2Path provides a unifying interface to implement different CBN models, which are utilized to facilitate the quantification, visualization, and analysis of mutational pathways. The CBN2Path has three main functionalities.
(a) The original implementation of the CT-CBN and H-CBN models, in which case the associated workflow for pathway quantification, is shown in Figure 1. In this setting, the genotype matrix and a given poset are used as inputs for the CBN models (Step 1), which output the estimated λ values and MLE poset structure. Subsequently, these outputs are used as inputs for pathway quantification and visualization functions (Step 2), which outputs the ultimate pathway probability distributions. These outputs are then utilized by downstream analysis functions (Step 3), which quantify the different properties of the pathway probability distributions, such as predictability, robustness, and compatibility.
(b) The second workflow was specifically designed to analyze mutational quartets ( Figure 2). In this setting, only a genotype matrix is required as the input, and specifying a given poset is not required. Basically, all potential 219 posets are considered and so the CT-CBN model is executed 219 times, leading to 219 different λ vectors, which are used to estimate 219 different probability distributions that will be aggregated to derive the ultimate probability distribution. The posets are weighted using an MCMC approach in the B-CBN-based approach, whereas they are weighted using their reciprocal rank in the R-CBN approach.5 Note that in the second workflow, unlike in the first one, there is no sequential input-output arrangement; rather, we have one single input (the genotype matrix) and one single output (the ultimate probability distribution), and the intermediate functions are called internally without a direct interface with the user.
(c) CBN2Path also provides the necessary functions for visualizing fitness landscapes and quantifying their associated pathway probabilities using evolutionary models that operate based on the Strong-Selection Weak-Mutation (SSWM) assumption ( Figure 3).
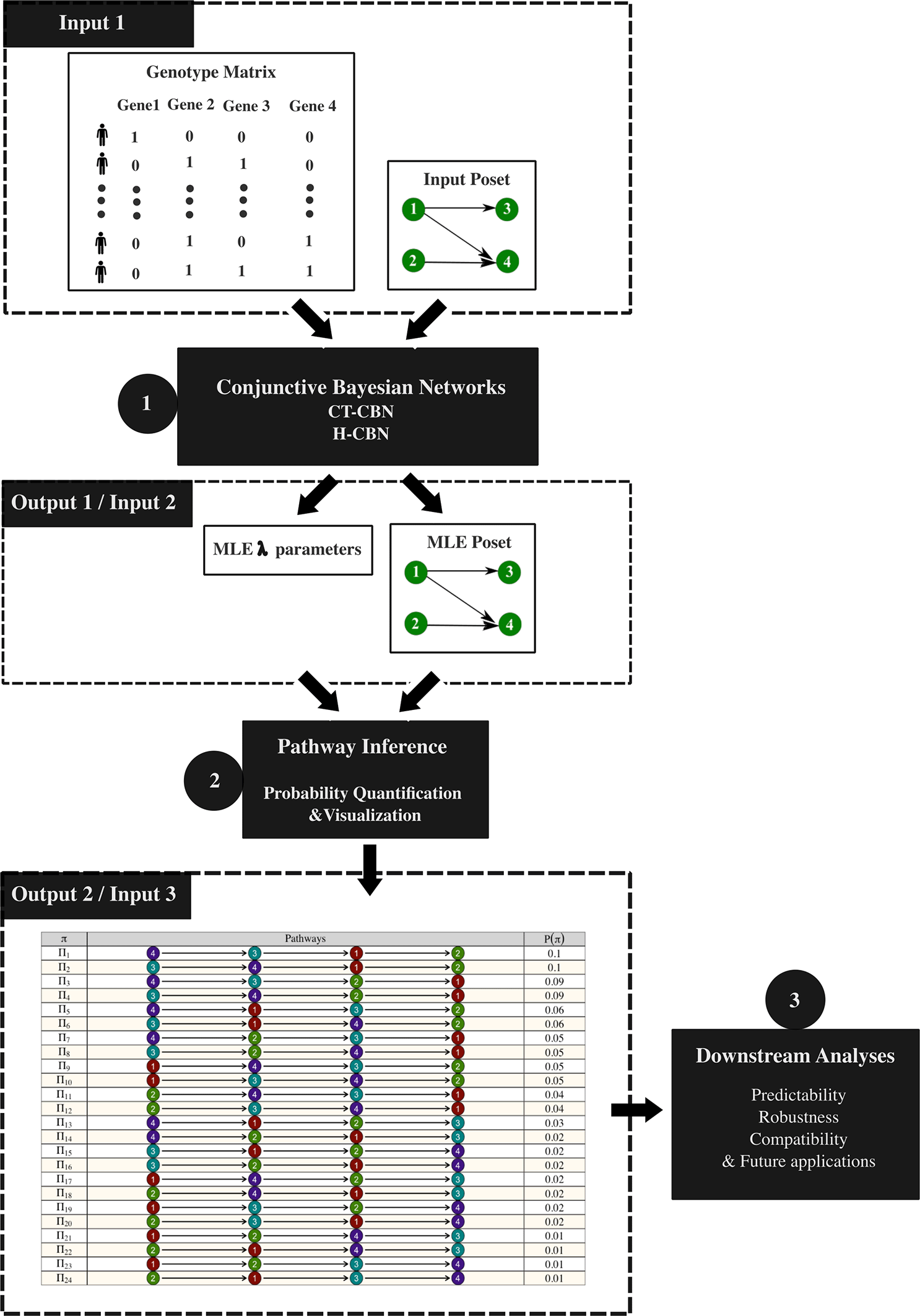
CBN models (CT-CBN or H-CBN) take the genotype matrix and a given poset as input, and then output the estimated λ vector and the MLE poset (step 1), which will be used by the pathway inference functions to produce the inferred pathway probability distribution (step 2) that will be subsequently used by other downstream functions to measure different properties of the pathway probabilities (step 3).
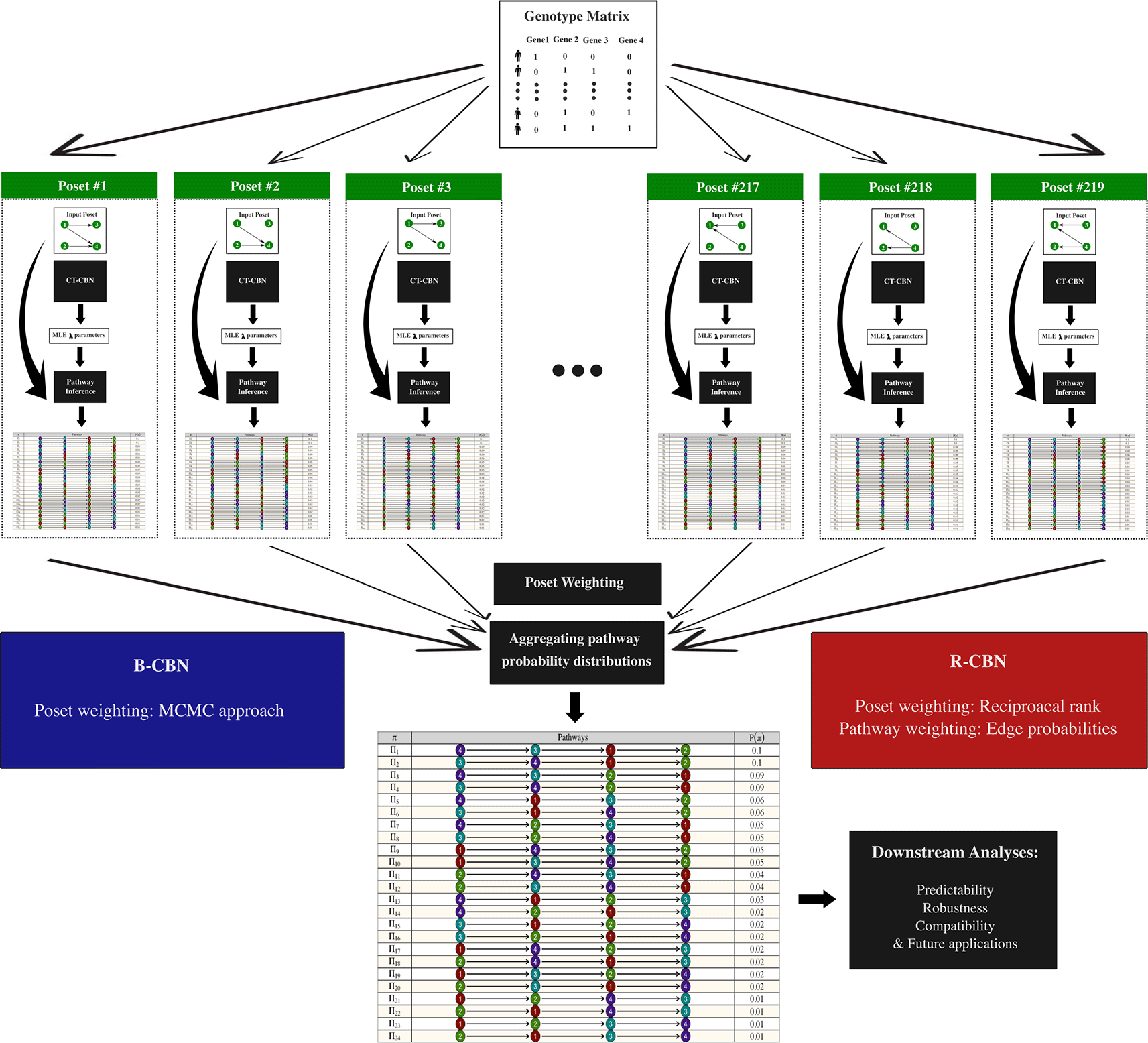
The R-CBN and B-CBN approaches require an alternative workflow for quantifying the pathway probability distributions, which only takes a genotype matrix as the input. Basically, under all 219 potential posets, the λ parameters are estimated using CT-CBN. Consequently, 219 different probability distributions are derived, which are then aggregated to generate the ultimate pathway probability distribution that will be used by the downstream functions for further analyses. Note that the B-CBN method utilizes an MCMC approach for weighting the posets, which is needed in the aggregation step.4 In contrast, in the R-CBN method, the likelihood outputted from the CT-CBN model under each of the 219 posets are considered, and pathways are weighted based on their reciprocal rank in terms of likelihood. Furthermore, R-CBN weights the pathways and updates their probabilities using their corresponding edge (marginal) probabilities.5 Note that in the workflow II there is no sequential input-output arrangement, but rather we have one single input (the genotype matrix) and one single output (the ultimate probability distribution). In other words, the intermediate functions are called internally, without a direct interface with the user.
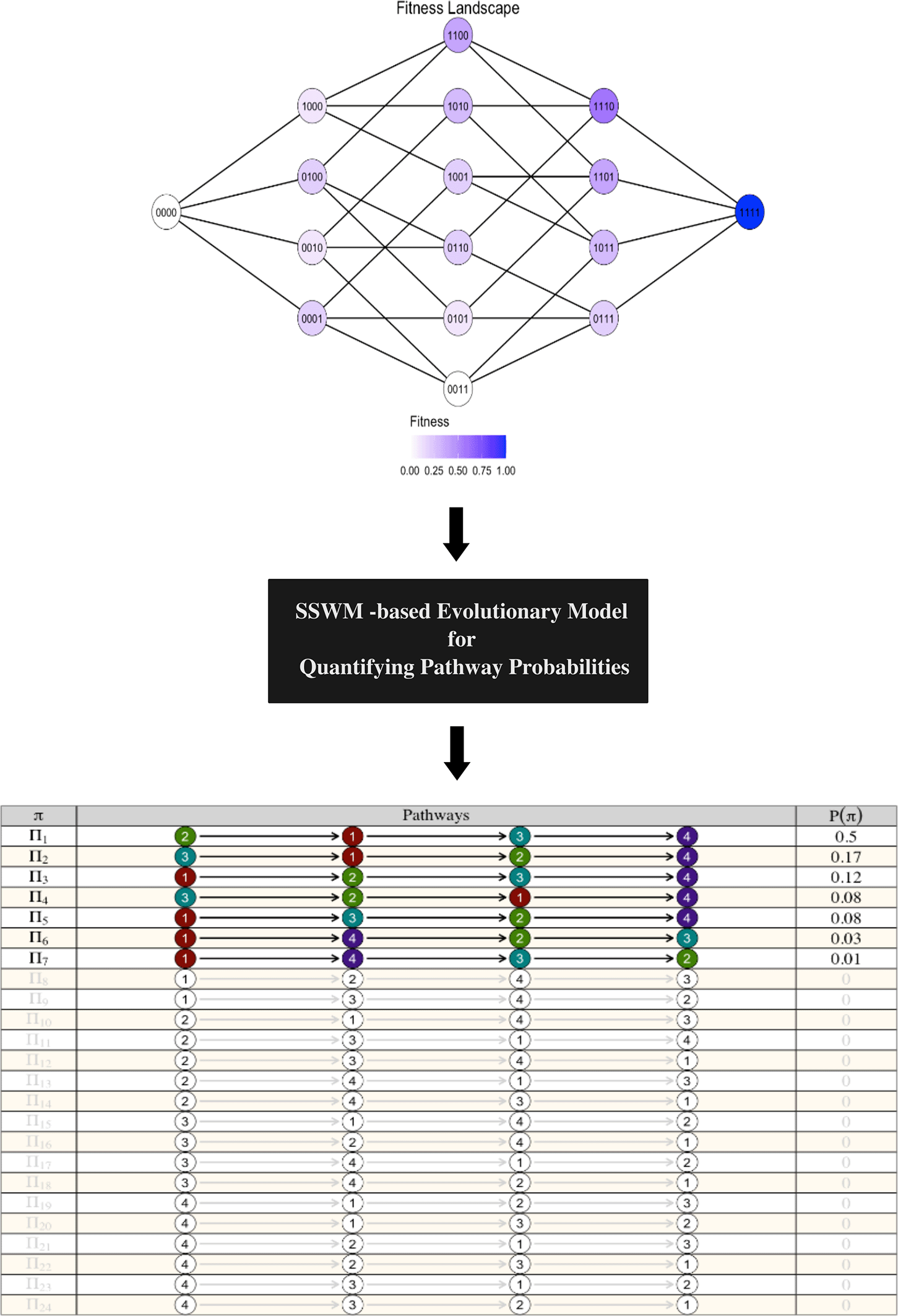
CBN2Path enables visualization of fitness landscapes and quantifying pathway probability distributions based on evolutionary models under the Strong-Selection Weak-Mutation (SSWM) assumption.7
Preparing the input data
As shown in Figure 2, the original implementation of the CT-CBN and H-CBN models requires two input files: i) a “.pat” file, which contains binary genotype data, and ii) a “.poset” file that encodes a given poset. CBN2Path avoids reading files but accepts two matrices that are obtained after reading the above files. Importantly, to store input posets and genotype matrices, CBN2Path implements its own data structure, Spock, which includes read_pattern and read_poset methods to read, respectively the “.pat” and “.poset” files in the spock-data type.
library(CBN2Path) example_path <- getExamples()[1] input_poset <- readPoset(example_path) input_pattern <- readPattern(example_path) input_1 <- Spock$new( poset = input_poset$sets, numMutations = input_poset$mutations, genotypeMatrix = input_pattern )
Alternatively, input matrices can be created directly without reading from a file. For example:
# The poset dag <- matrix(c(3, 3, 4, 4, 1, 2, 1, 2), 4, 2) # The genotype matrix set.seed(100) gen_1<-c(rep(0,150),sample(c(0,1),25,replace=TRUE),rep(0,25)) gen_2<-c(rep(0,175),sample(c(0,1),25,replace=TRUE)) gen_3<-c(rep(0,50),sample(c(0,1),100,replace=TRUE),rep(1,50)) gen_4<-c(sample(c(0,1),100,replace=TRUE),rep(0,50),rep(1, 50)) g_mat<-matrix(c(gen_1, gen_2, gen_3, gen_4), 200, 4) g_mat<-cbind(1, g_mat) # Preparing input of the ct-cbn/h-cbn methods input_2 <- Spock$new( poset = dag, numMutations = 4, genotypeMatrix = g_mat )
Note that the first column of the genotype matrix must always be one, whereas each of the other columns corresponds to a given mutational event. Therefore, the number of columns in the genotype matrix must be equal to the number of mutations considered plus one.
In the second example, the genotypes are generated such that the mutation orders never violate the restrictions in the temporal ordering between mutations imposed by the corresponding poset. For example, mutations 1 and 2 occur when mutations 3 and 4 have already occurred. To allow violation of the restrictions, one can use the genotypeMatrixMutator function to add false positives and false negatives of a given rate. In the following example, the g_mat matrix is converted to the g_mat_mut matrix by adding false positive and false negative rates of 0.3 and 0.2, respectively:
temp <- g_mat[,2:5] temp_mut <- genotypeMatrixMutator(temp, 0.3, 0.2) g_mat_mut <- cbind(1, temp_mut) # Preparing input of the ct-cbn/h-cbn methods input_3 <- Spock$new( poset = dag, numMutations = 4, genotypeMatrix = g_mat_mut )
Note that the first column of the genotype matrix must always remain one. Therefore, we did not pass the first column to genotypeMatrixMutator function.
Running the CBN models
Having prepared the input files, it is now easy to run the CBN models using ctcbnSingle and hcbnSingle.
# CT-CBN results_c1 <- ctcbnSingle(input_1) results_c2 <- ctcbnSingle(input_2) results_c3 <- ctcbnSingle(input_3) # H-CBN results_h1 <- hcbnSingle(input_1) results_h2 <- hcbnSingle(input_2) results_h3 <- hcbnSingle(input_3)
Below, we can see how to obtain the estimated λ values and the corresponding likelihood for the first example.
# The estimated lambda values ml_lambda_c1 <- results_c1[[1]]$lambda # The likelihood loglikelihood_c1 <- results_c1[[1]]$summary[4]
Furthermore, the maximum-likelihood poset can be identified and visualized using visualizeCBNModel function.
# The MLE poset ml_poset_c1 <-results_c1[[1]]$poset$sets # visualizing the MLE visualizeCBNModel(ml_poset_c1)
It is important to mention that we have an alternative implementation of the CBN models, namely the ctcbn and hcbn functions, which accept a list of posets as input and accordingly produce a list of λ vectors, a list of likelihood values, and a list of MLE posets. This strategy is utilized in the second workflow, which is specifically suited for analyzing mutational quartets and pathways of length four.
# The collection of all 219 potential posets posets <- readRDS(system.file("extdata", "Posets.rds", package = "CBN2Path")) # Input preparation input_4 <- Spock$new( poset = posets, numMutations = 4, genotypeMatrix = g_mat ) # Running the ctcbn function results_c4 <- ctcbn(input_4) # Running the hcbn function results_h4 <- hcbn(input_4)
Note that the collection of all 219 potential posets for analyzing mutational quartets is already accessible within the package, which is read and stored in the first line of the above code.
Inferring pathway probability distributions
The output of the CBN models, namely the estimated λ values and the MLE poset, can be used as the input of the pathProbCBN function, which quantifies the pathway probability distribution (P(Π)). In the example below, the results of the second example obtained in the previous section (results_c2 and results_h2) are used.
# The first input: The MLE poset (the output of the CBN models) dag_c2 <- results_c2[[1]]$poset$sets dag_h2 <- results_h2[[1]]$poset$sets
#The second input: The estimated Lambda values (the output of the CBN models) lambda_c2 <- as.numeric(results_c2[[1]]$lambda) lambda_h2 <- as.numeric(results_h2[[1]]$lambda) # Quantifying the pathway probability distributions prob_c2 <- pathProbCBN(dag_c2, lambda_c2, 4) prob_h2 <- pathProbCBN(dag_h2, lambda_h2, 4)
In this example, prob_c2 and prob_h2 are vectors of length 24, each representing one of the 24 pathways.
Downstream analyses
The quantified pathway probability distributions are used as the input of other functions used in the downstream steps for visualization (visualizeProbabilities) and quantification of the predictability (predictability), or measuring the divergence between probability distributions (jensenShannonDivergence):
# Visualization of pathways and their probabilities visualizeProbabilities(prob_c2) visualizeProbabilities(prob_h2) # Quantification of predictability score for a given probability distribution pred_c2 <- predictability(prob_c2, 4) pred_h2 <- predictability(prob_h2, 4) # Quantification of the Jensen-Shannon Divergence (JSD) between a pair of distributions jsd <- jensenShannonDivergence(prob_c2, prob_h2)
The second workflow for quantifying pathway probabilities was designed specifically for implementing the R-CBN and B-CBN algorithms to enable the robust inference of pathway probability distributions. It is specifically suited for analyzing mutational quartets and pathways of length 4. The ctcbn function that takes the exhaustive list of 219 posets as input is an integral part of this workflow, which makes it easy to work with, as the user only needs to input a genotype matrix.
Running the R-CBN model
R-CBN weighs the 219 posets based on their reciprocal rank in terms of likelihood, and a second pathway-based weighting layer is employed. However, the user only needs to work directly with the pathProbQuartetRCBN function, because intermediate functions such as posetWeightingRCBN, pathwayWeightingRCBN, edgeMarginalized, pathEdgeMapper and pathNormalization are taken care of internally.
g_mat2 <- g_mat[,2:5] prob_r2 <- pathProbQuartetRCBN(g_mat2)
Note that this function only needs a genotype matrix as the input and does not require the first column of the matrix to be one; therefore, we needed to remove the first column from the gMat matrix that we previously produced.
Running the B-CBN model
Although the B-CBN algorithm is fundamentally different from the R-CBN algorithm, particularly in terms of how the posets are weighted, which strongly affects the internal implementation of the intermediate functions, the user interface is exactly the same. The pathProbQuartetBCBN function is defined as
prob_b2 <- pathProbQuartetBCBN(g_mat2)
CBN2Path also provides a similar implementation for CT-CBN and H-CBN.
prob_c2 <- pathProbQuartetCTCBN(g_mat2) prob_h2 <- pathProbQuartetHCBN(g_mat2)
Having determined the pathway probabilities, downstream analysis can be performed similarly to those in the first workflow. Furthermore, pathway compatibilities (c(Π)) can be measured directly from a genotype matrix, and their correlation with pathway probabilities (P(Π)) can be calculated as
pathway_c2 <- pathwayCompatibilityQuartet(g_mat2) rho_c2 <- cor(pathway_c2, prob_c2, method = "spearman")
CBN2Path also provides functions for the analysis and visualization of fitness landscapes. For example, after assigning a fitness vector f to the set of binary genotypes of length four, which can be enumerated by the generateMatrixGenotypes function, we can calculate the corresponding pathway probability distribution under the SSWM-based evolutionary model using the pathProbSSWM function as follows:
f <- c(0, 0.1, 0.2, 0.1, 0.2, 0.4, 0.3, 0.2, 0.2, 0.1, 0, 0.6, 0.4, 0.3, 0.2, 1) g <- generateMatrixGenotypes(4) Prob_w<-pathProbSSWM(f,4)
Furthermore, the fitness landscape can be visually inspected using the visualizeFitnessLandscape function, as follows:
visualizeFitnessLandscape(f)
In summary, CBN2Path provides a unifying platform for the efficient implementation of the CT-CBN, H-CBN, B-CBN, and R-CBN methods, which facilitates robust quantification, visualization, and analysis of cancer progression pathways from pre-processed binary mutational data.
• Source code available from: https://github.com/rockwillck/CBN2Path
• Software will be available from: https://bioconductor.org/packages/CBN2Path
• Archived software available from: https://doi.org/10.5281/zenodo.16791480
• License: MIT.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the rationale for developing the new software tool clearly explained?
Partly
Is the description of the software tool technically sound?
No
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?
Yes
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?
No
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?
No
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Areas of expertise: - software engineering, machine learning, federated learning, Bayesian networks, clinical data science
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | |
|---|---|
| 1 | |
|
Version 1 29 Aug 25 |
read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)