Artificial Intelligence and Intelligent Tutoring Systems in Mathematics Education: A Bibliometric Analysis (2001–2025)

Search strategy

The search strategy was developed to capture research at the intersection of Artificial Intelligence (AI), Intelligent Tutoring Systems (ITS), and mathematics education. To do so, a specific query was run on the Scopus database in July 2025:

The initial search yielded 239 documents published between 2001 and 2026. Of these, one article published in 2026 was excluded as it fell outside the analysis range (2001–2025), and one Spanish-language article was excluded for not meeting the language criterion. The final dataset therefore consisted of 237 documents, including journal articles and conference proceedings. Only peer-reviewed publications were included, while book chapters, editorials, and non-scholarly documents were excluded. Scopus was selected as the sole database due to its extensive coverage of reputable journals in education, computer science, and related interdisciplinary fields (Pranckutė, 2021).

Screening and data cleaning

The screening process was carried out in three stages. First, duplicates and inconsistent metadata (e.g., variations in author names, affiliations, or keywords) were identified and removed using OpenRefine 3.7.6. Second, documents irrelevant to mathematics education or not explicitly addressing AI/ITS were excluded. Third, ambiguous records were manually reviewed to ensure alignment with the study’s focus. Following this rigorous cleaning process, 237 valid documents were retained for bibliometric analysis.

Data extraction and coding

Bibliographic information, including authors, titles, abstracts, keywords, affiliations, sources, and references, was exported in CSV format. To ensure reliability, the dataset was cross-verified with Scopus records and checked independently by two researchers. Author keywords (DE) and Keywords Plus (ID) were standardized through clustering, merging terms with equivalent meanings (e.g., “mathematics learning” vs. “mathematical learning,” “educational technology” vs. “educational technologies”). All derived bibliometric data and analytical outputs generated during this process are openly available in Zenodo (Kuncoro et al., 2025).

Bibliometric analysis

The cleaned dataset was analyzed using the Bibliometrix R-package (v.4.2.2) and its Biblioshiny web interface (Aria & Cuccurullo, 2017). The analyses included:

This review adhered to the PRISMA 2020 reporting guidelines, and the completed PRISMA checklist and flow diagram are publicly available in Zenodo (Kuncoro et al., 2026).

Validity and reliability

To ensure transparency and reproducibility, all search queries, inclusion/exclusion criteria, and data-cleaning procedures were documented. The combination of Scopus indexing with bibliometric software ensured validity and comparability with other large-scale analyses in the field of educational technology (Donthu et al., 2021).

Main information

This bibliometric analysis covers 237 documents published across 160 different sources during the period 2001–2026. The relatively high ratio between the number of documents and sources indicates that research in this field is disseminated through diverse publication outlets, including journals in education, computer science, psychology, and mathematics. This finding confirms the interdisciplinary nature of research focusing on Artificial Intelligence (AI), Intelligent Tutoring Systems (ITS), adaptive learning, and mathematics education. A summary of the dataset’s main information is presented in Table 1.

The average age of the documents (4.89 years) shows that this collection is relatively recent, while the average of 16.55 citations per document reflects a fairly strong level of impact. The total number of references reached 8,775, or about 37 references per document, indicating that the research is grounded in a broad and comprehensive body of literature. In terms of content, there are 924 Keywords Plus and 612 Author’s Keywords, reflecting thematic diversity. Keywords Plus illustrates the broad scope of the field, whereas Author’s Keywords capture more specific research focuses, ranging from ITS, adaptive learning, and artificial intelligence to mathematics education.

Author involvement also indicates a high degree of collaboration. A total of 702 authors contributed to the 237 documents, averaging 3.45 authors per document. Only 38 documents were single-authored, highlighting that this research is largely collaborative. International collaboration accounted for 18.57%, which, although not dominant, demonstrates cross-country networking in this field. The distribution of document types shows a balance between journal articles (132 documents) and conference proceedings (105 documents). Journal articles reflect more in-depth contributions that have undergone peer review, whereas conference proceedings highlight the need to disseminate emerging findings quickly within dynamic communities such as AI and ITS.

Annual scientific production

Annual scientific production in this field reveals a clear trajectory from slow growth toward more rapid expansion. Between 2001 and 2010, the number of publications was still relatively low and sporadic, rarely exceeding five documents per year, reflecting the early stage of research on Artificial Intelligence (AI) and Intelligent Tutoring Systems (ITS) in mathematics education. A more notable increase began in 2012, marking the onset of more sustained academic interest. After 2015, annual output stabilized within the range of 7–13 publications, indicating moderate but consistent growth. This development is illustrated in Figure 2.

Figure 2. Annual scientific production on AI and Intelligent Tutoring Systems in mathematics education (2001–2025).

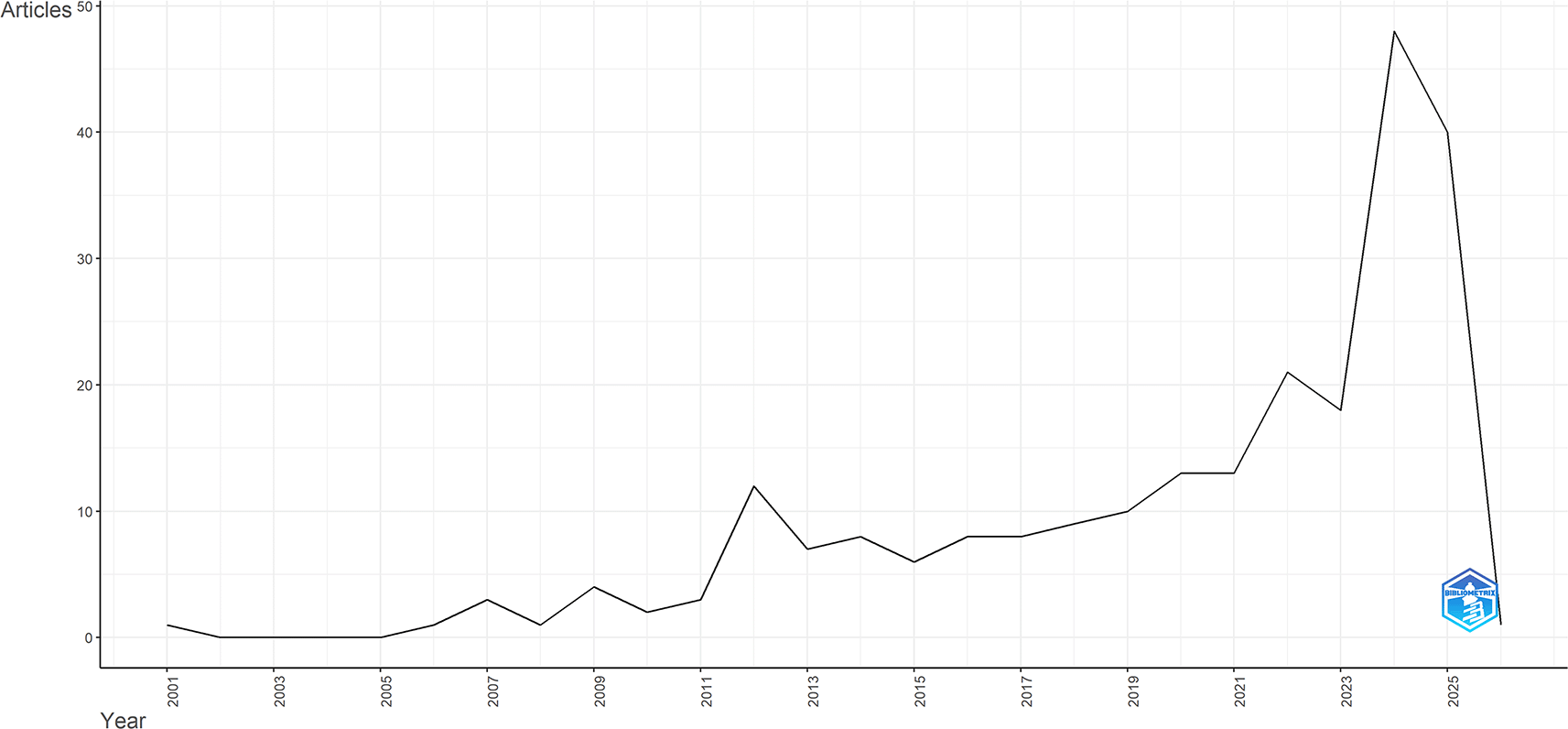
A significant turning point appeared after 2019, when the number of publications rose more sharply, surpassing 20 documents in 2021. This upward trend peaked in 2024 with nearly 50 publications, representing the highest figure across the entire observation period. The surge coincided with the global boom in AI-based research, particularly the application of machine learning and large language models in education. The apparent decline in 2025–2026 should be interpreted with caution, as it is more likely due to indexing delays of recent publications than to a real decrease in research activity. The findings suggest that research on AI and ITS in mathematics education has evolved from a relatively marginal topic in the early 2000s into a rapidly expanding field over the past decade. This pattern reflects Price’s Law, which anticipates exponential growth in publications within emerging disciplines, and it highlights the increasing significance of adaptive and intelligent technologies in shaping the future of mathematics teaching and learning (Cotič et al., 2024; Samala et al., 2024).

Three-Field plot

The Three-Field Plot illustrates how authors (AU), their countries of origin (AU_CO), and research keywords (DE) intersect within studies on Artificial Intelligence (AI), Intelligent Tutoring Systems (ITS), and mathematics education. On the author side, key contributors include Fancsali S. E., Ritter S., Aleven V., McLaren B. M., Arroyo I., Berman S. R., Koedinger K. R., Hausmann R. G. M., Woolf B. P., Borchers C., and Hu X., who stand out as leading figures in the field. The majority of authors are closely connected with institutions in the United States, while figures such as Hausmann RGM and Borchers C are affiliated with Germany, and Hu X is linked to China. These connections are illustrated in Figure 3.

Figure 3. International research linkages among authors, countries, and keywords in AI- and ITS-based mathematics education (2001–2025).

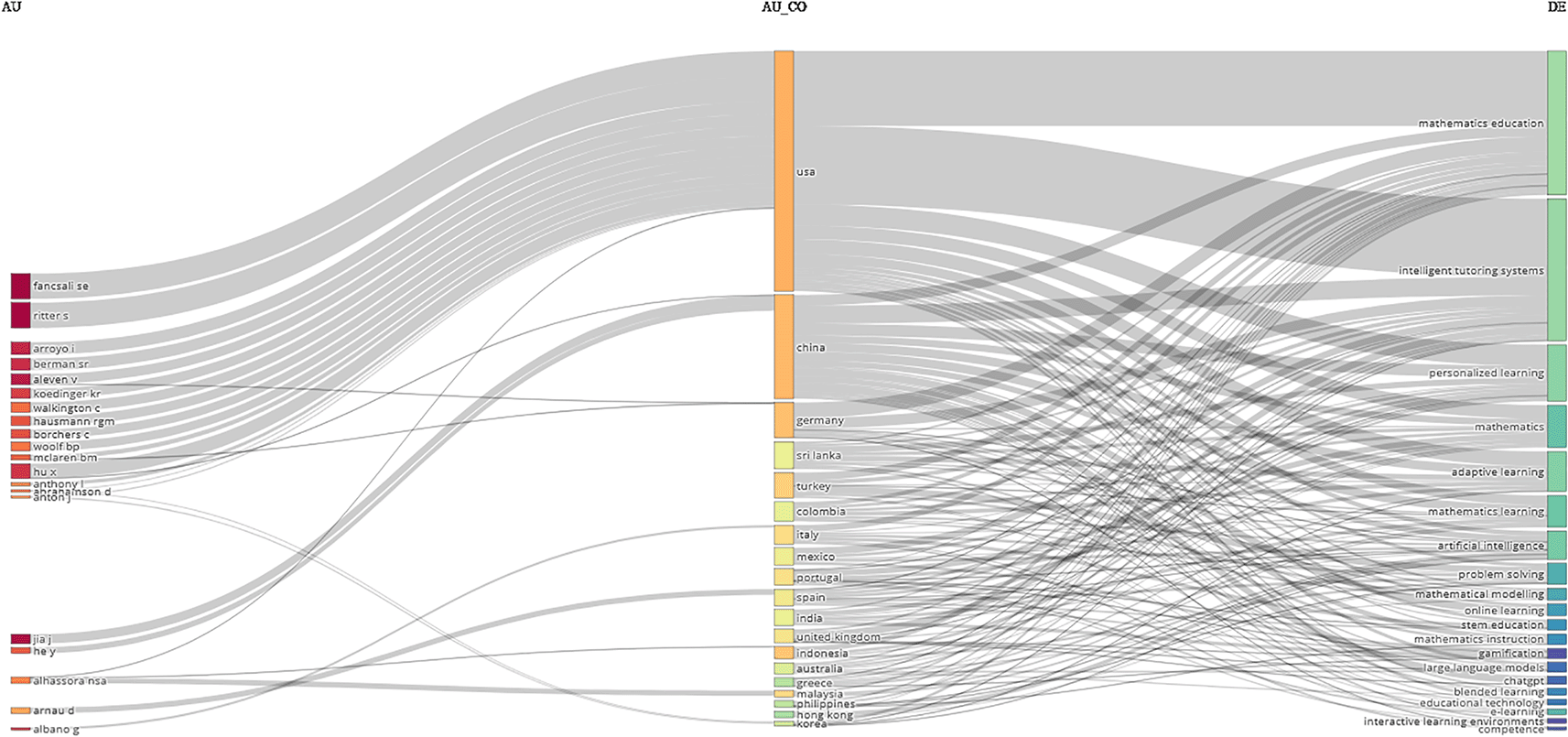
In the country column (AU_CO), the USA dominates research productivity, followed by China and Germany. Other countries such as Sri Lanka, Turkey, Colombia, Italy, Mexico, Portugal, Spain, India, the United Kingdom, Indonesia, and Australia also contribute, though in smaller numbers. The connections between countries and keywords indicate that the USA and China are most frequently associated with core themes such as mathematics education, intelligent tutoring systems, personalized learning, and adaptive learning.

From the keyword side (DE), mathematics education, intelligent tutoring systems, personalized learning, and adaptive learning emerge as the most dominant research themes. In addition, keywords such as mathematics learning, artificial intelligence, problem solving, and mathematical modelling appear frequently. Newer terms such as large language models and ChatGPT have also begun to surface, though with lower frequency, signaling the emergence of the latest research trends in this field.

Authors’ production over time

The Authors’ Production Over Time plot represents the publication trajectories of leading scholars in AI and Intelligent Tutoring Systems (ITS) for mathematics education. Each horizontal line shows a researcher’s active publishing period, while bubbles mark the number of articles per year. Larger bubbles represent higher productivity, whereas darker colors indicate higher annual citation impact (TC/year). This visualization is presented in Figure 4.

Figure 4. Author productivity over time in AI and Intelligent Tutoring Systems research in mathematics education (2001–2025).

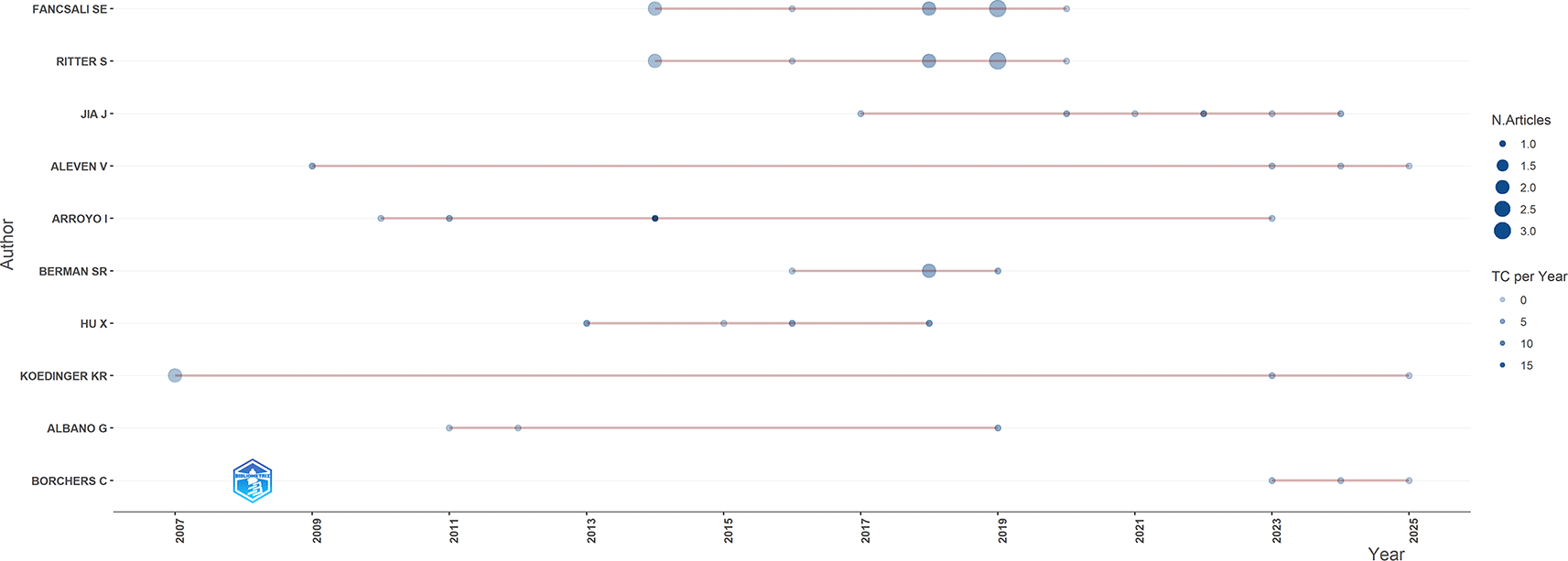
Figure 4 reveals several key patterns. First, senior authors such as Koedinger KR and Aleven V demonstrate long publication spans—2007–2023 and 2009–2024 respectively—with consistent contributions. Second, authors with more concentrated impact periods, such as Arroyo I (2011–2023, peaking in 2014 with the highest TCpY of 17.5) and Hu X (2013–2018, with medium to high impact publications), show significant productivity within narrower timeframes. Third, there is a group of authors with productivity concentrated in specific years, including Fancsali SE, Ritter S, and Berman SR, who contributed mainly during 2018–2019 on formative assessment in ITS. Fourth, newer authors such as Borchers C (active since 2023, co-publishing with Aleven and Koedinger) and Jia J (steady since 2016, peaking in 2022 with TCpY of 8.5) reflect the emergence of a new generation of researchers. Meanwhile, Albano G shows sporadic activity (2011–2019) with contributions such as the integration of GeoGebra in e-learning (2019, TCpY 3.7).

Author productivity through Lotka’s Law

Figure 5 shows that the distribution of author productivity follows the characteristic pattern of Lotka’s Law. The majority of authors produced only a single publication, accounting for more than 60%. The number of authors with two publications declines sharply, and even fewer authors generated three or more publications. The observed curve (solid line) aligns with the theoretical Lotka curve (dashed line), though slight deviations are visible in the categories of authors with one or two publications. Overall, this distribution forms a long-tail pattern, where most contributions come from low-productivity authors, while only a small core group of authors consistently contribute multiple publications.

Figure 5. Distribution of author productivity according to Lotka’s Law.

The findings in Figure 5 confirm the relevance of Lotka’s Law in the bibliometric context of AI and ITS research in mathematics education. They also indicate that this field is largely shaped by widespread contributions from sporadic authors, with a small nucleus of highly productive authors maintaining the continuity of research.

Corresponding author’s countries

Figure 6 presents the distribution of publications based on the country of the corresponding author, distinguishing between Single Country Publications (SCP) and Multiple Country Publications (MCP). The chart shows that the United States (USA) dominates with the largest contribution (32 articles), followed closely by China (30 articles), while Germany ranks third with 10 articles.

Figure 6. Country distribution of corresponding authors and international collaboration.

Countries with medium-level contributions include Turkey (9 articles), Indonesia (8 articles), the United Kingdom (6 articles), Italy (5 articles), and Australia, South Korea, and Malaysia (4 articles each). Other countries such as Mexico, Spain, India, the Netherlands, Norway, the Philippines, Thailand, Belgium, Colombia, and Finland contributed smaller numbers of publications. In terms of collaboration patterns, the USA and China produced more domestic publications (SCP), while Germany showed a balance between SCP and MCP with a high ratio of international collaboration. Some smaller contributors, such as Belgium, published exclusively MCP articles, indicating a complete orientation toward collaboration. The findings in Figure 6 highlight that research on AI and ITS in mathematics education is global in nature—dominated by major countries but also strengthened by significant contributions from developing nations through international collaboration.

Trend topics

The Trend Topics chart in Figure 7 illustrates the evolution of research terms from 2010 to 2024 in the fields of Artificial Intelligence, Intelligent Tutoring Systems, adaptive learning, and mathematics education. Bubble size reflects the annual median frequency of a term, while the horizontal line indicates the interquartile range (IQR), representing the period of emergence and consistency of each topic.

Figure 7. Trending research topics in AI and Intelligent Tutoring Systems research in mathematics education.

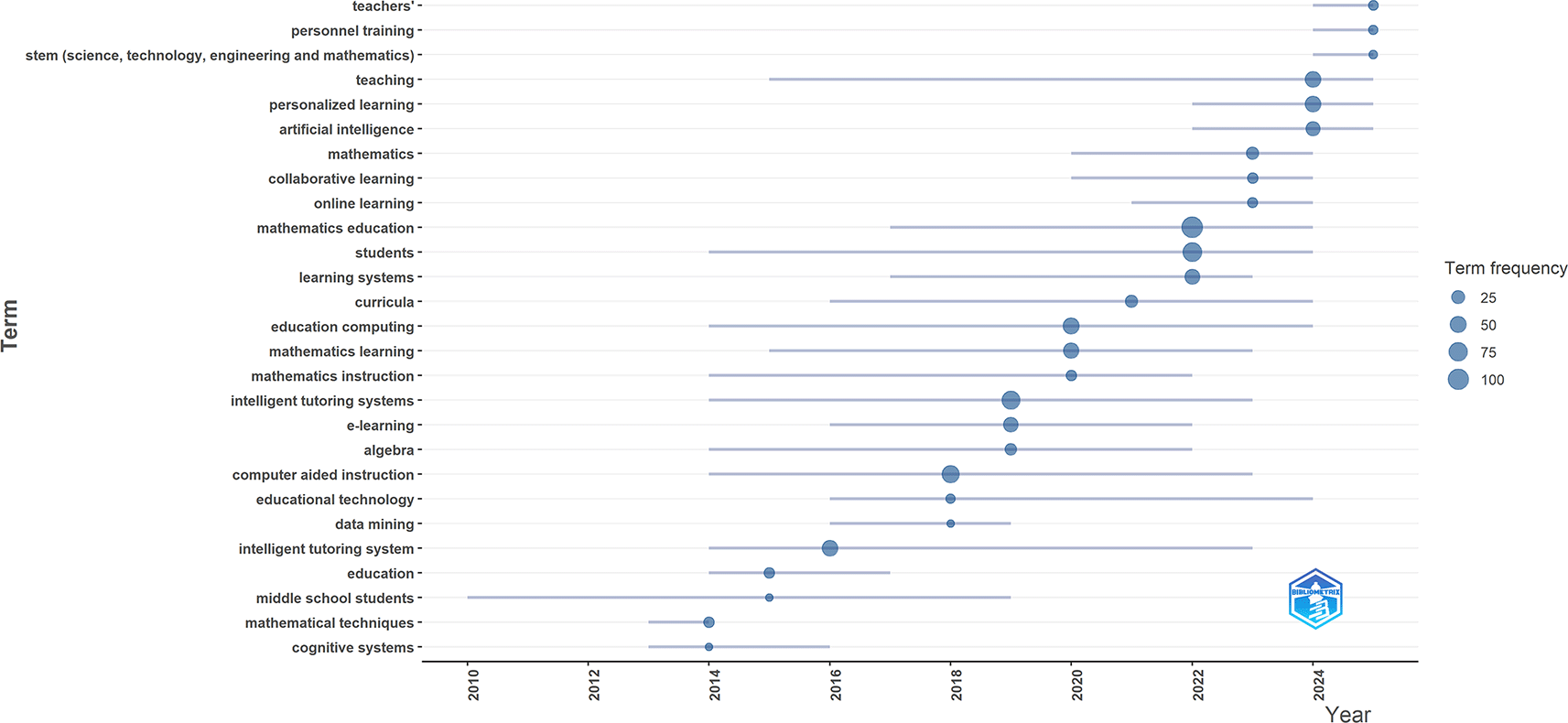
In the early phase (2010–2017), terms that appeared were mainly associated with conventional educational technologies such as cognitive systems, educational technology, computer-aided instruction, e-learning, as well as subject-specific topics like algebra and mathematical techniques. Research also focused on specific groups, such as middle school students. In the middle phase (2018–2020), research became more consolidated, with a rise in pedagogically oriented terms including intelligent tutoring systems, mathematics instruction, mathematics learning, and online learning, which began to dominate. The term collaborative learning also emerged during this period.

In the most recent phase (2021–2024), there was a sharp increase in terms such as artificial intelligence and personalized learning, with the largest bubbles across the entire timeline, marking a clear shift in research focus. STEM education also gained strength, reflecting a broader interdisciplinary perspective. By 2023–2024, terms such as teachers and personnel training appeared, indicating a growing awareness of the role of teachers and the importance of professional development. Several terms remained consistent throughout the period, particularly mathematics education, intelligent tutoring systems, and online learning, which continue to be central in this research domain. These findings confirm that Figure 7 represents a transition in research focus from conventional instruction toward the integration of AI and personalized learning.

Co-occurrence network

The keyword co-occurrence network analysis in Figure 8 provides a visual representation of the cognitive structure of research in Artificial Intelligence (AI), Intelligent Tutoring Systems (ITS), adaptive learning, and mathematics education. Larger nodes represent keywords with higher frequency, while edges indicate the strength of connections between keywords. Node colors represent thematic communities formed through clustering algorithms. Four dominant keywords were identified: mathematics education, students, intelligent tutoring system, and computer-aided instruction. These four terms form the core of the network and act as cross-theme connectors. Strong associations are especially evident in the pairs mathematics education–students and intelligent tutoring system–computer-aided instruction, reflecting close conceptual linkages in the literature.

Figure 8. Keyword co-occurrence network in AI and Intelligent Tutoring Systems research in mathematics education.

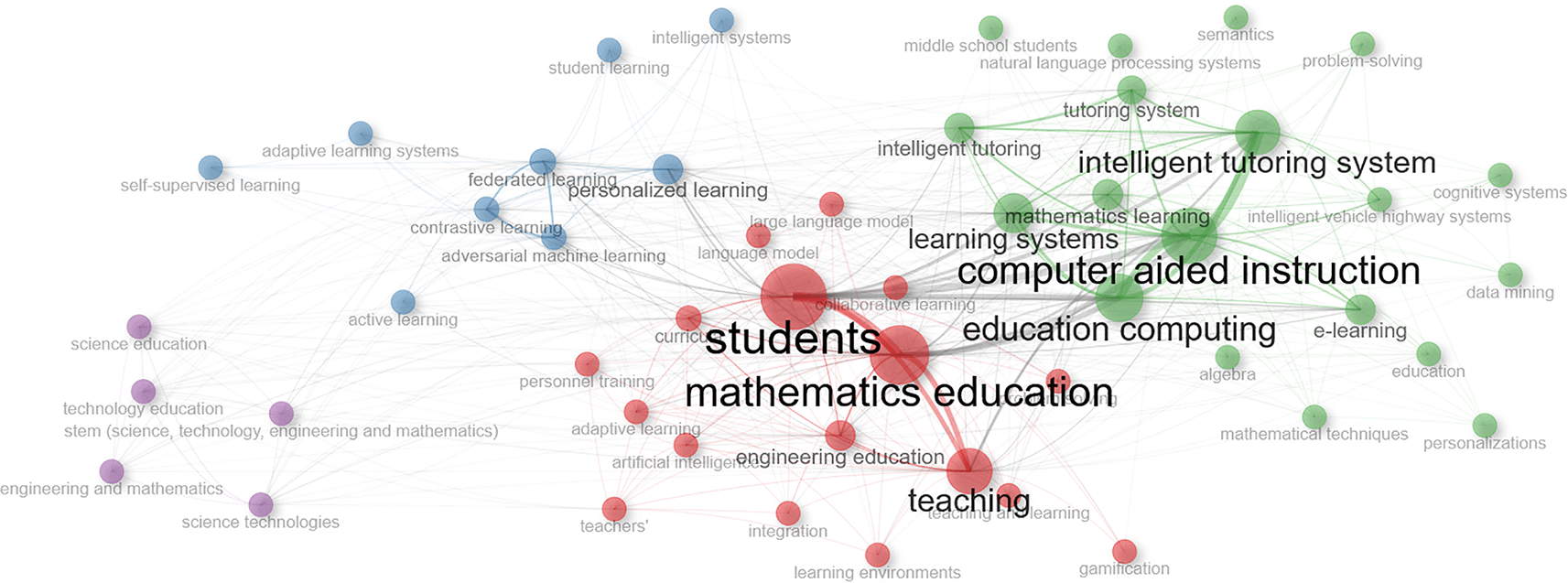
In addition, the network reveals four main clusters:

The findings in Figure 8 emphasize that research on AI and ITS in mathematics education has a complex thematic structure, with a strong central core while simultaneously expanding toward cutting-edge technological frontiers.

Thematic map

The Thematic Map in Figure 9 illustrates the distribution of research themes across two main dimensions: relevance (centrality) and level of development (density). From the analysis, four theme categories can be identified.

Figure 9. Thematic map of research themes in AI and Intelligent Tutoring Systems research in mathematics education.

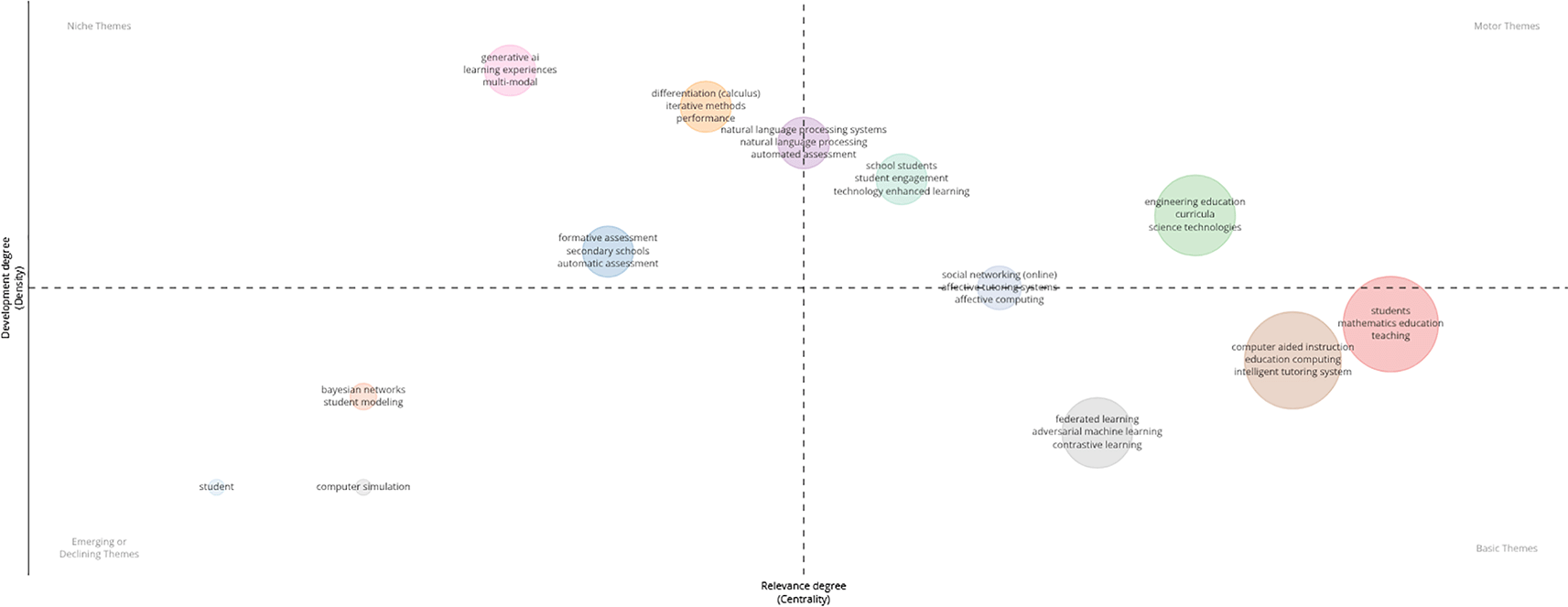
First, Niche Themes (upper-left quadrant) include topics with high density but low relevance. Themes such as generative AI, multimodal, learning experiences, differentiation (calculus), natural language processing systems, and automated assessment fall into this group. These represent deep and focused research but remain limited in scope. Second, Motor Themes (upper-right quadrant) are characterized by both high centrality and density, marking them as the driving forces of research. Keywords such as engineering education, curricula, and science technologies appear dominant. This highlights the key role of engineering education and science–technology integration in shaping current research developments. Third, Emerging or Declining Themes (lower-left quadrant) consist of topics with low density and low relevance. Examples include Bayesian networks, student modeling, and computer simulation. Their position indicates that these themes are either in the early stages of development or are losing relevance. Fourth, Basic Themes (lower-right quadrant) are defined by high relevance but low density. Key keywords here include students, mathematics education, teaching, computer-aided instruction, intelligent tutoring system, education computing, and advanced AI methods such as federated learning and adversarial machine learning. The findings in Figure 9 confirm that research on AI and ITS in mathematics education combines well-established themes, driving themes, and rapidly developing frontiers, offering a comprehensive picture of the dynamics and future direction of the field.

Thematic evolution

The thematic evolution analysis in Figure 10 highlights shifts in research focus in Artificial Intelligence (AI), Intelligent Tutoring Systems (ITS), adaptive learning, and mathematics education from 2001 to 2026.

Figure 10. Thematic evolution of research topics in AI and Intelligent Tutoring Systems research in mathematics education.

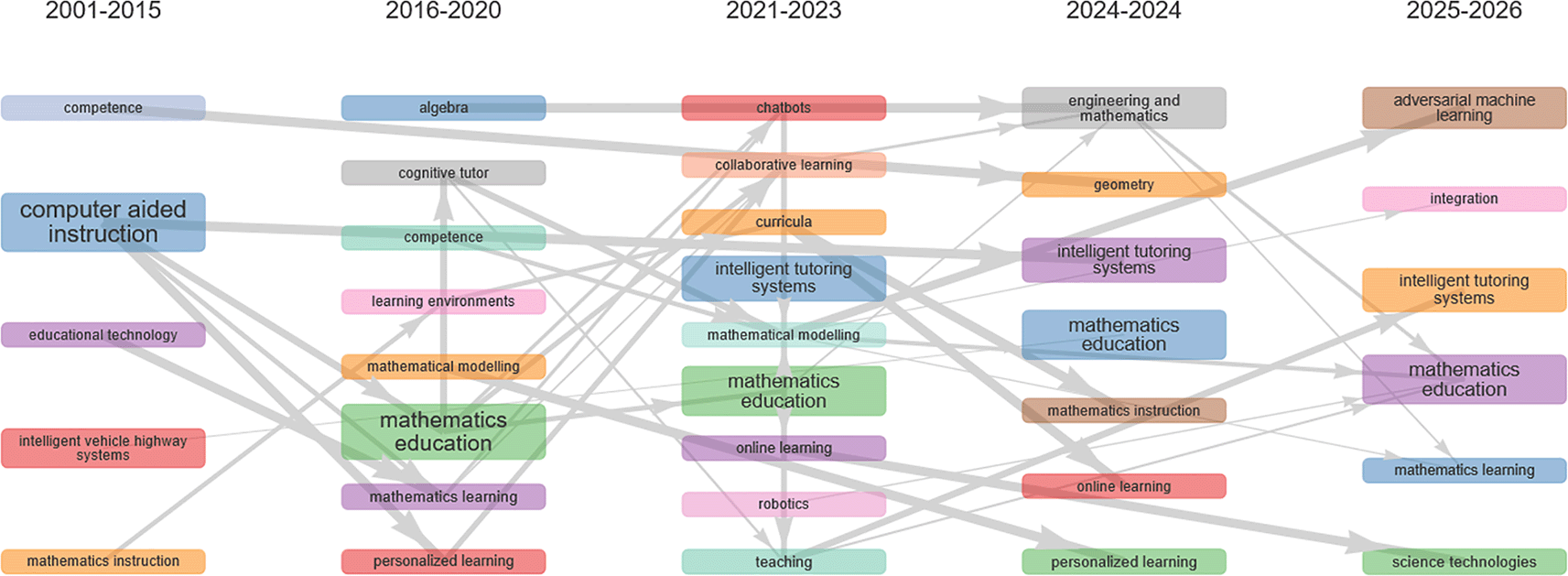
Overall, Figure 10 demonstrates that mathematics education and intelligent tutoring systems have remained consistent throughout, serving as the backbone of research evolution even as surrounding technological contexts shifted significantly.

Factorial analysis

The Factorial Analysis in Figure 11 presents a conceptual structure map explaining the intellectual framework of research on Artificial Intelligence (AI), Intelligent Tutoring Systems (ITS), adaptive learning, and mathematics education. Two main dimensions—Dimension 1 (40.08%) and Dimension 2 (30.93%)—together account for 71.01% of the data variance, indicating a robust conceptual structure.

Figure 11. Conceptual structure map based on multiple correspondence analysis (MCA) of AI and Intelligent Tutoring Systems research in mathematics education.

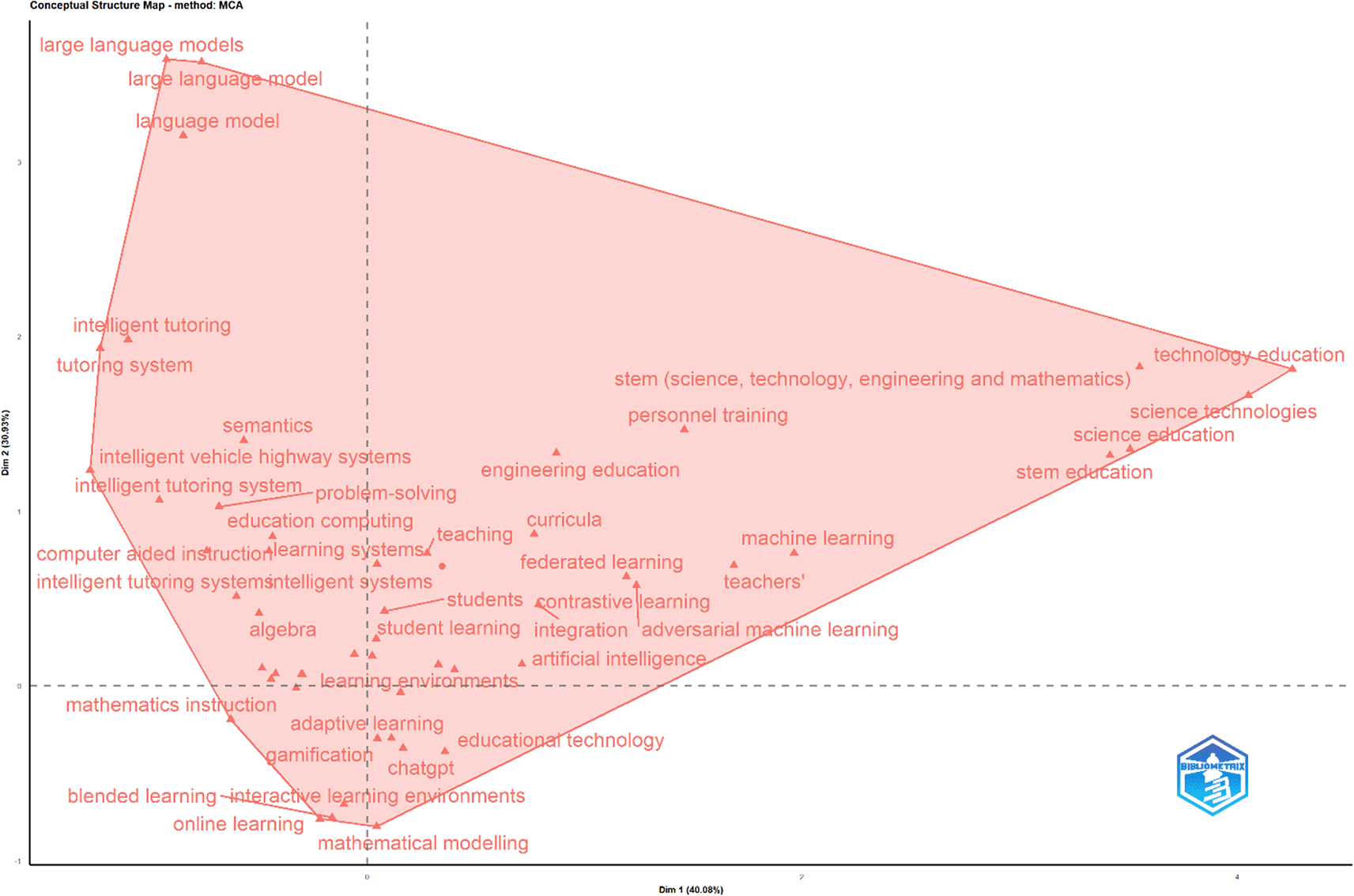
Several main clusters were identified:

In addition, central keywords near the origin, such as artificial intelligence, students, teaching, and computer-aided instruction, represent the common foundation of research. Meanwhile, peripheral terms such as large language models, federated learning, science technologies, and online learning point to specialized, emerging, or frontier areas. The findings in Figure 11 confirm that the conceptual structure of this research field is anchored in well-established foundations while also extending toward rapidly evolving frontiers aligned with the latest AI trends.

RQ1 – Scientific publication trends

The bibliometric results show that research in Artificial Intelligence (AI), Intelligent Tutoring Systems (ITS), adaptive learning, and mathematics education has developed dynamically with a strong interdisciplinary character, involving computer science, education, psychology, and mathematics. The main information findings in Table 1 indicate that this research collection is relatively recent, with an average document age of less than five years, and has significant impact, with an average of more than 16 citations per article. This confirms that publications in this field provide not only theoretical relevance but also tangible practical contributions. Authorship patterns reveal strong collaboration at both national and international levels, though there is still room to strengthen global networks. The distribution between conference proceedings and journal articles also reflects the dual character of the field: a drive for rapid dissemination through conferences alongside a commitment to deeper, peer-reviewed contributions in journals.

Viewed over time in Figure 2, research growth reveals distinct stages of development. Between 2001 and 2010, publications appeared only sporadically, reflecting an early phase in which the use of AI and STI in mathematics education was mainly limited to small-scale trials. From 2012 onwards, output increased more steadily, marking the first signs of consolidation. A decisive turning point occurred after 2019, coinciding with rapid progress in machine learning and, in particular, the emergence of large language models (LLMs), which drew global attention to the potential of AI in education. Recent studies highlight how AI-driven scaffolding, adaptive feedback, and personalized learning approaches can improve mathematics learning outcomes (Horvers et al., 2025; H. Li et al., 2025b; Yohannes & Chen, 2024).

The surge in publications—reaching nearly 50 in 2024—mirrors the trajectory predicted by Price’s Law, which holds that emerging research fields expand exponentially until they mature. Within this framework, AI and ITS have moved beyond their early niche status to become an increasingly recognized and established area of international research. The fact that recent trend topics have been dominated by keywords such as artificial intelligence, personalized learning, and mathematics education further reinforces the argument that the field has undergone substantial transformation and is moving toward a stage of research maturity.

The implication is that future research will likely place greater emphasis on diversifying AI applications, including the use of multimodal intelligent tutors, adaptive systems powered by big data, and the integration of generative AI in test construction, hint provision, and the design of interactive tutoring systems. Thus, the annual publication trend reflects not only an increase in research quantity but also a paradigmatic transformation in the ways AI is being used to shape the future of mathematics education.

RQ2 – Key authors & productivity (Lotka’s Law)

The Authors’ Production over Time analysis in Figure 4 highlights diverse patterns of contribution within the AI and ITS research community in mathematics education. Senior figures such as Aleven and Koedinger demonstrate long-term continuity in productivity, reflecting their roles as thought leaders who have shaped the field’s trajectory from its early stages to contemporary issues, including the integration of tutoring and mentoring roles in intelligent learning systems (Borchers et al., 2025; L. N. Son et al., 2025). By contrast, authors with shorter but high-impact periods of contribution—such as Arroyo, Hidayat, and Nygren—demonstrate that innovations addressing cognitive, metacognitive, and affective dimensions can have a strong influence even within a limited timeframe (Arroyo et al., 2014; Hidayat et al., 2023; Nygren et al., 2019).

Figure 4 shows the collaboration between Fancsali, Ritter, and Berman, illustrating the value of team research, especially in promoting ITS-driven formative assessment, which remains a cornerstone of adaptive education (Fancsali et al., 2018; Fancsali & Ritter, 2019; Fisher et al., 2020; Ritter et al., 2019; Zheng et al., 2019). At the same time, new contributors such as Borchers and Jia signal a generational shift in the field, drawing attention to cutting-edge technologies such as large language models (LLMs), intelligent proctoring, and adaptive prompt design (Borchers et al., 2023, 2025; Jia et al., 2020, 2023; Jia & He, 2022; Jia & Miao, 2021; Jia & Yu, 2017; H. T. Nguyen et al., 2024). These advances suggest that the field is expanding not only in scale but also in focus, thanks to sustained contributions from senior scholars, the impact of specific studies, and the incorporation of new researchers who push the technological boundaries (D. Li et al., 2025a). An analysis of author productivity using Lotka's Law confirms this distributional pattern, as shown in Figure 5. The majority of publications come from researchers with only one or two articles, while a smaller group—including Aleven, Koedinger, Arroyo, and Hu—maintains a consistent output over the long term. This is consistent with Lotka's prediction that a handful of highly productive authors dominate output, while the majority contribute intermittently.

The scholarly implications of these findings are notable. First, international collaboration needs to be strengthened to reduce dependence on a small group of senior authors. Second, the contributions of these established researchers must be sustained and extended through broader networks and generational renewal, as their work continues to shape both theory and methodology. Third, the large proportion of new authors demonstrates that the field remains open, offering significant opportunities for early-career researchers. Finally, creating a balanced research ecosystem—where widespread participation is complemented by the depth of work of lead authors—will require deliberate mentoring and capacity-building strategies to ensure long-term productivity. Taken together, the analysis of RQ2 shows that author productivity in AI and ITS research within mathematics education reflects not only the distribution of publications but also the broader social and academic structures that guide the growth of the field (Borchers et al., 2025; D. Li et al., 2025a; H. Liu et al., 2024; Lyu et al., 2025; H. T. Nguyen et al., 2024).

RQ3 – Patterns of international collaboration

The examination of international collaboration through the Three-Field Plot and Corresponding Author’s Countries reveals that progress in Artificial Intelligence (AI), Intelligent Tutoring Systems (ITS), adaptive learning, and mathematics education has been driven not only by individual scholars but also by increasingly interconnected global networks (See Figure 3). Findings suggest that research activity is still concentrated in a few major countries, particularly the United States, China, and Germany. The United States occupies a leading position, contributing extensively to central themes such as mathematics education, ITS, personalized instruction, and adaptive learning. China ranks just behind, showing a comparable research profile that reflects its rapid growth in AI-based educational technologies. Germany also plays a pivotal role, serving as a hub for cross-border collaboration that strengthens the reach and visibility of European contributions on the global stage.

From a topic perspective, the predominance of keywords such as mathematics education and intelligent tutoring systems highlights the global focus on leveraging AI to enhance mathematics learning. However, the emergence of new keywords such as large language models and ChatGPT reflects a shifting trend toward integrating generative AI into ITS (Chohan & Khan, 2024; J. Liu et al., 2025; Ru & Li, 2025; Xuan et al., 2025; Yunianto et al., 2024). This indicates that while the core topics remain relatively stable, the research community is also open to cutting-edge innovations such as conversational tutors, automatic problem generation, and adaptive feedback. Therefore, these collaboration patterns and topic orientation affirm that the field is dynamic and continuously evolving alongside cutting-edge technological developments.

An analysis of the corresponding authors' countries in Figure 6 reveals distinctive contribution patterns. The United States and China lead the publication volume; however, their high proportion of Single Country Publications (SCPs) shows that much of this work is domestically focused. While this reflects strong domestic research capacity, the relatively low proportion of Multi-Country Publications (MCPs) suggests that their global influence could grow further through broader international partnerships. Germany, in contrast, stands out for its high degree of cross-border collaboration, with a SCP share of 50%. While its overall output is lower, its openness to cooperation generates more diverse perspectives and greater international visibility. Similar trends are observed in Belgium, Malaysia, Spain, and Finland, where a relatively modest number of publications is offset by a strong commitment to collaboration.

Countries with average research output, such as Indonesia, Turkey, and the United Kingdom, also play a prominent role. Indonesia and Turkey produce primarily domestic studies, but their growing publication trends point to great potential for greater global engagement. The United Kingdom, on the other hand, records a comparatively high rate of MCPs, allowing it to act as a bridge between major research centers and broader academic communities. Taken together, the findings from RQ3 indicate that research on AI, ITS, and mathematics education is driven not only by major players such as the United States and China, but also by countries that prioritize collaboration. This pattern highlights the importance of international networks for the advancement of ITS and adaptive learning, as they facilitate the exchange of ideas, technologies, and pedagogical approaches on a global scale. For developing countries, active participation in such networks is particularly vital to strengthen research capacity, increase visibility, and ensure that AI-based educational innovations remain inclusive and globally relevant.

RQ4 – Dominant research themes & conceptual evolution

The progression of research topics reveals a clear paradigm shift: from conventional technology-based instruction to Artificial Intelligence (AI) and personalized learning as the new foundation (see Figure 7). Early studies focused mainly on computer-assisted instruction in specific subjects such as algebra. In the intermediate phase, attention shifted to adaptive learning systems, with greater emphasis on mathematical modeling and cognitive tutors. A major turning point emerged after 2021, when AI-based tutors and personalized learning approaches became dominant, underscoring the central role of AI in data-driven adaptive systems (Alvarez, 2024; Walkington et al., 2024). The growing importance of STEM education further reflects a trend toward interdisciplinary approaches, which place mathematics in a broader framework, aligned with the competencies required in the 21st century (Barana et al., 2024). Another notable trend is the increasing use of terms such as teacher and staff training, which highlights a growing awareness that successful technology integration depends largely on teachers' ability to manage and facilitate digital learning (D. Li et al., 2025a).

Keyword co-occurrence analysis also sheds light on the structure of the field, as shown in Figure 8. Two main pillars stand out: pedagogical practices and technology-based teaching systems. Within this framework, the red cluster highlights teaching strategies, while the green cluster emphasizes teaching technologies that support student learning. The blue cluster points to new research frontiers, with studies exploring areas such as federated learning and adversarial machine learning, indicating a growing concern for privacy and security in adaptive systems (H. T. Nguyen et al., 2024; R. Wang & Wu, 2023). On the other hand, the purple cluster points to the expansion of work in global STEM contexts, showing that ITS are no longer considered in isolation, but as part of a broader movement to strengthen scientific and technological literacy (Le & Taherdoost, 2025). Together, these patterns confirm the transition from traditional instruction to an AI-powered STEM education ecosystem that values both inclusivity and adaptability.

The thematic map in Figure 9 highlights the diversity of AI and ITS research in mathematics education across four categories. First, specific topics such as generative AI and multimodal learning represent specialized but rapidly expanding frontiers, particularly in the design of multimodal learning experiences (D. Li et al., 2025a). Second, key topics such as engineering education and science technologies act as cohesive hubs of innovation, driving the integration of AI into STEM curricula (Portillo & Alvarado, 2025). Third, basic themes including students, mathematics education, and intelligent tutoring systems serve as foundational anchors, showing continuity from earlier research to present adaptive approaches (Horvers et al., 2025). Fourth, Emerging or Declining Themes show the decline of student modeling and Bayesian networks, signaling a transition toward newer methods or potential revitalization if combined with frontier AI. Accordingly, the thematic map functions as a diagnostic tool to identify mature areas, promising frontiers, and shifting themes.

Longitudinally, the field has transitioned from simple instructional experiments to frontier AI-driven ecosystems (see Figure 10). In the early phase (2001–2015), research focused on computer-aided instruction emphasizing digital instructional tools (Arroyo et al., 2014; Craig et al., 2013; Ersoy & Akbulut, 2014; Harskamp & Suhre, 2006; Jurkovic, 2001; Kinnari-Korpela, 2015; Underwood, 2007). The consolidation phase (2016–2020) marked a turning point with mathematics education, cognitive tutors, and data mining gaining prominence, shifting the orientation toward data-driven adaptive systems (Albano & Dello Iacono, 2019; Greefrath, 2020; Nabiyev et al., 2016; Nygren et al., 2019; Wu, 2019). The transition phase (2021–2023) saw the integration of ITS and AI with topics like chatbots and collaborative learning, expanding approaches toward social and collaborative dimensions (Chau et al., 2025; Lee & Yeo, 2022; Neto & Fernandes, 2019; Rodríguez-Martínez et al., 2023; S. Sun et al., 2023; Taranto et al., 2024). The contemporary phase (2024) reflects the adoption of generative AI tools such as ChatGPT and the diversification of research into STEM areas, including geometry and engineering education (Chohan & Khan, 2024; Copur-Gencturk et al., 2024; Murdan, 2024; Opesemowo & Ndlovu, 2024; Torres-Peña et al., 2024). Looking ahead, the prospective phase (2025–2026) is expected to focus on frontier topics such as adversarial machine learning and system integration, with strong emphasis on security, privacy, and multimodal learning (Borchers et al., 2025; Cosentino et al., 2025; H. Li et al., 2025b; J. Liu et al., 2025; Lyu et al., 2025; C. Sun et al., 2025). Taken together, this trajectory illustrates the field’s progression from early digital tools to advanced intelligent systems that respond to the complex challenges of the generative AI era.

The factorial analysis as shown in Figure 11, uncovers layered conceptual structures within AI and ITS research. The first dimension illustrates the shift from specific pedagogical research such as mathematics instruction toward broader integration in STEM education (Barana et al., 2024). The second dimension distinguishes between foundational pedagogy-based research such as online learning and frontier AI-based research such as large language models (Alvarez, 2024). Established areas continue to include ITS, e-learning, and mathematics instruction, while emerging areas include LLMs and federated learning, now being explored in adaptive contexts (H. T. Nguyen et al., 2024). Cross-theme interactions highlight the importance of keywords such as artificial intelligence and teachers as connectors between pedagogy and frontier technology (X. Li et al., 2024). Strategically, four implications arise: (1) integrating advanced AI into ITS, (2) strengthening the synergy between pedagogy and frontier AI, (3) enhancing teacher professional development for technological adaptation, and (4) expanding personalized learning within STEM contexts more holistically (Le & Taherdoost, 2025). Thus, factorial analysis affirms that the future of research will be determined by a balance between technological sophistication and pedagogical needs.

Despite these contributions, several limitations should be noted. First, this study relied on a single database (Scopus) and restricted inclusion to English-language journal articles and conference papers, which may underrepresent relevant work indexed elsewhere or published in other languages and formats; moreover, recent-year patterns (especially 2024–2025) may be affected by indexing delays, and bibliometric indicators cannot directly evaluate instructional effectiveness, learning outcomes, or causal mechanisms. Second, science-mapping results depend on author keywords and metadata quality; variations in terminology (e.g., ITS vs. adaptive learning systems, LLM vs. generative AI) may influence cluster formation and thematic evolution. These constraints imply that the findings should be interpreted as a macroscopic “research landscape” rather than a substitute for pedagogical impact evidence, yet they still offer actionable implications: (i) scholars can use the identified thematic pillars and emerging fronts to position novelty and avoid duplication, (ii) institutions and funders can target capacity building in under-connected regions to strengthen international collaboration and knowledge transfer, and (iii) policymakers and practitioners should treat teacher professional development, governance, and responsible AI (privacy, security, robustness) as co-requisites of scaling AI/ITS in mathematics education rather than afterthoughts. Accordingly, further research is recommended to (1) expand coverage using multi-database designs (e.g., Scopus + WoS + ERIC) and multilingual retrieval, (2) integrate bibliometrics with systematic or scoping reviews and, where feasible, meta-analytic evidence to link research growth with demonstrated learning benefits, (3) conduct comparative empirical studies on generative-AI-enabled tutoring (e.g., feedback quality, misconception diagnosis, equity effects, and classroom orchestration), and (4) develop shared benchmarks and reproducible evaluation protocols that explicitly test privacy-preserving and security-aware approaches (e.g., federated learning, adversarial robustness) in authentic mathematics learning settings.