Keywords
occupancy, population viability analysis, extinction, range loss, presence/absence survey, detection probability, Gulo gulo, Sierra Nevada
occupancy, population viability analysis, extinction, range loss, presence/absence survey, detection probability, Gulo gulo, Sierra Nevada
Detection of rare species is one of the fundamental problems in conservation biology. A species cannot be managed for unless its presence is known. Consequently, presence-absence surveys are common first steps in guiding management policies. But, while formal surveys are very good at confirming a species presence, determining if a species is absent from a management unit is more problematic. The crux of the problem lies in the omnipresent possibility that nondetection does not indicate a species absence. Clearly, incorporating nondetection probability, through its inverse, detection probability, is a critical component to both the design and interpretation of presence-absence surveys, and there are well-developed methods for doing so [e.g.,1,2].
The simplest of these methods assume that detection probabilities depend only on survey effort1. Consequently, designing a survey with a small chance of failing to detect a species present in a management unit depends only on knowing detection probabilities, which can be estimated from surveys conducted in areas of known occupancy [e.g.,1,3]. In the absence of reliable information from surveys in known occupied areas, detection probability is often estimated from similar species4 or simulation5,6.
Of course, detection probabilities do not depend only on survey effort. At the very least, the size of the population within the survey area influences detection probabilities; smaller populations are more difficult to detect than larger ones. Moreover, the influence of population size on detection probability is nonlinear such that the loss of an individual has a larger impact on the detection probability of a small population than of a large one7. This relationship has two underappreciated consequences for designing and interpreting presence-absence surveys. First, the effort required to detect a small population increases at an accelerating pace as population size dwindles. Second, determining the survey effort required to have an acceptably small nondetection probability requires specifying the size of the population being looked for (hereafter, target population size).
Given limited resources, it generally will not make sense to dedicate a lot of resources to ensure a high probability of detecting the last individual of a species within a management unit. In other words, it is inefficient to spend limited resources to detect a species which may technically be present within a management unit but is effectively locally extinct. It would be more efficient to design a survey to detect a population of two individuals, but such a population would still likely require a large effort to detect and would still face a high risk of local extinction in the near term. It would generally be even more efficient to design a survey based on a target population of three individuals, but because increasing population size generally has a diminishing effect on both detection probability and extinction risk (assuming no Allee effect8), the gain in efficiency would not be as large as the gain in efficiency realized from designing for a target population of two vs. one.
Ideally, a survey design avoids two sources of inefficiency: failing to detect a population that persists into the near future and detecting a population that fails to persist into the near future. As such, the target population size should account for the effects of population size on both detection probability and extinction risk (Figure 1). This can be done thinking of survey power not in terms of the probability of failing to detect a population, but in terms of the probability of failing to detect a viable population. The latter is the equivalent of the product of both the probability of failing to detect at least one individual, which is an increasing function of population size, and the probability of a population persisting into the near future, which is a decreasing function of population size. Framing a presence-absence survey in terms of detecting a viable population also changes the interpretation of null survey results. Rather than a null result implying a species absence, a null result implies that if the species is present in a management unit, its population is so small that it is unlikely to persist into the near future.
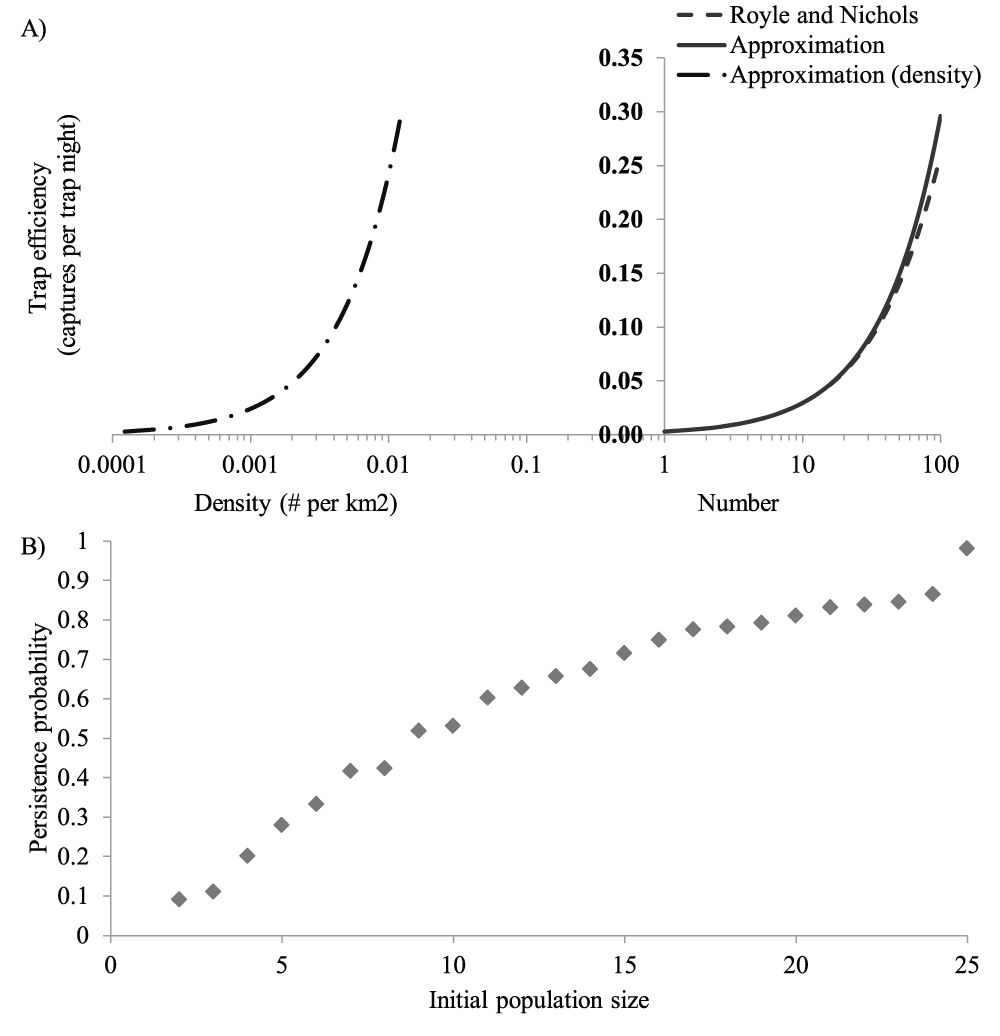
A) Lines to the right of the Y-axis depict how trap efficiency increases with population size calculated using the methods of Royle and Nichols7 (dashed line) and the approximation presented in this paper (solid line). The line to the left of the Y-axis shows how trap efficiency increases with increasing density. Density values correspond to the population sizes used in the right-hand side of the graph interacting in an 8171 km2 area. Trap efficiencies were calculated assuming an individual capture probability of 0.003 or reference trap efficiency of 0.024 for a reference population size of 8 individuals at a corresponding reference density of 0.0024 animals per square km. The X-axis is plotted on a log10 scale to emphasize small population numbers. For raw data, please see Dataset 1. B) Points indicate the probability that a population starting at the population size on the X-axis persists for 25 years predicted by PVA (see text for details). For raw data, please see Dataset 2.
In this paper, we develop a framework for survey design which incorporates small population effects on both detection probability and short-term persistence. We then demonstrate the application of this framework to the design and interpretation of a presence-absence survey for wolverines in Sequoia-Kings Canyon National Parks, California, USA. Finally, we discuss the implications of the wolverine survey for wolverine management in California and the circumstances under which the framework developed here is, and is not, appropriate for designing and interpreting presence-absence surveys.
We developed methods for optimizing survey effort to detect a viable population given that one persists in the survey region, and for a post-hoc analysis of survey power which serves as the basis for evaluating negative survey results in terms of the probability of overlooking a population that will persist into the near future. A good survey has two critical components: 1) an appropriate method to detect the species of interest, and 2) adequate sampling effort to have a low probability of overlooking the species if it is present. Here we focus on how to determine the amount of survey effort required once appropriate methods have been chosen. Although we envision a survey based on baited camera traps, with detections based on photographing an animal visiting a bait station, the methods described work with any survey protocol for which effort can be quantified in discrete units (e.g., trap-nights, kilometers traversed, etc.) and detection probability can be expressed per unit of effort.
Assuming that additional traps do not interfere with one another, the probability of detecting a species (D) for a given amount of effort is:
D=1-(1-E)T (equation 1)
where E is the trap efficiency (i.e., the probability of a detection during a single unit of survey effort) and T is the number of trap-days (i.e., total survey effort) in the study. If all individuals within the surveyed population have the same chance of being detected, trap efficiency will be related to population size as E=1-(1-e)N7, where e is the probability that a particular individual is detected and N is the number of individuals in the survey area. After substitution and simplification, Equation 1 can then be rewritten to account for population size as:
D(N)=1-((1-e)N)T (equation 2)
To calculate the survey effort required assuming a population size N, to achieve the desired detection probability (D(N)), we solve for T(N):
T(N)=ln(1-D(N))/ln((1-e)N) (equation 3)
Note that as the population size of the target species in the survey region approaches zero, the required effort approaches infinity. The nonlinear relationship between T and N as N approaches zero means that surveys designed to detect the lowest possible size (i.e., a single individual within the survey area) are likely to be prohibitively large.
The next step to optimize survey effort is to consider the effects of population size not only on detection probability, but also on near-term population viability (i.e., the probability that a population persists beyond some time, t, in the near future). There are many ways to determine the relationship between density and population viability using population viability analysis (PVA). Choosing the most appropriate type of PVA depends on what data are available for the species9. Commonly used count-based PVA, which treats changes in the (log) population size as a diffusion process, explicitly assumes a relationship between population size and extinction risk. For more complex population dynamics (e.g., density dependent or age structured populations), the relationship can be determined by simulation9. Here, we assume that there is some relationship between near-term population viability and the current population size (Z(N)) and that this relationship has been determined using PVA (e.g., Figure 1B).
When taking population viability into account, the relevant statistic is probability of failing to detect a viable population given that the species inhabits the survey area at a given population size:
P(N)=(1-Z(N))×(1-D(N))
Substituting for D(N) and simplification yields
P(N)=(1-Z(N))×(((1-e)N)T) (equation 4)
The maximum value of P(N), as N varies in equation 4, approximates the probability that a survey failed to detect a population that will persist into the near future. The exact probability is equal to the integral of the product of P(N) and the probability that the population being surveyed has N individuals over all possible values of N. However, the latter probability distribution is extremely unlikely to be known or even estimable for populations which are the focus of presence/absence surveys. Approximating this interval at the maximum value of P(N) results in an estimate of P(N) that is biased high, which for most applications of this analysis will be a conservative bias.
Because most power analyses calculate the probability of success (e.g., that a study will show a significant difference given that observed groups do differ), it is tempting to estimate survey power as 1-P(N). We caution against doing so because this quantity is difficult to interpret; it is the union of the probabilities that a population is detected or goes extinct in the near future, not the probability that a population is detected given that a viable population persists in the survey area, nor the probability that an undetected population goes extinct.
To determine the optimal trap effort, one must first determine the desired level of risk for overlooking a viable population independent of population size, P(•). Choosing a critical value for P(•)=(Pcrit) and rearranging equation 4 to solve for T yields
T=(ln(Pcrit)-ln(1-Z(N)))/ln((1-e)N) (equation 5)
At N=0, equation 5 evaluates to infinity, reflecting that no amount of effort can detect an extinct viable population (itself a logical impossibility). As N increases, equation 5 has a maximum value which indicates the optimal survey effort. If Z(N) is a differentiable function, Tmax can be calculated analytically. If Z(N) was determined by simulation then Tmax must be determined by iterating equation 5, but since extinction risk generally decreases sharply with population size, iterations will typically only have to span a small range of N. Note that if population viability and reference detection probabilities are provided in terms of population density rather than population numbers, equation 5 may still be used by defining N as population density.
Pre-survey power analysis. We applied the techniques outlined above to design and interpret a presence-absence survey for wolverines in Sequoia-Kings Canyon National Parks (SKCNP) to address concerns related to the impact that a proposed translocation of wolverines into the southern Sierra Nevada would have on a possible remnant population. The concerns arise from a contradiction between management agencies’ — in particular, California Department of Fish and Wildlife and SKCNP — stance that wolverines persist and should be managed for in the Sierra Nevada10,11 and published conclusions that the species has been extirpated from the state12,13. The conflicting stances largely stem from differences in opinion about how to treat unverified reports by citizen observers and a failure of formal surveys to address survey power. Because most carnivore surveys in the Sierra Nevada take place in the summer2,14, when wolverines are not likely to visit bait stations (there are no published records of summertime efforts which have trapped wolverines), it is not unreasonable to suppose that formal surveys may have overlooked a small remnant population in the Sierra Nevada given numerous reported sightings of the species. The recent discovery of an immigrant male wolverine more than 250 km north of SKCNP15 has done little to quell the debate.
In order to resolve this conflict, we carried out a winter survey for wolverines using baited camera stations in SKCNP designed to have a high power to detect a wolverine population large enough to have a reasonable probability of persisting at least 25 years. Given a 75-year absence of physical evidence of wolverine presence in the area13, we assumed that if wolverines did remain in the parks, they persisted in low densities compared to areas where detection probabilities were available from previous winter surveys. Consequently, it was clear that the effect of population size on detection probability needed to be accounted for.
Only two published winter carnivore surveys provide estimates of both detection rates from baited camera stations and wolverine density16,17, and none report both the trap efficiency and population estimate within the effective trap area. Consequently, it is not possible to estimate the per capita detection probability (e) of a wolverine. However, when N and e are small, E is closely approximated by (N/N*)E* where E* is the trap efficiency at a reference site with population size N* (Figure 1A). Application of this approximation for E into equation 5 yields:
T=(ln(Pcrit)-ln(1-Z(N)))/ln(1-(N/N*)E*) (equation 6)
Assuming a constant area, changes in density (d) are equivalent to changes in population size, such that N/N* may be replaced by d/d*. The average trap efficiency and density estimates from these studies were E*=0.024 detections per trap-night and d*=0.0098 wolverines per km2. Corresponding trap efficiencies over a range of wolverine densities are shown in Figure 1A.
We determined how wolverine population size affects extinction risk using the PVA modeling program VORTEX (v.9.7.2, Chicago Zoological Society 2007) parameterized with demographic rates taken from the published literature (see Appendix A). VORTEX is a widely used, flexible, individual based simulation18 that has been found to perform relatively well compared to other PVA packages19. We set initial population size between 2 and 25 animals and simulated population dynamics for 25 years, corresponding to 5 to 8 wolverine generations. We estimated short-term extinction risk at each initial population size as the fraction of 10,000 replicate simulated populations that went extinct before the end of the simulation (Figure 1B).
Because published detection probabilities are tied to population densities and extinction risk is tied to population size, we had to translate population size to density in the survey area. Our PVA assumed a well-mixed population without spatial structuring. We therefore assumed that the corresponding area allowed a juvenile at the center of the population to interact with all other animals in the population if it covered the average dispersal distance. The average distance covered by a dispersing wolverine is 51 km20, so we divided population size by 8171 km2 to calculate the corresponding density.
Maximizing equation 5 using the density dependent detection and extinction risks shown in Figure 1 and Figure 2, we calculated that 1160 trap-nights would be sufficient to have a less than 5% probability of failing to detect a viable population of wolverines inhabiting SKCNP (Figure 2A). Assuming that baited camera stations would be available for 2.5 months (75 days), this effort would require a minimum of 16 stations.
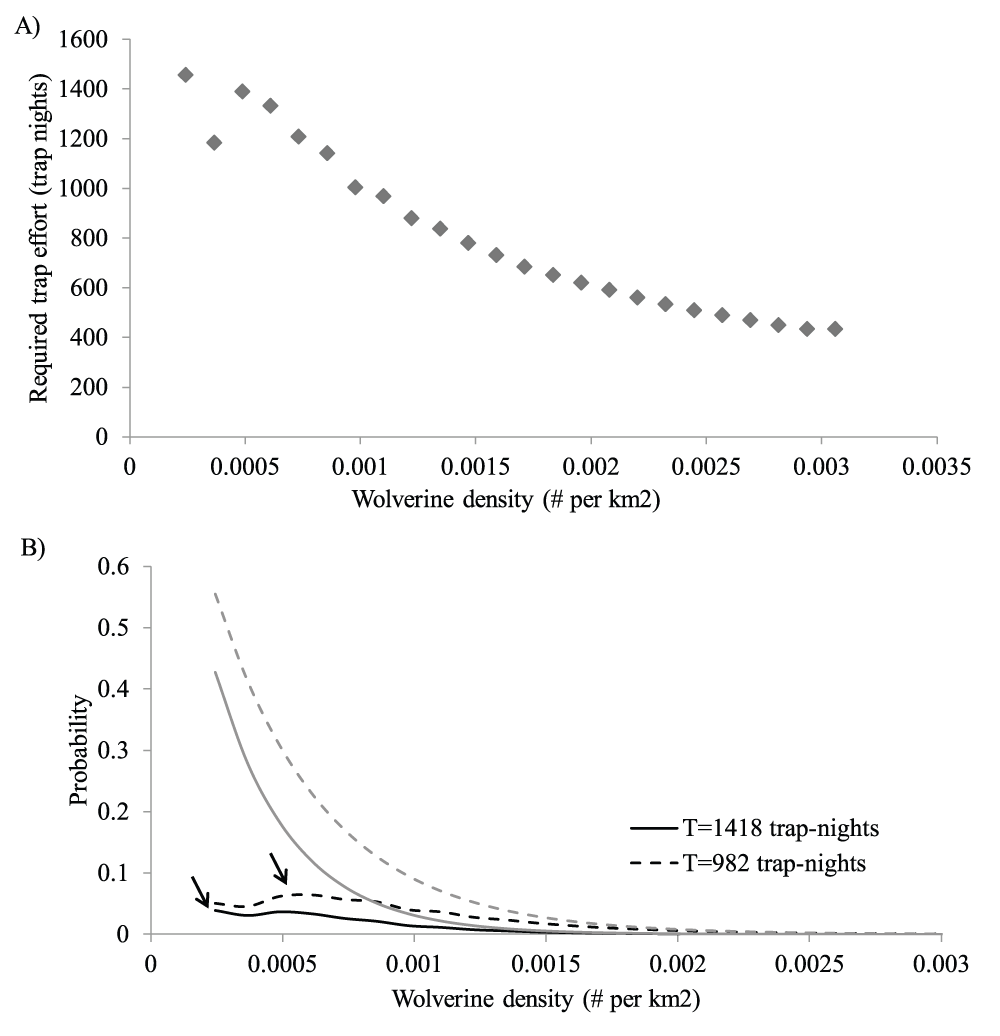
Top panel A) shows the trap effort required to have 95% probability of detecting a viable wolverine population given that wolverines inhabit the survey area at the density indicated on the X-axis. The apparent dip of the second point from the left reflects a dramatic decrease in population viability but not detection probability for a population of three compared to one of four individuals. The bottom panel (B) shows the realized power of the survey. The grey lines indicate the probability of failing to detect at least one wolverine and the dark lines indicate the probability of failing to detect a member of a viable wolverine population given that wolverines are present in the study region at the density indicated by the X-axis. Probabilities were calculated from equation 2 and equation 4, respectively, assuming a trap effort of 1418 (solid line) or 982 (dashed line) trap-nights, and reference trap efficiency of 0.024 captures per trap-night at a reference density of 0.0098 wolverines per square km. Black arrows indicate maximum values reported in text. For raw data, please see Dataset 3.
Survey methods. We placed 18 baited camera stations throughout SKCNP between January 26 and 28, 2006. Baited camera stations have been successfully used to detect wolverines outside our survey region15–17,21, and to detect other mesocarnivores in the southern Sierra Nevada12,14. We exceeded the recommended 16 stations so that camera malfunctions or other unforeseen circumstances affecting up to two stations would not reduce our survey power below 95%.
Each station consisted of a 1.2 m × 10 cm × 10 cm wooden post wrapped in barbed wire held 0.46 m from a tree by an aluminum frame. On top of each post was a ~0.5 m × 0.5 cm steel pole holding 1 to 5 kg of meat, bone, and hair cut from a pig carcass and wrapped in hardware cloth. We also attached a perforated can of wet cat food injected with Gusto (a combination of skunk glands and beaver castor oil; Caven’s Quality Animal Lures) to each post to provide a scent lure. The bottom of each station was placed approximately 1 m above snow level so that the bait was approximately 3 m above snow level (approximately 5–6 m above ground). We mounted a heat/motion triggered camera to a second tree 1.5–5 m away from and 0.5–1 m above the bait station. We constructed camera units using PixControl™ control boards equipped with passive infrared (PIR) sensors and Sony P32 digital cameras with 256 MB memory cards. All components were mounted in waterproof plastic boxes.
We established survey stations by helicopter on 26–28 January 2006 (Table 1). To ensure adequate coverage across the parks, a 20 km × 20 km grid was overlaid on the park and at least one station was placed in suitable wolverine habitat in each cell (Figure 3). This represents one station per average female home range area (400 km2) or two stations per male home range area (800 km2) at low wolverine density. We placed additional stations in cells that contained a high number of alleged wolverine sightings reported in the 25 years prior to the survey.
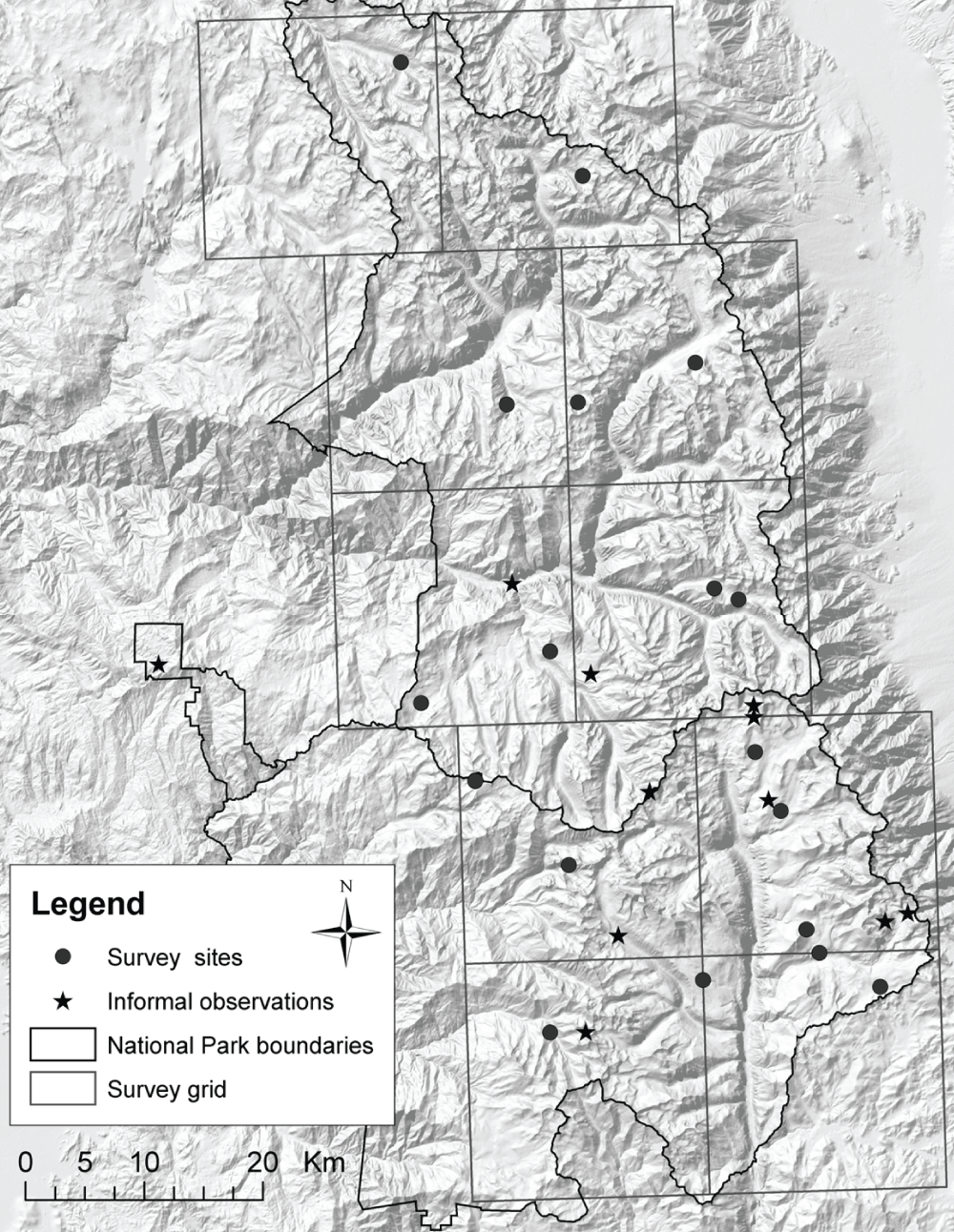
Black dots indicate locations of baited survey stations; stars indicate locations of informal wolverine sightings reported to Sequoia-Kings Canyon National Parks (courtesy NPS) since 1980. Map generated by IWS staff using ArcGIS and World Shaded Relief (ESRI 2009).
The primary determinants of station locations within each grid were elevations within approximately 200 m elevation of treeline (2744–3506 m), the availability of trees for anchoring bait stations and cameras, and proximity to safe helicopter landing sites. We also considered the accessibility of locations to monitoring teams that were to check the stations and the location of reported wolverine sightings within the past 25 years. The two sites located below 2500 m were placed within 1 km of where purported wolverine tracks were photographed during snow surveys in 1979 and 1980 (T. Andrews, unpublished data) and in the Mineral King area where many unsubstantiated sightings have been reported since 1980.
Fourteen of the camera stations were checked at least once between 18 February and 1 May 2006 by Institute for Wildlife Studies personnel, California snow survey teams, or park staff. The person checking each station replaced the camera batteries and memory cards. Frequent snow storms and high avalanche risk prevented surveyors from checking four of the most remote stations until they were taken down by helicopter in early May. Stations remained active for up to 105 days. We reviewed all pictures taken from each camera after memory cards were removed from the cameras during mid-survey checks, and at the end of the survey. We recorded all animals photographed by each camera, days during which photos indicated a camera was obscured by snowfall, how many days the station was available (see results), and the date the last photo was taken.
Camera performance. Overall, the PIR-triggered cameras worked very well under a wide range of conditions. We collected 2939 pictures during our survey excluding pictures taken while surveyors set up, maintained, and took down the stations. Pictures were taken during all hours of the day and night throughout the entire survey period. Animals were visible in 602 pictures (Figure 4); most remaining photographs were probably triggered by rapid changes in ambient temperature or by wind-blown branches. An additional 400 pictures were used to identify periods when cameras were operable. These included pictures taken during and immediately following snow events which obscured the camera lens, subsequent pictures indicating that the lens had been cleared, and pictures of surveyors approaching the camera before switching out memory cards or taking down survey stations.

Panels show four carnivores identified at four stations: a) black bear (Ursus americanus), b) coyote (Canis latrans), c) fisher (Martes pennanti), and d) marten (Martes americana).
In total, cameras were considered operable for 1418 survey-days from 27 January through 11 May. Individual stations were available for between 20 and 105 days (Table 1). A station was judged to be operable from the day it was set up to the day the last photograph of the bait station was taken, excluding days when snow accumulation either obscured the camera lens or buried the bait station. The camera lenses at five stations were temporarily obscured by snowfall accumulating on the camera case and were judged unavailable until the time of the next unobscured photo. This period ranged from 10 minutes to four days. There were no photos taken more than six hours after the first obscured photo that remained obstructed by snow accumulation. Any station known to have been obscured for more than one hour was deemed unavailable for at least one day. Stations were also judged to be unavailable when the bait was buried by snow or was missing.
| Site | Latitude | Longitude | Elevation (m) | Last picturea | Days closed | Days availableb | 1st carnivorec | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MK | 36 | 26 | 11 | 118 | 35 | 21 | 2400 | 24-Apr | 13 | 74 | 9-Feb |
| SP | 36 | 28 | 32 | 118 | 16 | 2 | 3338 | 25-Mar | 0 | 57 | NA |
| RC | 36 | 29 | 43 | 118 | 19 | 33 | 2955 | 11-May | 0 | 104 | 29-Jan |
| CP | 36 | 29 | 49 | 118 | 26 | 34 | 3161 | 9-May | 16 | 86 | 3-Feb |
| GF | 36 | 31 | 30 | 118 | 21 | 13 | 3234 | 10-May | 0 | 103 | 26-Mar |
| TL | 36 | 34 | 54 | 118 | 34 | 7 | 2839 | 21-Feb | 0 | 25 | 7-Feb |
| WC | 36 | 36 | 19 | 118 | 22 | 30 | 3311 | 10-May | 0 | 103 | 28-Mar |
| TM | 36 | 37 | 10 | 118 | 38 | 4 | 3149 | 11-May | 20 | 84 | 27-Mar |
| TC | 36 | 37 | 45 | 118 | 23 | 36 | 3165 | 11-May | 0 | 104 | 30-Jan |
| BD | 36 | 40 | 56 | 118 | 43 | 43 | 2773 | 26-Apr | 4 | 85 | 31-Jan |
| MC | 36 | 44 | 42 | 118 | 37 | 37 | 2154 | 7-Apr | 4 | 66 | 1-Feb |
| CL | 36 | 46 | 13 | 118 | 25 | 4 | 3268 | 10-May | 6 | 97 | 5-Mar |
| BL | 36 | 46 | 21 | 118 | 23 | 52 | 3260 | 4-May | 0 | 97 | 7-Mar |
| GB | 36 | 56 | 57 | 118 | 37 | 18 | 2505 | 16-Feb | 0 | 20 | 7-Feb |
| HL | 36 | 56 | 58 | 118 | 35 | 2 | 3092 | 24-Mar | 4 | 52 | 5-Feb |
| MI | 36 | 57 | 0 | 118 | 27 | 14 | 3290 | 10-May | 0 | 103 | 29-Mar |
| DB | 37 | 5 | 42 | 118 | 33 | 9 | 3450 | 13-Apr | 0 | 76 | 29-Jan |
| EV | 37 | 10 | 24 | 118 | 42 | 57 | 3012 | 20-Apr | 1 | 82 | 23-Mar |
We detected no wolverines. Species detected included nine mammals and four birds. Martens (Martes americana Turton) were recorded in 419 pictures from 14 stations (Dataset 4). Other mesocarnivore species detected include coyote (Canis latran, Say), fisher (Martes pennanti Erxleben), and black bear (Ursus americanus Pallas). We also recorded northern flying squirrels (Glaucomys sabrinus Shaw), Douglas’ squirrels (Tamiasciurus douglasi Bachman), golden-mantle ground squirrel (Spermophilus lateralis Say), deer mouse (Peromyscus maniculatus Wagner), white-tailed jackrabbit (Lepus townsendii Bachman), Clark’s nutcrackers (Nucifraga columbiana Wilson), dark-eyed juncos (Junco hyemalis Linnaeus), green-tailed towhee (Pipilo chlorurus Audubon), and white-crowned sparrow (Zonotrichia leucophrys Forster).
Post-hoc power analysis. Assuming 1418 trap-nights and the density dependent detection and persistence probabilities from Figure 1 and Figure 2, maximizing equation 4 yields an estimated probability for failing to detect a viable wolverine population of P=0.039 (Figure 2B). Because most wolverine surveys are conducted following a pre-bait period, we also calculated the power of our survey assuming that survey stations were not effective until the average date of first visitation by mesocarnivores to the 17 stations that were visited by at least one mesocarnivore (February 21). This reduced the effective survey time to 982 trap-days, increasing the estimated probability of failing to detect a viable wolverine population to P=0.064 (Figure 2B).
A growing literature is devoted to inferring true occupancy from spatially replicated surveys1, and incorporating density effects on detection rates to infer extinction probabilities from temporally replicated surveys2,7 and population size from detection patterns22. The framework presented here extends the application of these methods to the special but important case where replicated surveys fail to detect a species on any occasion. We accomplish this by extending the analyses to simultaneously consider the effects of population size on detection and population processes (i.e., trap efficiency and persistence probability). This extension makes two important advances to the design and interpretation of presence-absence surveys. First, explicitly acknowledging that extremely small populations are very difficult to detect but unlikely to persist facilitates efficient survey designs with enough power to detect species which need to be managed without wasting effort on effectively extinct populations. Second, the framework presented here shifts the interpretation of a failure to detect a species from the conclusion that zero individuals remain within the survey area to the conclusion that no more than a very small number could be within the survey area.
Choosing a target population density based on the effects of small populations on both detection and persistence probabilities was critical to design of an efficient survey. If only a single wolverine inhabited the park, the survey would require 3730 trap days to have 5% failure probability. In contrast, consideration of small population effects on persistence led to the choice of target density that required less than one-third the effort, and expense, to have the same power to detect a viable population.
A consequence of choosing a target population size greater than one is that while the lack of detections during our survey does provide strong evidence that there is not a viable wolverine population within SKCNP, it does not necessarily mean that recent informal sightings are false (somebody could have seen the last remaining individual). We see this as a useful uncertainty when making management decisions. Evaluating null results in terms of a viable population rather than simple occupancy provides a basis for making management decisions that are scientifically justified regardless of the credibility of informally reported observations. When survey results indicate no viable population is present based on density dependent detection and persistence probabilities, informal sightings do not bear on estimates of future occupancy because 1) the possibility that one or a few individuals inhabit the region, and their potential to contribute to future occupancy, has been accounted for, and 2) it is generally not possible to quantify accurately the effort that could lead to an informal observation. Informal sightings often suffer the additional weakness that the probability of misidentification cannot be quantified.
Wolverines are but one of many charismatic, yet elusive species, for which informal sightings contradict current published range limits distributions inferred from formal surveys. Other notable examples include several heavily managed species such as pumas (Puma concolor)23, fisher (Martes pennant)24, Iberian lynx (Lynx pardinus)25, or koalas (Phascolarctos cinereus)26. At the core of this conflict are the different types of errors possibly committed when interpreting informal sightings and unsuccessful formal surveys. The interpretation of a lack of verifiable evidence from formal surveys as evidence for extinction may lead to the error of accepting a false negative (i.e., the species is present but undetected). Alternatively, interpretation of informal sightings, particularly sightings unaccompanied by verifiable physical evidence, as confirmation of an extant population despite negative results from formal surveys may lead to the error of rejecting a true negative (i.e., the species was undetected by surveys because it is truly absent). The variety of classification schemes and the evidentiary value of different types of observations in the published literature highlight the range of willingness among biologists to accept one type of error over the other13,23,24. Differences in opinion about which of these errors is more egregious are not merely academic, as the allocation of limited resources often depends on the presence or absence of charismatic species24.
Appropriate application of the methods presented in this paper depends on choosing the proper time horizon to evaluate population viability. Density dependent persistence for time horizons near or below the species’ generation time or for thousands of generations will rarely vary (from near 100% and 0%, respectively) and therefore contribute little to enhancing survey design or interpreting negative results. Worse, using persistence probabilities estimated for time periods beyond the management horizon may yield misleading results. Incorporating small population effects on both detection and population processes to shift analyses from present to future occupancy should only be done if the latter is pertinent to management goals. For example, when the population in question comprises the entirety of a species, even the last pair has high conservation value.
A management challenge particularly suited to the methods developed in this paper is evaluating the appropriateness of translocations as a management strategy. Translocations are powerful tools to reintroduce extirpated species or to prevent local extinction when populations decline to levels highly susceptible to demographic, environmental, and genetic stochastic events or suffer from Allee effects. However, translocations may have the unintended effects of eroding genetic diversity when relatively large numbers are introduced into small but viable populations. For example, the historic Sierra Nevada wolverine population was highly differentiated from other North American populations evidenced by alleles not known from any other population27. Uncertainty about the status of wolverines in the Sierra Nevada caused by numerous informal sightings in SKCNP weighs against translocating animals into the region as a strategy to restore healthy populations to the area, while translocations would be the only recourse if the species truly is extirpated from the region. By evaluating formal survey efforts in terms of near future occupancy, we can conclude from our negative result that even if a small number of wolverines inhabit the parks, their persistence is so tenuous that any contribution they may make to species-wide genetic diversity will most likely be lost to extinction in the absence of translocations. Consequently, translocations may be viewed as the most appropriate strategy to restore a healthy wolverine population to the southern Sierra Nevada regardless of the validity of informal sightings.
Incorporating the concurrent effects of small populations on multiple processes, such as detection and persistence probabilities, has utility for many ecological applications. For example, fish stocking programs face the problem of preventing disease transfer to stocked populations. Disease monitoring of source populations must balance concerns about overlooking a pathogen against logistical constraints, especially because destructive sampling is often necessary for pathogen detection. The detection effort required to achieve some certainty of pathogen detection depends on pathogen prevalence28, which also determines the risk of disease transfer if pathogens are present but not detected. Disease prevalence is often unknown, and assumed at an arbitrary level29. A better strategy would be to determine sampling effort based on the product of prevalence dependent detection and transfer probabilities. Similar problems are faced in determining the success of nonnative eradication efforts. For example, optimal efforts to remove golden eagles (Aquila chrysaetos) from the California Channel Islands because they threaten endemic fox populations would account for increasing costs to find eagles and reduced impact of eagles on foxes as eagle density on the islands approaches zero30. Perhaps the most important benefit of considering the simultaneous effects of population size on detection and population processes is that doing so frames detection studies and their interpretation in terms directly related to their management application and away from the onerous task of proving something does not exist.
BH and DG conceived the study and collected the field data. BH conducted the analysis and prepared the manuscript. Both authors were involved in the revision of the draft manuscript and have agreed to the final content.
We thank Sequoia-Kings Canyon National Parks staff, particularly D. Graber, H. Werner, and R. Mazur. We are grateful to C. Rall, who headed IWS monitoring efforts, with C. Miles and B. Czibesz, J. Nelson, and K. Thompson, and to J. King and the California Snow Surveyors who checked stations for us and D. Johnson, M. Potter, R. Rall, and G. Schmidt. Comments from K. Aubry, R. Powell, N. Haddad, and K. Pollock substantially improved this paper.
| Parameter | Value | Notes (parameter origin) |
|---|---|---|
| Age of first reproduction | 3 yrs | 31, 32 |
| Maximum age of reproduction | 13 yrs | 31 |
| Maximum progeny/year | 4 | 32 |
| Sex ratio at birth (M:F) | 45:55 | 32a |
| % Adult females breeding | 50 | 32b |
| Mean offspring/female/yr | 1.5 | 31, 32b |
| Std | 0.1 | 32c |
| Mortality | ||
| juv male | 0.135 | 31d |
| juv female | 0.175 | 31d |
| subadult male | 0.1775 | 31d |
| subadult female | 0.175 | 30d |
| adult male | 0.1775 | 31d |
| adult female | 0.175 | 31d |
| % males breeding | 33 | Corresponds to 4 female home ranges/male home rangee |
| Initial population size | 2–25 | |
| Carrying capacity | 100 | 33 |
b Persson et al.32 report 53% of females ≥ 3 reproduce with a mean annual birth rate of 0.74 kits/female. We assumed 0.5 females breeding * 1.5 kit/breeding female =0.75 kits/female. This assumption approximates the 0.375 female kits/female adult/year reproductive rate assumed by Krebs et al.31.
c Persson et al.32 report litter sizes between 1–4, averaging 1.88 kits/litter and a 95% CI 1.68–2.07, corresponding to a std of 0.1.
d Mortality rates were calculated as an average of mortality from natural causes of radio-tracked wolverines in montane habitats from both trapped and untrapped sites, weighted by effort in each site type31.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Competing Interests: No competing interests were disclosed.
Competing Interests: No competing interests were disclosed.
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 1 06 Nov 13 |
read | read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
- It is impractical to search for the very last individual in a region, and also not interesting to find the very last individual because if there is only one the population is already effectively extinct.
- If the species is present, there is no prior information about what population size may be.
- Larger populations are both more likely to be detected for a given effort and of greater interest (i.e. less likely to go extinct in the near future, and thus more likely to need management). This is an issue for ecologists when: trying to determine regional extinctions, trying to identify major range reductions, trying to determine removal of invasive species, or trying to determine pathogen presence. In the case of wolverines, public support for a reintroduction of wolverines into the Sierra Nevada depends on the historic native population being extinct. In cases of invasive species removal, it can be applied to post eradication attempt monitoring when encounter rates are not known from pre-attempt monitoring. Recent approaches using occupancy models to infer population parameters assume relatively small, replicated units being monitored with some units being occupied by the target species. Those methods do not apply to region-wide surveys without any occupied subunits, and cannot be used to infer regional absence as, without any occupied subunits, there is no information available on detection probabilities.
You are correct that Equation (4) should be P(N)=(1-probability of extinction given N)*(1-probability of detection given N). We incorrectly implied that Z(N) is the probability of persistence in the preceding paragraph, it should be the probability of extinction, and the application of equation 6 (derived from equation 4) assumes Z(N) is extinction probability.I agree that integrating over N would preferable, but only if there is a justified probability distribution for N. Again, the Royle (2004) method is aimed for fitting data to replicated transects with nonzero count data at some sites. The methods appear to do poorly when most observed counts are zero (based on their simulation study), and do not apply when all observed counts are zero. However, if survey data from other regions where the species of interest is present in known numbers can be used to generate an expected population, or to provide a maximum population size, in the target region, one could calculate the probability of possible population sizes p[N] from a Poisson or uniform distribution respectively. Integrating p[N]*P(N) over N=1 to (max N) would then yield a better estimate of the true probability of overlooking a viable population. While I agree this is worth further development, I expect the calculation will be sensitive to the choice of probability distribution for N, and since we did not have information for the motivating case of wolverines in the Sierra Nevada, we relied on the simpler approximation, which effectively represents the case where N is assumed to be equal to the value yielding the greatest probability of overlooking a viable population, and is thus a conservative estimate.
Lastly, while a single value of Pcrit is assumed, because N is unknown, we do indeed maximize Equation (5) over a range of N=[1,25].
- It is impractical to search for the very last individual in a region, and also not interesting to find the very last individual because if there is only one the population is already effectively extinct.
- If the species is present, there is no prior information about what population size may be.
- Larger populations are both more likely to be detected for a given effort and of greater interest (i.e. less likely to go extinct in the near future, and thus more likely to need management). This is an issue for ecologists when: trying to determine regional extinctions, trying to identify major range reductions, trying to determine removal of invasive species, or trying to determine pathogen presence. In the case of wolverines, public support for a reintroduction of wolverines into the Sierra Nevada depends on the historic native population being extinct. In cases of invasive species removal, it can be applied to post eradication attempt monitoring when encounter rates are not known from pre-attempt monitoring. Recent approaches using occupancy models to infer population parameters assume relatively small, replicated units being monitored with some units being occupied by the target species. Those methods do not apply to region-wide surveys without any occupied subunits, and cannot be used to infer regional absence as, without any occupied subunits, there is no information available on detection probabilities.
You are correct that Equation (4) should be P(N)=(1-probability of extinction given N)*(1-probability of detection given N). We incorrectly implied that Z(N) is the probability of persistence in the preceding paragraph, it should be the probability of extinction, and the application of equation 6 (derived from equation 4) assumes Z(N) is extinction probability.I agree that integrating over N would preferable, but only if there is a justified probability distribution for N. Again, the Royle (2004) method is aimed for fitting data to replicated transects with nonzero count data at some sites. The methods appear to do poorly when most observed counts are zero (based on their simulation study), and do not apply when all observed counts are zero. However, if survey data from other regions where the species of interest is present in known numbers can be used to generate an expected population, or to provide a maximum population size, in the target region, one could calculate the probability of possible population sizes p[N] from a Poisson or uniform distribution respectively. Integrating p[N]*P(N) over N=1 to (max N) would then yield a better estimate of the true probability of overlooking a viable population. While I agree this is worth further development, I expect the calculation will be sensitive to the choice of probability distribution for N, and since we did not have information for the motivating case of wolverines in the Sierra Nevada, we relied on the simpler approximation, which effectively represents the case where N is assumed to be equal to the value yielding the greatest probability of overlooking a viable population, and is thus a conservative estimate.
Lastly, while a single value of Pcrit is assumed, because N is unknown, we do indeed maximize Equation (5) over a range of N=[1,25].