Keywords
Molecular dynamics, Arrhenius, unfolding rate
Molecular dynamics, Arrhenius, unfolding rate
Molecular dynamics (MD) simulations have become an important tool in understanding chemical and biochemical processes at the molecular level. Through the use of Newtonian mechanics and an empirically derived force-field, simulations have been used to investigate the interactions of drug molecules and their targets as well as to predict the behaviour of proteins and peptides (Vasquez et al., 1994). Originally simulations were carried out in vacuo, but now with the increasing power of computers, simulations are usually carried out using periodic boundary conditions in water.
Increasingly realistic simulations lead to a better understanding of processes such as protein folding and unfolding at the molecular level (Lindorff-Larsen et al., 2012; Scheraga et al., 2007). The literature on molecular dynamics simulations for protein folding and unfolding is extensive. This can include very large simulations that can be simplified using coarse-graining, down to simulations of small proteins or peptides. One area where MD simulations have been particularly widely used is in the simulation of prion proteins and the protein mis-folding diseases associated with them (Shamsir & Dalby, 2005; Shamsir & Dalby, 2007; van der Kamp & Daggett, 2010; van der Kamp & Daggett, 2011).
Molecular dynamics simulations give us a detailed view of protein folding and unfolding pathways and their rates of unfolding (Daggett, 2002). Temperature is often used to accelerate protein unfolding and it has been shown that this does not affect the protein unfolding pathway (Day et al., 2002). It is often difficult to relate the simulated results to experimental data. A review of simulated folding times has shown that the times predicted by MD and the experimental rates for thermal unfolding are in good agreement (Snow et al., 2005). Atomic force microscopy data is another possibility and this has been used to investigate protein folding of T4 lysozyme (Peng & Li, 2008).
The rate of protein folding at increasing temperatures should be described by the Arrhenius equation over a limited range of temperatures (Alberty):
Where k is the rate of the reaction, A is a constant (pre-exponential factor) Ea is the energy of activation, T is the Temperature in Kelvin and R is the Universal Gas Constant.
A rearrangement of the Arrhenius equation taking natural logarithms gives the linear function:
A plot of the natural logarithm of the rate ln(k) against 1/Temperature will be a straight line if the simulations obey the Arrhenius equation.
The Arrhenius equation has been used in solid-state chemistry calculations but currently no studies have tested whether it is valid in MD simulations of protein folding (Huwe et al., 1999). This paper presents a MD simulation study using a small protein (crambin) to test whether the models do agree with the predicted linear behaviour.
Crambin was chosen as the model protein for simulation of its size as it only has 46 amino acids (Caves et al., 1998). A high resolution crystal structure of crambin (3NIR.pdb) was downloaded from the RCSB Protein Databank (Rose et al., 2011; Schmidt et al., 2011). Molecular dynamics simulations were carried out using Gromacs 4.6.4 on an Ubuntu 12.04 machine with GPU acceleration (Hess et al., 2008).
The protein was solvated using periodic boundary conditions and a surrounding distance of 4nm around the protein. Simulations were run at 500K to 560K at 10K intervals using the OPLS forcefield. At temperatures of 570K and above the simulations fail to complete. The models were initially equilibrated using the canonical (nvt) and isothermal-isobaric (npt) ensembles. At 500K the simulations were run for 10ns with a time-step of 2fs. At 560K the simulations were run for 1ns with a time-step of 2fs. Secondary structure was calculated using DSSP (Dodge et al., 1998) (the data is available in dssp_files.zip). RMSD deviations from the original crystal structure were calculated in Gromacs and displayed in Grace (the data is available in rmsd_grace_datafiles.zip). All of the scripts for equilibration dynamics and analysis can be found in the accompanying data files (the Gromacs files are in gromacs_files.zip and the shell script to run all the simulations and analysis is gromacs_runs_complete_analysis.sh).
The statistical analysis of the rate data was carried out using SPSS version 22 (IBM_Corp., 2013). The line of best fit to the mean data was fitted using linear regression (the data files are available as md_arrhenius_crambin_averaged.sav, md_arrhenius_crambin_averaged.spv). The line of best fit for the complete dataset was calculated using the general linear model (the data files are available as md_arrhenius_crambin.sav, md_arrhenius_crambin.spv). All of the scripts and data for the statistical analysis are available in the supplementary materials.
Over these time periods crambin did not unfold as much as had been expected. As it is such a small protein it seems to be particularly stable to rises in temperature. There were three possible end points that could be used in determining the rate:
It was not clear which of the measures would be the most reliable and so time was taken for all three. There were however missing values because the end points were not reached during the simulations. This was particularly apparent in the 540K simulations, which seem to be anomalous as can be seen in the boxplots for the reaction times from the simulations (Figure 2A–C). The boxplots show the expected downward trend, although there is considerable variation between the times taken for the repeated simulations. This variability declines at higher temperatures as rates become faster. A summary of the times to the three different end points are given in Table 1–Table 3.
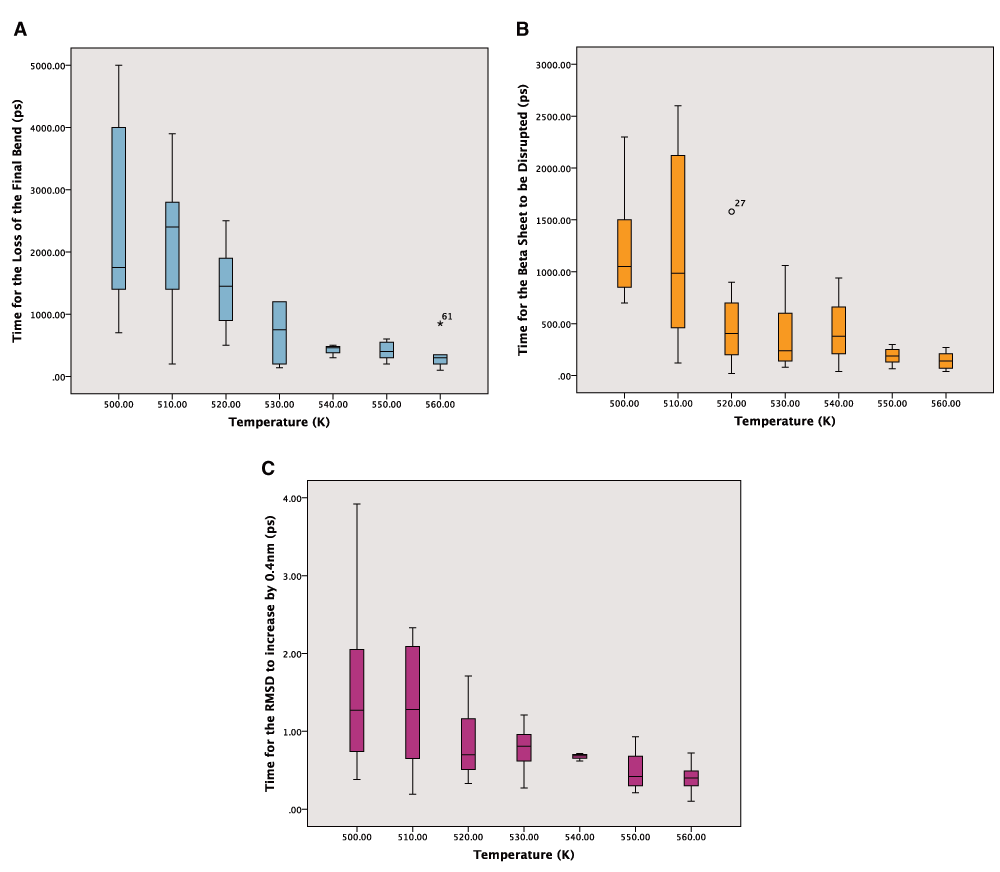
A: Boxplot of the times for the loss of the final bend from the secondary structure in picoseconds. Outliers are labelled. B: Boxplot of the times for the loss of the beta sheet in picoseconds. Outliers are labelled as circles or numbers if they are extreme. C: Boxplot of the times for the RMSD to go above 0.4nm from the crystal structure in picoseconds.
The Arrhenius plot can be constructed using either the mean values for the different temperatures or all of the values for the repeats. In both cases a linear model is produced but the correlation is much stronger for the averaged values, which also give a narrower confidence interval for the line of best fit (Figure 3A–C). The wider confidence intervals for all of the data and the extent of the scatter can be seen in Figure 4A–C.
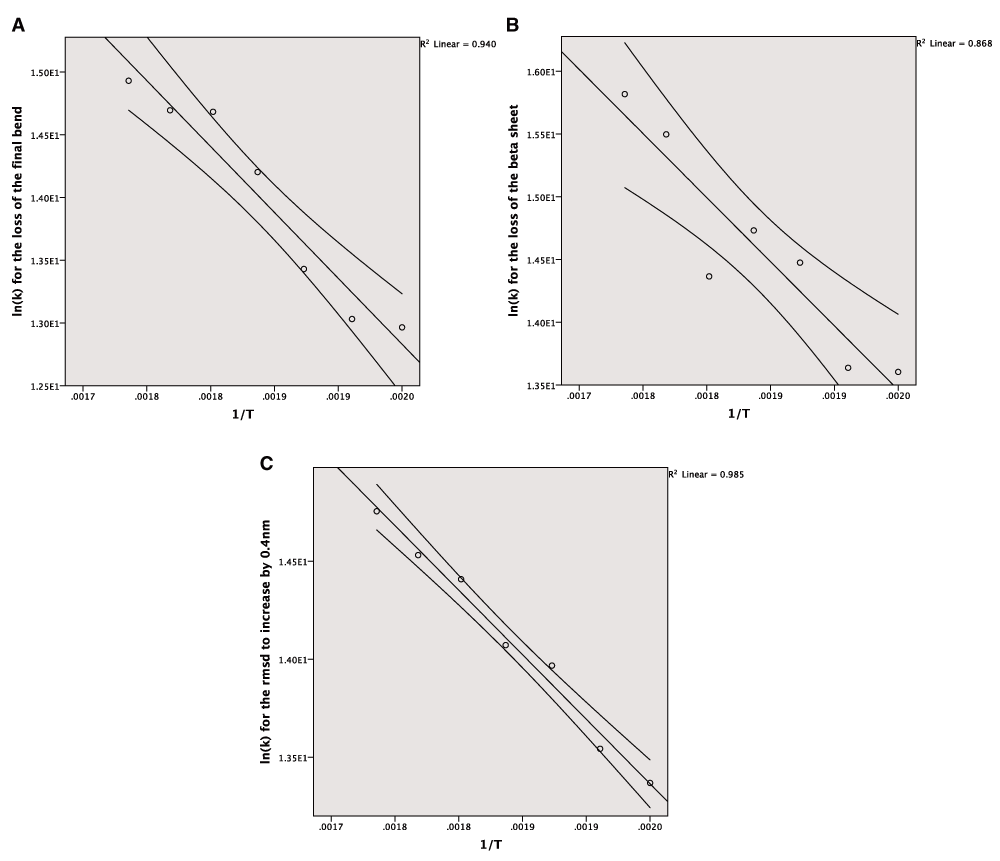
A: The Arrhenius plot for the unfolding of the final bend using the averaged data. B: The Arrhenius plot for the unfolding of the beta sheet using the averaged data. C: The Arrhenius plot for the increase of the RMSD by 0.4nm from the crystal structure using the averaged data.
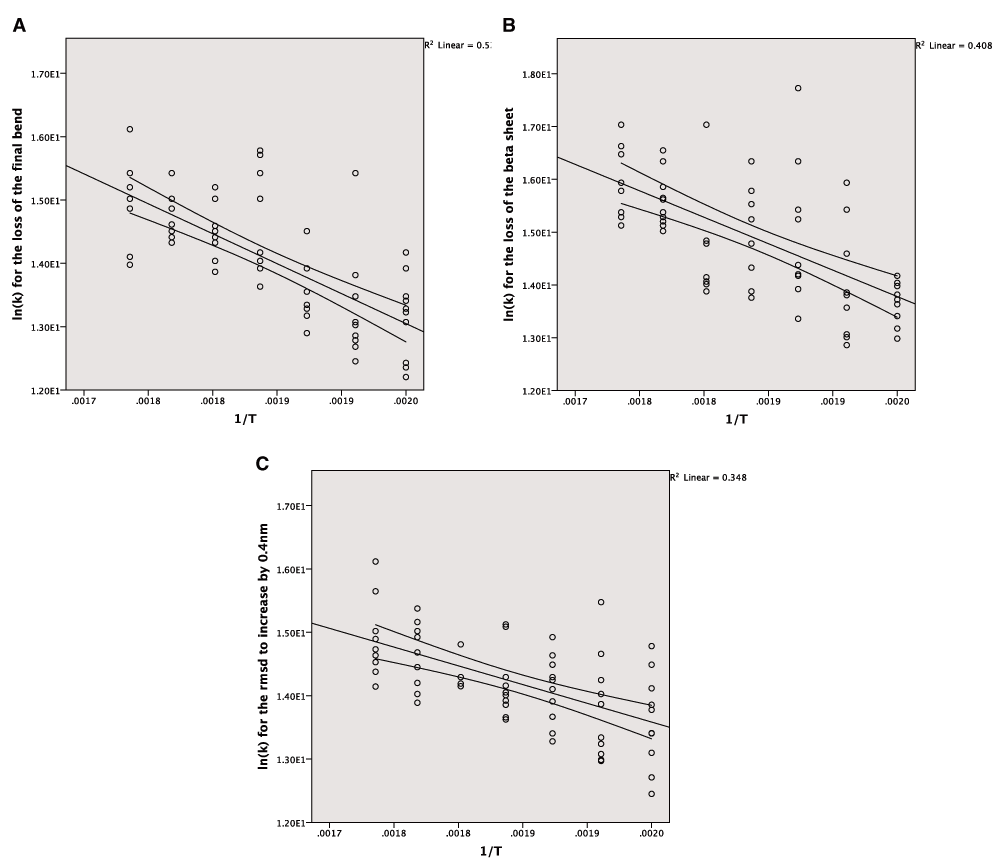
A: The Arrhenius plot for the unfolding of the final bend using the complete data. B: The Arrhenius plot for the unfolding of the beta sheet using the complete data. C: The Arrhenius plot for the increase of the RMSD by 0.4nm from the crystal structure using the complete data.
The parameters for the lines of best fit using all of the data and only the mean values are given in Table 4 and Table 5.
All three of the end points used produce a linear model in the Arrhenius plot with a high degree of correlation. This suggests that in these cases the MD simulations are following Arrhenius behaviour and that these models can be used to predict rates of unfolding.
Of the three end points the RMSD variation is the easiest to calculate and least ambiguous, but it is also difficult to understand what this signifies at the protein level, when compared to using the disruption of secondary structure as a metric. The other advantage of using the unfolding of the secondary structure is that experimental values are available for unfolding of proteins and so if an appropriate end point can be found in the simulations then the gradients of the Arrhenius plot can be used to calculate the activation energy for unfolding.
This study also highlights the high degree of variability between the trajectories of different simulations. This variability is very high at lower temperatures. Simulations were repeated ten times and this resulted in values for the standard errors for the time of unfolding that could be up to 25% of the time. These standard errors are large and so the number of simulations that are run needs to be increased in order to reduce them. As the standard errors falls with the square root of the sample size this would mean a 4-fold increase in the number of simulations is needed to reduce the standard error by half. This would suggest that more reliable results could be obtained by carrying out 40 simulations at each of the temperatures, which is a considerable additional computational burden.
The large amount of variation also affected the quality of the lines of best fit to the Arrhenius equation. The coefficient of determination was much lower when considering all of the data but nonetheless there is clear evidence of the simulations following Arrhenius behaviour. The confidence intervals for the linear models using all the data and the average data are similar. The variation in the gradient is too large for making comparisons with experimentally derived energies of unfolding and this is another reason why a larger number of simulations will be needed in future studies.
There was a surprising degree of agreement in the slopes and intercepts of the bend loss and beta sheet loss end-points. This suggests that the energies involved in stabilising the beta sheet and final bend are similar. This consistency is encouraging and suggests that detailed energy predictions will be possible from MD simulations.
Crambin was not an ideal case for using in this study. Although it is very small and allows the simulations to be run in a shorter time, the protein does not unfold very much and so longer time-scales are needed within the simulations. Prion protein is another possible model that could be used to test unfolding as this has been shown to unfold over short simulation times (< 10ns) (Shamsir & Dalby, 2005). The other alternative is longer simulations times in order to produce clearer and less ambiguous end-points for the simulations.
All of the code and data required for carrying out the simulations is available from http://dx.doi.org/10.5281/zenodo.20550. The shell script used to perform the simulations is available from http://dx.doi.org/10.5281/zenodo.20544. The dssp plots and the RMSD graphs for the simulations are available from http://dx.doi.org/10.5281/zenodo.20548. The SPSS data files and output files that include the details of how the analysis was carried out are available from http://dx.doi.org/10.5281/zenodo.20549. The software is released under a MIT license.
ARD conceived the study and designed the experiments. ARD and MSS carried out the simulations and the analysis. ARD and MSS were involved in all of the versions of the manuscript and have agreed to the final content.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Competing Interests: No competing interests were disclosed.
Competing Interests: No competing interests were disclosed.
Competing Interests: No competing interests were disclosed.
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | |||
|---|---|---|---|
| 1 | 2 | 3 | |
|
Version 1 20 Aug 15 |
read | read | read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)