Signal-processing tools for core-collection selection from genetic-resource collections

Ernesto Borrayo; Masaru Takeya

doi:10.12688/f1000research.6391.1

Home Browse Signal-processing tools for core-collection selection from genetic-resource...

ALL Metrics

-

Views

-

Downloads

Get PDF

Get XML

Export

▬

✚

Method Article

Signal-processing tools for core-collection selection from genetic-resource collections

[version 1; peer review: peer review discontinued]

Ernesto Borrayo¹, Masaru Takeya²

PUBLISHED 23 Apr 2015

Author details Author details

¹ Gene Research Center, University of Tsukuba, Tsukuba City, Ibaraki, 605-8572, Japan
² Genetic Resources Center, National Institute of Agrobiological Sciences, Tsukuba City, Ibaraki, 305-8602, Japan

OPEN PEER REVIEW

PEER REVIEW DISCONTINUED

This article is included in the Japan Institutional Gateway gateway.

Abstract

Selecting a representative core collection (CC) is a proven and effective strategy for overcoming the expenses and difficulties of managing genetic resources in gene banks around the globe. Because of the diverse applications available for these sub-collections, several algorithms have been successfully implemented to construct them based on genotypic, phenotypic, passport or geographic data (either by individual datasets or by consensus). However, to the best of our knowledge, no single comprehensive dataset has been properly explored to date.
Thus, researchers evaluate multiple datasets in order to construct representative CCs; this can be quite difficult, but one feasible solution for such an evaluation is to manage all available data as one discrete signal, which allows signal processing tools (SPTs) to be implemented during data analysis.
In this research, we present a proof-of-concept study that shows the possibility of mapping to a discrete signal any type of data available from genetic resource collections in order to take advantage of SPTs for the construction of CCs that adequately represent the diversity of two crops. This method is referred to as 'SPT selection.'
All available information for each element of the tested collections was analysed under this perspective and compared, when possible, with one of the most used algorithms for CC selection.
Genotype-only SPT selection did not prove as effective as standard CC selection algorithms; however, the SPT approach can consider genotype alongside other types of information, which results in well-represented CCs that consider both the genotypic and agromorphological diversities present in original collections.Furthermore, SPT-based analysis can evaluate all available data both in a comprehensive manner and under different perspectives, and despite its limitations, the analysis renders satisfactory results. Thus, SPT-based algorithms for CC selection can be valuable in the field of genetic resources research, management and exploitation.

Keywords

Core collection, Fast Fourier Transform, Genetic resource management, Rice, Foxtail millet

Corresponding authors: Ernesto Borrayo, Masaru Takeya

Competing interests: No competing interests were disclosed.

Grant information: This research is supported in part by the SATREPS project by JST and JICA, Diversity Assessment and Development of Sustainable Use of Mexican Genetic Resources and in part by JSPS Grant-in-Aid 25257416.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2015 Borrayo E and Takeya M. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Data associated with the article are available under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original data is properly cited.

How to cite: Borrayo E and Takeya M. Signal-processing tools for core-collection selection from genetic-resource collections [version 1; peer review: peer review discontinued]. F1000Research 2015, 4:97 (https://doi.org/10.12688/f1000research.6391.1) First published: 23 Apr 2015, 4:97 (https://doi.org/10.12688/f1000research.6391.1) Latest published: 23 Apr 2015, 4:97 (https://doi.org/10.12688/f1000research.6391.1)

Background

One of the most promising techniques for conserving the diversity of genetic resources is ex situ genebank germoplasm collection. A significant effort has been made on a global scale to preserve, characterize, distribute and utilise genetic resources in order to understand their biological phenomena and to confront the vulnerable situation regarding the sustainability of future human development^1,2. As the size of germoplasm collections increase, it becomes difficult to appropriately manage and extensively evaluate them³; thus, the core collection (CC) concept⁴ has become a fundamental genetic resource management approach and exploits the potential of a complete collection in terms of viable data management and monetary expenses^5–8.

Different CCs have different purposes, characteristics and evaluation criteria^7,9–11; thus, several different algorithms and informatics tools have been developed and implemented^12–15 with different approaches for satisfying particular needs of each CC. Because these CCs are constructed mainly on the basis of genotypic, phenotypic, passport or geographic data (either by individual datasets or by consensus)¹⁶, there is a lack of all-inclusive datasets; this limits the possibility of generating a CC that may satisfy most basic and applied genetic resource research programs. To the best of our knowledge, no single comprehensive dataset has been properly explored to date. One possible method to create a comprehensive dataset is to represent the available data as numerical values. Several methods exist that represent genomic information into numerical values¹⁷ and agromorphological traits (ATs) into scores¹⁸. Through this mapping process, treating each data vector as a discrete signal that can, in turn, be analysed by signal processing tools (SPTs) is possible, thus providing an effective tool for a comprehensive evaluation of datasets. We present a proof-of-concept study that shows the possibility of mapping to a discrete signal any type of data available from genetic resource collections in order to take advantage of SPTs for CC selections; this possibility provides new decision-making criteria for genetic resource management and research.

Methods

Mapping data

Each input data must be mapped to a numerical value. This is a fundamental process of the algorithm because it enables different datasets to be analysed together, regardless of their nature. In this manner, dissimilar passport data, single nucleotide polymorphisms (SNPs), restriction fragment length polymorphisms (RFLPs), geographic information and phenotypical traits can be included in one comprehensive dataset. To consistently represent each data type, reference tables are implemented according to the nature of each particular data: genetic information (originally represented as character elements) is now represented by a numerical vector, and trait variation, simple sequence repeat (SSR) molecular markers and passport data can be represented as either binary or normalized data depending on the quantitative/qualitative nature of the data. The original data and reference tables for this study are available in supplementary material 1. Data transformation for this study rendered a matrix containing the representation of MC samples (i₁, i₂, i₃, …i_n) with (j₁, j₂, j₃, … j_m) elements each, where n is the total number of samples, and m is the number of included samples characteristics, represented by a numerical value as data_{(i, j)}.

Signal construction

Numerical representations of each jth data element can be treated as frequency values in m data time in such a manner that each ith sample is treated as a discrete signal. The i signal corresponds to the information behaviour from each sample. This perspective will enable the implementation of SPTs such as the discrete Fourier transform and power spectrum comparison. Although SPTs can be implemented on all data available for each sample, not all data elements contain the same informativeness value to discriminate between samples. To overcome the informative difference in each j element of data, a principal component analysis (PCA) can be performed to rearrange data into a new matrix that has the high informative elements of data at the beginning and that arranges subsequent elements according to their informativeness, discarding those whose variance equals 0. This process renders two new matrices: the original characteristics mapped vectors matrix (x) and rearranged variance value matrix (X). Matrix X, therefore, contains n samples that are formed by a numerical vector with m=m-(non informative characteristics).

Fast Fourier transform

The main objective of Fourier transform is the decomposition of any signal into a complex histogram of frequencies. Signal function is then represented as a vectorial function whose angle and magnitude determine a sampled point in the signal¹⁹. The original Fourier model is expressed as follows:

\hat{f} (ξ) = \int_{- \infty}^{\infty} f (x) e^{- 2 π i x ξ_{d x}} (1)

where x is the temporal variable, ξ it the frequential variable, i is a -1 square root and e is the natural exponent. From equation 1, a derivative can be determined for any point ξ sampled in the signal.

f (x) [\cos^{(2 π e ξ)} + i * ​ \sin^{(2 π e ξ)}] (2)

Fourier transform can be implemented into any complex numerical series, but in a practical sense, the computational cost increases exponentially. Thus, fast Fourier transform (FFT) is more often implemented and can be defined according to Cooley-Tukey algorithm²⁰ as follows:

X_{k} = \sum_{n = 0}^{N - 1} x_{n} e^{- i π k \frac{n}{N}} (3)

where N is the vector length, x is the temporal variable, i is a -1 square root and e is the natural exponent; in such matter that an euclidean representation - with the angle, magnitude and phase that corresponds to their position in the signal - exists for any signal dot.

Therefore, mapping any signal into a vectorial representation that contains information from every original signal dot is possible. From this complex vector, useful data can be retrieved to establish a comparison between them that indirectly represents the original signal’s juxtaposition²¹.

Distance matrix computation

Inspired by the genomic signal processing alignment-free distance (GAFD) model²², each signal corresponding to the PCA-mapped accessions data in a set Ŝ_i was converted into its frequency representation by applying discrete Fourier transform. Its power spectrum ${\hat{F}}_{i}$ was then computed. Subsequently, the distance d(i, j) for a given pair of comprehensive data signals was calculated by obtaining the mean squared error (MSE) of their respective power spectra:

D (i, j) = {\sum_{x} ({\hat{F}}_{i} (x) - {\hat{F}}_{j} (x))}^{2} (4)

Finally, a distance matrix (DM) was created by performing a pairwise comparison of all sequences in the set.

In parallel, we constructed a point-to-point (RAW) DM on the basis of the MSE given to a pair of signals prior to the PCA analysis.

Core collection selection

Selecting a CC by this method requires the generation of a DM for each sample of the MC; this provides the interrelations among samples and enables adequate selection. A schematic of the complete workflow is presented in Figure 1.

Figure 1. General workflow of the FFT-based core collection selection algorithm.

PCA: Principal Component Analysis; FFT: Fast Fourier Transform; CC: Core Collection.

In the past, several methodological procedures have been implemented to select K elements from an MC on the basis of information provided by its DM; among such procedures, the most frequently used one is the hierarchical clustering method¹¹. However, the current algorithm does not rely on hierarchical clustering for CC selection, instead - similar to the least distance stepwise sampling method²³ - CC elements are selected by an iterative process, where r samples are selected by different criteria (which may be individually implemented) on each iteration.

Selection criteria (based on the DM without hierarchical clustering) for the current algorithm is as follows:

• a) The ith sample with the most lower distance values among jth elements.
• b) The ith sample with the most higher distance values among jth elements.
• c) The ith sample with a lower distance average.
• d) The ith sample with a higher distance average.
• e) The ith sample with a lower overall distance.
• f) The ith sample with a higher overall distance.

In cases where multiple samples share selection values, an appearance priority will complete the criteria.

An example of selection process is presented in Figure 2 and its final result is presented in Figure 3.

Figure 2.

First three principal component’s distribution of Rdata (a), methodology’s first (b), second (c) and third (d) iterations; final K=72 distribution is presented in (e).

Figure 3. First three principal component’s distributions of K=72 CC selection (X) from Rdata MC.

Once the selected samples (r) are included in the future CC, they (along with others that are identical to them (s)) are removed from X for the next iteration; then, a DM₂ with n₂ = n–r–s is calculated. This process will continue Z times until R >= K, where R = (r₁ + r₂….r_Z ) and K = predefined CC elements desired.

Evaluation of the selected core collection

As discussed previously, the best way to evaluate a CC depends on the purpose of that CC, and even if it can be evaluated from the same dataset from which it was constructed, evaluating it with a different dataset⁷ is desirable. In this study, we use other datasets for our evaluation whenever possible. The list given below provides the evaluation parameters implemented in this study.

a) The average distance between each MC sample and the nearest CC sample (ANE) can be calculated using the equation as follows:
$A N E_{t o t} = \frac{1}{L} \sum_{k = 1}^{K} \sum_{j = 1}^{J} D (k - c M C_{j}) (5)$
where K is all CC elements, k is each CC element and D is the distance between k and each jth cMC element whose closest CC element is k, including itself, thus rendering L total comparisons. The ideal ANE value is 0, where each sample of the CC represents itself and those similar to it. This parameter evaluates the homogeneity of the represented MC diversity.
b) The average distance between each CC sample and the nearest CC sample (ENE) can be calculated using the equation as follows:
$E N E_{t o t} = \frac{1}{L} \sum_{k = 1}^{K} D (k - c C C) (6)$
where K is all CC elements, k is each CC element and D is the distance between k and its closest CC element cCC, excluding itself, in L total comparisons. With such an evaluation parameter, higher dispersion renders higher scores with the aim of evaluating the dispersion among selected CC elements.
c) The average distance between CC samples (E) can be calculated using the equation as follows:
$E_{t o t} = \frac{1}{L} \sum_{k = 1}^{K} \sum_{j = 1}^{J} D (k - c C C_{j}) (7)$
where K is all CC elements, k is each CC element and D is the distance between k and all other jth CC elements cCC, excluding itself, in L total comparisons. This evaluation parameter indicates higher scores when CC elements have greater distances between themselves.
While previous evaluation parameters are useful for data dispersion analysis, such parameters will not evaluate how well the distribution of the MC is represented on the CC; therefore, the distribution comparisons tests that were included are as follows:
d) The homogeneity test (F – test for variances and t – test for means; α = 0.05) between the CC and MC for each trait can be represented as a percentage of traits that are statistically different (MD for means and VT for variances)⁹.
e) The coincidence rate (CR) can be calculated using the equation as follows:
$C R = \frac{1}{M} \sum_{m = 1}^{M} \frac{R_{C C}}{R_{M C}} * 100 (8)$
where R is the range of each m trait, and M represents the number of traits.
f) The variable rate (CV) can be calculated using the equation as follows:
$C V = \frac{1}{M} \sum_{m = 1}^{M} \frac{C V_{C C}}{C V_{M C}} * 100 (9)$
where CV is the coefficient of the variation of each m trait in the CC and MC, and M is the number of traits.
According to Hu et al.¹⁰, a valid CC has CR > 80 and MD < 20, which are the limits for the ideal representation of the identity and distribution of the MC.
g) The alleles coverage (CA) can be calculated using the equation as follows:
$C A = [| 1 - (| 1 - A C C | / A M C) |] * 100 (10)$
where ACC is a set of alleles in the CC, and AMC is a set of alleles in the MC; ACC measures the percentage of alleles from the MC that are present in the CC¹².

To compare the obtained CCs with an established methodology, we implemented Core Hunter 2 (CH)¹³ as a reference and used it with the program’s default parameters on the agrological and genomic datasets.

Experimental datasets

To determine the efficiency of the analysis of data behaviour by a point-to-point direct comparison, a synthetic dataset was constructed using binary data (Sdata) with manageable n and m elements (supplementary material 1).

To test the algorithm in real biological-context scenarios, the CCs from different MCs were constructed and evaluated.

To test the algorithm’s CCs versus the scores of the MCs, 780 rice (Oriza sativa(L.)) accession and 423 foxtail millet (Setaria italica subsp. italica (L.) P. Beauv.) accession data were retrieved from the National Institute of Agrobiological Sciences (NIAS) http://www.gene.affrc.go.jp/databases_en.php.

According to the available data, different datasets were assembled. The 762 SNPs from the 780 rice accessions retrieved from the NIAS database (Rdata) were divided arbitrarily into two subsets of 331 SNPs each for constructing two smaller datasets (RdataI and RdataIII). In addition, ATs were categorized and mapped into the binary data for 273 of the 780 accessions, resulting in 38 variables (RdataII). The variables from the 423 foxtail millet genotypes with transposon displays²⁴ were used as a single dataset (Fdata). For a subset of 141 accessions (FdataI), 9 ATs were categorized and mapped into binary data, resulting in 28 variables (FdataII). The substitution tables used during this mapping are presented as supplementary material 1.

Implementation

All methodological procedures (except for CH, which was implemented according to the software’s default parameters and which is available for download at www.corehunter.org) were performed using FreeMat v4.2 (www.freemat.sourceforge.net). All original codes are available as supplementary material 1.

Results and discussion

Selection and evaluation

The selection criteria were chosen to look for the best possible distribution of selected CC elements within the DM. Although hierarchical clustering has proven to be an effective method for determining collection structure and sampling CC²⁵ and although it has been implemented in different crops^26,27 and included in various selection algorithms¹¹, hierarchical reconstruction presents the challenge of selecting an appropriate model for biological interpretation that can be applied to everything from unweighted pair-group averages to Markov models in Bayesian estimations²⁸. To avoid the challenge of selecting a reconstruction model, we decided to work strictly with the DM. By selecting the items described in this methodology, we aimed to retrieve representative elements from among the distributions of collections; however, because of its iterative nature, this methodology may render high redundancy under certain data distributions. Despite this limitation, the methodology has proven to be capable of selecting representative elements of the MC’s diversity.

Evaluation criteria were applied according to Odong et al.⁷ without excluding the classic criteria used in 9,10. The selected CCs render proper results in general terms. As expected, selected CCs did not always reach for optimal values for MD and CR, this is due the fact that it is not the aim of the selection method to render a CC with similar distribution to that of the MC, but to make sure to include as much diversity as possible.

It is our belief that scoring the CC sets obtained with these methodologies will enable genetic resource banks to provide clear descriptors of what their CC strengths and limitations are with respect to the MC from which they come and will provide adequate tools for determining the possible purposes of the selected CCs.

Mapping

Although several representations of genotypic characteristics (particularly those involving DNA sequences^29–31) have been proposed, real-number-based mappings have not been discarded; indeed, this type of mapping has been highly studied for signal analysis even when they share two principal problems: the preferential magnitude of some nucleotides and the non-equidistance of all nucleotides^32,33. The arbitrary values selected for SNPs’s numerical representation of genotypes aim to maintain equidistant relations among purines and among pyrimidines in such a manner that the same distance is also preserved between at least one of them and the undetermined values. ATs are represented as binary data. This representation may prove useful for discrete data but requires a clustering procedure for continuous data. In this study, we arbitrarily generated clusters for the latter and then represented them as the former. Although this implementation may not be the most accurate regarding biological or agronomical significance, it serves as the first approach for testing the feasibility of the use of signal processing techniques when merging several datasets to construct one CC.

RAW versus FFT

The RAW comparison establishes a distance value on the basis of the average distance between each mapped value on each element while the FFT power spectra implementation compares the signals in the frequency domain. Using FFT, establishing a DM on the basis of how data ’shifted’ rather than on the basis of average point-to-point comparisons was possible. The FFT approach provides a different DM, where its compared elements are clustered based on the similarity of the shift among data, regardless of whether the shift is in the opposite phase. We believe that this procedure may reveal additional information about the relations not only between elements but also between the individual components within each element.

FFT comparisons of signals without PCA are a good approach for CC selection. Nevertheless, PCA implementation enables us to avoid possible misleads in random data arrangements, as, for example, palindromic data that could result in the same power spectra. Moreover, through PCA, we could organize data according to their levels of impact on the difference between accessions, which - when their magnitudes were obtained - inherently rendered a representation of informativity relations among values. This ’data behaviour’ was used as the element for pairwise comparisons, and although this approach clusters differently from RAW comparisons, we believe that it will provide a new perspective for CC selection and open the possibility of further data exploration.

Our first approach was to measure the comparisons under different K values. We compared the approach of the RAW signals with the PCA-FFT-treated signals. Results from Sdata, Fdata and Rdata are presented in Table 1–Table 3. As expected, most evaluation criteria improved as K increased.

Table 1. ∆ K selected CC scores from MC Sdata Raw and PCA Signal evaluated with Sdata.

	Sdata PCA			Sdata RAW
K	12	18	24	12	18	24
ANE	0.2348	0.2311	0.2164	0.2697	0.2287	0.2164
ENE	0.339	0.3386	0.3401	0.3696	0.3228	0.3214
E	0.5562	0.5622	0.5547	0.5558	0.5333	0.5299
MD	0	0	0	0	0	0
VT	41.6667	50	41.6667	33.3333	58.3333	41.6667
CR	64.8403	71.6918	73.7154	60.6447	75.2465	80.4716
CV	9080.798	61.2074	86.0876	136.6446	139.1418	280.8481
AR	74.3363	81.4159	89.3805	61.9469	77.8761	80.531

Table 2. ∆ K selected CC scores from MC Fdata Raw and PCA Signal evaluated with Fdata.

	Fdata PCA			Fdata RAW
K	48	72	96	48	72	96
ANE	0.6454	0.6423	0.6407	0.6489	0.6431	0.643
ENE	0.646	0.6472	0.6474	0.65	0.6448	0.6452
E	0.7297	0.7301	0.7304	0.7231	0.7236	0.7239
MD	1.1799	0.59	0.59	1.7699	1.4749	1.4749
VT	50.4425	53.6873	56.6372	50.7375	56.0472	55.1622
CR	83.6883	87.0605	88.9709	83.5334	86.9308	87.7461
CV	0.8494	0.419	0.7357	1.1037	4.74	0.7361
VA	96.3945	97.7652	98.5995	95.3516	97.497	97.4374

Table 3. ∆ K selected CC scores from MC Rdata Raw and PCA Signal evaluated with Rdata.

	Rdata PCA			Rdata RAW
K	48	96	156	48	96	156
ANE	0.6013	0.5966	0.5942	0.6118	0.6052	0.6042
ENE	0.5939	0.5944	0.5981	0.6106	0.6085	0.609
E	0.7105	0.7074	0.7051	0.703	0.7038	0.7054
MD	9.1146	5.9896	3.9062	10.1562	5.4688	4.4271
VT	42.4479	48.6979	58.0729	57.5521	72.9167	70.0521
CR	70.5716	78.477	83.2957	69.9022	78.1045	80.0167
CV	1.0171	0.4343	0.3137	7.9407	0.4375	1.1344
VA	92.6758	96.8992	98.5298	93.9856	98.1823	98.5031

The use of FFT signals renders better overall scores than the use of RAW signals in Sdata and Fdata; however, this advantage diminishes in Rdata. We speculate that this difference can be explained by the mapping procedures used; further research regarding this matter is encouraged.

Using the CHs’ rendered K values, we used both CH and FFT to generate the CCs on the above datasets. The evaluation of these CCs is summarized in Table 4 and in Figure 4, Figure 5. Both methodologies rendered similar results, yet PCA rendered better results on parameters representing MC distribution; this could be an effect of the selection method’s intrinsic redundancy.

Table 4. CCs selected from MC Sdata, Fdata and Rdata using PCA signals and Core Hunter compared with respective same data.

	Sdata		Fdata		Rdata
	PCA	CH	PCA	CH	PCA	CH
K	12		84		156
ANE	0.2348	0.2314	0.6407	0.6392	0.5942	0.5952
ENE	0.339	0.3906	0.6474	0.6386	0.5981	0.6047
E	0.5562	0.563	0.7304	0.7176	0.7051	0.7017
MD	0	0	0.59	1.1799	3.9062	5.4688
VT	41.6667	58.3333	56.6372	66.6667	58.0729	86.7188
CR	65.6045	76.1001	88.9709	93.0119	83.2957	89.6723
CV	9080.978	132.6078	0.7357	0.429	0.3137	0.4001
AR	74.3363	76.9912	98.5995	98.4803	98.5298	99.3852

Figure 4.

First two principal component’s distributions of k=11 CC (orange) selected by CH (a), PCA (b) and RAW (c) in Sdata distribution (blue).

Figure 5.

First two principal component’s distributions of k=84 CC (orange) selected by CH (a) and PCA (b) in Fdata distribution (blue).

Thus far, the proposed CC selection method and algorithm appear worthy of further exploration. We are aware that two particular fundamental elements require immediate attention. First, a better mapping solution for both genotypic and AT numerical representation needs to be determined. Second, the selection system developed by us is directly based on the DM and is prone to high redundancy in some data distributions. As discussed earlier, this selection system was chosen in order to avoid the problems associated with hierarchical clustering and further allocation selections^13,34. Both issues should be addressed in the near future.

Comprehensive data analysis

To demonstrate that FFT-based CC selection can include and analyse data regardless of its origin, we concatenated corresponding signals from FdataI with FdataII as well as RdataI and RdataIII with RdataII to construct MFdata, MRdataI and MRdataIII. The comprehensive sets were used to construct CCs; the sets were then compared with both their original genotype and phenotype MCs. These comparisons are shown in Table 5–Table 8, and their distributions are represented in Figure 6–Figure 9.

Table 5. CCs selected from MC FdataI and MC MFdata PCA signals and evaluated with FdataI and FdataII

	vs FdataI		vs FdataII
	FdataI	MFdata	FdataII	MFdata
K	24
ANE	0.6333	0.6356	0.4049	0.4093
ENE	0.6413	0.6423	0.4374	0.4351
E	0.7194	0.7113	0.623	0.5914
MD	1.7668	2.4735	0	0
VT	66.0777	33.9223	46.42	64.2857
CR	89.4908	89.8198	80.677	82.1913
CV	45.7033	35.6847	21.8658	132.1517
AR	91.7647	92.7206	97.5904	94.3775

Table 6. CCs selected from MC RdataI, MRdataI, RdataIII and MRdataIII PCA signals and evaluated with RdataI.

	vs RdataI
	RdataI	MRdataI	RdataIII	MRdataIII
K	24
ANE	0.6148	0.6156	0.6251	0.6169
ENE	0.5989	0.6107	0.621	0.6194
E	0.6962	0.6909	0.6985	0.6934
MD	8.8542	8.5938	7.2917	6.7708
VT	52.0833	63.5417	52.0833	53.3854
CR	80.7367	83.768	81.7278	81.8623
CV	56.3949	59.6279	45.6875	199.9377
AR	86.5097	88.144	86.5651	90.7202

Table 7. CCs selected from MC RdataI, MRdataI, RdataIII and MRdataIII PCA signals and evaluated with RdataIII.

	vs RdataIII
	RdataI	MRdataI	RdataIII	MRdataIII
K	24
ANE	0.6285	0.6276	0.6314	0.623
ENE	0.6273	0.6294	0.6368	0.6267
E	0.7036	0.7054	0.7226	0.7056
MD	8.0729	7.5521	7.2917	10.4167
VT	52.8646	60.6771	51.5625	46.875
CR	79.5995	81.0356	79.6809	84.53
CV	28.3673	56.3689	90.0475	60.7279
AR	88.9071	88.7705	87.5956	93.0471

Table 8. CCs selected from MC RdataI, MRdataI, RdataIII and MRdataIII PCA signals and evaluated with RdataII.

	vs RdataII
	RdataII	MRdataI	MRdataIII
K	24
ANE	0.4594	0.4652	0.4618
ENE	0.4796	0.4896	0.4742
E	0.6402	0.6205	0.6169
MD	0	5.2632	0
VT	39.4737	42.1053	60.5263
CR	63.8082	61.8988	68.2437
CV	3.8262	2.2285	4.1332
AR	95.4268	98.7805	98.7805

Figure 6.

First two principal component’s distributions of k=24 CC (orange) selected by PCA from FDataI (a) and MDataI (b) in FdataI distribution (blue).

Figure 7.

First two principal component’s distributions of k=24 CC (orange) selected by PCA from FDataII (a) and MDataI (b) in FdataII distribution (blue).

Figure 8.

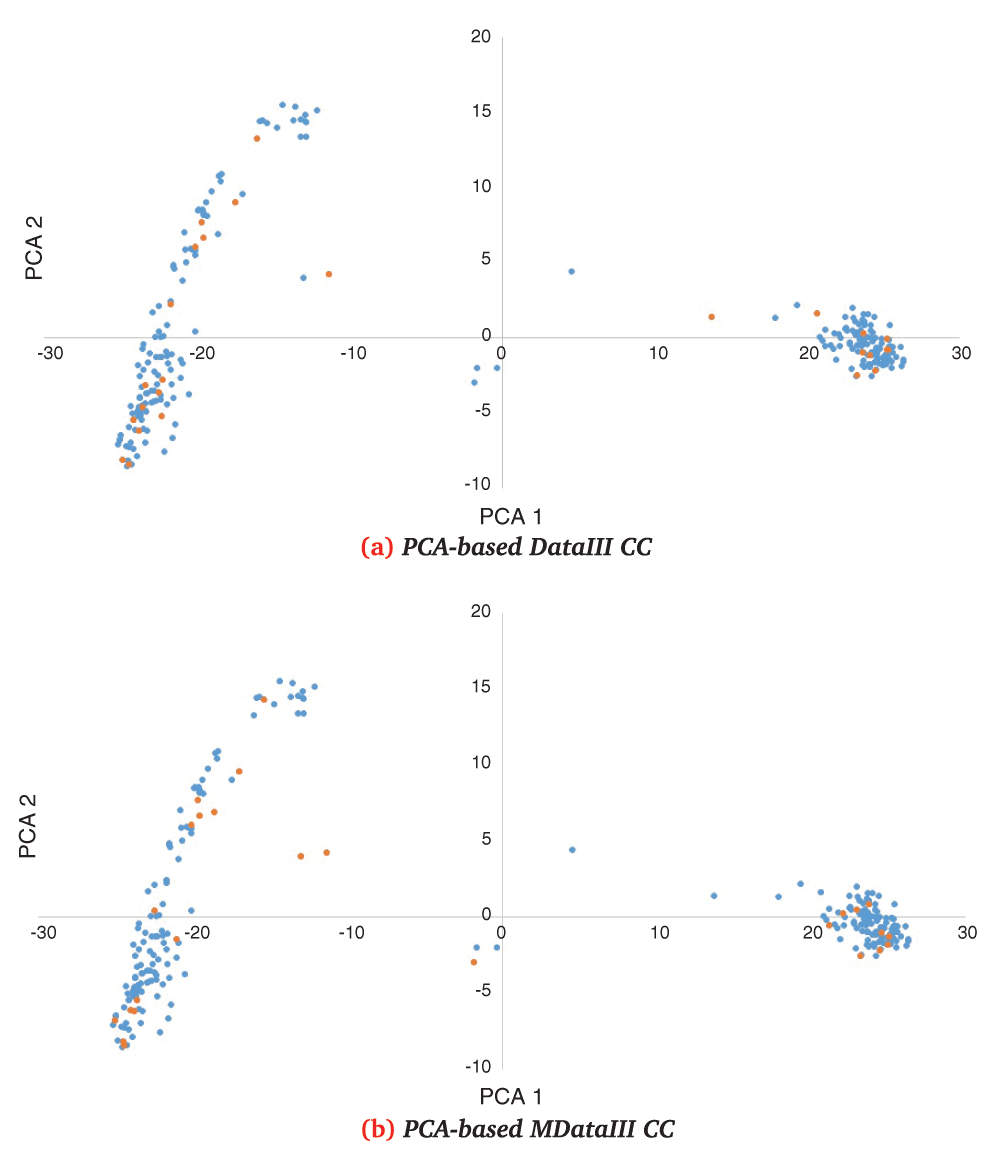
First two principal component’s distributions of k=24 CC (orange) selected by PCA from RDataIII (a) and MDataIII (b) in RDataI distribution (blue).

Figure 9.

First two principal component’s distributions of k=24 CC (orange) selected by PCA from RDataII (a) and MRDataI (b) in RdataII distribution (blue).

These comprehensive CCs showed overall better scores than genotypic-only CCs when compared with genotypic-only data. On the contrary, there was a better overall score in phenotypic-only CCs when compared against phenotypic-only data. In the latter case, it should be kept in mind that comprehensive data also consider genotypic data; this could explain why better selections are made when only phenotypic data are considered because genotypic variations may reduce the impact of some phenotypic traits in the PCA analysis.

The generation of a DM based on signal comparisons originating from mixed data construction enables us to explore one of the most interesting applications of this algorithm. By mapping genotypic and AT data, constructing a single signal with all data available for a particular accession is possible. The possibility of including genotypic data with phenotypic traits, geographical locations, climates, habitats, nutritional requirements, symbiotic relationships and so forth provides an opportunity for determining the best information to be included in the selection process in order to cope with the particular objectives for which that CC is being selected. This concept, in addition to adequate scoring systems, may prove useful in designing tailored CCs that comply with specific research/breeding objectives.

Conclusions

The use of SPTs in CC selection, as presented in this algorithm, enables us to analyse all available data comprehensively and from different perspectives. Despite its limitations, this signal construction makes it possible to analyse all available data regarding each accession in CC selection with good results. The efficiency of SPTs in CC selection suggests that the use of these tools in MC analysis may provide useful information not only for CC but also for other purposes. The implementation of current and other SPTs in all-inclusive MC-mapped signals is worth further exploration, and we believe that it will be an important asset to genetic resource management and exploitation.

Author contributions

EB conceived and designed the algorithm, performed the implementation, analysed the data and wrote the manuscript. MT contributed to the design of the algorithm, data analysis and manuscript drafting and correction. Both authors have read and approved the final manuscript.

Competing interests

No competing interests were disclosed.

Grant information

This research is supported in part by the SATREPS project by JST and JICA, Diversity Assessment and Development of Sustainable Use of Mexican Genetic Resources and in part by JSPS Grant-in-Aid 25257416.

I confirm that the funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Acknowledgements

We would like to thank F1000Research for the free-submission prize awarded at ISCB-ASIA 2014.

Supplementary Material 1

Genomic and AT numerical mapping equivalences and Original Codes

SyntheticData.cvs : Synthetic Data representing binary information.
FoxtailATMap.cvs : Mapped Rice AT where 1=’presence’; 0=’absence’ (corresponds to FdataII).
FoxtailGenMap.cvs : Mapped Foxtail Genotype where 1=’presence’; 0=’absence’ (corresponds to FdataI).
RiceATMap.cvs : Mapped Rice AT where 1=’presence’; 0=’absence’ (corresponds to RdataII).
RiceGenIMap.cvs : Mapped RICE SNPs where 1="T"; 2="C"; 4="N"; 6="G" and 7="A" (corresponds to RdataI).
RiceGenIIIMap.cvs : Mapped RICE SNPs where 1="T"; 2="C"; 4="N"; 6="G" and 7="A" (corresponds to RdataIII).

Codes are enclosed as scripts in FFTCoreCollCodes.rar, available online at https://zenodo.org/badge/doi/10.5281/zenodo.16895.svg Refer to README.m for details.

Faculty Opinions recommended

References

1. Watanabe KN, Iwanaga M: Plant Genetic Resources and its Global Contribution. Plant Biotechnol. 1999; 1(16): 7–13. Reference Source
2. Dulloo ME, Hunter D, Borelli T: Ex situ and in situ conservation of agricultural biodiversity: major advances and research needs. Not Bot Horti Agrobot Cluj Napoca. 2010; 38(2): 123–135. Reference Source
3. Upadhyaya HD, Gowda CLL, Sastry D: Plant genetic resources management: collection, characterization, conservation and utilization. J SAT Agricultural Res. 2008; 1–16. Reference Source
4. Brown HD: Core collections: a practical approach to genetic resources management. Genome. 1989; 31(2): 818–824. Publisher Full Text
5. Guo Y, Li Y, Hong H, et al.: Establishment of the integrated applied core collection and its comparison with mini core collection in soybean (Glycine max). The Crop Journal. 2014; 2(1): 38–45. Publisher Full Text
6. Studnicki M, Madry W, Schmidt J: Efficiency of Sampling Strategies to Establish a Representative in the Phenotypic-based Genetic Diversity Core Collection of Orchardgrass (Dactylis glomerata). Czech J Genet Plant Breed. 2013; 2013(1): 36–47. Reference Source
7. Odong TL, Jansen J, van Eeuwijk FA, et al.: Quality of core collections for effective utilisation of genetic resources review, discussion and interpretation. Theor Appl Genet. 2013; 126(2): 289–305. PubMed Abstract | Publisher Full Text | Free Full Text
8. Richards CM, Volk GM: Selection of stratified core sets representing wild apple (Malus sieversii). J Am Soc Hortic Sci. 2009; 134(2): 228–235. Reference Source
9. Franco J, Crossa J, Warburton ML, et al.: Sampling Strategies for Conserving Maize Diversity When Forming Core Subsets Using Genetic Markers. Crop Sci. 2006; 46(2): 854–864. Publisher Full Text
10. Hu J, Zhu J, Xu HM: Methods of constructing core collections by stepwise clustering with three sampling strategies based on the genotypic values of crops. Theor Appl Genet. 2000; 101(1–2): 264–268. Publisher Full Text
11. Wang JC, Hu J, Huang XX, et al.: Assessment of different genetic distances in constructing cotton core subset by genotypic values. J Zhejiang Univ Sci B. 2008; 9(5): 356–62. PubMed Abstract | Publisher Full Text | Free Full Text
12. Thachuk C, Crossa J, Franco J, et al.: Core Hunter: an algorithm for sampling genetic resources based on multiple genetic measures. BMC Bioinformatics. 2009; 10: 243. PubMed Abstract | Publisher Full Text | Free Full Text
13. De Beukelaer H, Smýkal P, Davenport GF, et al.: Core Hunter II: fast core subset selection based on multiple genetic diversity measures using Mixed Replica search. BMC Bioinformatics. 2012; 13: 312. PubMed Abstract | Publisher Full Text | Free Full Text
14. Jansen J, van Hintum T: Genetic distance sampling: a novel sampling method for obtaining core collections using genetic distances with an application to cultivated lettuce. Theor Appl Genet. 2007; 114(3): 421–8. PubMed Abstract | Publisher Full Text
15. Gouesnard B, Bataillon TM, Decoux G, et al.: MSTRAT: An algorithm for building germ plasm core collections by maximizing allelic or phenotypic richness. J Hered. 2001; 92(1): 93–94. PubMed Abstract | Publisher Full Text
16. Franco J, Crossa J, Ribaut JM: A method for combining molecular markers and phenotypic attributes for classifying plant genotypes. Theor Appl Genet. 2001; 103(6–7): 944–952. Publisher Full Text
17. Kwan HK, Arniker SB: Numerical representation of DNA sequences. In IEEE International Conference on Electro/Information Technology. 2009; 307–310. Publisher Full Text
18. Dossou-aminon I, Loko LY, Adjatin A, et al.: Genetic divergence in Northern Benin Sorghum (Sorghum bicolor L. Moench) landraces as revealed by agromorphological traits and selection of candidate genotypes. ScientificWorldJournal. 2015; 2015: e916476. PubMed Abstract | Publisher Full Text | Free Full Text
19. Stein EM, Weiss G: The Fourier Transform. In Introduction to Fourier analysis on Euclidean Spaces. Princeton University Press. 1971. Reference Source
20. Cooley JW, Tukey JW: An algorithm for the machine calculation of complex Fourier series. Math Comput. 1965; 297–301. Publisher Full Text
21. Nagarajan N, Keich U: FAST: Fourier transform based algorithms for significance testing of ungapped multiple alignments. Bioinformatics. 2008; 24(4): 577–8. PubMed Abstract | Publisher Full Text
22. Borrayo E, Mendizabal-Ruiz EG, Vélez-Pérez H, et al.: Genomic signal processing methods for computation of alignment-free distances from DNA sequences. PLoS One. 2014; 9(11): e110954. PubMed Abstract | Publisher Full Text | Free Full Text
23. Wang JC, Hu J, Xu HM, et al.: A strategy on constructing core collections by least distance stepwise sampling. Theor Appl Genet. 2007; 115(1): 1–8. PubMed Abstract | Publisher Full Text
24. Hirano R, Naito K, Fukunaga K, et al.: Genetic structure of landraces in foxtail millet (Setaria italica (L.) P. Beauv.) revealed with transposon display and interpretation to crop evolution of foxtail millet. Genome. 2011; 54(6): 498–506. PubMed Abstract | Publisher Full Text
25. Odong TL, van Heerwaarden J, Jansen J, et al.: Determination of genetic structure of germplasm collections: are traditional hierarchical clustering methods appropriate for molecular marker data? Theor Appl Genet. 2011; 123(2): 195–205. PubMed Abstract | Publisher Full Text | Free Full Text
26. Cericola F, Portis E, Toppino L, et al.: The population structure and diversity of eggplant from Asia and the Mediterranean Basin. PLoS One. 2013; 8(9): e73702. PubMed Abstract | Publisher Full Text | Free Full Text
27. Mei Y, Zhou J, Xu H, et al.: Development of sea island cotton (’Gossypium barbadense’L.) Core collection using genotypic values. Aust J Crop Sci. 2012; 6(4): 673–680. Reference Source
28. Redelings BD, Suchard MA: Joint Bayesian estimation of alignment and phylogeny. Syst Biol. 2005; 54(3): 401–18. PubMed Abstract | Publisher Full Text
29. Cristea PD: Conversion of nucleotides sequences into genomic signals. J Cell Mol Med. 2002; 6(2): 279–303. PubMed Abstract | Publisher Full Text
30. Rosen GL, Sokhansanj BA, Polikar R, et al.: Signal processing for metagenomics: extracting information from the soup. Curr Genomics. 2009; 10(7): 493–510. PubMed Abstract | Publisher Full Text | Free Full Text
31. Wang L, Schonfeld D: Mapping Equivalence for Symbolic Sequences: Theory and Applications. IEEE Trans Signal Process. 2009; 57(12): 4895–4905. Publisher Full Text
32. Almeida JS, Vinga S: Universal sequence map (USM) of arbitrary discrete sequences. BMC Bioinformatics. 2002; 3(1): 6. PubMed Abstract | Publisher Full Text | Free Full Text
33. Akhtar M, Epps J, Ambikairajah E: Signal Processing in Sequence Analysis: Advances in Eukaryotic Gene Prediction. IEEE J Sel Top Signal Process. 2008; 2(3): 310–321. Publisher Full Text
34. Franco J, Crossa J, Taba S, et al.: A Sampling Strategy for Conserving Genetic Diversity when Forming Core Subsets. Crop Sci. 2005; 45(3): 1035–1044. Publisher Full Text

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 23 Apr 2015

Author details Author details

¹ Gene Research Center, University of Tsukuba, Tsukuba City, Ibaraki, 605-8572, Japan
² Genetic Resources Center, National Institute of Agrobiological Sciences, Tsukuba City, Ibaraki, 305-8602, Japan

Competing interests

No competing interests were disclosed.

Grant information

This research is supported in part by the SATREPS project by JST and JICA, Diversity Assessment and Development of Sustainable Use of Mexican Genetic Resources and in part by JSPS Grant-in-Aid 25257416.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (1)

version 1

Published: 23 Apr 2015, 4:97

https://doi.org/10.12688/f1000research.6391.1

Copyright

© 2015 Borrayo E and Takeya M. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Data associated with the article are available under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original data is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

Borrayo E and Takeya M. Signal-processing tools for core-collection selection from genetic-resource collections [version 1; peer review: peer review discontinued]. F1000Research 2015, 4:97 (https://doi.org/10.12688/f1000research.6391.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Peer review discontinued

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 23 Apr 2015

Peer review discontinued

At the request of the author(s), this article is no longer under peer review.

What does this mean?

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

[1] 1. Watanabe KN, Iwanaga M: Plant Genetic Resources and its Global Contribution. Plant Biotechnol. 1999; 1(16): 7–13. Reference Source

[2] 2. Dulloo ME, Hunter D, Borelli T: Ex situ and in situ conservation of agricultural biodiversity: major advances and research needs. Not Bot Horti Agrobot Cluj Napoca. 2010; 38(2): 123–135. Reference Source

[3] 3. Upadhyaya HD, Gowda CLL, Sastry D: Plant genetic resources management: collection, characterization, conservation and utilization. J SAT Agricultural Res. 2008; 1–16. Reference Source

[4] 4. Brown HD: Core collections: a practical approach to genetic resources management. Genome. 1989; 31(2): 818–824. Publisher Full Text

[5] 5. Guo Y, Li Y, Hong H, et al.: Establishment of the integrated applied core collection and its comparison with mini core collection in soybean (Glycine max). The Crop Journal. 2014; 2(1): 38–45. Publisher Full Text

[6] 6. Studnicki M, Madry W, Schmidt J: Efficiency of Sampling Strategies to Establish a Representative in the Phenotypic-based Genetic Diversity Core Collection of Orchardgrass (Dactylis glomerata). Czech J Genet Plant Breed. 2013; 2013(1): 36–47. Reference Source

[7] 7. Odong TL, Jansen J, van Eeuwijk FA, et al.: Quality of core collections for effective utilisation of genetic resources review, discussion and interpretation. Theor Appl Genet. 2013; 126(2): 289–305. PubMed Abstract | Publisher Full Text | Free Full Text

[8] 8. Richards CM, Volk GM: Selection of stratified core sets representing wild apple (Malus sieversii). J Am Soc Hortic Sci. 2009; 134(2): 228–235. Reference Source

[9] 9. Franco J, Crossa J, Warburton ML, et al.: Sampling Strategies for Conserving Maize Diversity When Forming Core Subsets Using Genetic Markers. Crop Sci. 2006; 46(2): 854–864. Publisher Full Text

[10] 10. Hu J, Zhu J, Xu HM: Methods of constructing core collections by stepwise clustering with three sampling strategies based on the genotypic values of crops. Theor Appl Genet. 2000; 101(1–2): 264–268. Publisher Full Text

[11] 11. Wang JC, Hu J, Huang XX, et al.: Assessment of different genetic distances in constructing cotton core subset by genotypic values. J Zhejiang Univ Sci B. 2008; 9(5): 356–62. PubMed Abstract | Publisher Full Text | Free Full Text

[12] 12. Thachuk C, Crossa J, Franco J, et al.: Core Hunter: an algorithm for sampling genetic resources based on multiple genetic measures. BMC Bioinformatics. 2009; 10: 243. PubMed Abstract | Publisher Full Text | Free Full Text

[13] 13. De Beukelaer H, Smýkal P, Davenport GF, et al.: Core Hunter II: fast core subset selection based on multiple genetic diversity measures using Mixed Replica search. BMC Bioinformatics. 2012; 13: 312. PubMed Abstract | Publisher Full Text | Free Full Text

[14] 14. Jansen J, van Hintum T: Genetic distance sampling: a novel sampling method for obtaining core collections using genetic distances with an application to cultivated lettuce. Theor Appl Genet. 2007; 114(3): 421–8. PubMed Abstract | Publisher Full Text

[15] 15. Gouesnard B, Bataillon TM, Decoux G, et al.: MSTRAT: An algorithm for building germ plasm core collections by maximizing allelic or phenotypic richness. J Hered. 2001; 92(1): 93–94. PubMed Abstract | Publisher Full Text

[16] 16. Franco J, Crossa J, Ribaut JM: A method for combining molecular markers and phenotypic attributes for classifying plant genotypes. Theor Appl Genet. 2001; 103(6–7): 944–952. Publisher Full Text

[17] 17. Kwan HK, Arniker SB: Numerical representation of DNA sequences. In IEEE International Conference on Electro/Information Technology. 2009; 307–310. Publisher Full Text

[18] 18. Dossou-aminon I, Loko LY, Adjatin A, et al.: Genetic divergence in Northern Benin Sorghum (Sorghum bicolor L. Moench) landraces as revealed by agromorphological traits and selection of candidate genotypes. ScientificWorldJournal. 2015; 2015: e916476. PubMed Abstract | Publisher Full Text | Free Full Text

[19] 19. Stein EM, Weiss G: The Fourier Transform. In Introduction to Fourier analysis on Euclidean Spaces. Princeton University Press. 1971. Reference Source

[20] 20. Cooley JW, Tukey JW: An algorithm for the machine calculation of complex Fourier series. Math Comput. 1965; 297–301. Publisher Full Text

[21] 21. Nagarajan N, Keich U: FAST: Fourier transform based algorithms for significance testing of ungapped multiple alignments. Bioinformatics. 2008; 24(4): 577–8. PubMed Abstract | Publisher Full Text

[22] 22. Borrayo E, Mendizabal-Ruiz EG, Vélez-Pérez H, et al.: Genomic signal processing methods for computation of alignment-free distances from DNA sequences. PLoS One. 2014; 9(11): e110954. PubMed Abstract | Publisher Full Text | Free Full Text

[23] 23. Wang JC, Hu J, Xu HM, et al.: A strategy on constructing core collections by least distance stepwise sampling. Theor Appl Genet. 2007; 115(1): 1–8. PubMed Abstract | Publisher Full Text

[24] 24. Hirano R, Naito K, Fukunaga K, et al.: Genetic structure of landraces in foxtail millet (Setaria italica (L.) P. Beauv.) revealed with transposon display and interpretation to crop evolution of foxtail millet. Genome. 2011; 54(6): 498–506. PubMed Abstract | Publisher Full Text

[25] 25. Odong TL, van Heerwaarden J, Jansen J, et al.: Determination of genetic structure of germplasm collections: are traditional hierarchical clustering methods appropriate for molecular marker data? Theor Appl Genet. 2011; 123(2): 195–205. PubMed Abstract | Publisher Full Text | Free Full Text

[26] 26. Cericola F, Portis E, Toppino L, et al.: The population structure and diversity of eggplant from Asia and the Mediterranean Basin. PLoS One. 2013; 8(9): e73702. PubMed Abstract | Publisher Full Text | Free Full Text

[27] 27. Mei Y, Zhou J, Xu H, et al.: Development of sea island cotton (’Gossypium barbadense’L.) Core collection using genotypic values. Aust J Crop Sci. 2012; 6(4): 673–680. Reference Source

[28] 28. Redelings BD, Suchard MA: Joint Bayesian estimation of alignment and phylogeny. Syst Biol. 2005; 54(3): 401–18. PubMed Abstract | Publisher Full Text

[29] 29. Cristea PD: Conversion of nucleotides sequences into genomic signals. J Cell Mol Med. 2002; 6(2): 279–303. PubMed Abstract | Publisher Full Text

[30] 30. Rosen GL, Sokhansanj BA, Polikar R, et al.: Signal processing for metagenomics: extracting information from the soup. Curr Genomics. 2009; 10(7): 493–510. PubMed Abstract | Publisher Full Text | Free Full Text

[31] 31. Wang L, Schonfeld D: Mapping Equivalence for Symbolic Sequences: Theory and Applications. IEEE Trans Signal Process. 2009; 57(12): 4895–4905. Publisher Full Text

[32] 32. Almeida JS, Vinga S: Universal sequence map (USM) of arbitrary discrete sequences. BMC Bioinformatics. 2002; 3(1): 6. PubMed Abstract | Publisher Full Text | Free Full Text

[33] 33. Akhtar M, Epps J, Ambikairajah E: Signal Processing in Sequence Analysis: Advances in Eukaryotic Gene Prediction. IEEE J Sel Top Signal Process. 2008; 2(3): 310–321. Publisher Full Text

[34] 34. Franco J, Crossa J, Taba S, et al.: A Sampling Strategy for Conserving Genetic Diversity when Forming Core Subsets. Crop Sci. 2005; 45(3): 1035–1044. Publisher Full Text

Signal-processing tools for core-collection selection from genetic-resource collections

Abstract

Keywords

Background

Methods

Mapping data

Signal construction

Fast Fourier transform

Distance matrix computation

Core collection selection

Figure 1. General workflow of the FFT-based core collection selection algorithm.

Figure 2.

Figure 3. First three principal component’s distributions of K=72 CC selection (X) from Rdata MC.

Evaluation of the selected core collection

Experimental datasets

Implementation

Results and discussion

Selection and evaluation

Mapping

RAW versus FFT

Table 1. ∆ K selected CC scores from MC Sdata Raw and PCA Signal evaluated with Sdata.

Table 2. ∆ K selected CC scores from MC Fdata Raw and PCA Signal evaluated with Fdata.

Table 3. ∆ K selected CC scores from MC Rdata Raw and PCA Signal evaluated with Rdata.

Table 4. CCs selected from MC Sdata, Fdata and Rdata using PCA signals and Core Hunter compared with respective same data.

Figure 4.

Figure 5.

Comprehensive data analysis

Table 5. CCs selected from MC FdataI and MC MFdata PCA signals and evaluated with FdataI and FdataII

Table 6. CCs selected from MC RdataI, MRdataI, RdataIII and MRdataIII PCA signals and evaluated with RdataI.

Table 7. CCs selected from MC RdataI, MRdataI, RdataIII and MRdataIII PCA signals and evaluated with RdataIII.

Table 8. CCs selected from MC RdataI, MRdataI, RdataIII and MRdataIII PCA signals and evaluated with RdataII.

Figure 6.

Figure 7.

Figure 8.

Figure 9.

Conclusions

Author contributions

Competing interests

Grant information

Acknowledgements

Supplementary Material 1

References

Comments on this article Comments (0)

Peer review discontinued

Comments on this article Comments (0)

Peer review discontinued

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated