Keywords
minimally frustrated models, biomolecular dynamics, frustrated protein models, protein structure model, x-ray crystallography, nuclear magnetic resonance, Direct coupling analysis
minimally frustrated models, biomolecular dynamics, frustrated protein models, protein structure model, x-ray crystallography, nuclear magnetic resonance, Direct coupling analysis
High-resolution structural techniques (e.g., X-ray crystallography and nuclear magnetic resonance) have provided the data necessary to develop and refine a multitude of potential energy functions used in the simulation of biomolecules. In particular, these structures provide the parameterization for simplified models that are based on the energy landscape theory of protein folding. These models construct an energetically unfrustrated (ideal) funneled landscape by including stabilizing interactions between native contacts (i.e., amino acid pairs that are nearby in the three-dimensional native structure of a protein). In cases in which experimental structures are lacking or insufficient, it becomes necessary to supplement these models with other sources of contact information. An emerging technique for contact estimation is via the statistical analysis of residue co-evolution in families of protein sequences. Combinations of high-resolution structural data and predictions from residue co-evolution are proving to be invaluable tools for building models to study protein structure and dynamics.
Understanding the fundamental process of how a heterogeneous polypeptide can reversibly fold into a distinct native three-dimensional structure on biological timescales led to the development of the energy landscape theory of biomolecular folding. This theory is based on the principle of minimal frustration1 and the folding funnel concept2,3. These physical principles describe an energy landscape that has been molded by evolution such that the native interactions (i.e., the molecular interactions present in low free-energy configurations of folded proteins and RNAs) are, on average, more stabilizing than non-native interactions. The consequence of proteins having sufficiently reduced energetic frustration is that geometry dominates energetic roughness in determining folding mechanisms. Thus, a description of the effective energetics of the folding phenomenon can be attained by including a set of native stabilizing interactions consistent with the native basin of attraction. Potential energy functions of this type, which use experimental information to determine such native interactions, are known as “structure-based models” (SBMs)4–6 and, when employed in dynamical models, are powerful tools for understanding the connection between structure, folding, and function. Although these SBMs have been successfully applied to different biomolecules, we will be focusing on proteins for clarity in this review.
Structural information, however, may be limited for many interesting systems. This is particularly true for functional configurations that are transient or partially disordered or both. The recent explosion in genomic information has enabled complementary methods for discovering functionally important amino acid interactions. The minimal frustration principle applies equally to any sequence of amino acids that can robustly fold to a particular native structure. Thus, in a family of sequences where most of them fold to a common structure, residue positions that are in contact will display a correlated mutational record because of the global evolutionary constraint that the native structure imposes for foldability. Of course, additional constraints beyond folding affect sequence evolution, including maintenance of molecular assemblies, enzymatic activity, and allosteric motions. Signals of these functionally relevant contacts are necessarily mixed with those providing robust folding. To identify such relevant interactions involved in folding and function, a number of methodologies have been developed in recent years that have been successful in uncovering such molecular couplings from sequence data. One of them is direct coupling analysis (DCA)7,8, which is designed to infer a global statistical model from a multiple sequence alignment (MSA) of a single protein family. Using a maximum entropy approach, DCA infers the parameters of an effective energy function consisting of single-site fields and pairwise couplings that is able to approximately reproduce the empirically observed single-site and pairwise amino acid frequencies from the input sequence alignment. The DCA energy function is known as a Potts model, a generalized Ising model that includes non-nearest neighbor interactions and non-constant spin-spin interactions. In practice, couplings of varying strength are computed between all possible pairs of sequence positions. In the past, accurate and tractable approximations of such global models were elusive and detection of direct correlations, as opposed to an aggregate of direct and indirect correlations, was challenging. Other methods are derived from similar theoretical perspectives but have varying computational demands and accuracies9–12. Using an inferred effective energy function, one can estimate pairwise direct probabilities at a particular pair of residue sites. Calculating the Kullback–Leibler divergence between these joint probabilities and single marginal frequencies gives the direct information (DI) score for that residue pair. DI is a proxy of how “directly correlated” two sites are in an MSA. When compared with crystal structures, high DI scores correlate highly with native contacts, and more than 80% overlap, on average, for the top residue pairs in many protein families7,13. The full set of highly scoring contacts amounts to a superset of minimally frustrated and functionally important residue pairs that are spatially localized in the functional configurations of the members of a protein family. Here, we will review the current progress in using residue co-evolution for modeling the structure and dynamics of proteins with a focus on its combination with SBMs.
In their simplest form, SBMs idealize minimally frustrated protein energy landscapes by including only native interactions. This model removes any residual non-native energetic roughness and clarifies analysis of the geometrical and topological aspects of protein dynamics and folding. These models faithfully represent the local geometry through bond, angle, dihedral, and excluded volume terms at either single-bead-per-residue or all-atom resolutions. Non-local interactions consist of stabilizing pairwise potentials applied between residue (or atom) pairs that are nearby in the native structure. These pairwise interactions are called native contacts, and the entire set is known as a native contact map. All of the interactions, local and non-local, are set to have an explicit minimum at the native structure, hence the name “structure-based”. The simplified construction of the potential energy function permits for reduced computational requirements, and the explicitly encoded native interactions provide a baseline model that can be used for molecular modeling or studying physical perturbations. For a detailed discussion of the theoretical foundation and construction of SBMs, we refer you to the following reviews,14–16, and the references therein.
The quality of contact maps derived from DCA and similar methods have been benchmarked against contact maps calculated from crystallographic structures, and their accuracy is promising. In general, the larger and more diverse the family of sequences, the higher the quality of contact prediction. The high level of DCA accuracy provided sufficient tertiary constraints to allow folding single domain proteins to within 3 Å from the crystal structure when given knowledge of the secondary structure17–21. A rule of thumb is that the number of sequences should be larger than 1000 with less than 80% identity; however, others propose an even lower requirement of a minimum number of sequences close to the length L of the protein polypeptide chain, provided that they are diverse18. The notoriously difficult problem of predicting membrane protein structures has also been aided by considering evolutionarily coupled pairs22,23.
A native contact map derived from a single native structure is often not sufficient to encode all the functionally relevant, minimally frustrated interactions. This led to the development of a variety of “multi-basin” models, where multiple experimental structures or structural constraints are included in a single SBM24–26. As described above, residue pairs with the highest DI scores, the high DI pairs (HDPs), are consistent with the native contact maps. Thus, in an analogous fashion, predicted contact constraints from co-evolution can be merged with contact maps computed from experimental structures in order to more fully capture the true underlying biomolecular energy landscape, including functional transitions and conformations, and therefore to be consistent with multiple structures27–29.
Interactions between proteins are fundamental to cellular processes. Where these interactions involve direct contact, multimeric structures, both long-lived and transient, leave correlated mutational patterns between interacting surface residues. A pioneering study used the HDPs between a histidine kinase and its response regulator to make a prediction of the transient protein complex enabling phosphotransfer30. This allowed a prediction for the histidine kinase TM0853 and its response regulator TM0468 that was later confirmed experimentally to be within 3.3 Å31. These predictions are made by minimizing a contact-based energy function consisting of dimeric HDPs. Where dimerization only weakly perturbs the monomer structure, refined rigid-body modeling in combination with co-evolutionary constrains can be employed to estimate protein complexes. When combined with experimental observations, directly coupled amino acids can unveil protein interfaces relevant for the study of disease32. Larger monomer distortions can be readily sampled with SBMs coupled with simulated annealing33. Current protocols involving HDPs have allowed the large-scale prediction of both homodimers34 and heterodimers35,36. The HDP contact map for a protein family that forms homodimers is a prime example of how ambiguity can arise in co-evolutionary information. The co-evolving dimeric interfacial contacts are mixed with HDPs selected for monomeric folding, but the dimeric contacts can in general be sorted from the monomeric contacts when there is a known monomer structure34. But rarely are there true dichotomies in biology; the existence of domain swapping37,38 and structural symmetry26,39 highlights some difficulties in assigning particular roles to each HDP. Also, some protein-protein interactions are mediated by disordered regions that order upon binding. The utility of DCA in these cases remains to be tested.
In addition to homo-multimerization, the set of conformations encoded in HDP contact maps can include functional motions. Multi-domain proteins can undergo conformational changes, for example, to accommodate ligands40 or in response to phosphorylation41. In periplasmic ligand binding proteins, there exists an open, ligand-free configuration and a closed, ligand-bound configuration. Molecular dynamics simulations can be performed by using an SBM specific to an open configuration but overlaid with an additional potential term consisting of a set of attractive, short-range interactions for each HDP27. Figure 1 illustrates an example of this for the leucine-binding protein. The native contact maps for two crystal structures of leucine-binding protein are shown in Figure 1A: “open” without ligand and “closed” with ligand. The closed contact map has additional contacts not present in the open structure. The DCA contact map, shown as the lower triangular map in Figure 1B, contains a superset of both the open and closed configuration contacts. An SBM is constructed that is specific to the open structure (Figure 1D) and additionally contains contact potentials stabilizing all the “non-native” DCA contacts (i.e., any DCA contacts that are not already in the open structure). These additional contacts are each given a stabilizing potential with a minimum at 8 Å. Molecular dynamics simulations of this hybrid SBM+DCA Hamiltonian show two clusters, each within 2 Å of either the open or closed state. Overlaying the DCA contacts does not disrupt the stability of the open structure, and additionally reveals the closed state without including any information from the closed crystal structure. This shows that co-evolutionary information can be used to uncover intermediary, hidden, and functionally relevant conformational states present in many protein families27.
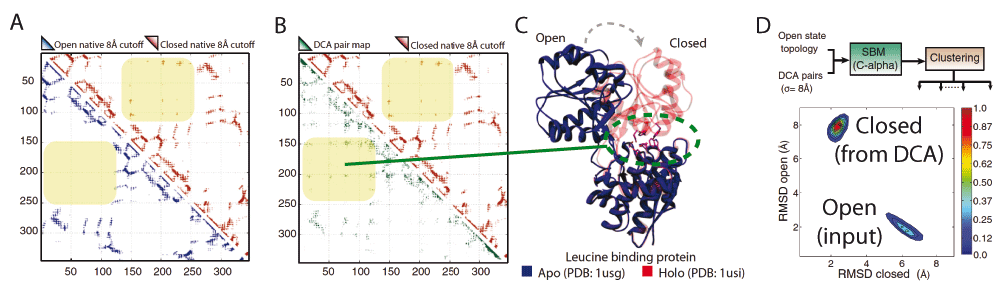
(A) Leucine-binding protein (LBP) contact maps derived from crystal structures: “open” without ligand and “closed” bound to a ligand. Each triangular region in the map shows a mark if residue pairs are less than 8 Å apart in the experimental structure. The closed contact map (upper triangle) has additional contacts not present in the open structure. (B) The DCA contact map inferred from residue co-evolution (lower triangle) contains a superset of contacts from both open and closed conformations. (C) A cartoon representation of the aligned open (apo) and closed (holo) LBP structures shows a large conformational change upon ligand binding. (D) A structure-based model (SBM) is defined from the apo structure plus contact potentials stabilizing DCA contacts that are not already in the open structure. A two-dimensional root mean square deviation (RMSD) distribution of the states explored by molecular dynamics simulations of this hybrid Hamiltonian shows two peaks within 2 Å of the open and closed states. This shows the ability to uncover functional states via co-evolutionary couplings.
So far, we have discussed how HDP contact maps can be used for structural modeling. However, the fundamental output of the DCA algorithm is not direct information about co-evolving pairs but rather a Potts model Hamiltonian describing the effective energies of interaction for all pairs of residues in a protein family. This Hamiltonian, though not transferable to any sequences outside the family, should, in principle, be able to provide a quantitative window into the stabilities provided by each amino acid in a protein. Strong evidence of the utility of the effective energies comes from their ability to predict the stability changes of single-site mutants42,43 and significant correlations to folding rates44. Including the so-called single-site fields in addition to the pairwise energies provides even better predictive power45. These results suggested that the pairwise energies calculated from co-evolution could be used to inform thermodynamic models of protein folding. Indeed, folding simulations using SBMs with DCA-weighted native contact potentials can better capture transition state ensembles46. DCA energies have also been shown to correlate with physical potentials when summed over the entire sequence47. Confidence in the ability to estimate energies at both the single-mutant and full-sequence levels is allowing novel methods for investigating the effective energy landscape of evolution, and bridging the gap between biophysics and sequence evolution47,48. These developments are important for integrating the energetics of protein folding and function with protein evolution and selection, which will be crucial to understanding drug resistance and cancer development going forward.
The marriage between co-evolutionary information and physical models of biomolecules has been shown to be a fertile research field, where the most important results are yet to come. This field has been focused on rigorously validating the connection and usefulness between evolutionary information with structural modeling and experimental information. However, the true utility of co-evolutionary information is that it allows us to go places that are hard to access by current experimental technologies; important examples are those of membrane protein structure22,23 and dynamics, systems with transient conformational states, as well as investigation of large molecular assemblies that resist crystallographic characterization. Although crystal structures exist for FtsH AAA peptidase and the 30S ribosome, recent studies on these two systems28,49 show the promise of co-evolutionary information for discovering structural constraints in molecular assemblies. The ability to detect relevant evolutionary interactions has repercussions to our understanding of biomolecular assembly and function. Hopefully, these new tools can be used to alter protein conformation and rewire their interfaces. This has potential applications in the field of protein engineering, as well as systems biology. There is no conceptual hurdle to resisting the application of these ideas to RNA structure and function as well as protein-RNA interactions. Ultimately, we would hope to use all this knowledge to tackle biomedical problems that would help advance human health.
DCA, direct coupling analysis; DI, direct information; HDP, high direct information pair; MSA, multiple sequence alignment; SBM, structure-based model.
This work was supported by the Center for Theoretical Biological Physics sponsored by the National Science Foundation (grants PHY-1427654 and NSF-MCB-1214457). Jeffrey K. Noel is supported in part by the Welch Foundation (grant C-1792).
I confirm that the funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Competing Interests: No competing interests were disclosed.
Competing Interests: No competing interests were disclosed.
Competing Interests: No competing interests were disclosed.
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | |||
|---|---|---|---|
| 1 | 2 | 3 | |
|
Version 1 26 Jan 16 |
read | read | read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)