Keywords
mutational context, signatures, cancer aetiology
This article is included in the RPackage gateway.
mutational context, signatures, cancer aetiology
The existence of context-specific DNA mutational signatures as a response to carcinogens has been known for some time (see e.g. Pfeifer et al.1), but the last three years have seen progress to bioinformatic inference of mutational signatures from large scale cancer sequencing studies2–4 such as TCGA (http://cancergenome.nih.gov/) and ICGC (icgc.org).
These methods of signature discovery, while important, do not translate to clinical application. First of all, they are reliant on a large corpus of samples for their efficacy, making them impractical to be run repeatedly for each new patient. Secondly, even with a large corpus, the results for one individual can theoretically change depending on the identities of the other patients in the corpus, which is undesirable in practice. Therefore there is great value in methods such as those recently presented by Rosenthal et al.5 that can, for a single sample, break a vector of observed mutation counts into constituent signature components.
In the Cancer Research UK funded oesophageal adenocarcinoma ICGC project we have taken a similar view to Rosenthal et al.5 for the decomposition of a single sample, but rather than decomposing mutational contexts into signatures by fitting iterative linear models (ILM), we have viewed the question as lying within the framework of quadratic programming (QP). By mutational contexts, we commonly mean the 96 trinucleotide contexts consisting of the 6 distinguishable mutations and the 16 combinations of immediately preceding and following bases. More general definitions are possible3 and can be accommodated in both the QP and ILM approaches, but we assume the standard 96 in what follows.
In brief, we want to minimize the difference between the normalized observed vector of mutation contexts m (a 96 × 1 vector) and Sw (where S is a 96 × k matrix, each column of which represents the contributions of mutational contexts to one signature, k is the number of known mutational signatures, and w is a k × 1 matrix of weights to be estimated). Our problem, then, is to:
which is equivalent to:
which is the classical quadratic programming problem that can be solved quickly (given the form of STS) and easily using the core linear algebra functionality of R (version 3.2.4)6 and the quadprog package (version 1.5-5)7, which implements the dual method of Goldfarb and Idnani8,9 to find the solution. Practical details of the implementation can be found in the ‘Data and Software Availability’ section of this note.
In most circumstances, both the ILM and QP approaches work well. Illustrating them on an example from the OCCAMS consortium’s whole-genome sequencing of oesophageal adenocarcinoma10, we see that the ILM and QP approaches are highly concordant (See Figure 1). The ILM approach has the advantages of familiarity of interpretation, and enforcement of parsimony should this be desired (while parsimony is generally desirable if building a predictor, if we are trying to model an underlying truth then it represents a strong assumption). More importantly, taking advantage of the linear modelling framework, it would be easy to generalize this approach to use other error models or to include additional structure should one e.g. wish to simultaneously investigate several related samples.
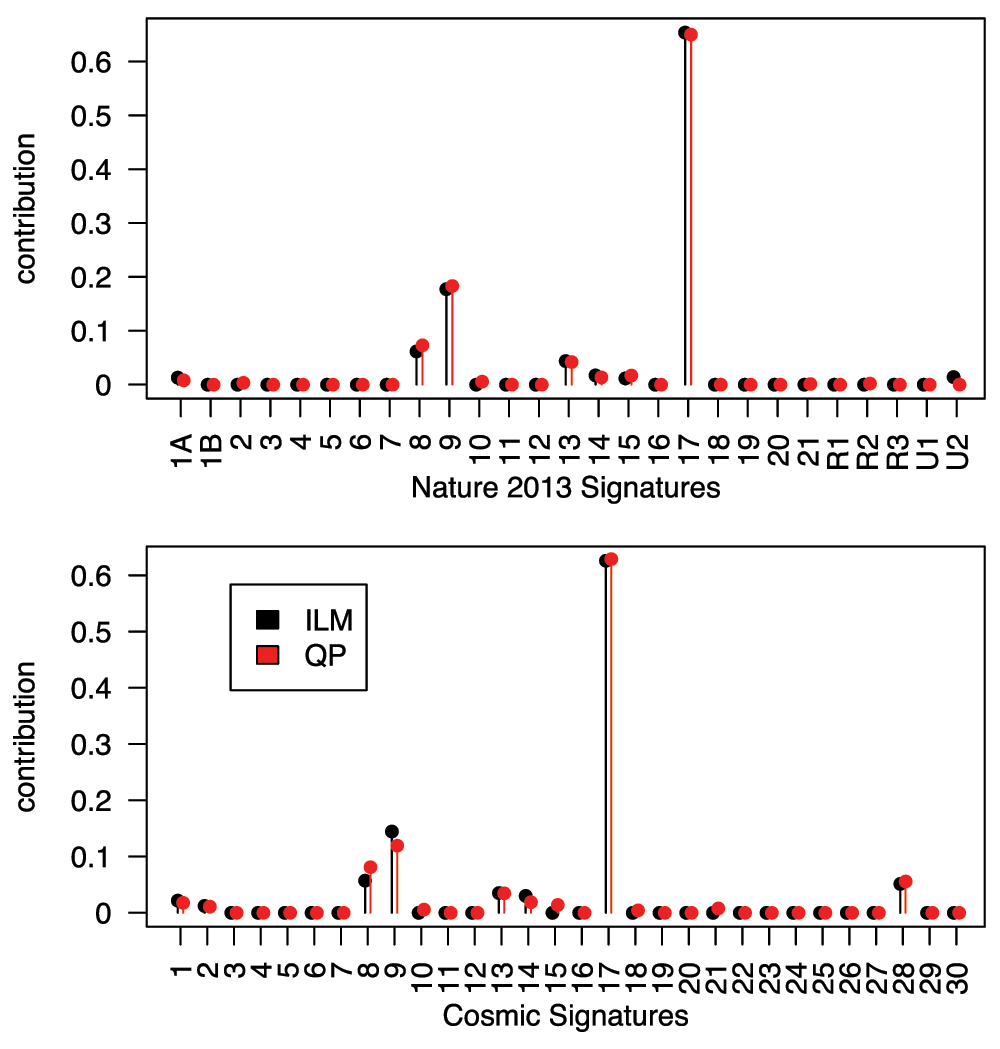
18, 916 SNVs from sequencing library SS6003314 (tumour) compared to library SS6003313 (matched normal tissue)10 are considered. Using the two signature sets included with the deconstructSigs package (Top: the original Nature 2013 signatures2. Bottom: the COSMIC11 signatures) both methods identify the same signatures as being active and produce estimates of contribution weight that are remarkably similar. Note that we are not adjusting for frequencies of contexts in the genome in these analyses.
The disadvantage of the ILM approach comes from its having to define a subset of signatures to include in the model. While the signature matrix is of full rank, with noise in the system it is sometimes possible to approximate an observed vector with several different linear combinations of signatures, and an ILM approach is not guaranteed to give consideration to the correct combination of signatures. Even if the correct solution is reached, it can be a substantially slower approach. It is not difficult to simulate a combination of signatures that takes thousands of iterations and thousands of times longer to run than the QP approach.
If one simulates a flat combination of all available signatures, then the ILM approach performs worse than the QP approach. A fairer comparison would be to consider all equal combinations of just two signatures (with noise added). Of 351 possible such combinations using the Nature 2013 signature set2,5, the majority are well inferred using both the ILM and QP approaches, while one (the combination of signatures 1B and 3) performs poorly for both methods. Aside from these, there is a definite set of combinations for which the ILM approach performs markedly worse than the QP approach (See Figure 2). Pairs involving signature 1B, or signature 5, appear to cause the most problems. It is not the case that the problematic pairs are themselves highly correlated, but the 1B and U2 signatures are, possibly explaining the outlying nature of the U2-R2 pair. This exercise took approximately 5 seconds using the QP approach, and approximately 15 minutes using the ILM approach (on a well-specified desktop).
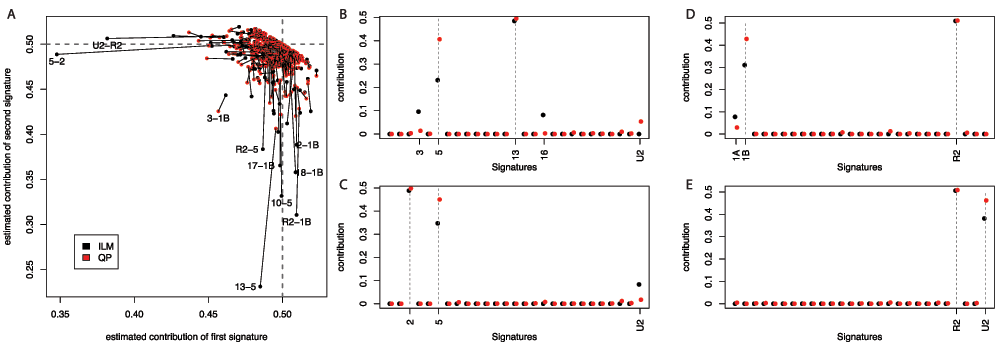
A. 351 simulated datasets were constructed, one for each possible pair of the 27 Nature 2003 signatures, with equal weighting given to both of the signatures and independent uniform errors applied to each mutational context count (ranging from –5% to +5%). The contributions for the two signatures that should be detected are illustrated, with a line linking the estimates from the ILM and QP methods. Perfect performance would see contributions of 0.5 estimated for both signatures in all cases. The identities of outlying signature-pairs are indicated. B. The contributions estimated from the combination of signatures 13 and 5. C. The contributions estimated from the combination of signatures 2 and 5. D. The contributions estimated from the combination of signatures 1B and R2. E. The contributions estimated from the combination of signatures R2 and U2. In all four cases, both methods underestimate the contribution of one signature, but the ILM method more drastically. The ILM method is also more prone to the erroneous detection of other signatures.
Since it makes use of well-established and core R code in a classical mathematical context, no new software is required to use the QP approach (see Data and software availability and Supplementary material for details of implementation). The speed and improved performance of the QP approach makes it an attractive alternative to the ILM method and complements the additional functionality of the deconstructSigs package5.
F1000Research. Dataset 1: An R Markdown document that when compiled will reproduce all the results presented, 10.5256/f1000research.8918.d12418113.
The raw oesophageal adenocarcinoma data for library SS6003314, from which some of these counts are derived, are available from the European Genome-phenome Archive (EGA; accession EGAD00001000704).
AGL was supported in this work by a Cancer Research UK programme grant [C14303/A20406] to Simon Tavaré.
AGL acknowledges the support of the University of Cambridge, Cancer Research UK and Hutchison Whampoa Limited. Whole-genome sequencing of oesophageal adenocarcinoma was part of the oesophageal International Cancer Genome Consortium (ICGC) project. The oesophageal ICGC project was funded through a programme and infrastructure grant to Rebecca Fitzgerald as part of the OCCAMS collaboration.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
WGS sequencing pipelines for the oesophageal ICGC project are managed by Lawrence Bower.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Competing Interests: No competing interests were disclosed.
References
1. Rosenthal R, McGranahan N, Herrero J, Taylor BS, et al.: DeconstructSigs: delineating mutational processes in single tumors distinguishes DNA repair deficiencies and patterns of carcinoma evolution.Genome Biol. 2016; 17: 31 PubMed Abstract | Publisher Full TextCompeting Interests: No competing interests were disclosed.
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 1 07 Jun 16 |
read | read |
Click here to access the data.
Spreadsheet data files may not format correctly if your computer is using different default delimiters (symbols used to separate values into separate cells) - a spreadsheet created in one region is sometimes misinterpreted by computers in other regions. You can change the regional settings on your computer so that the spreadsheet can be interpreted correctly.
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)