SCODE: A Cytoscape app for supervised complex detection in protein-protein interaction graphs

Sarah Mohamed; Nick Janus; Yanjun Qi

doi:10.12688/f1000research.9184.1

Home Browse SCODE: A Cytoscape app for supervised complex detection in protein-protein...

ALL Metrics

-

Views

-

Downloads

Get PDF

Get XML

Export

▬

✚

Software Tool Article

SCODE: A Cytoscape app for supervised complex detection in protein-protein interaction graphs

[version 1; peer review: 2 approved with reservations]

Sarah Mohamed¹, Nick Janus¹, Yanjun Qi¹

PUBLISHED 14 Jul 2016

Author details Author details

¹ Department of Computer Science, University of Virginia, Charlottesville, USA

OPEN PEER REVIEW

REVIEWER STATUS

This article is included in the Cytoscape gateway.

Abstract

Protein complexes are groups of interacting proteins unified by a common biological function. Identifying complexes amid a network of thousands of interacting proteins poses a difficult computational challenge. Traditional approaches to this problem rely on clique-like topography in order to identify complexes. Supervised learning is an alternative approach that leverages real-valued data in order to extract the features of protein complexes and identify candidates that do not conform to traditional, dense clique structures. SCODE (Supervised Complex Detection), an application for the Cytoscape App Store, implements a supervised learning algorithm for the detection of protein complexes in protein-protein interaction networks.

Keywords

supervised learning, complex, Bayesian network, protein-protein interaction, search

Corresponding author: Yanjun Qi

Competing interests: No competing interests were disclosed.

Grant information: This work was supported by the National Science Foundation under Grant No. 1453580 (awarded to Dr. Yanjun Qi). Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2016 Mohamed S et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Data associated with the article are available under the terms of the Creative Commons Zero "No rights reserved" data waiver (CC0 1.0 Public domain dedication).

How to cite: Mohamed S, Janus N and Qi Y. SCODE: A Cytoscape app for supervised complex detection in protein-protein interaction graphs [version 1; peer review: 2 approved with reservations]. F1000Research 2016, 5:1699 (https://doi.org/10.12688/f1000research.9184.1) First published: 14 Jul 2016, 5:1699 (https://doi.org/10.12688/f1000research.9184.1) Latest published: 14 Jul 2016, 5:1699 (https://doi.org/10.12688/f1000research.9184.1)

Introduction

Protein-protein interaction (PPI) networks provide information about the biochemical relationships in a cell’s molecular machinery. Each node in the network represents a protein, with edges connecting proteins that physically interact with one another. Complexes are clusters of interacting proteins in the network which are together responsible for some biological function. The discovery of complexes in a PPI network has implications in the study of the molecular basis of diseases, drug targets, and biological pathways¹.

Existing tools for complex detection in PPI networks rely on assumptions about a common topography observed among most protein complexes. These tools often assume that protein complexes can be identified based on the density of interactions (edges) among the set of its nodes. As a result, the problem is often reduced to clique detection². While many complexes often take the form of edge-dense protein clusters, this is not the only observed topology. Real-valued data indicate that a variety of other features, including but not limited to edge density, are typical of complexes among PPI networks³.

SCODE, an application for supervised complex detection, seeks to make more informed predictions about potential clusters in PPI networks. It applies supervised learning, a strategy for making predictions based on training data that has already been labeled (as a complex or a non-complex, for example). In order to predict novel complexes, SCODE uses a naive Bayesian classifier to determine the likelihood that potential protein clusters are true complexes.

SCODE allows the user to define a set of features that determine whether a protein cluster forms a complex or not. The probability distribution of this set of features, dependent on whether or not a cluster is a complex, is encoded using naive Bayesian networks. Based on information in the training data, this probability distribution determines which predicted protein clusters conform to the observed features of known complexes. Not only does this identify more qualified candidate complexes, it also provides the user with more autonomy to describe what characteristics are important.

Overall, SCODE performs four major functions: (1) train a Bayesian network, (2) search a PPI graph for candidate complexes, (3) score candidate complexes, and (4) optionally, evaluate the quality of the returned complexes. Figure 1 illustrates the pipeline of these functions in SCODE.

Figure 1. SCODE’s pipeline, with direct arrows demonstrating links from one stage of the procedure to the next, and a dashed arrow indicating the implicit relationship between training the Bayesian network and the scoring function.

Methods

Search

The search algorithm uses a form of iterative simulated annealing in which complexes are expanded to include neighboring proteins at each cycle. The user may specify a set of "seed" proteins from which to begin the search, or allow the program to randomly select a set of starting nodes.

Beginning from each of the seed proteins, the program iteratively performs the following steps:

1. Maintain a record of the neighbor that produces the highest score when added to the complex. For each neighbor of the seed:
- (a) Calculate the complex score if the neighboring protein is added
- (b) If the complex score exceeds the record, then update the record’s value
2. If the record exceeds the current score of the complex, then add the associated protein to the complex
3. If the record does not exceed the current score of the complex, then calculate the probability of adding the protein to the complex as a function of the score and the temperature. SCODE then adds the protein to the complex with probability as follows: P(exp(Record – Score(complex))/Temperature)

Three variations on this algorithm are available: iterative simulated annealing (ISA), greedy iterative simulated annealing (Greedy ISA), and sorted-neighbor iterative simulated annealing (Sorted-Neighbor ISA). In ISA, at each iteration a node is randomly selected from the neighbors of the candidate complex and scored in order to determine if it should be kept in the complex. Greedy ISA scores all neighbors of the candidate complex and retains only the best one (or none, if no neighbors improve the score). Sorted-Neighbor ISA sorts the neighbors of the complex by degree and evaluates the top N neighbors (N is a parameter set by the user).

Scoring

SCODE offers two scoring options to the user. The first does not perform learning, while the second option does (by training a Bayesian model).

The first scoring option performs a simple calculation based on the mean weight among edges in the proposed protein cluster. It does not require any information regarding known complexes and does not perform learning. This option may be used as a reference for comparing the complexes produced by the second scoring method.

The second scoring option, relying on supervised learning, calculates scores using a likelihood equation that is generated based on a trained Bayesian network. It reflects the conditional probability distribution that each feature is demonstrated in a complex versus the distribution for a non-complex. The sample Bayesian network from Figure 2 would use the following calculation to determine the likelihood that a candidate protein cluster, x, represents a true complex, given the prior probability that x is a complex (P(x₁)) or a non-complex (P(x₀)):

L i k e l i h o o d_{x} = log \frac{(P (D e n s i t y_{x} | x_{1}) P (M a x D e g r e e_{x} | x_{1}) P (x_{1})}{(P (D e n s i t y_{x} | x_{0}) P (M a x D e g r e e_{x} | x_{0}) P (x_{0})}

Figure 2. A simple Bayesian template with two independent features given the root node.

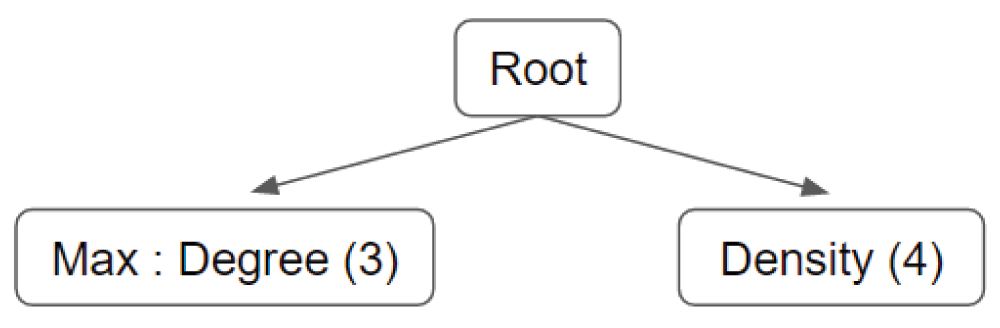
The root indicates whether the candidate cluster is a complex or not.

Here P(f₁|x₁) denotes the conditional probability that feature f₁ is observed given that x is a complex (x₁). P(f₁|x₀) indicates the conditional probability that feature f₁ is observed given that x is not a complex (x₀). This equation may be extended to any naive Bayesian network, with f₁…f_n representing the features of the model:

L i k e l i h o o d_{x} = log \frac{P (f_{1} | x_{1}) P (f_{2} | x_{1}) ... P (f_{n} | x_{1}) P (x_{1})}{P (f_{1} | x_{0}) P (f_{2} | x_{0}) ... P (f_{n} | x_{0}) P (x_{0})} (1)

Training

Bayesian networks (BNs) are directed acyclic graphs (DAGs) that describe the conditional dependency relationships among a set of nodes representing random variables. In SCODE, Bayesian networks are used to describe the joint probability distribution of the features describing complexes, as well as the joint probability distribution of the features describing non-complexes in the PPI graph. After training the networks to calculate each of the conditional probabilities in Equation 1, these networks are used to score complexes that are discovered during the search phase.

A feature describes a particular property of a candidate complex, such as size or density. Each node in the trained Bayesian model represents a discrete value, or subset of values, of a feature. For example, a binary feature is represented in the trained model using two nodes, with one node for each of its two possible values. A feature with continuous values is discretized by subdividing its range into a set of equally-sized bins. This representation of the Bayesian model allows the conditional probability of each discrete value (or range of values) of a feature to be stored in the Cytoscape network as an edge table attribute. However, as Figure 3 demonstrates, this structure is incredibly verbose and requires multiple nodes to separate the bins for a single feature. We instead provide a simpler way for users to design a Bayesian template (an example is shown in Figure 2).

Figure 3. Representation of the Bayesian networks produced after training in SCODE.

Users may define custom Bayesian templates using Cytoscape’s native graph-building or importing tools. These templates must use a specialized syntax for naming nodes, wherein each node other than the root (labeled ‘Root’) specifies a feature. The syntax for a feature is as follows:

Statistic : Feature (Bins)

"Statistic" is an optional prefix that indicates an operation to perform on the values of a feature (such as taking the max, mean, or median). A statistic must be applied to a feature that produces a list of values rather than a singular value. Applying the statistic results in a single floating-point value, which may then be assigned to the appropriate bin. The available statistics include: Mean, Median, Count, and ordinals such as 1st, 2nd, 3rd, etc.

For example, Figure 2 illustrates a simple Bayesian network with two features that are conditionally independent given the root node. The feature labeled "density" may have continuous values in the range (0, 1], divided equally among 4 bins. In the second feature, "degree" represents the number of neighbors of each node in a candidate cluster. Applying the "max" statistic produces the highest degree among all the nodes in a cluster. The range of this feature is (0, n], where n is the highest degree of any node in the positive training data.

Once its features are defined, the template is trained using a set of user-provided positive training complexes and a set of randomly-generated negative training clusters. First, two nearly-identical representations of the Bayesian template are created, with the root node of the first labeled ‘Root Cluster’ and the root node of the second labeled ‘Root Non-Cluster’. A separate node is then created for each bin of each feature, resulting two networks whose respective sizes are, identically, the sum of the number of bins for each feature plus the root node. Figure 3 illustrates the two networks produced after training the template in Figure 2.

The positive Bayesian network (‘Root Cluster’) is trained using the positive complexes provided by the user, and the negative Bayesian Network (‘Root Non-Cluster’) is trained using the randomly-generated negative protein clusters. In both training procedures, the program records the frequency at which the values representing each node in the Bayesian network are encountered among the training clusters; this translates to the frequency for each feature bin.

By the end of training, the node frequencies are used to encode the conditional probabilities, P(f_b|RootCluster) and P(f_b|RootNon − Cluster) for bin b of feature f, as follows:

P (f_{b} | R o o t) = \frac{C o u n t_{f_{b}} + 1}{T o t a l N u m b e r O f C l u s t e r s + T o t a l N u m b e r O f B i n s_{f}} (2)

We may then use Equation 1 to produce a log-likelihood score for a candidate cluster based on the conditional probability of each feature bin in both the positive and negative Bayesian networks. Conditional probabilities on the root node are maintained as properties of the edges in the returned Cytoscape network, which represents both halves of the trained Bayesian model; in doing so, trained models may be saved and recycled for later use in Cytoscape session files.

Evaluation

The search phase returns a set of predicted complexes and their associated likelihood scores, which may be visualized and analyzed independently using Cytoscape tools. SCODE also provides a tool for evaluating discovered complexes against a user-provided set of known complexes in the network, allowing the program to quantify its overall performance.

To perform the evaluation, the user must supply a file containing a list of complexes known to exist in the PPI graph. These complexes may include the positive examples used to train the Bayesian network, but they will be filtered out when calculating the evaluation score.

The evaluation provides two metrics: recall and precision. Recall measures the ability of the program to discover complexes from the known set, while precision measures the accuracy of the discovered complexes.

When comparing a predicted complex against a known complex,

• Let A be the number of proteins only in the predicted complex
• Let B be the number of proteins only in the known complex
• Let C be the number of proteins in both the predicted and the known complex

A predicted complex is said to have identified a known complex³ if

\frac{C}{A + C} > p and \frac{C}{B + C} > p (3)

Here p is a hyperparameter specified by the user. Recall and precision are calculated as follows:

Recall = \frac{Num Known complexes identified}{Total num known complexes}

P r e c i s i o n = \frac{Num predicted that recover Known}{Total num predicted}

Implementation

SCODE is organized among three packages. The statistic package contains implementations of the abstract class ’Statistic’, which specifies methods for operating on a list of feature values and calculating the overall range of those values for binning. A second package, feature, contains implementations of the abstract FeatureSet class. FeatureSet specifies methods for getting feature values, applying statistics to them, and returning the bins for a complex. The list of statistics that is applied to a feature is stored as a protected member of the FeatureSet class.

The third package contains the remaining code for gathering input and executing the search, scoring, and training tasks. The entry point to SearchTask and TrainingTask creation is in SupervisedComplexTaskFactory. TrainingTask initiates the process of loading the appropriate template network or trained model network, which is then used to create the internal representation of the Bayesian network in the SupervisedModel class. SupervisedModel represents both the positive and negative Bayesian graphs via the Graph class, which also specifies methods for training the graph and scoring candidate complexes during search.

From the initial searchTask, an IsaSearch object is created to divide the starting nodes among separate threads and to begin searching on each one. The core search algorithm is located in the SeedSearch class, where candidate complexes are expanded and scored. Complexes are represented internally as Cluster objects and returned as CySubNetworks once the search has been completed.

Operation

Taking advantage of its new modular architecture, SCODE requires Cytoscape version 3.2 or above to operate. Upon launch, SCODE accepts user input and displays a summary of the results from the SCODE tab in the Control Panel. Mirroring its pipeline, SCODE’s interface is divided into subsections for each of the search, scoring, training, and evaluation tasks.

The user may adjust the following input parameters for the search stage:

• Variation of Simulated Annealing : The program offers three variants of the Iterative Simulated Annealing algorithm: ISA, Sorted-Neighbor ISA, and Greedy ISA.
- ISA : Fastest performance but tends to produce low-scoring complexes.
- Greedy ISA : Slower than ISA, but tends to produce more, larger, higher-scoring candidate complexes.
- Sorted-Neighbor ISA : Slower than ISA and sometimes slower than Greedy ISA, depending on the density of the PPI graph. Tends to produce higher scoring complexes.
• Search Limit : Specifies the maximum number of iterations of the search.
• Initial Temperature : Sets the starting temperature of the search. Higher temperature increases the likelihood that a protein will be added to the complex.
• Temperature Scaling Factor : The rate at which the temperature decreases over time.
• Overlap Limit : The maximum proportion of nodes that two distinct complexes may share.
• Use Seeds From File : Optional; the user may select an external file containing a list of seed nodes from which to begin the search.
• Number of Random Seeds : Allows the program to randomly select the specified number of seed nodes.
• Number of Results to Display : The number specified here will be the number of results visible at the end of the search.

The scoring section accepts the following parameters:

• Minimum Complex Score : When the results are shown to the user, only candidate complexes with scores equal to or greater than this input will be displayed.

The training section accepts the following parameters:

• Cluster Probability Prior : The prior probability, P(x₁), that a group of proteins forms a complex.
• Generate Negative Examples : Specifies the number of negative training examples that the program will randomly generate.
• Ignore Missing Nodes : During training, if one of the proteins in a positive training example cannot be found in the PPI network, selecting this option will allow the program to disregard the training example.

The training section takes additional input parameters relating to the Bayesian network. The first set of parameters specifies the Bayesian network itself. The user may either use a default model provided by the application, or a custom Bayesian network that has been constructed using Cytoscape. The custom network may be either trained or untrained; in the latter case, the user must provide an input file containing a set of known complexes that will be used to train the model. Trained models can be saved and loaded from Cytoscape session files, which store networks for later use.

SCODE includes a number of predefined features for building Bayesian templates, enumerated below. The features of the built-in Bayesian template are provided in Table 2, but are not exhaustive. In the following descriptions, G indicates a PPI graph with edges, E, and nodes, N:

• Complex Size : Takes the length of a list of complexes of size |N|.
• Clustering Coefficient : How many triangles contain the node n as a vertex. Calculated using the equation CC_n = 2e_k/(k_n * (k_n − 1)), where k_n is the number of neighbors of n and e_k is the number of edges between those neighbors.
• Degree : For a node in N, the number of edges connected to that node.
• Degree Correlation : For a node in N, the average number of neighbors among its adjacent nodes.
• Density : The ratio of the number of observed edges to the number of possible edges in G: D = |E|/|Ep|.
• Density at Cutoff : The same as above, once edges with a weight below the cutoff are removed from the set of observed edges.
• Edge Weight : A measure of the strength of the interaction between a pair of nodes. Must be provided as an edge table column in the PPI network.
• Edge Table Column : Produces a vector of values from a Cytoscape graph table’s column for each edge in the graph.
• Edge Table Correlation : Produces a set of vectors from a set of columns in a Cytoscape table and returns a list containing the correlation coefficients for each pair of vectors.
• Node Table Column : The same as the edge table feature, but applied to each node.
• Node Table Correlation : The same as the edge table correlation feature, but applied to nodes.
• Singular Values : The singular values for each graph correspond to the graph’s shape. For instance, A linear graph’s values will consistently differ from those of a clique.
• Topological Coefficient : For a node n, the topological coefficient measures the connectivity of n’s neighbors, where f (a, b) is the number of neighbors in common between neighbors a and b, while k_n is the number of neighbors: TC_n = avg(f (a, b))/k_n

Use cases

Dataset 1.Demo Using CYC2008 and TAP06 Complexes.

This demo includes the following files: CYC2008 complexes for training/testing, TAP06 complexes for training/testing, a PPI graph, and a Cytoscape session file (.cys) pre-loaded with the PPI graph. Please see ‘data description.txt’ for a description of the files.

We demonstrate the app using training/evaluation datasets constructed from two sources: the CYC2008 catalogue of manually curated protein complexes⁴, and the TAP06 dataset of complexes screened using affinity purification and mass spectrometry⁵, which were each filtered to a random sampling of 50 complexes with 4–6 nodes. Both files are supplied in a tab-separated format.

The graph on which search is performed features 396 proteins (those featured among the CYC2008 and TAP06 complexes) and 5141 edges. The set of interactions in this graph is generated from the STRING database of known and predicted protein-protein interactions⁶. The graph is also in tab-separated format and must be loaded into Cytoscape as a network; the network may then be saved in a session file (.cys) for later use. All of the data used in this demonstration can be found online and is provided below under ‘Data Availability’.

At the end of the search, discovered complexes will be returned as Cytoscape networks under the ‘Network’ tab in the Control Panel.

Search parameters

For this demonstration, we employ the parameters shown in Figure 4. The number of random seeds matches the number of nodes in the graph. This number, to some degree, dictates the likelihood of identifying complexes of good quality. With a low starting seed count in a large PPI graph, the probability of beginning the search from a protein that is a member of a "true" complex is low. For the purposes of our evaluation, we provide the ideal conditions for the search to return true complexes. This includes using Greedy ISA so that all nodes neighboring a complex are scored before selecting one for expansion.

Figure 4. Parameters used to search the PPI graph.

Training parameters

We choose to employ the built-in Bayesian template for training, with features shown in Table 1. Since the PPI graph is under 500 nodes, we use a prior probability of 0.5 for clusters, and generate 50 negative examples. Two rounds of training and search are performed, the first using the abridged set of CYC2008 complexes for training and the TAP06 complexes for evaluation, and the second using the reverse (with all other parameters held constant). The minimum complex score is set to 0.

Table 1. Features of the built-in Bayesian template.

Feature	Bins
Mean : Degree	4
Variance : Degree	4
Max : Degree	4
Median : Degree	4
Mean : Weight	4
Variance : Weight	4
Count : Node	5
Density at Cutoff [1.0, 1.2, 1.5, 1.8, 2.2, 2.6, and 3.0]	6
Density	4
Mean : Degree Correlation	4
Variance : Degree Correlation	4
Max : Degree Correlation	4
Mean : Clustering Coefficient	3
Variance : Clustering Coefficient	3
Max : Clustering Coefficient	3
Mean : Topological Coefficient	3
Variance : Topological Coefficient	3
Max : Topological Coefficient	3
1st : Singular Value	4
2nd : Singular Value	2
3rd : Singular Value	2

Evaluation

Once the search is complete, the top M results (specified under the search parameters) are displayed under the ‘Network’ tab in the Cytoscape Control Panel. All protein clusters produced by the search, including but not limited to those displayed, are considered during evaluation. The Evaluation section appears directly below the Scoring section after ‘Analyze Network’ is clicked (Figure 6).

Figure 5. Parameters used to select a scoring option and train the Bayesian template.

Figure 6. Parameters used to evaluate the search results.

We supply p=0.5 for Equation 3, such that all predicted complexes with a majority of proteins from a known testing complex are said to have "recovered" that complex. After clicking "Evaluate Results", the evaluation scores for recall and precision appear in a dialog (Figure 7).

Figure 7.

Evaluation scores using CYC2008 to train and TAP06 to test (a) or TAP06 to train and CYC2008 to test (b).

Summary

SCODE expands the detection of protein complexes in weighted PPI networks by applying a supervised learning algorithm with a set of known training complexes. Users may discover topologically non-traditional protein complexes by leveraging more information about the features of its PPI graph. The Bayesian network encodes the desired characteristics of complexes beyond density and is used to score the likelihood that a candidate discovered during a search of the PPI network represents a complex. Each version of the ISA search heuristic discovers complexes of varying quality and size, in accordance with the degree to which the algorithm exhausts the search space.

Data availability

F1000Research: Dataset 1. Demo Using CYC2008 and TAP06 Complexes, 10.5256/f1000research.9184.d128878⁸

Software availability

1. Software available from:
http://apps.cytoscape.org/apps/scode
2. Latest source code: https://github.com/DataFusion4NetBio/Paper16-SCODE
3. Archived source code as at time of publication: http://dx.doi.org/10.5281/zenodo.57163⁹
4. Software license: MIT License (https://opensource.org/licenses/MIT)

Author contributions

YQ conceived of, funded, and supervised the project. NJ and SM implemented the app. SM, NJ, and YQ authored this article.

Competing interests

No competing interests were disclosed.

Grant information

This work was supported by the National Science Foundation under Grant No. 1453580. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.

The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Acknowledgements

We thank Leonard Ramsey of the University of Virginia for his feedback and assistance in improving the functionality and supporting documentation of the app.

Faculty Opinions recommended

References

1. Ideker T, Sharan R: Protein networks in disease. Genome Res. 2008; 18(4): 644–652. PubMed Abstract | Publisher Full Text | Free Full Text
2. Bader GD, Hogue CW: An automated method for finding molecular complexes in large protein interaction networks. BMC Bioinformatics. 2003; 4: 2. PubMed Abstract | Publisher Full Text | Free Full Text
3. Qi Y, Balem F, Faloutsos C, et al.: Protein complex identification by supervised graph local clustering. Bioinformatics. 2008; 24(13): i250–i268. PubMed Abstract | Publisher Full Text | Free Full Text
4. Pu S, Wong J, Turner B, et al.: Up-to-date catalogues of yeast protein complexes. Nucleic Acids Res. 2009; 37(3): 825–31. PubMed Abstract | Publisher Full Text | Free Full Text
5. Gavin AC, Aloy P, Grandi P, et al.: Proteome survey reveals modularity of the yeast cell machinery. Nature. 2006; 440(7084): 631–6. PubMed Abstract | Publisher Full Text
6. Szklarczyk D, Franceschini A, Wyder S, et al.: STRING v10: protein-protein interaction networks, integrated over the tree of life. Nucleic Acids Res. 2015; 43(Database issue): D447–52. PubMed Abstract | Publisher Full Text | Free Full Text
7. Mewes HW, Frishman D, Gruber C, et al.: MIPS: a database for genomes and protein sequences. Nucleic Acids Res. 2000; 28(1): 37–40. PubMed Abstract | Publisher Full Text | Free Full Text
8. Mohamed S, Janus N, Qi Y: Dataset 1 in: SCODE: A Cytoscape app for supervised complex detection in protein-protein interaction graphs. F1000Research. 2016. Data Source
9. Mohamed S, Janus N, Qi Y, et al.: SCODE: Supervised Complex Detection. Zenodo. 2016. Data Source

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 14 Jul 2016

Author details Author details

¹ Department of Computer Science, University of Virginia, Charlottesville, USA

Competing interests

No competing interests were disclosed.

Grant information

This work was supported by the National Science Foundation under Grant No. 1453580 (awarded to Dr. Yanjun Qi). Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (1)

version 1

Published: 14 Jul 2016, 5:1699

https://doi.org/10.12688/f1000research.9184.1

Copyright

© 2016 Mohamed S et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Data associated with the article are available under the terms of the Creative Commons Zero "No rights reserved" data waiver (CC0 1.0 Public domain dedication).

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

Mohamed S, Janus N and Qi Y. SCODE: A Cytoscape app for supervised complex detection in protein-protein interaction graphs [version 1; peer review: 2 approved with reservations]. F1000Research 2016, 5:1699 (https://doi.org/10.12688/f1000research.9184.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 1

VERSION 1

PUBLISHED 14 Jul 2016

Views

4

Reviewer Report 04 Apr 2017

T.M. Murali, Department of Computer Science, Virginia Tech, Blacksburg, VA, USA

Approved with Reservations

https://doi.org/10.5256/f1000research.9883.r20480

4th April 2017: This referee report was mistakenly published with a Not Approved status - we have now corrected this to the intended Approved with Reservations.

The manuscript present a Cytoscapp app called SCODE for supervised detection ... Continue reading

4th April 2017: This referee report was mistakenly published with a Not Approved status - we have now corrected this to the intended Approved with Reservations.

The manuscript present a Cytoscapp app called SCODE for supervised detection of protein complexes. In principle, the motivation of the work is strong: learning the features of known complexes in a protein interaction network is a viable strategy to compute new complexes. However, the manuscript requires a significant amount of revision.

The authors motivate the usefulness of supervised learning of complexes by saying that the problem is often reduced to clique detection. They are considerably simplifying the literature in making this claim, since there are literally dozens of algorithms for computing protein complexes in protein networks and they cite only one publication (the MCODE paper) to support the claim.

The authors claim that "Real-valued data indicate that a variety of other features, including but not limited to edge density, are typical of complexes among PPI networks." In support, they cite an earlier paper from 2008 (citation 5). In citation 5, the authors of that paper show a few example of complexes that are not-cliques. It is possible that algorithms developed since 2008 may compute such subgraphs. This manuscript will be improved if the authors provide some more recent and updated data to support the claim.

It is unclear how the SCODE algorithm differs from the method published in citation 5. The manuscript should clarify if the two methods differ in any essential features or if this manuscript focuses on presenting a Cytoscape app that implements the method from citation 5.

In either case, the precision of SCODE is very low (around 0.1) when the recall is around 0.5. The manuscript will be much improved by a quantitative comparison to other algorithms (supervised or not) in terms of its precision and recall.

A difficulty that a user of the SCODE app will find is that it has a surfeit of parameters. When faced with so many choices, a user is likely to settle for the defaults without knowledge of whether these values will lead to good results or not. The usability of the app can be dramatically improved by decreasing the number of parameters and providing some guidelines to the user on how to tune them for a particular dataset. In the section on "Search parameters", the authors do state "For the purposes of our evaluation, we provide the ideal conditions for the search to return true complexes." They should explain how they determined that these parameters provide ideal conditions to find true complexes.

The descriptions of some features are confusing and unclear. For example, "Complex size" is "Takes the length of a list of complexes of size |N|." Do the authors mean that the feature is for a complex c, the number of proteins in c? They use this type of language for features such as degree and clustering coefficient. In the definition of density, what is Ep? What are the values in "Edge Table Column"? What are the singular values of a graph? How do the authors compute them? What is their biological meaning?

More generally, some features are defined for nodes, some for edges, some for pairs of nodes, some for the entire graph. It will be helpful to group them by this categorization and explain how the different types of features fit into the training framework.

Competing Interests: No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Respond or Comment

Views

12

Reviewer Report 28 Nov 2016

Narayanaswamy Srinivasan, Molecular Biophysics Unit, Indian Institute of Science, Bangalore, India

Approved with Reservations

https://doi.org/10.5256/f1000research.9883.r16428

Authors employ a supervised learning algorithm for prediction of protein complexes from protein-protein interaction networks. This manuscript requires considerable work. I am listing what I think as most crucial points for authors to work on:

The

Authors employ a supervised learning algorithm for prediction of protein complexes from protein-protein interaction networks. This manuscript requires considerable work. I am listing what I think as most crucial points for authors to work on:

The input to the proposed development is protein-protein interaction network. This information usually comes from laboratory studies. While there is always an element of accuracy and completeness associated with the data, once a network is constructed what are the protein assemblies within the network is intuitively obvious. Why do we need a development such as the one proposed in this manuscript? Where is the question of “prediction” of assemblies? – the interaction information is already firmly coded in the network and information on assemblies is part of construction of the network. This is a fundamental and serious problem authors must address.
Authors have come up with a computational development. But there is no assessment on how well the method works.
There is no application shown using a protein-protein interaction network.
Manuscript reads too technical with too much jargon.
Figures could be lot more informative. For example the two parts of Figure 3 are extremely similar and the message from the figure is not clear.

Competing Interests: No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Respond or Comment

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 14 Jul 2016

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 1 14 Jul 16	read	read

Narayanaswamy Srinivasan, Indian Institute of Science, Bangalore, India
T.M. Murali, Virginia Tech, Blacksburg, USA

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

Back to all reports

Reviewer Report

4 Views

04 Apr 2017 | for Version 1

T.M. Murali, Department of Computer Science, Virginia Tech, Blacksburg, VA, USA

4 Views Cite this report Responses(0)

Approved With Reservations

4th April 2017: This referee report was mistakenly published with a Not Approved status - we have now corrected this to the intended Approved with Reservations.

The manuscript present a Cytoscapp app called SCODE for supervised detection of protein complexes. In principle, the motivation of the work is strong: learning the features of known complexes in a protein interaction network is a viable strategy to compute new complexes. However, the manuscript requires a significant amount of revision.

The authors motivate the usefulness of supervised learning of complexes by saying that the problem is often reduced to clique detection. They are considerably simplifying the literature in making this claim, since there are literally dozens of algorithms for computing protein complexes in protein networks and they cite only one publication (the MCODE paper) to support the claim.

The authors claim that "Real-valued data indicate that a variety of other features, including but not limited to edge density, are typical of complexes among PPI networks." In support, they cite an earlier paper from 2008 (citation 5). In citation 5, the authors of that paper show a few example of complexes that are not-cliques. It is possible that algorithms developed since 2008 may compute such subgraphs. This manuscript will be improved if the authors provide some more recent and updated data to support the claim.

It is unclear how the SCODE algorithm differs from the method published in citation 5. The manuscript should clarify if the two methods differ in any essential features or if this manuscript focuses on presenting a Cytoscape app that implements the method from citation 5.

In either case, the precision of SCODE is very low (around 0.1) when the recall is around 0.5. The manuscript will be much improved by a quantitative comparison to other algorithms (supervised or not) in terms of its precision and recall.

A difficulty that a user of the SCODE app will find is that it has a surfeit of parameters. When faced with so many choices, a user is likely to settle for the defaults without knowledge of whether these values will lead to good results or not. The usability of the app can be dramatically improved by decreasing the number of parameters and providing some guidelines to the user on how to tune them for a particular dataset. In the section on "Search parameters", the authors do state "For the purposes of our evaluation, we provide the ideal conditions for the search to return true complexes." They should explain how they determined that these parameters provide ideal conditions to find true complexes.

The descriptions of some features are confusing and unclear. For example, "Complex size" is "Takes the length of a list of complexes of size |N|." Do the authors mean that the feature is for a complex c, the number of proteins in c? They use this type of language for features such as degree and clustering coefficient. In the definition of density, what is Ep? What are the values in "Edge Table Column"? What are the singular values of a graph? How do the authors compute them? What is their biological meaning?

More generally, some features are defined for nodes, some for edges, some for pairs of nodes, some for the entire graph. It will be helpful to group them by this categorization and explain how the different types of features fit into the training framework.

Competing Interests

No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

12 Views

28 Nov 2016 | for Version 1

Narayanaswamy Srinivasan, Molecular Biophysics Unit, Indian Institute of Science, Bangalore, India

12 Views Cite this report Responses(0)

Approved With Reservations

Authors employ a supervised learning algorithm for prediction of protein complexes from protein-protein interaction networks. This manuscript requires considerable work. I am listing what I think as most crucial points for authors to work on:

The input to the proposed development is protein-protein interaction network. This information usually comes from laboratory studies. While there is always an element of accuracy and completeness associated with the data, once a network is constructed what are the protein assemblies within the network is intuitively obvious. Why do we need a development such as the one proposed in this manuscript? Where is the question of “prediction” of assemblies? – the interaction information is already firmly coded in the network and information on assemblies is part of construction of the network. This is a fundamental and serious problem authors must address.
Authors have come up with a computational development. But there is no assessment on how well the method works.
There is no application shown using a protein-protein interaction network.
Manuscript reads too technical with too much jargon.
Figures could be lot more informative. For example the two parts of Figure 3 are extremely similar and the message from the figure is not clear.

Competing Interests

No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

Respond to this report

Responses (0)

[1] 1. Ideker T, Sharan R: Protein networks in disease. Genome Res. 2008; 18(4): 644–652. PubMed Abstract | Publisher Full Text | Free Full Text

[2] 2. Bader GD, Hogue CW: An automated method for finding molecular complexes in large protein interaction networks. BMC Bioinformatics. 2003; 4: 2. PubMed Abstract | Publisher Full Text | Free Full Text

[3] 3. Qi Y, Balem F, Faloutsos C, et al.: Protein complex identification by supervised graph local clustering. Bioinformatics. 2008; 24(13): i250–i268. PubMed Abstract | Publisher Full Text | Free Full Text

[4] 4. Pu S, Wong J, Turner B, et al.: Up-to-date catalogues of yeast protein complexes. Nucleic Acids Res. 2009; 37(3): 825–31. PubMed Abstract | Publisher Full Text | Free Full Text

[5] 5. Gavin AC, Aloy P, Grandi P, et al.: Proteome survey reveals modularity of the yeast cell machinery. Nature. 2006; 440(7084): 631–6. PubMed Abstract | Publisher Full Text

[6] 6. Szklarczyk D, Franceschini A, Wyder S, et al.: STRING v10: protein-protein interaction networks, integrated over the tree of life. Nucleic Acids Res. 2015; 43(Database issue): D447–52. PubMed Abstract | Publisher Full Text | Free Full Text

[7] 7. Mewes HW, Frishman D, Gruber C, et al.: MIPS: a database for genomes and protein sequences. Nucleic Acids Res. 2000; 28(1): 37–40. PubMed Abstract | Publisher Full Text | Free Full Text

[8] 8. Mohamed S, Janus N, Qi Y: Dataset 1 in: SCODE: A Cytoscape app for supervised complex detection in protein-protein interaction graphs. F1000Research. 2016. Data Source

[9] 9. Mohamed S, Janus N, Qi Y, et al.: SCODE: Supervised Complex Detection. Zenodo. 2016. Data Source

SCODE: A Cytoscape app for supervised complex detection in protein-protein interaction graphs

Abstract

Keywords

Introduction

Figure 1. SCODE’s pipeline, with direct arrows demonstrating links from one stage of the procedure to the next, and a dashed arrow indicating the implicit relationship between training the Bayesian network and the scoring function.

Methods

Search

Scoring

Figure 2. A simple Bayesian template with two independent features given the root node.

Training

Figure 3. Representation of the Bayesian networks produced after training in SCODE.

Evaluation

Implementation

Operation

Use cases

Search parameters

Figure 4. Parameters used to search the PPI graph.

Training parameters

Table 1. Features of the built-in Bayesian template.

Evaluation

Figure 5. Parameters used to select a scoring option and train the Bayesian template.

Figure 6. Parameters used to evaluate the search results.

Figure 7.

Summary

Data availability

Software availability

Author contributions

Competing interests

Grant information

Acknowledgements

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

The problem

How to fix it

Competing Interests Policy

Stay Updated