Keywords
Tumour heterogeneity, diffusion, random-effects, MCMC, Markov chain Monte Carlo, Bayesian, spatial statistical modelling
This article is included in the University College London collection.
Tumour heterogeneity, diffusion, random-effects, MCMC, Markov chain Monte Carlo, Bayesian, spatial statistical modelling
Numerous investigations have demonstrated a surprising level of intra-tumour heterogeneity in a variety of cancers1–3. In particular, a picture is emerging in which intra-tumour genetic regional differences can be as great as those observed between cases. It has become widely accepted that spatial heterogeneity underlies the tumour evolutionary process itself. Thus, tumour growth is conceived as a Darwinian process in which spatially heterogeneous mutations occur. The implications are enormous, and intra-tumour heterogeneity poses challenges and questions for those searching for effective treatments. For example, it has been suggested that drug resistance is an inevitable consequence of intra-tumour genetic diversity, and that the presence of many different genomes increases the probability that a particular population of cells develop resistance. It is also suggested that a given drug might kill a majority of tumour cells, leaving those that are resistant to become dominant in a Darwinian-like selection processes. Thus, according to this proposition, selection is driven by the treatment itself. Furthermore, clinical decision making and patient management based on a standard biopsy must be questionable and the very notion of personalised medicine might be a greater challenge than initially conceived. The realisation that treatment can drive the evolutionary process might indicate a need to revise current treatment strategies4.
Many papers have appeared in the biomedical imaging literature dealing with tumour spatial heterogeneity and proposing a variety of methods for characterising the resulting distributions. Quantile estimates are commonly used for this purpose, but a variety of other methods have been adopted including, for example, measures based on the departure of the observed data from a simple idealised spatial structure5 and functional principal components analysis6. A key feature of the majority of these analyses is their two-stage nature in which voxel-by-voxel parameter estimates are derived from the image data, followed by a second-stage analysis of the resulting parameter distribution. The present paper outlines a single-stage approach to characterising tumour heterogeneity in DWI images based on so-called random effects modelling. A key feature of the method is that a formal spatial model is included in the statistical procedure used to extract the diffusion parameter estimates from the signal intensity data. In fact, given the paucity of the DWI data used in the present analyses, the spatial random effects treatment is an indispensable component of the estimation method.
A key tenet underlying the application of diffusion MRI (dMRI) to cancer patient management is the notion that the apparent diffusion coefficient (ADC) is a surrogate marker of altered cellularity. Despite numerous investigations into the relationship between cellularity and MRI surrogate markers7–14 several issues remain to be resolved. One might question whether positive tests of association, including correlation coefficient tests, are sufficient to justify the surrogate-marker claim. A relatively weak relationship can be sufficient to yield a statistically significant test result. It might be argued that the requirements of a biomarker/surrogate marker should meet the criteria of a surrogate endpoint in clinical trials (see, for example, 15). Secondly, some of the published evidence is based on statistical models that might be judged inadmissible. Furthermore, some researchers use p-values as the sole supporting evidence of biomarker validity. Although p-values may provide a measure of the strength of evidence (recognising that this contravenes the rules governing the frequentist approach to statistical inference), a p-value does not provide a measure of the strength of the effect/association under consideration (see, for example, 16). Among the complications is the p-value dependence on sample size. Moreover, the p-value provided by an association test does not address the key issues of specificity and sensitivity.
Working under the assumption that the ADC is a valid surrogate marker of cellularity, researchers have focussed on a variety of tumour ADC measures, including various global spatial heterogeneity and dispersion/distribution indicators (see, for example 9 or 17). Some have examined the spatial dependence of the ADC in the vicinity of the tumour boundary (see, for example, 14, or 17) while others have focussed their efforts on the elucidation of the underlying causes of the diffusion changes11,18, or have adopted an entirely empirical approach and examined the relationship between survival and one or other DWI measure19–22. The latter studies aim to address the central clinical issue and provide a direct answer to the fundamental question regarding the prognostic/diagnostic value of dMRI. This literature provided the motivation for the present statistical modelling work. Although the mechanistic basis of the ADC changes that occur during tumour development may remain elusive, this does not preclude the possibility that dMRI might have the potential to provide a useful prognostic indicator. In keeping with this empirical approach, the present study was undertaken to develop a formal statistical modelling procedure for tumour DWI spatial heterogeneity estimation. The main focus is robust voxel-specific ADC estimation and an examination of the ADC dependence on distance from the tumour boundary. This is prompted by a number of reports indicating that some tumours exhibit a boundary-distance dependence in ADC, the magnitude of which might carry prognostic information14,17,22. In particular, we examine the magnitude and significance of the boundary-distance effect that remains after simultaneously adjusting for an underlying random 2D heterogeneity in ADC. In addition, heterogeneity in the boundary region is compared with that in the core. As stated above, this is based on the premise that empirical measures might provide useful prognostic information in the absence of an understanding of the mechanistic basis of the spatial variation and temporal changes in diffusion that have been observed to occur in a variety of tumours.
The tumour heterogeneity analysis outlined in this paper is based on a Bayesian spatial random effects (random coefficients) analysis of paediatric DWI data. Key to this approach is the provision of robust estimates of the voxel-specific diffusion parameters, as required to obtain reliable measures of spatial heterogeneity. The random coefficient estimates are expected to be more robust than the voxel-specific parameter estimates provided by an independent-voxels (separate voxel-by-voxel) analysis. In common with all Bayesian analyses, prior distributions are a central part of the statistical model. These provide a formal mechanism for incorporating existing information and model assumptions. In the present study Markov random field prior distributions were adopted for a number of parameters, including the voxel-specific anisotropic diffusion coefficients, as outlined below and in the Methods section. The reason why Bayesian random effect models have the potential to provide improved parameter estimates, relative to those given by an independent-voxels analysis, is because they make good use of the available data through so-called information borrowing. In the present context, the signal behaviour in adjacent voxels influences the parameter estimates obtained for each voxel under consideration. Formal borrowing of information across a region and the resulting improvement in estimation is mediated via the prior distributions that are assigned to each model parameter. Restated, the distributional priors underlie the information borrowing that is key to random effects modelling. (The distributional assumptions required to construct an hierarchical random effects model are priors, by definition, regardless of the analytical framework, be it frequentist or Bayesian.) The resulting estimators are referred to as shrinkage estimators, the aim being to provide some shrinkage towards the typical behaviour, and thus achieve some level of smoothing. Specifically, shrinkage refers to the condition where more extreme estimates are pulled towards more typical values, as determined by the distribution characteristics (spatial correlation structure in the present application) of the ensemble of units (voxels in the present study) under consideration. More robust estimates of the underlying and unknown parameters are thus obtained, improving on those that might be derived from an independent units (isolated voxel-by-voxel) analysis. Necessarily, one accepts a trade-off between bias and improved variance. Nevertheless, in any situation in which there is a true, non-negligible underlying variation between the units under consideration, combined with a non-negligible measurement error, neither completely-pooled estimation (averaging over the ROI) nor the estimates obtained through a set of separate analyses are uncompromised. This issue is discussed in Sections 5.4 and 5.5 of the textbook by Gelman et al.23, where they use a simple dataset to compare the results given by a random effects treatment with the completely pooled result and an independent units analysis. They make a convincing case for random effects modelling.
Among the research disciplines in which Bayesian spatial random effects modelling is especially prominent is epidemiological disease mapping. Disease mapping and the present tumour heterogeneity study share a similar objective, namely the extraction of an underlying spatial structure, given data that are typically corrupted by noise. Sparseness/rarity of the observed events is a problem in some disease mapping applications, which is not dissimilar to the sparse data problem that arises in the present study. Markov random field priors are common among those adopted in the disease mapping literature24–26. Note S1 provides a brief introduction to Markov processes and Markov random field models which, together with references given in the Methods section, serves as an entry point to the literature. The analyses outlined in this paper were performed using a so-called conditional autoregressive (CAR) form of Markov random field prior, as explained in Note S1.
Given a Bayesian hierarchical random effects model, some procedure is required for computing the posterior probability distribution. This invariably involves complicated high-dimensional integrals that have no analytical solution. MCMC is often adopted as a method that circumvents the analytical intractability of this kind of problem23,27,28. The Gibbs sampler is among the most widely used MCMC algorithms; it is based on an iterative sampling of a set of conditional distributions. The CAR prior referred to in the preceding paragraph (a conditional distribution by definition), thus fits naturally into the Gibbs sampler algorithm, and the resulting computational efficiency is among the appealing features of adopting this prior when performing a Bayesian spatial analysis using the Gibbs sampler. Computer software for performing Bayesian spatial data analyses is readily available, including Gibbs sampler implementations. The MCMC analyses outlined in this paper were performed using WinBUGS/GeoBUGS29,30.
In summary, the purpose of the present study was to develop a model for tumour ADC spatial heterogeneity. This was motivated by current biomedical research indicating that tumour heterogeneity has important implications in the search for improved cancer treatment strategies and for the investigation of tumour pathophysiology1–3. We have adopted a spatial random effects modelling approach to characterising heterogeneity, implemented using MCMC. Despite the merits of performing an MCMC analysis, the method is not infallible. Reliable statistics depend on achieving convergence to a stationary distribution. Convergence assessment is, therefore, an essential part of any MCMC analysis. In order to guard against misleading heterogeneity measures, we have paid reasonable attention to the convergence issue, in addition to addressing the question of model adequacy. The latter was achieved by using posterior predictive simulation to examine key features of the spatial statistical modelling results, as described in the Methods section.
The data used in this study are the same as those used in a previous study22 for which ethical approval was granted by the National Research Ethics Service Committee London – Bloomsbury. Therefore, no additional approval was required. Patient details and related information are given in 22. The subset of patients selected for the present work were imaged using a Siemens Magnetom Symphony scanner, capable of generating magnetic field gradients of amplitude up to 30 mT m–1. DWI data were acquired using a diffusion-sensitized single-shot echo planar imaging sequence (acquisition matrix 128 × 128, image matrix 256 × 256, field-of-view 230 × 230 mm, twenty 5mm slices separated by 2.5mm, TR 3600 ms, TE 107 ms). In addition to a single b0 image, 6 diffusion-weighted images were acquired with b-values 500 and 1000 s mm–2 for each of 3 orthogonal directions. The total imaging/sequence time was 56s.
The data were not formally blinded because the investigation does not take the form of a clinical trial. Instead, the purpose of the study was to develop a statistical model, with parameter estimation as the objective, focussing on tumour heterogeneity measures. Thus the goal is parameter estimation as distinct from hypothesis testing. That said, the model development and data analyses were performed by MDK, using image signal intensity data provided in NIFTI format, with all sources of identification removed. The FSL utility tools (Version 4.1.5) fslview, fslslice and fsl2ascii (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/Fslutils) were used to identify the location of each tumour, and to extract the DWI signal intensity data from the tumour region, with conversion to ASCII format.
Region-of-interest selection was based on an inspection of ADC maps. A core ROI of 15-by-15 voxels was placed at a position well removed from the tumour boundary, as shown for one case in Figure 1. Tumour boundary ROIs were selected in that portion of the tissue where the boundary is easily identified due to the presence of adjacent oedematous voxels. A subject-specific ADC threshold was chosen and used to define tumour versus extra-tumour voxels. These thresholds were based on an inspection of the ADC values in oedematous voxels, together with a visual examination of the segmentation obtained with alternative values. ADC profile plots were used to select the boundary ROI width, as judged by the number of voxels over which the boundary distance effect vanishes, and the ADC becomes indistinguishable from typical core values. Boundary distance was equated to the minimum of the row and column distances. (No marked differences occurred when the analyses were performed using minimum Euclidean distances.) Figure 1 includes a magnified portion of the ADC image to show the boundary ROI in greater detail. It also shows part of the corresponding array of ADC values. In this case a threshold of 117 was used to distinguish tumour versus oedematous voxels. This study is of an exploratory nature, and tumour boundary identification and ROI selection are among the issues that require refinement, given the fact that the tumour boundary is never well defined in its entirely. We return to the ROI selection and automation problem in the Discussion.

The left panel shows an ADC image with the core ROI (square region) and boundary ROI (irregular region) superimposed. The boundary ROI is shown with increased magnification in the upper right panel. The array of ADC values given in the lower right panel are taken from the subregion indicated by the white box. The lines superimposed on the ADC array correspond to the ROI boundary.
The main purpose of the modelling study outlined in this paper is to determine whether DWI data obtained from PNET (primitive neuroectodermal tumour) cases provide statistical evidence to support the proposition that water diffusivity in the boundary region of some tumours exhibits a dependence on distance from the boundary, in excess of an underlying 2D spatial heterogeneity in diffusion. Tumour ADC dependence on boundary-distance has been reported in previous publications, and the principal objective is to determine whether this effect can be demonstrated given a model that includes additional 2D spatial variation. The distinction is between a monotonic change in diffusion in a direction approximately normal to the boundary, compared with an underlying and general 2D spatial dependence, with no distinct orientation relative to the tumour boundary. Specifically, an inverse tumour boundary-distance term is included in the diffusion model, together with additional random effect diffusion terms to capture the underlying 2D spatial heterogeneity (spatial correlation structure). Separate random effect terms are assigned to each of the three (read, phase and slice) diffusion coefficients. Interest focusses on the magnitude and statistical significance of the inverse-distance coefficient, in order to determine whether a formal spatial model provides robust evidence for a boundary effect. The statistical model allows the boundary voxels to differ from core voxels in their spatial correlation/heterogeneity, thus facilitating a comparison of the two regions. Furthermore, the model deals with the complication that arises from non-monoexponential signal-intensity dependence on gradient amplitude, combined with an additional limitation arising from our using existing DWI data acquired with a standard clinical image acquisition protocol. The main limitation of the clinical data is a lack of replication. Thus each DWI dataset consists of 7 images only, namely, a single b0 image plus single acquisitions with gradient sensitisation in the x, y and z directions and b-values of 500 and 1000 s mm–2. The lack of b0 data replication coupled with the non-monoexponential decay is the main challenge because a standard analysis cannot yield estimates of the true b0 signal intensities separated from the accompanying noise. An additional limitation of the clinical data is the restriction to two non-zero b-value observations in each direction, again with no replication. The required diffusion parameter estimates can be obtained, however, under the spatial model outlined below, despite the departure from exponential dependence on magnetic field gradient amplitude and lack of replication. In essence the model assumes an exponential dependence in a b-value range that includes the b500 to b1000 observations, and captures the departure of the b0 signal intensity from the exponential curve using an offset parameter (δi in equation 3). The latter is incorporated in the form of a random effect term, and it is among those that are assigned a spatial CAR prior distribution (the CAR prior is outlined in Note S1). The essential features of the measurement model are illustrated in Figure 2. To re-iterate, an offset term captures the low b-value signal decay and yields a b0 signal intensity estimate, separated from the noise contribution, despite the lack of b0 replication. The b0 signal intensity estimates are subject to two constraints, namely the underlying spatial distribution referred to above, together with a measurement error distribution with variance equal to the error variance of the finite b-value observations. This approach is preferable to treating the b0 observations as error free. The resulting voxel-specific signal intensity and diffusion parameter estimates were used to calculate a summary parameter, ADC0.5 (given the symbol d′ in the following equations), based on the half-maximum-intensity b-value estimates, thus circumventing the non-monoexponential decay problem. The model details are as follows.
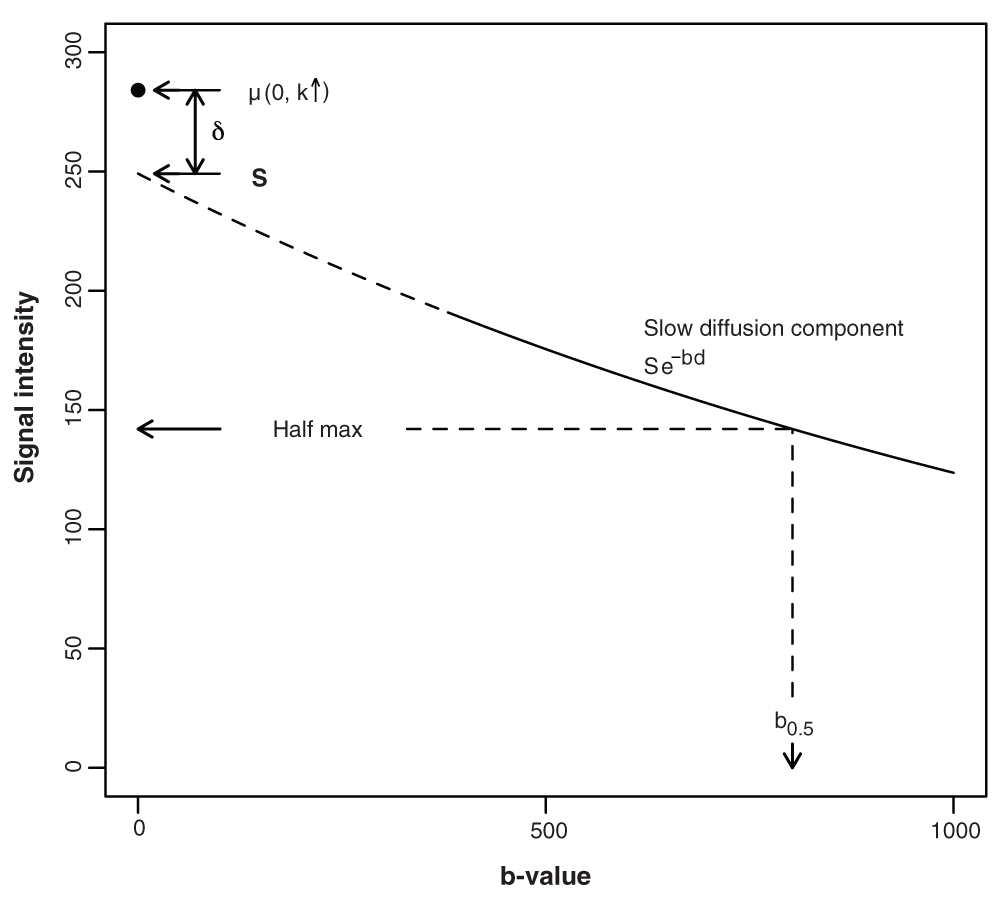
Signal attenuation from a b-value of 380 s mm–2 up to 1000 s mm–2, and beyond, is assumed to be exponential, with a voxel-specific diffusivity characterised by ADCs (slow diffusion ADC component). The model allows for a departure from mono-exponential behaviour, which is assumed to occur below a b-value of 380 s mm–2. (The need to assume that the mono-exponential behaviour extends down to 380 s mm–2 arises because some of the estimates (definition given below), which are used to calculate the ADC0.5 estimates, are less than 500 s mm–2, the lowest falling at approximately 380 s mm–2. In contrast, the mono-exponential assumption underlying the ADCs calculations is restricted to the b-value range 500 s mm–2 to 1000 s mm–2.) An offset term, δ, captures the additional signal attenuation that occurs over the b-value range 0 to 380 s mm–2, thus accounting for the expected departure from mono-exponential behaviour at low b-value. δ is the difference between the true b0 signal intensity and the intercept, S, given by the mono-exponential expression for signal intensity. The dashed curve shows this exponential behaviour extrapolated to zero b-value. As outlined in the Statistical model subsection of the Methods section, ADC0.5 is calculated using where is the b-value at the half-maximum signal intensity, noting that the subscript labels used in the main text (indicating that each of these parameters is voxel specific) have been dropped for the sake of simplicity. Similarly, the associated random effect terms are not included in the schematic.
The measurement model takes the form
where yi(.) is a signal intensity observation in the ith voxel, the symbol ~ indicates ‘distributed as’ and N(µi (.), 1/τr) is the normal distribution with mean µi(.) and residual variance = 1/τr (i.e., τr is the precision of the measurements). The subscript labels k1 = k4 = x, k2 = k5 = y, k3 = k6 = z refer to the magnetic field gradient directions, b1 = b2 = b3 = 500 and b4 = b5 = b6 = 1000 are the DWI b-values (s mm–2), while k ↑ indicates that k is not defined when b = 0. Si is the b0 intercept in the monoexponential signal intensity expression for the ith voxel, dikj are voxel- and direction-specific apparent diffusion coefficients and δi a voxel-specific term that captures the departure from monoexponential dependence at low b-values. The following equations complete the statistical model, where the subscripts b and c are used to indicate boundary and core voxels, respectively. (Note that several model parameters are completely defined within the hierarchical set of equations and do not require further definition.) where Nc and NT are the number of core voxels and total number of voxels, respectively, µs, µδ, µdkc and µdkb are intercept terms, θip, p = 1,2, are spatial random effects and l is the boundary distance. (In equation 7 and equation 8, the acquisition label, j, that appears as a subscript in equation 2 has been dropped.) The coefficient α captures the magnitude of the boundary-distance dependence in the departure from monoexponential behaviour and β captures the boundary-distance dependence in the diffusion coefficients. The random coefficients θik in equation 7 and equation 8 were assigned ROI-specific prior distributions to allow the boundary and central regions to differ in their level of spatial correlation, noting that in the boundary region this 2D spatial heterogeneity is supplementary to the inverse boundary-distance effect on diffusion. Each of the eight sets of random effect terms was assigned a spatial CAR (conditional autoregressive) prior as follows: where and are conditional variance parameters, ri is the number of voxels adjacent to the ith voxel, and are conditional means given by in which ∂i is the set of voxel labels belonging to the neighbours of the ith voxel. The CAR priors were implemented using the GeoBUGS car.normal function (see below) with dispersion specified as precision parameters, i.e., reciprocal variance, each of which was assigned a Gamma(0.5, 0.0005) distribution at the next level in the prior hierarchical structure. The measurement precision, τr, and intercept terms were assigned an uninformative gamma prior and flat prior distributions, respectively. An important feature of equation 8 is the contribution provided by the inverse distance term. This contrasts with the linear dependence on distance adopted by some analysts. A linear distance dependence is a counter-intuitive model for decay, given a non-negative diffusion coefficient. Thus, an inverse distance dependence was adopted because it approaches zero asymptotically. In particular, it cannot become negative when β is positive.In summary, the model includes a spatial random effects term (θi1) to cater for between-voxel variation in the b0 intercept of the slow-diffusion component (i.e., Si in equation 2), specified as having a conditional variance common to both boundary and core voxels, a spatial random effect term (θi2) to allow for between-voxel variation in the fast-diffusion component, i.e., the departure from mono-exponential decay, again with a conditional variance common to the two regions, and spatial random-effect contributions (θik, k = x, y, z) to the magnetic field gradient direction-specific diffusion coefficients, with separate conditional variances assigned to the core and boundary and to each direction. A diffusion summary parameter (d′) was adopted to circumvent the complication that arises due to non-exponential b-value dependence. This is based on the assumption that the direction-specific mono-exponential expression for signal attenuation given in equation 2 applies over the range b380 to b2000. (With the exception of a few outliers with larger values, the voxel-specific estimates, referred to below, lie within this b-value range. It might be noted that a proportion of these estimates lie outside the b500 and b1000 range, which is not ideal. This problem is a reflection of our using retrospective clinical data obtained with an imaging sequence that was designed for routine DWI, as opposed to detailed statistical modelling.) Accordingly, a voxel-specific half-maximum signal-intensity b-value was calculated using (0, k↑))/di, where di = (dix + diy + diz)/3 is the mean diffusivity (the subscript i is the voxel label, not to be confused with the convention where it is used to indicate an isotropic parameter). This is used, in turn, to calculate the summary parameter d′i = log(2)/. For the sake of conciseness and readability the voxel subscript is dropped in the Results and Discussion sections, and the abbreviations ADCs, ADC0.5 and µ0 are used for di, di′ and µi (0, k ↑), respectively, i.e., the slow-diffusion ADC component, the ADC based on an estimate of the half-maximum signal intensity, and the b0 signal intensity estimate. A schematic showing the relationship between the key model parameters and the b-value dependence in signal intensity is shown in Figure 2.
The summary parameters ADCs and ADC0.5 were calculated using the definitions given above. The various range statistics were generated by evaluating the relevant minimum and maximum voxel-specific values at each MCMC iteration. Thus the resulting statistics include all sources of variation/error, including uncertainty in the identity of the voxels responsible for the extreme values. The boundary-region 2D heterogeneity ADCs statistics listed in Table 2 were derived from the average of the three magnetic field gradient-specific diffusion coefficients, as obtained for each voxel with the boundary effect (β/li) removed (i.e., based on dik = µdkb + θik, i = Nc + 1, . . ., NT; k = x, y, z; compare with equation 8). The third data column in Table 2 lists the boundary distance-effect (β/li, i = Nc + 1, . . ., NT) ranges, as given by the difference between the maximum and minimum voxel-specific values.
Bayesian spatial modelling and its implementation using MCMC is well documented (see, for example, 24–26,31). We have previously demonstrated the application of this modelling approach to the crossing-fibre problem that arises in diffusion tensor imaging32 and the sparse data problem that often arises in MR perfusion and diffusion image analyses33,34. Gibbs sampling was performed using the WinBUGS/GeoBUGS package (Version 1.4.3)29,30,35,36, which was downloaded from http://www.mrc-bsu.cam.ac.uk/bugs. Three parallel chains were generated for each of the five analyses (5 cases examined in total), each chain consisting of 5000 samples after thinning. (Thinning is the name given to the common practice whereby a specified proportion of the MCMC output is discarded, the remaining samples being stored for subsequent processing. It has been discussed by a number of analysts, including Carlin and Louis (2009) (Section 3.4.5 in 28). The reason for thinning the MCMC output is to produce a chain with reduced sample autocorrelation. The aim is to reduce both the storage and post-simulation CPU demands of an analysis without suffering much loss in precision. A thinning factor of 40 was used in the majority of the simulations, excepting the posterior predictive analyses, which were performed using a thinning factor of 10. Thus, 1 in 40 (or 1 in 10) samples was stored and used in subsequent calculations). The first of each set of three chains was started at an arbitrary position in parameter space, while the other two were started at over-dispersed positions. A burn-in set of samples was acquired prior to storing each chain of 5000 samples. The burn-in samples were discarded.
An informal assessment of convergence was performed by inspecting selected overlaid trace plots for visual signs of convergence failure. (MCMC convergence analysis is a topic that has been discussed by many analysts, as summarised in several textbooks, (Gelman et al23, and Carlin and Louis28, for example) and discussion papers37,38. Our approach is based partly on their recommendations.) This visual assessment was followed by a semi-formal analysis (see 39 for a review of the methods) which was performed using three convergence test procedures, namely the Gelman-Rubin shrink factor diagnostic and associated shrink factor plots (which is based on an ANOVA-like assessment of the between-chain and within-chain variances), the Geweke Z-score diagnostic and Z-score plots (based on spectral density variance estimation and a Z-score comparison of chain segments), and the Raftery-Lewis diagnostic procedure (which provides a variety of data, including an estimate of the number of iterations required to obtain a given quantile to some specified accuracy, taking into account the correlation between samples). Particular attention was paid to the accuracy obtained for the key measures of spatial variation. These convergence analyses were performed using the R CODA (Convergence Diagnosis and Output Analysis) package40 (R version 2.15.2, CODA version 0.16-1).
Model assessment was undertaken using posterior predictive simulation (41–43; Chapter 6 in 23, provides a useful introduction.) This is an established procedure which can be used to calculate so-called posterior predictive p-values or Bayesian p-values, which serve to determine whether some aspect of the data is unexpected under the model, indicating potential model inadequacy. The objective is to adopt tests that probe the capacity of the model to capture features in the data that are key to the scientific question underlying the research (see, for example, page 172 in 23). In the present study the resulting Bayesian p-values are used as probabilistic measures of the extent to which the observed signal intensities are more extreme than the posterior predictive data (yrep). In short, the p-values provide a measure of discrepancy. Following Gelman et al.23, page 162, and noting that in the present analysis the test quantity depends only on the data,
taken jointly over the posterior predictive distribution of yrep and the posterior distribution of the model parameters (θ). An estimate of pB is given by the proportion of L simulations satisfyingIn those instances where this yields a p-value greater than 0.5, the sign of the test is reversed. Thus improbable test results are indicated by Bayesian p-values near zero.
The preceding mathematical expressions differ from those given in 23, the latter using discrepancy measures that depend on unknown parameters, in addition to the data. In the present study, posterior predictive tests were all performed using signal intensity in isolation as a measure of discrepancy. (Thus T(y, θl), as given on page 163 of 23, becomes T(yi) = yi, where i is the voxel label.) The rationale behind focusing on discrepancies between the observed signal intensities and replicate data generated under the model was as a simple procedure to detect potential outliers, and to determine whether these are associated with extreme ADC estimates, leading to spurious heterogeneity measures, noting that tumour heterogeneity is the focus of the study.
The Results section of this paper is organised as follows. The first subsection reports the main findings of the tumour spatial heterogeneity analysis, which compares the level of heterogeneity observed in the core and boundary region of five tumours. This is followed by two subsidiary sections, the first of which examines the boundary distance effect in greater detail, followed by a subsection dealing with potential anisotropic behaviour in the observed spatial heterogeneity. The final subsection provides a brief summary of the MCMC convergence and simulation accuracy analyses, together with a summary of the posterior predictive simulation results.
The main motivation for the ADC analysis outlined in this paper is the MRI literature suggesting that the ADC in the boundary region of some tumours exhibits a voxel-specific dependence on distance from the tumour boundary14,17,22. The aim was to determine whether an analysis based on a formal spatial model provides supporting evidence for a boundary effect after adjusting for an underlying random 2D spatial heterogeneity. In this context the statistical model accommodates several parameters of potential interest. These include a term, specific to the boundary ROI, which assumes an inverse dependence of the anisotropic diffusion coefficients on distance from the tumour boundary. This effect is superimposed on an underlying random 2D spatial heterogeneity that is assumed to exist in both the boundary and core regions. The latter general heterogeneity is incorporated in the form of so-called spatial random effect terms. The magnitude of the resulting 2D spatial heterogeneity is allowed to differ between the two regions. Interest focusses on potential subject-specific differences in heterogeneity between the boundary and core regions, together with the magnitude of the boundary distance effect. A note of explanation might assist readers unfamiliar with the Bayesian terminology used in this paper. Each of the model parameters is estimated with error. This uncertainty is captured by the posterior probability distribution. The posterior median provides a point estimate of the true parameter value, while the tail quantiles give an indication of the uncertainty in the estimate. 95% posterior intervals are given for every parameter estimate, including the various range parameters which are used as measures of spatial heterogeneity. In the latter case, the 95% posterior intervals provide a measure of the range of uncertainty in the ADC range estimates.
Table 1 lists the minimum and maximum voxel-specific ADCs estimates, as obtained for the core and boundary regions in five subjects, together with the corresponding range statistics. The main result that emerges from this table is that heterogeneity in the core is not consistently less than that observed in the boundary region, despite the additional boundary distance-effect contribution to the latter. Thus, although heterogeneity in the boundary region ADCs is substantially larger than that observed in the core in 3 of the 5 cases, in one of the remaining cases (Subject 2) the core region exhibits a greater level of heterogeneity.
*The median of the posterior distribution obtained for each of the specified ADCs parameters is listed, together with the 0.025 and 0.975 quantiles, which are given in brackets.
Core and boundary-region minimum and maximum voxel-specific ADCs estimates are listed, together with the corresponding ranges (difference between the maximum and minimum of the voxel-specific estimates). The ADCs range estimates, which are used as measures of ADCs dispersion, are derived from the raw MCMC sample, as opposed to subtracting the listed minimum and maximum values, hence the apparent discrepancy between some of the extreme-value and corresponding range statistics.
Table 2 provides estimates of the magnitude of the random 2D spatial heterogeneity contribution to the boundary-region variation in diffusivity, as captured by the spatial random effects, together with the variation attributable to the deterministic boundary-distance effect, which operates close to the boundary, and the magnitude of the random 2D spatial heterogeneity in the core. Again, these are expressed in the form of ADCs range statistics, as given by the difference between the minimum and maximum voxel-specific ADCs values. The core-region range statistics are included for completeness, although these are identical to those given in Table 1. No consistent pattern emerges from a comparison of the boundary and core spatial random effect ranges (ie the random 2D heterogeneity effect). In particular, there is no indication of a consistently greater level of heterogeneity in one region compared with the other. A comparison of the boundary distance-effect ranges with the corresponding boundary random 2D heterogeneity ranges suggests that both are important sources of spatial variation, although the 2D heterogeneity component dominates in two of the five cases (Subjects 4 and 5).
*The median of the posterior distribution obtained for each ADCs range estimate (10−3 mm2 s−1) is listed, together with the 0.025 and 0.975 quantiles, which are given in brackets.
Range statistics are used as measures of ADCs dispersion in order to determine the relative contribution of the underlying sources of spatial variation. ADCs dispersion in the boundary region is composed of a random 2D spatial heterogeneity contribution and a deterministic boundary-distance effect which operates close to the tumour boundary. In contrast, dispersion in the core is restricted to a random 2D heterogeneity effect, which is permitted to differ in magnitude to the 2D spatial variation observed within the boundary region. Core region ADCs ranges are listed in the first data column, as determined by the difference between the maximum and minimum voxel-specific ADCs values within the selected region. ADCs range estimates attributable to the boundary-region 2D spatial heterogeneity component are listed in the second data column. The third data column lists the contribution of the boundary-distance effect, again expressed as an ADCs range equal to the difference between the voxel-specific maximum and minimum values within the boundary region.
Having examined the relative magnitude of the ADCs heterogeneity in the boundary-region with that in the core, Table 3 focusses on ADC0.5. ADC0.5 (denoted d′ in the Methods section) is a diffusion summary parameter that captures the signal intensity departure from an exponential dependence on b-value as it approaches zero, in addition to the slow diffusion component. It is based on an estimate of the b-value at the half-maximum signal intensity. (In contrast, ADCs is based on the monoexponential expression for diffusion (slow diffusion component) that is assumed to apply at b-values between 500 s mm–2 and 1000 s mm–2. The ADC0.5 calculation supposes that the departure from mono-exponential dependence occurs below 380 s mm–2. Details of the ADCs and ADC0.5 estimation method are given in the Methods section.) Again, no consistent pattern emerges, noting that in one of the five subjects (Subject 3) the core region appears markedly more heterogeneous than the boundary region.
*The median of the posterior distribution generated for the specified ADC0.5 parameter is listed, together with the 0.025 and 0.975 quantiles, which are given in brackets.
The core and boundary-region minimum and maximum voxel-specific posterior ADC0.5 (denoted d′ in the Methods section) estimates are given, together with the corresponding ranges. ADC0.5 is derived from the half-maximum signal intensity point on the mono-exponential decay curve as outlined in the Methods section. Spatial variation in the boundary region includes contributions from a random 2D heterogeneity in ADCs (captured by the diffusion coefficient random effect terms), a deterministic boundary-distance effect on diffusion and a boundary distance contribution to heterogeneity in the b0 signal intensity. The range statistics are derived from the raw MCMC sample, as opposed to subtracting the listed maximum and minimum values, hence the apparent discrepancy between some of the extreme value estimates and corresponding range statistics.
The results given in the preceding section indicate that the boundary-distance effect on diffusion (captured by the term β/l in equation 8) makes an important contribution to the spatial heterogeneity in ADC that is observed in the vicinity of the tumour boundary. In this section the effect is examined in greater detail. In addition to diffusion-coefficient dependence on boundary distance, an inverse distance term has also been added to the expression for the b0 signal intensity in the boundary region (α/l in equation 6), although there is no prior reason for assuming that this term will be important. The regression-parameter posterior median estimates are given in Table 4, together with the corresponding posterior 0.025 and 0.975 quantiles. With the exception of the posterior interval listed for α in Subject 2, the remaining 0.95 posterior intervals all exclude zero. This provides statistical evidence for the presence of a boundary distance effect on the slow diffusion component in all five cases, together with evidence for a boundary effect on the low b-value portion of the signal intensity curve (rapidly attenuated fast diffusion component) in 4 of the 5 cases.
*10−3 mm2 s−1 × (voxel size); **image intensity units × (voxel size). (Note the inverse distance dependencies in equation 6 and equation 8.)
Regression coefficient posterior median estimates are listed together with the 0.025 and 0.975 posterior quantiles, which are given in brackets. β is the coefficient in the term that captures the boundary inverse-distance dependence of each of the 3 (phase, read and slice) voxel-specific diffusion coefficients, while α is the coefficient in a term that allows for boundary inverse-distance dependence in the b0 signal intensities. The regression model details are given in the Methods section.
A visual representation of the magnitude of the boundary effect is given in Figure 3. The upper row shows the voxel-specific median ADCs estimates plotted against distance from the boundary. The corresponding ADC0.5 plots are given in the lower row. Superimposed on each graph is a median curve showing the boundary-distance dependence in ADCs, as given by the β/l term in equation 8. These curves have an arbitrary intercept (because the expression for diffusion includes additional random effect and intercept terms) and are shown with an intercept chosen to give a mid point equal to the overall median. The scatter in ADCs values at a given distance is attributable to the diffusion coefficient spatial random effect terms and provides a visual indication of the magnitude of the underlying 2D spatial heterogeneity in the diffusion coefficients (slow diffusion component). Consistent with the results given in the preceding section, and the statistics listed in Table 4, these plots show that the boundary distance effect makes a marked contribution to the spatial dependence in ADCs and that it is not completely dominated by the 2D spatial heterogeneity captured by the diffusion coefficient random effect terms. The relationship between ADC0.5 and β/l is less obvious indicating the importance of other sources of spatial variation. Scatter in the ADC0.5 values at a given distance from the boundary is accounted for by the entire set of random effect terms that are incorporated into the model, including those that capture the 2D spatial heterogeneity in the fast diffusion component.
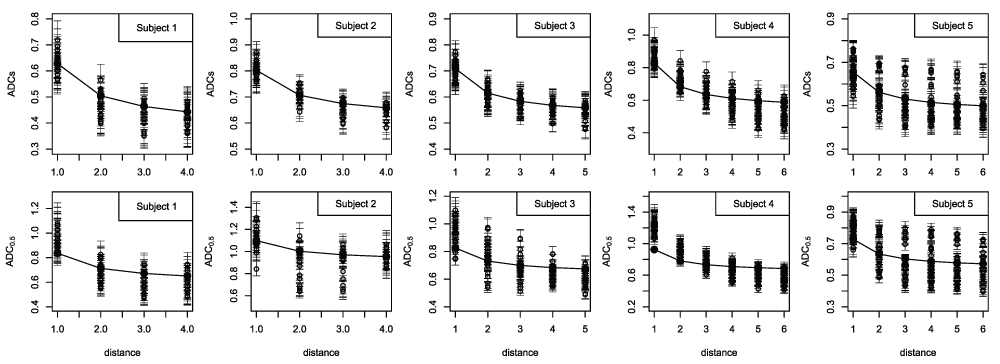
Voxel-specific ADCs estimates (top row) and ADC0.5 estimates (bottom row) in the boundary region plotted against distance from the boundary (distance given in units equal to the voxel size). ADCs is the slow ADC component, while ADC0.5 is derived from the half-maximum signal intensity estimate, and captures the signal attenuation that occurs at low b-value in addition to the slow component. The voxel-specific posterior medians are shown as dots while the posterior 0.025 and 0.975 quantiles are shown as bars. Although the figure does not show which of the medians belongs to each pair of quantiles, it does serve to provide an indication of the between-voxel differences in ADC together with the uncertainty in the estimates. Each plot includes a curve showing the dependence given by the inverse-distance diffusion term (β/l in equation 8), each of which is plotted with an intercept chosen to give a mid point equal to the overall median ADC value.
A comparison of the data shown in Figure 3 with those given in Table 3 reveals small differences between the two, particularly with respect to the ADC0.5 maxima, some of those listed in the table being noticeably larger than shown in the figure. In fact, all of the minimum and maximum ADC0.5 values listed in the table are more extreme than shown in the figure, although in some cases the difference is negligible. Focusing on the estimated maxima, the differences arise because the figure shows the median voxel-specific ADC0.5 estimates (and quantiles) while the table lists the median (with 95% posterior interval) of the maximum ADC0.5 estimates. The latter are not voxel-specific, but take account of uncertainty in the voxel associated with the maximum values. The median of the maximum ADC0.5 estimates tend to be larger than the maximum of the median voxel-specific estimates, which is expected. Similar differences arise in the ADCs results, but are less obvious. The estimates given in the tables provide the required characterisation of tumour heterogeneity. On the other hand, Figure 3 provides a visual impression of the heterogeneity among the voxel-specific ADC estimates, and the dependence on boundary distance. Restated, the maximum of the voxel-specific median ADC values does not equal the median of the maximum ADC estimates, within the selected region. It is the latter that are used to derive the ADC range statistics, because these capture uncertainty in the identity of the voxels responsible for the extreme values. The capacity to account for all sources of variation/error is among the advantages of the MCMC modelling approach adopted in this study. Among the limitations of a standard independent-voxels analysis (i.e., one based on independent voxel-specific estimates) is the lack of a formal mechanism for achieving this.
Finally we focus on the spatial-CAR precision parameters associated with the three diffusion coefficients (phase, read and slice-direction coefficients). They determine the magnitude of the dispersion in the diffusion coefficient spatial random effects, i.e., the underlying 2D spatial heterogeneity in ADCs. The boundary and core-region parameter estimates are listed in Table 5, after conversion to standard deviations in order to show these on the same scale as the ADC estimates. Inspection of these data suggests the presence of considerable anisotropy in the level of diffusion heterogeneity, together with substantial between-subject differences. The values obtained for the core region in Subject 2 are particularly large, raising questions regarding the robustness of these statistics. We return to this issue in the Discussion.
*The posterior median estimate of each standard deviation is listed together with the 0.025 and 0.975 quantiles, which are given in brackets.
CAR precision parameter values are listed after conversion to standard deviations. These provide a measure of local spatial dispersion and are shown on the same scale as the ADCs estimates. Specifically, the CAR precision (inverse variance) parameters determine the magnitude of local dispersion in the spatial random effects, i.e., the level of 2D spatial heterogeneity in the gradient-specific diffusion coefficients. It should be noted that the CAR precision parameters are conditional (by definition), and that a direct comparison with the other measures of dispersion given in this paper is invalid. Restated, measures of local dispersion are not, in general, directly related to global variability.
It should be noted that the standard deviations reported in Table 5 (square root of the inverse CAR precision parameter values) are not necessarily interpretable because they relate to local spatial structure as opposed to global variation over the entire ROI. Thus, in general, it is not meaningful to compare these conditional (local) dispersion parameters with standard measures of dispersion (see the Discussion for additional comments). As it happens, we do observe a relationship between each of the precision parameters and the corresponding region-specific diffusion-coefficient range of values. But this relationship is not guaranteed. We include Table 5 only because these data appear to suggest a considerable anisotropy in spatial structure.
Convergence to a stationary distribution is a critical requirement in any statistical modelling analysis performed using MCMC. In the absence of convergence the resulting parameter estimates can be meaningless. In accordance with accepted procedure, an initial convergence assessment was performed using overlaid parallel-chain trace plots. Given a set of chains started at overdispersed positions in parameter space, a failure to achieve a good coverage of the region of parameter space supported by the posterior distribution is usually revealed by visual inspection. An additional semi-formal analysis was performed using the diagnostic tests listed in the Methods section. These tests were mainly restricted to the derived heterogeneity measures that are the focus of the study, including α, β, the boundary- and core-region ADCs range variables, the boundary- and core-region ADC0.5 range variables, a derived parameter equal to the boundary spatial range with the β/l contribution removed, and the CAR precision parameters. In addition a few voxel-specific ADCs parameters were also examined. The resulting convergence test and simulation accuracy results are given in Note S2. In summary, there were no instances of compromise due to convergence failure. Regarding simulation accuracy, Raftery-Lewis calculations indicated that 5000 samples (after thinning) were more than sufficient to provide the majority of nominal 95% credible intervals with a true coverage of between 94% and 96%, with probability 0.95. Where this was not achieved, the results indicate a true coverage of between 93% and 97%, with probability 0.95. We regard this level of accuracy to be satisfactory, noting that the heterogeneity statistics provided in this paper are generated after combining the three individual chains generated for each case, thus providing an accuracy greater than given here for the individual chains.
As stated previously, convergence and simulation accuracy are not the only considerations. Clearly, model adequacy is central to the present analysis because an incapacity to capture the true DWI signal intensities is expected to give rise to meaningless measures of ADC heterogeneity. Posterior predictive simulation was used to examine the MCMC output for signs of model inadequacy. It provides a mechanism for distinguishing between observations that are unexpected under the model (i.e., indicative of model failure), and observations that are compatible with the model despite appearing extreme. Details are given in Note S2. Although there are instances where a very low Bayesian p-value was obtained, this is not unexpected given the relatively large number of signal-intensity observations involved in each image dataset. Paying attention to the Bayesian p-values obtained for those voxels that give rise to the extreme parameter values that determine each of the reported heterogeneity estimates (i.e., the various range statistics), there are no instances where the p-value falls below 0.01. The conclusion is that there are no instances where an extreme ADC estimate gives rise to a spurious measure of heterogeneity, i.e., where an inflated heterogeneity estimate arises due to a spurious signal intensity observation or due to model failure. Re-stated, the model appears adequate in terms of its capacity to capture the true underlying tumour ADC heterogeneity.
The focus of this study is a statistical modelling procedure for characterising intra-tumour heterogeneity. This was motivated by a well-established literature indicating that tumour heterogeneity has major implications for the development of improved treatment strategies and for the basic understanding of tumour development and pathophysiology. Among the important features of the approach that has been adopted is a single-stage analysis in which spatial heterogeneity is modelled simultaneously with signal intensity fitting. This is achieved by using a Bayesian spatial random effects model, implemented using MCMC. Some might question the need to adopt a formal spatial model, as opposed to a standard independent voxels (i.e., voxel-by-voxel) analysis. A brief statement of the general advantages of random effects modelling over an independent-units analysis is given in the Section on Bayesian random effect models that is included in the Introduction. In particular, we refer to the improvement in parameter precision that arises due to so-called information borrowing. Among the main ingredients of the random effects treatment adopted in this study are the spatial distributional constraints imposed by the CAR priors. These introduce a degree of spatial smoothing, referred to as shrinkage in the random effects context. The resulting voxel-specific ADC estimates and range statistics will, in general, be less extreme than those obtained from an independent-voxels analysis. In particular, the various range estimates are expected to be smaller than those obtained by subtracting the voxel-specific maximum and minimum ADC values obtained in an independent-voxels analysis. In that sense, the present random effects model analysis yields robust/conservative measures of heterogeneity.
The tumour heterogeneity analysis yields a variety of spatial statistics that are potentially useful from a clinical perspective. The main conclusions are that the previously reported relationship between diffusion and boundary proximity remains observable and achieves statistical significance (the 95% posterior intervals exclude zero) after adjusting for an underlying random 2D spatial heterogeneity in the diffusion model parameters. In addition, the results suggest that the tumour core and boundary regions are distinguishable in terms of the ADC spatial structure captured by the random effect terms, notwithstanding the additional deterministic boundary effect. A comparison of the magnitude of the deterministic boundary distance-effect with the underlying random 2D boundary heterogeneity suggests that both are important sources of variation in the vicinity of the boundary. No consistent pattern emerges from a comparison of the boundary and core spatial heterogeneity. In particular, the level of heterogeneity in the core is not consistently less than that observed in the boundary region, despite the additional boundary distance-effect contribution to the latter.
A potentially interesting observation is that the diffusion coefficient CAR-prior precision parameters (these conditional parameters are measures of local heterogeneity) exhibit a significant degree of anisotropy, which suggests that combining the direction-specific diffusion coefficients to obtain ADC measures of heterogeneity is accompanied by a loss of information. But caution is required given the possibility of over-interpretation due to over-fitting the data which consists of only seven signal intensity observations per voxel. The present study suffers a deficiency that is not uncommon in the MRI field, namely existing imaging data acquired using a standard clinical imaging sequence were used in a retrospective modelling exercise. The DWI acquisition protocol was designed to produce clinical ADC maps sufficient for visual inspection. Data of this type are unlikely to be optimum from a modelling perspective. In the present context a lack of replication within each dataset, especially the lack of b0 replication, is particularly problematic. Obviously, the restriction to two non-zero b-values is an additional and severe limitation, noting the need to cater for departure from mono-exponential behaviour. Given signal intensity data consisting of 7 observations per voxel (b0, b500x, b500y, b500z, b1000x, b1000y, b1000z) the calculations are barely tractable. Clearly, b0 data replication would provide a more robust estimate of the true b0 signal intensity, thus facilitating estimation of the magnitude of the departure from mono-exponential behaviour and the noise contribution to the b0 signal intensity observation. Given the present data, this is achieved only through the combined constraints provided by the error distribution and the autoregressive spatial prior associated with the b0 signal-intensity observation. The residual error variance would be estimated with improved precision given a reasonable amount of replication.
An additional compromise arises in relation to the ADC0.5 statistics, because these are based on an estimate of the b-value at half-maximum signal intensity which, for some voxels, lies below 500 s mm–2. Clearly it would be preferable to acquire data using a protocol that gives a better coverage of the critical range of b-values, and with suitable replication. Scan time is, however, a limiting factor in achieving this ideal. Furthermore, replication of the entire DWI dataset and/or the entire imaging session would allow a formal assessment of the robustness of the various heterogeneity measures, and the suggestion of anisotropy in the CAR precision parameters. Unfortunately, given the need to work in a standard clinical setting, comprehensive within-scan replication coupled with replicate scanning is not a realistic option. In the absence of replicate data, a question arises regarding the plausibility of some of the dispersion statistics reported in this paper, in particular the larger of the standard deviations given in Table 5. Although the latter conditional dispersion statistics cannot be interpreted as measures of global heterogeneity, some might appear greater than expected. Nevertheless, these are not incompatible with the ADC data provided by Bull et al., (2012), as obtained by averaging over the entire tumour44. They report that subject-specific PNET average ADC values lie in the interval 0.67 × 10–3 to 1.23 × 10–3 mm2 s–1, based on an examination of 22 cases.
As originally conceived, the main purpose of a simultaneous spatial modelling analysis of core and boundary regions was improved parameter estimation. An initial working assumption was that the underlying random 2D spatial heterogeneity in the core and boundary regions would be similar, with the boundary-distance effect superimposed close to the boundary. Given a set of common spatial parameters, the information provided by the core would lead to improved precision in the boundary-specific parameter estimates. It became immediately obvious, however, that this preliminary assumption was wrong and that the level of 2D spatial correlation in the core and boundary regions is distinguishable, regardless of the additional boundary-distance terms that were included in the model. The model was modified accordingly. Although the more general model does not offer the advantage of improved boundary parameter estimation based on information borrowed from the core, the precision of the resulting parameter estimates is nevertheless sufficient. In particular, a characterisation of the difference between the core and boundary regions is provided by the modified model, in addition to an estimate of the magnitude of the boundary-distance effect. In summary, the core and boundary regions differ in their spatial correlation structure, requiring our initial model to be modified through the inclusion of region-specific spatial random effect terms. Although this complicates the comparison of the boundary-distance effect with the underlying random 2D spatial heterogeneity, it is possible to obtain sufficiently precise estimates of the magnitude of these two sources of spatial variation.
A comment is required concerning the partial volume problem that arises in MRI due to finite resolution. Related issues include point spread function and zero filling effects. These must impact on the boundary distance coefficient estimates obtained in this study. For example, given the extreme case in which a step change occurs at the tumour boundary, partial volume/finite resolution effects, combined with image processing distortions, will cause a dispersion of the underlying step change in tissue characteristics. This interesting issue is related to the distinction between modelling the image-intensity data and modelling the underlying tissue structure. In keeping with standard practice among analysts engaged in MRI post-processing work, the results presented in this paper are based on modelling the image intensity data. An alternative approach might be sought in which a latent variables model is constructed, aimed at capturing the unobserved underlying tissue structure, combined with a model for the point spread function and zero-filling effects. A latent variables model must deal with all sources of image degradation. The resulting model will be complicated, however, and this will cause parameter estimation/precision problems, especially when working with sparse DWI data. A second point relates to the prognostic modelling literature that motivated this study. As stated in the Introduction, it has been suggested that PNET patient survival is a function of the tumour-boundary ADC gradient. Even in the extreme case in which a step change in tissue structure occurs at the tumour boundary, the magnitude of the gradient derived from the DW image will be related to the magnitude of the underlying step change. In particular, the magnitude of the ADC gradient will tend to zero as the step change tends to zero, and the relationship between them is expected to be monotonic. For this reason it is reasonable to assume that patient outcome will remain a function of any sensible regression coefficient derived from the tumour boundary DWI data, despite the degradation cause by imaging constraints and data processing, if a relationship genuinely exists between the underlying structure and survival. Existing literature suggests that the DWI data carry prognostic information, despite image degradation. We do acknowledge that a comparison of a given boundary-distance coefficient and the various measures of 2D heterogeneity is compromised, if the former is interpreted as a direct indicator of real underlying structure. For those readers preferring to dismiss the observed boundary decay in ADC as largely artefactual, caused by image degradation, we add the following rejoinder. The fact remains that the statistical model must include one or more terms to deal with the boundary effect, even if it is an imaging/data-processing artefact. The boundary-distance coefficient will be a function of the magnitude of the assumed step change that occurs at the boundary, coupled with imaging effects. From this perspective, the boundary distance-effect statistics listed in Table 2 and Table 4 might be regarded as measures of the magnitude of the imaging artefact, relative to the true 2D spatial heterogeneity in the region of the tumour boundary. We wish to stress that the notion of a tumour ADC dependence on boundary distance is not ours, and the main purpose of this study was to determine whether the boundary effect disappears after adjusting for an underlying 2D spatial heterogeneity in ADC. The present statistical analysis is not compromised by the possibility that the ADC boundary-distance effect is partly artefactual. The statistical model applies to the image data as opposed to the underlying structure. As it happens, the distance effect remains statistically significant, regardless of its origin. An additional note is warranted. This paper does not address any issues arising from the assertion that tumour ADC provides a reliable biomarker of cellularity, apart from the statements made in the Introduction regarding the limitations of simple correlation analyses and the criteria that should be met before claiming to have a reliable surrogate marker.
Posterior predictive simulation was performed as a mechanism for assessing model adequacy. In essence this is a simulation approach to comparing an observed statistic, designed to capture some key feature of the data, with that given by the model (chapter 6 in 23,41–43). Bayesian p-values are commonly adopted as a measure of discrepancy between an observed statistic and that obtained under the model. We note that the approach has received some criticism. For example, the predictive probabilities are not calibrated (in general, the posterior predictive p-values do not have a uniform distribution under the null hypothesis45). Some data analysts have suggested that the very notion of Bayesian p-values is a contradiction. (An indication of the nature of the paradox is given on page 87 of 28.) A number of eminent statisticians remain enthusiastic about this approach to model evaluation, however. The early BUGS documentation46 included a section on goodness-of-fit tests based on Bayesian p-values. Gelman, who is a notable advocate, argues that a statistical model can seldom be perfectly true (see page 158 in 23, or page 776 in 42), but that it is important to demonstrate that it is adequate for the intended purpose, even if it is deficient in some other aspect. Posterior predictive simulation provides a useful tool for performing this kind of model assessment. Nevertheless, we acknowledge that controversy remains regarding some aspects of this approach, including the calibration issue referred to above and an uncertainty regarding the p-value threshold that is used to indicate a problem. Thus the simple analysis adopted in the present study is undertaken without reference to the expected distribution under a satisfactory model. The purpose is to verify that there are not too many instances where an observation appears unexpected under the model. In the present study it was used as an approach for detecting potentially spurious signal intensities and/or instances of model failure, and to determine whether these are associated with extreme ADC estimates. We found two individual signal intensity observations with extremely low p-values. Given the nature of DWI and its sensitivity to movement, spurious observations might be expected. Thus, extremely low Bayesian p-values might be attributed to the simplicity of the error term, which ignores the possibility of spurious observations caused by motion and other imaging problems, as opposed to an inadequacy in the deterministic and/or spatial components of the model. That said, these two DWI observations did not give rise to extreme ADC estimates. Thus, exaggerated spatial heterogeneity measures arising from spurious DWI observations do not appear to be a problem. Accordingly, we conclude that the heterogeneity statistics given in this paper are robust to the presence of outlier signal intensities. Nevertheless, some might take the view that some form of model refinement should have been undertaken in an attempt to deal with the occurrence of a number of small Bayesian p-values. As a rejoinder we would argue that model assessment requires more comprehensive data than that provided by a standard clinical DWI acquisition. As stated previously, replication is desirable at several levels, including repeated acquisition within individual DWI datasets (as opposed to signal accumulation) and within-session DWI dataset replication. Given a reasonable level of replication, model refinement based on residuals analysis and other criteria becomes realistic. Furthermore, as stated above, replication at the DWI-dataset and/or imaging-session level would also facilitate an assessment of the robustness of the results.
Despite the limited number of observations per voxel and the resulting compromises, the signal intensity residuals were examined for signs of model inadequacy, as a complement to the assessment that was performed using posterior predictive simulation. In addition to a small number of relatively large residuals which are attributable to spurious signal intensity observations, the residual plots do display a degree of remaining spatial dependence. This does indicate a degree of model inadequacy, including a potential deficiency in the form of distance dependence that was adopted and/or the assumptions underlying the random effects. For example, the present random effects treatment is based on spatially invariant CAR precision parameters (these determine the level of local smoothing), and this might be an oversimplification. A spatially adaptive model might be investigated, although this is not a trivial undertaking. Alternatively, the error term might be modified to capture the remaining spatial structure, thus dropping the independent residuals assumption and substituting some form of autoregressive error behaviour. In order to adopt the latter approach as a sensible solution, the magnitude of the residuals must remain small relative to the total spatial variation in signal amplitude, thus ensuring that the majority of the spatial variation is captured by the random effect and boundary effect terms. Restated, the spatial heterogeneity estimates derived from the analyses will be compromised if a substantial proportion of the intra-tumour variation is captured by the error term. A heavy-tailed error distribution might provide a mechanism for dealing with spurious observations arising from a sensitivity to motion. Clearly, the model that was adopted in this study cannot be regarded as definitive. As stated above, model assessment and refinement, including an examination of the assumptions underlying the error term, would be facilitated by data replication. In particular, a comprehensive dataset with replication would permit a meaningful examination of alternative boundary decay models.
A final comment on the form of the model used in this study relates to the decision to adopt CAR priors for the spatial random effect terms. As stated in the Results section, the CAR prior precision parameters cannot be used as direct measures of global tumour heterogeneity because these relate to local spatial correlation structure as opposed to global structure. Trial analyses were performed using a global model of spatial heterogeneity based on so-called exchangeable priors. This would have offered the advantage of providing more direct measures of heterogeneity. Unfortunately, this model tended to produce poorly distributed residuals due to over-fitting, a problem that might be expected given the lack of replicate signal intensity observations and poor coverage of the b-value range. For this reason, given the present data, models based on exchangeable priors were abandoned as a potential alternative to the present CAR-prior models.
The preceding qualifications regarding the validity of the spatial model and/or error term prompt us to make a final comment regarding the value of this study. The question is whether it was sensible to embark on a study using clinical data that are sub-optimum from a modelling perspective. In our view, the paediatric data available to us represent a valuable and rare resource, despite the limitations arising from the acquisition constraints of a standard clinical imaging environment. We suggest that using these data in an exploratory study is justified, and provides a valid mechanism for gaining insight into the utility of the information that might be derived from these data. There is no possibility of re-scanning these children using an experimental imaging protocol for the sole purpose of undertaking an exploratory study of the potential benefits of a given kind of analysis. The results obtained from this preliminary study using existing data gives an indication of the possibilities, enabling a decision to be made regarding the development of this approach. A clear indication of the manner in which the imaging protocol might be improved also emerges, although any proposed changes are subject to the constraints that inevitably arise in a clinical setting. We have shown that despite the limitations of an analysis based on standard clinical DWI data (mainly a lack of replication), the heterogeneity summary measures have sufficient precision to be useful. The spatial model does achieve a separation of the noise contribution from the effects of departure from mono-exponential dependence, despite the absence of replication in the b0 signal intensity observation. The constraints imposed by the CAR spatial prior and the spatially invariant error distribution render the problem tractable. The key is a simultaneous modelling of a collection of voxels, since the separate estimation of the true signal intensity and noise contributions to a single b0 observation is impossible in an independent-voxels analysis. A comparison of the ADC estimates (both ADCs and ADC0.5) obtained with the current spatial model and a simple voxel-by-voxel fitting of the DWI signal intensity data (treating the b0 observations as error free) indicates marked differences in some voxels, which is expected and attributable to the shrinkage/smoothing properties of the random effects model.
Another matter that requires attention is ROI selection. In this study boundary ROIs were positioned where the tumour border is very well defined, working under the assumption that boundary effects might be more pronounced in that region. More sophisticated approaches should be investigated if the models outlined in this paper are to be adopted for prognostic modelling. Apart from the practical issues of tumour segmentation and automation, a modified approach will be required to cater for the expectation that tumour boundary heterogeneity is itself position dependent. Averaging heterogeneity over the entire boundary might obscure important prognostic information if, for example, tumour evolution is not uniform over the boundary. It would not be surprising to find improved performance among survival/prognostic models that retain position dependent heterogeneity information, compared with those based on averaged data or data taken from arbitrary regions.
In summary, the present study suggests that heterogeneity measures can be derived from standard clinical DWI datasets, despite their limited information content. Particular attention is paid to heterogeneity close to the tumour boundary, in order to determine whether water diffusivity in the boundary region of some tumours exhibits a deterministic dependence on distance from the boundary. The results indicate that the boundary-distance effect retains statistical significance after adjusting for an underlying and general 2D spatial heterogeneity. The level of spatial heterogeneity in the region of the boundary is not consistently greater than that observed in the core. The analysis could be extended to determine whether the heterogeneity parameters provide useful prognostic indicators in a survival analysis. Obviously, the same approach could be adopted using data acquired with a purpose-designed sequence, the advantage being that an increase in the accuracy and precision of the heterogeneity measures will be an advantage if these do carry useful prognostic information. In addition to assessing these heterogeneity measures as useful predictors in a survival analysis, the question arises regarding the relationship between these measures and intra-tumour genetic spatial heterogeneity. A biomarker of genetic heterogeneity would provide a powerful tool with applications in both patient management and in cancer research. Clearly, any imaging method that fulfils this role has the potential to provide clinical insights relevant to individual treatment and the pursuit of a better understanding of cancer biology.
F1000Research: Dataset 1. Diffusion-weighted MR signal intensity observations and voxel adjacency data. 10.5256/f1000research.9355.d13281648
MDK conceived, designed and performed the analyses and wrote the manuscript. MG-S collated and selected the data, read the manuscript and suggested improvements.
The authors thank Prof D. Gadian for reading early drafts of this paper and making substantial suggestions, each leading to marked improvements. Matthew Grech-Sollars thanks Prof Chris A. Clark and Prof Andrew C. Peet for support received as a participant in the research undertaken by the Children’s Cancer and Leukaemia Groups (CCLG) Functional Imaging Group. Martin King thanks Prof Chris A. Clark for covering the costs of attending a number of workshops held by the CCLG Functional Imaging Group. Various presentations given at these workshops provided the initial motivation for the statistical modelling work outlined in this paper.
Markov random field models and the conditional autoregressive prior Markov random field models are well known among fMRI researchers, but a brief overview follows, as it applies to the present study. Markov processes are particularly prominent in time-series data analysis. In that setting a first order Markov process is defined as a stochastic process in which the conditional probability of some future state is determined by the present state, unaffected by past history. Thus the process is first order autoregressive (AR(1)) given by Xt = αXt–1 + Zt (see, for example, page 35 in 47) where Zt is some random process with zero mean (Xt is the autoregressive process). An extension of this kind of conditional independence to the spatial case leads to Markov random field models in which the probability distribution of a random variable at some position in space is completely determined by conditioning on a set of neighbouring values. Thus a Markov random field characterisation of a spatial process is based on the assumption that the conditional distribution of some variable at a given location depends only on the value of this variable at a subset of immediately neighbouring locations. In the present context, this is the prior assumption, and it is modified by the information provided by the data, as expressed in the likelihood. The magnitude of the estimated differences between neighbouring voxels, ie., the extent to which the voxel-specific estimates are shrunk towards less extreme values, depends on the information content of the data, relative to the prior.
An intuitive Markov random field model, widely used as a prior distribution, is the intrinsic Gaussian conditional autoregressive (CAR) model which, for some parameter U, takes the form (see, for example, 24–26,31)
where Ui |Uv is the probability distribution of Ui given Uv, the symbol ~ indicates ‘distributed as’, N(mean, variance) is the normal distribution with the specified conditional mean and conditional variance, is a variance parameter, ri is the number of neighbours belonging to the ith voxel and ∂i denotes the set of voxel labels belonging to those voxels in the immediate neighbourhood of the ith voxel (i.e., those voxels sharing a corner or edge with the ith voxel); v belongs to that set. Thus, the prior conditional mean is the average of the neighbouring values. It happens that the conditional nature of this prior offers a considerable computational advantage in Bayesian analyses implemented using Markov chain Monte Carlo (MCMC). The CAR prior is adopted in the present work.Convergence tests, simulation accuracy, posterior predictive simulation and Bayesian p-values
Convergence tests were performed as outlined in the Methods section. There were no instances in which the Gelman-Rubin diagnostic suggested convergence failure. The majority of the Geweke Z-scores were also satisfactory, although several chains yielded a Z-score above 2. In only one case was the Z-score extreme (a value of 4.4 was obtained for one of the 3 chains of the boundary-region ADCs range parameter in Subject 1). Despite these indications of some non-ideal Z-scores, a comparison of the parameter median estimates and 95% posterior intervals given by the individual chains indicated good agreement. Thus, we conclude that there is no instance of unreliable measures of heterogeneity caused by compromised convergence.
The Raftery-Lewis results indicated that in many cases 5000 samples (after thinning) were more than sufficient to provide the 0.025 quantile estimates with an accuracy of ±0.005 with probability 0.95. Thus the resulting nominal 95% credible intervals have a true coverage of between 94% and 96%, with probability 0.95. There were, however, many other instances where this level of simulation accuracy was not achieved. Nevertheless, in these cases, the accuracy was at least ±0.01 with probability 0.95, which provides nominal 95% credible intervals with a true coverage of between 93% and 97%, with probability 0.95. It should be noted that the heterogeneity statistics provided in this paper are generated after combining the three individual chains, and that the resulting accuracy will be greater than given here for the individual chains.
Model adequacy is of central importance to the present analysis because an incapacity to capture the true DWI signal intensities is expected to give rise to meaningless measures of ADC heterogeneity. There were several instances where an observed DWI signal intensity appears extreme and the corresponding signal intensity estimate exhibits shrinkage towards a more typical value. This behaviour is expected under a random effects model, and is not necessarily an indication of model failure. Posterior predictive simulation provides a mechanism for distinguishing between observations that are unexpected under the model (i.e., indicative of model failure), and observations that are compatible with the model despite appearing extreme. To this end, Bayesian p-values were calculated for every observation. The focus of this paper is tumour heterogeneity, as characterised by the extremes in ADC0.5 and ADCs. Thus, particular attention is paid to the Bayesian p-values obtained for those voxels that give rise to the extreme parameter values that determine each of the reported heterogeneity estimates (i.e., the various range statistics), noting that extreme signal-intensity observations do not necessarily give extreme ADC values, and vice versa. In three of the five cases, no observation yielded a Bayesian p-value less than 0.001. The exceptions were Subject 2 and 4, which, taken together, yielded a total of three p-values of approximately 6 × 10–4. These 2 cases yielded a number of additional observations with a p-value < 0.05, as did the other 3 cases. Given the relatively large number of signal-intensity observations in each of the image datasets this is expected regardless of model adequacy. The largest number of observations with low p-values was obtained for Subject 1, with 20 p-values in the range 0.001 < p-value < 0.01. Inspection of the raw signal intensity data and diffusion weighted images indicates that, in this particular case, a small image artefact contributes to the apparent discrepancy between the model and observed data. Focusing on those voxels with extreme ADC0.5 and ADCs values, as expected some voxels yield Bayesian p-values in the tails of the distribution (p-value < 0.05), but there are no instances where the p-value falls below 0.01. This is consistent with the conclusion that the estimated ADC extremes are not invalid, i.e., attributable to the excessive influence of spurious signal intensity observations or model failure. In contrast, the model appears adequate in terms of its capacity to capture the true underlying tumour ADC heterogeneity. The low Bayesian p-values obtained for some observations do suggest, however, that potential improvements to the model might be sought. An inspection of various plots (not shown) indicates the presence of some spatial structure in the residuals. Thus, despite the apparent complexity of the random effects model adopted in this study and the limited number of observations, just seven per voxel, the low Bayesian p-values obtained for some observations might indicate scope for model refinement. The Discussion takes up the model refinement issue.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Competing Interests: No competing interests were disclosed.
At the request of the author(s), this article is no longer under peer review.
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | |
|---|---|
| 1 | |
|
Version 1 26 Aug 16 |
read |
Click here to access the data.
Spreadsheet data files may not format correctly if your computer is using different default delimiters (symbols used to separate values into separate cells) - a spreadsheet created in one region is sometimes misinterpreted by computers in other regions. You can change the regional settings on your computer so that the spreadsheet can be interpreted correctly.
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)