Keywords
climate change, agricultural yields, cropland extensification, econometrics, decision trees, international trade
This article is included in the Agriculture, Food and Nutrition gateway.
This article is included in the Machine learning: life sciences collection.
climate change, agricultural yields, cropland extensification, econometrics, decision trees, international trade
A consensus has emerged that recent climate change has had a negative effect on crop yields around the world (e.g., 1–4). Accelerating climate change is likely to put even more downward pressure on agricultural productivity around the world in coming years. Further, demand for food will grow quickly as the world races to a population of ~12 billion by 21005. Therefore, the vital question is: How can the world’s farmers increase crop productivity, as necessitated by global population growth, despite the expected drag on yields caused by climate change, while leaving the socially desirable amount of forest, grasslands, and other semi-natural land cover around the world?6
Before suggesting a way forward on this issue, we first have to determine what agricultural inputs are most important to yield growth around the world. Here we use global yield and agricultural input data from 1975 to the mid-2000s to determine what agricultural production inputs were most responsible for the growth in global and regional yields during this time period. The inputs we consider include growing season weather, crop choice, investment in irrigation capability, land, and machinery, agricultural science and management, fertilizer use, cropped footprint7, and cropped soil quality. We find that improvements in agricultural science and management (e.g., technology and chemical use), increased fertilizer use, and changes in crop mix around the world explained most of the gain in global crop yields from 1975 to the mid-2000s. Improvements in agricultural science and management were particularly important drivers of yield growth in the temperate region and changes in crop mix and increased fertilizer use were particularly important drivers of yield growth in the tropics. Further, the deleterious impacts of climate change on yield were small compared to the yield-augmenting factors noted above. Finally, cropland extensification over the last 40 years has dragged average global yields down as well, sometimes as much as climate change has.
Our results indicate that 1) transferring better agricultural science and management and other inputs to the tropics, 2) encouraging countries to exclusively concentrate on growing the crops most suited to their soil-climate conditions (and trading for the rest of the crops their consumers want), and 3) focusing on increasing the productivity of existing cropland in lieu of concentrating on cropland extensification will be the most effective ways to ameliorate climate change’s expected drag on global yields.
We used two analytical methods to measure relative importance of agricultural inputs to the growth in global and regional crop yields between 1975 and the mid-2000s.
First, we estimated country-level yield functions with a fixed-effects econometric model using a 1975 to the mid-2000s global panel dataset (Supplementary Table 1 and Supplementary Table 2; Dataset 1 and Dataset 28,9). We estimated country-level yield functions using both Mg ha-1 and M kcals ha-1 yield metrics: Mg or M kcal production across all crops in a country in year t divided by hectares of cropland in the country in year t. Second, we used the estimated yield functions and the panel data to obtain annual expected country-level yields, both in Mg ha-1 and M kcals ha-1, for the 1975 to the mid-2000s time period. Third, we generated global and regional expected crop yields in year t by taking the weighted average of expected country-level yields in year t using country-level cropped hectarage as weights. This process generated three expected “all-crop” yield curves, one for the globe, one for the temperate region, and one for the tropics region (see Figure 1 for the global Mg ha-1 and M kcals ha-1 expected yield functions).

The counterfactual global yield curves were constructed by holding all country-level agricultural inputs at 1975 levels except growing season weather. These graphs are based on “long” model results (based on the dataset with 1975 to 2007 data). Expected global yield grew 46.5% when measured in Mg ha-1 (A) and 58.8% when measured in M kcals ha-1 (B) between 1975 and 2007. Under the numeraire counterfactual global yield fell 2.1% when measured in Mg ha-1 (A) and 2.5% when measured in M kcals ha-1 (B) between 1975 and 2007. The light gray line indicates observed global yields.
To estimate the overall contribution of an agriculture production input or a group of inputs on 1975 to mid-2000s global or regional crop yield trends, we again found the expected global or region yield curve (as explained above) while holding the input or inputs in question fixed at observed 1975 levels (all other variables took on observed values). For example, to measure the impact of the change in cropped land soil quality on yield trends, the “soil quality” counterfactual yield curves were estimated with the quality of cropped land soil around the world remaining fixed at 1975 levels while all other inputs varied as observed. Then by integrating over the gap formed between the expected global or regional yield curve and the counterfactual global or regional yield curve we have measured the relative contribution of that input or group of inputs to 1975 to mid-2000s growth in global or regional yields, all else equal. The larger a counterfactual’s integral (in absolute terms), the greater the impact that the input or group of inputs in question had on global or regional yield trends from 1975 to the mid-2000s. A positive (negative) integral means that the 1975 to mid-2000s changes in the input in question had, on net, a positive (negative) impact on average global or regional yield.
When discussing results below, we normalize the size of a counterfactual’s integral by measuring its size relative to the size of the integral formed by the numeraire counterfactual. In a numeraire counterfactual all inputs are held at 1975 levels, except growing season weather over each country’s crop production area, which varied as observed (the numeraire counterfactuals always form the largest integrals). We refer to a numeraire counterfactual’s integral as the ‘Mg gap’ or the ‘kcals gap’ (Figure 2). For example, the mean global “crop mix” counterfactual has an integral of 9.11 over the 1975 to 2007 period when yield is measured in Mg ha-1. The mean global “numeraire Mg” counterfactual produces an integral of 30.53. Thus, the mean global “crop mix” counterfactual makes up or explains 9.11/30.53 = 29.83% of the 1975 to 2007 global Mg gap. The larger the percentage, positive or negative, the more important the counterfactual’s input or group of inputs was to determining the 1975 to mid-2000s global or regional yield trend.

In (A) an estimated global or regional counterfactual yield curve (one or more inputs are held fixed at 1975 levels in each country), measured in Mg, is given by the dotted black line. Assume the integral of the area between the expected global or regional yield curve (the solid black line) and the estimated counterfactual global or region yield curve is 10.00. Further, assume the integral of the area between the expected global or regional yield curve (the solid black line) and the numeraire counterfactual yield curve (the solid blue line) is 30.53. Then the counterfactual explains 10/30.53 or 33% of the “global Mg gap.” In (B) the estimated global or regional counterfactual explains −5/30.53 or −16% of the “global Mg gap.”
We also used decision tree algorithms to obtain a “second opinion” on which agricultural inputs were most important in explaining the growth in global and regional crop yields between 1975 and the mid-2000s. A decision tree segregates a process’ outcomes (in our case, annual changes in observed country-level yields) based on the attributes of a process (in our case, annual changes in each country’s input levels). A tree can be interpreted as the rules that map attributes of a process to the outcome of the process. In our case we find rules – ranges in annual changes in input levels – that predicted annual changes in country-level yields best (Supplementary Figure 1–Supplementary Figure 12; Dataset 310). When using econometric techniques to build a yield function, we made several assumptions regarding the variable-generating process. In the decision tree analysis, a machine learning algorithm, we identified key features of the data without committing to statistical assumptions.
For each analytical method we discuss two sets of results. In one case, we derive results for the time period 1975 to 2007. However, this set of results does not include fertilizer as a production input. In the other case we derive results for the time period 1975 to 2002. This set of results does include fertilizer use as an explanatory variable. The source of much of our agriculture data changed their fertilizer collection methods beginning in 200311. Harmonizing the two fertilizer databases was not practical. Below we will refer to results derived from the 1975 to 2002 dataset as the “wide” results and results derived from the 1975 to 2007 dataset as the “long” results.
Improvements in agricultural science and management, crop-mix change, and increased fertilizer use has explained most recent yield growth. When using either the long and wide datasets, time was the largest contributor to crop yield growth (both in terms of Mg ha-1 and M kcals ha-1) at the global and temperate region levels (Table 1 and Table 2 for the wide and long results, respectively). (Unless otherwise stated, we discuss mean results in the text.) At the global level, the time counterfactual’s integral makes up approximately 57% or 72% of the Mg gap (always wide and long results, respectively, unless otherwise stated) and 37% or 47% of the kcal gap. In the time counterfactual, we held the year variable fixed at 1975. In the temperate region, the time counterfactual makes up 79% or 90% of the Mg gap and 62% and 67% of the kcal gap. At the other extreme, the time counterfactual only explains -1.5% or 24% and -12.5% or 18% of the tropic’s Mg and kcal gaps, respectively.
The global model uses all countries while the regional models only use countries in the given region. The “Low” estimates are calculated with the 25th percentile annual yield estimates in each country. The “High” estimates are calculated with the 75th percentile annual yield estimates in each country. The cells in black indicate the integral if all agricultural inputs other than weather are fixed at 1975 levels (the numeraire counterfactuals; see Figure 1 and Figure 2). All other cells have an increasingly dark shade of green (red) as the integrals get more positive (negative). Pure white occurs at 0.
See the legend of Table 1 for more details.
Our econometric model’s time trend jointly captures the impact of several agricultural inputs that are omitted from our global panel database. Between 1975 and the mid-2000s, agricultural technology, agriculture management science, pesticide use, and international trade of agricultural commodities (variables missing from our dataset) increased around the world12. That greater technology, better management, and more pesticides increased yield is intuitive. However, the impact of increasing globalization on yields was important as well. Greater liberalization of agricultural production policies around the world and advancements in shipping technology meant that farmers were able to access international markets at increasingly lower costs13. And this increased market access spurred greater investment in farms (e.g., 14). Further, as cropland around the world became scarcer relative to the supply of rural labor, farmers increasingly became motivated to maximize yield rather than economize on labor use (e.g., 15). The time trend crudely accounts for the joint impact of these unobserved factors on yields (including fertilizer use in the long results but not in the wide results, which explicitly includes fertilizer use). Our results make it clear that the recent growth in agricultural technology, input use, farm management, globalization, and market liberalization disproportionally benefited the farmers of more developed nations in the temperate region than it did farmers of tropical countries.
When using either the wide or long datasets, change in crop mix was the largest net contributor to yield growth in the tropics. The tropical region’s integral from the crop mix counterfactual, where we kept the relative mix of crop hectarage in each country frozen at 1975 levels, makes up 55% or 61% and 58% or 65% of the tropic’s Mg and kcals gaps, respectively. Between 1975 and 2007 oil crops, sugarcane, roots and tubers, and fruit became a larger part of cropped area in the tropic region (Figure 3). According to the econometrically estimated yield models (Supplementary Table 1 and Supplementary Table 2), replacing wheat and other grain production with sugarcane, roots and tubers, and fruit production was particularly important to improving overall crop yield in the tropics. The gain in yield due to this crop switching can partly be explained by a simple substitution effect: Tropical cropland was increasingly used to grow denser fruits and roots and tubers versus less dense grains. However, this also reflects a comparative advantage effect, as wheat and most grains are most effectively grown in cooler climates while fruits are most cost-effectively grown in the tropics16. In comparison to its impact in the tropics, change in crop mix in the temperate region had little impact on yield when measured in Mg and only slightly improved yield when measured in M kcals.

Cropped area by crop type (crop mix) across the globe (A), across countries in the temperate region (B), and across countries in the tropical region (C). These graphs give the weighted average of area planted in each crop group across the globe or region over time. We use cropped hectarage in country c in year t as weights. Red (black) indicates a decrease (increase) in the crop or crop group’s share in the overall mix between 1975 and 2007. The percentage change indicates the change between 1975 and 2007.
The change in a country’s crop mix from 1975 to the mid-2000s was most likely driven by changes in global demand for various foodstuffs (e.g., 17,18) and the increasing globalization of crop production and trade12. As an example of the former effect, retail sales of foods with high oil and fat content increased dramatically in many countries from 1983 to 2002. Further, the number of calories that the average global person obtained from cereals fell while the number of calories they obtained from fruits and vegetables rose from 1996 to 200219. As an example of the globalization effect, consider that the reduction of several trade barriers in the early 1990s was largely responsible for the doubling of soybean production in Brazil20. Other potential explanations for country-level changes in crop mix include farmers adapting to climate change. However, there is little evidence of adaptation being a large driver of crop mix change.
Increasing fertilizer use across the globe from 1975 to 2002 (Table 3) was the next most important contributor to the steady gains in yield over that time period (only the wide dataset includes fertilizer data). When yield is measured in Mg ha-1, the fertilizer counterfactual makes up 23% to 32% to 38% of the Mg gaps (the temperate, global, and tropics Mg gaps, respectively). When yield is measured in M kcals ha-1, fertilizer makes up 12% to 23% to 42% of the kcals gaps (again, the temperate, global, and tropics Mg gaps, respectively). Further, the time trend no longer has a positive effect on the tropical yield when using the wide dataset. In fact, the time counterfactual produces a negative kcal gap in the tropics.
All averages are weighted by cropped area in each country in each year.
| 1975 – 77 average | 2000 – 02 average | % Change | |
|---|---|---|---|
| Globe | 84.17 | 128.56 | 52.73% |
| Temperate | 99.64 | 152.82 | 53.37% |
| Tropics | 34.37 | 68.46 | 99.16% |
Recent climate change slightly dampened yield growth. Compared to time, crop mix, and fertilizer use, the impact of the other agricultural inputs on recent global and regional yield was much less significant in terms of magnitude. When using the long or wide datasets, recent increases in daytime growing season temperatures (DGSTs; Table 4) negatively affected global and regional yields. When yield is measured in Mg ha-1, the DGST counterfactual makes up –4% or –6% of the global Mg gap (as before, the order is always wide and long results, respectively, unless otherwise stated). When yield is measured in M kcals ha-1, the DGST counterfactual makes up –4% or –5% of the global kcals gap. In the DGST counterfactual we fixed DGSTs around the world at 1975–1977 averages. The negative impact of increasing DGSTs on global yield was almost entirely explained by its drag on tropical yields; the impact of increasing DGSTs on temperate region yields was almost non-existent.
All averages are weighted by cropped area in each country in each year.
All else equal, warm days and cool nights allow for vigorous plant growth during the day and efficient plant respiration at night21–24. In contrast, warmer nighttime temperatures cause more wasteful respiration and less energy for growth during the day, all else equal. Therefore, we were surprised to find that increasing nighttime growing season temperatures (NGSTs) at the global and tropical region scales (Table 4) were associated with a boost in yields. The NGST counterfactual makes up ~10% of tropic’s Mg and kcal gaps. However, in the temperate region we find evidence of the expected impact of increasing NGS temperatures on yield: the NGST counterfactual makes up –3% or –4% and –3% or –2% of the temperate region’s Mg and kcal gaps, respectively. Changes in growing season precipitation had no effect on global or regional yields.
Recent change in cropped soil quality and cropland footprint had a negligible effect on yield growth. Recent changes in the quality of cropped land around the world have had a mixed effect on yield growth. One way we measure the change in the quality of land a country crops on is by measuring the change in its cropped soil’s nutrient availability and retention capacity as its cropland footprint shifts across the landscape25. We also measure a country’s extensive change in footprint by tracking its net areal change in cropland over time. The extensive change in cropped area is a catch-all for the change in land quality conditions not measured by the change in the nutrient availability and retention capacity of cropped soils. We assume that a country’s most productive land has long been used for crops and net growth in cropland extent since 1975 will have had a negative impact on yield as only more marginal lands were available for cropping after 1975. For example, most of the globe’s 1975 to mid-2000s growth in cropland extent occurred in the tropics (Table 4). Further, the decline in the overall quality of cropped soil has been more dramatic in the tropics as more and more tropical forest area and their poor soils have been used for crops since 197526.
A general worsening in the nutrient availability and retention capacity of cropped soils across the globe was associated with slightly lower yields (Table 1 and Table 2). However, the extent of the loss was very small (the soil quality counterfactual makes up –0.2% to –1.2% of global Mg and kcal gaps). As expected, net growth in a cropped area was associated with a decline in global and tropical Mg yields. Again, however, the extent of the negative impact is relatively minor (the area cultivated counterfactual makes up –13% or –2% to of global Mg gaps and –7% or –5% of tropical Mg gaps). In contrast, and contrary to expectations, net growth in cropped area was associated with an increase in global and temperate region yields when measured in M kcals ha-1. Again, however, the extent of the gap created by net change in cropped area in these cases is relatively small (the area cultivated counterfactual makes up 5% or 16% of global kcals gaps and 12% or 19% of temperate region kcals gaps).
The counterintuitive positive relationship between net cropland expansion and higher M kcal ha-1 yield in the temperate region may hold for several reasons. First, it may be that land that was marginal for crops grown earlier in the 20th century became more suitable for the more kcal-denser crop mixes grown over the last 40 years. Second, land that was marginal given earlier technology and cultivars may have become increasingly productive, especially for kcal-rich crops, with emerging technology. Third, cropland across the world has generally become better connected to transportation infrastructure, thereby encouraging farmers to invest in their operations and potentially more than compensating for their land’s quality shortcomings14,27. Finally, we note that these counter intuitive results are less noticeable when using the wide dataset. In other words, the yield curves estimated with the long dataset may be biased upwards with respect to the area cultivated variable due to the omitted fertilizer variable.
Investment in land, machinery, and irrigation had little impact on recent yield growth. Surprisingly, investment in irrigation capacity and investment in land and equipment and machinery (Table 4) had very little effect on global and regional yields (see the irrigation capability and investment in land and equipment counterfactuals in Table 1 and Table 2). Increases in irrigation capacity had a positive effect on Mg and kcal yield across the globe and in both regions but no irrigation capacity counterfactual produced an integral larger than 4% of a gap. Further, investment in land and farm machinery and equipment appears to have contributed little to yield growth over time. Investment in land may have had little effect on yield because land development investment per cropped hectare only increased by 10% around the globe between 1975 and 2007 and actually fell over this time period in the tropics (Table 4). However, the lack of investment in land in the tropics was countered by a contemporaneous 60% increase in the value of farm machinery and equipment per cropped hectare in the region. The large increase in machinery and equipment use in the tropics vis-à-vis the temperate region may explain why the tropical integrals for the investment in land, machinery, and equipment counterfactual are larger than the analogous integrals for the temperate region. The investment in land, machinery, and equipment counterfactual makes up 6% of the tropic’s Mg gap (with both the wide and long model estimates) and 8% or 1% of the tropic’s kcal gap (with the wide and long model estimates, respectively).
Before we analyzed our two panel datasets with decision trees, we first transformed them into annual change datasets. These annual change datasets begin with each country’s 1975 to 1976 changes and end with each country’s 2001 to 2002 changes (wide dataset) or 2006 to 2007 changes (long dataset). Further, we transformed the continuous distributions of annual change in country-level yields into discrete distributions of three tertiles; low annual change (L), moderate annual change (M), and high annual change (H) (see Table 5 for an exact numerical definition of these categories).
Notes: A high yield change (“H”) in a country is given by a one year change of (0.158,10.1] Mg ha-1 or (0.354,30.2] M kcals ha-1 with the long dataset and (0.17,7.66] Mg ha-1 or (0.401,30.2] M kcals ha-1 with the wide dataset. A low yield change (“L”) in a country is given by a one year change of ([-10.2,-0.0647] Mg ha-1 or [-30.7,-0.197] M kcals ha-1 with the long dataset and [-10.2,-0.0703] Mg ha-1 or [-30.7,-0.208] M kcals ha-1 with the wide dataset. Input names in black refer to crop mix inputs, names in red refer growing season weather inputs, and names in blue refer to other input types.
The decision tree algorithm recursively partitions the dataset, eventually settling on n sets of decision sequences that predict outcomes of L, M, and H (n traversals of a tree, from the “root” that contains all the data to a “leaf” that contains a subset of the data)28–30. The partitioning of the data can be constrained by one or more pruning rules. We pruned trees to make them easier to interpret and to increase our confidence in their predictive power. Here, we pruned trees by mandating that each leaf node in a tree has at least 50 records that support the decision sequence leading to the leaf node. In other words, sets of country-level year-to-year changes in inputs could not be mapped as a branch unless at least 50 instances of that set were observed in the data. After meeting the pruning rules, the decision tree algorithm produced the sets of annual changes in agricultural inputs that best predicted whether a country had an L, M, or H categorical change in annual yield.
Unique combinations of yield metric {Mg ha-1, M kcals ha-1}, scale {globe, temperate, tropics}, and dataset {wide dataset, long dataset} means that we created 12 unique trees of annual yield change predictions. (see Supplementary Figure 1–Supplementary Figure 12). We summarize the 12 decision trees in several ways. First, we report on the accuracy and complexity of each tree (Table 5; Dataset 310). Second, we list all of the inputs that are found in the first three levels of a tree. We highlight these inputs because they do the most towards predicting annual change in a country’s yield. Third, we highlight the traversal in each tree with the highest number of records. These traversals indicate the annual changes in agricultural inputs that are most common across space and time. Finally, we indicate the traversals that generate the greatest proportion of high (H) and low (L) annual country-level yield changes in a tree. These traversals give the ranges in annual input change that, respectively, best predict a high and low annual yield change in a country.
We find that the trees constructed from the wide dataset are simpler (fewer traversals) than those constructed from the long dataset and the trees constructed with the change in Mg ha-1 yield metric are simpler than those constructed with the change in M kcal ha-1 yield metric. (The econometric analysis also indicates that the wide dataset with yield measured in Mg ha-1 fits the yield model better than the other three yield measure - dataset combinations.) In terms of prediction accuracy, the trees constructed over the temperate countries are better than the trees generated over all countries and tropical countries only, and the trees generated with yield measured in M Kcals ha-1 are better than the trees generated with yield measured in Mg ha-1. Therefore, annual yield changes in the temperate countries are explained by a narrower set of annual input changes than annual yield changes in the tropics. To put it another way, explanations of changes in tropical yields are messier.
Next we describe the inputs found closest to the roots of trees where the root of the tree contains all the data. We define “close to the root” as the first three levels of a tree from its root (the first three decisions). Changes in a country’s crop mix – change in relative area devoted to sugarcane, roots and tubers, and wheat – appear close to the roots of all 12 trees. In particular, sugarcane is found close to the root of all 12 trees and the roots and tubers crop category is found close to the root of all three trees formed with the long dataset when yield is measured in Mg ha-1. The annual change in DGSTs is close to the root of three of the four trees estimated over the tropical countries. Finally, change in cultivated area is found close to the root of the two trees estimated over the temperate countries when yield is measured in Mg ha-1. Therefore, the decision trees indicate that recent annual changes in yield across the globe were most associated with changes in crop mix and that each region had idiosyncratic drivers of yield change as well.
(In the decision tree analysis we de-trended the data by using annual changes; in the fixed-effects analysis we de-trended the data by including time as an explanatory variable. This means the decision tree analysis cannot account for the various unobserved inputs that are correlated with time.)
A gain in the proportion of a country’s crop mix devoted to sugarcane is the best predictor of high (H) yield change in five of the six trees created with the wide dataset and four of the six trees created with the long dataset. Prediction of the H category is a bit more complicated in the global trees estimated with the long dataset. According to trees estimated with the long dataset, gains in wheat and roots and tubers in the proportional mix of a country’s crop profile, modest changes in sugarcane’s contribution to the proportional mix, and growing seasons that had cooler daytime temperatures than the previous growing season were most likely to have led to a high annual gain in a country’s yield.
The best set of predictors for a negative change in annual yield (the L yield category) is a bit more expansive than the sets of best predictors for the H yield category. Not surprisingly, losses in proportion of a country’s crop mix devoted to sugarcane are found in all tree branches with the highest proportion of L observations. In the tropics, a one-year gain in DGST and NGST were also associated with yield losses from one year to the next. Finally, an increase in a country’s cultivated area from one year to the next was associated with a negative change in a temperate country’s Mg ha-1 yield.
When we compare the decision trees (Table 5) to the econometrically estimated counterfactual results (Table 1 and Table 2) several similarities and differences emerge. First, both analyses highlight that changes in crop mix have been one of the most important contributions to the gain in crop yields over the last 40 years. The decision tree analysis also reinforces the econometric evidence that gains in DGSTs dampened gains in yields more in the tropics than in the temperate region. The trees, like the counterfactual analysis, also suggest that investment in irrigation, land, machinery, and equipment and the quality of cropped soil had little effect on yield change. The counterfactual and the decision tree analyses disagree on the importance of fertilizer use in explaining yield gains over the last 40 years, however; the counterfactual analysis deems this input more important than the decision tree analysis.
Improvements in agricultural technology, management, and science, changes in crop mix, and increased fertilizer use were responsible for the lion’s share of yield improvement around the world from 1975 to 2007. The negative yield impacts associated with increases in growing season temperatures were smaller. In some cases, the changes in the quality of land used for crops and cropland footprint were just as detrimental to yields as changes in climate.
The downward pressure on crop yields due to climate change will worsen in the future (e.g., 31). We see two paths to continued yield improvements despite this growing drag on yields. First, investment in agricultural technology, chemical inputs, management, and science in the tropics is vitally important (the so-called closing of “yield gaps”15). As indicated by the “time” counterfactuals, the tropics have not yet experienced the agricultural science and management revolution that the temperate region has. Second, if each country can increasingly specialize in the crops best suited for their (changing) climate and trade for the rest of their crop needs, then the spatial allocation of crops will become more efficient. For example, our results suggest the continued divestment in grain production in the tropics and greater investment in grain production in the temperate zone would do much to boost food production in the future. Further, greater fruit and sugarcane production in the tropics relative to the temperate zone would also help accelerate food production32. More trade liberalization and the reduction or even elimination of national crop subsidy programs will make it easier for each country to grow the crops best suited for their soil-climate conditions13.
Several suggested paths to greater food production are not supported by our analysis. Cropland extensification contributed little to yield gains in the immediate past and are not likely to do so in the future27. Instead, switching to more climate-appropriate crops, using more fertilizers, chemicals and improved cultivars, and improving the nutrient retention capability of already existing cropland appears to be a more effective strategy for increasing worldwide yields and, ultimately, food production (i.e., land sparing versus land sharing; 33). This strategy would also leave more land for nature in an increasingly populated world. Further, we are also skeptical that an emphasis on investment in infrastructure in of itself (i.e., machinery and irrigation capacity) will significantly increase yields in the future; these investments did not do much to boost crop production in the recent past. Machinery that is compatible with precision agriculture (i.e., technology) is likely to be more effective than just more tractors and other machinery. Of course, the recommendation on investment in irrigation could change if climate change severely disrupts current rainfall patterns.
This analysis is limited by several data issues. First, our treatment of weather data (see Materials and Methods) did not allow us to isolate changes in growing season weather due to spatial reallocation of cropland versus changes in the atmospheric system. Separating these trends would help us better understand the effect of recent climate change on crop yields around the world. Another shortcoming of this analysis is that it does not specifically account for farmer reaction to climate change; this omission could bias our results. For example, if the changes in the spatial pattern of production and crop choice were partially affected by climate change, then we have underestimated the impact of climate change and overestimated the impact of crop choice and cropped-footprint change on recent yield trends. In addition, we are missing data for all countries that were in the Soviet Union and many Warsaw Pact countries (e.g. Poland and Hungary). One of the data sources we used to construct our panel datasets does not contain a consistent set of data back to 1975 for these countries. Most of these countries are in the temperate region. Therefore, our analysis, especially the temperate region analysis, could be biased due to the omission of these countries from the dataset. Further, the source of our gridded crop maps stopped providing annual grid cell maps of global cropland beyond 200734. Thus our dataset ends with 2007 data and cannot be extend into the early 2010s. Finally, to conduct this analysis, we either had to summarize the native grid-level data on cropped soil quality and growing season weather at the country level or we had to decompose the native country-level data on production, crop mix, and investment to the grid-cell level. We used the former approach.
A limitation of our decision tree analysis is that trees are constructed in a “greedy” fashion, iteratively splitting on the most powerful agricultural inputs (in a predictive sense) as the branches are built; this can lead to suboptimal trees when there are nonlinear interactions among the variables. Quinlan’s C4.5 algorithm28 for the decision tree approach strives to mitigate the biasing effect of the iterative tree-building approach by repeatedly building a tree with a subset of the data and assessing its quality on the held-out data to find the most robust trees; the RWeka decision-tree packaged used for this analysis is a slightly updated version of C4.5. Additionally, we could do more to explore the sensitivity of tree results to different transformations of the data, for example, whether the trees would have greater explanatory power if change in yield outcomes were transformed to a discrete distribution of four categories instead of three.
First, we used the method of least squares to estimate a fixed effects model of annual per hectare crop yield at the country level from years ṯ through t̄.
where Yct is the production of all crops grown in country c in harvest year t, measured either in metric tons (Mg) or millions of kilocalories (M kcals), divided by harvested hectares in country c in harvest year t (harvest year t refers to crops harvested in year t, but not necessarily planted in year t; for example, grain can be planted in October and harvested the next March in many southern hemisphere countries). Further, αc is the fixed effect intercept for country c, Xct is a vector of harvested hectare percentages across crop or crop groups in country c in harvest year t (collectively Xct gives a country’s “crop mix” in harvest year t; see the Supplementary Methods for more on Xct, 11), Kct contains variables that measure investment in agricultural land and agricultural machinery and equipment per harvested hectare c in harvest year t (11; http://faostat3.fao.org/home/E) Act is the harvested or cropped hectarage in country c in year t11, Sct summarizes the quality of soil used to grow crops in country c in harvest year t25, Ict is the percentage of harvested area equipped for irrigation in c in harvest year t11, Zct is a vector of statistics that summarize the weather that occurred over country c’s cropland during the growing season of harvest year t8,9, and Fct measures kg ha-1 of fertilizers used in country c in year t11.The land investment variable in vector Kct measures major improvements in the quantity, quality or productivity of land or prevention of deterioration. Activities such as land clearance, land contouring, creation of wells and watering holes are integral to the land improvement. The concept of land improvement includes 1) field improvements undertaken by farmers (e.g., making boundaries, irrigation channels) and 2) other activities undertaken by government and other local bodies such as irrigation works, soil-conservation works, and flood-control structure. The machinery and equipment investment variable in vector Kct measures the value of tractors, harvesters and thrashers, milking machines and hand tools in a country.
See the section ‘Creating country-level data for crop yield model and decision tree analysis’ for more information on how we constructed the variables in the vector Zct.
In the estimate of model (1) using the “long” dataset (Dataset 29) Fct is not included and time ṯ equals 1975 and time t̄ equals 2007. In the estimate of model (1) using the “wide” dataset (Dataset 18) Fct is included and time ṯ equals 1975 and time t̄ equals 2002. We estimate the long and wide versions of model (1) with all countries, tropical countries only, and temperate countries only. A country’s regional affiliation is defined by the latitude of the country’s capital and the Tropics of Cancer and Capricorn. Model (1) was estimated with the reg command in Stata 12.1. See Supplementary Table 1 and Supplementary Table 2 for estimates of model (1), including estimated standard errors and p-values. Stata code and related databases can be found in Supplementary materials under Stata Files.
We built expected yield curves for country c, Ŷct for years ṯ through t̄, by running the country’s input data from years ṯ to t̄ through an estimate of model (1),
where a “^” indicates an estimate (see Supplementary Table 1 and Supplementary Table 2 for estimated coefficients). Each country has eight expected yield curves, one for each unique combination of yield measure {Mg ha-1, M kcals ha-1}, scale {globe, appropriate region}, and dataset {long, wide}. Using these country-level yield curves we calculated four expected global yield curves, one for each unique combination of yield {Mg ha-1, M kcals ha-1} and dataset {long, wide} and eight expected regional yield curves, one for each unique combination of yield measure {Mg ha-1, M kcals ha-1}, scale {temperate, tropics}, and dataset {long, wide}. To construct a global or regional yield curve, Ŷrt for years ṯ through t̄, we averaged Ŷct for each year t across all c in r (globe, temperate, tropics) weighed by each country’s cropped hectarage in year t,In Figure 1, we present the global Ŷrt for years 1975 through 2007 (the long dataset) where yield is measured in Mg ha-1 (black solid curve in Figure 1A) and M kcals ha-1 (black solid curve in Figure 1B).
We built counterfactual yield curves for country c, Ỹct for years ṯ through t̄, by running the country’s input data from years ṯ to t̄ through an estimate of model (1), holding one or more of c’s inputs fixed at 1975 levels (the exception is a growing season weather counterfactual; in those cases, we fix the appropriate input at the 1975–1977 annual average). Each country has 84 counterfactual yield curves for the years ṯ through t̄, one for each unique combination of yield measure {Mg ha-1, M kcals ha-1}, scale {globe, appropriate region}, and 10 counterfactuals with the long dataset and 11 counterfactuals with the wide dataset. Using these country-level counterfactual yield curves, we calculated 42 counterfactual global-yield curves, one for each unique combination of yield measure {Mg ha-1, M kcals ha-1} and 10 counterfactuals with the long dataset and 11 counterfactuals with the wide dataset and 84 expected regional yield curves, one for each unique combination of yield measure {Mg ha-1, M kcals ha-1}, scale {temperate, tropics}, and 10 counterfactuals with the long dataset and 11 counterfactuals with the wide dataset. To construct a global or regional counterfactual yield curve, Ỹrt for years ṯ through t̄, we averaged Ỹrt for each year t across all c in r, weighed by each country’s cropped hectarage in year t,
where Act = Ac,1975 for all t in the numeraire and “area cultivated” counterfactuals. In Figure 1, we present the global Ỹrt for the numeraire counterfactual (all inputs other than weather inputs are fixed at 1975 levels) for years 1975 through 2007 (the long dataset) where yield is measured in Mg ha-1 (blue solid curve in Figure 1A) and M kcals ha-1 (blue solid curve in Figure 1B).In the mean columns of Table 1 and Table 2 we present the counterfactual integrals,
where q indexes the counterfactual, m indicates yield measure {Mg ha-1, M kcals ha-1}, r indicates scale {globe, temperate, tropics}, and d indicates dataset {long, wide} (Figure 2). To normalize these integrals we also present the fraction of the numeraire counterfactual integral, λconterfactual,m,r,d, that counterfactual q’s integral “explains,” where we call λcounterfactual,mrd r’s “m” gap using dataset d.The counterfactual analyses were conducted with MATLAB R2013a. MATLAB code and related databases can be found in Supplementary materials under MATLAB Code for Table 1 and Table 2.
We generated the “low” and “high” results for each q, m, r, and d counterfactual combination in the following manner (Table 1 and Table 2). First, we created 1000 unique vectors of model (1) coefficients by randomly drawing from the multivariate normal distribution with a mean of (the estimated vector of beta coefficients) and a covariance matrix of,
where σ is estimated model (1)’s root mean square error, N is the number of observations in the dataset, is a random variable with a chi-square distribution with N degrees of freedom, and vcov is estimated model (1)’s variance-covariance matrix for all β’s. (We do not vary the estimated αc coefficients.)Second, using the 1000 randomly generated β coefficient vectors, we generated 1000 values of Ŷctmd for all c and t for each unique m and d combination and 1000 values of Ỹqctmd for all c and t for each unique q, m, and d combination. Third, we generated expected 25th and 75th percentile yield curves for each country and each unique m and d combination by selecting the 25th percentile and 75th percentile values of Ỹctmd at each t. Fourth, we generated counterfactual 25th and 75th percentile yield curves for each country and each unique q, m, and d combination by selecting the 25th percentile and 75th percentile values of Ỹqctmd at each t. Fifth, we calculated a region or the globe’s expected percentile yield in year t with,
for each unique m and d combination where the superscripts “25” and “75” indicate the 25th and 75th percentile, respectively. Sixth, we calculated the globe or region’s counterfactual percentile yield in year t with, for each unique q, m and d combination. Finally, in the low and high columns of Table 1 and Table 2 we present the percentile counterfactual integrals for a given region r,We constructed decision trees using the RWeka package in R (RWeka 0.4-24 and RWekajars 3.7.12.-1) and J48 classifiers in particular. These are a reimplementation of Quinlan’s C4.5 algorithm28. We evaluated trees for prediction accuracy using a 10-fold cross-validation strategy. Decision trees are given in Supplementary Figure 1–Supplementary Figure 12, and the results are summarized in Table 5. In the analysis reported here, “leaf nodes” (the resulting subsets of the data after the branching of the tree on decision variables) were required to contain at least 50 observations, using the M option to control the minimum number of instances per leaf. This approach was used to yield trees with higher human interpretability as well as higher prediction accuracy. While 50 is somewhat arbitrary, we explored other values and empirically found it to lead to high prediction accuracy and greater interpretability in the resulting trees. (Interestingly, this approach also worked better for this data than using the C option to control the “confidence” in the pruned trees.)
To create country-level summary statistics of the quality of cropped soil (Sct) and growing season weather over cropland (contained in vector Zct) in each country in each harvest year t we used annual global grid cell maps of cropped land34 along with gridded global maps of soil quality25, monthly weather8, and growing season months9. (Ramankutty and Foley stopped updating annual global grid-cell maps of cropped land after releasing the 2007 data. Thus, our dataset ends with 2007 data.) By combining the gridded maps on soil, weather, and growing season months with gridded cropland maps we were able to create summary statistics that preserved the observed spatial heterogeneity in agronomic conditions across a county in any given year. For example, consider the landscape in Figure 4. Suppose the square landscape represents a country. Assume the large number in each grid cell in Figure 4A represents the number of cropland hectares in that cell in harvest year t (the small number in the corner of a cell is its ID number). In Figure 4B each cell’s nutrient availability score is given where a 1 indicates ‘No or slight nutrient constraint’, 2 indicates ‘moderate nutrient constraint’, 3 indicates ‘severe nutrient constraint’, 4 indicates ‘very severe nutrient constraint’, and 5 indicates ‘mainly non-soil’ (in other words, lower scores mean better soil quality; see 25. Nutrient availability (Nct) is decisive for successful low-level-input farming and, in some cases, intermediate-input-level farming. A country’s composite nutrient availability score on cropland in harvest year t is the weighted average of the nutrient availability scores across all cropland area in the country in harvest year t or,
where j ∈ c is the set of grid cells in country c, Nj is grid cell j’s nutrient availability score, and Ajt is grid cell j’s cropland area in harvest year t34. In the illustrative country represented in Figure 4 Nct is equal to,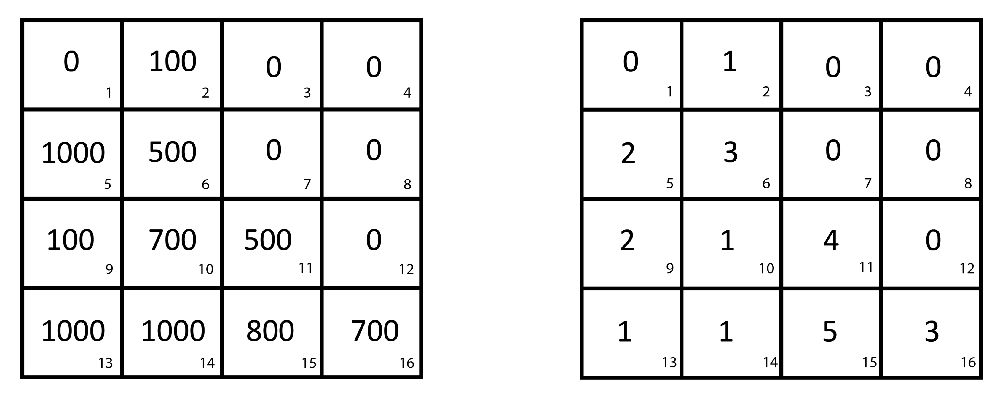
Harvested hectares in each grid cell in an illustrative country (A) where the small numbers in the corner of a grid cell indicate cell ID. Nutrient availability score (Nct) in each grid cell (B) where 1 indicates ‘No or slight nutrient constraint’, 2 indicates ‘moderate nutrient constraint’, 3 indicates ‘severe nutrient constraint’, 4 indicates ‘very severe nutrient constraint’, and 5 indicates ‘mainly non-soil’25.
We use the same method to calculate a country’s nutrient retention score, given by Uct. Nutrient retention capacity is of particular importance for the effectiveness of fertilizer applications and is therefore of special relevance for intermediate and high input level cropping conditions. The explanatory soil statistic used in the model, Sct, is the average of Nct and Uct.
The weather vector Z includes weather statistics that summarize the weather conditions over a country’s cropland during the growing season. We summarized each weather variable at the country level in year t with a procedure very similar to that used to find the country-level cropland soil statistic S. Let DGSTjmt and NGSTjmt indicate the average daytime high and nighttime low temperature in grid cell j in month m of harvest year t (measured in degrees Celsius)8. Let DGSTjt and NGSTjt indicate the average of DGSTjmt and NGSTjmt, respectively, across grid cell j’s growing season months of harvest year t where we use a grid cell’s growing season months for maize to define growing season. Let Pjt be the total precipitation in grid cell j during the cell’s growing season in harvest year t (measured in millimeters). If a crop was harvested in the spring of year t then some of the weather that contributes to DGSTjt, NGSTjt, and Pjt occurred in the final months of year t – 1. Let DGSTct, NGSTct, and Pct measure the average monthly daytime high, monthly nighttime low, and growing season precipitation, respectively, over c’s cropland during the course of growing season t where weather data is weighted by cropland density in grid cell j.
where Ajt is the area of grid cell j that was cropped in year t. The weather vector Zct in model (1) also includes the squares of DGSTct, NGSTct, and Pct.MATLAB code was used to construct Sct, DGSTct, NGSTct, and Pct. The code and related databases can be found in Supplementary materials under MATLAB Code for creating country-level variables.
Maps of 1975 – 1977 to 2005 – 2007 country-level changes in various model (1) inputs are given in Supplementary Figure 13–Supplementary Figure 21. These figures can be found Supplementary material under the zip file Supplementary Figures.
Dataset 1. “Wide” dataset. doi, 10.5256/f1000research.10419.d1463388
1. ID: UNFAO Country Code
2. Year
3. Tropical: a 1 indicates that that country is a tropical country and a 0 indicates that the country is a temperate country
4. tons/ha: a country's crop yield in year t in metric tons/ha (I summed all tons of crops produced in a country and divided by total cropped hectares in a country)
5. million kcals/ha: a country's crop yield in year t in millions of kcals/ha (I summed all kcals of crops produced in a country and divided by total cropped hectares in a country)
6. soilscore: The composite soil quality score of the land that was cropped in year t in country k (on a 1 to 5 scale with lower numbers indicating better soil).
7. ha: total cropped hectares in year t in country k
8. rice: percentage of cropped area in rice in year t in country k
9. wheat: percentage of cropped area in wheat in year t in country k
10. sugar: percentage of cropped area in sugarcane in year t in country k
11. grains: percentage of cropped area in coarse grains in year t in country k
12. oil: percentage of cropped area in oil crops in year t in country k
13. fruits: percentage of cropped area in fruits in year t in country k
14. roots: percentage of cropped area in roots and tubers in year t in country k
15. other: percentage of cropped area in all other crops in year t in country k
16. davg: The composite average daytime temperature over cropped lands during the growing season year t in country k (Celsius)
17. navg: The composite average nighttime temperature over cropped lands during the growing season year t in country k (Celsius)
18. pavg: The total rainfall over cropped lands during the growing season year t in country k (mm)
19. irr: Fraction of cropped lands that are equipped for irrigation in year t in country k
20. land: total money invested in agricultural land development divided by cropped hectares in year t in country k (2005 constant US $/ha)
21. eqp: total money invested in agricultural equipment divided by cropped hectares in year t in country k (2005 constant US $/ha)
22. fert: kilograms of fertilizer used in the country divicde by cropped hectares in year t in country k.
Dataset 2. “Long” dataset. doi, 10.5256/f1000research.10419.d1463399
1. ID: UNFAO Country Code
2. Year
3. Tropical: a 1 indicates that that country is a tropical country and a 0 indicates that the country is a temperate country
4. tons/ha: a country's crop yield in year t in metric tons/ha (I summed all tons of crops produced in a country and divided by total cropped hectares in a country)
5. million kcals/ha: a country's crop yield in year t in millions of kcals/ha (I summed all kcals of crops produced in a country and divided by total cropped hectares in a country)
6. soilscore: The composite soil quality score of the land that was cropped in year t in country k (on a 1 to 5 scale with lower numbers indicating better soil).
7. ha: total cropped hectares in year t in country k
8. rice: percentage of cropped area in rice in year t in country k
9. wheat: percentage of cropped area in wheat in year t in country k
10. sugar: percentage of cropped area in sugarcane in year t in country k
11. grains: percentage of cropped area in coarse grains in year t in country k
12. oil: percentage of cropped area in oil crops in year t in country k
13. fruits: percentage of cropped area in fruits in year t in country k
14. roots: percentage of cropped area in roots and tubers in year t in country k
15. other: percentage of cropped area in all other crops in year t in country k
16. davg: The composite average daytime temperature over cropped lands during the growing season year t in country k (Celsius)
17. navg: The composite average nighttime temperature over cropped lands during the growing season year t in country k (Celsius)
18. pavg: The total rainfall over cropped lands during the growing season year t in country k (mm)
19. irr: Fraction of cropped lands that are equipped for irrigation in year t in country k
20. land: total money invested in agricultural land development divided by cropped hectares in year t in country k (2005 constant US $/ha)
21. eqp: total money invested in agricultural equipment divided by cropped hectares in year t in country k (2005 constant US $/ha)
Dataset 3. Accuracy of decision trees. doi, 10.5256/f1000research.10419.d14634010
E.J.N. did everything other than construct the decision trees. C.B.C constructed the decision trees. C.B.C. also wrote and edited portions of the text.
The authors wish to thank Jae Bradley, Clarissa Hunnewell, and Isabel Schwartz, undergraduates at Bowdoin College, for help with putting datasets together and analyzing data.
Supplementary Figures 1–21:
Click here to access the data.
(1) Decision tree for globe, yield measured in Mg ha-1, using the “long” dataset.
(2) Decision tree for temperate region, yield measured in Mg ha-1, using the “long” dataset.
(3) Decision tree for tropics, yield measured in Mg ha-1, using the “long” dataset.
(4) Decision tree for globe, yield measured in M kcals ha-1, using the “long” dataset.
(5) Decision tree for temperate region, yield measured in M kcals ha-1, using the “long” dataset.
(6) Decision tree for tropics, yield measured in M kcals ha-1, using the “long” dataset.
(7) Decision tree for globe, yield measured in Mg ha-1, using the “wide” dataset.
(8) Decision tree for temperate region, yield measured in Mg ha-1, using the “wide” dataset.
(9) Decision tree for tropics, yield measured in Mg ha-1, using the “wide” dataset.
(10) Decision tree for globe, yield measured in M kcals ha-1, using the “wide” dataset.
(11) Decision tree for temperate region, yield measured in M kcals ha-1, using the “wide” dataset.
(12) Decision tree for tropics, yield measured in M kcals ha-1, using the “wide” dataset.
(13) Percentage change in 1975–1977 to 2005–2007 growing season daytime temperature by country.
(14) Percentage change in 1975–1977 to 2005–2007 growing season nighttime temperature by country.
(15) Percentage change in 1975–1977 to 2005–2007 growing season precipitation by country.
(16) Percentage change in 1975–1977 to 2005–2007 soil score by country.
(17) Percentage change in 1975–1977 to 2005–2007 hectares of irrigation capacity per cropped hectare by country.
(18) Percentage change in 1975–1977 to 2005–2007 equipment investment ($2005) per cropped hectare by country.
(19) Percentage change in 1975–1977 to 2005–2007 land investment ($ 2005) per cropped hectare by country.
(20) Percentage change in 1975–1977 to 2005–2007 all crop M kcals per hectare yield by country.
(21) Percentage change in 1975–1977 to 2005–2007 all crop Mg per hectare yield by country.
Supplementary Table 1: Econometric estimates of fixed effects model (1) with the “long” global, tropics, and temperate datasets. Estimated coefficients with standard errors in parentheses. Standard errors are robust standard errors. ‘***’ indicates statistical significance at p = 0.01, ‘**’ indicates statistical significance at p = 0.05, and ‘*’ indicates statistical significance at p = 0.10. Country fixed effect coefficients and SE are available upon request.
Click here to access the data.
Supplementary Table 2: Econometric estimates of fixed effects model (1) with the “wide” global, tropics, and temperate datasets.
Click here to access the data.
Supplementary Methods: Crop groups used to define crop mix.
Click here to access the data.
MATLAB Code for Tables 1 and 2.
Click here to access the data.
MATLAB Code for creating country-level variables.
Click here to access the data.
Stata Files.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
References
1. Evenson RE, Gollin D: Assessing the impact of the green revolution, 1960 to 2000.Science. 2003; 300 (5620): 758-62 PubMed Abstract | Publisher Full TextCompeting Interests: No competing interests were disclosed.
Competing Interests: No competing interests were disclosed.
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 1 29 Dec 16 |
read | read |
Click here to access the data.
Spreadsheet data files may not format correctly if your computer is using different default delimiters (symbols used to separate values into separate cells) - a spreadsheet created in one region is sometimes misinterpreted by computers in other regions. You can change the regional settings on your computer so that the spreadsheet can be interpreted correctly.
Click here to access the data.
Spreadsheet data files may not format correctly if your computer is using different default delimiters (symbols used to separate values into separate cells) - a spreadsheet created in one region is sometimes misinterpreted by computers in other regions. You can change the regional settings on your computer so that the spreadsheet can be interpreted correctly.
Click here to access the data.
Spreadsheet data files may not format correctly if your computer is using different default delimiters (symbols used to separate values into separate cells) - a spreadsheet created in one region is sometimes misinterpreted by computers in other regions. You can change the regional settings on your computer so that the spreadsheet can be interpreted correctly.
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)