Keywords
Gene Ontology, Graphical Model, Gene Set Enrichment Analysis
Gene Ontology, Graphical Model, Gene Set Enrichment Analysis
Term Enrichment Analysis (TEA) is a common technique for finding functional patterns, specifically overrepresented ontology terms, in a set of experimentally identified genes1. The most common approach, which we refer to as Frequentist TEA, is a one-tailed Fisher’s Exact Test (based on the hypergeometric distribution, which models the number of term-associations if the gene set was chosen by chance), with a suitable correction for multiple hypothesis testing. Frequentist TEA has been implemented many times on various platforms1–8.
A model-based alternative to Frequentist TEA, which more directly addresses some of the multiple testing issues (for example, by modeling the ways that an observed gene list can be broken down into complementary gene sets), is Bayesian TEA. In contrast to Frequentist TEA, which just rejects a null hypothesis that genes are chosen by chance, the Bayesian TEA explicitly models the alternative hypothesis that the gene set was generated from a few random ontology terms. This approach was introduced by 9 and further developed by 10, who implemented model-based testing in Java and R11. However, the model-based approach remains significantly less well-explored than frequentist approaches.
The graphical model underpinning Bayesian TEA is sketched in Figure 1. For each of the m terms there is a boolean random variable Tj (“term j is activated”). For each of the n genes there is a directly-observed boolean random variable Oi (“gene i is observed in the gene set”), and one deterministic boolean variable Hi (“gene i is activated”) defined by Hi = 1 − (1 − Tj), where Gi is the set of terms associated with gene i (including directly annotated terms, as well as ancestral terms implied by transitive closure of the directly annotated terms). The probability parameters are π (term activation), α (false positive) and β (false negative), and the respective hyperparameters are p = (p0, p1), a = (a0, a1) and b = (b0, b1).

Other variables and hyperparameters are defined in the text. Circular nodes indicate continuous-valued variables or hyperparameters; square nodes indicate discrete-valued (boolean) variables. Dashed lines indicate deterministic relationships; shaded nodes indicate observations. Plates (rounded rectangles) indicate replicated subgraph structures.
The model is
with π ∼ Beta(p), α ∼ Beta(a) and β ∼ Beta(b). The model of 10 is similar, but uses an ad hoc discretized prior for π, α and β .
Most Bayesian and Frequentist TEA implementations are designed for desktop use. Several Frequentist TEA implementations are designed for the web, such as DAVID-WS6 and Enrichr8,12,13, which has a rich dynamic web front-end. However, web-facing Frequentist TEA implementations generally require a server-hosted back end that executes code. Further, there are no JavaScript-based Bayesian TEA implementations, and no web-facing implementations other than the Java-based Ontologizer which can be loaded via Java Web Start.
In order to further explore the model-based TEA and compare it to Frequentist TEA, and to make these investigations accessible to researchers in a way that would be easily embeddable in static websites, we developed WTFgenes, a JavaScript implementation of both approaches with (for time-sensitive applications) a parallel C++ implementation that is numerically identical.
We note in passing that Fisher’s Exact Test—which we call Frequentist TEA—was originally motivated by a blind tea-tasting challenge14.
In developing our Bayesian TEA sampler, we introduce a collapsed version of the model in Figure 1 by integrating out the probability parameters. Let cp = Tj count the number of activated terms, cg = Hi the activated genes, ca = Oi (1 – Hi) the false positives and cb = Oi Hi the false negatives.
Then
P(T, O|a, b, p) = Z(cp;m, p)Z(ca; n – cg, a)Z(cb; cg, b)
where
is the beta-Bernoulli distribution for k ordered successes in N trials with hyperparameters A= (A0, A1), using the beta function
Integrating out probability parameters improves sampling efficiency and allows for higher-dimensional models where, for example, we observe multiple gene sets and give each term its own probability πj or each gene its own error rates (αi, βi). Our implementation by default uses uninformative priors with hyperparameters a = b = p = (1, 1), but this can be overridden by the user.
The MCMC sampler uses a Metropolis-Hastings kernel15. Each proposed move perturbs some subset of the term variables. The moves include flip, where a single term is toggled; step, where any activated term and any one of its unactivated ancestors or descendants are toggled; jump, where any activated term and any unactivated term are toggled; and randomize, where all term variables are uniformly randomized. The relative rates of these moves can be set by the user.
The sampler of 10 implemented only the flip move. To test the relative efficacy of the newly-introduced moves we measured the autocorrelation of the term variables for a dataset of 17 S.cerevisiae genes involved in mating (The gene IDs used in this evaluation, for purposes of reproduction, were: STE2, STE3, STE5, GPA1, SST2, STE11, STE50, STE20, STE4, STE18, FUS3, KSS1, PTP2, MSG5, DIG1, DIG2, STE12. Other representative gene sets for yeast may be obtained from the Gene Ontology website at http://geneontology.org/experimental/enrichment-genesets/yeast/ and several of these are bundled with the example dataset in the WTFgenes repository). The results, shown in Figure 2, led us to set the MCMC defaults, such that the flip, step, and jump moves are equiprobable, while randomize is disabled.
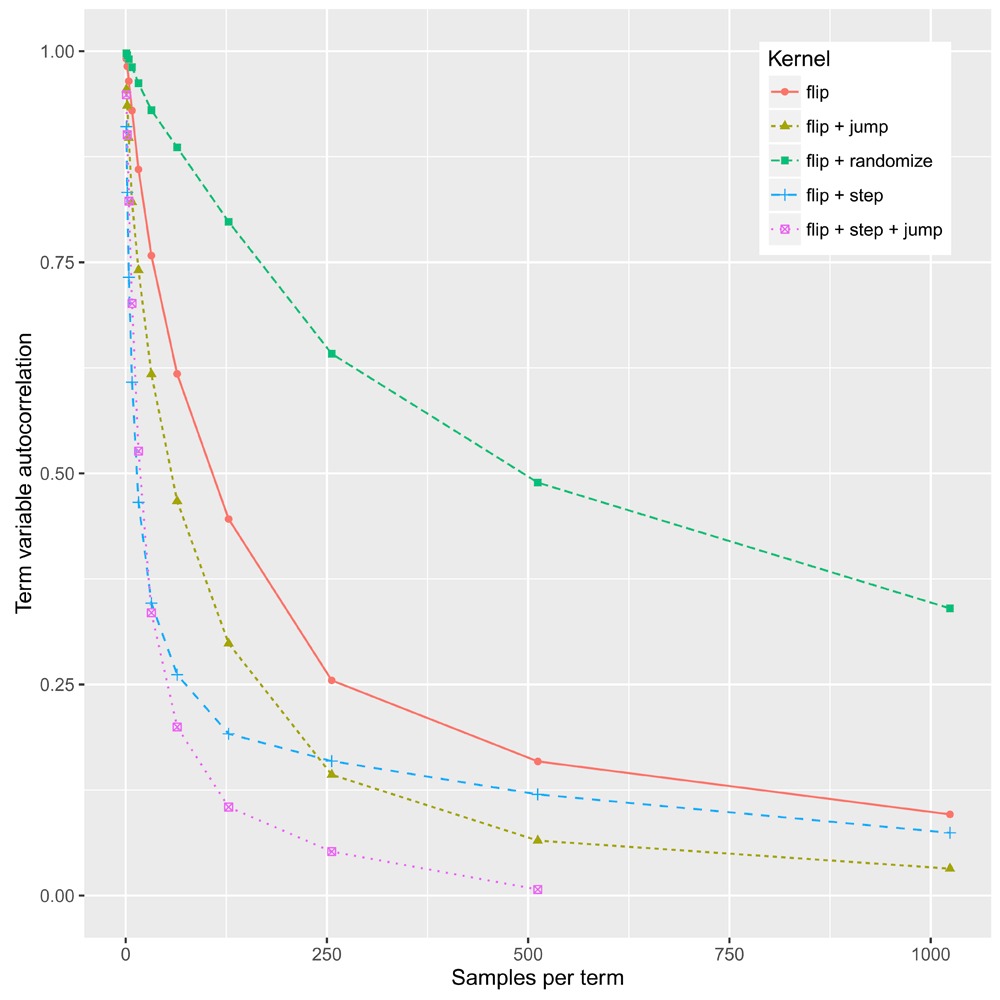
A rapidly-decaying curve indicates an efficiently-mixing kernel. The kernel incorporating flip, step and jump moves (defined in the text) mixes most efficiently.
We have implemented both Frequentist TEA (with Bonferroni correction) and Bayesian TEA (as described above), in both C++11 and JavaScript. The JavaScript version can be run as a command-line tool using node, or via a web interface in a browser, and includes extensive unit tests. The two implementations use the same random number generator and yield numerically identical results.
Our JavaScript software, when used as a web application, offers a “quick report” view using Frequentist TEA. For the slower-running, but more powerful, Bayesian TEA, the software plots the log-likelihood during an MCMC sampling run, for visual feedback. The repository includes setup scripts allowing the tool to be deployed as a “static site”, i.e. consisting only of static files (HTML, CSS, JSON, and JavaScript) that can be hosted via a minimal web server with no need for dynamic code execution. This has considerable advantages: static web hosting is generally much cheaper, and far more secure, than running server-hosted web applications.
An example WTFgenes static site, configured for the GO-basic ontology and GO-annotated genomes from the Gene Ontology website, can be found at https://evoldoers.github.io/wtfgo.
An earlier version of this article can be found on bioRxiv (doi: 10.1101/114785).
When compiled using clang, the C++ version of WTFgenes is about twice as fast as the JavaScript version: a benchmark of Bayesian TEA on a late-2014 iMac (4GHz Intel Core i7), using the above mentioned 17 yeast mating genes and the relevant subset of 518 GO terms, run for 1,000 samples per term, took 37.6 seconds of user time for the C++ implementation and 79.8 seconds in JavaScript.
By contrast, the Frequentist TEA approach is almost instant. However, its weaker statistical power is apparent from Figure 3, which compares the recall vs specificity of Bayesian and Frequentist methods on simulated datasets (The full workflow for this simulation is available at http://doi.org/10.5281/zenodo.40060816). For values of N from 1 to 4, we sampled N terms from the S.cerevisiae subset of the Gene Ontology, and generated a corresponding set of yeast genes with false positive rate 0.1% and false negative rate 1%. The MCMC sampler was run for 100 iterations per term, and this experiment was repeated 100 times. The model-based approach has vastly superior recall to the Fisher exact test, and the difference grows with the number of terms.
JavaScript genome browsers, such as JBrowse17, represent a broader web trend of producing static sites where possible, for reasons of security and performance. We have implemented such a static site generator for ontological term enrichment analysis of gene sets that offers both Bayesian and frequentist tests. In contrast with existing web services for Frequentist TEA, such as DAVID-WS or Enrichr, it requires no server resources and allows comparison of Bayesian and Frequentist approaches.
Model-based TEA is versatile: it can readily be extended to allow for datasets that are structured temporally18, spatially19, or by genomic region20; to use domain-specific biological knowledge21; or to incorporate additional lines of evidence such as quantitative data22. We hope our development of a collapsed likelihood, and evaluation of different MCMC kernels, will assist these efforts.
Latest source code: https://github.com/evoldoers/wtfgenes
Archived source code as at time of publication: http://doi.org/10.5281/zenodo.40060623
Software license: BSD3
A demonstration for the Gene Ontology is usable at https://evoldoers.github.io/wtfgo.
A Makefile-driven simulation study underpinning results reported in this paper is available at http://doi.org/10.5281/zenodo.40060816.
IH designed the method, wrote the software, performed the analyses, and wrote the manuscript. CM suggested the idea, consulted on the design of the software and corrected errors in the manuscript.
IHH was partially supported by NHGRI (grant HG004483). CJM was partially supported by Office of the Director (R24-OD011883) and the Director, Office of Science, Office of Basic Energy Sciences, of the US Department of Energy (Contract No. DE-AC02-05CH11231).
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the rationale for developing the new software tool clearly explained?
Yes
Is the description of the software tool technically sound?
Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?
Partly
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?
Partly
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?
Partly
Competing Interests: No competing interests were disclosed.
Is the rationale for developing the new software tool clearly explained?
Partly
Is the description of the software tool technically sound?
Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?
Partly
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?
Partly
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?
No
References
1. Pan KH, Lih CJ, Cohen SN: Effects of threshold choice on biological conclusions reached during analysis of gene expression by DNA microarrays.Proc Natl Acad Sci U S A. 2005; 102 (25): 8961-5 PubMed Abstract | Publisher Full TextCompeting Interests: No competing interests were disclosed.
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 1 04 Apr 17 |
read | read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)