A simple mathematical approach to the analysis of polypharmacology and polyspecificity data

Gerry Maggiora; Vijay Gokhale

doi:10.12688/f1000research.11517.1

Home Browse A simple mathematical approach to the analysis of polypharmacology...

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

A simple mathematical approach to the analysis of polypharmacology and polyspecificity data

[version 1; peer review: 3 approved, 1 approved with reservations]

Gerry Maggiora ¹, Vijay Gokhale¹

PUBLISHED 06 Jun 2017

Author details Author details

¹ BIO5 Institute, University of Arizona, 1657 East Helen Street, Tucson, AZ, 85719, USA

OPEN PEER REVIEW

REVIEWER STATUS

This article is included in the Cheminformatics gateway.

Abstract

There many possible types of drug-target interactions, because there are a surprising number of ways in which drugs and their targets can associate with one another. These relationships are expressed as polypharmacology and polyspecificity. Polypharmacology is the capability of a given drug to exhibit activity with respect to multiple drug targets, which are not necessarily in the same activity class. Adverse drug reactions (‘side effects’) are its principal manifestation, but polypharmacology is also playing a role in the repositioning of existing drugs for new therapeutic indications. Polyspecificity, on the other hand, is the capability of a given target to exhibit activity with respect to multiple, structurally dissimilar drugs. That these concepts are closely related to one another is, surprisingly, not well known. It will be shown in this work that they are, in fact, mathematically related to one another and are in essence ‘two sides of the same coin’. Hence, information on polypharmacology provides equivalent information on polyspecificity, and vice versa.
Networks are playing an increasingly important role in biological research. Drug-target networks, in particular, are made up of drug nodes that are linked to specific target nodes if a given drug is active with respect to that target. Such networks provide a graphic depiction of polypharmacology and polyspecificity. However, by their very nature they can obscure information that may be useful in their interpretation and analysis. This work will show how such latent information can be used to determine bounds for the degrees of polypharmacology and polyspecificity, and how to estimate other useful features associated with the lack of completeness of most drug-target datasets.

Keywords

drugs, drug targets, polypharmacology, polyspecificity, networks, edge-colored, bipartite networks, latent information,

Corresponding author: Gerry Maggiora

Competing interests: No competing interests were disclosed.

Grant information: The author(s) declared that no grants were involved in supporting this work.

Copyright: © 2017 Maggiora G and Gokhale V. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Maggiora G and Gokhale V. A simple mathematical approach to the analysis of polypharmacology and polyspecificity data [version 1; peer review: 3 approved, 1 approved with reservations]. F1000Research 2017, 6(Chem Inf Sci):788 (https://doi.org/10.12688/f1000research.11517.1) First published: 06 Jun 2017, 6(Chem Inf Sci):788 (https://doi.org/10.12688/f1000research.11517.1) Latest published: 06 Jun 2017, 6(Chem Inf Sci):788 (https://doi.org/10.12688/f1000research.11517.1)

Introduction

The study of drug-target interactions and their manifestation in polypharmacology and polyspecificity is playing a major role in the growing field of chemogenomics in particular, and in drug research in general. Polypharmacology describes the multiplicity of drug targets against which a given compound exhibits some form of biological activity^1–6. A less appreciated characteristic of drug targets is their polyspecificity, namely the ability of multiple, structurally dissimilar drugs to exhibit biological activity against the same target.

The principal manifestation of polypharmacology is adverse drug reactions (‘side effects’), a phenomenon that has been recognized ever since the administration of the first drug^7,8. In an interesting turnabout, side-effect similarity has recently been used to identify drug targets⁹. A useful public data source called SIDER has also been developed; it links approximately 1000 drugs to nearly 1500 side effects¹⁰. An emerging role of polypharmacology is in the repositioning of existing drugs for new therapeutic indications¹¹.

The term polyspecificity was primarily used to describe antibody recognition, and has been around for more than three decades^12,13. It is only in the last few years, however, that it has been employed in the context of drug-target interactions. Consequently, there are fewer papers on this topic, and many of them deal with transporters and the efflux pumps that confer drug resistance^14–18, which is hardly a broad sample of biological activity. This is somewhat surprising, given that the polyspecificity of drugs has not always been explicitly recognized as such. For a number of years, it has been manifest in many different forms in drug research, under the guise of multiple lead series¹⁹, scaffold hopping²⁰, and pharmacophore-based structure-activity studies²¹. All of these applications suggest that diverse structures may nevertheless exhibit biological activity with respect to the same target. This view is further supported by more recent evidence on the surprising prevalence of similarity cliffs²², and indirectly by the enhanced effectiveness of group fusion in identifying new active compounds²³. These examples and the widespread occurrence of drug side effects suggest that some type of relationship might exist between polypharmacology and polyspecificity.

The alternative terminologies ‘drug promiscuity’ and ‘target promiscuity’ that are sometimes used instead of polypharmacology and polyspecificity, are slightly more general since they do not require the occurrence of biological activity, only that drugs and their targets interact (e.g., bind) in some specific fashion. Likewise, the term drug-target is sometimes replaced by the more general terms ligand-target or compound-target. However, the more popular although less general terms polypharmacology, polyspecificity, and drug-target will be used throughout the remainder of this work, with the caveat that their usage may sometimes be too narrow and may not always be strictly correct.

Recognition of the growing importance of polypharmacology in drug research and in biological research in general has resulted in the development of a number of drug-target databases^24–32 summarized in Table 1. A cursory examination of these databases shows that most drugs, as well as many xenobiotics, apparently exhibit very high degrees of polypharmacology. However, the data in these databases needs to be considered with caution, because it may not be of uniform quality since many experimental methods or computational techniques of varying accuracy may have been used in its generation. This is further exacerbated by the fact that reproducing biological data can be difficult even when the same experimental method is used in different laboratories, or even in the same ones! The paper by Jasial³³ provides an interesting discussion that is relevant to this point.

Table 1. Sample of drug-target databases available over the Internet given by name, web address, and reference number in this work.

	Name	Web Address	Reference
1	DrugBank	www.drugbank.ca	24
2	STITCH	stitch.embl.de	25
3	WOMBAT	sunsetmolecular.com	26
4	PubChem BioAssay	ncbi.nlm.nih.gov/pcassay	27
5	BindingDB	bindingdb.org/bind/index.jsp	28
6	ChEMBL	ebi.ac.uk/chembl/target	29
7	canSAR	cansar.icr.ac.uk	30
8	PROMISCUOUS	bioinformatics.charite.de/promiscuous	31
9	MATADOR	omictools.com/matador-tool	32

To counter this issue database developers have established ‘reliability scores’ based on criteria of data quality, but there is no uniform procedure that is applied in all cases. Hence, drug-target datasets assembled with data obtained from multiple, diverse sources are unlikely to be of uniform quality. And this can give rise to significant uncertainties in the inferences that are drawn from analyses of such datasets.

By contrast, a number of more stringent evaluations have led to significantly reduced values for degrees of polypharmacology of many drugs^33–36. But these values represent lower bounds to the true values, since the datasets from which these results are drawn are typically incomplete, an issue that is discussed further in this section. Additional study is certainly warranted in order to determine the true degree of polypharmacology for most drugs. As discussed in the following section, the multiplicity of ways that drugs can bind to a wide variety of different structural features in protein targets suggests the possibility that polypharmacology may be more prevalent than the most conservative view suggests. It does not, however, provide incontrovertible support for the extremely high degrees of polypharmacology implied by the data in many drug-target databases.

Data quality is not the only issue associated with drug-target datasets; another important concern is that of data completeness, as discussed in a recent paper by Mestres et al.³⁷. Data on all of the possible drug-target interactions within a given dataset of drugs and targets is generally unavailable, making a complete analysis of these interactions impossible. This issue is aggravated by the fact that almost all drug-target databases only report data on active compounds. The most complete datasets undoubtedly can be found in the laboratories of pharmaceutical companies, but since their data is proprietary it is of little value to researchers outside of these companies. The problem of data availability is also affected by biases that arise from the popularity of particular research areas such as GPCRs, ion channels, protein kinases, and proteases, which make up a significant portion of all targets in drug discovery research³⁸.

The crux of this paper is based on an analysis of the relationship between polypharmacology and polyspecificity, and it is demonstrated that they represent mathematical duals of one another. We describe (1) a rigorous mathematical relationship between polypharmacology and polyspecificity, based on a simple mathematical argument, and (2) an analysis of the latent information associated with drug-target interactions, described by edge-colored bipartite drug-target networks. The use of edge-colored networks provides the means for establishing bounds on the degrees of polypharmacology and polyspecificity. A simple example of a drug-target network is presented in order to clarify a number of the technical points raised in this paper. Currently, there is greater research focus on polypharmacology, since it has a seemingly more direct relationship to the pharmacological behavior of drugs. However, as far as we can determine, a definitive study rigorously linking polypharmacology and polyspecificity has yet to be published by other authors.

Structural basis of drug-target interactions

It is important to recognize that polypharmacology and polyspecificity are purely phenomenological concepts. As such, they do not contain or require any specific structural information on the drugs or the targets they interact with. This is akin to classical chemical thermodynamics where, for example, the entropy, enthalpy, and free energy functions are purely phenomenological and do not in any way take account of the structural features of molecules³⁹. In the case of drug-target interactions, all that is needed is some measure of the degree of interaction, such as an activity, inhibition constant, or an IC₅₀ value, all of which are phenomenological constants.

It has been generally assumed that in most instances of polypharmacology, the drug binding-site of one target or the domain within which it resides is in some fashion structurally related to the binding-site or domain of other targets that the drug interacts with^40–42. A number of papers^43–46 have taken a more high-resolution approach that focuses on individual groups within binding sites. The work from these laboratories has dramatically expanded the rather limited contemporary view of the structural requirements of drug-target interactions^43–46. It counters the widely held, albeit changing, belief that if similar ligands bind to different proteins they must bind to structurally similar subsites in these proteins. The paper by Ehrt, et al.⁴⁷ provides an overview of this developing area of research.

Recent work from Shoichet’s group at UCSF is based on detailed structural studies of the binding of 59 different ligands in 116 complexes, where the binding of a given ligand involved pairs of proteins with different folds. In almost half of the protein pairs examined, a given ligand interacted with unrelated residues in the two proteins. Even in cases with similar binding-site environments, the ligands interacted with different residues. All of this shows that multiple patterns of residues and binding site environments are capable of interacting with highly structurally similar, even identical ligands. The investigators concluded that “There appears to be no single pattern-matching ‘code’ for identifying binding sites in unrelated proteins that bind identical ligands”. This view is in line with what has been espoused by Mathews for protein-DNA interactions almost two decades earlier⁴⁸.

Mathematical representations of drug-target interactions

Drug-target relationships

Mathematically, drug-target interactions can be characterized as binary relations, R(D,T), that describe an association between a set of drugs

D = {d_{1}, d_{2}, \dots, d_{n}} (1)

and a set of drug targets

T = {t_{1}, t_{2}, \dots, t_{m}} . (2)

These relations are described by ordered-pairs of elements, (d_{_i},t_{_j}), formed by the Cartesian product of these two sets, D × T, i.e.

(d_{i}, t_{j}) \in R (D, T) \subseteq D \times T for all d_{i} \in D and t_{j} \in T . (3)

The meaning associated with ordered-pairs in a given relation depends on the nature of the relation. In this work we are interested in whether a drug is active with respect to a specific target. This is given by the characteristic function r(d_{_i}, t_{_j}) ∈ R associated with the relation, which satisfies

r (d_{i}, t_{j}) = {\begin{array}{l} 1 if d_{i} is active with respect to t_{j} \\ 0 if d_{i} is inactive with respect to t_{j} \end{array}, (4)

where the activity values are equal to or greater than a threshold value that typically lies in the range of 1μM -10 μM. The elements r(d_{_i}, t_{_j}) are generally collected into a n × m dimensional matrix,

R = [\begin{matrix} r (d_{1}, t_{1}) & r (d_{1}, t_{2}) & \dots & r (d_{1}, t_{m}) \\ r (d_{2}, t_{1}) & r (d_{2}, t_{2}) & \dots & r (d_{2}, t_{m}) \\ ⋮ & ⋮ & ⋱ & ⋮ \\ r (d_{n}, t_{1}) & r (d_{n}, t_{2}) & \dots & r (d_{n}, t_{m}) \end{matrix}] . (5)

Now consider the transpose of the relation, R(D,T)′ = R(T,D). This changes the order of the elements in the ordered-pairs, i.e.

(d_{i}, t_{j}) \in R (D, T) \to (t_{j}, d_{i}) \in R {(D, T)}^{'} (6)

Nothing has fundamentally changed, except the arrangement of the elements of the relation; their values remain the same

R^{'} = [\begin{matrix} r (t_{1}, d_{1}) & r (t_{1}, d_{2}) & \dots & r (t_{1}, d_{n}) \\ r (t_{2}, d_{1}) & r (t_{2}, d_{2}) & \dots & r (t_{2}, d_{n}) \\ ⋮ & ⋮ & ⋱ & ⋮ \\ r (t_{m}, d_{1}) & r (t_{m}, d_{2}) & \dots & r (t_{m}, d_{n}) \end{matrix}] . (7)

Now the relation can be viewed from the ‘target perspective’. This clearly shows that however the values of the elements of R(D,T) or R(D,T)′ are obtained, i.e. from the drug perspective r(d_{_i},t_{_j}), which is associated with polypharmacology, or from the target perspective r(t_{_j},d_{_i}), which is associated with polyspecificity, the two views are completely comparable. The above argument is the basis for showing that polypharmacology and polyspecificity are mathematical duals of one another.

In order to simplify and clarify all subsequent discussion, the following three categories of relations associated with ordered drug-target pairs are defined:

(1) ‘active’, which includes all drug-target pairs whose activity has been experimentally measured or computationally estimated to meet or exceed the designated activity threshold value;

(2) ‘inactive’, which includes all drug-target pairs whose activity value has been experimentally measured or computationally estimated to fall below the designated activity threshold value; and

(3) ‘unknown’, which includes all drug-target pairs whose activities have neither been measured experimentally nor estimated computationally.

The following simple, illustrative example shows that the 8 × 4 dimensional drug-target interaction matrix and its transpose, the 4 × 8 target-drug interaction matrix, contain entirely equivalent information – only the ‘viewpoint’ has changed:

\begin{matrix} R_{+} = [\begin{matrix} 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 \\ 1 & 1 & 1 & 1 \\ 0 & 0 & 1 & 1 \end{matrix}], & R_{+}^{'} = [\begin{matrix} 1 & 0 & 1 & 1 & 0 & 1 & 1 & 0 \\ 1 & 1 & 0 & 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \end{matrix}] \end{matrix} . (8)

In R₊, the rows correspond to drugs and the columns to targets, while in $R_{+}^{'}$ the rows correspond to targets and the columns to drugs. The positive subscript indicates that the matrix represents active drug-target pairs.

Bipartite networks

It may also be desirable to represent the information in Equations (5), (7), and (8) as a network^49,50, since a considerable amount of the data on biological interactions is presented in the literature as networks. When the entities that are being compared belong to different sets, for example drugs and targets, a bipartite network such as that given in Equation (9) is commonly used:

N = 〈 D \cup T, E 〉 . (9)

These networks are comprised of sets of drug and target nodes, D and T, that are non-overlapping, i.e. D ∩ T = ∅. Edges only link nodes between D and T; there are no edges linking pairs of nodes within either D or T. Thus, the edge set can be defined as

E = {e (d_{i}, t_{j}) | if (d_{i}, t_{j}) is an' active' drug-target pair} (10)

In networks, pairs of nodes directly linked by edges are said to be adjacent and constitute the elements of the (n + m) × (n + m) dimensional adjacency matrix:

{\tilde{A}}_{(n + m) \times (n + m)} = [\begin{array}{l} 0_{n \times n} & A_{n \times m} \\ {A^{'}}_{m \times n} & 0_{m \times m} \end{array}], (11)

where

A = [\begin{matrix} a (d_{1}, t_{1}) & a (d_{1}, t_{2}) & \dots & a (d_{1}, t_{m}) \\ a (d_{2}, t_{1}) & a (d_{2}, t_{2}) & \dots & a (d_{2}, t_{m}) \\ ⋮ & ⋮ & ⋱ & ⋮ \\ a (d_{n}, t_{1}) & a (d_{n}, t_{2}) & \dots & a (d_{n}, t_{m}) \end{matrix}], (12)

is called a biadjacency⁵¹ or incidence matrix⁴⁹, although the latter usage is not strictly correct. The elements of A indicate which nodes of D are adjacent (i.e. linked or connected) to those of T. This provides what could be called drug-based view of the network. Since A′ is the transpose of A, its elements now indicate which nodes of T are adjacent to those of D (Cf. Equation (6)). This can be said to provide a target-based view of the network. Because the same information is contained in both matrices, the corresponding network has no directionality and is thus an undirected network. Moreover, the network topology is independent of which representation is used.

While not technically correct, for simplicity in this work A will be termed the adjacency matrix of 𝒩, since it contains all of the information in 𝒩. The zero valued submatrices in $\tilde{A}$ show that there are no links among nodes within D or among those within T. Since the elements of A are in one-to-one correspondence with the elements of R, the two matrices are isomorphic. Hence, R and A, and by implication 𝒩, contain essentially the same information.

Figure 1 depicts the bipartite network corresponding to the drug-target interaction matrix R₊ given Equation (8). From the discussion of the general relationship of R and A in the previous paragraphs it follows that

A_{+} = [\begin{matrix} 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 \\ 1 & 1 & 1 & 1 \\ 0 & 0 & 1 & 1 \end{matrix}] = R_{+} . (13)

Note that

R_{+}^{'}

and

A_{+}^{'}

interchange the positions of the nodes of the corresponding network, so that the target nodes now lie on the left hand side of the network diagram and the target nodes lie on the right hand side. This changes nothing, since the topology of the network is the same in both cases.

Figure 1. Simple example of a bipartite drug-target network made up of eight drugs and four targets.

Drug-target networks

Network data

Yildrim, et al.⁵² provided the earliest example of drug-target networks. Vogt and Mestres⁵³ have also discussed a number of issues associated with such networks including, as mentioned earlier, the issue of data completeness³⁷. Other related databases have also been developed such as those based on drug-side effects¹⁰ and gene-disease networks⁵⁴.

While it is true that drug-target networks provide dramatic views of the complex interrelationships amongst drugs and their putative targets, they are difficult to interpret when the number of drug-target pairs becomes too large, as is demonstrated by several of the figures depicted in references 52 and 53. In those cases networks merely provide a visual sense of drug-target relationships and their overall complexity.

Because of this, such networks are rarely used directly to draw detailed inferences. Rather, as the information contained within them is available in various matrices such as the adjacency matrices shown in Equations (11) – (13), it can be analyzed by algebraic procedures, some of which are described in this work. However, even the matrix algebraic approach becomes limiting for the adjacency matrices of large drug-target systems, which are quite sparse. In such cases, normal matrix-algebraic procedures become very inefficient. Storing the limited amount of data in such large sparse matrices is also very wasteful. This necessitates the development of efficient data structures and algorithmic procedures that facilitate the management and analysis of large drug-target datasets⁵⁵. The fact that so many large networks such as the Internet have been analyzed has led to the development of highly efficient algorithms that are more than capable of handling the size problems typically encountered with drug-target networks. The last part of the book by Newman⁴⁹ describes a number of these algorithms. They are not employed here, since the goal of the current work is the development of an understanding of some of the overlooked characteristics of drug-target network data and their analysis. Consequently, a very simple example is used as a basis for describing the underlying principles.

Many databases have been developed in order to provide a more unified source of experimental and computational data on drug-target interactions. Table 1 provides a summary of some useful drug-target databases. References to the various experimental methods used can best be found in the databases themselves. Because of the size and complexity of the chemogenomic space, computational methods have begun to play a larger role in determining drug-target interactions. A sample of some of the many computational techniques is given in the following references^6,56–59.

Polypharmacology and polyspecificity

The work described here is based on a phenomenological model of interactions between a set of drugs and a corresponding set of targets. Thus, as noted earlier, there is no requirement for any information on the molecular structure of the drugs, their targets, or any details on the nature of their inter- molecular interactions.

The degree of a given drug node is equal to the number of edges connected to that node, which is equivalent to the degree of polypharmacology of the drug associated with that node. The degree of a given target node is equivalent its degree of polyspecificity. It should be clear from Figure 1 that knowing the polypharmacology associated with the drug nodes is tantamount to knowing the degree of polyspecificity of the target nodes, and vice versa.

That this is the case can also be seen from the relational matrix, R₊, given by Equation (8) or from the adjacency matrix, A₊, given by Equation (13). In both instances, the rows represent drugs and the columns targets. Rows can be thought of as binary vectors associated with each of the drugs whose components are the targets the drugs can potentially interact with; correspondingly, columns can be thought of as binary vectors associated with each of the targets whose components are the drugs they can potentially interact with. Thus, all of the information on the degrees of polypharmacology and polyspecificity are contained in R₊ and A₊. Polypharmacology data, polyspecificity data, or some combination of the two can be used to ‘fill in’ the elements of R₊ and A₊. The degrees of polypharmacology and polyspecificity can then be computed by the expressions given in Equation (14) where the row and column sums correspond to the usual nodal degrees of the drug and target nodes, k̂₊(d_{_i}) and k̂₊(t_{_j}), which are equivalent to their corresponding degrees of polypharmacology and polyspecificity, π̂_{_PP}(d_{_i}) and π̂_{_PS}(t_{_j}), i.e.

\begin{array}{l} {\hat{k}}_{+} (d_{i}) \equiv {\hat{π}}_{PP} (d_{i}) = \sum_{t_{j} \in T} a_{+} (d_{i}, t_{j}), for all d_{i} \in D \\ {\hat{k}}_{+} (t_{j}) \equiv {\hat{π}}_{PS} (t_{j}) = \sum_{d \in D} a_{+} (d_{i}, t_{j}), for all t_{j} \in T \end{array}, (14)

where the a₊(d_{_i}, t_{_j}) are elements of A₊. Note that use of the caret or circumflex symbol "∧" follows customary statistical usage and indicates that these values are estimates. This will be used consistently throughout this manuscript to indicate parameters estimated from data in the corresponding relational or adjacency matrices. As noted earlier, the adjacency or relational matrices contain all of the information needed to determine the degrees of polypharmacology and polyspecificity, in this case for the set of eight drugs and four targets, regardless of how the data are created. Having information about one of them automatically provides information on the other, since r(d_{_i},t_{_j}) = r(t_{_j},d_{_i}) and a(d_{_i},t_{_j}) = a(t_{_j},d_{_i}).

Table 2 summarizes the degrees of polypharmacology and polyspecificity for the sets of drugs and targets in the example depicted in Figure 1, and represented by the adjacency matrix in Equation (13). But there is more that needs to be considered.

Table 2. Active drug-target interactions.

The rows correspond to drugs and the columns to targets. The far right hand column gives values for the degree of polypharmacology, while the bottom most row gives values for the degree of polyspecificity. The binary values at the center of the table show whether a given drug-target pair is active (1) or inactive (0) or of unknown activity (0).

	t₁	t₂	t₃	t₄	Polypharmacology
d₁	1	1	0	1	3
d₂	0	1	1	0	2
d₃	1	0	0	0	1
d₄	1	1	1	0	3
d₅	0	1	0	1	2
d₆	1	0	0	1	2
d₇	1	1	1	1	4
d₈	0	0	1	1	2
Polyspecificity	5	5	4	5	19

Limitations of network representations

The network representation of drug-target interactions effectively captures the information associated with active drug-target pairs, but in many instances it does not capture comparable information on inactive drug-target pairs or pairs whose activities have not been evaluated experimentally or computationally. This can lead to considerable uncertainty in the dataset and can be a latent source of error in the determination of degrees of polypharmacology and polyspecificity. The situation is exacerbated by the fact that most drug-target databases do not report data on drugs that are inactive, even if such data exists. In those cases, the drug-target pair must be assumed to belong to the category of pairs with unknown activity. How this affects the analysis of drug-target interactions is described in the sections that follow.

It is quite likely that within larger datasets, the activity of many of the drug-target pairs has not been evaluated experimentally or computationally. Since some of these may nevertheless be active, it follows that the degrees of polypharmacology and polyspecificity are typically underestimated and hence only provide approximate lower bounds to the true values. They are not true lower bounds because the data used for their determination are not always entirely consistent or accurate. Hence their reliability may be questionable.

Even though the number of drug-target pairs in the inactive and unknown categories is small in the example given here, in reality the number can be substantial and generally exceeds the number of active drug-target pairs. This makes total sense given that the number of active compounds in large corporate databases is generally only a few percent of the total number of compounds in their database. Thus, the problem now becomes how to obtain data on drugs in a dataset that are known to be inactive. As mention earlier, this is a significant problem for two reasons. First, activity data in corporate databases, where such information is likely to exist, is generally unavailable to the general research community. Second, most databases accessible by the non-industrial research community either do not report or report very little data on inactive drugs. Because of this, it is difficult to determine the contributions of drugs to the inactive category, which directly affects our knowledge of drugs in the category of unknown activity status. As will be seen in a forthcoming section, this impacts the size of the bounds to the degrees of polypharmacology and polyspecificity. Thus, while data on inactive drug-target pairs does not provide information that is useful for identifying drug targets, its availability reduces the size of the category of drugs of unknown activity, which improves the bounds on the degrees of polypharmacology and polyspecificity. The details of this argument are presented in a forthcoming section and are exemplified by the expression given in Equation (22).

More importantly, in many cases the number of possible drug-target pairs whose activity status is unknown may be significant. If they were experimentally or computationally determined, at least some of these might have activity values that meet or exceed the desired activity threshold. Not including these data will result in a less reliable estimation of the degrees of polypharmacology and polyspecificity. It may also suggest that the observed drug-target interactions involve a more limited region of target space than is actually the case. All of these issues raise questions as to how such data can be effectively incorporated into an analysis of drug-target interactions. One way to address this issue is by extending the current networks to include the class of edge-colored bipartite networks.

Edge-colored bipartite networks

An edge-colored bipartite network is depicted in Figure 2 for the simple example shown in Figure 1. Edges corresponding to active drug-target pairs are colored green, those corresponding to inactive pairs are colored red, and those corresponding to pairs of unknown activity are colored black. Thus, all of the possibilities are now incorporated into a single edge-colored network. Figure 3a represents a separation of this network into its three components, corresponding to active (+), inactive (−), and unknown (*) bipartite subnetworks. Figure 3b depicts their respective adjacency matrices, A₊, A_-, and A_*, where the colored squares correspond to matrix elements with value ‘1’ and the uncolored squares correspond to matrix elements with value ‘0’. An examination of Figure 3b shows that the matrix elements of A, A₊, A_-, and A_* satisfy

\begin{array}{l} a (d_{i}, t_{j}) = a_{+} (d_{i}, t_{j}) + a_{-} (d_{i}, t_{j}) + a_{*} (d_{i}, t_{j}) = 1 \\ for all d_{i} \in D and t_{j} \in T \end{array} (15)

The elements of the three matrices cover all possible drug-target interactions and are non-overlapping. Thus, they represent a partition of the matrix elements of A, all of whose elements have value unity.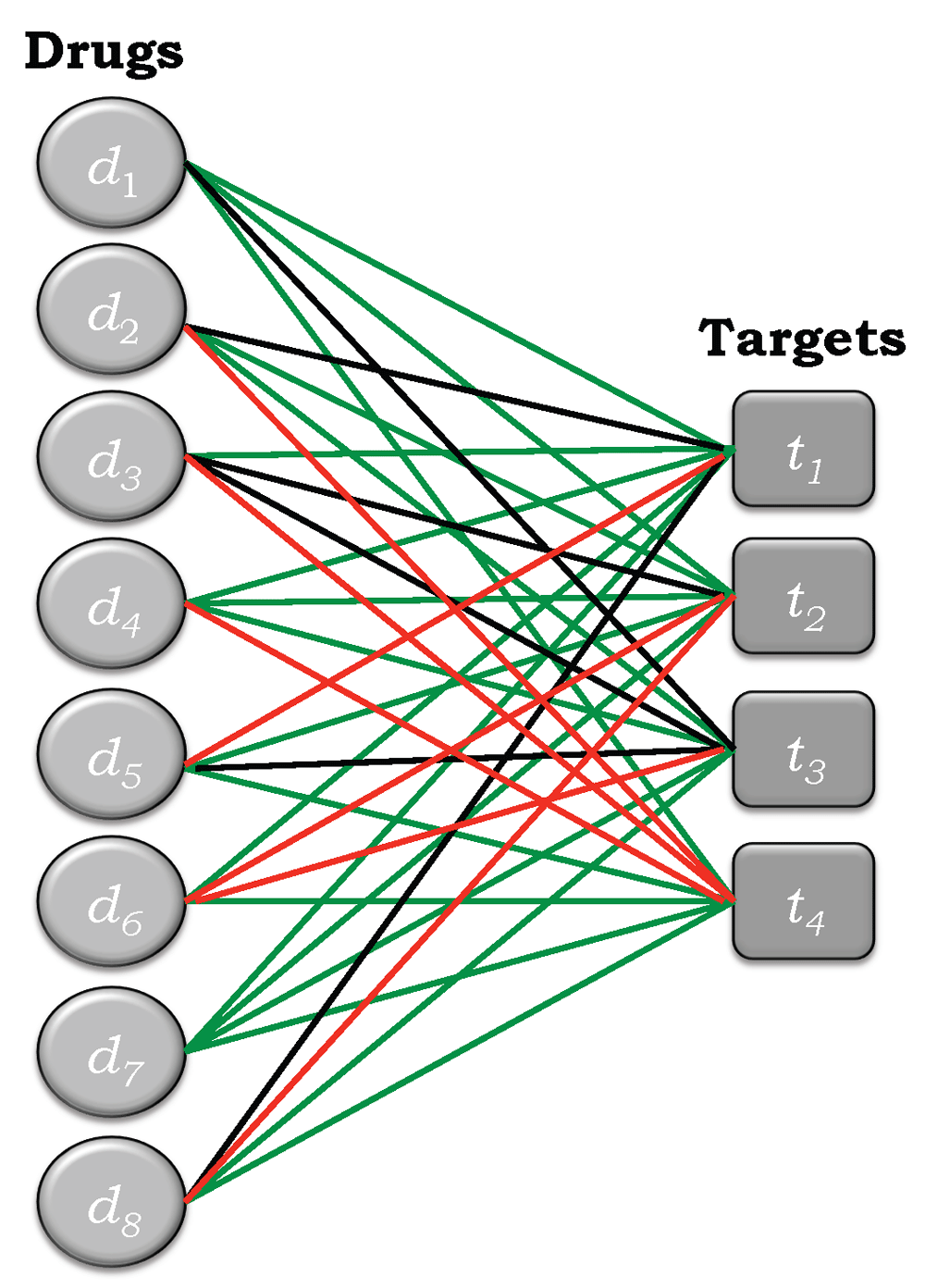

Figure 2. Example of the network in Figure 1 represented as an edge-colored network, where the green edges correspond to active drug-target pairs, the red edges to inactive drug-target pairs, and the black edges to drug-target pairs of unknown activity status.

Figure 3.

(a) Decomposition of the bipartite, edge-colored network depicted in Figure 2 into its three component subnetworks, namely drug-target pairs that are active, inactive, and of unknown activity status. (b) The adjacency matrices corresponding to the bipartite, edge-colored subnetworks given in (a). The colored cells correspond to a value of unity and the uncolored cells to zero values.

Because of this, it is possible to determine the degrees of nodes for each of the subnetworks independently. Thus, the row and column sums for the three colored networks associated with A₊, A_-, and A_*, are given, respectively, by

\begin{array}{l} {\hat{k}}_{η} (d_{i}) = \sum_{y_{j} \in Y} a_{η} (d_{i}, t_{j}) for all d_{i} \in X \\ {\hat{k}}_{η} (t_{j}) = \sum_{x_{i} \in X} a_{η} (d_{i}, t_{j}) for all t_{j} \in Y \end{array} (16)

where η ≜ +, –, *. Equation (14) shows the equivalences k̂₊(d_{_i}) ≡ π̂_{_PP}(d_{_i}) and k̂₊(t_{_j}) ≡ π̂_{_PS}(t_{_j}). As is discussed in detail in forthcoming sections, the terms k̂_*(d_{_i}) and k̂_*(t_{_j}) are equivalent to error terms that provide uncertainty measures with respect to the degrees of polypharmacology and polyspecificity. In order to emphasize this property and to make their association with π̂_{_PP}(d_{_i}) and π̂_{_PS}(t_{_j}) clear, the following equivalences are defined: k̂_*(d_{_i}) ≡ ε̂_{_PP}(d_{_i}) and k̂_*(t_{_j}) ≡ ε̂_{_PS}(t_{_j}) for all d_{_i} ∈ D and t_{_j} ∈ T.

The results for the simple example depicted in Figure 1–Figure 3 are collected in Table 3 and Table 4. In Table 3, k̂_-(d_{_i}) corresponds to the right hand column designated ‘Row-Sum’, and k̂_-(t_{_j}) corresponds to the bottom row designated ‘Col-Sum’, and similarly for ε̂_{_PP}(d_{_i}) and ε̂_{_PS}(t_j), respectively, in Table 4. These latter quantities associated with the drug-target pairs of unknown activity are important since they contain information, albeit latent information, that bears on the degrees of polypharmacology and polyspecificity for any drug-target dataset. As noted earlier, some of the drugs known to be inactive may nonetheless fall in the category of drugs of unknown activity, because inactivity data is not generally incorporated into many of the widely available drug-target databases. Moreover, the terms associated with inactive drug-target pairs k_-(d_{_i}) and k_-(t_{_j}) provide useful information since they eliminate the possibility of being considered as active pairs. They also have an effect on the sizes of ε̂_{_PP}(d_{_i}) and ε̂_{_PS}(t_j), as discussed in a forthcoming section.

Table 3. Inactive drug-target interactions.

The rows correspond to drugs and the columns to targets. The far right hand column gives values for the row sums (‘Row-Sum’), while the bottom most row gives values for the corresponding column sums (‘Col-Sum’). The binary values at the center of the table show whether a given drug-target pair is inactive (1) or active (0) or of unknown activity (0).

	t₁	t₂	t₃	t₄	Row-Sum
d₁	0	0	0	0	0
d₂	0	0	0	1	1
d₃	0	0	0	1	1
d₄	0	0	0	1	1
d₅	1	0	0	0	1
d₆	0	1	1	0	2
d₇	0	0	0	0	0
d₈	0	1	0	0	1
Col-Sum	1	2	1	3	7

Table 4. Unknown drug-target interactions.

The rows correspond to drugs and the columns to targets. The far right hand column gives values for the row sums (‘Row-Sum’), while the bottom most row gives values for the corresponding column sums (‘Col-Sum’). The binary values at the center of the table show whether a given drug-target pair is of unknown activity (1) or active (0) or inactive (0).

	t₁	t₂	t₃	Row-Sum
d₁	0	0	1	1
d₂	1	0	0	1
d₃	0	1	1	2
d₄	0	0	0	0
d₅	0	0	1	1
d₆	0	0	0	0
d₇	0	0	0	0
d₈	1	0	0	1
Col-Sum	2	1	3	6

The information in Table 2–Table 4 can be represented as three-dimensional Euclidean vectors

\begin{array}{l} k_{PP} (d_{i}) = ({\hat{π}}_{PP} (d_{i}), {\hat{k}}_{-} (d_{i}), {\hat{ε}}_{PP} (d_{i})) \\ k_{PS} (t_{j}) = ({\hat{π}}_{PP} (t_{j}), {\hat{k}}_{-} (t_{j}), {\hat{ε}}_{PP} (t_{j})) \end{array} (17)

that can be plotted in three dimensions as depicted in Figure 4. Although not examined in this work, Euclidean vectors also allow computation of inter-vector distances and cosine-based similarities²³, either of which can be used to cluster the data points by a variety of well-known methods⁶⁰.

In the case where the activities of all of the drug-target pairs have been measured, ideally the points will lie entirely within the ‘Active-Inactive’ plane. In general, the information provided exceeds that of typical bipartite drug-target networks, because of the explicit inclusion of data on drug-target pairs of inactive and unknown activity.

Figure 4.

(a) Three-dimensional plots of the information in Table 2–Table 4 for drugs. (b) Three-dimensional plots of the information in Table 2–Table 4 for targets.

Measures of data completeness

Global measures

A global measure of data completeness that accounts for experimentally determined or computationally estimated activities of drug-target pairs is given by

{\hat{C}}_{DT} = \frac{{\hat{μ}}_{+} + {\hat{μ}}_{-}}{{\hat{μ}}_{+} + {\hat{μ}}_{-} + {\hat{μ}}_{*}} (18)

where μ̂₊ is an estimate of the total number of experimentally or computationally determined active pairs, μ̂₋ is an estimate of the total number of experimentally or computationally determined inactive pairs and μ̂_* is an estimate of the total number of pairs of unknown activity status. Thus,

{\hat{μ}}_{η} = \sum_{d_{i} \in D} \sum_{t_{j} \in T} a_{η} (d_{i}, t_{j}) (19)

where η ≜ +, −, *. The denominator of Equation (18) is a known constant because it is equal to the total number of possible drug-target pairs in the dataset, | D × T | = n·m. Hence, there are only two degrees of freedom for the estimated quantities, and the value of μ̂_* is specified directly if the values of μ̂₊ and μ̂₋ are known.

In the example given in Figure 2 and Figure 3 and Equation (8) and Equation (13), and μ̂₊ = 19, μ̂₋ = 7, μ̂_* = 6. Thus,

C_{DT} = (19 + 7) / (19 + 7 + 6) = 26 / 32 = 0.813, (20)

which satisfies 0 ≤ C_{_DT} ≤ 1. Obviously, the closer C_{_DT} is to unity, the more accurate the estimates of polypharmacology and polyspecificity will be, but it provides no information on the degrees of polypharmacology and polyspecificity associated with individual drugs or targets.

Local measures

In many instances, it is desirable to have local measures that are associated with individual drug or target nodes. One possible local measure is related to the nodal degrees of bipartite subnetworks associated with drug-target pairs of unknown activity status, ε̂_{_PP}(d_{_i}) and ε̂_{_PS}(t_i), which can be viewed as measures of error or uncertainty. Fractional measures could also be defined by dividing each of them by | T | and | D |, respectively, but this will not be done here.

In order to develop these measures, the nodal degrees are combined with respect to all three types of relations given by Equation (16) for each of the nodes d_{_i} ∈ D and t_j ∈ T. Combining and simplifying terms using Equation (15) yields

\begin{array}{l} {\hat{π}}_{pp} (d_{i}) + {\hat{k}}_{-} (d_{i}) + {\hat{ε}}_{pp} (d_{i}) = | T | for all d_{i} \in D \\ {\hat{π}}_{PS} (t_{j}) + {\hat{k}}_{-} (t_{j}) + {\hat{ε}}_{PS} (t_{j}) = | D | for all t_{j} \in T \end{array} . (21)

As was the case for the variables in the denominator of Equation (18), the sum of terms in either expression in Equation (21) is equal to a constant, and hence there are two degrees of freedom. Once values for the first two terms in either expression of Equation (21) are obtained by appropriately summing the experimentally or computationally determined elements of their corresponding adjacency matrices A₊ and A₋, the values of the remaining error terms, ε̂_{_PP}(d_{_i}) and ε̂_{_PS}(t_i), are automatically specified. Nevertheless, uncertainties in these terms remain because it is not known which of their elements, a_{_*}(d_i, t_j), correspond to active drug-target pairs, i.e. which have a value of unity, and which do not.

Knowing that the values of k₋(d_{_i}) and k₋(t_{_j}) are useful is seen by rearranging Equation (21)

\begin{array}{l} {\hat{ε}}_{PP} (d_{i}) = | T | - {\hat{π}}_{PP} (d_{i}) - k_{-} (d_{i}) \\ {\hat{ε}}_{PS} (t_{j}) = | D | - {\hat{π}}_{PS} (t_{j}) - k_{-} (t_{j}) \end{array} . (22)

The following example illustrates this point. Consider a specific drug, say d_p, with unknown activity with respect to a subset of two of the targets under study; hence, ε̂_{_PP}(d_p) = 2. Now experimentally or computationally determine the activity of the drug with respect one of the targets, say t_q. The drug will either be active or inactive. Regardless of which, it will diminish the size of ε̂_{_PP}(d_p) = 2 and, as will be seen in the following section, will tighten the bounds on π̂_{_PP}(d_p). Hence, even though the compound has no particular value as a drug for that target, knowing that it is inactive improves the estimate of its degree of polypharmacology with respect to the entire set of targets under study. This affords a clear example of the usefulness of information on the inactivity of drugs towards specific targets. An exactly analogous argument can be made regarding targets, although the details will not be given here.

Bounds for the degrees of polypharmacology and polyspecificity

Bounds to the values of π̂_{_PP}(d_{_i}) and π̂_{_PS}(t_{_j}) can be derived in a relatively straightforward manner from two basic assumptions:

(1) all (d_i, t_j) pairs of unknown activity are actually active, i.e. a_{_*}(d_i, t_j) ⇒ a₊(d_i, t_j) = 1, for all a_{_*}(d_i, t_j) ∈ A_*; and

(2) all (d_i, t_j) pairs of unknown activity are actually inactive, i.e a_{_*}(d_i, t_j) ⇒ a₋(d_i, t_j) = 1 for all a_{_*}(d_i, t_j) ∈ A_*.

In the first case the magnitudes of ε̂_{_PP}(d_{_i}) and ε̂_{_PS}(t_{_j}) determine the respective uncertainties of π̂_{_PP}(d_{_i}) and π̂_{_PS}(t_{_j}), while in the second case, assuming that all (d_i, t_j) pairs of unknown activity are in fact inactive gives values of π̂_{_PP}(d_{_i}) and π̂_{_PP}(t_{_j}) that are lower bounds to their true values. But as noted earlier their true values may be lower because of measurement, computational, or other types of errors.

The mathematical expressions in Equation (23) show that the true values, π_{_PP}(d_{_i}) and π_{_PS}(t_{_j}), are bounded, i.e.

\begin{array}{l} {\hat{π}}_{PP} (d_{i}) \leq π_{PP} (d_{i}) \leq {\hat{π}}_{PP} (d_{i}) + {\hat{ε}}_{PP} (d_{i}) \\ {\hat{π}}_{PS} (t_{j}) \leq π_{PS} (t_{j}) \leq {\hat{π}}_{PS} (t_{j}) + {\hat{ε}}_{PS} (t_{j}) \end{array} (23)

and thus they depend directly on the magnitudes of their corresponding uncertainties, ε̂_{_PP}(d_{_i}) and ε̂_{_PS}(t_{_j}). Maximum upper bounds to these quantities are given by max[π̂_{_PP}(d_{_i})] = | T | and max[π̂_{_PS}(t_{_j})] = | D |, since the maximum connectivity of any d_{_i} node is equal to the total number of t_{_j} nodes, | T |, and similarly the maximum connectivity of any t_{_j} node is equal to the total number of d_{_i} nodes, | D |. If all of the d nodes are connected to all of the t nodes the network is fully connected, and thus would be a complete bipartite network. This result is clearly seen in Figure 2 if all of the edges were colored green and in Equation (13) if all of the matrix elements a₊(d_i, t_j) = 1, a situation that is only achieved in the case where there are no inactive or unknown elements, i.e. a_(d_i, t_j) = a_{_*}(d_i, t_j) = 0 for all and d_{_i} ∈ D and t_{_j} ∈ T. Lastly, consider the case where all of the edges correspond to active or inactive drug-target pairs, i.e. there are no drug-target pairs of unknown activity. In this case, all of the edges in the network are either green or red, and the elements of the three adjacency matrices satisfy a₊(d_i, t_j) + a₋(d_i, t_j) = 1 and a_{_*}(d_i, t_j) = 0 for all d_{_i} ∈ D and t_{_j} ∈ T.

Applying the expressions in Equation (23) to the data in Table 2 and Table 4 yields the bounds given in Table 5 and Table 6. As discussed earlier, these bounds are unrealistically small, since in real cases the sizes of ε̂_{_PP}(d_{_i}) and ε̂_{_PS}(t_{_j}) are likely to be much larger than those used in the simple example presented here. Nevertheless, it illustrates a number of relevant points. In carrying out this analysis it is important to remember that all drug-target pairs whose activity has not been determined must be included in the class of drug-target pairs of unknown activity, which directly contributes to the uncertainty in π̂_{_PP}(d) and π̂_{_PS}(t).

Table 5. Upper and lower bounds to the degree of polypharmacology for the set of eight drugs in the simple example described in this work.

	Lower	Upper
d₁	3	4
d₂	2	3
d₃	1	3
d₄	3	3
d₅	2	3
d₆	2	2
d₇	4	4
d₈	2	3

Table 6. Upper and lower bounds to the degree of polyspecificity for the set of four targets in the simple example described in this work.

	Lower	Upper
t₁	5	7
t₂	5	6
t₃	4	7
t₄	5	5

Summary and conclusions

The study of polypharmacology is becoming increasingly important in drug research because it raises awareness of the inherent lack of specificity of drugs and xenobiotics for specific targets. Moreover, it provides a basis for understanding the prevalence of side effects and the rationale behind the repurposing of drugs for new therapeutic indications. The concept of polyspecificity, on the other hand, affords support for the lack of specificity of drug targets. A simple mathematical argument shows that these seemingly disparate characteristics of drugs and targets are, in fact, closely related, a result that to the best of our knowledge has not been previously published by other authors. This is supported by a growing number of structural studies that suggest that the variety of different structural patterns arising in drug-target interactions is so large it is highly unlikely that high degrees of specificity in these interactions will occur.

Constructing networks is a popular enterprise in biology nowadays. Although useful, these networks have some significant limitations. For example, while they offer a highly visual depiction of the interrelationships among entities associated with the nodes in the network it is difficult to extract detailed information from them when the number of entities is large, a situation that also obtains in the case of drug-target networks. The issue can be overcome by utilizing the adjacency matrix of the network, which provides a faithful representation of its edge structure, and thus preserves the relations associated with active drug-target pairs. Because of this the degrees of polypharmacology and polyspecificity can be computed directly from adjacency matrices.

There is other information associated with drug-target pairs that is rarely if ever dealt with. Representing this information involves the use of the edge-colored bipartite drug-target networks introduced in this paper. In addition to representing active drug-target pairs, which is the case with standard drug-target networks, these augmented networks represent data associated with inactive drug-target pairs and with pairs of unknown activity. By including this heretofore latent data it is possible to compute global and local measures of data completeness as well as bounds for the degrees of polypharmacology and polyspecificity. These parameters can be viewed as diagnostics of the suitability of a given analysis of a drug-target network.

In the simple example describe here, the values for the uncertainties ε̂_{_PP}(d) and ε̂_{_PS}(t) are quite small, and hence the upper bounds lie close to the values of π̂_{_PP}(d) and π̂_{_PS}(t). This is not likely to be the case in larger, more realistic drug-target networks. In such cases, the uncertainties will be considerably larger due to a lack of data availability. As noted above, the reliability of the analysis can be increased by the use of experimentally or computationally determined data on inactive drug-target pairs. Unfortunately, such data is not as readily available in many publicly accessible databases where the focus is largely on drugs that are active with respect to specific targets. Assuming drugs without activity data are inactive, as is the case in the use of ‘decoys’ to test various computational methodologies, clearly leads to a loss of information. This trend needs to be reversed.

Although the analysis presented here is useful, it is just a start and by no means exhausts the possibilities for further study. Three areas for to consider for future research include:

(1) Expanding statistical analysis of drug-target network properties;

(2) Examining higher-order drug-target interactions; and

(3) Developing weighted and fuzzy representations of drug-target networks.

A lot of work is still needed in order to provide a suitably rigorous formalism for treating drug-target networks in ways that allow maximum extraction of information, which clarifies a number of the subtle issues associated with these biologically important networks.

Author contributions

GM and VG both conceived the study and both contributed to the general outline of the work. GM wrote most but not all of the initial draft of the manuscript. VG contributed his expertise in database searching and analysis and how it applied to the work carried out for this manuscript. GM contributed his mathematical expertise and formulated most of the mathematical material. Both authors were involved in the revision of the manuscript and have agreed to its final content.

Competing interests

No competing interests were disclosed.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Acknowledgments

GM wishes to thank Professor Jürgen Bajorath and Dr. Martin Vogt, both from Department of Life Science Informatics, B-IT, Rheinische Friedrich-Wilhelms-Universität in Bonn, Germany, for a number of useful comments regarding this work.

Faculty Opinions recommended

References

1. Peters JU, Ed: Polypharmacology in Drug Discovery. John Wiley & Sons, New York. 2012. Publisher Full Text
2. Hopkins AL: Network pharmacology: the next paradigm in drug discovery. Nature Chem Biol. 2008; 4(11): 682–690. PubMed Abstract | Publisher Full Text
3. Hopkins AL: Introduction: The case for polypharmacology. In Polypharmacology in Drug Discovery. Peters JU, Ed., John Wiley & Sons, 2012; 1–6. Publisher Full Text
4. Anighoro A, Bajorath J, Rastelli G: Polypharmacology: Challenges and opportunities in drug discovery. J Med Chem. 2014; 57(19): 7874–7887. PubMed Abstract | Publisher Full Text
5. Tan Z, Chaudhai R, Zhang S: Polypharmacology in Drug Development: A Minireview of Current Technologies. ChemMedChem. 2016; 11(12): 1211–1218. PubMed Abstract | Publisher Full Text
6. Achenbach J, Tiikkainen P, Franke L, et al.: Computational tools for polypharmacology and repurposing. Future Med Chem. 2011; 3(8): 961–968. PubMed Abstract | Publisher Full Text
7. Pérez-Nueno VI, Souchet M, Karaboga AS, et al.: GESSE: Predicting drug side effects from drug-target relationships. J Chem Inf Model. 2015; 55(9): 1804–1823. PubMed Abstract | Publisher Full Text
8. Lounkine E, Keiser MJ, Whitebread S, et al.: Large-scale prediction and testing of drug activity on side-effect targets. Nature. 2012; 486(7403): 361–367. PubMed Abstract | Publisher Full Text | Free Full Text
9. Campillos M, Kuhn M, Gavin AC, et al.: Drug target identification using side-effect similarity. Science. 2008; 321(5886): 263–266. PubMed Abstract | Publisher Full Text
10. Kuhn M, Campillos M, Letunic I, et al.: A side effect resource to capture phenotypic effects of drugs. Mol Syst Biol. 2010; 6: 343. PubMed Abstract | Publisher Full Text | Free Full Text
11. Barratt MJ, Frail DE: Drug Repositioning – Bringing New Life to Shelved Assets and Existing Drugs. John Wiley & Sons, New York. 2012. Publisher Full Text
12. Dimitrov JD, Pashov AD, Vassilev TL: Antibody polyspecificity: what does it matter? Adv Exp Med Biol. 2012; 750: 213–226. PubMed Abstract | Publisher Full Text
13. Van Regenmortel MH: Specificity, polyspecificity, and heterospecificity of antibody-antigen recognition. J Mol Recog. 2014; 27(11): 627–639. PubMed Abstract | Publisher Full Text
14. Young DD, Jockush S, Turro NJ, et al.: Synthetase polyspecificity as a tool to modulate protein function. Bioorg Med Chem Lett. 2011; 21(24): 7502–7504. PubMed Abstract | Publisher Full Text | Free Full Text
15. Martinez L, Arnaud O, Henin E, et al.: Understanding polyspecificity within the substrate-binding cavity of the human multidrug resistance P-glycoprotein. FEBS J. 2014; 281(3): 673–682. PubMed Abstract | Publisher Full Text
16. Lyons JA, Parker JL, Solcan N, et al.: Structural basis for polyspecificity in the POT family of proton-coupled oligopeptide transporters. EMBO Rep. 2014; 15(8): 886–893. PubMed Abstract | Publisher Full Text | Free Full Text
17. Lytvynenko I, Brill S, Oswald C, et al.: Molecular basis of polyspecificity of the small multidrug resistance efflux pump AbeS from Acinetobacter baumannii. J Mol Biol. 2016; 428(3): 644–657. PubMed Abstract | Publisher Full Text
18. Esser L, Zhou F, Pluchino KM, et al.: Structures of the multidrug transporter P-glycoprotein reveal asymmetric ATP binding and the mechanism of polyspecificity. J Biol Chem. 2017; 292(2): 446–461. PubMed Abstract | Publisher Full Text | Free Full Text
19. Blass BE: Basic Principles of Drug Discovery and Development. Academic Press, New York. 2015. Reference Source
20. Brown N, Ed: Scaffold Hopping in Medicinal Chemistry. Wiley-VCH, New York. 2014. Publisher Full Text
21. Saha R, Tanwar O, Alam NM, et al.: Pharmacophore based virtual screening, synthesis and SAR of novel inhibitors of Mycobacterium sulfotransferase. Bioorg Med Chem Lett. 2015; 25(3): 701–707. PubMed Abstract | Publisher Full Text
22. Iyer P, Stumpfe D, Vogt M, et al.: Activity Landscapes, Information Theory, and Structure - Activity Relationships. Mol Inform. 2013; 32(5-6): 421–430. PubMed Abstract | Publisher Full Text
23. Maggiora GM: Introduction to molecular similarity and chemical space. In Foodinformatics: Applications of Chemical Information to Food Chemistry. Martinez-Mayorga K, Medina-Franco JL, Eds. Springer International Publishing Switzerland; 2014; 1–81. Publisher Full Text
24. Law V, Knox C, Djoumbou Y, et al.: DrugBank 4.0: shedding new light on drug metabolism. Nucleic Acids Res. 2014; 42(Database issue): D1091–D1097. PubMed Abstract | Publisher Full Text | Free Full Text
25. Szklarczyk D, Santos A, von Mering C, et al.: STITCH 5: augmenting protein-chemical interaction networks with tissue and affinity data. Nucleic Acids Res. 2016; 44(D1): D380–D384. PubMed Abstract | Publisher Full Text | Free Full Text
26. Olah M, Rad R, Ostopovici L, et al.: WOMBAT and WOMBAT-PK: Bioactivity Databases for Lead and Drug Discovery. In Chemical Biology: From Small Molecules to Systems Biology and Drug Design. Schreiber SL, Kapoor T, Wess G, Eds., John Wiley & Sons, New York; 2008; 760–786. Publisher Full Text
27. Kim S, Thiessen PA, Bolton EE, et al.: PubChem Substance and Compound databases. Nucleic Acids Res. 2016; 44(D1): D1202–D1213. PubMed Abstract | Publisher Full Text | Free Full Text
28. Liu T, Lin Y, Wen X, et al.: BindingDB: a web-accessible database of experimentally determined protein-ligand binding affinities. Nucleic Acids Res. 2007; 35(Database issue): D198–D201. PubMed Abstract | Publisher Full Text | Free Full Text
29. Gaulton A, Hersey A, Nowotka M, et al.: The ChEMBL database in 2017. Nucleic Acids Res. 2017; 45(D1): D945–D954. PubMed Abstract | Publisher Full Text | Free Full Text
30. Tym JE, Mitsopoulos C, Coker EA, et al.: canSAR: an updated cancer research and drug discovery knowledgebase. Nucleic Acids Res. 2016; 44(D1): D938–D943. PubMed Abstract | Publisher Full Text | Free Full Text
31. von Eichborn J, Murgueitio MS, Dunkel M, et al.: PROMISCUOUS: a database for network-based drug-repositioning. Nucleic Acids Res. 2011; 39(Database issue): D1060–D1066. PubMed Abstract | Publisher Full Text | Free Full Text
32. Günther S, Kuhn M, Dunkel M, et al.: SuperTarget and Matador: resources for exploring drug-target relationships. Nucleic Acids Res. 2008; 36(Database issue): D919–D922. PubMed Abstract | Publisher Full Text | Free Full Text
33. Jasial S, Hu Y, Bajorath J: Determining the degree of promiscuity of extensively assayed compounds. PLoS One. 2016; 11(4): e0153873. PubMed Abstract | Publisher Full Text | Free Full Text
34. Hu Y, Gupta-Osterman D, Bajorath J: Exploring compound promiscuity patterns and multi-target activity spaces. Comput Struct Biotechnol J. 2014; 9(13): e201401003. PubMed Abstract | Publisher Full Text | Free Full Text
35. Hu Y, Bajorath J: How promiscuous are pharmaceutically relevant compounds? A data-driven assessment. AAPS J. 2013; 15(1): 104–111. PubMed Abstract | Publisher Full Text | Free Full Text
36. Hu Y, Bajorath J: Exploring molecular promiscuity from a ligand and target perspective. In Frontiers in Molecular Design and Chemical Information Science. Bajorath J, Ed. ACS Symposium Series, American Chemical Society, 2016; 1222. : 19–34. Publisher Full Text
37. Mestres J, Gregori-Puigjané E, Valverde S, et al.: Data completeness--the Achilles heel of drug-target networks. Nat Biotechnol. 2008; 26(9): 983–984. PubMed Abstract | Publisher Full Text
38. Santos R, Ursu O, Gaulton A, et al.: A comprehensive map of molecular drug targets. Nat Rev Drug Discov. 2017; 16(1): 19–34. PubMed Abstract | Publisher Full Text
39. Klotz IM, Rosenberg RM: Chemical Thermodynamics: Basic Concepts and Methods. 7^th Edition. John Wiley & Sons, New York 2008. Publisher Full Text
40. Milletti F, Vulpetti A: Predicting polypharmacology by binding site similarity: from kinases to the protein universe. J Chem Inf Model. 2010; 50(8): 1418–1431. PubMed Abstract | Publisher Full Text
41. Moya-García AA, Ranea JA: Insights into polypharmacology from drug-domain associations. Bioinformatics. 2013; 29(16): 1934–1937. PubMed Abstract | Publisher Full Text
42. Moya-Garcia AA, Dawson NL, Kruger FA, et al.: Structural and functional view of polypharmacology. Preprint posted online 18 March 2016 (not peer reviewed). 2017. Publisher Full Text
43. Bareller S, Sterling T, O’Meara MJ, et al.: The recognition of identical ligands by unrelated proteins. ACS Chem Biol. 2015; 10(12): 2772–2784. PubMed Abstract | Publisher Full Text | Free Full Text
44. Kahraman A, Morris RJ, Laskowski RA, et al.: Shape variation in protein binding pockets and their ligands. J Mol Biol. 2007; 368(1): 283–301. PubMed Abstract | Publisher Full Text
45. Kahraman A, Morris RJ, Laskowski RA, et al.: On the diversity of physicochemical environments experienced by identical ligands in binding pockets of unrelated proteins. Proteins. 2010; 78(5): 1120–1136. PubMed Abstract | Publisher Full Text
46. Sturm N, Desaphy J, Quinn RJ, et al.: Structural insights into the molecular basis of the ligand promiscuity. J Chem Inf Model. 2012; 52(9): 2410–2421. PubMed Abstract | Publisher Full Text
47. Ehrt C, Brinkjost T, Koch O: Impact of Binding Site Comparisons on Medicinal Chemistry and Rational Molecular Design. J Med Chem. 2016; 59(9): 4121–4151. PubMed Abstract | Publisher Full Text
48. Matthews BW: Protein-DNA interaction. No code for recognition. Nature. 1988; 335(6188): 294–295. PubMed Abstract | Publisher Full Text
49. Newman ME: Networks. An Introduction. Oxford University Press, Oxford, UK. 2010. Publisher Full Text
50. Van Steen M: Graph Theory and Complex Networks. An Introduction. M van Steen Publisher; 2010. Reference Source
51. Asratian AS, Denley TM, Häggkvist R: Bipartite Graphs and Their Applications. Cambridge University Press, Cambridge, UK. 1999. Publisher Full Text
52. Yildirim MA, Goh KI, Cusick ME, et al.: Drug-target network. Nat Biotechnol. 2007; 25(10): 1119–1126. PubMed Abstract | Publisher Full Text
53. Vogt I, Mestres J: Drug-Target Networks. Mol Inform. 2010; 29(1–2): 10–14. Publisher Full Text
54. Bauer-Mehren A, Rautschka M, Sanz F, et al.: DisGeNET: a Cytoscape plugin to visualize, integrate, search and analyze gene-disease networks. Bioinformatics. 2010; 26(22): 2924–2926. PubMed Abstract | Publisher Full Text
55. Kolaczyk ED: Statistical Analysis of Network Data: Methods and Models. Springer, New York. 2009. Publisher Full Text
56. Cheng F, Liu C, Jang J, et al.: Prediction of drug-target interactions and drug repositioning via network-based inference. PLoS Comput Biol. 2012; 8(5): e1002503. PubMed Abstract | Publisher Full Text | Free Full Text
57. Yamanishi Y, Araki M, Gutteridge A, et al.: Prediction of drug-target interaction networks from the integration of chemical and genomic spaces. Bioinformatics. 2008; 24(13): i232–i240. PubMed Abstract | Publisher Full Text | Free Full Text
58. Lu Y, Guo Y, Korhonen A: Link prediction in drug-target interactions network using similarity indices. BMC Bioinformatics. 2017; 18(1): 39. PubMed Abstract | Publisher Full Text | Free Full Text
59. Peng L, Liao B, Zhu W, et al.: Predicting drug-target interactions with multi-information fusion. IEEE J Biomed Health Inform. 2017; 21(2): 561–572. PubMed Abstract | Publisher Full Text
60. Jain AK, Dubes RC: Algorithms for Clustering Data. Prentice Hall, Englewood Cliffs, New Jersey. 1988. Reference Source

Comments on this article Comments (1)

Version 1

VERSION 1 PUBLISHED 06 Jun 2017

Reader Comment 13 Mar 2018

Francois Berenger, Kyushu University, Japan

13 Mar 2018

Reader Comment

I see many [Math Processing Error] in the text.
Am I the only one?
Competing Interests: No competing interests were disclosed.
I see many [Math Processing Error] in the text.
Am I the only one?
I see many [Math Processing Error] in the text.
Am I the only one?
Competing Interests: No competing interests were disclosed. Close
Report a concern
Comment

Author details Author details

¹ BIO5 Institute, University of Arizona, 1657 East Helen Street, Tucson, AZ, 85719, USA

Competing interests

No competing interests were disclosed.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Article Versions (1)

version 1

Published: 06 Jun 2017, 6:788

https://doi.org/10.12688/f1000research.11517.1

© 2017 Maggiora G and Gokhale V. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

Maggiora G and Gokhale V. A simple mathematical approach to the analysis of polypharmacology and polyspecificity data [version 1; peer review: 3 approved, 1 approved with reservations]. F1000Research 2017, 6(Chem Inf Sci):788 (https://doi.org/10.12688/f1000research.11517.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Current Reviewer Status: ?

Key to Reviewer Statuses VIEW HIDE

ApprovedThe paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approvedFundamental flaws in the paper seriously undermine the findings and conclusions

Version 1

VERSION 1

PUBLISHED 06 Jun 2017

Views

Reviewer Report 20 Jun 2017

Tudor I. Oprea, Translational Informatics Division, Department of Internal Medicine, University of New Mexico School of Medicine, Albuquerque, NM, USA

Approved with Reservations

https://doi.org/10.5256/f1000research.12441.r23321

This subject is relevant for the drug discovery community. The theoretical approach is potentially sound, as far as I can tell - but (full disclosure) while familiar with statistics and matrices algebra, I believe someone more competent in such mathematics should judge that part of the publication.

The problem is genuine: Indeed, after more than a century of pharmaceutical research, it has become clear (owing to high throughput screening of large chemical libraries) that many drugs bind to multiple targets. This problem is compounded by other aspects such as tissue distribution, on- and off- dissociation constants, half-life and other pharmacokinetics parameters. Target and drug (*see below) specific elements influence the relevance of both polypharmacology and polyspecificity.

Which begs the question, how relevant is target polyspecificity? The authors encode "structurally dissimilar drugs" in their definition (see Abstract and Introduction). This in itself is a slippery slope, considering Maggiora's 2006 Commentary that similar molecules do not always share the same activity landscape. The implication being that structural similarity does not always work. So, dis-similarity would have to be defined... at the 2D level (which fingerprints)? 3D? (shape? electrostatics? etc.). In my opinion, polyspecificity does NOT require "dissimilar" in the definition.

Polyspecificity is relevant when one considers drugs co-administered simultaneously - with the possibility of exacerbating some side-effects or, perhaps, staying "on target". This is likely to occur, considering that 15% of U.S. adults are likely to use 5 or more prescription drugs (aka polypharmacy). Thus, the issue of target polyspecificity is relevant and ought to be investigated more in the context of co-prescribed medications.

The main topic of this paper is polypharmacology. The issue of potency appears to be brushed aside, as shown in the assumption that "drug-target interactions can be characterized as binary relations" (see Drug-Target Relationships). This, of course, implies that Drug D1, with a Ki of 1 nM (10^-9 M) has the same relevance for polypharmacology and polyspecificity as Drug D2, with a Ki of 1 mM (10^-3 M). In practice, this is not likely to be the case.

Polypharmacology is not a binary issue of binding or not binding. The bi-partite drug-target network in Figure 1, therefore, not only has nodes and edges, but edges have values: D1 binds to target T1 with potency P1, D1 binds to T2 with P2 and so on... Which would change Table 2 into something more familiar to medicinal chemists, i.e., a Structure-Activity Table.

The issue of what's "active" vs. "inactive" (e.g., Fig 3) is a somewhat subjective issue. Take for example ropinirole: "although the anti-Parkinsonian drug ropinirole is more potent at the D₃ receptor than the D₂ receptor by an order of magnitude, we annotate the D₂ receptor as the mechanism of action target because D₂ receptors, but not D₃ receptors, are expressed in the substantia nigra, the pathologically relevant tissue for anti-Parkinsonian drugs". Our own DrugCentral entry shows other targets, such as the 5-HT_1A and alpha-_2B adrenergic receptors, with potency similar to D₂ receptors. Is that relevant? Should all targets with potency below 6 (on the negative log scale) be considered "inactive"? The answer to these questions depends on the problem at hand.

By the same token, the issue of polyspecificity may be regarded differently given a target for which over 20 potent (approved) drugs are known (some Receptor Tyrosine Kinases fit this profile), compared to a target for which only 2 drugs are approved (e.g., cyclin-dependent kinases 4 and 6).

Given the wealth of data for drug-target interactions from a variety of sources such as ChEMBL, DrugBank, DrugCentral or GuideToPharmacology, it is recommended that real examples are used in this paper. Although "data completeness" remains an issue, the authors can no doubt identify a subset of 20-50 drugs, say anti-depressants or anti-psychotics, for which a wealth of in vitro bioactivity data are available through various channels, including PDSP in addition to the above.

That would provide clear and immediate utility to the upper and lower bounds for the degree of polypharmacology (Table 5), which would make this paper more impactful. The authors are clearly aware of this, as discussed in Conclusions...

I found the discussion related to the limitations of network biology representations particularly interesting. Perhaps that section could be expanded...

(*) Footnote. Two simple scenarios are discussed. These do not include target mutations (e.g., causing drug resistant cancers or infections), allelic variation, or other population-specific phenomena.

The target is in the CNS, but the drug itself is an ABCB1 substrate (see for example the impact of ABCB1 on CNS side-effects), or the drug lacks blood-brain barrier permeability - in which case the potency of the drug in vitro is irrelevant in vivo.
The drug can have significant in vitro potency on many targets, e.g., dobutamine hits over 20 human targets according to DrugCentral. However, its half-life is 2 minutes. Therefore, these "off target effects" are irrelevant.

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

I cannot comment. A qualified statistician is required.
Are all the source data underlying the results available to ensure full reproducibility?

No source data required
Are the conclusions drawn adequately supported by the results?

Partly

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Cheminformatics, pharmacoinformatics, drug target analytics, drug target curation

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Author Response 23 Jun 2017

Gerry Maggiora, BIO5 Institute, University of Arizona, 1657 East Helen Street, Tucson, 85719, USA

23 Jun 2017

Author Response

Oprea raises the issue of "how relevant is target polyspecificity?" and he also takes issue with usage of the terminology "structurally dissimilar drugs" with regard to the concept of polyspecificity, ... Continue reading Oprea raises the issue of "how relevant is target polyspecificity?" and he also takes issue with usage of the terminology "structurally dissimilar drugs" with regard to the concept of polyspecificity, noting that "similar molecules do not always share the same activity landscape". Moreover, he states that in his opinion "polyspecificity does NOT require 'dissimilar' in the definition". These three points are addressed in order.

First, The relevance of polyspecificity is not explicitly addressed in the paper, rather the focus is on the fact that polyspecificity is closely (and mathematically) related to polypharmacology, a concept that most will agree is quite relevant to drug research. The point is that both concepts are related to one another, and as stated in the paper are metaphorically "two sides of the same coin".

Second, the reason that 'structurally dissimilar drugs' was mentioned explicitly in the definition of polyspecificity is that polyspecificity implies multiple specificities and hence a diversity of drug structures.

Third, that structurally similar molecules will interact with the same protein is generally expected, although as Oprea has pointed out above, "similar molecules do not always share the same activity landscape". While the 'spirit' of this quote is relevant, it is not entirely accurate since an activity landscape is associated with the target being assayed. The molecules that make up the dataset will all lie on that particular activity landscape. Although relatively rare, two structurally similar molecules may nevertheless exhibit widely different activities, an occurrence that gives rise to 'activity cliffs' on the landscape.

Oprea also opines that the issue of target polyspecificity is relevant and ought to be investigated more in the context of co-prescribed medications. This seems like a very relevant application of polyspecificity especially, as pointed out by Oprea, that "15% of US adults are likely to use 5 or more prescription drugs. Moreover, it should be noted that geriatric patients generally are on two or more times as many drugs as younger patients making such an analysis even more desirable.

Oprea brings up the important subject of potency, pointing out that it is not specifically addressed in the formulation presented in the paper. For example, he states that "The bipartite drug-target network in Figure 1, therefore, not only has nodes and edges, but the edges have values...". While this statement is technically correct, with regard to the paper the point he is making is incorrect since it is addressed, albeit in limited fashion, by the fact that the bipartite networks employed in our work are threshold networks. By choosing activity values that are greater than or equal to a given threshold value, say 100 nM, ensures that all of the edges in the network correspond to drug-target pairs of reasonable activity with respect to the targets assayed. Hence, Oprea's point "that Drug D1, with a Ki of 1 nM has the same relevance for polypharmacology and polyspecificity as Drug D2, with a Ki of 1 mM" is not correct. For example, for a threshold value of 100 nM an edge would be drawn between Drug D1 and its target, while no edge would be drawn between Drug D2 and the same target. It is true, however, that not dealing explicitly with drug-target activity values results in a loss of information, but this can be accounted for if one uses weighted bipartite networks, which are more complicated and require a higher level of theory. Hence, we chose to explore the issues associated with drug-target networks using the simplest level of theory first, but we intend to deal with weighted drug-target networks in a future publication.

Oprea raises a number of important issues regarding the inherent subjectivity of interpreting drug activity with respect to different targets. He makes the point that receptors with lower activity for a given drug may, nevertheless, be more pharmacologically/biologically relevant than other receptors for which the drug has a higher affinity. His point is well taken and, no doubt, needs to be addressed when assessing the pharmacological/biological relevance of a particular drug-target interaction. However, doing so is a much more demanding task than identifying putative polypharmacologies and polyspecificities and requires significant additional information on pathways, biopharmaceutical properties, and drug metabolism. Our aim in this paper was merely to address drug-target interactions within an in vitro setting.

An additional complication in the study of drug-target interactions, most of which involve in vitro and ex vivo experiments, is that the information in drug-target databases is very heterogeneous since it is made up of data obtained from a wide variety off different sources. As noted in the paper, even experiments carried out in the same lab using the same experimental protocol on different days can result in significantly divergent experimental values. Further complicating this issue is the fact, also stated in the paper, that a growing number of values are obtained computationally. All of these factors conspire to raise the uncertainty of the information used to construct drug-target networks. Lastly, it is assumed, mostly tacitly, that drug-target interactions, which are generally determined in in vitro and ex vivo experiments, can be used to interpret complicated in vivo biological phenomena. However, this must be done with caution. For example, protein-protein interaction data are used in the construction of biological pathways, when in fact most such data are determined in in vitro experiments that are far removed from the context in which the pathways reside. Nevertheless, while such data may be problematic in some cases, they can be useful in advancing our understanding of the biological functionality of many processes taking place in living systems, with the caveat that care must be used in drawing inferences from such potentially problematic data.

Oprea suggests that data from such databases a ChEMBL, DrugBank, DrugCentral, or GuideToPharmacology be used to construct an example from 'real data'. This is an excellent suggestion and one that we are currently working on. There are two main issues that we wanted to highlight in the paper: (1) the relationship between polypharmacology and polyspecificity and (2) the development of a method for estimating error bounds for drug-target network parameters such as the degrees of polypharmacology and polyspecificity. Hence, we focused our attention on the mathematical relationships that exemplify these network properties, and we left the development of actual examples for future work.
Oprea raises the issue of "how relevant is target polyspecificity?" and he also takes issue with usage of the terminology "structurally dissimilar drugs" with regard to the concept of polyspecificity, noting that "similar molecules do not always share the same activity landscape". Moreover, he states that in his opinion "polyspecificity does NOT require 'dissimilar' in the definition". These three points are addressed in order.

First, The relevance of polyspecificity is not explicitly addressed in the paper, rather the focus is on the fact that polyspecificity is closely (and mathematically) related to polypharmacology, a concept that most will agree is quite relevant to drug research. The point is that both concepts are related to one another, and as stated in the paper are metaphorically "two sides of the same coin".

Second, the reason that 'structurally dissimilar drugs' was mentioned explicitly in the definition of polyspecificity is that polyspecificity implies multiple specificities and hence a diversity of drug structures.

Third, that structurally similar molecules will interact with the same protein is generally expected, although as Oprea has pointed out above, "similar molecules do not always share the same activity landscape". While the 'spirit' of this quote is relevant, it is not entirely accurate since an activity landscape is associated with the target being assayed. The molecules that make up the dataset will all lie on that particular activity landscape. Although relatively rare, two structurally similar molecules may nevertheless exhibit widely different activities, an occurrence that gives rise to 'activity cliffs' on the landscape.

Oprea also opines that the issue of target polyspecificity is relevant and ought to be investigated more in the context of co-prescribed medications. This seems like a very relevant application of polyspecificity especially, as pointed out by Oprea, that "15% of US adults are likely to use 5 or more prescription drugs. Moreover, it should be noted that geriatric patients generally are on two or more times as many drugs as younger patients making such an analysis even more desirable.

Oprea brings up the important subject of potency, pointing out that it is not specifically addressed in the formulation presented in the paper. For example, he states that "The bipartite drug-target network in Figure 1, therefore, not only has nodes and edges, but the edges have values...". While this statement is technically correct, with regard to the paper the point he is making is incorrect since it is addressed, albeit in limited fashion, by the fact that the bipartite networks employed in our work are threshold networks. By choosing activity values that are greater than or equal to a given threshold value, say 100 nM, ensures that all of the edges in the network correspond to drug-target pairs of reasonable activity with respect to the targets assayed. Hence, Oprea's point "that Drug D1, with a Ki of 1 nM has the same relevance for polypharmacology and polyspecificity as Drug D2, with a Ki of 1 mM" is not correct. For example, for a threshold value of 100 nM an edge would be drawn between Drug D1 and its target, while no edge would be drawn between Drug D2 and the same target. It is true, however, that not dealing explicitly with drug-target activity values results in a loss of information, but this can be accounted for if one uses weighted bipartite networks, which are more complicated and require a higher level of theory. Hence, we chose to explore the issues associated with drug-target networks using the simplest level of theory first, but we intend to deal with weighted drug-target networks in a future publication.

Oprea raises a number of important issues regarding the inherent subjectivity of interpreting drug activity with respect to different targets. He makes the point that receptors with lower activity for a given drug may, nevertheless, be more pharmacologically/biologically relevant than other receptors for which the drug has a higher affinity. His point is well taken and, no doubt, needs to be addressed when assessing the pharmacological/biological relevance of a particular drug-target interaction. However, doing so is a much more demanding task than identifying putative polypharmacologies and polyspecificities and requires significant additional information on pathways, biopharmaceutical properties, and drug metabolism. Our aim in this paper was merely to address drug-target interactions within an in vitro setting.

An additional complication in the study of drug-target interactions, most of which involve in vitro and ex vivo experiments, is that the information in drug-target databases is very heterogeneous since it is made up of data obtained from a wide variety off different sources. As noted in the paper, even experiments carried out in the same lab using the same experimental protocol on different days can result in significantly divergent experimental values. Further complicating this issue is the fact, also stated in the paper, that a growing number of values are obtained computationally. All of these factors conspire to raise the uncertainty of the information used to construct drug-target networks. Lastly, it is assumed, mostly tacitly, that drug-target interactions, which are generally determined in in vitro and ex vivo experiments, can be used to interpret complicated in vivo biological phenomena. However, this must be done with caution. For example, protein-protein interaction data are used in the construction of biological pathways, when in fact most such data are determined in in vitro experiments that are far removed from the context in which the pathways reside. Nevertheless, while such data may be problematic in some cases, they can be useful in advancing our understanding of the biological functionality of many processes taking place in living systems, with the caveat that care must be used in drawing inferences from such potentially problematic data.

Oprea suggests that data from such databases a ChEMBL, DrugBank, DrugCentral, or GuideToPharmacology be used to construct an example from 'real data'. This is an excellent suggestion and one that we are currently working on. There are two main issues that we wanted to highlight in the paper: (1) the relationship between polypharmacology and polyspecificity and (2) the development of a method for estimating error bounds for drug-target network parameters such as the degrees of polypharmacology and polyspecificity. Hence, we focused our attention on the mathematical relationships that exemplify these network properties, and we left the development of actual examples for future work.
Competing Interests: The authors have no competing issues. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 23 Jun 2017

Gerry Maggiora, BIO5 Institute, University of Arizona, 1657 East Helen Street, Tucson, 85719, USA

23 Jun 2017

Author Response

Oprea raises the issue of "how relevant is target polyspecificity?" and he also takes issue with usage of the terminology "structurally dissimilar drugs" with regard to the concept of polyspecificity, ... Continue reading Oprea raises the issue of "how relevant is target polyspecificity?" and he also takes issue with usage of the terminology "structurally dissimilar drugs" with regard to the concept of polyspecificity, noting that "similar molecules do not always share the same activity landscape". Moreover, he states that in his opinion "polyspecificity does NOT require 'dissimilar' in the definition". These three points are addressed in order.

First, The relevance of polyspecificity is not explicitly addressed in the paper, rather the focus is on the fact that polyspecificity is closely (and mathematically) related to polypharmacology, a concept that most will agree is quite relevant to drug research. The point is that both concepts are related to one another, and as stated in the paper are metaphorically "two sides of the same coin".

Second, the reason that 'structurally dissimilar drugs' was mentioned explicitly in the definition of polyspecificity is that polyspecificity implies multiple specificities and hence a diversity of drug structures.

Third, that structurally similar molecules will interact with the same protein is generally expected, although as Oprea has pointed out above, "similar molecules do not always share the same activity landscape". While the 'spirit' of this quote is relevant, it is not entirely accurate since an activity landscape is associated with the target being assayed. The molecules that make up the dataset will all lie on that particular activity landscape. Although relatively rare, two structurally similar molecules may nevertheless exhibit widely different activities, an occurrence that gives rise to 'activity cliffs' on the landscape.

Oprea also opines that the issue of target polyspecificity is relevant and ought to be investigated more in the context of co-prescribed medications. This seems like a very relevant application of polyspecificity especially, as pointed out by Oprea, that "15% of US adults are likely to use 5 or more prescription drugs. Moreover, it should be noted that geriatric patients generally are on two or more times as many drugs as younger patients making such an analysis even more desirable.

Oprea brings up the important subject of potency, pointing out that it is not specifically addressed in the formulation presented in the paper. For example, he states that "The bipartite drug-target network in Figure 1, therefore, not only has nodes and edges, but the edges have values...". While this statement is technically correct, with regard to the paper the point he is making is incorrect since it is addressed, albeit in limited fashion, by the fact that the bipartite networks employed in our work are threshold networks. By choosing activity values that are greater than or equal to a given threshold value, say 100 nM, ensures that all of the edges in the network correspond to drug-target pairs of reasonable activity with respect to the targets assayed. Hence, Oprea's point "that Drug D1, with a Ki of 1 nM has the same relevance for polypharmacology and polyspecificity as Drug D2, with a Ki of 1 mM" is not correct. For example, for a threshold value of 100 nM an edge would be drawn between Drug D1 and its target, while no edge would be drawn between Drug D2 and the same target. It is true, however, that not dealing explicitly with drug-target activity values results in a loss of information, but this can be accounted for if one uses weighted bipartite networks, which are more complicated and require a higher level of theory. Hence, we chose to explore the issues associated with drug-target networks using the simplest level of theory first, but we intend to deal with weighted drug-target networks in a future publication.

Oprea raises a number of important issues regarding the inherent subjectivity of interpreting drug activity with respect to different targets. He makes the point that receptors with lower activity for a given drug may, nevertheless, be more pharmacologically/biologically relevant than other receptors for which the drug has a higher affinity. His point is well taken and, no doubt, needs to be addressed when assessing the pharmacological/biological relevance of a particular drug-target interaction. However, doing so is a much more demanding task than identifying putative polypharmacologies and polyspecificities and requires significant additional information on pathways, biopharmaceutical properties, and drug metabolism. Our aim in this paper was merely to address drug-target interactions within an in vitro setting.

An additional complication in the study of drug-target interactions, most of which involve in vitro and ex vivo experiments, is that the information in drug-target databases is very heterogeneous since it is made up of data obtained from a wide variety off different sources. As noted in the paper, even experiments carried out in the same lab using the same experimental protocol on different days can result in significantly divergent experimental values. Further complicating this issue is the fact, also stated in the paper, that a growing number of values are obtained computationally. All of these factors conspire to raise the uncertainty of the information used to construct drug-target networks. Lastly, it is assumed, mostly tacitly, that drug-target interactions, which are generally determined in in vitro and ex vivo experiments, can be used to interpret complicated in vivo biological phenomena. However, this must be done with caution. For example, protein-protein interaction data are used in the construction of biological pathways, when in fact most such data are determined in in vitro experiments that are far removed from the context in which the pathways reside. Nevertheless, while such data may be problematic in some cases, they can be useful in advancing our understanding of the biological functionality of many processes taking place in living systems, with the caveat that care must be used in drawing inferences from such potentially problematic data.

Oprea suggests that data from such databases a ChEMBL, DrugBank, DrugCentral, or GuideToPharmacology be used to construct an example from 'real data'. This is an excellent suggestion and one that we are currently working on. There are two main issues that we wanted to highlight in the paper: (1) the relationship between polypharmacology and polyspecificity and (2) the development of a method for estimating error bounds for drug-target network parameters such as the degrees of polypharmacology and polyspecificity. Hence, we focused our attention on the mathematical relationships that exemplify these network properties, and we left the development of actual examples for future work.
Oprea raises the issue of "how relevant is target polyspecificity?" and he also takes issue with usage of the terminology "structurally dissimilar drugs" with regard to the concept of polyspecificity, noting that "similar molecules do not always share the same activity landscape". Moreover, he states that in his opinion "polyspecificity does NOT require 'dissimilar' in the definition". These three points are addressed in order.

First, The relevance of polyspecificity is not explicitly addressed in the paper, rather the focus is on the fact that polyspecificity is closely (and mathematically) related to polypharmacology, a concept that most will agree is quite relevant to drug research. The point is that both concepts are related to one another, and as stated in the paper are metaphorically "two sides of the same coin".

Second, the reason that 'structurally dissimilar drugs' was mentioned explicitly in the definition of polyspecificity is that polyspecificity implies multiple specificities and hence a diversity of drug structures.

Third, that structurally similar molecules will interact with the same protein is generally expected, although as Oprea has pointed out above, "similar molecules do not always share the same activity landscape". While the 'spirit' of this quote is relevant, it is not entirely accurate since an activity landscape is associated with the target being assayed. The molecules that make up the dataset will all lie on that particular activity landscape. Although relatively rare, two structurally similar molecules may nevertheless exhibit widely different activities, an occurrence that gives rise to 'activity cliffs' on the landscape.

Oprea also opines that the issue of target polyspecificity is relevant and ought to be investigated more in the context of co-prescribed medications. This seems like a very relevant application of polyspecificity especially, as pointed out by Oprea, that "15% of US adults are likely to use 5 or more prescription drugs. Moreover, it should be noted that geriatric patients generally are on two or more times as many drugs as younger patients making such an analysis even more desirable.

Oprea brings up the important subject of potency, pointing out that it is not specifically addressed in the formulation presented in the paper. For example, he states that "The bipartite drug-target network in Figure 1, therefore, not only has nodes and edges, but the edges have values...". While this statement is technically correct, with regard to the paper the point he is making is incorrect since it is addressed, albeit in limited fashion, by the fact that the bipartite networks employed in our work are threshold networks. By choosing activity values that are greater than or equal to a given threshold value, say 100 nM, ensures that all of the edges in the network correspond to drug-target pairs of reasonable activity with respect to the targets assayed. Hence, Oprea's point "that Drug D1, with a Ki of 1 nM has the same relevance for polypharmacology and polyspecificity as Drug D2, with a Ki of 1 mM" is not correct. For example, for a threshold value of 100 nM an edge would be drawn between Drug D1 and its target, while no edge would be drawn between Drug D2 and the same target. It is true, however, that not dealing explicitly with drug-target activity values results in a loss of information, but this can be accounted for if one uses weighted bipartite networks, which are more complicated and require a higher level of theory. Hence, we chose to explore the issues associated with drug-target networks using the simplest level of theory first, but we intend to deal with weighted drug-target networks in a future publication.

Oprea raises a number of important issues regarding the inherent subjectivity of interpreting drug activity with respect to different targets. He makes the point that receptors with lower activity for a given drug may, nevertheless, be more pharmacologically/biologically relevant than other receptors for which the drug has a higher affinity. His point is well taken and, no doubt, needs to be addressed when assessing the pharmacological/biological relevance of a particular drug-target interaction. However, doing so is a much more demanding task than identifying putative polypharmacologies and polyspecificities and requires significant additional information on pathways, biopharmaceutical properties, and drug metabolism. Our aim in this paper was merely to address drug-target interactions within an in vitro setting.

An additional complication in the study of drug-target interactions, most of which involve in vitro and ex vivo experiments, is that the information in drug-target databases is very heterogeneous since it is made up of data obtained from a wide variety off different sources. As noted in the paper, even experiments carried out in the same lab using the same experimental protocol on different days can result in significantly divergent experimental values. Further complicating this issue is the fact, also stated in the paper, that a growing number of values are obtained computationally. All of these factors conspire to raise the uncertainty of the information used to construct drug-target networks. Lastly, it is assumed, mostly tacitly, that drug-target interactions, which are generally determined in in vitro and ex vivo experiments, can be used to interpret complicated in vivo biological phenomena. However, this must be done with caution. For example, protein-protein interaction data are used in the construction of biological pathways, when in fact most such data are determined in in vitro experiments that are far removed from the context in which the pathways reside. Nevertheless, while such data may be problematic in some cases, they can be useful in advancing our understanding of the biological functionality of many processes taking place in living systems, with the caveat that care must be used in drawing inferences from such potentially problematic data.

Oprea suggests that data from such databases a ChEMBL, DrugBank, DrugCentral, or GuideToPharmacology be used to construct an example from 'real data'. This is an excellent suggestion and one that we are currently working on. There are two main issues that we wanted to highlight in the paper: (1) the relationship between polypharmacology and polyspecificity and (2) the development of a method for estimating error bounds for drug-target network parameters such as the degrees of polypharmacology and polyspecificity. Hence, we focused our attention on the mathematical relationships that exemplify these network properties, and we left the development of actual examples for future work.
Competing Interests: The authors have no competing issues. Close
Report a concern

Views

Reviewer Report 19 Jun 2017

John Van Drie, Van Drie Research LLC, North Andover, MA, USA

Approved

https://doi.org/10.5256/f1000research.12441.r23318

This is as close to 'publish as is' as I've ever seen. Excellent work, well articulated, good overview of literature.

My only suggestion is that a paragraph at the end would be helpful, laying out the experimental implications of this theory, i.e. if this theory holds or if such analyses pan out, how would an experimentalist change their research plan?

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

No source data required
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests: No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Author Response 28 Jun 2017

Gerry Maggiora, BIO5 Institute, University of Arizona, 1657 East Helen Street, Tucson, 85719, USA

28 Jun 2017

Author Response

I completely agree with Van Drie's comment and will include a discussion regarding the experimental implications of our work in the subsequent version of the paper.
Competing Interests: I have no competing interest that would influence my judgment.
I completely agree with Van Drie's comment and will include a discussion regarding the experimental implications of our work in the subsequent version of the paper.
I completely agree with Van Drie's comment and will include a discussion regarding the experimental implications of our work in the subsequent version of the paper.
Competing Interests: I have no competing interest that would influence my judgment. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 28 Jun 2017

Gerry Maggiora, BIO5 Institute, University of Arizona, 1657 East Helen Street, Tucson, 85719, USA

28 Jun 2017

Author Response

I completely agree with Van Drie's comment and will include a discussion regarding the experimental implications of our work in the subsequent version of the paper.
Competing Interests: I have no competing interest that would influence my judgment.
I completely agree with Van Drie's comment and will include a discussion regarding the experimental implications of our work in the subsequent version of the paper.
I completely agree with Van Drie's comment and will include a discussion regarding the experimental implications of our work in the subsequent version of the paper.
Competing Interests: I have no competing interest that would influence my judgment. Close
Report a concern

Views

Reviewer Report 19 Jun 2017

Karina Martinez-Mayorga, Institute of Chemistry, National Autonomous University of Mexico, Mexico City, Mexico

Approved

https://doi.org/10.5256/f1000research.12441.r23316

This is an original and nice contribution to the field. The authors propose a mathematical approach to analyse the relation between polypharmacology and polyspecificity, that are, as presented here “two concepts running on the same avenue”. I particularly like the idea of extracting latent information to describe relationships between the degrees of these two complementary features.

This work highlights the inherent complexity of biological systems providing a view of drug-target interactions as a pattern where both sides have an array of possibilities. Pattern recognition involved in the perception of odorants provides an additional example (See for instance DOI: 10.1038/81774) of the complexity involved in the recognition of ligands by biomacromoleules. It could be envisioned that the mathematical approach described in this paper will be attractive to parallel areas of biological processes governed by pattern interactions.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

References

1. Araneda RC, Kini AD, Firestein S: The molecular receptive range of an odorant receptor.Nat Neurosci. 2000; 3 (12): 1248-55 PubMed Abstract | Publisher Full Text

Competing Interests: No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Respond or Comment

Views

Reviewer Report 09 Jun 2017

Jose L. Medina-Franco, DIFACQUIM Research Group, Department of Pharmacy, School of Chemistry, National Autonomous University of Mexico, Mexico City, Mexico

Approved

https://doi.org/10.5256/f1000research.12441.r23317

This well-written and organized manuscript addresses an extremely timely topic in drug discovery.

The authors starts defining the basic concepts of polypharmacology and polyspecificity. Then, in a very clear and didactic manner (using nice illustrations), propose a general and intuitive mathematical approach to quantify the degrees of both concepts. It is clear from the manuscript the mathematical relationship of polypharmacology and polyspecificity (e.g., paraphrasing the authors “the two sides of the same coin”). The new measures address at some extent data incompleteness that is a major issue of chemogenomics data sets. As the authors point out in the Conclusions, this paper sets the ground to implement these metrics to public or private chemogenomics data sets. In particular, I found quite innovative and clear the edge-colored bipartite networks introduced in this manuscript.

I strongly support indexing of this paper. Minor suggestions to further improve the manuscript:

The term “frequent hitter” related to polypharmacology can be added in the Introduction.
Comment on the effect of drug concentration in chemogenomics data sets. For instance, adverse drug reactions, and drug-interaction networks in general, will depend on the drug concentrations.
Page 4: Include reference related to the statement: “Recent work from Shoichet’s group at UCSF …”. I believe the authors refer to the paper published in ACS Chem. Biol. 2015¹. This manuscript is not included in the Reference section of the current version.
Spell out "UCSF" (University of California at San Francisco).

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

References

1. Barelier S, Sterling T, O'Meara MJ, Shoichet BK: The Recognition of Identical Ligands by Unrelated Proteins.ACS Chem Biol. 2015; 10 (12): 2772-84 PubMed Abstract | Publisher Full Text

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Computer-aided drug design, chemoinformatics

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Author Response 28 Jun 2017

Gerry Maggiora, BIO5 Institute, University of Arizona, 1657 East Helen Street, Tucson, 85719, USA

28 Jun 2017

Author Response

Medina-Franco suggests that "The term 'frequent hitter' related to polypharmacology can be added in the Introduction". We chose not to include it in our initial version of the manuscript because ... Continue reading Medina-Franco suggests that "The term 'frequent hitter' related to polypharmacology can be added in the Introduction". We chose not to include it in our initial version of the manuscript because we felt that the term was too general since it also includes drug-target interactions induced by a variety of non-specific modes of interaction that do not typically lead to genuine pharmacological responses. However, we will include a mention of it in the next version of the paper along with relevant caveats regarding non-specific modes of interaction.

Medina-Franco also suggest that a comment should be made regarding the effect of drug concentration in chemogenomics datasets since, for example, "...adverse drug reactions and drug-interaction networks in general, will depend on the drug concentrations". While it is certainly true that drug concentration has a significant effect on biological processes it does not per se directly affect the structure of the drug-target threshold networks described in our paper because the presence of an edge between two network nodes is solely dependent on the activity value, e.g. a pK_i or IC₅₀, and the activity threshold imposed.

Medina-Franco has noted that reference to the work in Shoichet's lab at the University of California at San Francisco (UCSF) is apparently missing. The missing citation is reference [43].
Medina-Franco suggests that "The term 'frequent hitter' related to polypharmacology can be added in the Introduction". We chose not to include it in our initial version of the manuscript because we felt that the term was too general since it also includes drug-target interactions induced by a variety of non-specific modes of interaction that do not typically lead to genuine pharmacological responses. However, we will include a mention of it in the next version of the paper along with relevant caveats regarding non-specific modes of interaction.

Medina-Franco also suggest that a comment should be made regarding the effect of drug concentration in chemogenomics datasets since, for example, "...adverse drug reactions and drug-interaction networks in general, will depend on the drug concentrations". While it is certainly true that drug concentration has a significant effect on biological processes it does not per se directly affect the structure of the drug-target threshold networks described in our paper because the presence of an edge between two network nodes is solely dependent on the activity value, e.g. a pK_i or IC₅₀, and the activity threshold imposed.

Medina-Franco has noted that reference to the work in Shoichet's lab at the University of California at San Francisco (UCSF) is apparently missing. The missing citation is reference [43].
Competing Interests: I have no competing interest that could be construed to influence my response to the referee's comments. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 28 Jun 2017

Gerry Maggiora, BIO5 Institute, University of Arizona, 1657 East Helen Street, Tucson, 85719, USA

28 Jun 2017

Author Response

Medina-Franco suggests that "The term 'frequent hitter' related to polypharmacology can be added in the Introduction". We chose not to include it in our initial version of the manuscript because ... Continue reading Medina-Franco suggests that "The term 'frequent hitter' related to polypharmacology can be added in the Introduction". We chose not to include it in our initial version of the manuscript because we felt that the term was too general since it also includes drug-target interactions induced by a variety of non-specific modes of interaction that do not typically lead to genuine pharmacological responses. However, we will include a mention of it in the next version of the paper along with relevant caveats regarding non-specific modes of interaction.

Medina-Franco also suggest that a comment should be made regarding the effect of drug concentration in chemogenomics datasets since, for example, "...adverse drug reactions and drug-interaction networks in general, will depend on the drug concentrations". While it is certainly true that drug concentration has a significant effect on biological processes it does not per se directly affect the structure of the drug-target threshold networks described in our paper because the presence of an edge between two network nodes is solely dependent on the activity value, e.g. a pK_i or IC₅₀, and the activity threshold imposed.

Medina-Franco has noted that reference to the work in Shoichet's lab at the University of California at San Francisco (UCSF) is apparently missing. The missing citation is reference [43].
Medina-Franco suggests that "The term 'frequent hitter' related to polypharmacology can be added in the Introduction". We chose not to include it in our initial version of the manuscript because we felt that the term was too general since it also includes drug-target interactions induced by a variety of non-specific modes of interaction that do not typically lead to genuine pharmacological responses. However, we will include a mention of it in the next version of the paper along with relevant caveats regarding non-specific modes of interaction.

Medina-Franco also suggest that a comment should be made regarding the effect of drug concentration in chemogenomics datasets since, for example, "...adverse drug reactions and drug-interaction networks in general, will depend on the drug concentrations". While it is certainly true that drug concentration has a significant effect on biological processes it does not per se directly affect the structure of the drug-target threshold networks described in our paper because the presence of an edge between two network nodes is solely dependent on the activity value, e.g. a pK_i or IC₅₀, and the activity threshold imposed.

Medina-Franco has noted that reference to the work in Shoichet's lab at the University of California at San Francisco (UCSF) is apparently missing. The missing citation is reference [43].
Competing Interests: I have no competing interest that could be construed to influence my response to the referee's comments. Close
Report a concern

Comments on this article Comments (1)

Version 1

VERSION 1 PUBLISHED 06 Jun 2017

Reader Comment 13 Mar 2018

Francois Berenger, Kyushu University, Japan

13 Mar 2018

Reader Comment

I see many [Math Processing Error] in the text.
Am I the only one?
Competing Interests: No competing interests were disclosed.
I see many [Math Processing Error] in the text.
Am I the only one?
I see many [Math Processing Error] in the text.
Am I the only one?
Competing Interests: No competing interests were disclosed. Close
Report a concern
Comment

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2	3	4
Version 1 06 Jun 17	read	read	read	read

Jose L. Medina-Franco, National Autonomous University of Mexico, Mexico City, Mexico
Karina Martinez-Mayorga, National Autonomous University of Mexico, Mexico City, Mexico
John Van Drie, Van Drie Research LLC, North Andover, USA
Tudor I. Oprea, University of New Mexico School of Medicine, Albuquerque, USA

Comments on this article

All Comments(1)

Add a comment

Browse by related subjects

Back to all reports

Reviewer Report

20 Views

20 Jun 2017 | for Version 1

Tudor I. Oprea, Translational Informatics Division, Department of Internal Medicine, University of New Mexico School of Medicine, Albuquerque, NM, USA

20 Views Cite this report Responses(1)

Approved With Reservations

The target is in the CNS, but the drug itself is an ABCB1 substrate (see for example the impact of ABCB1 on CNS side-effects), or the drug lacks blood-brain barrier permeability - in which case the potency of the drug in vitro is irrelevant in vivo.
The drug can have significant in vitro potency on many targets, e.g., dobutamine hits over 20 human targets according to DrugCentral. However, its half-life is 2 minutes. Therefore, these "off target effects" are irrelevant.

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

I cannot comment. A qualified statistician is required.
Are all the source data underlying the results available to ensure full reproducibility?

No source data required
Are the conclusions drawn adequately supported by the results?

Partly

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Cheminformatics, pharmacoinformatics, drug target analytics, drug target curation

Respond to this report

Responses (1)

Author Response

23 Jun 2017

Gerry Maggiora, BIO5 Institute, University of Arizona, 1657 East Helen Street, Tucson, 85719, USA

Oprea raises the issue of "how relevant is target polyspecificity?" and he also takes issue with usage of the terminology "structurally dissimilar drugs" with regard to the concept of polyspecificity, noting that "similar molecules do not always share the same activity landscape". Moreover, he states that in his opinion "polyspecificity does NOT require 'dissimilar' in the definition". These three points are addressed in order.

First, The relevance of polyspecificity is not explicitly addressed in the paper, rather the focus is on the fact that polyspecificity is closely (and mathematically) related to polypharmacology, a concept that most will agree is quite relevant to drug research. The point is that both concepts are related to one another, and as stated in the paper are metaphorically "two sides of the same coin".

Second, the reason that 'structurally dissimilar drugs' was mentioned explicitly in the definition of polyspecificity is that polyspecificity implies multiple specificities and hence a diversity of drug structures.

Third, that structurally similar molecules will interact with the same protein is generally expected, although as Oprea has pointed out above, "similar molecules do not always share the same activity landscape". While the 'spirit' of this quote is relevant, it is not entirely accurate since an activity landscape is associated with the target being assayed. The molecules that make up the dataset will all lie on that particular activity landscape. Although relatively rare, two structurally similar molecules may nevertheless exhibit widely different activities, an occurrence that gives rise to 'activity cliffs' on the landscape.

Oprea also opines that the issue of target polyspecificity is relevant and ought to be investigated more in the context of co-prescribed medications. This seems like a very relevant application of polyspecificity especially, as pointed out by Oprea, that "15% of US adults are likely to use 5 or more prescription drugs. Moreover, it should be noted that geriatric patients generally are on two or more times as many drugs as younger patients making such an analysis even more desirable.

Oprea brings up the important subject of potency, pointing out that it is not specifically addressed in the formulation presented in the paper. For example, he states that "The bipartite drug-target network in Figure 1, therefore, not only has nodes and edges, but the edges have values...". While this statement is technically correct, with regard to the paper the point he is making is incorrect since it is addressed, albeit in limited fashion, by the fact that the bipartite networks employed in our work are threshold networks. By choosing activity values that are greater than or equal to a given threshold value, say 100 nM, ensures that all of the edges in the network correspond to drug-target pairs of reasonable activity with respect to the targets assayed. Hence, Oprea's point "that Drug D1, with a Ki of 1 nM has the same relevance for polypharmacology and polyspecificity as Drug D2, with a Ki of 1 mM" is not correct. For example, for a threshold value of 100 nM an edge would be drawn between Drug D1 and its target, while no edge would be drawn between Drug D2 and the same target. It is true, however, that not dealing explicitly with drug-target activity values results in a loss of information, but this can be accounted for if one uses weighted bipartite networks, which are more complicated and require a higher level of theory. Hence, we chose to explore the issues associated with drug-target networks using the simplest level of theory first, but we intend to deal with weighted drug-target networks in a future publication.

Oprea raises a number of important issues regarding the inherent subjectivity of interpreting drug activity with respect to different targets. He makes the point that receptors with lower activity for a given drug may, nevertheless, be more pharmacologically/biologically relevant than other receptors for which the drug has a higher affinity. His point is well taken and, no doubt, needs to be addressed when assessing the pharmacological/biological relevance of a particular drug-target interaction. However, doing so is a much more demanding task than identifying putative polypharmacologies and polyspecificities and requires significant additional information on pathways, biopharmaceutical properties, and drug metabolism. Our aim in this paper was merely to address drug-target interactions within an in vitro setting.

An additional complication in the study of drug-target interactions, most of which involve in vitro and ex vivo experiments, is that the information in drug-target databases is very heterogeneous since it is made up of data obtained from a wide variety off different sources. As noted in the paper, even experiments carried out in the same lab using the same experimental protocol on different days can result in significantly divergent experimental values. Further complicating this issue is the fact, also stated in the paper, that a growing number of values are obtained computationally. All of these factors conspire to raise the uncertainty of the information used to construct drug-target networks. Lastly, it is assumed, mostly tacitly, that drug-target interactions, which are generally determined in in vitro and ex vivo experiments, can be used to interpret complicated in vivo biological phenomena. However, this must be done with caution. For example, protein-protein interaction data are used in the construction of biological pathways, when in fact most such data are determined in in vitro experiments that are far removed from the context in which the pathways reside. Nevertheless, while such data may be problematic in some cases, they can be useful in advancing our understanding of the biological functionality of many processes taking place in living systems, with the caveat that care must be used in drawing inferences from such potentially problematic data.

Oprea suggests that data from such databases a ChEMBL, DrugBank, DrugCentral, or GuideToPharmacology be used to construct an example from 'real data'. This is an excellent suggestion and one that we are currently working on. There are two main issues that we wanted to highlight in the paper: (1) the relationship between polypharmacology and polyspecificity and (2) the development of a method for estimating error bounds for drug-target network parameters such as the degrees of polypharmacology and polyspecificity. Hence, we focused our attention on the mathematical relationships that exemplify these network properties, and we left the development of actual examples for future work.

View more View less

Competing Interests

The authors have no competing issues.

Back to all reports

Reviewer Report

12 Views

19 Jun 2017 | for Version 1

John Van Drie, Van Drie Research LLC, North Andover, MA, USA

12 Views Cite this report Responses(1)

Approved

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

No source data required
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests

No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (1)

Back to all reports

Reviewer Report

13 Views

19 Jun 2017 | for Version 1

Karina Martinez-Mayorga, Institute of Chemistry, National Autonomous University of Mexico, Mexico City, Mexico

13 Views Cite this report Responses(0)

Approved

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

References

1. Araneda RC, Kini AD, Firestein S: The molecular receptive range of an odorant receptor.Nat Neurosci. 2000; 3 (12): 1248-55 PubMed Abstract | Publisher Full Text

Competing Interests

No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

21 Views

09 Jun 2017 | for Version 1

Jose L. Medina-Franco, DIFACQUIM Research Group, Department of Pharmacy, School of Chemistry, National Autonomous University of Mexico, Mexico City, Mexico

21 Views Cite this report Responses(1)

Approved

The term “frequent hitter” related to polypharmacology can be added in the Introduction.
Comment on the effect of drug concentration in chemogenomics data sets. For instance, adverse drug reactions, and drug-interaction networks in general, will depend on the drug concentrations.
Page 4: Include reference related to the statement: “Recent work from Shoichet’s group at UCSF …”. I believe the authors refer to the paper published in ACS Chem. Biol. 2015¹. This manuscript is not included in the Reference section of the current version.
Spell out "UCSF" (University of California at San Francisco).

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

References

1. Barelier S, Sterling T, O'Meara MJ, Shoichet BK: The Recognition of Identical Ligands by Unrelated Proteins.ACS Chem Biol. 2015; 10 (12): 2772-84 PubMed Abstract | Publisher Full Text

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Computer-aided drug design, chemoinformatics

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (1)

Author Response

28 Jun 2017

Gerry Maggiora, BIO5 Institute, University of Arizona, 1657 East Helen Street, Tucson, 85719, USA

Medina-Franco suggests that "The term 'frequent hitter' related to polypharmacology can be added in the Introduction". We chose not to include it in our initial version of the manuscript because we felt that the term was too general since it also includes drug-target interactions induced by a variety of non-specific modes of interaction that do not typically lead to genuine pharmacological responses. However, we will include a mention of it in the next version of the paper along with relevant caveats regarding non-specific modes of interaction.

Medina-Franco also suggest that a comment should be made regarding the effect of drug concentration in chemogenomics datasets since, for example, "...adverse drug reactions and drug-interaction networks in general, will depend on the drug concentrations". While it is certainly true that drug concentration has a significant effect on biological processes it does not per se directly affect the structure of the drug-target threshold networks described in our paper because the presence of an edge between two network nodes is solely dependent on the activity value, e.g. a pK_i or IC₅₀, and the activity threshold imposed.

Medina-Franco has noted that reference to the work in Shoichet's lab at the University of California at San Francisco (UCSF) is apparently missing. The missing citation is reference [43].

View more View less

Competing Interests

I have no competing interest that could be construed to influence my response to the referee's comments.

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

[1] 1. Peters JU, Ed: Polypharmacology in Drug Discovery. John Wiley & Sons, New York. 2012. Publisher Full Text

[2] 2. Hopkins AL: Network pharmacology: the next paradigm in drug discovery. Nature Chem Biol. 2008; 4(11): 682–690. PubMed Abstract | Publisher Full Text

[3] 3. Hopkins AL: Introduction: The case for polypharmacology. In Polypharmacology in Drug Discovery. Peters JU, Ed., John Wiley & Sons, 2012; 1–6. Publisher Full Text

[4] 4. Anighoro A, Bajorath J, Rastelli G: Polypharmacology: Challenges and opportunities in drug discovery. J Med Chem. 2014; 57(19): 7874–7887. PubMed Abstract | Publisher Full Text

[5] 5. Tan Z, Chaudhai R, Zhang S: Polypharmacology in Drug Development: A Minireview of Current Technologies. ChemMedChem. 2016; 11(12): 1211–1218. PubMed Abstract | Publisher Full Text

[6] 6. Achenbach J, Tiikkainen P, Franke L, et al.: Computational tools for polypharmacology and repurposing. Future Med Chem. 2011; 3(8): 961–968. PubMed Abstract | Publisher Full Text

[7] 7. Pérez-Nueno VI, Souchet M, Karaboga AS, et al.: GESSE: Predicting drug side effects from drug-target relationships. J Chem Inf Model. 2015; 55(9): 1804–1823. PubMed Abstract | Publisher Full Text

[8] 8. Lounkine E, Keiser MJ, Whitebread S, et al.: Large-scale prediction and testing of drug activity on side-effect targets. Nature. 2012; 486(7403): 361–367. PubMed Abstract | Publisher Full Text | Free Full Text

[9] 9. Campillos M, Kuhn M, Gavin AC, et al.: Drug target identification using side-effect similarity. Science. 2008; 321(5886): 263–266. PubMed Abstract | Publisher Full Text

[10] 10. Kuhn M, Campillos M, Letunic I, et al.: A side effect resource to capture phenotypic effects of drugs. Mol Syst Biol. 2010; 6: 343. PubMed Abstract | Publisher Full Text | Free Full Text

[11] 11. Barratt MJ, Frail DE: Drug Repositioning – Bringing New Life to Shelved Assets and Existing Drugs. John Wiley & Sons, New York. 2012. Publisher Full Text

[12] 12. Dimitrov JD, Pashov AD, Vassilev TL: Antibody polyspecificity: what does it matter? Adv Exp Med Biol. 2012; 750: 213–226. PubMed Abstract | Publisher Full Text

[13] 13. Van Regenmortel MH: Specificity, polyspecificity, and heterospecificity of antibody-antigen recognition. J Mol Recog. 2014; 27(11): 627–639. PubMed Abstract | Publisher Full Text

[14] 14. Young DD, Jockush S, Turro NJ, et al.: Synthetase polyspecificity as a tool to modulate protein function. Bioorg Med Chem Lett. 2011; 21(24): 7502–7504. PubMed Abstract | Publisher Full Text | Free Full Text

[15] 15. Martinez L, Arnaud O, Henin E, et al.: Understanding polyspecificity within the substrate-binding cavity of the human multidrug resistance P-glycoprotein. FEBS J. 2014; 281(3): 673–682. PubMed Abstract | Publisher Full Text

[16] 16. Lyons JA, Parker JL, Solcan N, et al.: Structural basis for polyspecificity in the POT family of proton-coupled oligopeptide transporters. EMBO Rep. 2014; 15(8): 886–893. PubMed Abstract | Publisher Full Text | Free Full Text

[17] 17. Lytvynenko I, Brill S, Oswald C, et al.: Molecular basis of polyspecificity of the small multidrug resistance efflux pump AbeS from Acinetobacter baumannii. J Mol Biol. 2016; 428(3): 644–657. PubMed Abstract | Publisher Full Text

[18] 18. Esser L, Zhou F, Pluchino KM, et al.: Structures of the multidrug transporter P-glycoprotein reveal asymmetric ATP binding and the mechanism of polyspecificity. J Biol Chem. 2017; 292(2): 446–461. PubMed Abstract | Publisher Full Text | Free Full Text

[19] 19. Blass BE: Basic Principles of Drug Discovery and Development. Academic Press, New York. 2015. Reference Source

[20] 20. Brown N, Ed: Scaffold Hopping in Medicinal Chemistry. Wiley-VCH, New York. 2014. Publisher Full Text

[21] 21. Saha R, Tanwar O, Alam NM, et al.: Pharmacophore based virtual screening, synthesis and SAR of novel inhibitors of Mycobacterium sulfotransferase. Bioorg Med Chem Lett. 2015; 25(3): 701–707. PubMed Abstract | Publisher Full Text

[22] 22. Iyer P, Stumpfe D, Vogt M, et al.: Activity Landscapes, Information Theory, and Structure - Activity Relationships. Mol Inform. 2013; 32(5-6): 421–430. PubMed Abstract | Publisher Full Text

[23] 23. Maggiora GM: Introduction to molecular similarity and chemical space. In Foodinformatics: Applications of Chemical Information to Food Chemistry. Martinez-Mayorga K, Medina-Franco JL, Eds. Springer International Publishing Switzerland; 2014; 1–81. Publisher Full Text

[24] 24. Law V, Knox C, Djoumbou Y, et al.: DrugBank 4.0: shedding new light on drug metabolism. Nucleic Acids Res. 2014; 42(Database issue): D1091–D1097. PubMed Abstract | Publisher Full Text | Free Full Text

[25] 25. Szklarczyk D, Santos A, von Mering C, et al.: STITCH 5: augmenting protein-chemical interaction networks with tissue and affinity data. Nucleic Acids Res. 2016; 44(D1): D380–D384. PubMed Abstract | Publisher Full Text | Free Full Text

[26] 26. Olah M, Rad R, Ostopovici L, et al.: WOMBAT and WOMBAT-PK: Bioactivity Databases for Lead and Drug Discovery. In Chemical Biology: From Small Molecules to Systems Biology and Drug Design. Schreiber SL, Kapoor T, Wess G, Eds., John Wiley & Sons, New York; 2008; 760–786. Publisher Full Text

[27] 27. Kim S, Thiessen PA, Bolton EE, et al.: PubChem Substance and Compound databases. Nucleic Acids Res. 2016; 44(D1): D1202–D1213. PubMed Abstract | Publisher Full Text | Free Full Text

[28] 28. Liu T, Lin Y, Wen X, et al.: BindingDB: a web-accessible database of experimentally determined protein-ligand binding affinities. Nucleic Acids Res. 2007; 35(Database issue): D198–D201. PubMed Abstract | Publisher Full Text | Free Full Text

[29] 29. Gaulton A, Hersey A, Nowotka M, et al.: The ChEMBL database in 2017. Nucleic Acids Res. 2017; 45(D1): D945–D954. PubMed Abstract | Publisher Full Text | Free Full Text

[30] 30. Tym JE, Mitsopoulos C, Coker EA, et al.: canSAR: an updated cancer research and drug discovery knowledgebase. Nucleic Acids Res. 2016; 44(D1): D938–D943. PubMed Abstract | Publisher Full Text | Free Full Text

[31] 31. von Eichborn J, Murgueitio MS, Dunkel M, et al.: PROMISCUOUS: a database for network-based drug-repositioning. Nucleic Acids Res. 2011; 39(Database issue): D1060–D1066. PubMed Abstract | Publisher Full Text | Free Full Text

[32] 32. Günther S, Kuhn M, Dunkel M, et al.: SuperTarget and Matador: resources for exploring drug-target relationships. Nucleic Acids Res. 2008; 36(Database issue): D919–D922. PubMed Abstract | Publisher Full Text | Free Full Text

[33] 33. Jasial S, Hu Y, Bajorath J: Determining the degree of promiscuity of extensively assayed compounds. PLoS One. 2016; 11(4): e0153873. PubMed Abstract | Publisher Full Text | Free Full Text

[34] 34. Hu Y, Gupta-Osterman D, Bajorath J: Exploring compound promiscuity patterns and multi-target activity spaces. Comput Struct Biotechnol J. 2014; 9(13): e201401003. PubMed Abstract | Publisher Full Text | Free Full Text

[35] 35. Hu Y, Bajorath J: How promiscuous are pharmaceutically relevant compounds? A data-driven assessment. AAPS J. 2013; 15(1): 104–111. PubMed Abstract | Publisher Full Text | Free Full Text

[36] 36. Hu Y, Bajorath J: Exploring molecular promiscuity from a ligand and target perspective. In Frontiers in Molecular Design and Chemical Information Science. Bajorath J, Ed. ACS Symposium Series, American Chemical Society, 2016; 1222. : 19–34. Publisher Full Text

[37] 37. Mestres J, Gregori-Puigjané E, Valverde S, et al.: Data completeness--the Achilles heel of drug-target networks. Nat Biotechnol. 2008; 26(9): 983–984. PubMed Abstract | Publisher Full Text

[38] 38. Santos R, Ursu O, Gaulton A, et al.: A comprehensive map of molecular drug targets. Nat Rev Drug Discov. 2017; 16(1): 19–34. PubMed Abstract | Publisher Full Text

[39] 39. Klotz IM, Rosenberg RM: Chemical Thermodynamics: Basic Concepts and Methods. 7^th Edition. John Wiley & Sons, New York 2008. Publisher Full Text

[40] 40. Milletti F, Vulpetti A: Predicting polypharmacology by binding site similarity: from kinases to the protein universe. J Chem Inf Model. 2010; 50(8): 1418–1431. PubMed Abstract | Publisher Full Text

[41] 41. Moya-García AA, Ranea JA: Insights into polypharmacology from drug-domain associations. Bioinformatics. 2013; 29(16): 1934–1937. PubMed Abstract | Publisher Full Text

[42] 42. Moya-Garcia AA, Dawson NL, Kruger FA, et al.: Structural and functional view of polypharmacology. Preprint posted online 18 March 2016 (not peer reviewed). 2017. Publisher Full Text

[43] 43. Bareller S, Sterling T, O’Meara MJ, et al.: The recognition of identical ligands by unrelated proteins. ACS Chem Biol. 2015; 10(12): 2772–2784. PubMed Abstract | Publisher Full Text | Free Full Text

[44] 44. Kahraman A, Morris RJ, Laskowski RA, et al.: Shape variation in protein binding pockets and their ligands. J Mol Biol. 2007; 368(1): 283–301. PubMed Abstract | Publisher Full Text

[45] 45. Kahraman A, Morris RJ, Laskowski RA, et al.: On the diversity of physicochemical environments experienced by identical ligands in binding pockets of unrelated proteins. Proteins. 2010; 78(5): 1120–1136. PubMed Abstract | Publisher Full Text

[46] 46. Sturm N, Desaphy J, Quinn RJ, et al.: Structural insights into the molecular basis of the ligand promiscuity. J Chem Inf Model. 2012; 52(9): 2410–2421. PubMed Abstract | Publisher Full Text

[47] 47. Ehrt C, Brinkjost T, Koch O: Impact of Binding Site Comparisons on Medicinal Chemistry and Rational Molecular Design. J Med Chem. 2016; 59(9): 4121–4151. PubMed Abstract | Publisher Full Text

[48] 48. Matthews BW: Protein-DNA interaction. No code for recognition. Nature. 1988; 335(6188): 294–295. PubMed Abstract | Publisher Full Text

[49] 49. Newman ME: Networks. An Introduction. Oxford University Press, Oxford, UK. 2010. Publisher Full Text

[50] 50. Van Steen M: Graph Theory and Complex Networks. An Introduction. M van Steen Publisher; 2010. Reference Source

[51] 51. Asratian AS, Denley TM, Häggkvist R: Bipartite Graphs and Their Applications. Cambridge University Press, Cambridge, UK. 1999. Publisher Full Text

[52] 52. Yildirim MA, Goh KI, Cusick ME, et al.: Drug-target network. Nat Biotechnol. 2007; 25(10): 1119–1126. PubMed Abstract | Publisher Full Text

[53] 53. Vogt I, Mestres J: Drug-Target Networks. Mol Inform. 2010; 29(1–2): 10–14. Publisher Full Text

[54] 54. Bauer-Mehren A, Rautschka M, Sanz F, et al.: DisGeNET: a Cytoscape plugin to visualize, integrate, search and analyze gene-disease networks. Bioinformatics. 2010; 26(22): 2924–2926. PubMed Abstract | Publisher Full Text

[55] 55. Kolaczyk ED: Statistical Analysis of Network Data: Methods and Models. Springer, New York. 2009. Publisher Full Text

[56] 56. Cheng F, Liu C, Jang J, et al.: Prediction of drug-target interactions and drug repositioning via network-based inference. PLoS Comput Biol. 2012; 8(5): e1002503. PubMed Abstract | Publisher Full Text | Free Full Text

[57] 57. Yamanishi Y, Araki M, Gutteridge A, et al.: Prediction of drug-target interaction networks from the integration of chemical and genomic spaces. Bioinformatics. 2008; 24(13): i232–i240. PubMed Abstract | Publisher Full Text | Free Full Text

[58] 58. Lu Y, Guo Y, Korhonen A: Link prediction in drug-target interactions network using similarity indices. BMC Bioinformatics. 2017; 18(1): 39. PubMed Abstract | Publisher Full Text | Free Full Text

[59] 59. Peng L, Liao B, Zhu W, et al.: Predicting drug-target interactions with multi-information fusion. IEEE J Biomed Health Inform. 2017; 21(2): 561–572. PubMed Abstract | Publisher Full Text

[60] 60. Jain AK, Dubes RC: Algorithms for Clustering Data. Prentice Hall, Englewood Cliffs, New Jersey. 1988. Reference Source

A simple mathematical approach to the analysis of polypharmacology and polyspecificity data

Abstract

Keywords

Introduction

Table 1. Sample of drug-target databases available over the Internet given by name, web address, and reference number in this work.

Structural basis of drug-target interactions

Mathematical representations of drug-target interactions

Drug-target relationships

Bipartite networks

Figure 1. Simple example of a bipartite drug-target network made up of eight drugs and four targets.

Drug-target networks

Network data

Polypharmacology and polyspecificity

Table 2. Active drug-target interactions.

Limitations of network representations

Edge-colored bipartite networks

Figure 2. Example of the network in Figure 1 represented as an edge-colored network, where the green edges correspond to active drug-target pairs, the red edges to inactive drug-target pairs, and the black edges to drug-target pairs of unknown activity status.

Figure 3.

Table 3. Inactive drug-target interactions.

Table 4. Unknown drug-target interactions.

Figure 4.

Measures of data completeness

Global measures

Local measures

Bounds for the degrees of polypharmacology and polyspecificity

Table 5. Upper and lower bounds to the degree of polypharmacology for the set of eight drugs in the simple example described in this work.

Table 6. Upper and lower bounds to the degree of polyspecificity for the set of four targets in the simple example described in this work.

Summary and conclusions

Author contributions

Competing interests

Grant information

Acknowledgments

References

Comments on this article Comments (1)

Open Peer Review

Comments on this article Comments (1)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated