Keywords
paternal age, de novo mutations, IQ, demographic models
paternal age, de novo mutations, IQ, demographic models
The DNA of a child is not exactly a composition of its father’s and mother’s DNA. De novo mutations, base pair changes, do occur during meiosis and throughout the parent’s life, including in male gametes. It has been widely reported (Cannon, 2009; Gauthier & Rouleau, 2012; Kong et al., 2012) that parental age at the time of conception is one factor contributing to a higher mutation rate. The number of de novo mutations rises particularly with the age of the father. Paternal de novo mutations have been found (Kong et al., 2012) to increase by about 2.01 base pairs per year. For example, an age of 45 at conception entails an average 52.5 more de novo mutations in offspring than an age of 20.
Kong et al. showed that the father's age is the dominant factor in determining the number of de novo mutations in a child. By sequencing the genomes of 78 parent-child trios, Kong et al. found that the number of mutations increases (Gauthier & Rouleau, 2012; Kong et al., 2012) with the father's age (P = 3.6 × 10-19) at an estimated rate of 2.01 mutations per year (standard error = 0.17). Some of Kong et al.’s rate dimensions imply a first-order relationship whereas others imply rather a zero-order dependency: i.e. respectively reporting an exponential increase with a doubling of paternal mutations every 16.5 years as well as a yearly rate of 2.01 de novo mutations. A first- or zero-order rate are of course two different propositions and, short off alleging a governing influence of a decay in DNA repair and replication, the formation of de novo mutations is proportional to the size of the genome, thus, implying rather zero order kinetics. Either way, for the reported comparison of two extrema of the age at conception the difference in order only affects the assessment of intermediate de novo mutation levels.
The paternal age effect describes the sensitivity of individual health to the average increase in de novo mutations in offspring due to elevated paternal age: e.g. 30 years of elevated paternal age resulting in ~60 more base pair changes. As per Kong et al.’s reported standard error, the yearly de novo mutation rate has been considered as quasi linear and can thus be considered as of constant logarithmic order of magnitude throughout a man’s life.
Regardless of the age at conception, de novo mutations present a constant limit to the conservation of DNA and a constant degrading effect on an organism’s health, statistically detectable within one generation and even more significant when considered for historic time scales.
Increasing paternal age has been linked (Cannon, 2009) to a statistically detectable mental decline, an average IQ decline of six points for children of fathers aged 50 (at conception) compared to younger fathers, aged 20, as reported by Cannon. The correlation between de novo mutations and paternal age effect, with respect to the average IQ, might have been considered unexpected due to the logarithmic orders of magnitude separating the number of de novo mutations and the size of the entire human genome, as well as the small fraction of protein coding exon-DNA. A direct link to this statistical effect is nevertheless not only plausible, considering the influence of mutations in intron-DNA on the level of gene expression, but might also be negligent to discard considering the drastic outcome that this might entail for persistent trends of elevated paternal age. This paper presents a model that simulates the paternal age effect on IQ for societies and super-positions it with other effects: e.g. the Flynn effect, which is an increase in IQ points (Flynn, 1987) per generation, that has been found particularly during the 20th century’s development of parenting and education. It has been disputed whether this is a temporal effect as the increases have been most prominent in data from well within the 20th century. Since then the average paternal age has continued to increase. The simulation presented in this paper super-positioned the Flynn effect with rising paternal age and yielded a good agreement with the recently observed halt or decrease of the Flynn effect (Sundet et al., 2004).
The relevance of paternal age, that is, the relevance of a limited number of de novo mutations, for neurological and psychiatric disorders becomes consistent when considering not only rare mutations in protein coding DNA but also much more frequent genetic alteration in introns, which impacts protein expression, as evidenced by findings that confirmed the long suspected significant role of non-protein coding DNA in protein expression (Le Hir et al., 2003; Nott et al., 2003). Hence, increased random errors in DNA, due to increased paternal age, might plausibly yield statistical decreases in cognitive abilities.
The developed model can aid to assess these and:
1. couple de novo mutation accumulation simulations with correlations for IQ decline or probabilities for other health impacts statistically related to paternal age,
2. be useful for both, investigating genetic alteration depending on potentially relevant factors under investigation, such as environmental influences and demographic patterns in terms of reproduction,
3. assess dynamic distributions of neurological and psychiatric disorders (Gauthier & Rouleau, 2012) along multiple generations,
4. simulate the health of organisms and its interconnected dynamic properties during evolution and bottlenecks in evolution,
explain uncertainty in demographic models which heretofore didn’t consider dependencies between these organism properties and reproductive patterns.
A prerequisite to embarking some of the considerations mentioned above, is to recognize that long term developments of properties such as the average IQ belong to the vital interests of societies. Henceforth, even if cautioned that not all influences are yet quantified or even possible to quantify, potential decay factors, their impact potential and long-term impact should be anticipated and extrapolated, particularly assessing the order of magnitude of the potential change in the population’s IQ distribution based on contemporary reproductive trends (here elevated paternal age across multiple generations).
The developed model simulates reproduction, mutations and IQ individually for each person in the simulated population. The initial age distribution as well as reproductive dynamics can be supplied to the model via demographic data. Reproduction occurs at a particular age with varying probabilities, depending on demographic input data. It is also possible to set a gender bias in the sex ratio of newborns. A for-loop checks every month whether the demographic data suggest reproduction and the associated probability. This has been embedded with a weighted random number ρ and normal distributed random number ρn . Children are born every month based on the set sex ratio and with added de novo mutations according to the paternal age. The IQ is then set randomized as per a normal distribution normed to the parental IQ, plus Flynn effect, minus paternal age effect as per its correlation with the accumulated de novo mutations. Simulated individuals die as per supplied demographic input data. Matrix M contains columns denoting age, gender, life expectancy, de novo mutations, and IQ. Reproduction occurs based on the relation rl + ρ > 1 with l = Mi1 where r is a vector containing the reproductive probability depending on age. If wanted, correlations between intelligence and fertility can be taken into account by involving the IQ in this relation.
The IQ is denoted in M for a newborn s and calculated with and .
IQ is the relative average IQ, Δa is the fertile age interval, σ the spread of the normal distribution, and F is the assumed IQ increase as per the Flynn effect.
clear d y m f z i h b n s r t j c %PATERNAL AGE EFFECT: IQ 9/10/15 d=30; y=d*10; m=y*12; f(y,31)=0; z=f; %decades, years & months; records f i=2000; %initial population size i h=70*12; %highest age in months h b=1; %gender ration b: boys/girls n(1:h)=2.01; %dynamic de novo mutation rate n for c=20:50 %vary reproduction ages in loop clear M %Mij with j=1 age, 2 gender s=i; %dynamic population size s M(1:s,1:4)=0; %Mij, j=3 de novo m., 4 lifespan M(1:s,4)=h; %lifespan in colum 4 of M M(1:round(b*s/2),2)=1; %gender (1: males, 0: females) M(:,1)=linspace(1,70*12,s);M=round(M); %even initial age distribution M(:,5)=1; %initial average IQ r(1:h)=0; %reset reproduction probability r(c*12+1:(c+10)*12)=2.0/10; %fertile decade is varied r=r/12; n=n/12; %convert yearly values to months for t=1:m %simulate for all months m for j=1:s %simulate for all people s M(j,1)=M(j,1)+1; %people's aging if M(j,4)==M(j,1) %depart life after lifespan M(j,4)=-1; M(j,2)=0; end if M(j,2)==1 %if alive & male, then: M(j,3)=M(j,3)+n(M(j,1)); %collect de novo mutations if r(M(j,1))+rand>1 %reproduce per set probability s=s+1; %grow number of people q=.92+.08*(60-M(j,1)/12)/40; %age based Gauss f(IQ) M(s,5)=M(j,5)*1.05*(randn*.15+q);%assign random IQ M(s,1)=0; M(s,4)=h; %assign age & lifespan M(s,2)=round(b*rand); %gender as per gender bias M(s,3)=M(j,3); %inherit de novo mutations end end end if t/12==round(t/12) %record data yearly z(t/12,c-19)=sum(M(:,2))/b*2; %record population z & mean IQ f(t/12,c-19)=sum(M(:,2)'*M(:,5))/sum(M(:,2)); end end end
The simulated cases shown in Figure 1 and Figure 2 below have the specifications: 1.) A population of 20,000; 2.) 300 years; 3.) Average number of children is 2; 4.) No gender bias concerning delivery of baby boys and girls is assumed but could be accounted for by setting a different value for the sex ratio b; 5.) De novo mutation accumulation has been assumed to obey published data (Gauthier & Rouleau, 2012; Kong et al., 2012).
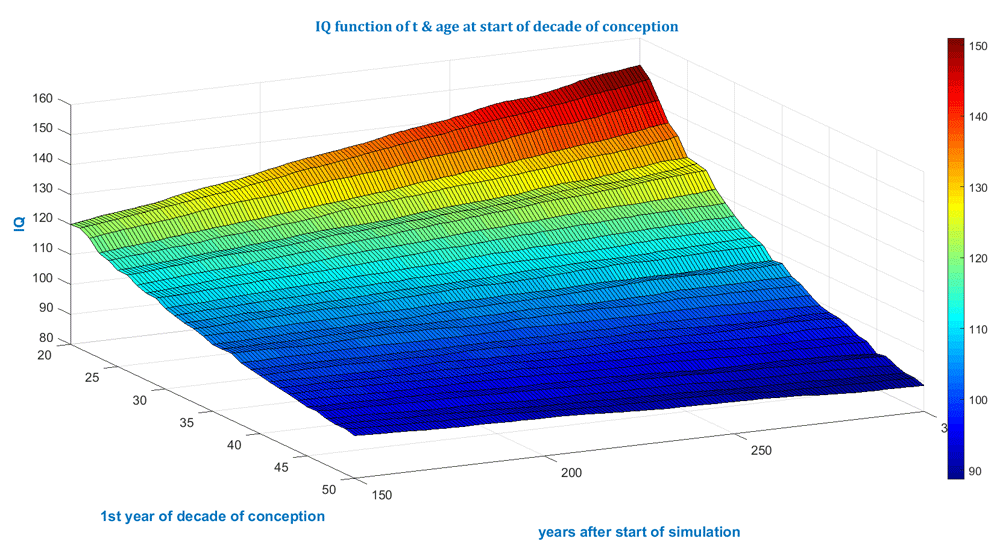
The start of the decade is varied from 20 to 50. The optimistic assumption of a continuous Flynn effect has been super-positioned.
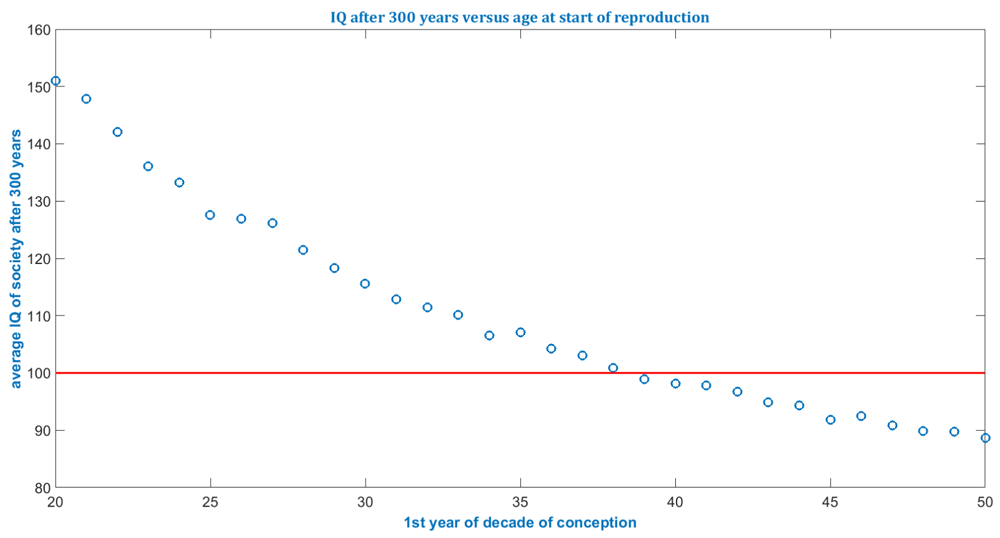
The start of the decade is varied from 20 to 50. The optimistic assumption of a continuous Flynn effect has been super positioned which yields very high IQs for young paternal ages after 300 y.
Life expectancy is of little relevance for the simulated results, considering that in most cases death occurs after the fertile age period.
A nonlinear de novo mutation accumulation rate, as plausibility due to changing cell division and DNA repair protein activity throughout life, can be used as already provided for by keeping y as vector. This can easily be incorporated with linear ratios (splines) between each data point yielding varying rates depending on age. The reproduction probability distribution can be set as per demographic data from any population of interest and represented as vector r. This particle type model illustrates that different effects can be conveniently superimposed. Furthermore, it allows to assess the order of magnitude of the problem as shown in the simulated cases where conception occurs in different paternal age intervals, starting with an interval from 20 to 30 and ending with an interval from 50 to 60. That means, 30 different reproductive patterns in terms of paternal age are simulated for comparison, the youngest assuming reproduction to occur between 20 and 30 and the oldest assuming paternal age at conception to be between 50 and 60.
Currently the model is intended to assess the order of magnitude of the impact of elevated paternal age after multiple generations - not to do forecasting for average properties - since several input distributions, such as for reproduction, age, life expectancy and gender ratios, are set to constant values. The model simulates each individual and thus requires much more computational capacity than models relying on partial differential equations which average every constituent into a continuum. Therefore, if populations >1 million, that is, whole societies or populations, are to be simulated, then supercomputers might support practicable computational times. Several conclusions can be gleaned from the simulation illustrated in Figure 1 to Figure 4 and listed in Table 1.


| Conclusions | |
|---|---|
| 1. | The correlation between continuous paternal accumulation of de novo mutations and intelligence has not been discovered before comparing different paternal age groups. Therefore, it might have been masked by other factors including reproductive patterns. To offset the paternal age effect, they must be sufficiently significant to constitute an uncertainty in various adjacent problems such as demographics. |
| 2. | Demographics, reproduction, and the paternal age effect, that is de novo mutation levels in newborns, are coupled, with both influencing each other, as supported by recent findings (Arslan et al., 2017). |
| 3. | The model permits to elucidate highly interconnected patterns of organism health and reproduction in evolution scenario (not only for humans). |
| 4. | The model (if run for small populations) indicates ill-posed, susceptible to random influences, behavior during evolutionary bottlenecks. This statistical particle model shows for the same initial conditions substantially varying outcomes, depending on the set of random numbers (for small populations, i.e. isolated communities or evolutionary bottlenecks). |
| 5. | Investigated demographic distributions should be empirically supplied to the model, such as: Correlation of intelligence with fertility, correlation of other health indicators with fertility, correlation of de novo mutation levels in newborns with later fertility. |
| 6. | To validate paternal age effect correlations, it is recommendable to include data from bioinformatics which detail affected genes’ functionality, rather than just macroscopic demographic distributions. |
| 7. | The effects of continuously elevated paternal age in society can be assessed, particularly with respect to the order of magnitude of the impacts, by super-positioning in simulations impacting and mitigating factors for investigated countries/regions. |
| 8. | For example, the simulation returned that, even under the optimistic assumption of a never-ending Flynn effect, if super-positioned with the paternal age effect, then an average paternal age above 40 would lead to the long-term decline of the average IQ in society. |
Obviously, limits in the conservation of DNA are usually outpaced by evolution, mating patterns or might be masked by improved social, environmental, parenting, etc. conditions – particularly the later are difficult to model.
And heretofore, a constant decay of any health indicator has not been observed. Therefore, there might be a set of mechanisms that effect reproductive patterns and compensate for the about 2 yearly paternal random de novo mutations in inherited DNA. It is not possible for us to identify (e.g. possibly mating choice based on facial symmetry, intelligence, etc.) or quantitatively assess these mechanisms as rigorous as the underlying de novo mutations that they might be mitigating.
Nevertheless, considering the constant pace of de novo mutations and detectable associated statistical impact, these mechanisms might entail a similar imminent and substantial response in reproductive patterns. Interestingly, therefore, possibly spelling another uncertainty for demographic modeling.
The model also illustrates the ill-posed fate and predictability for small populations. If the simulated population is small, e.g. 2,000, then individual fate will cause an uneven surface or curve as in Figure 3 and Figure 4 below. Figure 1 and Figure 2 above were produced from simulations for 20,000 individuals and look more even. Bigger populations should be simulated, e.g. a few hundred thousand, to even out individual fate and further smooth the surface.
De novo mutations are accumulated all the time regardless of age at about 2 base pair changes per year, also in children conceived at young age. Mitigating mating choices and reproductive patterns are merely given less opportunity to outpace de novo mutations in case of elevated paternal age. Yet the impact of de novo mutations and the correlation between continuous paternal accumulation of de novo mutations and mild IQ decay has not been discovered before comparing different paternal age groups. Therefore, the effect appears to have been masked by mitigating factors which constitute an uncertainty in modeling. Hence, assessing the paternal age effect due to accumulating de novo mutations in offspring across multiple generations is prone to uncertainty short off an understanding of complex mating dynamics. Nevertheless, simulated cases illustrate the drastic outcomes of persistent elevated paternal age over multiple generations at already one logarithmic order. The model results illustrate highly interconnected patterns in organism health and reproduction in evolution scenarios (not only for humans). The model, if run for small populations, indicates ill-posed, susceptible to random influences, behavior during evolutionary bottlenecks. This statistical particle model shows for the same initial conditions substantially varying outcomes, depending on the set of random numbers for small populations, i.e. isolated communities or evolutionary bottlenecks. Investigated demographic patterns should be empirically supplied to the model, such as: Correlations of intelligence with fertility, correlations of other health indicators with fertility, correlations of de novo mutation levels in newborns with later fertility. To validate paternal age effect correlations, it is recommendable to include data from bioinformatics, which detail affected genes’ functionality, rather than just macroscopic demographic distributions. The effects of continuously elevated paternal age in society can be assessed, particularly with respect to the order of magnitude of the impacts, by super-positioning in simulations impacting and mitigating factors for investigated countries/regions. For example, the simulation returned that, even under the optimistic assumption of a never-ending Flynn effect, if super-positioned with the paternal age effect, then an average paternal age above 40 would lead to the long-term decline of the average IQ in society.
The entirety of the model code is documented in the Methodology section. The code for plotting figures is documented in the Appendix. Input data such as population size and de novo mutation accrual rate are also detailed in the Methodology section. The model can be run on MATLAB 9 or Octave 4.2.
%1st fig.: IQ function of t & age at start of decade of conception figure('name','IQ function of t & age at start of decade of conception') surf(20:c,round(y/2):y,100*f(round(y/2):y,:)) %(for 2nd half of t-span) xlabel('1st year of decade of conception'); ylabel('years after start of simulation'); zlabel('IQ'); title('IQ function of t & age at start of decade of conception') %2nd fig.: Average IQ after simulated period depending on age at conception str=sprintf('IQ after %i years versus age at start of reproduction',y); figure('name',str) plot(20:c,100*f(y,:),'o'); hold on line(1:c-20+1)=100; plot(20:c,line,'red'); %initial average IQ comparison title(str) str=sprintf('average IQ of society after %i years',y); xlabel('1st year of decade of conception'); ylabel(str);
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the rationale for developing the new method (or application) clearly explained?
No
Is the description of the method technically sound?
No
Are sufficient details provided to allow replication of the method development and its use by others?
No
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?
Partly
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?
Partly
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Genetics, biomarkers and therapeutics in neurodegenerative diseases
Is the rationale for developing the new method (or application) clearly explained?
Partly
Is the description of the method technically sound?
Partly
Are sufficient details provided to allow replication of the method development and its use by others?
Partly
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?
Partly
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?
No
References
1. Arslan RC: Secular changes in sexual and natural selection against deleterious genetic mutations in humans (Dr. rer. nat.). University of Goettingen. 2017. Reference SourceCompeting Interests: No competing interests were disclosed.
Reviewer Expertise: paternal age, intelligence, demographics
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 1 22 Mar 18 |
read | read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)