Introduction
It is well-known that some genera of bacteria, such as Pseudomonas, Xanthomonas, Ferroxidans, Ralstonia, Acidobacillus1–3, have very interesting capacities as heavy metal remediating agents, since they are capable of extracting metals from solid substrates or transform them into harmless forms. Furthermore, bacteria can be used as bio absorbents for the recovery of metals and for the treatment of industrial effluents4,5. For this reason, the application of these technologies and research for continuous improvements is necessary.
In a previous study, the application of Photobacterium sp to remove lead from wastewater was shown to be possible6. However, understanding the behavior of this strain within the experimental conditions was not studied. Particularly, computational modeling of the growth kinetics that aims to extract information about interactions between bacteria, nutrients and in this case the pollutant (lead; Pb) could be useful. For this reason, the present study intends to analyze growth of Photobacterium sp using two well-known mathematical models, the Verhulst-Pearl growth model and the Malthusian growth model7. These models have a long history of application in the fields of ecology, environmental remediation and industrial fermentation8.
Methods
The study uses kinetics data collected from the previous study in Quito-Ecuador, which studied the application of Photobacterium sp to remove lead from wastewater6. Briefly in the previous experiments, Photobacterium sp was exposed to two concentrations of Pb (20–100 ppm) in a general growth broth. The experiments were performed in times ranging between 0 and 86 hours, under a controlled temperature (25°C) and unsupervised at room temperature, ranging 5–23°C6 at Quito-Ecuador.
Malthusian growth model
This model is often referred to as the mathematical exponential law (MEL). It is extensively adopted in the fields of agronomy, ecology or microbiology. The MEL is therefore seldom referred to as the Malthusian Law, which is a widely accepted view to study Malthusian growth in ecology and microbiology.
The following equation was applied to the kinetics data in the present study:
Pt = Poekt
Where, P(t) is the population in a time, Po is the initial population, k is the specific growth rate and t is the time in hours.
Verhulst-Pearl growth model
For values of t in the domain of real numbers, the S-shaped curve is denoted by the model below. The initial stage of growth is approximately stationary and subsequent is nearly exponential; then, as saturation begins, the growth slows, and at maturity, growth stops as shown:
The following equation was applied to the kinetics data in the present study:
Where, P(t) is the population in a time, Po is the initial population, km is the maximum growth rate and t is the time in hours. t0 represents the time to achieve the middle of the growth and A represents the carrying capacity of the broth tested.
Data analysis
All fittings were performed with sigmaplot 10, using minimum least squares, evaluating the goodness of fit using adjusted R-squared.
Results
Fitting a bacteria growth model aims to understand its kinetics. In Table 1 it is evident that Verhulst-Pearl model has a good performance since a R-squared > 0.90, which is considered as acceptable to model bacteria kinetics curves5,9. In these fitted curves, it is noticeable that room temperature parameters differed drastically from 25°C in carrying capacity (A) and middle time (to) to achieve middle biomass concentration. Therefore, these parameters suggest that 25°C controlled temperature increases the performance in both Pb concentrations. Room temperature seems to reduce the growth considering that Quito-Ecuador is located at 2800 m.a.s.l. Moreover, this model explains the reduction in maximum growth ratio due to the increase of Pb concentration. This effect is present at both temperature conditions (Figure 1).
Table 1. Results of modeling data with Verhulst-Pearl growth model.
Temp=temperature, Pb=lead concentration in ppm.
| Temp | Lead (ppm) | A | to | km | Po | R-Sq |
|---|
| 25°C | 20 | 6.8E+08 | 33 | 0.141 | 6.0E+07 | 0.987 |
| 25°C | 100 | 7.0E+08 | 41 | 0.081 | 8.8E+06 | 0.975 |
| Room | 20 | 5.2E+08 | 64 | 0.113 | 1.1E+08 | 0.916 |
| Room | 100 | 5.5E+08 | 62 | 0.085 | 1.4E+08 | 0.909 |
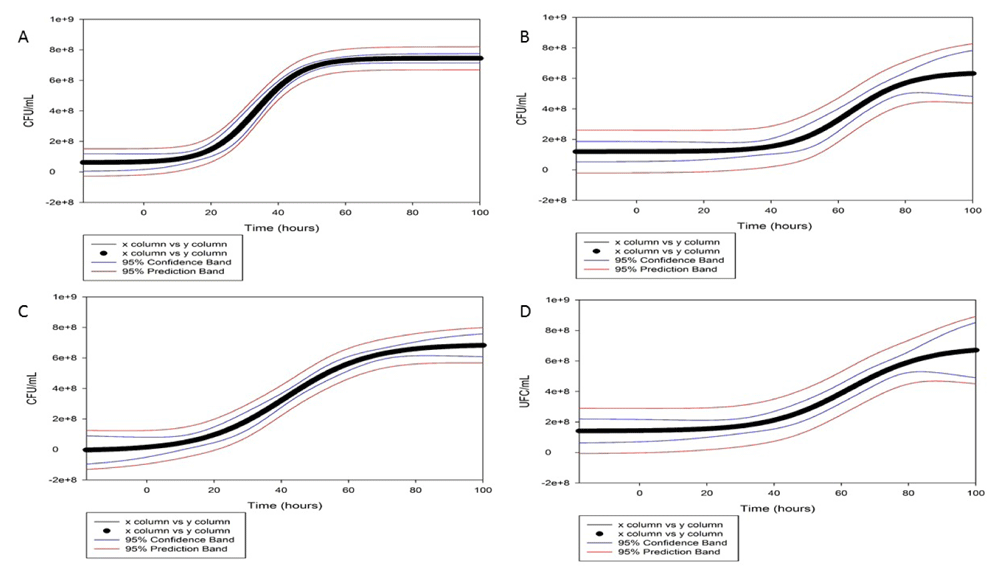
Figure 1. Modeling data with Verhulst-Pearl growth model.
(A) 25°C, 20ppm lead; (B) Room temperature, 20ppm lead; (C) 25°C, 100ppm lead; and (D) Room temperature, 100ppm lead.
Table 2 shows that the Malthusian growth model had an unacceptable goodness of fit, R-squared < 0.90 for all fitted curves. Therefore, this is considered as an unacceptable model for the bacteria kinetics curves tested. In these fitted curves, it is difficult see differences in temperature and Pb concentration. However, this model provides information about variations in growth ratio (Figure 2). It would be difficult to extend analysis since this model does not fit as well as the Verhulst-Pearl growth model.
Table 2. Results of modeling data with Malthusian growth model.
| Temp | Lead (ppm) | Po | km | R-Sq |
|---|
| 25°C | 20 | 2.33E+08 | 0.016 | 0.718 |
| 25°C | 100 | 1.27E+08 | 0.022 | 0.866 |
| Room | 20 | 7.22E+07 | 0.025 | 0.886 |
| Room | 100 | 1.05E+08 | 0.021 | 0.892 |
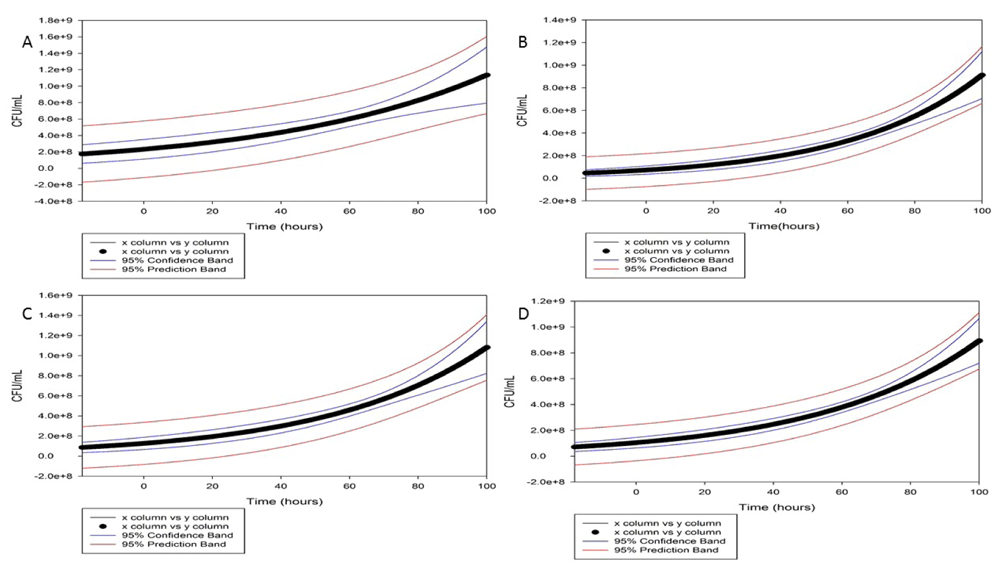
Figure 2. Modeling data with Malthusian growth model.
(A) 25°C, 20ppm lead; (B) Room temperature, 20ppm lead; (C) 25°C, 100ppm lead; and (D) Room temperature, 100ppm lead.
Dataset 1.Kinetics data obtained in Ramirez-Cando et al.6.
Uploaded with permission of all the authors.Conclusions
Analysing the goodness of fit reveals that the Verhulst-Pearl growth model is the best option to model the kinetics of Photobacterium sp instead of the Malthusian growth model, at least in this particular case. Photobacterium sp is also suitable to remove lead from water as shown in Ramirez-Cando et al.6. The Malthusian model has no manner to estimate Carrying capacity since parameters in the model are developed to explain only the exponential growth phase. Moreover, parameters determined by Verhulst-Pearl growth model are very important in design further research and scaling to preindustrial process in microbiology as well as Monods model10.
Data availability
Dataset 1: Kinetics data obtained in Ramirez-Cando et al.6. Uploaded with permission of all the authors.11
Competing interests
No competing interests were disclosed.
Grant information
This work was supported by Universidad Politecnica Salesiana.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Faculty Opinions recommendedReferences
- 1.
Soto C, Gutiérrez S, Rey León A, et al.:
Biotransformación de metales pesados presentes en lodos ribereños de los ríos Bogotá y Tunjuelo.
Nova.
2010; 8(4): 195–205. Publisher Full Text
- 2.
Mohanasrinivasan V, Mishra M, Paliwal JS, et al.:
Studies on heavy metal removal efficiency and antibacterial activity of chitosan prepared from shrimp shell waste.
3 Biotech.
2014; 4(2): 167–175. ISSN 2190-572X. PubMed Abstract
| Publisher Full Text
| Free Full Text
- 3.
Fu F, Wang Q:
Removal of heavy metal ions from wastewaters: a review.
J Environ Manage.
2011; 92(3): 407–18. ISSN 03014797. PubMed Abstract
| Publisher Full Text
- 4.
Sánchez J, Rodríguez J:
Fundamentos y Aspectos Microbiológicos: Biorremediación.
Universidad de Oviedo.
2010; 1: 12–16. Reference Source
- 5.
Shaw DR, Dussan J:
Mathematical Modelling of Toxic Metal Uptake and Efflux Pump in Metal-Resistant Bacterium Bacillus cereus Isolated From Heavy Crude Oil.
Water Air Soil Poll.
2015; 226(4): 112. ISSN 0049-6979. Publisher Full Text
- 6.
Ramirez-Cando LJ, Guerra S, Reinoso G:
IN VITRO EVALUATION OF LEAD REMOVAL IN WASTEWATER BY Photobacterium damselae.
La Granja.
2017; 26(2): 64–71. ISSN 1390-8596. Publisher Full Text
- 7.
Hogan JN, Daniels ME, Watson FG, et al.:
Longitudinal poisson regression to evaluate the epidemiology of Cryptosporidium, Giardia, and fecal indicator bacteria in coastal California wetlands.
Appl Environ Microbiol.
2012; 78(10): 3606–3613. ISSN 00992240. PubMed Abstract
| Publisher Full Text
| Free Full Text
- 8.
Krysiak-Baltyn K, Martin GJ, Stickland AD, et al.:
Computational models of populations of bacteria and lytic phage.
Crit Rev Microbiol.
2016; 42(6): 942–968. ISSN 1040-841X. PubMed Abstract
| Publisher Full Text
- 9.
Kallawicha K, Lung SC, Chuang YC, et al.:
Spatiotemporal distributions and land-use regression models of ambient bacteria and endotoxins in the greater Taipei area.
Aerosol Air Qual Res.
2015; 15(4): 1448–1459. ISSN 20711409. Publisher Full Text
- 10.
Shirsat N, Mohd A, Whelan J, et al.:
Revisiting Verhulst and Monod models: analysis of batch and fed-batch cultures.
Cytotechnology.
2015; 67(3): 515–530. ISSN 15730778. PubMed Abstract
| Publisher Full Text
| Free Full Text
- 11.
Ramirez-Cando LJ, Alvarez-Mendoza CI, Gutierrez-Salazar P:
Dataset 1 in: Verhulst-Pearl growth model versus Malthusian growth model for in vitro evaluation of lead removal in wastewater by Photobacterium sp.
F1000Research.
2018. Data Source
Comments on this article Comments (0)