Keywords
Maxwell Equation, magnetism, electromagnetism, field
Maxwell Equation, magnetism, electromagnetism, field
James Clerk Maxwell [1831–1879] was a pioneer in studying the propagation of electromagnetic waves1–5. He unified his observations with Faraday’s, Gauss’s and Ampere’s Laws into a set of four equations, known as Maxwell’s Equations (Figure 1)1–9. Maxwell’s Equations summarize the world of electromagnetics in four elegant equations that state: (a) an electric charge is the source of an electric field; (b) a moving electric charge results in a magnetic field; (c) a changing magnetic field results in an electric field; (d) a magnetic field has no source (Figure 1)1. As such, Maxwell’s Equations summarize the source of electric and magnetic fields, and also describe how they are interlinked. Simultaneously, Maxwell’s Equations also demonstrated for the first time that electromagnetic waves and visible light have the same speed and are essentially the same1,2,6. As such, the equations provide also an equation for light and its origin, making them of fundamental importance to physics and life. To illustrate their importance, the biblical quote “And God said let there be light, and there was light”10 has been jokingly altered by physicists and is also found displayed on various merchandise: “And God said [Maxwell’s equations], and there was light”11.

a, an electric charge is the source of an electric field1–9 (E: external electric field, A: area; Q: electric charge; ε0: dielectricty constant of the vacuum, εr: dielectricty constant of the material). b, a moving electric charge results in a magnetic field1–9 (B: magnetic field intensity, x: distance from current, μ0: permeability constant of the vacuum, μr: permeability constant of material, ε0: dielectricty constant of the vacuum, εr: dielectricty constant of the material, I: electric current, t: time, E: external electric field, A: area). c, a changing magnetic field results in an electric field1–9 (E: external electric field, x: distance from current, t: time, B: magnetic field intensity, A: area). d, a magnetic field has no source1–9 (B: magnetic field intensity, A: area).
Here, I revisit one of Maxwell’s Equations, which shows that a magnetic field has no source. By carefully reanalyzing how this equation was derived, I show that this equation ought to be adjusted as a substitution has not been made. After the revisions presented here, the equation now demonstrates that a magnetic field has a source, namely a moving electric charge. In fact, this adjusted equation confirms experimental observations. It is widely accepted and an undisputed experimental observation that a moving electric charge gives rise to a magnetic field5,6,12–14. Without a moving electric charge, or in other words without a source, no magnetic field exists. The calculations presented here identify that an essential substitution was not made in one of Maxwell’s Equations, which ought to be revised. When adjusted for the substitution, the equation shows a different conclusion: instead of showing that a magnetic field has no source, the equation now demonstrates that the magnetic field has an actual source, and that the source is a moving electric charge.
In physics, a field is a region in which each point is affected by a force5–7,9. For example, objects fall to the ground as they are affected by the force of a gravitational field15. An electrical field surrounds an electrical charge and it repels or attracts other charges5–7,9. An electromagnetic field is caused by the motion of an electric charge5–7,9. A stationary charge will only give rise to an electric field. Only if such charge is moving, a magnetic field is produced5–7,9.
An electric field can be described by two vectors: the external electric field E and the electric displacement field D, which is also known as the dielectric displacement field. D describes the vector field in a non-conducting medium, a dielectric, which is an electrically insulating material6. D is proportional to E, but they differ: External materials such as dielectrics change the effective electric field E, while D remains constant5,6. In other words, D can be regarded as a constant of the system being studied, while E is the variable vector of the electric field in that system. The relationship between E and D is summarized with the equation D = E ⋅ ε0 ⋅ εr, with ε0 being the dielectricity constant of the vacuum and εr the dielectricity of the material5,6.
Analogous to the electric fields E and D, two different vectors are used to describe magnetic fields: one is called magnetic flux density or magnetic induction, and is symbolized by B; the other is called magnetic field strength or magnetic field intensity, abbreviated as H. B is proportional to H, but they differ; external materials such as diamagnetics or ferromagnetics change the magnetic field intensity H, while B remains constant (Figure 2b)5,6. As such, B can be regarded as a constant of the system being studied, while H is the variable vector of the electric field in that system. The connection between B and H is represented by B = H ⋅ μ0 ⋅ μr, with μ0 being the permeability constant of the vacuum and μr the permeability constant of the material5,6.
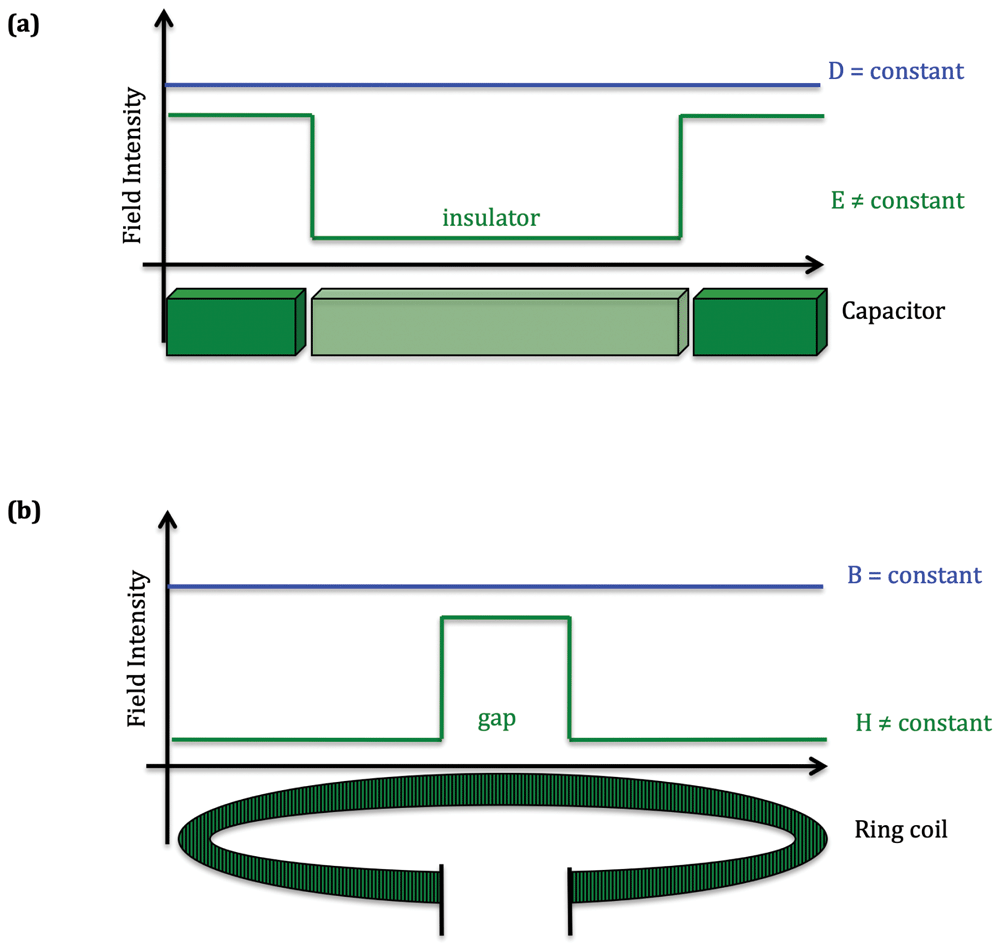
a, Example of an electric field along a capacitor: external factors such as capacitors and dielectrics change the external electric field (E) vector, while the electric displacement field (D) vector remains constant5,6. b, Example of a magnetic field along a ring coil: external factors such as gaps in a coil, diamagnetics or ferromagnetics change the magnetic field intensity (H) vector, while the magnetic induction field (B) vector remains constant5,6.
Even though E and B are the most commonly used field vectors to describe electric and magnetic fields, respectively, they are not equivalents. This is important to highlight. Instead, D and B are equivalents, as D and B both do not change upon the addition of external materials such as dielectrics or diamagnetics. Similarly, E and H are equivalents, as they are not influenced by such external materials (Figure 3)5,6.
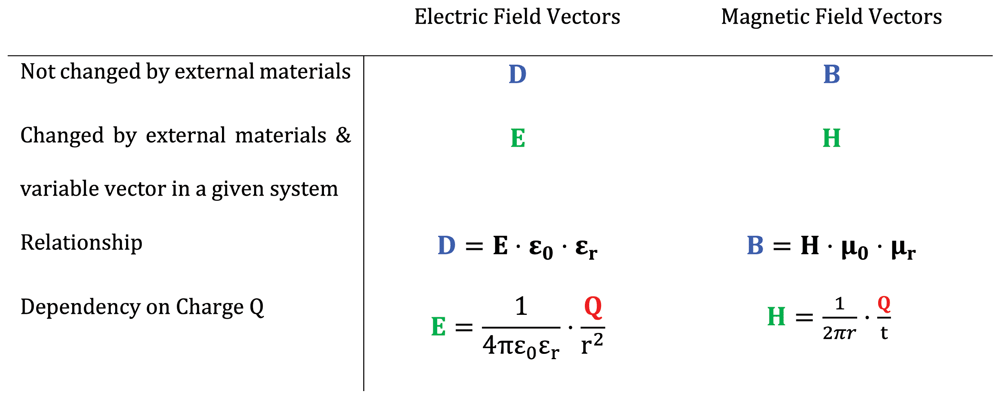
The vectors D and E both describe electric fields, while the vectors B and H describe magnetic fields. D and B are equivalent vectors, as both do not change upon the addition of external materials such as dielectrics or diamagnetics, respectively5,6. In contrast, E and H are equivalent vectors, as they are not influenced by such external materials. The relationships between D and E, and between B and H are interlinked with permeability (μ0 and μr) dielectricty (ε0 and εr) constants, respectively. Both E and H depend on the electric charge Q, and its distance r away from that charge, and in the case of H also on how the electric charge Q changes over time t5,6.
To describe the flow of an electric field through a given surface A, the electric flux 𝜓 is used. Similarly, the magnetic flux ϕ is a measure of a magnetic field through a given surface A5,6. Both depend on the field’s vectors: 𝜓 has been defined by E through 𝜓 = ∮E ⋅ dA, while ϕ has been defined through B, with ϕ = ∮B ⋅ dA5,6. Although these flux definitions might seem equivalent, they are not: 𝜓 has been defined using the electric field vector E that changes with external materials, while ϕ has been defined based on the magnetic field vector B, which remains constant if for example diamagenetics are introduced into the system. As such, within a given system, the flux of the electric field is defined by a variable vector of the electric field, namely E, which can change. However, the flux of the magnetic field has been defined by a constant vector of the magnetic field, B, which remains constant even if diamagenetics are introduced into the system. Hence, the flux of electricity and magnetisms are not equivalent, as 𝜓 is based on the variable vector E, while ϕ is based on a constant vector B5,6. However, B depends on the variable vector H, with B = H ⋅ μ0 ⋅ μr, and E on the constant vector D, with D = E ⋅ ε0 ⋅ εr5,6. As such, both 𝜓 and ϕ can also be described with constant or variable field vectors:
One of Maxwell’s Equation focuses on 𝜓, and shows that which demonstrates that an electric charge is the source of an electric field (Figure 1a)5,6. This equation is derived from 𝜓 = ∮E ⋅ dA, and is applied onto one electric point charge Q5,6: the electric field of an electric point charge is defined by radial coordinates. As such, E is proportionate to the point charge Q, but decreases with increased radial distance away from that charge. The electric field dependency on an electric charge is summarized by the following equation (Figure 3)5,6. Substituting E within the 𝜓 equation, gives rise to Maxwell’s equation that shows that an electric charge it the source of an electric field1,2,5–9.
Analogous to the above, another of Maxwell’s equations focuses on ϕ, and states that ϕ = ∮B ⋅ dA = 05,6. This equation illustrates that a magnetic field has no source5,6. This equation is derived based on the argument that B is constant, and does not change. As such, B entering an area (B1) and B exiting (B2) the same area is the same. With B1 = B2, the following Maxwell equation was derived1,2,4–9:
Both of the above equations by Maxwell are derived from the equation describing the flux of the electric or magnetic field through a surface A, as shown in Equation (3) and Equation (5)1,2,4–9. However, unlike 𝜓, which is usually represented by the variable vector E, ϕ is most commonly represented by the constant vector B1,2,4–9. However, both electric and magnetic flux can ultimately be described by variables of the electric or magnetic fields, as shown in Equation (1) and Equation (2). As such, they also ultimately depend on such variables and have to be taken into account. If not, relationships and dependence of variables are eliminated incorrectly.
For example, as outlined above in Equation (3), Maxwell has shown that 𝜓 can be expressed through 1–9. To derive this equation, the variable E was replaced by the electric charge Q (Figure 3)1–9. He applied Coulomb’s law1–9. However, what if he instead of used for the substitution, which is derived from the relationship D = E ⋅ ε0 ⋅ εr1–9. If E is substituted by in the 𝜓 equation, the following relationship is obtained, in which ψ is only represented by constants and a constant vector.
Next, following Maxwell’s argument that he used in deriving his Equation (4): D, as well as ε0 and εr are constants that do not change. As such, D entering an area (D1) and D exiting (D2) the same area is the same. Also, the material constants ε0 and εr remain the same. As such, . Following Maxwell’s reasoning and calculation (4), the following conclusions could be made:
The above reasoning leading to calculation (7), which Maxwell applied to his calculations with ϕ1–9, one would obtain an equation shown below (8), which illustrates that an electric field has no source.
Although Equation (8) might appear mathematically correct, it is not: 𝜓 is experimentally dependent on the variable E, which in turn is dependent on the electric charge Q, summarized in Coulomb’s law (Figure 3)1–9. Hence, because of E’s dependence on Q, 𝜓(Q), ∮E ⋅ dA ≠ 0, if Q is not zero.
Overall, functions are defined by variables that cannot be ignored as otherwise wrong conclusions are drawn. However, this is what occurred when the equation ∮B ⋅ dA = 0 was derived1–9: Even though B is a constant, it is dependent on H, a variable of the magnetic field. This dependence was not considered in the calculation of one of Maxwell’s equations that analyzed the source of the magnetic flux ϕ1–9.
As such, here, the ϕ calculation is reanalyzed: ϕ is defined by B in a given area A, through ϕ = ∮B ⋅ dA1–9. The magnetic field and the vector B are known to depend on an electric current I, which is a variable of B and cannot be ignored5,6. Analogous to Coulomb’s law that describes E5,6, the Biot-Savart law, describes the dependence of B on I5,6: B is proportionate to the electric current I along its path x, but decreases with increased radial distance r away from I (Figure 4a)5,6. This is true for B along a straight current-carrying wire. For an arbitrary shape current, for example surrounding a moving charge, an integral calculation can be carried out (Figure 4b)5,6. Since the electric current I is defined by the rate of flow of an electric charge through 5,6, B can also be defined as:
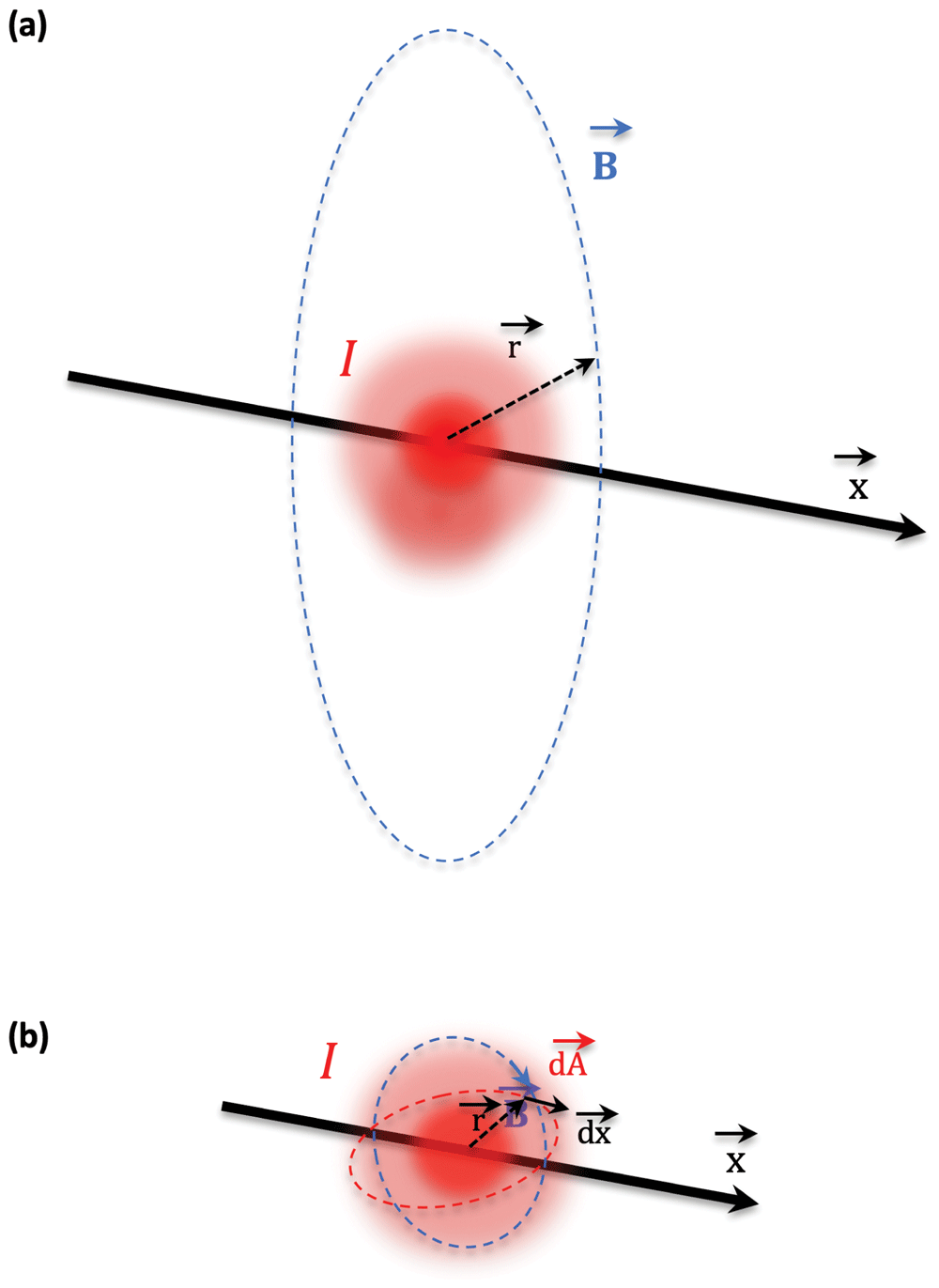
a, The magnetic induction field (B) is dependent on several variables: the electric current (I) and the radial distance away from I, as well as μ0, and μr, with μ0 being the permeability constant of the vacuum and μr the permeability constant of the material5–8,13. b, Illustration of the magnetic induction field going through a surface surrounding a point charge5–8,13: the magnetic induction field (B) going through a circular surface A perpendicular to B can be described by the electric current (I) and the vectors r and dx defining the circular surface A, with dA = 2π ⋅ r ⋅ dx. All vectors r, x and B are perpendicular to each other.
In the integral ϕ equation over an area, the area A can be also be replaced by two vectors representing the area, r and x, with x being the vector along the path of the electric charge Q, while r is the distance between Q and the position of B (Figure 4b). All vectors are perpendicular to each other. In case of one electric point charge, the magnetic field at that point can be best described by a circular surface area dA = 2π ⋅ r ⋅ dx (Figure 4b). Furthermore, since describe the velocity ν of the electric charge Q, the following equation can be derived:
Therefore, the following relationship for the magnetic field can be derived:
The equation ∮B ⋅ dA = μ0 ⋅ μr ∫Q ⋅ dν illustrates that a charge in motion is the source of the magnetic field. As such, one could also write the magnetic field as ϕ(Q, ν), analogous to 𝜓(Q), which summarizes the electric field’s dependence on the electric charge Q. The above equation summarizes what is already well known in physics: a moving electric charge is the source of a magnetic field5–7,12–14: only when no electric charge is in motion, no magnetic field exists5–7,12–14. This is what has been also experimentally verified and is widely accepted5–7,12–14.
As a control for the calculations above that lead to ∮B ⋅ dA = μ0 ⋅ μr ∫Q ⋅ dν one could also consider Ampere’s law: Ampere’s law states 5,6. As a simple control, when adding an additional dimension to Ampere’s law through the addition of another vector dx, newly derived equation from above is derived, confirming Equation (11) in a different way ϕ = ∮B ⋅ dA = μ0 ⋅ μr ∫Q ⋅ dν.
Maxwell’s Equations summarize the electromagnetic field1–9. One of the equation’s, ∮B ⋅ dA = 0, deduces that a magnetic field has no source1. This is in contrast to what is experimentally known, namely that a moving electric charge gives rise to the magnetic field5–7,12–14. Also, a magnetic field cannot be created without this source, hence, it has a source, namely a moving electric charge. This is essential, as without this source, no magnetic field exists5–7,12–14.
Here, after carefully reevaluating how Maxwell derived the equation ∮B ⋅ dA = 01, a shortcoming was identified: A substitution has not been made, eliminating an existing experimental finding1. Although ∮B ⋅ dA = 0 still applies when a charge is not in motion, Maxwell’s equation ignored the dependence of the magnetic field on variables1. Here, when taking into account such variables and making appropriate substitutions, the adjusted Maxwell’s equation instead demonstrates that the source of a magnetic field is a moving charge: ∮B ⋅ dA = μ0 ⋅ μr ∫Q ⋅ dν
This adjustment has consequences on science. For example, Schrödinger’s Equation that describes the probability waves of small particles, has been for example applied to describe the hydrogen atoms characteristics16–19. It used Maxwell’s Equation ∮B ⋅ dA = 0 to derive such characteristics16–19. However, with ∮B ⋅ dA = μ0 ⋅ μr ∫Q ⋅ dν, Schroedinger’s Equation ought to be revisited, as it is only true when a moving charge is not in motion.
Overall, it is important to adjust one of Maxwell’s Equations1, to have a more complete understanding and representation of the world through formulas. After all, if “God said ∮B ⋅ dA = 01, there would be no light”.
All data underlying the results are available as part of the article and no additional source data are required.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the topic of the opinion article discussed accurately in the context of the current literature?
Yes
Are all factual statements correct and adequately supported by citations?
Partly
Are arguments sufficiently supported by evidence from the published literature?
Yes
Are the conclusions drawn balanced and justified on the basis of the presented arguments?
Yes
References
1. Al-Mdallal Q, Indumathi N, Ganga B, Abdul Hakeem A: Marangoni radiative effects of hybrid-nanofluids flow past a permeable surface with inclined magnetic field. Case Studies in Thermal Engineering. 2020; 17. Publisher Full TextCompeting Interests: No competing interests were disclosed.
Reviewer Expertise: Computational Fluid Dynamics, heat transfer, nanofluids.
Is the topic of the opinion article discussed accurately in the context of the current literature?
No
Are all factual statements correct and adequately supported by citations?
No
Are arguments sufficiently supported by evidence from the published literature?
No
Are the conclusions drawn balanced and justified on the basis of the presented arguments?
No
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Mathematical Physics, Electrodynamics, Differential geometry, General Relativity.
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 1 04 Sep 20 |
read | read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)