Catheter placement selection for convection-enhanced delivery of therapeutic agents to brain tumors

Lisa H. Antoine; Roy P. Koomullil; Timothy M. Wick; Louis B. Nabors; Ahmed K. Abdel Aal; Mark S. Bolding

doi:10.12688/f1000research.27699.1

Home Browse Catheter placement selection for convection-enhanced delivery of therapeutic...

ALL Metrics

-

Views

-

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Catheter placement selection for convection-enhanced delivery of therapeutic agents to brain tumors

[version 1; peer review: 2 not approved]

Lisa H. Antoine ¹, Roy P. Koomullil², Timothy M. Wick¹, Louis B. Nabors³, Ahmed K. Abdel Aal⁴, Mark S. Bolding⁵

Lisa H. Antoine ¹, Roy P. Koomullil², [...] Timothy M. Wick¹, Louis B. Nabors³, Ahmed K. Abdel Aal⁴, Mark S. Bolding⁵

PUBLISHED 07 Dec 2020

Author details Author details

¹ School of Engineering, University of Alabama at Birmingham, Birmingham, Alabama, 35294, USA
² Department of Mechanical Engineering, University of Alabama at Birmingham, Birmingham, Alabama, 35294, USA
³ Department of Neurology, University of Alabama at Birmingham, Birmingham, Alabama, 35210, USA
⁴ Department of Diagnostic and Interventional Imaging, University of Texas Health Science Center at Houston, Houston, Texas, 77030, USA
⁵ Department of Radiology, University of Alabama at Birmingham, Birmingham, Alabama, 35294, USA

Lisa H. Antoine
Roles: Conceptualization, Data Curation, Formal Analysis, Funding Acquisition, Investigation, Methodology, Project Administration, Software, Validation, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Roy P. Koomullil
Roles: Conceptualization, Formal Analysis, Funding Acquisition, Investigation, Methodology, Project Administration, Software, Supervision, Validation, Visualization, Writing – Review & Editing

Timothy M. Wick
Roles: Conceptualization, Funding Acquisition, Methodology, Project Administration, Supervision, Validation, Visualization, Writing – Review & Editing

Louis B. Nabors
Roles: Conceptualization, Data Curation, Methodology, Project Administration, Validation, Visualization, Writing – Review & Editing

Ahmed K. Abdel Aal
Roles: Conceptualization, Data Curation, Methodology, Validation, Visualization, Writing – Review & Editing

Mark S. Bolding
Roles: Conceptualization, Formal Analysis, Methodology, Validation, Visualization, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

Abstract

Background: Convection-enhanced delivery (CED) of therapeutic agents to brain tumors allows clinicians to bypass the blood-brain barrier (BBB) to infuse virus therapy, biological, or chemotherapy directly into a brain tumor through convection. However, the effectiveness of infusions via CED may depend on catheter placement.
Methods: This study used diffusion maps from magnetic resonance imaging (MRI) of human brain tumors and computational fluid dynamics (CFD) simulations to assess therapy volume distribution percentages based on catheter placement locations.
Results: The primary outcome showed differences in volume distribution based on the catheter placement location. Total tumor volume filled ranged from 144.40 mm³ to 317.98 mm³. Percent filled of tumor volume ranged from 2.87% to 6.32%.
Conclusions: The selection of the location for catheter placement using the region with the highest volume filled may provide optimal therapeutic effect. The researchers conclude that CFD may provide guidance for catheter placement in CED of therapeutic agents.

Keywords

tumor, catheter, convection-enhanced delivery, diffusion, computational fluid dynamics

Corresponding author: Lisa H. Antoine

Competing interests: Ahmed K Abdel Aal reports consultancies with Boston Scientific, Bard, Baxter, Trisalus, Esai, and Terumo.

Grant information: This work was funded by the University of Alabama at Birmingham Blazer Graduate Research Fellowship and NIH grant number 5K12GM088010-12.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2020 Antoine LH et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Antoine LH, Koomullil RP, Wick TM et al. Catheter placement selection for convection-enhanced delivery of therapeutic agents to brain tumors [version 1; peer review: 2 not approved]. F1000Research 2020, 9:1415 (https://doi.org/10.12688/f1000research.27699.1) First published: 07 Dec 2020, 9:1415 (https://doi.org/10.12688/f1000research.27699.1) Latest published: 07 Dec 2020, 9:1415 (https://doi.org/10.12688/f1000research.27699.1)

Introduction

When using intravenous therapy to treat brain tumors, the blood-brain barrier (BBB) appears to hinder the effectiveness of the therapy. The BBB consists of glial cells and pericytes, which enclose the endothelial layer of the blood vessels, and restricts fluid flow into the brain¹. Glucose, electrolytes, vitamins, peptides, regulatory proteins, and ~2% of small-molecule drugs (<~400 Dalton (Da) with <~8 hydrogen bonds) can cross the BBB; however, large-molecule drugs and ~98% of small-molecule drugs cannot adequately cross the BBB^2,3. Therefore, clinicians may consider direct injection of therapeutic agents into the tumor instead of delivering the agent intravenously.

Molecules diffuse from the site of injection at different rates. Wolak et al.⁴ compiled diffusion coefficients for selected molecules at 37°C and found that the diffusion rate for sucrose (342 Da) is 7×10^-4 mm²/s; whereas, the diffusion rates for inulin (5000 Da), transferrin (80,000 Da), and PHPMA (515,000 Da) were 2.44×10^-4 mm²/s, 7.50×10^-5 mm²/s, and 1.29×10^-5 mm²/s, respectively. Therapeutic agents are typically larger molecules that diffuse at slower rates.

Within the brain, stand-alone diffusion is slow and therapeutic agents may migrate only 1 mm from the source in three days⁵. Stand-alone diffusion in simulations for our study caused therapy to migrate a maximum distance of 6.68 mm from the source. Convection (i.e. injection of therapeutic agents under pressure) can improve the distribution of the therapeutic agents, as opposed to diffusion, which is passive and occurs during molecule movement from an area of higher concentration to an area of lower concentration.

Bobo et al.⁶ developed the CED method to increase therapeutic distribution in the brain. To bypass the BBB and deliver therapeutic agents directly to tumors, CED uses a catheter inserted into a cannula, which connects to a syringe pump. The pump introduces and maintains a pressure gradient, which activates mass fluid movement or convection. Using convection, Bobo et al.⁶ observed at least a 100-fold increase in therapy distribution. However, this 100-fold increase did not necessarily translate to success in clinical trials.

Stine et al.¹ reviewed more than 15 trials and found that the outcomes using CED did not produce better results than standard treatment. For these trials, 10 clinical groups reported median survival, which ranged from 18.5 to 60 weeks^7–13. These results suggest that either the therapy or the procedure needs improvement.

When modeling therapy distribution using CED, Støverud et al.¹⁴ considered a region of the gray and white matter of the brain, not including tumor, along with porosity and patient-specific diffusivity and permeability parameters. They found that the therapy distribution followed the white matter region more than the gray matter region. Using tumor shapes that ranged from oblate to prolate, Sefidgar et al.¹⁵, found that larger tumors decreased therapeutic agent distribution in the interstitial fluid and that the prolate shape resulted in a wider range of distribution than other shapes. Zhan et al.¹⁶ modeled distribution using a patient-specific tumor geometry and constant parameters for pressure, permeability, and diffusivity and found that the therapy type and infusion locations influenced the distribution. When infusing therapy from the tumor center, uniform distribution mostly occurred. However, infusion from peripheral locations seemed to limit spatial distribution closer to that location.

Recently Bhandari et al.¹⁷ compared distribution of three different therapies within the brain tumor using constant diffusivity, but variable permeability and porosity based on tumor to contrast agent correlation. These researchers found that at the outset distribution appears greater in higher permeability regions, but then shifts and appears greater in higher porosity regions with more available space. Tumor cell density appeared to be an effectiveness indicator and noticeably varied by therapy and time. Conversely, Zhan et al.¹⁸ observed that the permeability minimally affected the therapy distribution volume but did alter the distribution shape in space. CED appeared to cause the interstitial fluid pressure to increase near the infusion location.

The aim of this study is to assess therapy distribution in the tumor based on catheter placement location. Measurement of the volume distribution was a predictor of therapy effectiveness^19–23.

Using CFD this study calculated therapy distribution percentages and total tumor volume filled with therapy. The study simulated transient therapy distribution in a patient-specific brain tumor using a pressure-based solver. The model analyzes the effect of convection and tumor properties such as geometry, diffusivity, permeability, porosity, and interstitial fluid pressure on therapy distribution within the tumor.

T1-weighted imaging (T1W) and diffusion-weighted imaging (DWI) provided patient-specific geometry, diffusivity, and permeability information. Using patient-specific brain tumor characteristics may improve the accuracy of the volume distribution prediction. The researchers conducted sixteen simulations by dividing the tumor into four regions and within each region introduced therapy into four random locations.

Methods

Model development

Previously, the investigators, using a two-dimensional domain, detailed the image processing and simulation pre-processing stages, the order of convergence for the mesh, and the numerical scheme accuracy for this analysis²⁴. In the model development, simulation results for a two-dimensional domain closely agreed with the analytical results and mesh spacing was 0.5% of the domain length²⁴. Average mesh spacing for this phase of the study was approximately 0.64% of the domain length. An examination of results from the numerical schemes, which included the first order, second order, power law, quick scheme, and third order scheme suggested that higher order schemes compared favorably to the analytical results²⁴.

Tumor geometry

The tumor geometry, which represents initial diagnosis, for this simulation resulted from an MRI brain exam obtained on a 3 Tesla Phillips Ingenia MRI machine (Phillips Ingenia scanner, Netherlands) at the University of Alabama at Birmingham Hospital. The use of patient-specific information requires a review by the Institutional Review Board (IRB) to determine human subjects research status. After reviewing the submitted application the IRB determined that this research is not human subjects research. The acquired sagittal T1W gradient-echo images (Figure 1a) included slice thickness, repetition time, and echo time of 1.2 mm, 6.8 ms, and 3.3 ms, respectively. Axial diffusion tensor images resulted from the DWI of the same patient (Figure 1b). The patient received the standard of care, which is fractionated radiation therapy and chemotherapy with the drug temozolomide at a dose of 0.1 mL/hour for 6 hours. Repetition time and echo time of the DWI were 7927.7 ms, and 70.0 ms, respectively. The b-value, in-plane resolution, and slice thickness were 800 s/mm², 1.75 mm, and 2 mm, respectively, with 33 diffusion directions performed. Images used in this study are available as Underlying data²⁵.

Figure 1. Patient-specific T1W and DWI.

(a) Sagittal view of the T1-weighted scan. The tumor (red arrow) locates in the frontal lobe. (b) Axial view of the DWI shows restricted diffusion in tumor (red arrow)

The stereolithography (stl) tumor geometry (see Figure 2) resulted from the Lesion GNB version 2 software²⁶. Investigators utilized the Ansys version 19.1 ICEM meshing tool to generate the computational mesh from the stl²⁷.

Figure 2. Tumor computational mesh included 21,033 elements, 43,481 faces, and 4,259 nodes.

Ansys calculated the therapy concentration at the center of each element. Lengths along the x, y, and z axis were 12.86 mm, 30.4 mm, and 37.43 mm, respectively. Tumor volume was 5031.35 mm³

DWI to T1W transformation

The researchers used DSI Studio to transform the DWI onto the T1W^28,29. The transformation, which produced the diffusion tensor and fiber tracking images (Figure 3), was necessary to ensure that the diffusion tensors aligned to the geometry spatial locations. MATLAB allowed further validation of the transformation with the spatial plotting of the geometry with the diffusion tensors overlaid (Figure 4)³⁰. Validation can also be performed using GNU Octave.

Figure 3. DWI to T1W transformation and fiber tracking.

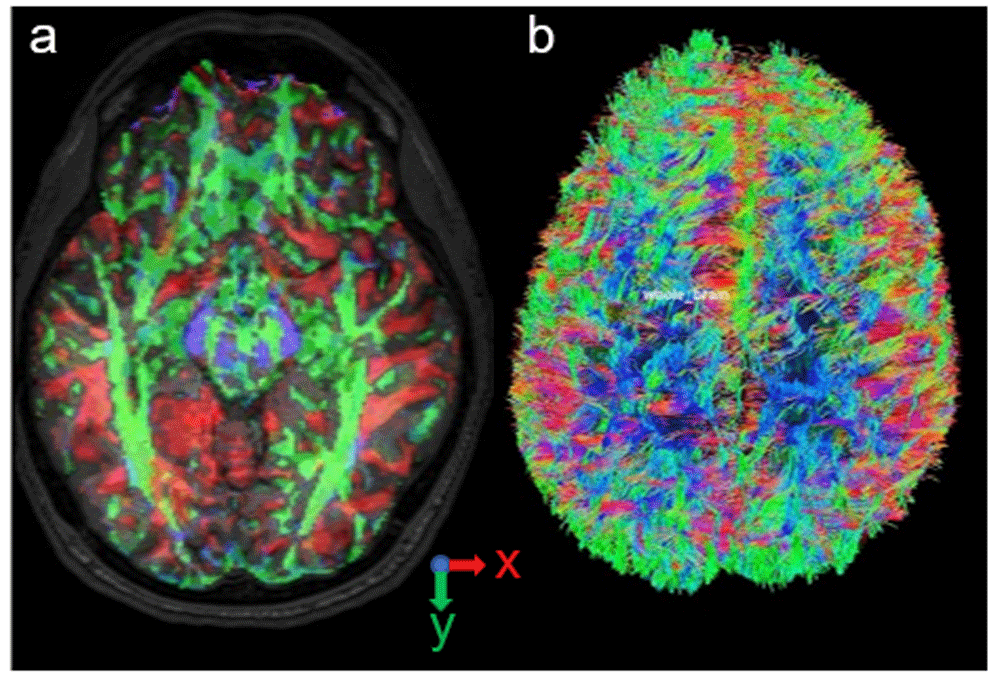
(a) Diffusion tensor orientation at the spatial locations. Red represents the x component of the tensor. Green represents the y component. Blue represents z. (b) Fiber tracking included the anisotropy threshold of 0.16, angular threshold from 15 ° to 90 °, step size from 0.5 voxels to 1.5 voxels, and track length from 30 mm to 300 mm

Figure 4. DWI to T1W transformation validation.

Tumor geometry displayed in the xyz volume with diffusion tensor locations overlaid (points).

Diffusion tensors

Variable tensors included Dxx, Dyy, Dzz (principal and main diagonal diffusion rates and directions) and Dxy, Dxz, Dyz (off-diagonal diffusion rates and directions) aligned with the x, y, and z locations within the tumor. Minimum domain extents of the mesh were -21.24 mm, -0.75 mm, and 20.11 mm for x, y, and z. Maximum domain extents of the mesh were -8.38 mm, 29.65 mm, and 57.54 mm for x, y, and z. Because the diffusion tensors from the medical imaging analysis are Cartesian in nature, the researchers used these tensors and trilinear interpolation to derive tensors based on the cell center of the mesh element. The tumor geometry (Figure 5) encompassed four regions with four catheter placement locations per region. See Table 1 for input coordinates for each location. For each location, the radius was constant at 1.5 mm, which accounts for the radius of the catheter.

Figure 5. Tumor geometry with four catheter placement locations per region.

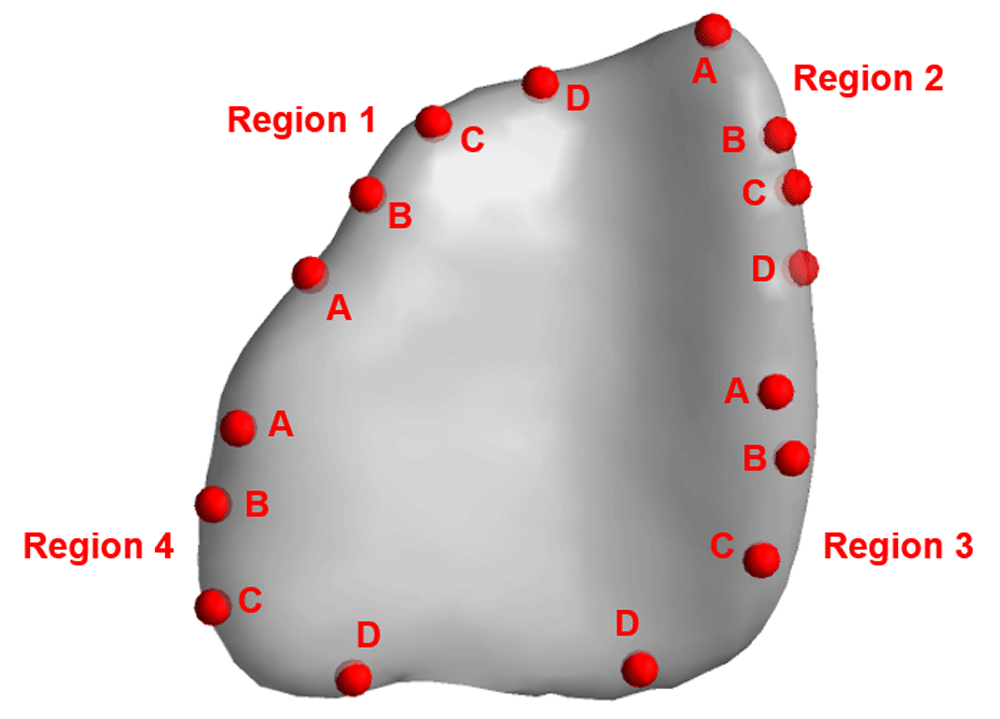
Each region includes locations A, B, C, and D with the corresponding x, y, and z coordinates as shown in Table 1.

Table 1. Input coordinates for each catheter placement location.

Region	Catheter Placement Location	X (mm)	Y (mm)	Z (mm)
1	A	-12.0712	26.4458	44.1864
	B	-12.0910	28.1581	39.7368
	C	-12.7864	29.1803	35.1615
	D	-14.7261	27.5785	29.7284
2	A	-11.8511	25.5153	21.4311
	B	-10.1577	19.8160	21.6308
	C	-10.3928	17.2347	22.3890
	D	-10.0346	13.7872	24.2536
3	A	-8.4733	9.6618	28.6031
	B	-8.7321	6.4828	29.7097
	C	-9.1972	3.0720	33.5995
	D	-12.1838	1.4350	41.3137
4	A	-10.5698	22.3697	51.2323
	B	-11.7206	19.7583	54.2218
	C	-11.8917	15.5437	56.9510
	D	-12.3269	8.8005	53.1614

Simulations

Using Ansys, the researchers conducted 16 simulations of therapy distribution within the tumor²⁷. Diffusivity and main diagonal permeability location-dependent variable tensors resulted from the following governing equations^6,7,31.

\frac{\partial C}{\partial t} + u \cdot \nabla c = \nabla \cdot (D \nabla c) (1)

$\frac{\partial C}{\partial t}$ represents concentration change with respect to time, u · ∇c represents convection, and ∇ · (D∇c) represents diffusion due to the concentration gradient.

K_{0} = ξ Λ^{'} ξ^{T} (2)

K₀ represents permeability tensor. ξ represents diffusion tensor eigenvectors. Λ′ represents permeability and eigenvalues.

A generation rate, defined as follows, was necessary to consider the effects of the infusion rate, source volume, and the density in the transport equation.

S_{ϕ} = \frac{I R}{S_{v}} ρ (3)

S_ϕ represents generation rate. IR represents infusion rate. S_v represents source volume and ρ is density. The source represents the catheter placement location infused with one milliliter of an oncolytic herpes simplex virus for six hours³². Therefore, IR was 0.1 mL/hr. The minimum dose was 1×10^-10 mL/m³ (1×10^-19 mL/mm³).

For the simulations, the solver type was pressure-based with absolute velocity formulation and transient solver time. The model was viscous and laminar. The solution method was a third-order spatial discretization. The stability condition for a numerical scheme determined an acceptable time step size that did not cause non-physical solutions. The following equation is useful for calculating the maximum time step size (M_TSS) and resolving the unsteadiness of the instance²⁷.

M_{TSS} = Min (\frac{.3 L_{scale}}{U}, \frac{L_{scale}^{2}}{v}) (4)

where L_scale (conservative) represents MIN(L_vol, L_ext), U is maximum velocity at the domain boundary, L_vol represents $\sqrt[3]{V}$ , V is the domain volume, L_ext represents MAX(L_x, L_y, L_z), L_x, L_y, L_z are domain extents (x,y,z direction), and ν is the kinematic viscosity. The M_TSS and time steps were 10 seconds and 2,160 steps, respectively. Tumor porosity and average interstitial fluid pressure (IFP) of 0.6 and 266.65 Pa resulted from previous studies^33,34.

Results

Infusion time for all simulations was 21,600 seconds (6 hours) with 0.6 mL of therapy infused per catheter. Simulations for four unique infusion locations per region resulted in therapy concentration ranges as depicted in Figure 6–Figure 9. The average velocity magnitude and pressure were 3.43×10^-7 mm/s and 443.66 Pa, respectively. Average distance from the source was 7.4 mm. The investigators ranked each location based on at least 1×10^-10 mL/m³ (1×10^-19 mL/mm³) distribution throughout the tumor (see Table 2).

Figure 6. Therapy distribution based on catheter placement location.

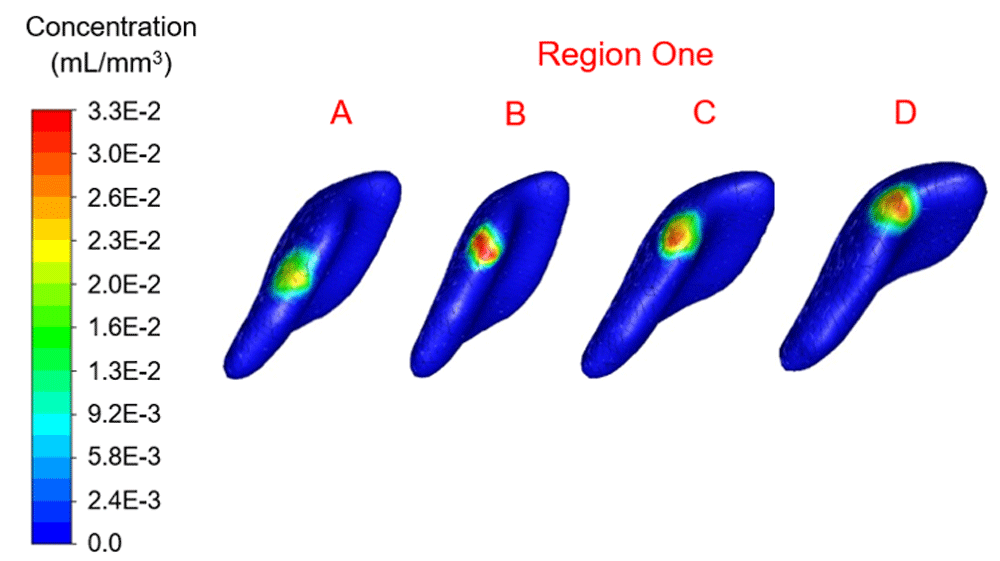
Concentration range from 0.0 to 3.3×10^-2 mL/mm³. Location A shows the highest percentage filled at 6.26%.

Figure 7. Therapy distribution based on catheter placement location.

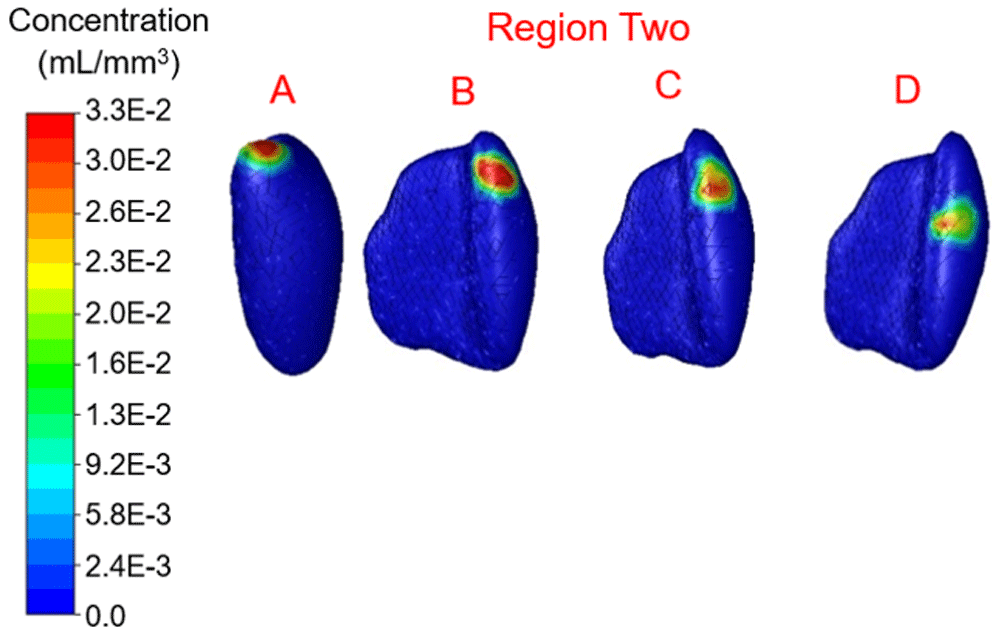
Concentration range from 0.0 to 3.3×10^-2 mL/mm³. Location D shows the highest percentage filled at 6.32%

Figure 8. Therapy distribution based on catheter placement location.

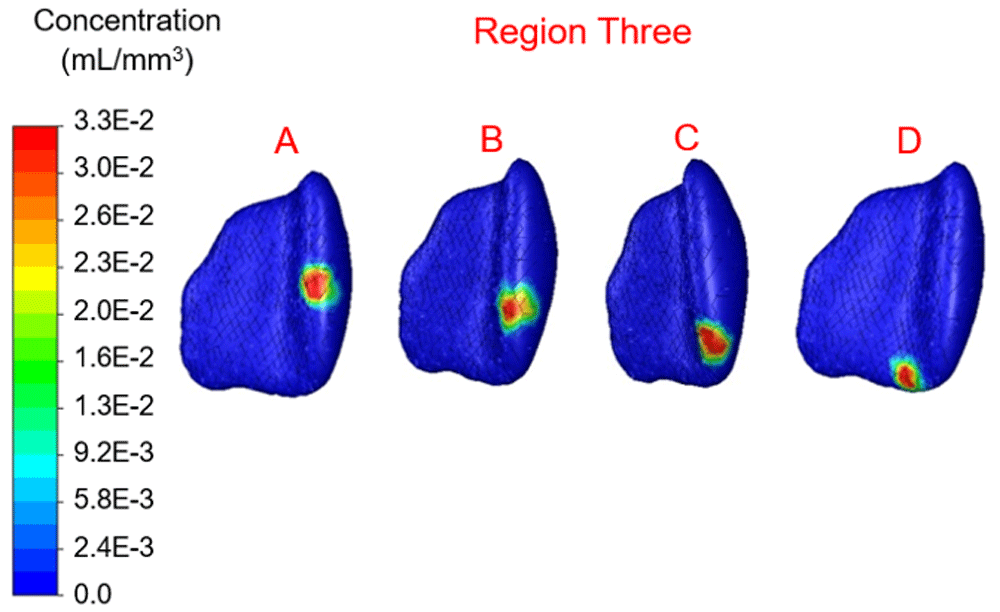
Concentration range from 0.0 to 3.3×10^-2 mL/mm³. Location B shows the highest percentage filled at 5.3%.

Figure 9. Therapy distribution based on catheter placement location.

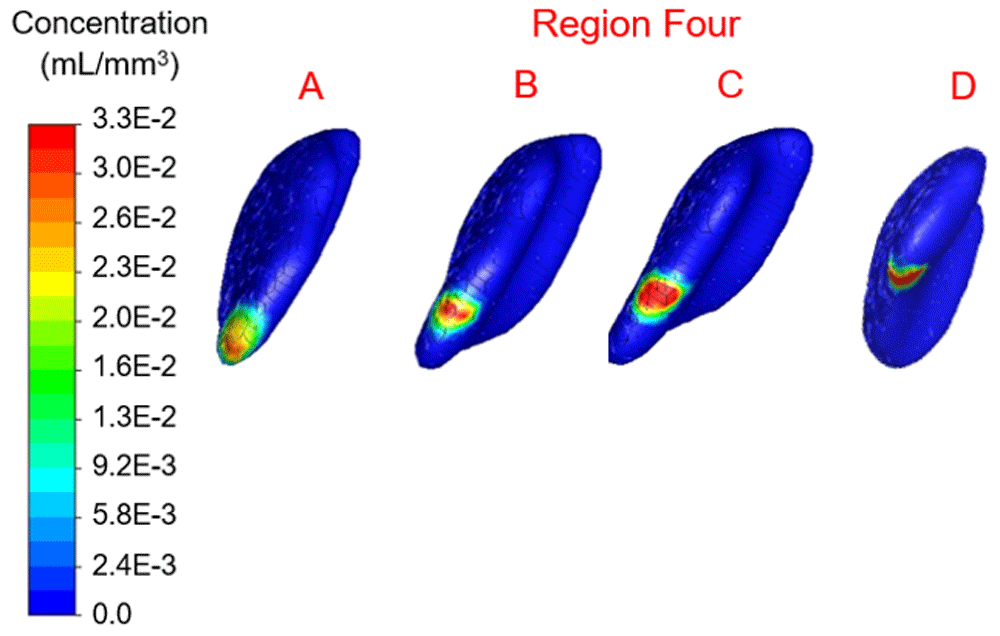
Concentration range from 0.0 to 3.3×10^-2 mL/mm³. Location B shows the highest percentage filled at 4.47%.

Table 2. Catheter placement location rankings based on a infused therapy amount of at least 1×10^-10 mL/m³ (1×10^-19 mL/mm³) throughout the tumor.

Region	Catheter Placement Location	Total Volume Filled (mm³)	% Volume of Tumor Filled	Rank
One	A	314.96	6.26	1
	B	213.83	4.25	4
	C	240.50	4.78	3
	D	273.20	5.43	2
Two	A	195.72	3.89	3
	B	191.69	3.81	4
	C	293.33	5.83	2
	D	317.98	6.32	1
Three	A	266.16	5.29	2
	B	266.66	5.30	1
	C	209.81	4.17	4
	D	250.06	4.97	3
Four	A	208.30	4.14	2
	B	224.90	4.47	1
	C	202.26	4.02	3
	D	144.40	2.87	4

In region one the location with maximum therapy distribution was A with 314.96 mm³or 6.26% and a maximum Euclidean distance from this location of 9.6 mm. Location B (-12.09 mm, 28.16 mm, 39.74 mm) represented the least therapy distribution at 213.83 mm³ or 4.25%. In region two the location with maximum distribution was D with 317.98 mm³or 6.32% and a maximum distance from this location of 8.56 mm. Location B (-10.16 mm, 19.82 mm, 21.63 mm) represented the least therapy distribution at 191.69 mm³ or 3.81%. In region three the location with the maximum distribution was B with 266.66 mm³ or 5.30% and a maximum distance from this location of 8.27 mm. Location C (-9.20 mm, 3.07 mm, 33.60 mm) represented the least distribution for region three and was 209.81 mm³ or 4.17%. In region four the location with the maximum distribution was B with 224.90 mm³ or 4.47% and a maximum distance from this location of 8.32 mm. Location D (-12.33 mm, 8.80 mm, 53.16 mm) in region four represented the lowest distribution percentage and was 2.87% or 144.40 mm³.

The tumor volume was 5031.35 mm³. The number of locations with volume filled greater than 250 mm³was six, while the locations less than 250 mm³ was ten (see Figure 10).

Figure 10. Histogram of catheter placement locations based on the total volume filled.

Discussion

The primary outcome of this research showed differences in the therapy volume distribution based on the catheter placement location and suggested that location may influence the distribution and therapeutic value. Total volume filled by the therapy ranged from 144.40 mm³ to 317.98 mm³. Percent filled of tumor volume ranged from 2.87% to 6.32%. The average velocity range of 2.45×10^-7 mm/s to 4.49×10^-7 mm/s caused the therapy to displace from the source by an average of 7.4 mm, which was reasonable based on an infusion time of six hours.

Previously, research groups defined therapeutic value using the ratio between specific therapy volume of distribution (V_d) and volume of infusion (V_i), which is the therapy plus carrier fluid^22,35–37. In vivo rodent and nonhuman primates’ experiments allowed these researchers to determine V_d by using image processing to measure the distribution of the specific therapy in the brain. Distribution for oncolytic viruses appeared to be unavailable because this distribution varies based on infusion location, tumor parameters, and therapy clearance³⁸. The researchers in this study did not identify any in vivo V_d results for the oncolytic virus. However, clinicians at the authors’ institution are currently conducting a clinical trial to investigate immunotherapy in canines³⁹. The trial is a regional collaboration designed to assess brain tumor therapies in humans and animals. Nevertheless, oncolytic viruses can reproduce in tumor cells destroying these cells without harming normal cells³².

Clinicians in the authors’ institution select four catheter placement locations to maximize therapy volume distribution. If the clinicians select the four previously mentioned patient-specific locations from regions 1, 2, 3, and 4, the effectiveness of therapy may improve. The selection of locations within each region with the highest total volume filled or highest tumor percentage filled may provide the most optimal therapeutic value.

Researchers in this study analyzed 16 random locations, which provided a baseline mathematical prediction of the optimal catheter placement location. Clinicians may not currently use a mathematical model to select catheter placement locations, but instead select locations based on the avoidance of cell areas with visible signs of necrosis. This mathematical model may be an improvement over the current clinical method. In the next phase of this study the investigators will use a design optimization technique, which will allow the analysis of additional locations.

Conclusions

In this study, porosity and IFP resulted solely from previous studies; while diffusivity and permeability were mostly patient-specific. Patient-specific porosity and IFP may improve volume distribution accuracy. Although the authors did not consider retrograde infusion flow depending on tumor density and placement, it may improve the effectiveness of the treatment if future researchers consider the impact of retrograde flow.

The results presented suggest that computational fluid dynamic approaches using diffusivity and permeability parameters of actual patient data could greatly improve the treatment of adult and pediatric brain tumor patients by optimizing the placement of catheters in convection enhanced therapy. Using the specific anatomy of the patient, this novel method would optimize catheter placement to provide maximal tumor coverage of the therapeutic agent. This is the first report using diffusivity and permeability of real patient data and computational fluid dynamic modeling to guide catheter placement for convection enhanced delivery of a therapeutic agent. This predictive quantitative method to determine the ideal catheter placement location will assist clinicians in effectively treating brain tumors using CED.

Data availability

Harvard Dataverse: Catheter placement selection for convection-enhanced delivery of therapeutic agents to brain tumors. https://doi.org/10.7910/DVN/H7C6A2²⁵.

This project contains T1-weighted and diffusion-weighted images used in the present study.

Data are available under the terms of the Creative Commons Zero "No rights reserved" data waiver (CC0 1.0 Public domain dedication).

Author contributions

Lisa H Antoine substantially contributed to the study design, data (T1-weighted images and diffusion-weighted images) acquisition, analysis and interpretation, drafting and critically revising the article, and the final approval of the published version. Roy P Koomullil substantially contributed to the study conception and design, data analysis and interpretation, critically revising the article, and the final approval of the published version. Timothy M Wick, Louis B Nabors, and Mark S Bolding substantially contributed to the study design, data analysis and interpretation, critically revising the article, and the final approval of the published version. Ahmed K Abdel Aal substantially contributed to data acquisition, analysis and interpretation, critically revising the article, and the final approval of the published version.

Faculty Opinions recommended

References

1. Stine CA, Munson JM: Convection-Enhanced Delivery: Connection to and impact of interstitial fluid flow. Front Oncol. 2019; 9: 966. PubMed Abstract | Publisher Full Text | Free Full Text
2. Banks WA: From blood-brain barrier to blood-brain interface: new opportunities for CNS drug delivery. Nat Rev Drug Discov. 2016; 15(4): 275–292. PubMed Abstract | Publisher Full Text
3. Pardridge WM: Drug transport across the blood-brain barrier. J Cereb Blood Flow Metab. 2012; 32(11): 1959–1972. PubMed Abstract | Publisher Full Text | Free Full Text
4. Wolak DJ, Thorne RG: Diffusion of macromolecules in the brain: implications for drug delivery. Mol Pharm. 2013; 10(5): 1492–1504. PubMed Abstract | Publisher Full Text | Free Full Text
5. Jain RK: Delivery of novel therapeutic agents in tumors: physiological barriers and strategies. J Natl Cancer Inst. 1989; 81(8): 570–576. PubMed Abstract | Publisher Full Text
6. Bobo RH, Laske DW, Akbasak A, et al.: Convection-enhanced delivery of macromolecules in the brain. Proc Natl Acad Sci U.S.A. 1994; 91(6): 2076–2080. PubMed Abstract | Publisher Full Text | Free Full Text
7. Laske D, Youle R, Oldfield E: Tumor regression with regional distribution of the targeted toxin TF-CRM107 in patients with malignant brain tumors. Nat Med. 1997; 3(12): 1362–1368. PubMed Abstract | Publisher Full Text
8. Wersäll P, Ohlsson I, Biberfeld P, et al.: Intratumoral infusion of the monoclonal antibody, mAb 425, against the epidermal-growth-factor receptor in patients with advanced malignant glioma. Cancer Immunol Immunother. 1997; 44(3): 157–164. PubMed Abstract | Publisher Full Text
9. Voges J, Coenen HH, Wienhard K, et al.: Imaging-guided convection-enhanced delivery and gene therapy of glioblastoma. Ann Neurol. 2003; 54(4): 479–487. PubMed Abstract | Publisher Full Text
10. Weber FW, Floeth F, Asher A, et al.: Local convection enhanced delivery of IL4-Pseudomonas exotoxin (NBI-3001) for treatment of patients with recurrent malignant glioma. Acta Neurochir Suppl. 2003; 88: 93–103. PubMed Abstract | Publisher Full Text
11. Lidar Z, Nass D, Mardor Y, et al.: Convection-enhanced delivery of paclitaxel for the treatment of recurrent malignant glioma: a Phase I/II clinical study. J Neurosurg. 2004; 100(3): 472–479. PubMed Abstract | Publisher Full Text
12. Kunwar S, Westphal M, Chang S, et al.: Phase III randomized trial of CED of IL13-PE38QQR vs Gliadel wafers for recurrent glioblastoma. Neuro Oncol. 2010; 12(8): 871–881. PubMed Abstract | Publisher Full Text | Free Full Text
13. Desjardins A, Gromeier M, Herndon JE, et al.: Recurrent glioblastoma treated with recombinant poliovirus. N Engl J Med. 2018; 379(2): 150–161. PubMed Abstract | Publisher Full Text | Free Full Text
14. Støverud KH, Darcis M, Helmig R, et al.: Modeling concentration distribution and deformation during convection-enhanced drug delivery into brain tissue. Transp Porous Media. 2012; 92: 119–143. Publisher Full Text
15. Sefidgar M, Soltani M, Raahemifar K, et al.: Effect of tumor shape, size, and tissue transport properties on drug delivery to solid tumors. J Biol Eng. 2014; 8: 12. PubMed Abstract | Publisher Full Text | Free Full Text
16. Zhan W, Arifin D, Lee TK, et al.: Mathematical modelling of convection enhanced delivery of carmustine and paclitaxel for brain tumour therapy. Pharm Res. 2017; 34(4): 860–873. PubMed Abstract | Publisher Full Text
17. Bhandari A, Bansal A, Singh A, et al.: Comparison of transport of chemotherapeutic drugs in voxelized heterogeneous model of human brain tumor. Microvasc Res. 2019; 124: 76–90. PubMed Abstract | Publisher Full Text
18. Zhan W, Rodriguez Y, Baena F, et al.: Effect of tissue permeability and drug diffusion anisotropy on convection-enhanced delivery. Drug Deliv. 2019; 26(1): 773–781. PubMed Abstract | Publisher Full Text | Free Full Text
19. Zhan W: Convection enhanced delivery of anti-angiogenic and cytotoxic agents in combination therapy against brain tumour. Eur J Pharm Sci. 2020; 141: 105094. PubMed Abstract | Publisher Full Text
20. Stephen Z, Chiarelli P, Revia R, et al.: Time-Resolved MRI assessment of convection-enhanced delivery by targeted and nontargeted nanoparticles in a human glioblastoma mouse model. Cancer Res. 2019; 79(18): 4776–4786. PubMed Abstract | Publisher Full Text | Free Full Text
21. Vidotto M, Botnariuc D, De Momi E, et al.: A computational fluid dynamics approach to determine white matter permeability. Biomech Model Mechanobiol. 2019; 18(4): 1111–1122. PubMed Abstract | Publisher Full Text | Free Full Text
22. Singh R, Bellat V, Wang M, et al.: Volume of distribution and clearance of peptide-based nanofiber after convection-enhanced delivery. J Neurosurg. 2018; 129(1): 10–18. PubMed Abstract | Publisher Full Text
23. Lueshen E, Tangen K, Mehta A, et al.: Backflow-free catheters for efficient and safe convection-enhanced delivery of therapeutics. Med Eng Phys. 2017; 45: 15–24. PubMed Abstract | Publisher Full Text
24. Antoine LH, Koomullil RP, Wick TM, et al.: Model development to assess drug delivery to brain tumors. Early Career Technical Journal. 2018; 17: 73–79.
25. Lisa A: Catheter placement selection for convection-enhanced delivery of therapeutic agents to brain tumors. Harvard Dataverse, V1, 2020. http://www.doi.org/10.7910/DVN/H7C6A2
26. Griffis J, Allendorfer J, Szaflarski J: Voxel-based Gaussian naïve Bayes classification of ischemic stroke lesions in individual T1-weighted MRI scans. J Neurosci Methods. 2016; 257: 97–108. PubMed Abstract | Publisher Full Text | Free Full Text
27. ANSYS® [computer program] Version 19.1.
28. Yeh F, Van Jay W, Wen-Yih I: Generalized q-sampling imaging . IEEE Trans Med Imaging. 2010; 29(9): 1626–1635. PubMed Abstract | Publisher Full Text
29. Yeh F, Verstynen TD, Wang Y, et al.: Deterministic diffusion fiber tracking improved by quantitative anisotropy. PLoS One. 2013; 8(11): e80713. PubMed Abstract | Publisher Full Text | Free Full Text
30. MATLAB: [computer program] Version 2019a, Natick, Massachusetts: The MathWorks, Inc.,2019.
31. Støverud K: Modeling convection-enhanced delivery into brain tissue using information from magnetic resonance imaging. Master thesis; Universität Stuttgart, 2009.
32. Patel DM, Foreman PM, Nabors LB, et al.: Design of a phase I clinical trial to evaluate M032, a genetically engineered HSV-1 expressing IL-12, in patients with recurrent/progressive glioblastoma multiforme, anaplastic astrocytoma, or gliosarcoma. Hum Gene Ther Clin Dev. 2016; 27(2): 69–78. PubMed Abstract | Publisher Full Text | Free Full Text
33. Jain R: Transport of molecules in the tumor interstitium: a review. Cancer Res. 1987; 47(12): 3039–3051. PubMed Abstract
34. Boucher Y, Salehi H, Witwer B, et al.: Interstitial fluid pressure in intracranial tumours in patients and in rodents. Br J Cancer. 1997; 75(6): 829–836. PubMed Abstract | Publisher Full Text | Free Full Text
35. Asthagiri A, Walbridge S, Heiss J, et al.: Effect of concentration on the accuracy of convective imaging distribution of a gadolinium-based surrogate tracer. J Neurosurg. 2011; 115(3): 467–473. PubMed Abstract | Publisher Full Text | Free Full Text
36. Croteau D, Walbridge S, Morrison P, et al.: Real-time in vivo imaging of the convective distribution of a low-molecular-weight tracer. J Neurosurg. 2005; 102(1): 90–97. PubMed Abstract | Publisher Full Text
37. Bernal GM, LaRiviere MJ, Mansour N, et al.: Convection-enhanced delivery and in vivo imaging of polymeric nanoparticles for the treatment of malignant glioma. Nanomedicine. 2014; 10(1): 149–157. PubMed Abstract | Publisher Full Text | Free Full Text
38. Talimogene Laherparepvec. Accessed June 7, 2020. Reference Source
39. NCI Awards Cancer Moonshot℠ Grants in Five Areas of Precision Medicine Oncology. Accessed June 7, 2020. Reference Source

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 07 Dec 2020

Author details Author details

¹ School of Engineering, University of Alabama at Birmingham, Birmingham, Alabama, 35294, USA
² Department of Mechanical Engineering, University of Alabama at Birmingham, Birmingham, Alabama, 35294, USA
³ Department of Neurology, University of Alabama at Birmingham, Birmingham, Alabama, 35210, USA
⁴ Department of Diagnostic and Interventional Imaging, University of Texas Health Science Center at Houston, Houston, Texas, 77030, USA
⁵ Department of Radiology, University of Alabama at Birmingham, Birmingham, Alabama, 35294, USA

Lisa H. Antoine
Roles: Conceptualization, Data Curation, Formal Analysis, Funding Acquisition, Investigation, Methodology, Project Administration, Software, Validation, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Roy P. Koomullil
Roles: Conceptualization, Formal Analysis, Funding Acquisition, Investigation, Methodology, Project Administration, Software, Supervision, Validation, Visualization, Writing – Review & Editing

Timothy M. Wick
Roles: Conceptualization, Funding Acquisition, Methodology, Project Administration, Supervision, Validation, Visualization, Writing – Review & Editing

Louis B. Nabors
Roles: Conceptualization, Data Curation, Methodology, Project Administration, Validation, Visualization, Writing – Review & Editing

Ahmed K. Abdel Aal
Roles: Conceptualization, Data Curation, Methodology, Validation, Visualization, Writing – Review & Editing

Mark S. Bolding
Roles: Conceptualization, Formal Analysis, Methodology, Validation, Visualization, Writing – Review & Editing

Competing interests

Ahmed K Abdel Aal reports consultancies with Boston Scientific, Bard, Baxter, Trisalus, Esai, and Terumo.

Grant information

This work was funded by the University of Alabama at Birmingham Blazer Graduate Research Fellowship and NIH grant number 5K12GM088010-12.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (1)

version 1

Published: 07 Dec 2020, 9:1415

https://doi.org/10.12688/f1000research.27699.1

Copyright

© 2020 Antoine LH et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

Antoine LH, Koomullil RP, Wick TM et al. Catheter placement selection for convection-enhanced delivery of therapeutic agents to brain tumors [version 1; peer review: 2 not approved]. F1000Research 2020, 9:1415 (https://doi.org/10.12688/f1000research.27699.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 1

VERSION 1

PUBLISHED 07 Dec 2020

Views

0

Reviewer Report 24 May 2024

Ajay Bhandari, Department of Mechanical Engineering, Indian Institute of Technology, Kanpur, Kanpur, Uttar Pradesh, India

Not Approved

https://doi.org/10.5256/f1000research.30617.r78819

This research focuses on developing a computational model to predict the optimum catheter placement selection for convection-enhanced delivery (CED) of therapeutic agents to brain tumors. To make the computational model heterogeneous, authors have used diffusion-weighted imaging (DWI) data and have ... Continue reading

This research focuses on developing a computational model to predict the optimum catheter placement selection for convection-enhanced delivery (CED) of therapeutic agents to brain tumors. To make the computational model heterogeneous, authors have used diffusion-weighted imaging (DWI) data and have predicted therapy volume distributions based on different catheter locations. The reviewer thinks that most of the work regarding catheter design, placement and its effect on CED delivery has already been performed by Linninger et. Al. in this field. Check the following papers.

Linninger et al.(2008¹): “Computational methods for predicting drug transport in anisotropic and heterogeneous brain tissue”, Journal of Biomechanics, 2008
Linninger et al.(2008²): "Prediction of convection-enhanced drug delivery to the human brain, Journal of Theoretical Biology", 2008

Reviewers suggest the authors to improve the quality of the paper. Following comments can help the authors to enhance the quality of the research.

Comment 1: The literature review has not been done properly. There are several studies already been done in this field (CED). The authors have not properly acknowledged all of them. Neither the authors have properly mentioned the research gaps.
Comment 2: No detailed information has been provided for the DWI imaging. From where the data was acquired? What were the imaging parameters? How the analysis was carried out? How were the diffusion tensors along the white and grey matter of the brain obtained? Authors should read the following paper in this regard
Linninger et al.(2008²).
Comment 3: No details regarding the numerical simulations have been shown. What were the boundary conditions, discretization schemes especially for the convection term, simulation time, solvers? How the pressure velocity coupling was incorporated? Were the equations solved in a segregated or coupled manner?
Comment 4: Results and Discussion part is very weak. No proper clarifications have been given. No clinical implications have been given.

Is the work clearly and accurately presented and does it cite the current literature?

No
Is the study design appropriate and is the work technically sound?

No
Are sufficient details of methods and analysis provided to allow replication by others?

No
If applicable, is the statistical analysis and its interpretation appropriate?

No
Are all the source data underlying the results available to ensure full reproducibility?

No
Are the conclusions drawn adequately supported by the results?

No

References

1. Linninger AA, Somayaji MR, Erickson T, Guo X, et al.: Computational methods for predicting drug transport in anisotropic and heterogeneous brain tissue.J Biomech. 2008; 41 (10): 2176-87 PubMed Abstract | Publisher Full Text
2. Linninger AA, Somayaji MR, Mekarski M, Zhang L: Prediction of convection-enhanced drug delivery to the human brain.J Theor Biol. 2008; 250 (1): 125-38 PubMed Abstract | Publisher Full Text

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Bio-fluid mechanics, Image based numerical modeling, CFD, cancer drug delivery.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

CITE

Report a concern

Respond or Comment

Views

29

Reviewer Report 07 Jun 2021

Bryn A. Martin, Department of Chemical and Biological Engineering, University of Idaho, Moscow, ID, USA; Alcyone Therapeutics, Inc., Lowell, MA, USA

Not Approved

https://doi.org/10.5256/f1000research.30617.r83147

Summary
The selection of the location for catheter placement using the region with the highest volume filled may provide optimal therapeutic effect. The researchers conclude that CFD may provide guidance for catheter placement in CED of therapeutic agents. This ... Continue reading

Summary
The selection of the location for catheter placement using the region with the highest volume filled may provide optimal therapeutic effect. The researchers conclude that CFD may provide guidance for catheter placement in CED of therapeutic agents. This paper could be improved by the following overall modifications a) restating conclusions to be more directly related with study results, b) addition of details in discussion with respect to the study findings, c) addition of validation data to determine the degree of agreement between computational predictions versus in vivo findings.

Specific comments

Please provide T1W imaging in-plane resolution. Also, resolution seems coarse for the needed high-resolution application. Please explain in the text or reference a study showing that the results documented in your study would be independent of the spatial imaging resolution.
Catheter radius was specified as 1.5 mm. Please provide information on the exact catheter model utilized in the study. Also, please describe if the catheter geometry was added to the computational mesh.
For time step size, please reference a previous study, or provide supporting information, showing the time-step / mesh resolution you chose resulted in numerically-independent results.
Please provide information on the diffusion coefficient specified.
This model did not have interaction of interstitial spaces and pressure. Please explain why this was chosen and what are the drawbacks / benefits of that approach.
This model represented the end of the catheter by a source term. In reality, the source is from a catheter tip with parabolic flow profile. Please explain if this assumption may impact the results.
Please provide information on the external boundary conditions of pressure on the model walls.
Please provide information on how the total volume filled in the tumor was calculated. For example, was there a minimum therapeutic threshold defined that would specify if a region was included in the volume filled?
The total volume dosed over 6 hours was 600 uL (600 mm3). However, the simulations showed total volumes filled less than 600 uL. Please explain where the missing drug went.
Table 2 shows relatively small differences in % volume of tumor filled. Would be helpful to provide insight into if these differences are statistically significant or if they are artifacts of the simulation boundary conditions / limited resolution of input data.
Discussion “the primary outcome of this research showed differences in the therapy volume distribution based on the catheter placement location and suggested that location may influence the distribution and therapeutic value.” This statement is difficult to reconcile with regard to the significance of the “differences”. These differences are small. See comment 11 above.
The discussion of results is limited. Authors should consider a) how does this study compare to previous CED study results and modeling approach? b) what are the specific limitations to the model and how are they expected to impact the results, c) The model lacks validation with in vivo measurements, this should be discussed.
A significant portion of the discussion text relates to the researcher’s clinical trial. This seems like an unrelated topic and text should be shortened with respect to this trial.
The conclusion that the computational fluid dynamics could “greatly improve the treatment of adult and pediatric brain tumor patients by optimization…” seems overconfident on the implications of the results. Authors should consider toning down this statement to what the study results show directly.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

Partly
Are all the source data underlying the results available to ensure full reproducibility?

No source data required
Are the conclusions drawn adequately supported by the results?

No

Competing Interests: 1) Scientific Advisory Board member and consultant to Anuncia, Inc., 2) Scientific Advisory Board member, employee and shareholder at Alcyone Therapeutics, Inc., 3) Consultant to Genentech Corp., Roche Corp., Cerebral Therapeutics Inc., InviCRO Inc., Minnetronix Inc, SwanBio Therapeutics Inc., Cerevasc Inc., Flux Neuroscience LLC.

Reviewer Expertise: Computational, in vivo, and in vitro fluid dynamics of cerebrospinal fluid. CNS diseases.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

CITE

Report a concern

Respond or Comment

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 07 Dec 2020

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 1 07 Dec 20	read	read

Bryn A. Martin, University of Idaho, Moscow, USA; Alcyone Therapeutics, Inc., Lowell, USA
Ajay Bhandari, Indian Institute of Technology, Kanpur, Kanpur, India

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

Back to all reports

Reviewer Report

0 Views

24 May 2024 | for Version 1

Ajay Bhandari, Department of Mechanical Engineering, Indian Institute of Technology, Kanpur, Kanpur, Uttar Pradesh, India

0 Views Cite this report Responses(0)

Not Approved

This research focuses on developing a computational model to predict the optimum catheter placement selection for convection-enhanced delivery (CED) of therapeutic agents to brain tumors. To make the computational model heterogeneous, authors have used diffusion-weighted imaging (DWI) data and have predicted therapy volume distributions based on different catheter locations. The reviewer thinks that most of the work regarding catheter design, placement and its effect on CED delivery has already been performed by Linninger et. Al. in this field. Check the following papers.

Linninger et al.(2008¹): “Computational methods for predicting drug transport in anisotropic and heterogeneous brain tissue”, Journal of Biomechanics, 2008
Linninger et al.(2008²): "Prediction of convection-enhanced drug delivery to the human brain, Journal of Theoretical Biology", 2008

Reviewers suggest the authors to improve the quality of the paper. Following comments can help the authors to enhance the quality of the research.

Comment 1: The literature review has not been done properly. There are several studies already been done in this field (CED). The authors have not properly acknowledged all of them. Neither the authors have properly mentioned the research gaps.
Comment 2: No detailed information has been provided for the DWI imaging. From where the data was acquired? What were the imaging parameters? How the analysis was carried out? How were the diffusion tensors along the white and grey matter of the brain obtained? Authors should read the following paper in this regard
Linninger et al.(2008²).
Comment 3: No details regarding the numerical simulations have been shown. What were the boundary conditions, discretization schemes especially for the convection term, simulation time, solvers? How the pressure velocity coupling was incorporated? Were the equations solved in a segregated or coupled manner?
Comment 4: Results and Discussion part is very weak. No proper clarifications have been given. No clinical implications have been given.

Is the work clearly and accurately presented and does it cite the current literature?

No
Is the study design appropriate and is the work technically sound?

No
Are sufficient details of methods and analysis provided to allow replication by others?

No
If applicable, is the statistical analysis and its interpretation appropriate?

No
Are all the source data underlying the results available to ensure full reproducibility?

No
Are the conclusions drawn adequately supported by the results?

No

References

1. Linninger AA, Somayaji MR, Erickson T, Guo X, et al.: Computational methods for predicting drug transport in anisotropic and heterogeneous brain tissue.J Biomech. 2008; 41 (10): 2176-87 PubMed Abstract | Publisher Full Text
2. Linninger AA, Somayaji MR, Mekarski M, Zhang L: Prediction of convection-enhanced drug delivery to the human brain.J Theor Biol. 2008; 250 (1): 125-38 PubMed Abstract | Publisher Full Text

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Bio-fluid mechanics, Image based numerical modeling, CFD, cancer drug delivery.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

29 Views

07 Jun 2021 | for Version 1

Bryn A. Martin, Department of Chemical and Biological Engineering, University of Idaho, Moscow, ID, USA; Alcyone Therapeutics, Inc., Lowell, MA, USA

29 Views Cite this report Responses(0)

Not Approved

Summary
The selection of the location for catheter placement using the region with the highest volume filled may provide optimal therapeutic effect. The researchers conclude that CFD may provide guidance for catheter placement in CED of therapeutic agents. This paper could be improved by the following overall modifications a) restating conclusions to be more directly related with study results, b) addition of details in discussion with respect to the study findings, c) addition of validation data to determine the degree of agreement between computational predictions versus in vivo findings.

Specific comments

Please provide T1W imaging in-plane resolution. Also, resolution seems coarse for the needed high-resolution application. Please explain in the text or reference a study showing that the results documented in your study would be independent of the spatial imaging resolution.
Catheter radius was specified as 1.5 mm. Please provide information on the exact catheter model utilized in the study. Also, please describe if the catheter geometry was added to the computational mesh.
For time step size, please reference a previous study, or provide supporting information, showing the time-step / mesh resolution you chose resulted in numerically-independent results.
Please provide information on the diffusion coefficient specified.
This model did not have interaction of interstitial spaces and pressure. Please explain why this was chosen and what are the drawbacks / benefits of that approach.
This model represented the end of the catheter by a source term. In reality, the source is from a catheter tip with parabolic flow profile. Please explain if this assumption may impact the results.
Please provide information on the external boundary conditions of pressure on the model walls.
Please provide information on how the total volume filled in the tumor was calculated. For example, was there a minimum therapeutic threshold defined that would specify if a region was included in the volume filled?
The total volume dosed over 6 hours was 600 uL (600 mm3). However, the simulations showed total volumes filled less than 600 uL. Please explain where the missing drug went.
Table 2 shows relatively small differences in % volume of tumor filled. Would be helpful to provide insight into if these differences are statistically significant or if they are artifacts of the simulation boundary conditions / limited resolution of input data.
Discussion “the primary outcome of this research showed differences in the therapy volume distribution based on the catheter placement location and suggested that location may influence the distribution and therapeutic value.” This statement is difficult to reconcile with regard to the significance of the “differences”. These differences are small. See comment 11 above.
The discussion of results is limited. Authors should consider a) how does this study compare to previous CED study results and modeling approach? b) what are the specific limitations to the model and how are they expected to impact the results, c) The model lacks validation with in vivo measurements, this should be discussed.
A significant portion of the discussion text relates to the researcher’s clinical trial. This seems like an unrelated topic and text should be shortened with respect to this trial.
The conclusion that the computational fluid dynamics could “greatly improve the treatment of adult and pediatric brain tumor patients by optimization…” seems overconfident on the implications of the results. Authors should consider toning down this statement to what the study results show directly.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

Partly
Are all the source data underlying the results available to ensure full reproducibility?

No source data required
Are the conclusions drawn adequately supported by the results?

No

Competing Interests

1) Scientific Advisory Board member and consultant to Anuncia, Inc., 2) Scientific Advisory Board member, employee and shareholder at Alcyone Therapeutics, Inc., 3) Consultant to Genentech Corp., Roche Corp., Cerebral Therapeutics Inc., InviCRO Inc., Minnetronix Inc, SwanBio Therapeutics Inc., Cerevasc Inc., Flux Neuroscience LLC.

Reviewer Expertise

Computational, in vivo, and in vitro fluid dynamics of cerebrospinal fluid. CNS diseases.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

Respond to this report

Responses (0)

[1] 1. Stine CA, Munson JM: Convection-Enhanced Delivery: Connection to and impact of interstitial fluid flow. Front Oncol. 2019; 9: 966. PubMed Abstract | Publisher Full Text | Free Full Text

[2] 2. Banks WA: From blood-brain barrier to blood-brain interface: new opportunities for CNS drug delivery. Nat Rev Drug Discov. 2016; 15(4): 275–292. PubMed Abstract | Publisher Full Text

[3] 3. Pardridge WM: Drug transport across the blood-brain barrier. J Cereb Blood Flow Metab. 2012; 32(11): 1959–1972. PubMed Abstract | Publisher Full Text | Free Full Text

[4] 4. Wolak DJ, Thorne RG: Diffusion of macromolecules in the brain: implications for drug delivery. Mol Pharm. 2013; 10(5): 1492–1504. PubMed Abstract | Publisher Full Text | Free Full Text

[5] 5. Jain RK: Delivery of novel therapeutic agents in tumors: physiological barriers and strategies. J Natl Cancer Inst. 1989; 81(8): 570–576. PubMed Abstract | Publisher Full Text

[6] 6. Bobo RH, Laske DW, Akbasak A, et al.: Convection-enhanced delivery of macromolecules in the brain. Proc Natl Acad Sci U.S.A. 1994; 91(6): 2076–2080. PubMed Abstract | Publisher Full Text | Free Full Text

[7] 7. Laske D, Youle R, Oldfield E: Tumor regression with regional distribution of the targeted toxin TF-CRM107 in patients with malignant brain tumors. Nat Med. 1997; 3(12): 1362–1368. PubMed Abstract | Publisher Full Text

[8] 8. Wersäll P, Ohlsson I, Biberfeld P, et al.: Intratumoral infusion of the monoclonal antibody, mAb 425, against the epidermal-growth-factor receptor in patients with advanced malignant glioma. Cancer Immunol Immunother. 1997; 44(3): 157–164. PubMed Abstract | Publisher Full Text

[9] 9. Voges J, Coenen HH, Wienhard K, et al.: Imaging-guided convection-enhanced delivery and gene therapy of glioblastoma. Ann Neurol. 2003; 54(4): 479–487. PubMed Abstract | Publisher Full Text

[10] 10. Weber FW, Floeth F, Asher A, et al.: Local convection enhanced delivery of IL4-Pseudomonas exotoxin (NBI-3001) for treatment of patients with recurrent malignant glioma. Acta Neurochir Suppl. 2003; 88: 93–103. PubMed Abstract | Publisher Full Text

[11] 11. Lidar Z, Nass D, Mardor Y, et al.: Convection-enhanced delivery of paclitaxel for the treatment of recurrent malignant glioma: a Phase I/II clinical study. J Neurosurg. 2004; 100(3): 472–479. PubMed Abstract | Publisher Full Text

[12] 12. Kunwar S, Westphal M, Chang S, et al.: Phase III randomized trial of CED of IL13-PE38QQR vs Gliadel wafers for recurrent glioblastoma. Neuro Oncol. 2010; 12(8): 871–881. PubMed Abstract | Publisher Full Text | Free Full Text

[13] 13. Desjardins A, Gromeier M, Herndon JE, et al.: Recurrent glioblastoma treated with recombinant poliovirus. N Engl J Med. 2018; 379(2): 150–161. PubMed Abstract | Publisher Full Text | Free Full Text

[14] 14. Støverud KH, Darcis M, Helmig R, et al.: Modeling concentration distribution and deformation during convection-enhanced drug delivery into brain tissue. Transp Porous Media. 2012; 92: 119–143. Publisher Full Text

[15] 15. Sefidgar M, Soltani M, Raahemifar K, et al.: Effect of tumor shape, size, and tissue transport properties on drug delivery to solid tumors. J Biol Eng. 2014; 8: 12. PubMed Abstract | Publisher Full Text | Free Full Text

[16] 16. Zhan W, Arifin D, Lee TK, et al.: Mathematical modelling of convection enhanced delivery of carmustine and paclitaxel for brain tumour therapy. Pharm Res. 2017; 34(4): 860–873. PubMed Abstract | Publisher Full Text

[17] 17. Bhandari A, Bansal A, Singh A, et al.: Comparison of transport of chemotherapeutic drugs in voxelized heterogeneous model of human brain tumor. Microvasc Res. 2019; 124: 76–90. PubMed Abstract | Publisher Full Text

[18] 18. Zhan W, Rodriguez Y, Baena F, et al.: Effect of tissue permeability and drug diffusion anisotropy on convection-enhanced delivery. Drug Deliv. 2019; 26(1): 773–781. PubMed Abstract | Publisher Full Text | Free Full Text

[19] 19. Zhan W: Convection enhanced delivery of anti-angiogenic and cytotoxic agents in combination therapy against brain tumour. Eur J Pharm Sci. 2020; 141: 105094. PubMed Abstract | Publisher Full Text

[20] 20. Stephen Z, Chiarelli P, Revia R, et al.: Time-Resolved MRI assessment of convection-enhanced delivery by targeted and nontargeted nanoparticles in a human glioblastoma mouse model. Cancer Res. 2019; 79(18): 4776–4786. PubMed Abstract | Publisher Full Text | Free Full Text

[21] 21. Vidotto M, Botnariuc D, De Momi E, et al.: A computational fluid dynamics approach to determine white matter permeability. Biomech Model Mechanobiol. 2019; 18(4): 1111–1122. PubMed Abstract | Publisher Full Text | Free Full Text

[22] 22. Singh R, Bellat V, Wang M, et al.: Volume of distribution and clearance of peptide-based nanofiber after convection-enhanced delivery. J Neurosurg. 2018; 129(1): 10–18. PubMed Abstract | Publisher Full Text

[23] 23. Lueshen E, Tangen K, Mehta A, et al.: Backflow-free catheters for efficient and safe convection-enhanced delivery of therapeutics. Med Eng Phys. 2017; 45: 15–24. PubMed Abstract | Publisher Full Text

[24] 24. Antoine LH, Koomullil RP, Wick TM, et al.: Model development to assess drug delivery to brain tumors. Early Career Technical Journal. 2018; 17: 73–79.

[25] 25. Lisa A: Catheter placement selection for convection-enhanced delivery of therapeutic agents to brain tumors. Harvard Dataverse, V1, 2020. http://www.doi.org/10.7910/DVN/H7C6A2

[26] 26. Griffis J, Allendorfer J, Szaflarski J: Voxel-based Gaussian naïve Bayes classification of ischemic stroke lesions in individual T1-weighted MRI scans. J Neurosci Methods. 2016; 257: 97–108. PubMed Abstract | Publisher Full Text | Free Full Text

[27] 27. ANSYS® [computer program] Version 19.1.

[28] 28. Yeh F, Van Jay W, Wen-Yih I: Generalized q-sampling imaging . IEEE Trans Med Imaging. 2010; 29(9): 1626–1635. PubMed Abstract | Publisher Full Text

[29] 29. Yeh F, Verstynen TD, Wang Y, et al.: Deterministic diffusion fiber tracking improved by quantitative anisotropy. PLoS One. 2013; 8(11): e80713. PubMed Abstract | Publisher Full Text | Free Full Text

[30] 30. MATLAB: [computer program] Version 2019a, Natick, Massachusetts: The MathWorks, Inc.,2019.

[31] 31. Støverud K: Modeling convection-enhanced delivery into brain tissue using information from magnetic resonance imaging. Master thesis; Universität Stuttgart, 2009.

[32] 32. Patel DM, Foreman PM, Nabors LB, et al.: Design of a phase I clinical trial to evaluate M032, a genetically engineered HSV-1 expressing IL-12, in patients with recurrent/progressive glioblastoma multiforme, anaplastic astrocytoma, or gliosarcoma. Hum Gene Ther Clin Dev. 2016; 27(2): 69–78. PubMed Abstract | Publisher Full Text | Free Full Text

[33] 33. Jain R: Transport of molecules in the tumor interstitium: a review. Cancer Res. 1987; 47(12): 3039–3051. PubMed Abstract

[34] 34. Boucher Y, Salehi H, Witwer B, et al.: Interstitial fluid pressure in intracranial tumours in patients and in rodents. Br J Cancer. 1997; 75(6): 829–836. PubMed Abstract | Publisher Full Text | Free Full Text

[35] 35. Asthagiri A, Walbridge S, Heiss J, et al.: Effect of concentration on the accuracy of convective imaging distribution of a gadolinium-based surrogate tracer. J Neurosurg. 2011; 115(3): 467–473. PubMed Abstract | Publisher Full Text | Free Full Text

[36] 36. Croteau D, Walbridge S, Morrison P, et al.: Real-time in vivo imaging of the convective distribution of a low-molecular-weight tracer. J Neurosurg. 2005; 102(1): 90–97. PubMed Abstract | Publisher Full Text

[37] 37. Bernal GM, LaRiviere MJ, Mansour N, et al.: Convection-enhanced delivery and in vivo imaging of polymeric nanoparticles for the treatment of malignant glioma. Nanomedicine. 2014; 10(1): 149–157. PubMed Abstract | Publisher Full Text | Free Full Text

[38] 38. Talimogene Laherparepvec. Accessed June 7, 2020. Reference Source

[39] 39. NCI Awards Cancer Moonshot℠ Grants in Five Areas of Precision Medicine Oncology. Accessed June 7, 2020. Reference Source

Catheter placement selection for convection-enhanced delivery of therapeutic agents to brain tumors

Abstract

Keywords

Introduction

Methods

Model development

Tumor geometry

Figure 1. Patient-specific T1W and DWI.

Figure 2. Tumor computational mesh included 21,033 elements, 43,481 faces, and 4,259 nodes.

DWI to T1W transformation

Figure 3. DWI to T1W transformation and fiber tracking.

Figure 4. DWI to T1W transformation validation.

Diffusion tensors

Figure 5. Tumor geometry with four catheter placement locations per region.

Table 1. Input coordinates for each catheter placement location.

Simulations

Results

Figure 6. Therapy distribution based on catheter placement location.

Figure 7. Therapy distribution based on catheter placement location.

Figure 8. Therapy distribution based on catheter placement location.

Figure 9. Therapy distribution based on catheter placement location.

Table 2. Catheter placement location rankings based on a infused therapy amount of at least 1×10-10 mL/m3 (1×10-19 mL/mm3) throughout the tumor.

Figure 10. Histogram of catheter placement locations based on the total volume filled.

Discussion

Conclusions

Data availability

Author contributions

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated

Table 2. Catheter placement location rankings based on a infused therapy amount of at least 1×10^-10 mL/m³ (1×10^-19 mL/mm³) throughout the tumor.