Keywords
protein modelling, structural rearrangements, circular permutation, domain swapping, domain atrophy, Euclidean distance matrices
This article is included in the EMBL-EBI collection.
protein modelling, structural rearrangements, circular permutation, domain swapping, domain atrophy, Euclidean distance matrices
Most proteins fold into compact globular domains stabilised by hydrogen bonds and a hydrophobic core. Protein domains typically allow for sequence mutations and short indels, which have a minor effect on the domain core. Some domains additionally allow for larger structural rearrangements that conserve the majority of core interactions. Some examples are domain swapping, where two independent domains exchange secondary structures to form an intertwined dimer1 circular permutations, where the sequence order of the domain is rearranged, connecting the N and C-termini and introducing new termini at a specific "cut" position2 and domain atrophy, where complete core secondary structures of a domain are deleted3.
These structural rearrangements have been extensively studied both experimentally and computationally due to their importance for protein stability and function4–6. A number of methods have been devised to predict domains susceptible to circular permutations and domain swaps7–9. However, modelling the 3D structure of the alternate conformations proves challenging, often requiring complicated software pipelines and long simulations8,10. We present an alternative modelling approach that consists in representing domains as Euclidean distance matrices (EDMs) and generating rearranged structures by applying a series of matrix operations (Figure 1).
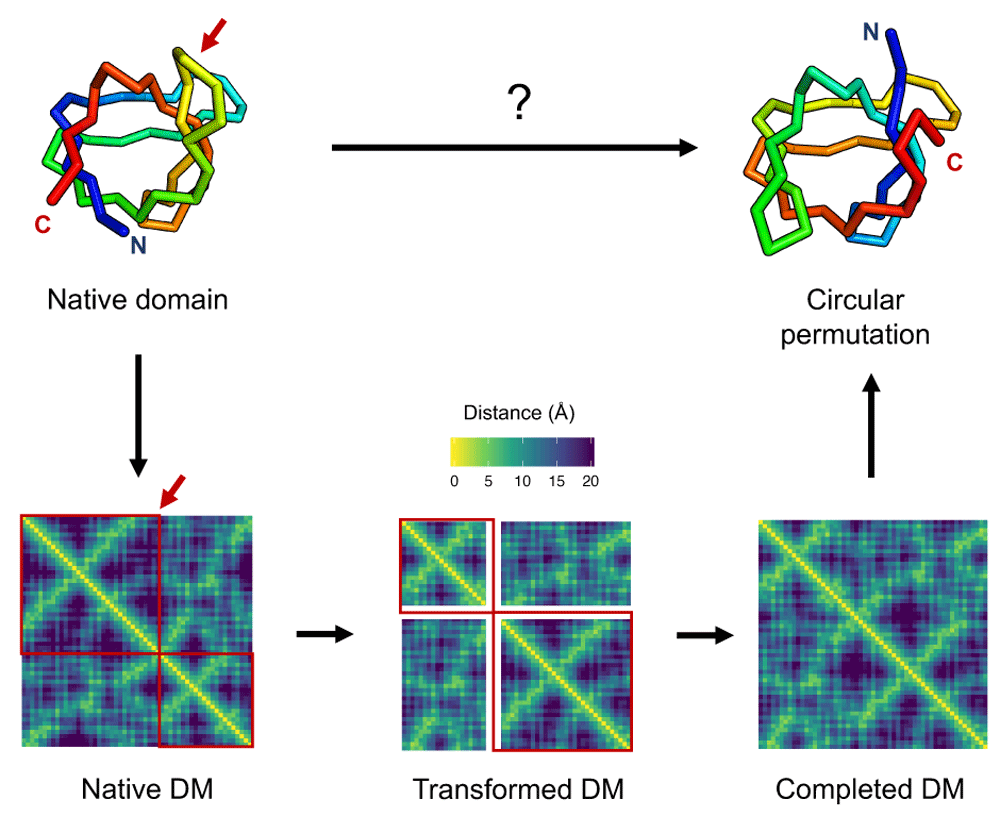
Atomic coordinates of the native SH3 domain (PDB:1SHG) structure (top left) are converted into a distance matrix (DM), shown at the bottom left as a heatmap of C-beta distances in a viridis color scale. A matrix transformation operation corresponding to the structural rearrangement is applied to the distance matrix (bottom middle), here shown as a red arrow for the circular permutation cut position and red boxes encapsulating conserved regions of the matrix. Values for unknown entries in the transformed distance matrix, shown as white stripes, are filled using an EDM completion algorithm to generate a complete EDM (bottom right). The distance matrix is finally converted to points in 3D corresponding to the atomic coordinates of the rearranged domain structure (top right).
EDMs are matrices of squared distances between points in an m-dimensional Euclidean space11. By definition, they are square and symmetric matrices with zero diagonal and non-negative off-diagonal values, fulfilling the triangle inequality. Thanks to their many useful properties they have been used for applications in sensor localisation, molecular conformation and dimensionality reduction, among others. In proteins, EDM-based algorithms have been previously used to model structures from distance constraints derived from nuclear magnetic resonance (NMR) experiments12. EDMs are especially well suited for modelling protein structural rearrangements, since most of the distances at the domain core are conserved and can therefore be used as known entries in the matrix. Here we describe in detail a modelling approach based on EDMs and demonstrate its applications for studying circular permutations, domain swaps and domain atrophy in proteins.
Given an input protein structure, its distance matrix can be computed as the Euclidean norm between all pairs of atoms. The distance matrix of a protein with n atoms will be n columns by n rows for a total of n2 entries. The granularity of the distance matrix can be easily adjusted by changing the number and type of atoms included from each protein residue. For example, a coarse-grained representation of a protein can be achieved using only C-alpha atoms.
Distance matrices are invariant to point rotations, translations, and mirror images. This means that proteins rotated and translated in space have the same distance matrix. To the advantage of protein structure analysis, distance matrices of similar proteins can be directly compared without the need to superpose them in space. On the other hand, a protein and its non-natural mirror image are also indistinguishable from their distance matrix. Distance matrices can be inverted into a set of points in an embedding space of m dimensions using a technique known as multidimensional scaling (MDS). Distance matrix inversions can be challenging for noisy and incomplete matrices. Thanks to the degeneracy in low-rank protein distance matrices, where the number of points is much higher than the number of dimensions (three), MDS can handle small levels of noise and produce accurate reconstructions. Atomic coordinates of proteins can be generated from distance matrices using MDS in three dimensions. If the MDS point reconstruction results in a non-natural mirror image of a protein, its natural stereoisomer can be obtained by simply changing the sign of the z dimension of all points.
Partial or incomplete EDMs, where only a subset of distances in the matrix are known, are a common problem in many applications. Finding values for the missing entries such that the resulting matrix is still an EDM is known as the EDM completion (EDMC) problem. Several different algorithms formulated as optimisation problems have been devised to complete EDMs, ranging from semidefinite programming (SDP) to numerical optimization, each with different loss functions and constraints.
EDMC algorithms only converge to an exact solution with zero loss, in which the resulting matrix is an EDM. In some cases, there are multiple exact solutions to the completion problem and algorithms will randomly converge to one of the solutions. In other cases, convergence will not be possible and algorithms will return a solution with minimal loss instead, corresponding to the closest matrix to an EDM.
For the purpose of protein modelling, the dissimilarity parameterization formulation (DPF) algorithm13 offers a suitable solution. The dimensions of the EDM embedding space and upper and lower bounds for unknown distances are built into the loss function and can be set as input parameters. Thus, atomic distance bounds can be used to avoid clashes and unrealistic conformations.
To obtain realistic protein conformations in EDM models, we use atomic distances extracted from experimental structures in order to set upper and lower bounds on unknown entries in protein distance matrices. We selected one manual representative domain from each architecture type of the Evolutionary Classification of Protein Domains (ECOD) database14. The set of 20 domain structures is of diverse length, secondary structure content and fold topology, and determined by high-resolution X-ray crystallography (below 2Å).
In total, we calculated over three million distances between backbone atoms (N, CA, CB, C, O) and grouped them by atom types and residue number separation along the peptide chain. Separations above five residues were grouped together into one. For each of the 270 pairs of atom types and residue separation groups, we constructed a lookup table of with the average value, the minimum value (lower bound) and the maximum value (upper bound). Outliers, defined as distances outside the 1/1,000 percentile, were discarded in the upper and lower bound calculations, for robustness. Given a partial protein distance matrix, lower and upper bounds for unknown distances are set to the corresponding values in the lookup table.
The average, upper and lower bounds for C-alpha and C-beta distances are shown in Figure 2A. As expected, the uncertainty around the average distance increases with the residue separation. The lower bound, however, reaches a minimum value of 3.70Å for C-alpha and 3.53Å for C-beta contacts. Values below 3Å are observed for C-alpha atoms of adjacent residues (separation equal to 1), which correspond to cis-Proline conformations. In order to simplify the lookup table of atomic distance bounds, we discarded cis-Prolines. A subset of the final distance bounds lookup table for two adjacent residues is shown in Figure 2B. Dark colours in the table represent distances with low variation, for example those between atoms that form the peptide bond plane (CA0, C0, O0, N1, CA1).

A) C-alpha (CA) and C-beta (CB) interatomic distances as a function of residue separation along the peptide chain. The average distances are shown as a black line with a grey area for lower and upper bounds. Upper bounds trimmed at 20Å . B) Table of average backbone interatomic distances between adjacent residues (0,1), excluding cis-Prolines. Colours indicate amount of variability as the difference between upper and lower bounds in Å, with darker colours for smaller variations.
Proteins with known pairs of native and rearranged structures have been selected from the Protein Data Bank (PDB) and used as modelling examples. The use of pairs has allowed the comparison of EDM models to their experimentally determined structures. For domain atrophy, a pair of close homologs were selected instead due to the lack of domain atrophied structures from the same protein.
The procedure to model structural rearrangements using EDMs is schematically shown in Figure 1 and starts by parsing the atomic coordinates of the domain structure from a PDB file and extracting a subset of atoms, either C-alpha or backbone atoms. Next, the distance matrix is calculated and its entries are rearranged, corresponding to the structural changes to be modelled. Unknown distances are bounded using the lookup table of atomic distance bounds and filled using EDM completion. Finally, the atomic coordinates of the rearranged structure are obtained using multidimensional scaling and substituted into the original PDB file, which is saved as the new model.
The EDM protein modelling approach presented here has been implemented in the R programming language, version 3.6. Protein structures are parsed and manipulated using the latest version (2.4) of the bio3d package15. The edmcr package version 1.016 is used for EDM completion and multidimensional scaling. The implementation requires minimal dependencies and only a few lines of code, and runs on a single CPU. A general script for each type of structural rearrangement has been created so that it can be applied to any query protein by simply changing the path to the input file.
A circular permutation of a protein domain is the alteration of its amino acid sequence order so that the N and C-terminal regions are interchanged at a specific "cut" position. The result is a new domain with a similar overall 3D structure and topology but different termini2.
The core of the domain remains largely the same, so atomic distances can be rearranged in the matrix, as shown in Figure 1. For a given native distance matrix D with n rows and columns, the distance matrix Dcp of a circular permutation at position k corresponds to:
Since the old N- and C-terminal residues are now connected in the circular permutation, their distances to other atoms are set to unknown in order to remove their constraints and let them to freely adopt a new conformation, effectively unfolding them. A linker of any length between the old domain termini can also be added to the circular permutant by inserting columns and rows of unknown distances in the matrix. Next, upper and lower bounds for all unknown distances are set using the lookup table of distance bounds. Finally, the matrix is completed and the coordinates of the atomic 3D points are reconstructed as described in the Methods section.The EDM completion algorithm will not converge to a solution if joining the domain termini is not geometrically possible. In that case, a longer linker or more unfolded terminal residues might have to be considered, as is the case for YibK methyltransferase. The distance between the N and C-terminal residues is 20Å, which means a linker is required to connect them. An experimental structure of a circular permuted YibK has five extra residues forming the termini linker loop17. Modelling the same circular permutation at position 82 with EDMs using only two unfolded terminal residues does not converge to a valid solution, with a large loss value over 20K and distance errors in the terminal loop region above 8Å. An EDM model with four unfolded residues neither converges to a solution, but has a smaller loss of 2K and errors on the order of 2Å. Using six unfolded terminal residues finally converges to an exact solution, shown in Figure 3A.
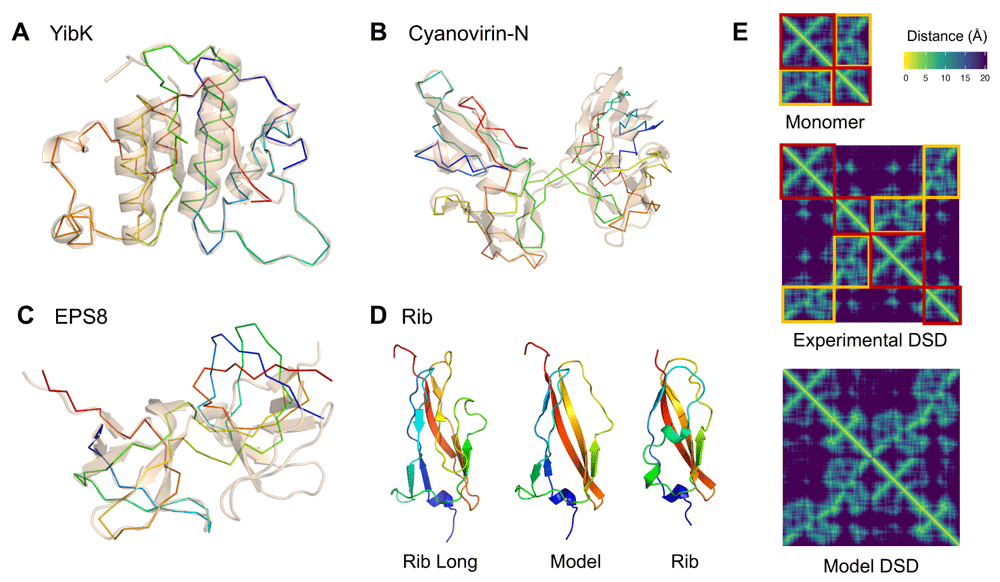
A) C-alpha model of the circular permutation of YibK methiltransferase as a rainbow backbone, superposed to the native structure (PDB: 1MXI) as transparent cartoon; B) Domain swap dimer model of Cyanovirin-N (PDB: 2EZM) as a rainbow backbone, superposed to its experimental domain swap dimer (PDB: 3EZM) as transparent cartoon; C) Domain swap dimer model of EPS8 SH3 domain (PDB: 1I0C) as a rainbow backbone, superposed to the left-most domain of its experimental domain swap dimer (PDB: 1I07) as transparent cartoon; D) Backbone EDM model of domain atrophied Rib domain (PDB: 6SX1) from the structure of Rib Long (PDB: 6S5W); and E) C-beta distance matrices of monomeric EPS8 domain (PDB: 1I0C), its experimental domain swap dimer (PDB: 1I07) and its model generated with EDMs. Conserved intra-domain contacts in the monomer distance matrix are highlighted as red boxes, while contacts swapped to inter-domain are highlighted as orange boxes.
Domain swapping refers to the reciprocal exchange of equivalent secondary structure elements between protein domains6. The swapping mechanism requires the extension of a short region of the native domain to form what is known as the "hinge loop" that bridges the two interacting domains. Although the core of the domain in a domain swap is formed by inter-domain interactions, as opposed to intra-domain interactions in the non-swapped conformation, its overall 3D structure is similar everywhere else apart from the "hinge loop" region. Therefore, like for circular permutations, atomic distances in the matrix can be rearranged to alter the pattern of residue interactions.
For a given distance matrix D from a monomeric domain with n atoms, the matrix Dsw for a domain swap with "hinge loop" centred at position k corresponds to a duplicated matrix with 2n columns and rows. Intuitively, interactions between atoms at each side of the "hinge loop" are changed to be inter-domain and interactions involving residues within each side are kept intra-domain, as shown in Figure 3E. This corresponds to the following matrix index rearrangements:
Similarly to the circular permutation case, distances involving residues that form the "hinge loop" have to be set as unknown to allow enough molecular flexibility to extend the loop and permit the interaction between the two domains. The number of "unfolded" residues needed as a "hinge loop" to make the domain swap geometrically possible is a parameter that has to be set before completing the matrix and can vary across domains.The structures of Cyanovirin-N and EPS8 SH3 domains have been experimentally determined both as monomeric and domain swapped dimers. The EDM model of the Cyanovirin-N domain swap structure from its monomer closely resembles the experimental domain swap at position 5118, as shown in Figure 3B. However, the EDM model of the EPS8 domain swap structure from its monomeric form converges to a valid solution, but has a different domain orientation to the experimental domain swap at position 3419, as shown in Figure 3C. These results imply that the domain swap of Cyanovirin-N has a lower flexibility than EPS8. The relative orientation between Cyanovirin-N domains is constrained and cannot change without disrupting natural protein geometry, while EPS8 domains have a greater range of possible orientations.
To model domain swap dimers, atomic coordinates can be directly assigned to two different chains. Another case is that of tandem domain swaps, where the two domains forming the swapped conformation are part of the same protein chain. In tandem domain swaps, an additional loop is required to connect the termini of the central domain at indices (n, n + 1), similar to the circular permutation case. The TAndem DOmain Swap Stability predictor (TADOSS) method9 already reports predictions for the "hinge loop" position and linker lengths required for the formation of tandem domain swaps. Hence, EDM modelling can be directly used to generate 3D models for TADOSS predictions. This feature has been implemented in the latest version of the method. The possibility to generate models for TADOSS predictions not only improves result visualisation and interpretability, but offers a new avenue to improve its accuracy.
Domain swapping is also found as a crystallisation artefact20–22. By inverting the domain swap matrix rearrangement, it is possible to "unswap" these structures using EDMs, facilitating its interpretation and comparison to other known domain structures.
Domain atrophy is the abrupt loss of entire secondary structures in the core of a protein domain, resulting in a shorter version of the domain3. Although it is a rare evolutionary event, it has been described for some of the most widespread and conserved domain folds, like immunoglobulins (Ig) and TIM barrels3,23.
A structural deletion between positions k and l in a domain can be modelled using EDMs by removing all columns and rows between indices k and l in the native distance matrix. Since residues k and l are connected through a peptide bond in the atrophied domain, constraints for adjacent residues from the lookup table of distance bounds have to be applied to the distance matrix accordingly.
Opposite to circular permutations and domain swaps, domain atrophy can have a more significant effect on the core of the domain, so it might have an impact on a higher fraction of native distances. As a result, the EDM completion is more likely to fail to converge to an exact solution. Proposed workarounds are to either "unfold" the residues around the deletion or to "relax" the native distances to intervals. Instead of using the exact distances, bounds can be set to a 10% interval of their native distances, for example. That way, the structure is given enough flexibility to adapt to the new conformation, while still conserving its overall 3D shape.
The domain atrophy in Rib domains involved the loss of a pair of beta strands core to its beta-sandwich topology23. The distance between the two ends of the deleted segment between positions 55 and 72 is, however, close enough so that a short linker can connect them, as captured by the EDM atrophy model shown in Figure 3D. The atrophy leaves, however, part of the domain core exposed to the surface. This gap is filled in the Rib domain by another part of the protein which adopts a helical turn conformation. This type of structural compensation is common in domain atrophy cases. Although such detailed structural consequences of domain atrophy can not be accounted for by EDM models, they provide a useful starting point to investigate them further.
The size of a distance matrix scales quadratically with the number of atoms in the input structure. This means that the running time and memory of EDM algorithms is expected to be at least 𝒪(n2).
Calculation of distance matrices and multidimensional scaling operations are very fast, and take less than a second for the modelling examples presented in Figure 3. The matrix completion step is, however, the bottleneck, varying from just a few seconds to few minutes, heavily dependent on the size of the input matrix, but also on the number and complexity of unknown entries and a random convergence factor.
Running times for modelling structural rearrangements of several domain structures is shown in Figure 4. C-alpha models take less than a minute for up to 200 residues, which is within the size of an average protein domain and suitable for large-scale analysis. C-alpha models of domains up to 400 residues run in less than ten minutes. In comparison, backbone models do not scale particularly well, with an expected factor of 25 times slower than C-alpha models due to their five atoms per residue. Hence, backbone models for domains over 200 residues are possible but not practical for most applications.
Running times were calculated on a single standard CPU with 8GB of RAM. The small computational resources needed to create a model allows multiple modelling jobs to run concurrently in large-scale analyses.
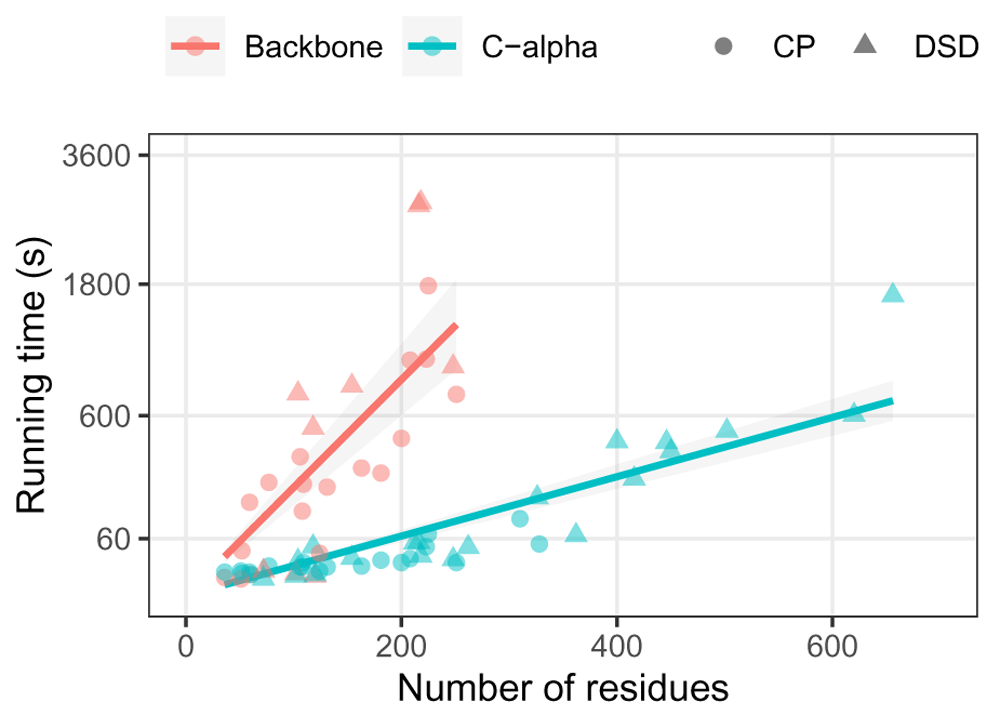
Time calculated for backbone and C-alpha models of circular permutations (CP) and domain swap dimers (DSD) of the 20 ECOD representative domains. Backbone models for domains over 300 residues are omitted. Quadratic fits of the form y = Ax2 for each model granularity are shown as lines with uncertainty grey shades. Running time shown as a square root scale.
We have described a new homology modelling approach for protein structures based on their distance matrices. The approach aims to be intuitive, flexible, light-weight and fast, being an alternative to more traditional modelling techniques based on simulation. Through a series of examples, we have demonstrated how EDMs can be handled to suit different modelling needs and its applications for protein structure analysis. We are also releasing an open code repository with an implementation of the method to the community, hoping that other researchers can explore the modelling cases presented in this study and extend the code for other applications.
Modelling protein structures with EDMs is well suited to tasks where a large proportion of atomic distances are known close to their exact values. As we have shown here, this is the case for structural rearrangements, where only a small subset of distances in the native matrix are perturbed. There are a number of other applications in protein modelling where this condition holds and that we have not explored here, including modelling of multidomain proteins by concatenating tandem or nested domains, docking protein subunits based on a subset of interface contacts, modelling allosteric conformational changes, and incorporating distance constraints from experimental techniques (NMR, cross-linking) and sequence co-evolution inferences.
Modelling protein structures using EDMs is far behind state-of-the-art techniques based on atomic energies and simulations, and therefore has its own limitations. EDM models are solely based on geometry, and it is not trivial how to incorporate other more complex energetic terms essential to protein structures. Additionally, there is a lack of specialised software libraries for EDM-based protein modelling, making it difficult to write efficient code for more sophisticated applications.
The current implementation in R does not scale well and proves impractical for inputs over 600 atoms, mainly due to the matrix completion bottleneck. This means most of the models are restricted to be coarse-grained (C-alpha or backbone only), even though the same approach described here can be used to generate full side-chain models. Adding residue side-chains to backbone models is, however, a common task in protein modelling and good tools already exist, for example Chimera’s Dock Prep24. The actual computational costs of EDM modelling can be reduced much further. On the software implementation side, matrix operations in R are two orders of magnitude slower than in other programming languages like C++ and Java. The use of an alternative library for faster EDM completion will have a big impact on the running time, but we are unaware of its existence. Algorithmically, the size of EDMs can be reduced exploiting rigid "cliques" of fully connected points. This technique is known as facial reduction and has been previously used to reduce the size of protein distance matrices12.
Despite its current limitations, several protein modelling tasks can benefit from the EDM modelling approach described in this article. As shown for structural rearrangements, EDM models prove to be another valuable tool in the protein structure analysis toolbox.
Zenodo: lafita/protein-edm-demo: Initial public release. https://doi.org/10.5281/zenodo.394538325 This project contains the following underlying data:
Data are available under the terms of the Creative Commons Attribution 4.0 International license (CC-BY 4.0).
Protein EDM modelling implementation in R.
Source code available from: https://github.com/lafita/protein-edm-demo
Archived source code at the time of publication: https://doi.org/10.5281/zenodo.394538325
License: MIT license
TADOSS method incorporating automatic generation of tandem domain swap models.
Source code available from: https://github.com/lafita/tadoss
Archived source code at the time of publication: https://doi.org/10.5281/zenodo.393915026
License: MIT license
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the rationale for developing the new method (or application) clearly explained?
Yes
Is the description of the method technically sound?
Yes
Are sufficient details provided to allow replication of the method development and its use by others?
Yes
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?
Yes
References
1. Alfakih AY: Euclidean Distance Matrices and Their Applications in Rigidity Theory. Springer. 2018.Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Convex optimization; numerical linear algebra.
Is the rationale for developing the new method (or application) clearly explained?
Partly
Is the description of the method technically sound?
Partly
Are sufficient details provided to allow replication of the method development and its use by others?
Yes
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?
Yes
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: I work on developing methods for protein structure prediction.
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 1 20 Jul 20 |
read | read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)