Introduction
Proteins are one of the basic building blocks of all life and we have learned much about them since they were ‘discovered’ about 200 years ago1, including their shapes, functionality, and uses. However, there are still many basic questions such as how proteins are able to transform from a useless linear assemblage of amino acids (primary structure) into a functional three-dimensional native structure, that remain unanswered2. The ability to accurately predict the functional form of a protein from its primary sequence would revolutionize many fields and has long been considered a ‘holy grail’ in Life Sciences research3.
The solution to the problem of computationally determining how proteins fold will involve multiple disciplines of science making it a very interesting topic to address. At its heart, it is a biochemical issue, rooted in both geometry and physics, which is faced by every cell on Earth. In Mathematical terms, it is an application of the ‘self-avoiding walk’ problem4 with some additional constraints. Since we know that there are many physical constraints on achieving a properly folded protein, it is also an NP-hard problem5 and therefore highly applicable to Computer Science.
Proteins are made up of a sequence of amino acids, of which there are many types but only 20 are typically used in biological proteins6. Each amino acid type can be placed into one of two categories: hydrophilic (P) and hydrophobic (H). While a protein’s primary sequence dictates the ordering of the amino acids, it must fold into a three-dimensional structure to be active7. Therefore, the goal of solving how proteins fold computationally is to determine the folding pattern of any protein starting from the primary sequence.
For the last 100 years, the two most employed methods for determining the folding pattern of a given protein are x-ray crystallography8 and nuclear magnetic resonance (NMR)9. Both can provide high resolution images of the folded-state of a protein but rely on the ability of scientists to purify the protein of interest to concentrations of 1 molar (NMR) to greater than 10 molar (x-ray crystallography), which is not an easy task. The x-ray crystallography method is further complicated by the need to determine the conditions for the growth of crystals of the protein and then waiting for those crystals to grow to a usable size and dimension10. The NMR method requires less purified protein, compared to x-ray crystallography; however, it is limited by the size of protein that can be analyzed10. Both of these more traditional methods also require a significant investment of time in order to achieve the folding pattern of a protein. Despite the significant time investment, these methods have persisted due to the fact that they are a very reliable way to determine protein structure. However, with the recent explosion of genomes being sequenced, which has resulted in the discovery of a plethora of new proteins and protein families, newer methods that will reliably determine the folding pattern of a protein in a shorter amount of time are called for11. One of these methods, de novo protein folding, uses only the primary sequence of a protein and a set of computer algorithms to determine its active, folded form. This may seem overly daunting at first, since even a relatively small protein can have a nearly infinite number of possible folding patterns. However, over the past 50–60 years biochemists have determined that the way a protein folds is quite conserved in a protein family12 and that chemical/physical forces significantly reduce the number of ways a protein can fold13–15. These two findings are very important and have the very real implication that computers can be used to predict the active, folded forms of a protein in a very short period of time.
One method often used to computationally determine how proteins fold is a Genetic Algorithm (GA). GAs are a type of optimization algorithm that models biological selection16,17 and are part of a family of optimizations algorithms called Heuristics18, which attempts to solve a problem by determining a solution and iteratively making the solution better. GAs have been very good at optimization of large complex domains, are a product of the field of Artificial Intelligence and can theoretically solve any problem that can be represented as the optimization of a continuous function. The theory behind GAs states that after many generations the intermediate solutions will eventually converge upon the correct answer19. Even in cases where GAs could not fully solve the problem, the answer produced was valuable, which is an aspect of GAs that makes them superior to other algorithms.
At their core, GAs model biological selection and provide multiple possible answers termed individuals, which are comprised of a string of characters. The GA begins by randomly generating a number of individuals (first generation) and then goes through multiple iterations of selection, crossover and mutation. In selection, pairs of individuals are picked for crossover. Individuals with higher fitness, as determined by a fitness function, are given an increased probability of being selected and an individual can be selected for crossover multiple times. In crossover, two individuals are picked and each is broken into two substrings at a randomly selected position that is at the same position in the string of characters for both thereby creating two new individuals. In mutation, the value of some of the characters in each individual can change based on a probability parameter. The processes described above results in a new generation of individuals and the process then repeats using the new generation (Table 1).
Table 1. GA vs. DSGA Pseudo-code.
| Line | GA Pseudo-code | DSGA Pseudo-code |
|---|
| 1 | Loop until termination
condition | Loop until termination condition |
| 2 | Select() | Seed Selection() |
| 3 | Crossover() | Selection() |
| 4 | Mutation() | Crossover() |
| 5 | End loop | Mutation() |
| 6 | | Seed Conservation() |
| 7 | | If (RLC mod Generation # = 0) |
| 8 | | Put current seeds on Tabu List |
| 9 | | Put any individuals with CL more
identical individuals on Tabu List |
| 10 | | Replace all individuals put on
Tabu List with randomly generated
individuals |
| 11 | | Increase radius by radius delta |
| 12 | | End if |
| 13 | | End loop |
Although GAs are good at solving the optimization of a continuous function, they have a difficult time solving multi-optima problems20. When multiple optima exist a traditional GA will often locate only one optimum and there is no guarantee that it is the global optimum and not a local one. To overcome this problem, specialized GAs, called Niche Genetic Algorithms (NGA), have been developed that can locate multiple optima20,21. There are a number of NGAs including De Jong22, Crowding Clustering Genetic Algorithm (CCGA)23 and Species Conserving Genetic Algorithm (SCGA)24. One NGA has been shown to be especially adept at solving problems with multiple optima21. It is called the Dynamic-radius Species-conserving Genetic Algorithm (DSGA)20 and is basically a modification of the SCGA24. DSGA enhances the traditional GA by the addition of seeds, a Tabu List20 and the ability to change the radius. A seed is a locally strong individual based upon some radius that is identified in each iteration of the loop and conserved (i.e. propagated into the next generation by replacing a locally weak individual). A Tabu List’s function, whose name comes from the Tabu Search25, is to store strong candidates for the global optima, which is determined by the Reevaluation Loop Count (RLC) and the Convergence Limit (CL).
Here we show that protein folding is a multi-optima problem and as a result NGAs are better suited for a solution. The DSGA has not previously been applied to the immense task of de novo protein folding. Therefore, as a proof of concept, we have shown two important results below: (1) the DSGA is very adept at predicting the folded state of proteins, which was shown by selecting a 20 amino acid protein and modeling the folds and all possible combinations; (2) the DSGA is better than a traditional GA and better able to derive the correct folding pattern of a protein. Below we present some preliminary testing data and have provided the source code, which is available for download at Zenodo.org (https://zenodo.org/record/11902).
Materials and methods
Seed Selection method
Each individual is evaluated from the most to the least fit. If no other seeds exist within the radius (r) of the individual then the individual is a seed. In the Seed Conservation method each seed will replace an individual in the newly created generation. If there are individuals in the next generation within r of the seed, the seed will replace the weakest of these individuals. If there are no individuals within r of the seed in the next generation, the seed will replace the globally weakest individual. But these seeds have to re-compete to be seeds in the next generation.
Generating the Tabu List
The Tabu List stores potential candidates for the global optima. As individuals are put on the Tabu List, the DSGA attempts to seek optima in other locations by using a Shared Fitness. Shared Fitness will decrease the fitness of an individual if it is too close to individuals on the Tabu List. This encourages exploration in other areas of the domain. The Shared Fitness function is defined in equation 1.
In equation 1, mi is defined by equation 2 where TLj is the jth individual on the Tabu List, Length(i) is the number of characters in individual i and Distance(i, TLj) is the distance between individual i and individual TLj.
The final term in the Shared Fitness equation is + 1. Individuals with a fitness of zero have no chance of being selected for crossover. By incrementing all Shared Fitness values by one, this gives these individuals a chance at selection and propagation into later generations.
Distance measurement
For this study, we selected chromosomal difference using Equation 3 below to calculate the distance between two individuals (i1 and i2).
Fitness function
This function determines how fit an individual is in relation to the fold it has adopted. The value of this function is determined by calculating the Free Energy and the algorithm prioritizes individuals with a greater ability to fold spontaneously (i.e. low value for Free Energy). Here, we calculated Free Energy by summing all of the possible contacts between adjacent, but not neighboring, hydrophobic amino acids as has been done previously26. The free energy between any two amino acids (i and j) can be found using the following formula:
The free energy (E) for a protein can be found by summing the free energy between all of the amino acids as follows:
E = Σ Δrijεij
Although proteins are three dimensional structures, it is common to use two dimensions. Using two dimensions reduces the search space in the domain. Issues with the algorithms can be addressed and future research can be published using three-dimensional models. This research uses a two dimensional model for protein folding.
Model for folding
In order to model protein folding, a simple method was selected where each gene of an individual has a value of zero, one, two or three. In our method, a zero, one, two or three denotes placing the next amino acid above, right, below or left the previous one, respectively. This method allows for greater simplicity and saves computing time as the number of genes needed in the individual is one less than the number of amino acids in the protein.
Keep Going
In some cases the model may produce a folding that isn’t physically possible (i.e. two amino acids occupying the same space). For example, the series of genes ‘13’ would not be physically possible as the second amino acid would be over top of the first. To handle these cases we employ a method we titled the Keep Going method. When directed to place an amino acid in a location that is already occupied, the algorithm will look for other positions to place it using a predictable pattern. If the folding sequence indicates placement of an amino acid in an occupied position, the algorithm will place it in the next available position in a clock-wise direction; however, if all positions are taken then the algorithm resolves this by setting the fitness to zero.
System requirements and input/output data
The Java-based DSGA and GA used here have been reliably run on a 1.86 GHz processor with 4 GB of memory (i.e. a standard MacBook Air). Minimal system requirements are a functional system that is able to support Java. Sample input data can be found in Supplementary File 1 but are basically an amino acid sequence with amino acids translated into hydrophilic (P) and hydrophobic (H) and the parameters for the DSGA. Sample output data are also provided (Supplementary File 2) but is basically a list of the best individuals with their corresponding calculated Free Energy value. All positive free energy values in the output should be interpreted as negative values, and vice versa. For example, a free energy value of ‘8’ for an individual in the output should be interpreted as ‘-8’. This is quite important as negative free energy values indicate spontaneous folding and positive values indicate that energy needs to be added to the system to get the protein to fold.
Results
To demonstrate that de novo protein folding is better addressed by DSGA, we have used two different methods. Two simple proteins and a method to model the protein folding were selected. All possible combinations of the folding were computed to demonstrate that there are multiple optima. Second a traditional GA was compared to DSGA to solve for a 20 amino acid protein.
Multioptimum problem
We selected a simple protein of four residues with the following sequence of hydrophilic (P) and hydrophobic (H) residues: HPHPP. The individual, which best represents how to fold the protein is 0121 (Figure 1). The first amino acid is placed in the center with the second one above (0121) the third to the right (0121), the fourth below (0121) and the last to the right (0121).
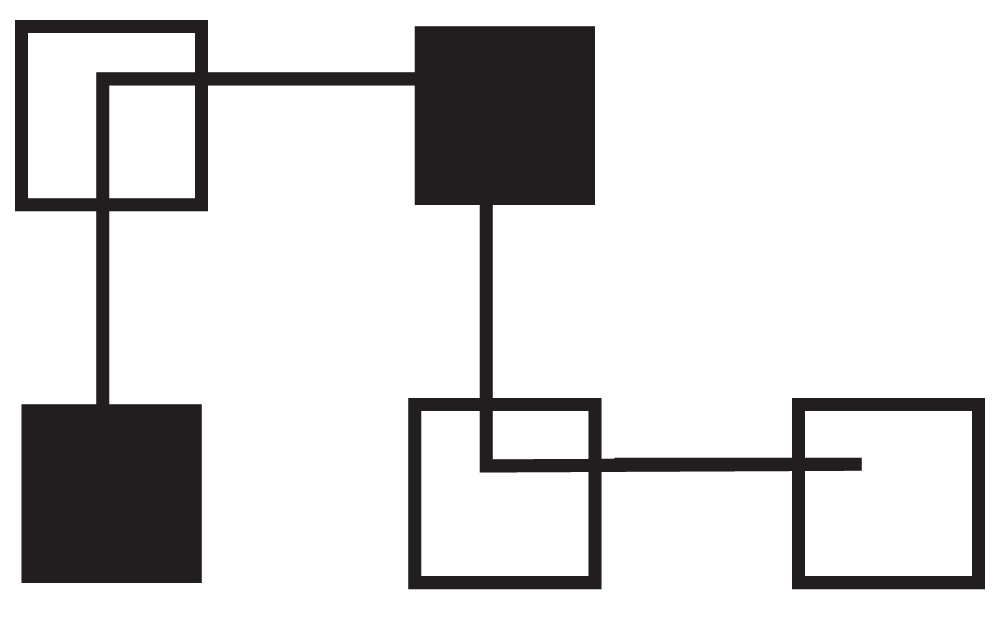
Figure 1. 0121 Folding of HPHPP.
Hydrophilic (P) residues are represented as non-shaded squares and hydrophobic (H) residues are shown as shaded squares.
Next, we moved to a more complex protein with ten amino acids, which translated into the following sequence of H and P residues: HPPHPPHPPH, and determined all the possible ways it could fold using the model described above. Since it has 10 amino acids, all the individuals generated by our DSGA will have nine genes. The values for each range from 000000000 (complete set of amino acids one above the other) to 333333333 (complete set of amino acids each one to the left of the other). Since there are four directions to place the next amino acids, there are 49 or 262,144 different ways to fold the amino acids.
Figure 2 shows a graph of all of the different ways to fold HPPHPPHPPH. The X-axis contains the different ways to fold the protein. The Y-axis is the free energy for the folding method. With this folding method there are eight global optima that each have a value of four and local optima with values of three, two or one. The optimal folding is seen in Figure 3.
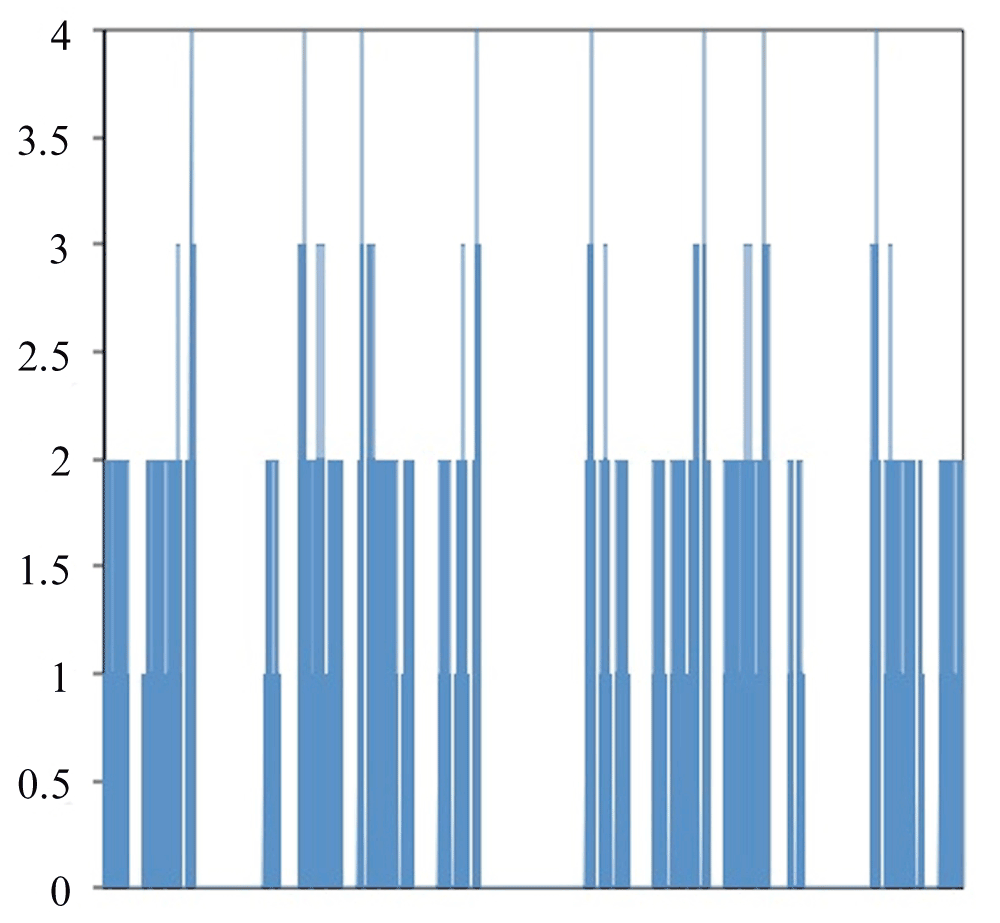
Figure 2. Free Energy for all methods to fold HPPHPPHPPH.
Left side of X-axis corresponds to 000000000 while the right side corresponds to 333333333.
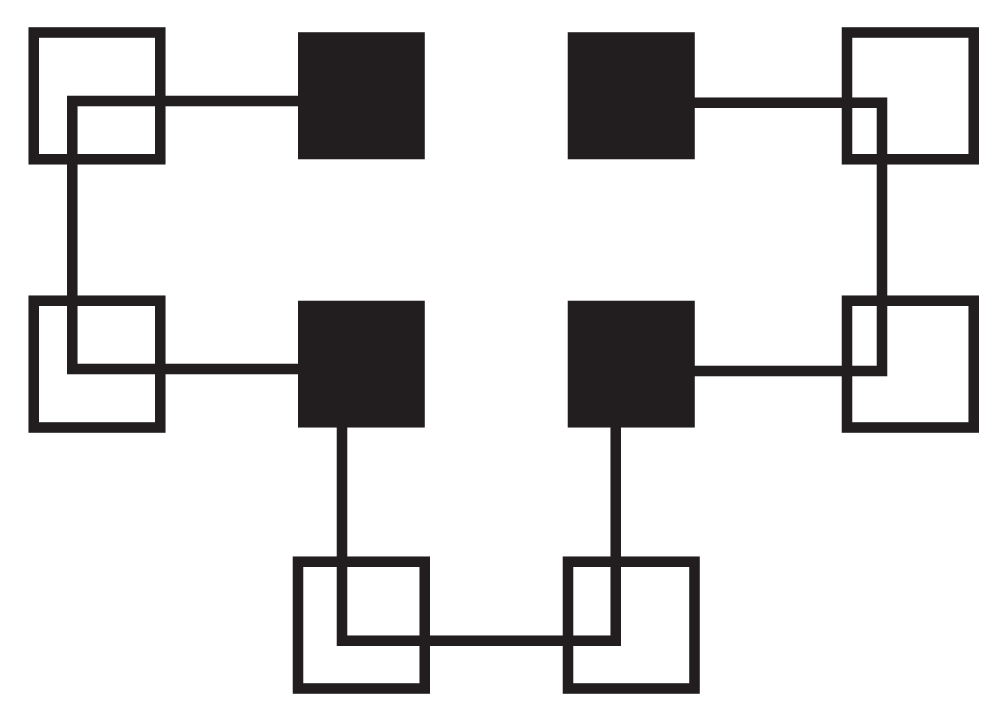
Figure 3. Correct Folding of HPPHPPHPPH.
Hydrophilic (P) residues are represented as non-shaded squares and hydrophobic (H) residues are shown as shaded squares.
Compare Traditional Genetic Algorithm to Niche Genetic Algorithm
Next, we executed our DSGA and a traditional GA26 (Table 1) at solving the folding for the following: HPHPPHHPHPPHPHHPPHPH. This protein of 20 amino acids was used previously27,28,29 and found to have an optimal folding pattern that resulted in a free energy of -9. Since DSGA usually takes longer to run than a traditional GA, two sets of results were created for the traditional GA. One contained the same number of generations as DSGA. The other had additional generations to get the total run-time the same between the two algorithms.
The parameters between DSGA and the traditional GA were kept consistent when possible; however, DSGA does have some additional parameters not used in traditional GAs (Table 2). The first set of results was from the traditional GA running the same number of generations as DSGA. The second set of results was the traditional GA running for the same amount of time as DSGA. In this example, a traditional GA running for 6,000 generations takes about the same amount of time as DSGA running for 1,000 generations. Table 3 shows the best individuals produced for each algorithm in 15 trials. In the case of DSGA the optimum is the best individual on the Tabu List. For the traditional GA the optimum is the best individual in the last generation.
Table 2. Parameter Values.
| Parameter | DSGA | GA | GA Running Same
Amount of Time |
|---|
| Population Size | 200 | 200 | 200 |
| Number of Generations | 1,000 | 1,000 | 6,000 |
| Mutation Rate (per gene) | 0.03 | 0.03 | 0.03 |
| Initial Radius | 4.0 | N/A | N/A |
| Radius Delta | 1.0 | N/A | N/A |
| Reevaluation Loop Count | 250 | N/A | N/A |
| Convergence Limit | 4 | N/A | N/A |
Table 3. Results of DSGA and GA attempting to fold HPHPPHHPHPPHPHHPPHPH.
| Trial | DSGA | GA | GA Running Same
Amount of Time |
|---|
| 1 | 9 | 4 | 3 |
| 2 | 9 | 4 | 3 |
| 3 | 9 | 4 | 4 |
| 4 | 9 | 4 | 5 |
| 5 | 9 | 2 | 4 |
| 6 | 9 | 3 | 3 |
| 7 | 9 | 3 | 3 |
| 8 | 9 | 3 | 3 |
| 9 | 9 | 3 | 4 |
| 10 | 9 | 4 | 3 |
| 11 | 9 | 3 | 4 |
| 12 | 9 | 3 | 3 |
| 13 | 9 | 3 | 3 |
| 14 | 9 | 3 | 4 |
| 15 | 9 | 2 | 3 |
Conclusion
Here we showed that even employing a simple modeling method for protein folding results in the generation of multiple local and global optima. The above also shows that using the DSGA, which is specialized for multiple optima domains, produces better results than a traditional GA. This should be instructive to researchers working on de novo techniques as many algorithms applied to protein folding are actually hybrid applications that use a GA27–29. It is possible that previous poor results could be caused by the GA’s weakness of finding local optima. Using an NGA in these algorithms could overcome this and produce improved results.
Software availability
Archived source code as at the time of publication
Zenodo: DSGA and GA from ‘Niche Genetic Algorithms are better than traditional Genetic Algorithms for de novo Protein Folding’ doi: 10.5281/zenodo.1190230
Software license
MIT License.
Author contributions
MB and JAC conceived the study and designed the experiments. MB and TB did the coding of the DSGA. MB performed the experiments. MB and JAC analyzed the data. JAC, MB, and TB wrote the paper.
Competing interests
No competing interests were disclosed.
Grant information
The author(s) declared that no grants were involved in supporting this work.
Acknowledgements
The authors would like to thank UMUC and all the members of the ITS Department for providing a positive space to perform our research.
Supplementary material
Supplementary File 1: Sample input data. This file contains a sample amino acid sequence (input data) and the meanings of each parameter that needs to be set.
Dynamic-radius Species-conserving Genetic Algorithm for de novo Protein Folding Instructions.
Dynamic-radius Species-conserving Genetic Algorithm for de novo Protein Folding is a Java application written in Java version 1.7, but it should run on other versions of Java.
There are 10 command line parameters that should be set:
# position 1 - population size
# position 2 - number of generations
# position 3 - mutation rate (decimal)
# position 4 - initial radius (decimal)
# position 5 - radius delta (decimal)
# position 6 - reevaluation loop count
# position 7 - convergence limit
# position 8 - protein
# position 9 - output file location
# position 10 - log status 0 few logs; 1 more logs; 2 most logs
An output file path must be placed in the file location for position 9.
Here is an example for running the application:
java -jar /Users/mbrown15/NetBeansProjects/DSGAProteinFolding/dist/DSGAProteinFoldingKG.jar 1000 2000 0.03 8.0 -1.0 500 4 HPPHPPHPPH //Users//mbrown15//Documents//genetic-algorithm-files// 1
This method allows multiple runs to be placed in a batch file, which can be set up as follows:
java -jar /Users/mbrown15/NetBeansProjects/DSGAProteinFolding/dist/DSGAProteinFoldingKG.jar 1000 2000 0.03 8.0 -1.0 500 4 HPPHPPHPPH //Users//mbrown15//Documents//genetic-algorithm-files// 1
1000 12000 0.03 8.0 -1.0 500 4 HPPHPPHPPH //Users//mbrown15//Documents//genetic-algorithm-files// 1
1000 20000 0.03 8.0 -1.0 500 4 HPPHPPHPPH //Users//mbrown15//Documents//genetic-algorithm-files// 1
Supplementary File 2: Sample output data. This file contains a sample of the output data.
TABU LIST
Individual 032321213 natural fittness 4.0
Individual 032320213 natural fittness 4.0
Individual 032320203 natural fittness 4.0
Individual 210012230 natural fittness 3.0
Individual 210212230 natural fittness 3.0
Individual 200212230 natural fittness 3.0
Individual 210212200 natural fittness 3.0
Individual 200212200 natural fittness 3.0
Individual 123320123 natural fittness 3.0
Individual 123310123 natural fittness 3.0
Individual 031321013 natural fittness 3.0
Individual 301133022 natural fittness 3.0
Individual 301133021 natural fittness 3.0
Best individual(s)
Individual = 032321213 4.0
Individual = 032320213 4.0
Individual = 032320203 4.0
Sample output data above are the result from the following input:
Population Size: 50
Number of generations: 5000
Mutation rate: 0.003
Initial radius: 12.0
Radius delta: -2.0
Reevaluation loop counter: 1000
Convergence limit: 3
Protein: HPPHPPHPPH
The output of the program is the full Tabu List and the best individuals for that run. The best individuals are determined by an individual’s free energy value. Free energy values are the last number in each row of the output data. So for the above sample output all three best individuals have a free energy value of -4.
NOTE: All positive free energy values in the output should be interpreted as negative values, and vice versa. For example, the above free energy value of ‘4’ for the best individuals should be interpreted as ‘-4’. This is quite important as negative free energy values indicate spontaneous folding and positive values indicate that energy needs to be added to the system to get the protein to fold.
Faculty Opinions recommendedReferences
- 1.
Teich M, Needham DM: in A Documentary History of Biochemistry, 1770–1940. (Rutherford, NJ : Fairleigh Dickinson University Press). 1992. Reference Source
- 2.
Khoury GA, Smadbeck J, Kieslich CA, et al.:
Protein folding and de novo protein design for biotechnological applications.
Trends Biotechnol.
2014; 32(2): 99–109. PubMed Abstract
| Publisher Full Text
| Free Full Text
- 3.
Dill KA, MacCallum JL:
The protein-folding problem, 50 years on.
Science.
2012; 338(6110): 1042–1046. PubMed Abstract
| Publisher Full Text
- 4.
Foster DP, Pinettes C:
Statistical mechanics of the two-dimensional hydrogen-bonding self-avoiding walk including solvent effects.
Phys Rev E Stat Nonlin Soft Matter Phys.
2008; 77(2 Pt 1): 021115. PubMed Abstract
| Publisher Full Text
- 5.
Unger R, Moult J:
Genetic algorithms for protein folding simulations.
J Mol Bio.
1993; 231(1): 75–81. PubMed Abstract
| Publisher Full Text
- 6.
Alberts B, Johnson A, Lewis J, et al.:
Molecular Biology of the Cell, Fifth Edition. (Garland Science). 2007. Reference Source
- 7.
Jung J, Han KY, Koh HR, et al.:
Effect of single-base mutation on activity and folding of 10–23 deoxyribozyme studied by three-color single-molecule ALEX FRET.
J Phys Chem B.
2012; 116(9): 3007–12. PubMed Abstract
| Publisher Full Text
- 8.
Coontz R, Fahrekamp-Uppenbrink J, Lavine M, et al.:
Going from Strength to Strength.
Science.
2014; 343(6175): 1091. PubMed Abstract
| Publisher Full Text
- 9.
Marion D:
An introduction to biological NMR spectroscopy.
Mol Cell Proteomics.
2013; 12(11): 3006–25. PubMed Abstract
| Publisher Full Text
| Free Full Text
- 10.
Henen MA, Coudevylle N, Geist L, et al.:
Toward rational fragment-based lead design without 3D structures.
J Med Chem.
2012; 55(17): 7909–19. PubMed Abstract
| Publisher Full Text
| Free Full Text
- 11.
Pantazes RJ, Grisewood MJ, Maranas CD:
Recent advances in computational protein design.
Curr Opin Struct Biol.
2011; 21(4): 467–72. PubMed Abstract
| Publisher Full Text
- 12.
Durand P, Lehn P, Callebaut I, et al.:
Active-site motifs of lysosomal acid hydrolases: invariant features of clan GH-A glycosyl hydrolases deduced from hydrophobic cluster analysis.
Glycobiology.
1997; 7(2): 277–84. PubMed Abstract
| Publisher Full Text
- 13.
Anfinsen CB:
Principles that govern the folding of protein chains.
Science.
1973; 181(4096): 223–230. PubMed Abstract
| Publisher Full Text
- 14.
Martí-Renom MA, Stuart AC, Fiser A, et al.:
Comparative protein structure modeling of genes and genomes.
Annu Rev Biophys Biomol Struct.
2000; 29: 291–325. PubMed Abstract
| Publisher Full Text
- 15.
Kaczanowski S, Zielenkiewicz P:
Why similar protein sequences encode similar three-dimensional structures?
Theor Chem Acc.
2009; 125(3–6): 643–50. Publisher Full Text
- 16.
Mitchell M: in An Introduction to Genetic Algorithms. (Cambridge, MA: MIT Press). 1996. Reference Source
- 17.
Wang C, Lefkowitz EJ:
Genomic multiple sequence alignments: refinement using a genetic algorithm.
BMC Bioinformatics.
2005; 6: 200. PubMed Abstract
| Publisher Full Text
| Free Full Text
- 18.
Ahn N, Park S:
Finding an upper bound for the number of contacts in hydrophobic-hydrophilic protein structure prediction model.
J Comput Biol.
17(4): 647–56. PubMed Abstract
| Publisher Full Text
- 19.
Holland JH: in Adaptation in Natural and Artificial Systems. (Ann Arbor, MI: University of Michigan Press). 1975. Reference Source
- 20.
Brown MS:
A Species-Conserving Genetic Algorithm for Multimodal Optimization (Doctoral dissertation). Available from Dissertations and Theses database. (UMI No. 3433233). 2010. Reference Source
- 21.
Brown MS, Pelsoi MJ, Dirska H:
Dynamic-Radius Species-Conserving Genetic Algorithm for the Financial Forecasting of Dow Jones Index Stocks.
Machine Learning and Data Mining in Pattern Recognition. Ed. P. Perner (Berlin: Springer). 2013; 7988: 27–41. Publisher Full Text
- 22.
De Jong KA:
An analysis of the behavior of a class of genetic adaptive systems. (Doctoral dissertation, University of Michigan).
Diss Abstr Int.
1975; 36(10): 5140B. (University Microfilms No. 76–9381). Reference Source
- 23.
Ling Q, Wa G, Yang Z, et al.:
Crowding clustering genetic algorithm for multimodal function optimization.
Appl Soft Comput.
2008; 8(1): 88–95. Publisher Full Text
- 24.
Li JP, Balazs ME, Parks GT, et al.:
A species conserving genetic algorithm for multimodal function optimization.
Evol Comput.
2002; 10(3): 207–234. PubMed Abstract
| Publisher Full Text
- 25.
Glover F:
Tabu Search – Part I.
ORSA Journal on Computing.
1989; 1(3): 190–206. Publisher Full Text
- 26.
Bremermann HJ:
The Evolution of Intelligence: The Nervous System as a Model of its Environment. (Technical Report, No.1, Contract No. 477, Issue 17). Seattle WA: Department of Mathematics, University of Washington. 1958. Reference Source
- 27.
Huang C, Yang X, He Z:
Protein folding simulations of 2D HP model by the genetic algorithm based on optimal secondary structures.
Comput Biol Chem.
2010; 34(3): 137–142. PubMed Abstract
| Publisher Full Text
- 28.
Su SC, Lin CJ, Ting CK:
An effective hybrid of hill climbing and genetic algorithm for 2D triangular protein structure prediction.
Proteome Sci.
2011; 9(Suppl 1): S19. PubMed Abstract
| Publisher Full Text
| Free Full Text
- 29.
Jiang T, Cui Q, Shi G, et al.:
Protein folding simulations of the hydrophobic-hydrophilic model by combing tabu search with genetic algorithms.
J Chem Phys.
2003; 119(8) 4592–4596. Publisher Full Text
- 30.
Brown M, Bennett T, Coker JA:
DSGA and GA from ‘Niche Genetic Algorithms are better than traditional Genetic Algorithms for de novo Protein Folding’
Zenodo.
2014. Data Source


Comments on this article Comments (0)