Keywords
Bayesian belief networks, higher education, marine biology, rocky shore, predictive models
Bayesian belief networks, higher education, marine biology, rocky shore, predictive models
While there are considerable differences between students’ understanding and academic strengths worldwide, within much of the native English speaking world large proportions of students studying life science disciplines at higher education level have weaknesses with numeracy, and associated topics, such as statistics (Feser et al., 2013). In many cases, ‘fears’ of mathematics have arisen and continued throughout their schooling, however, avoidance of numeric topics is not possible in many life science disciplines, especially in subjects such as ecology, where statistics form an important part of any independent research (e.g. Chalmers & Parker, 1989).
Many case studies have demonstrated that quantitative skills in ecology can be better taught if taught in a subject context (i.e. analysing data the students have collected in field based studies – Bäumer, 1999; Nolan & Speed, 1999; Yilmaz, 1996). Despite this, many students remain unconfident of quantitative elements of their courses, and few have the confidence apply even simple mathematics outside the confines of a few simple statistical tests (Grainger, 2010; Tariq, 2002; Tariq, 2004).
A possible solution to increase quantitative skills and confidence in students is the use of Bayesian belief networks. In their simplest form, Bayesian belief networks are a method of formalising uncertainty or probability from a number of events (Grover, 2013). From an ecological community perspective, this could amount to the calculated probability of a species decreasing in abundance, but based on known increases in both food supply and predation risk (Hammond & Ellis, 2002; Stafford et al., 2013). However, traditional Bayesian belief networks do not cope well with reciprocal interactions (such as competition between two species), and revised methods using some aspects of Bayesian inference have been developed (Stafford R. and Gardner E. unpublished data). These revised methods also have a simple, user-friendly interface. They use Microsoft Excel as an interface, with a hidden VBA script performing the calculations. As such, the software used is familiar to the students, rather than complex modelling environments or coding platforms often used for predictive models.
Given the identified need for quantitative skills in graduates, and even in post-doctoral researchers (Grainger, 2010), the aim of this study was determine if it was possible to introduce predictive modelling to students at an early point in their education, and whether this predictive modelling would benefit student learning about ecology in general, rather than being seen as extra, and unnecessary, complexity in learning key concepts. To do this, we combined a field visit to a rocky shore, followed by an afternoon using a predictive belief network, initially based on their knowledge of the rocky shore. We quantified the success of the technique both through student questionnaires and through examining the solutions they provided to problems requiring the use of the predictive networks.
The study group consisted of 12 students enrolled on a foundation degree (UK level 4) in Marine Ecology. The students were based in an educational college normally specialising in further education (pre-18 years old), but with some higher education (university level or post-18 courses) offered. The marine ecology course formed part of the higher education provision.
Students were in their second week of university level education, and from mixed backgrounds (~1/3rd mature students - 3 or more years after finishing school, and 2/3rds recent school or college leavers), however, none had previously formally studied ecology or ecological interactions beyond that covered in a typical school syllabus (UK A-levels or equivalent).
The field teaching session took place at Osmington Mills in Dorset, UK in early October 2014. Teaching consisted of an introduction lecture to rocky shore ecology, particularly examining ideas relating to vertical distribution of organisms (zonation) and exploring why small scale spatial patterns may have occurred (i.e. patches of green algae on the high shore, patches of barnacles). This gave a comprehensive introduction to physical limitations on organisms, as well as biological interactions (particularly interspecific competition and tropic interactions). Specifically eight key organisms were identified (Fucoid algae – Fucus spp., green algae – Enteromorpha spp., coralline algae - Corallina officinalis, barnacles – Chthalamalus and Semibalanus, dogwhelks – Nucella lapillus, periwinkles – Littorina littorea, topshells – Osilinus lineatus, and limpets Patella spp.), and after a 90 min field lecture, students were told to look for these species and consider their ecological interactions with each other (the lecture had given the basic ‘role’ of each species – i.e. grazer, filter feeder, predator; but had not provided details of interactions between the species). These eight organisms were all common on the mid shore, and were the species incorporated in the predictive model.
The full details of the belief network model used are provided as appendices (Supplementary File 1), as well as in VBA code within the downloadable Microsoft Excel files (Supplementary File 2). It comprised three ‘worksheets’ in a Microsoft Excel ‘workbook’. One worksheet asked for an indication of which species were directly interacting (i.e. competitively, trophically, mutualistically), and simply followed a grid system whereby a species in a column on the grid is effected by a species in the row on the grid. This worksheet automatically updates a second worksheet, indicating where ‘probabilities’ of species interactions need to be filled in. The top table on this second worksheet asks for a number between 0 and 1 indicating the probability of a target species increasing, assuming the probability of the ‘causing’ species is increasing. Largely, once this table is completed, typically with 15–20 different interaction probabilities (depending on how many interactions are specified on the previous worksheet), the model is complete. However, it is possible to specify non-reciprocal relationships if desired (for example, the probability of barnacles increasing, given an increase in predatory dogwhelks could be low (e.g. p = 0.1). The spreadsheet would update automatically to indicate a decrease in barnacles, if dogwhelks increased would be the reciprocal of this (p = 0.9), although these values could be manually altered if preferred. In this case, no students altered the other probability values.
The final worksheet contained the ‘prior’ probabilities of species changes. In this case, two scenarios were given to predict community level changes. Firstly, increases in dogwhelks, and secondly increases in periwinkles. These were described in the manner of actual experiments conducted at Osmington Mills (manipulation experiments designed to increase the abundance of these species – data set provided as Dataset 1). In these belief networks, only a prior probability of directly affected species should be altered, with the remainder of probabilities for species increases or decreases remaining at 0.5 for both increase and decrease. In the specific task set, students were asked to consider interactions over a three to four week period, partly to compare with experimental data that was collected over this time frame, and partly to simplify bottom up relationships (starvation is likely to take much longer than this in typical intertidal molluscs). Equally, while slow growing seaweeds will be unlikely to exhibit growth and therefore increased percentage cover, rapid growing green algae will be able to increase in abundance (Lubchenco, 1978).
Pressing a ‘calculate’ button then runs the VBA code and calculates posterior probabilities, indicating the likelihood of species increasing or decreasing. Results were then discussed in small groups, and where errors were made, the reasons for these errors were discussed.
A marine management scenario was then conducted, using the same spreadsheet template and underlying VBA code. A scenario based upon common commercial fish and shellfish (cod, haddock, whiting, sole and scallops) as well as important biotic habitat types (sea fans) was given. This time, however, trawling effort and fisher income were two non-biological interactions (Supplementary File 3). Students were asked complete the network in the same way, just considering what species or service was effected by others, and then parameterising the network with probabilities, in the same manner as before. In this case, they were asked to explore options for enhancing sea fan populations, without reducing fisher income.
An anonymous questionnaire was provided to each student, asking how much they had learned about various topics during the day (from rocky shore ecology through to understanding probability and uncertainty – Figure 1; Supplementary File 4). In addition to ranking each on a 1–10 scale, they were asked to provide an answer as to where they thought they had learned most about the topic (either during the field lecture, or the afternoon computer session). Again, this was on a 1–10 scale, where 1 was only from the morning field session, 5 was equally from both sessions, and 10 was only from the afternoon session. The collection of these data from students was approved by the Science, Technology and Health ethics committee of Bournemouth University.
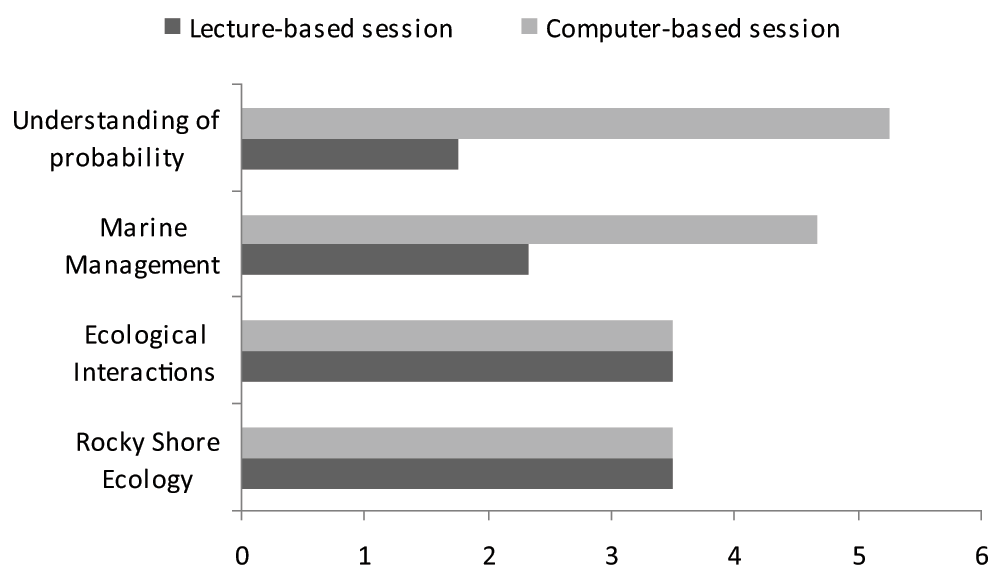
For each learning outcome examined, the median score was 7. Contribution was calculated using the equations C1 = M1*((10-M2)/10) and C2 = 10-C1, where C1 is the contribution made by field-based lecture, M1 is the median value of the students’ response to how much they learned about the topic (in this case, all equal to 7) and M2 is the median value of the students’ response to how much they learned from the different teaching methods (1 indicating fully from the field-based lecture and 10 indicating fully from the computer-based practical).
After a few questions regarding ‘what to do’, students (working in pairs) all produced sensible interaction links in the model. Typical initial questions involved which worksheets to fill in and a general reluctance to ‘break’ the software by doing something wrong. Filling in the probability values resulted in a minor problem of students not considering exactly what they were trying to predict (the probability of a species increasing, given that another species had increased – in this example, where most species interactions are negative, it may be easier to parameterise the model as probability of a species decreasing, given another had increased). Four of the six groups needed this re-explaining, however, once this was pointed out and otherwise independently, all groups managed to produce working belief network simulations which accurately predicted real results from previously conducted experiments. The only area where the majority of groups (five out of six) struggled was in complex, indirect interactions, which only occurred as a result of a tropic cascade. Most groups failed to predict the competitive interactions for space between seaweed species, despite correctly predicting the tropic relationships between grazers and green algae, but other than this one interaction, results were almost identical to the ‘expert’ parameterised networks created by the authors, and produced similar values to real experiments conducted on rocky shores (see Dataset 1 for real experimental data).
Student evaluations showed that students felt they had learned significant amounts about each topic, with median scores of 7 for all questions (with 25% and 75% quartiles between 6.5 and 9 in all cases). Knowledge of rocky shore ecology and ecological interactions was ranked as equally learned between the field and computer sessions (both with median values of 5) and knowledge of marine management and probability was greater in the computer based sessions (median scores of 7 and 8 respectively; Figure 1). In all cases, the full IQR was 2 or less indicating the majority of students scored in a similar manner (Dataset 2 provides the full data for each student – note, as the survey was optional, only 11 of the 12 students present completed this).
This study indicates that students (even at a very early stage in their academic journeys) are capable of understanding and applying quantitative techniques if presented in a logical and intuitive way. Furthermore, it demonstrates that their ability to learn these techniques can be integrated with development of ecological knowledge and understanding; acting not as a hindrance to, but as a compliment to the understanding of key concepts.
Much previous research has demonstrated that quantitative methods need to be taught in the context of the academic discipline (Bäumer, 1999; Nolan & Speed, 1999; Yilmaz, 1996). However, this approach can often seem rather forced to students, especially early in their studies. Examples are often based around simple data collecting exercises rather than conceptual issues or real research projects. Although students are capable of performing statistical tests, for example, on a specific dataset at the time, they find it difficult to remember and transfer the knowledge to a novel situation (Chance, 2002). However, embedding more quantitative elements regularly to courses to enhance learning of key concepts may result in less fear being associated with dealing with numbers, and a greater ability to synthesise more quantitative information such as inferential statistics when required.
The role of technology in education is becoming a prominent issue, with a number of case studies demonstrating how it can be useful in the classroom and even during field work (France & Welsh, 2012; Webb & Stafford, 2013; Welsh & France, 2012). Simulations have also been used to teach complex ecological concepts such as experimental design in place of (or in addition to) field or laboratory based studies (Stafford et al., 2010). With on-going improvements to technology (e.g. development of specific apps for tablet computers), it may be possible to use spreadsheet models such as this directly in the field. An advantage of such an approach would be that the simulation app could be combined with field guides and information on the species being studied, potentially allowing a more fully immersive learning experience.
The simplicity of use of belief networks, especially when combined with a familiar user interface, was clearly demonstrated here, with students being able to make, parameterise and run simulations of ecological systems and coupled socio-ecological systems. These results add further weight to the intuitiveness of the approach. Combined with uncertainty in detailed knowledge of many marine ecosystems (in terms of exact population sizes, recruitment and species interactions - Hilborn & Walters, 1992; Magnusson, 1995; Pope, 1991), and the need to adhere to what could be perceived as ‘crude’ policy measures (e.g. no decrease in the population size of a certain species – DEFRA, 2012), models such as these used in this study would fit well with the demands and requirements of policy makers, providing sufficient detail for achieving policy goals with limited data and in an intuitive manner.
F1000Research: Dataset 1. Data from manipulative experiment to assess community effects of dogwhelk manipulation (addition of 10 dogwhelks to each of 5 × ~1.5 × 1.5 × 1.5 m boulders) or periwinkle manipulation (addition of 10 periwinkles to 5 different, but similar sized boulders)., 10.5256/f1000research.5981.d41189 (Stafford & Williams, 2014a).
F1000Research: Dataset 2. Raw data values of student responses to surveys, 10.5256/f1000research.5981.d41190 (Stafford & Williams, 2014b).
RS wrote the code for the Bayesian belief model. RS and RLW both conceived the study, conducted the taught sessions and collected, analysed the results and contributed to writing the paper. Both authors have agreed the content of the final draft of the manuscript.
Supplementary File 1: Mathematical details and description of the belief network model.
Click here to access the data.
Supplementary File 2: Microsoft Excel file (with VBA script and macros) realising the belief network model for the rocky shore scenario.
The file is parameterised as per authors’ values, but is fully editable to allow students to alter these.
Click here to access the data.
Supplementary File 3: Microsoft Excel file (with VBA script and macros) realising the belief network model for the marine management scenario.
The file is parameterised as per authors’ values, but is fully editable to allow students to alter these.
Click here to access the data.
Supplementary File 4: Copy of survey provided to students to determine what they considered they learned, and whether they learned it from field lectures or computer based practical classes.
Note – survey was explained orally to students before completing it.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Competing Interests: No competing interests were disclosed.
References
1. Benn R: Discourse, social justice and the learning of mathematics. Studies in the Education of Adults. 2001; 24: 191-198Competing Interests: No competing interests were disclosed.
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 1 22 Dec 14 |
read | read |
Click here to access the data.
Spreadsheet data files may not format correctly if your computer is using different default delimiters (symbols used to separate values into separate cells) - a spreadsheet created in one region is sometimes misinterpreted by computers in other regions. You can change the regional settings on your computer so that the spreadsheet can be interpreted correctly.
Click here to access the data.
Spreadsheet data files may not format correctly if your computer is using different default delimiters (symbols used to separate values into separate cells) - a spreadsheet created in one region is sometimes misinterpreted by computers in other regions. You can change the regional settings on your computer so that the spreadsheet can be interpreted correctly.
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)