Keywords
methaphase chromosome, centromere detection, algorithm
This article is included in the Machine learning: life sciences collection.
methaphase chromosome, centromere detection, algorithm
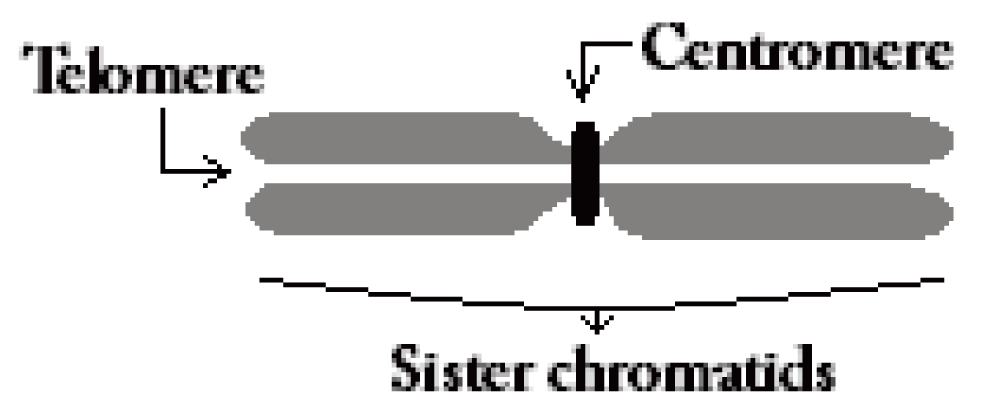
The centromere of a human chromosome (Figure 1) is the primary constriction to which the spindle fiber is attached during the cell division cycle (mitosis). The detection of this salient point is the key to calculating the centromere index which can lead to the type and the number of a given chromosome. The reliable detection of the centromere by image analysis techniques is challenging due to the high morphological variations of chromosomes on microscope slides. This variation is caused by various cell preparation and staining methods along with other factors that occur during mitosis. Irregular boundaries and large variations in chromosome morphology can cause a detection algorithm to miss the constriction, especially in high resolution chromosomes. Premature sister chromatid separation can also pose a significant challenge, since the degree of separation can vary from cell to cell, and even among chromosomes in the same cell. In such cases, the width constriction can be missed by image processing algorithms, and can result in incorrect localization of a centromere on one of the sister chromatids.
From an image analysis perspective, the high morphological variations in human chromosomes, due to their non rigid nature, pose a significant challenge. Cell preparation and staining techniques also vary among the laboratories. The end results obtained from clinical cytogenetic vs. reference biodosimetry laboratories can produce chromosome images that differ significantly in their appearance. As an example, chromosomes that were DAPI (4’,6-diamidino-2-phenylindole) stained shows different intensity features and boundary characteristics from chromosomes subjected only to Giemsa staining. Additionally, the stage of metaphase in which the cells were arrested along with environmental factors such as humidity during slide preparation can dictate the shape characteristics of individual cells and introduce a large variance to the data set. Furthermore, in some preparation methods, the cells are denatured, causing the detected chromosome boundary to be erratic. These same factors can also dictate the amount of premature sister chromatid separation in some of the cells. Effective algorithms for centromere detection need to be able to handle the high degree of shape variability present in different chromosomes, while correcting for artifacts such as premature sister chromatid separation. Figure 2 illustrates a sample set of shapes of chromosomes in the data set and their high morphological variations.

Depicts various degrees of sister chromatid separation present in some Giemsa stained chromosome images (Figure 2(a)–(c)) as well as some longer chromosomes characteristics of those prepared at a clinical cytogenetic laboratory (Figure 2(d)–(f)).
This research forms an essential component of detecting dicentric chromosomes (possessing two centromeres) which is used as a diagnostic test of radiation exposures in cytogenetic biodosimetry. The ability of the proposed algorithm to handle high degrees of morphological variation and also to detect and correct for the artifact created by premature sister chromatid separation in cell images is also critical to detecting dicentric chromosomal abnormalities.
Numerous computer algorithms have been proposed over time for chromosome analysis ranging from metaphase finding1, karyotype analysis2 to centromere and dicentric detection3,4. These methods are either constrained by the protocol used for staining the cell image or by the morphology of the chromosome. We have previously proposed an algorithm to locate the centromere by calculating a centerline with no spurious branches irrespective of boundary irregularities or the morphology of the chromosome5. This was later improved by using a Laplacian-based width-profile generation algorithm that integrates intensity measurements in a weighting scheme, biases the thickness measurement by tracing vectors across regions of homogeneous intensity6. Mohammad proposed an approach where he used our previous approach to derive the centerline and then used a curvature measure to localize the centromere location instead of the width measurements7. Another interesting approach by Jahani and Setarehdan involves artificially straightening chromosomes prior to creating the trellis structure using the centerline derived through morphological thinning8. Yet all these methods, including our previous approach, work well only with smooth object boundaries. The absence of a smooth boundary will directly affect the centerline and thus make the feature calculations noisy. Furthermore, the accuracy of all these methods is adversely impacted by sister chromatid separation. Although a commercial system exists for detecting dicentric chromosomes, it is semi-automatic and requires manual review of cells9. Furthermore, no published accuracy figures for detection of centromeres exist for this system. We propose a candidate based centromere localization algorithm capable of processing highly bent chromosomes prepared with a variety of staining techniques. This method can also detect and correct for artifacts introduced by premature sister chromatid separation.
To address image processing artifacts arising from sister chromatid separation, the proposed algorithm utilizes a new contour partitioning technique which identifies the telomere regions. This partitioning technique evaluates various combinations of salient points along the chromosome boundary by using machine learning together with a specially designed set of features. The partitioned contour is then used to generate a set of centromere candidates using local minima of the width profile. These centromere candidates are then classified using machine learning with a second set of features which incorporates contour shape as well as intensity information. This paper also introduces the Candidate-Based Centromere Confidence (CBCC) metric, which we use as an indicator of confidence of the detected location of the centromere. This metric is used in tests of the algorithm on a larger data set of chromosomes, with the aim of validating the performance of the algorithm.
The following section describes the proposed algorithm in detail. In section we show how this algorithm performed with a large data set and in section we comment on the performance and how it compares with other methods.
This section describes the proposed candidate based centromere detection algorithm in detail. This method can be functionally divided into the following steps for clarity,
1. Segmentation & centerline extraction
2. Contour partitioning & correcting for sister chromatid separation
3. Candidate point generation & metaphase centromere detection
Of these, step 1 was performed using algorithms that were published by us previously5,6. A brief description of this is included below for improved readability.
The chromosome database was created by manually selecting individual chromosomes that are well separated. During this process, images of cells with incomplete chromosome complements and those with higher densities of overlapping or touching chromosomes were discarded using a content-based classification procedure as described by others10. We have also developed Automated Dicentric Chromosome Identifier (ADCI) software which can automatically select individual chromosomes11. However, it was not used in this study.
Pre-processing steps for each chromosome image include application of a median filter followed by intensity normalization. The chromosome is then tresholded using Otsu’s method and the contour of that binary object is used as the starting point for Gradient Vector Flow (GVF) active contours. The use of GVF active contour algorithm produces a contour that is smooth and that converges to boundary concavities12.
In order to calculate the width profile of the chromosome using the thickness measuring algorithm, the chromosome contour is divided longitudinally into two approximately symmetric segments. We used Discrete Curve Evolution (DCE) based skeletal pruning5 to obtain an accurate centerline. DCE is a polygon evolution algorithm which evolves through vertex deletion based on a relevance measurement13. Using DCE, the chromosome boundary is reduced to the smallest possible polygon (a triangle). The shortest branch of the resulting skeleton is pruned to yield two points which belongs to the two ends (telomeres) and are used to obtain the centerline through the chromosome. These are called anchor points and denoted by EP.
Throughout this paper, we use the supercript P to refer to various point sets on the chromosome object contour C ∈ ℝ2. This set of points is used for contour partitioning in the next section.
Sister chromatid separation in chromosomes is an integral process that occurs during the metaphase stage of mitosis. Depending on the stage of mitosis at which the cells were arrested, varying degrees of sister chromatid separation may be evident. Furthermore long exposure to colcemid, a chemical agent which is used mainly as a preparatory chemical in biodosimetry studies to maximize the number of metaphase cells, can cause or exacerbate this condition and produce sister chromatid separation. It is important that the algorithm and associated software be able to analyze chromosomes with sister chromatid separation.
Accurate partitioning of the telomere region is necessary to identify evidence of sister chromatid separation and therefore correct for any such artifact as well as to split the contour into two segments accurately. Curvature of the contour is one of the most commonly used features for detecting salient points that can be used for partitioning14. An important requirement is that the location of these salient points needs to be highly repeatable under varying levels of object boundary noise. The DCE method described in the previous section was used again to provide a set of initial salient points on the contour of the chromosome outline. This is because this method performs well with boundaries regardless of whether they are smooth or not, yielding repeatable results15. The ability to terminate the process of DCE shape evolution at a given number of vertices further lends to its applicability. It was empirically established that a termination at 6 points would ensure that the required telomere end points will be retained within the set of candidate salient points. Two of those 6 points will include the anchor points, EP obtained in the previous step (section). Contour partitioning is performed by selecting the best 4 point combination (including the two anchor points) that represents all the telomere end points.
The approach for selecting the optimal contour partitioning point combination occurs in two stages. Initially, a SVM classifier using features (described below) was trained to detect and label preferred combinations from the given 12 possible combinations for each chromosome. At this stage, all the combinations across the data set are used as a pool of candidates to train the classifier. Then, the signed Euclidian distance from the separating hyperplane (say ρ) is computed for each of the candidates for a given chromosome, considering only the combinations of that chromosome. This process ranks all the candidates according to the likelihood they are a preferred candidate. Unlike traditional rule-based ranking algorithms, this approach requires very little high level knowledge of the desirable characteristics. The positioning of the separating hyperplane encapsulates this high level information through user-specified ground truth. The highest-ranked candidate is selected as the best combination of contour partitions for the given chromosome. The formal description of this procedure follows.
Let Φh be the curvature value at candidate point h and S ∈ ℝ2 be the skeleton of the chromosome with 6 DCE point stop criteria. We now define the following set of points (see Figure 3),
DP (⊂ C) is the set of six DCE vertices.
EP is the set of two anchor points
SP = DP – EP constitutes of all the points in DP except the anchor points (EP). These are the four telomere end-point candidates.
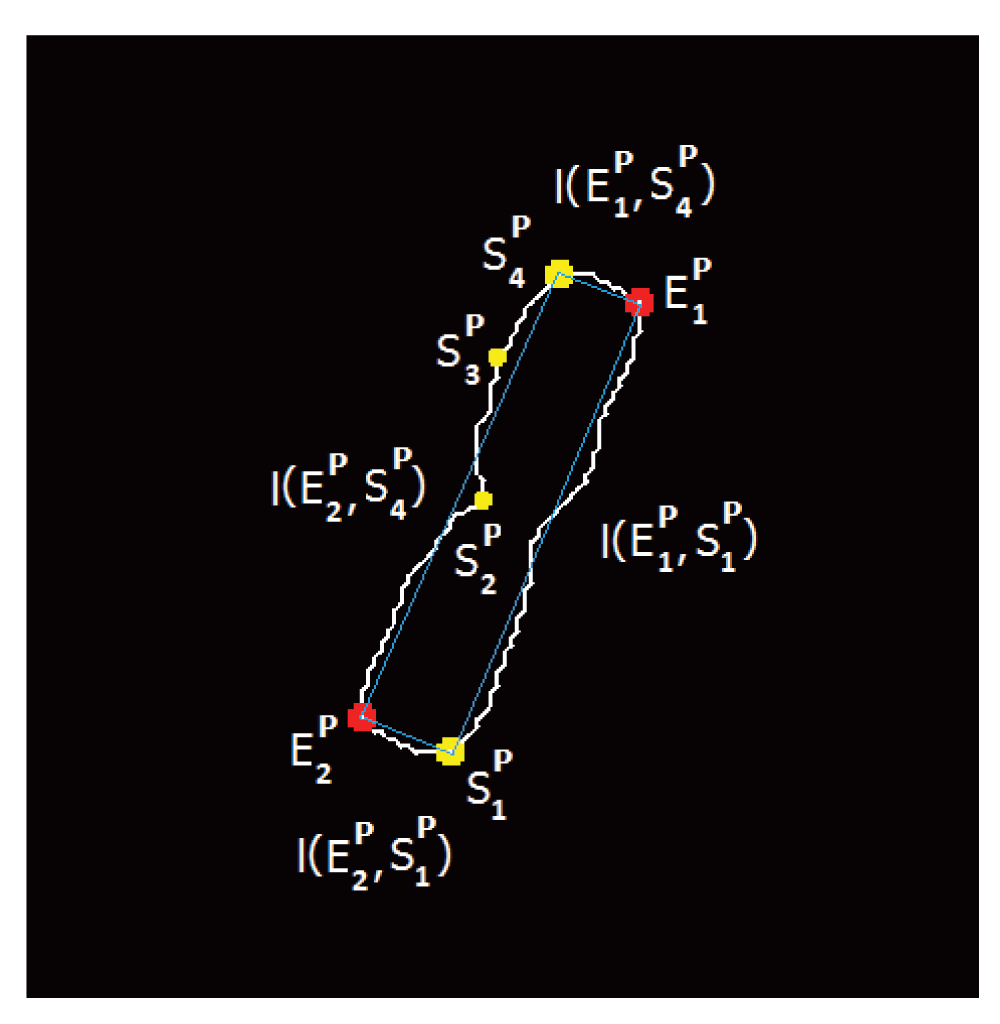
The (blue) line connects the set of points constituting the combination considered in this instance.
Then the family of sets TP for all possible combinations with the sets EP and SP would contain,
Figure 3 illustrates one such combination where the selected (connected by the blue line segments) combination for the contour partitioning points are given by .
In order to identify the best possible combination for contour partitioning, we have used a SVM classifier trained with the 11 different features () indicated below. Features and provide an indication to the saliency of the candidate point with respect to the skeletonization process. Features to are three normalized features which capture the positioning of each candidate in the given combination. and represent the shape or the morphology of the chromosome of interest (same values for all 12 combinations). The rationale behind the inclusion of these features is that they account for morphological variations across the cell images in the data set. and represent the curvature of the candidate points as well as the concavity/convexity of those locations. The features and are two Euclidean distance-based features which capture the proportion of each telomere region in the combination to the perimeter of the rectangle made by connecting the 4 candidate points. During our investigation, we observed a significant improvement of the accuracy of classification by the inclusion of these two features.
Let d (p, q) denote the Euclidean distance between the points p and q. Similarly let l (p, q) represent the length of the curve between p and q, which are points from the set DP. Then, for each contour partitioning combination in TP given by (where i and j are integer values such that 1 ≤ i, j ≤ 4 and i ≠ j), two main length measurement ratios (r1 and r2) are used for both calculating length based features, as well as for normalizing these features. r1 = yields the chromosome width/length with respect to the anchor point for the given contour partitioning combination (refer Figure 3). Similarly r2 = is calculated with respect to the anchor point . Then, the set of features Fs for each contour partitioning combination is defined as follows,
1. = 1 if the point belongs to a skeletal end point ( ∈ (S ∩ C)). Otherwise, = 0.
2. = 1 if the point belongs to a skeletal end point ( ∈ (S ∩ C)). Otherwise, = 0.
3. where 0 < < 1. This calculates the chromosome width/length ratio for each anchor point and the difference between the two measures. Two similar fractions would result in a high value for the feature .
4. where 0 < < 1. This calculates the chromosome width/length ratio with respect to the first anchor point (). Except for smallest chromosomes at the highest degree of metaphase condensation, the telomere axis is shorter than the longitudinal dimension of the chromosome. Therefore, a lower length ratio measurement is a higher value for the feature and is a desirable property.
5. where 0 < < 1. This is same as , but from the other anchor point, .
6. : ratio of length of the chromosome to area of the chromosome. This provides a measure of elongation of a chromosome.
7. : ratio value of perimeter of the chromosome to the area of the chromosome. This provides a measure of how noisy the object boundaries are.
8. : average of the curvature values Φh of the candidates. The curvature is an important measurement of the saliency of the candidate points.
9. : number of the negative curvature values (Φh < 0) of the candidates points ( and ). The telomere region end points are generally characterized by points with high convexity. The number of negative angles yield how concave the points of interest are.
10. where This feature calculates the normalized Euclidean distance between the anchor point and the candidate which makes up one telomere region.
11. where This is the same as feature , but calculated for the other anchor point.
A data set of 1400 chromosomes was collected from 40 metaphase cell images, which together yield 16,800 possible combinations of feature sets for contour partitioning. Three expert cytogeneticists marked the viable combinations of the salient points that capture the telomere regions for training the SVM classifier. The procedure involved training and testing with 2 fold cross validation (50% - train data, 50% - test data). We obtained accuracy, sensitivity and specificity values of 94%, 97% and 68%, respectively. The results demonstrate the ability of the feature set to effectively detect good combinations of candidate points for partitioning telomere regions. Although the low specificity suggests that some false positive telomeres were detected, this did not affect the accuracy of the contour partitioning, since the algorithm picks the optimal combination based on its rank rather than the classification label.
Correcting the deviation of the centerline for the effects of premature sister chromatid separation can be a difficult problem to solve. Once the best combination for the end points of the telomere region is selected, the telomere portions are segmented. Premature sister chromatid separation is detected from differences in the chromosome shape in the telomere region. This problem is solved with an algorithm that creates a set of features using functional approximation of the shape characteristics unique to premature sister chromatid separation and is derived from the coefficients calculated for each telomere6. A second SVM classifier is trained on these features to effectively detect these inherent shape variations of the sister chromatids. Once identified, correction is performed by extending the sample point (on the pruned centerline) to pass through the mid point of the partitioned telomere region. By getting the contour partitioned accurately, the correction process is significantly simplified.
In a previously described candidate-based approach, four candidate points were selected based on the minima values from the width profile16. However, this limits the number of possible locations that could be detected as the centromere location. Especially in cases where a high degree of sister chromatid separation is evident, limiting the search to just few candidates can have adverse effects. Therefore, we consider all possible local minima locations as candidates for the centromere location in a given chromosome, which are selected using the simple criteria given below.
Our notation p is used to refer to any other point(s), in general. Let the contour C be partitioned into two contour segments C1 (starting segment for tracing lines) and C2 (see Figure 4). Width profile was calculated using an intensity integrated Laplacian method6 which minimizes impact from irregular boundary of the chromosome segmentation by guiding the width profile trace lines to be contained within chromosome bands, which are regions with similar intensities. The width measurement of the normalized width profile at the discrete index λ (W (λ)) is obtained using the trace line which connects the contour points and from the two contours C1 and C2. Then, the set of candidate points for the centromere location pC (which stores the indices λ), where the local minima conditions of W(λ – 1) < W(λ) < W(λ + 1) and W(λ – 2) < W(λ) < W(λ + 2) are fulfilled for all valid locations λ of the width profile. In cases where the above condition failed to secure any candidates (mainly on extremely short chromosomes), the global minima was selected as the only candidate. Next, the following two sets of indices are created to correspond with each given element pC (α) of pC,
pmL(α) = W(β) where W(β) > W(γ), ∀γ < pC(α). Here pmL(α) stores the index of the global maxima for the portion (referred to as a regional maxima, henceforth) of the width profile prior to the candidate minima index pC(α).
pmR(α) = W(β) where W(β) > W(γ), ∀γ > pC(α). Similarly, pmR(α) stores the index of the global maxima for the portion of the width profile after the candidate minima index pC (α).
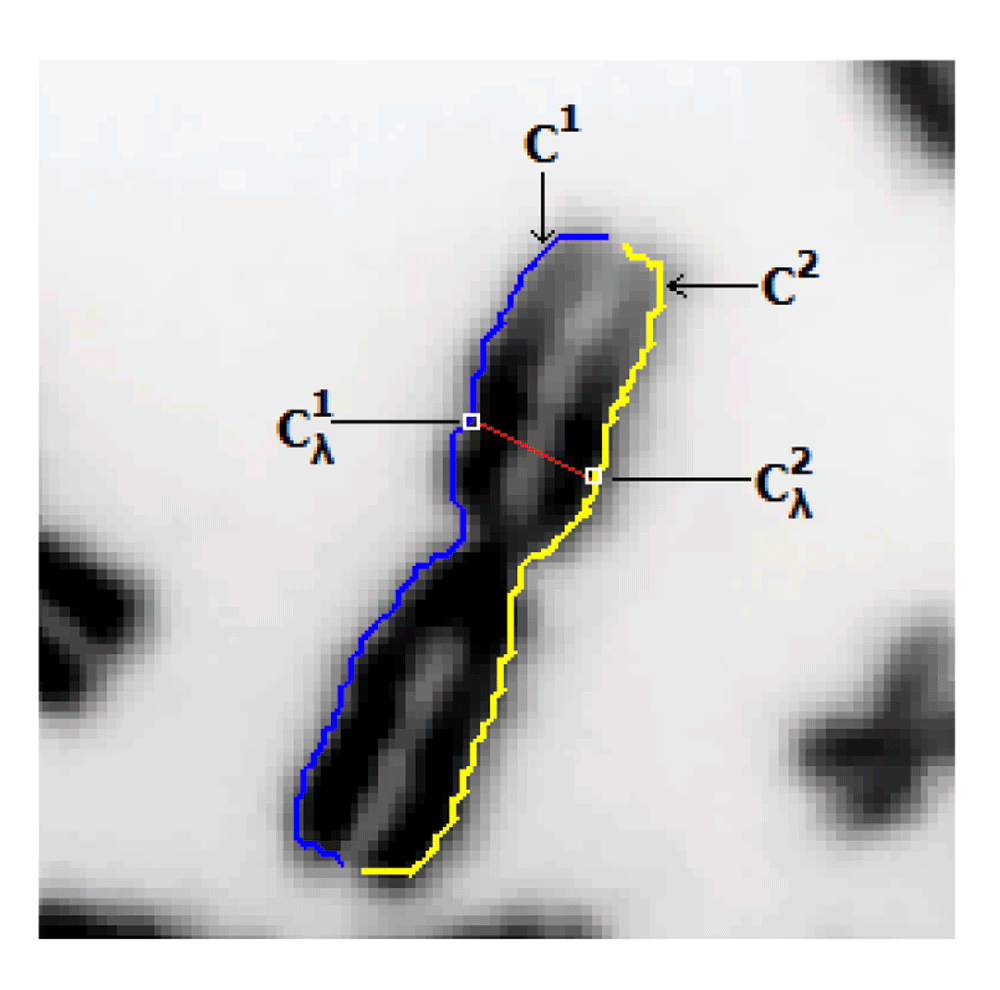
The width trace line, in red, connects the points and of the two contour segments.
Once the centromere candidate points pC and their corresponding maxima points pmL and pmR are calculated, the set of features Fc are calculated as given below. A set of 11 features – are proposed to train the third SVM classifier which will then be used to calculate the best candidate for a centromere location in a given chromosome. Features to provide an insight on the significance of the candidate point with respect to the general width profile distribution. The normalized width profile value itself is embedded in features and where the latter scales the minima based on the average value of the width profile. Features and capture the contour curvature values that are intrinsic to the constriction at the centromere location. Features , and include distance measures which indicate the positioning of the candidate point with respect to the chromosome as well as to the width profile shape. Finally the feature records the staining method used in the cell preparation. This gives the classifier a crucial piece of information that is then used to accommodate for specific shape features that may be the result of the particular laboratory procedure used to prepare and stain the sample.
Let i be a candidate member number assigned among the pool of centromere candidates. Also, let d(1, i) be the Euclidean distance along the midpoints of the width profile trace lines (centerline) from a telomere to the candidate point, and L be the total length of the chromosome. In the following description, represents the absolute value,
1. This feature calculates the absolute width profile difference between the candidate and the regional maxima prior to the candidate point on the width profile.
2. This feature calculates the absolute width profile difference between the candidate and the regional maxima beyond the candidate point on the width profile.
3. = + which calculates the combined width profile difference created by the candidate point.
4. = W(pC (i)). This captures the value of the width profile (0 ≤ ≤ 1) at the candidate point location.
5. is the local curvature value at the contour point which corresponds to the current centromere candidate location (where λ = pC (i)).
6. is the local curvature value at the contour point which corresponds to the current centromere candidate location (where λ = pC (i)).
7. = min (d(1, i), L – d(1, i))/L. Gives a measure where the candidate is located with respect to the chromosome as a fractional measure (0 ≤ ≤ 0.5).
8. = W(pC (i))/ , where is the average of the width profile of the chromosome. This includes the significance of the candidate point minima with respect to the average width of the given chromosome.
9. = d(pmL(i), pC (i))/L. This gives the distance between the candidate point location and the regional maxima value prior to the candidate point, normalized by the total length of the chromosome.
10. = d(pC (i), pmR(i))/L. This gives the distance between the candidate point location and the regional maxima value beyond the candidate point, normalized by the total length of the chromosome.
1. is a Boolean feature used to indicate the staining process used during cell preparation. A value of ‘0’ would indicate the use of DAPI chromosome staining while ‘1’ would indicate a Giemsa-stained cell.
The detection of the centromere location assumes that each chromosome at least contains one centromere location within the chromosome. This is a reasonable assumption, since the centromere region is an integral part of chromosome anatomy which is normally retained in cell division, with the exception of acentric fragments produced by excessive radiation exposure, or rarely in congenital and neoplastic conditions. This assumption transforms the detection problem into a ranking problem in which we pick the best candidate from a pool of candidates. Therefore, this enables the same approach to be adopted that was utilized for the contour partitioning algorithm (section); i.e. in which the distance from the separating hyperplane (ρ) represents a measure of goodness-of-fit for a given candidate. This metric reduces the multidimensional feature space to a single dimension, which inherently reduces the complexity of the ranking procedure for the candidate locations. Since the large margin binary classifier (SVM) orients the separating hyperplane in the feature space, the 1D distance metric directly relates to how well a given candidate fits into the general characteristics of a given class label. A detailed introduction to the candidate-based centromere confidence metric is provided in the following section.
Although existing measures of accuracy can establish performance of machine learning applications, these measures do not provide information on the reliability of the method. We developed a confidence metric for accurate detection of centromeres, which will be essential for assessment and ultimately adoption of this approach for diagnosis. We developed a Candidate Based Centromere Confidence metric (CBCC) to assess detection of a centromere location relative to alternatives. This value is obtained using the feature space derived via the classifier and the distance metric ρ. For a given set of candidate points, i.e. centromeres, of a chromosome pC, the goodness-of-fit (GF) of the optimal candidate point () is obtained by calculating , which is the average distance of all the remaining candidate points. In the ideal situation, the optimal candidate and the other candidates as support vectors for the classifier reside on opposite faces of the separating hyperplane (see Figure 5). Therefore the optimal candidate distance () is ≈ 1, while the average of the remaining candidate distances () is ≈ –1. The GF value is truncated at unity, since exceeding this value does not add additional information to the metric.
The complete data set used for developing and testing the algorithm discussed in this paper consists of 40 metaphase cell images, of which 38 consisted from irradiated samples obtained from cytogenetic biodosimetry laboratories and two were non-irradiated cells from a clinical cytogenetic laboratory. The chromosome data set comprised images of 18 Giemsa-stained cells and 22 DAPI-stained cells. The cells with minimal touching and overlapping chromosomes (a good metaphase spread) were manually selected from a pool of 1068 cell images for this experiment. Then 40 cell images were selected to represent both DAPI (55%) and Giemsa (45%) staining methods. During ground truth evaluation, the expert was presented with the set of centromere candidates generated by the algorithm and was asked to select the candidate that closely represented the correct chromosomal location, while explicitly marking other candidates as non-centromeres. In cases where all the candidates suggested by the algorithm were incorrect, all the positions were designated as negative candidates. Intra-observer variability between experts (ground truth) was minimal, as the laboratory directors differed in assessment in a single centromere out of > 500 chromosomes analyzed by both. The 1400 chromosome data set yielded 7058 centromere candidates. A randomly selected portion comprising 50% of this data set along with the corresponding ground truth centromere assignments were used for training a support vector machine for centromere localization. Next, the accuracy of centromere localization was calculated and is provided in Table 1. This provides a breakdown of the detection accuracy of the algorithm based on the presence or the absence of sister chromatid separation in the cell images for each staining method.
Table 2 depicts CBCC values for accurately detected chromosomes as opposed to inaccurately detected chromosomes. It also includes a third category termed "All nonviable candidate chromosomes" (a subset of the inaccurate centromere detection category), where none of the candidates for a given chromosome were marked as capturing the true centromere of the chromosome.
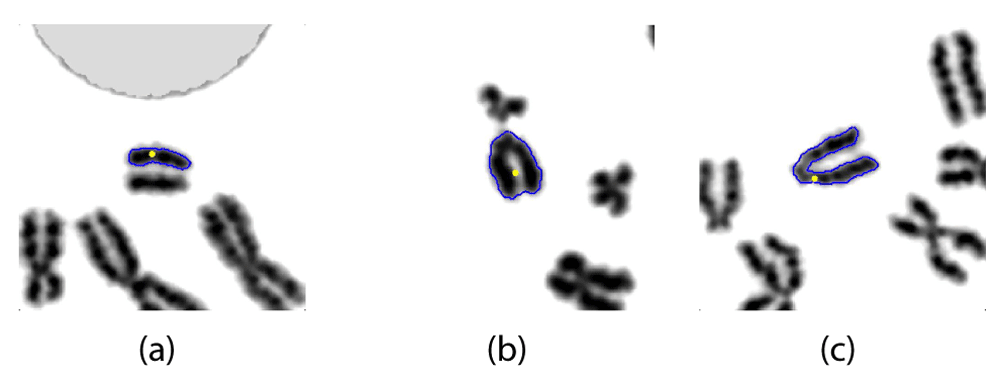
Figure 6 shows a representative sample of cases where the centromere was accurately localized. These cases include chromosomes with and without sister chromatid separation. The method does not detect centromere locations in all cases, some of which are impacted by the algorithm’s inability to fully correct for the adverse effects of sister chromatid separation (depicted in Figure 7).
| Chromosome morphology | Number of chromosomes | Number of accurate detections | Detection accuracy |
|---|---|---|---|
| DAPI without sc. sep. | 114 | 104 | 91.2% |
| DAPI with sc. sep. | 587 | 517 | 88.1% |
| Giemsa with sc. sep. | 699 | 599 | 85.6% |
| Category | Chromosomes | Mean (μ) | Std. Dev (σ) |
|---|---|---|---|
| Accurate detection | 1220 | 0.7861 | 0.3000 |
| Inaccurate detection | 180 | 0.3799 | 0.3293 |
| Nonviable candidates | 124 | 0.2696 | 0.2457 |

Figure 6(a) is a result from DAPI stained chromosomes while Figure 6(b)–(f) are results from Giemsa stained chromosomes. These results reported CBCC measures of (a) 1.000, (b) 1.000, (c) 1.000, (d) 0.995, (e) 1.000, (f) 0.661, respectively.
The detected centromere location (selected candidate) is depicted by a yellow dot while the segmented outline is drawn in blue. These results reported CBCC measures of (a) 0.368, (b) 0.066, (c) 0.655, respectively.
The candidate based approach for centromere detection used a trained SVM classifier based on half of the input chromosomes. The accuracy of the method was then tested using the remaining 50% of the data set (2 fold cross validation); accuracy, sensitivity and specificity were 92%, 96% and 72%, respectively. Two fold cross validation was used instead of other methods such as the leave-one-out method, since it yields a reasonable estimation of the accuracy with a low computational cost. The higher sensitivity of this algorithm relative to our previous efforts5 can be attributed to improvements in the performance of the classifier on both typical and sister chromatid separated chromosomes. The lower specificity is predominantly related to lower confidence detection by the integrated intensity Laplacian algorithm of centromeres in acrocentric chromosomes, in which the centromeric constriction is not readily apparent because of its close proximity to one of the telomeres.
The objective of this study was to accurately detect the preferred centromere location (points) for each chromosome, even though the SVM produces a set of candidate points that can each be classified separately. All candidates in each chromosome were analyzed separately and the best candidate from this set was selected based on the distance metric value (ρ) of which the results are produced in Table 1. Upon testing, the algorithm accurately located a correct centromere location in 1220 of 1400 chromosomes (87%). This is a clear improvement on our previous attempt with an accuracy of 81% (detected centromere within 5 pixels of the known location) which used a much smaller dataset of 226 chromosomes. It is notable that 124 of the 180 chromosomes that were missed were instances of non-viable candidate chromosomes. Some of these were caused by segmentation of acrocentric chromosomes, where the lighter intensity of the short-arm satellite regions were segmented out, while others were primarily the result of an extreme degree of sister chromatid separation, such that the pairs of telomeres from sister chromatids could not be unequivocally paired. The values in Table 1 further suggest a slight reduction in accuracy for Giemsa-stained images, which contained significantly higher levels of sister chromatid separation and noisy chromosome boundaries.
The proposed method performed centromere localization accurately for chromosomes with high morphological variations (see Figure 6). From a machine learning point of view, Figure 6(a)–(c) are fairly straightforward centromere localizations. The CBCC values for all three cases were 1.000 which was truncated from an even higher value. This further validates the CBCC metric, indicating that the selected candidate is preferable over the other candidates in the same chromosome. It is important to notice that the boundary conditions at the telomeric region of Figure 6(c) is similar in appearance to those in Figure 3 or Figure 4. However, with further separation and intensity fading between the two sister chromatid arms, the segmentation algorithm could converge to a concave morphology in the telomere region that links the sister chromatids. Figure 6(e) represents such an instance where sister chromatid separation has had a significant effect on the chromosome segmentation. However, as a result of correcting for this effect, the algorithm has localized the centromere accurately with a CBCC value of 1.000. The chromosome segmentation in Figure 6(d) demonstrates evidence of extensive sister chromatid separation and therefore the CBCC value is at 0.995, which still is a high value for the data set. The Figure 6(f) represents a chromosome which is highly bent and also presents with significant sister chromatid separation. Nevertheless, the algorithm was capable of localizing an accurate centromere location though the CBCC value was low (0.661), which indicates a less than ideal separation among the centromere candidates.
Some of the shortcomings of the proposed method are represented in Figure 7. Most of these (86%) were observed to be cases where none of the candidates were deemed to contain the actual centromere. This was mainly due to segmentation problems and add to high levels of sister chromatid separation. Figure 7(b) depicts an example where the segmentation algorithm failed to capture the constriction in an acrocentric chromosome. The CBCC value in this example was as low as 0.066, which indicates that the algorithm selected a weak candidate for the centromere. Figure 7(a) demonstrates a case where extreme sister chromatid separation has caused the segmentation algorithm to treat each individual chromatid separately. This chromosome had a low CBCC value of 0.368, which is consistent with the acentric nature (morphological) of the fragment. Figure 7(c) shows another impact of extreme sister chromatid separation on an acrocentric chromosome, namely, the incorrect connection of the long arm of a pair of sister chromatids, leading to an apparent, bent chromosome, instead of detecting sister chromatid separation. The CBCC measure fails to distinguish this chromosome from a normal bent chromosome, but nevertheless yielded a relatively high value of 0.655.
Although not the focus of this study, we carried out a preliminary analysis of the capability of this algorithm to detect both centromeres in a set of dicentric chromosomes, which were present among an excess of normal single centromere chromomes, due to irradiation of some of the cytogenetic samples analyzed. The constriction at the second centromere is similar morphologically to the first centromere in these chromosomes, and therefore, it should be feasible that it be among the candidates found by the algorithm. We hypothesized that along with the optimal candidate, the second centromere was also expected to exhibit a short distance to the hyperplane and be well separated from the other candidates. These distances were compared for all centromere candidates, and probable dicentric chromosomes were identified by determining if the correct, ground truth centromeres were among the top four ranked candidates. The breakdown of the candidates which captured the second centromere location is given in Table 3, where 20 cases (out of 31) reported the second centromere location as the second highest ranked candidate location. Among the 31 dicentric chromosomes present in the data set, the first candidate (the selected centromere) was accurate in all instances. There were only two instances where the second centromere was not among the top four candidates. In both of these cases, the chromosomes exhibited a high degree of sister chromatid separation. Nevertheless, the proposed method provides a good framework for detecting dicentric chromosomes in radiation biodosimetry applications.
We have described a novel candidate-based centromere detection algorithm for analysis of metaphase cells prepared by different culturing and staining methods. The method performed with an 87% accuracy level when tested with a data set of 1400 chromosomes from a composite set of metaphase images. The algorithm was capable of correcting for the artifact created by premature sister chromatid separation. The majority of chromosomes with centromere constrictions were detected with very high sensitivity. We have also tested a promising extension of the centromere detection algorithm to accurately identify dicentric chromosomes for cytogenetic biodosimetry. Loss of specificity in both monocentric and dicentric chromosomes was the result of segmentation errors in acrocentric chromosomes, as well as in chromosomes with extreme degrees of sister chromatid separation.
The framework used for adding intensity into the Laplacian thickness measurement algorithm can be easily extended to include other features besides the calculation of chromosome width. Further investigation aimed at both improving centromere detection accuracy and applications of this algorithm to other detection problems is warranted. The Candidate Based Centromere Confidence (CBCC) was introduced as a measure for confidence in each centromere detection. However, this metric can be applied to any problem which requires a selection of a candidate from a pool of candidates. We suggest that the CBCC metric may be extensible to indicate the relative quality of a given cell image or of a set of meta-phase cells from the same patient. If successful, the CBCC metric may eventually limit the amount of time required to evaluate samples both prior to and during centromere detection.
ZENODO: Chromosome images used for "Centromere detection of human metaphase chromosome images using a candidate based method", DOI: 10.5281/zenodo.5649017.
ZENODO: Matlab code for "Centromere detection of human metaphase chromosome images using a candidate based method", doi: 10.5281/zenodo.5649318.
Source code license: GPL v3
Akila Subasinghe developed all the algorithms, performed manual selection of chromosomes from the data sets, performed all the tests and wrote the first draft of this paper. Jagath Samarabandu provided advice on selection of algorithms, proposed the key idea of using combinations of vertices for contour partitioning, helped select suitable features for classification and provided substantial amount of review, editing and incorporating reviewer feedback. Peter Rogan and Joan Knoll provided guidance in algorithm development, validation of results, and contributed to writing the paper. Ruth Wilkins and Farrah Flegal provided curated images of gamma irradiated metaphase cells and chromosomes.
None of the authors have any competing interests in any commercial entities or funding agencies mentioned in this article.
Supported by the Western Innovation Fund (University of Western Ontario), Natural Sciences and Engineering Research Council of Canada and the DART-DOSE CMCR (5U01AI091173-02 from the US Public Health Service), the Canada Research Chairs Secretariat and the Canada Foundation for Innovation.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Competing Interests: No competing interests were disclosed.
Competing Interests: No competing interests were disclosed.
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 1 01 Jul 16 |
read | read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)