<i>2-DOF robot modelling by SimMechanics and PD-FL integrated controller for position control and trajectory tracking</i>

Tian Soon Lee; Esmail Ali Alandoli; V Vijayakumar

doi:10.12688/f1000research.72912.2

Home Browse 2-DOF robot modelling by SimMechanics and PD-FL integrated controller...

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Revised

2-DOF robot modelling by SimMechanics and PD-FL integrated controller for position control and trajectory tracking

[version 2; peer review: 1 approved, 1 approved with reservations]

Tian Soon Lee ¹, Esmail Ali Alandoli¹, V Vijayakumar²

PUBLISHED 17 Nov 2021

Author details Author details

¹ Faculty of Engineering and Technology, Multimedia University, 75450 Ayer Keroh, Melaka, Malaysia
² Faculty of Computing and Informatics, Multimedia University, 63100 Cyberjaya, Selangor, Malaysia

Tian Soon Lee
Roles: Conceptualization, Formal Analysis, Funding Acquisition, Investigation, Methodology, Software, Supervision, Validation, Writing – Review & Editing

Esmail Ali Alandoli
Roles: Conceptualization, Formal Analysis, Investigation, Methodology, Software, Validation, Writing – Original Draft Preparation

V Vijayakumar
Roles: Conceptualization, Formal Analysis, Investigation, Methodology, Software, Supervision, Validation, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

This article is included in the Research Synergy Foundation gateway.

Abstract

Background Due to the high demand of robots to perform several industrial tasks, such as welding, machining, pick and place, position control in robotics has attracted high attention recently. Controllers’ improvement is also continuous specifically in terms of design simplicity and performance accuracy. This research plans to obtain the SimMechanics model of a two-degree of freedom (DOF) robot and to propose an integrated controller of a proportional–derivative (PD) controller and a fuzzy logic (FL) controller.
Methodology The SimMechanics model of the 2-DOF robot is obtained using MATLAB SimMechanics toolbox from a CAD assembly design of the 2-DOF robot. Then, the proposed PD-FL integrated controller is designed and simulated in MATLAB Simulink. The PD controller is widely used for its simplicity, but it doesn’t have a satisfactory performance in difficult tasks. Furthermore, the FL controller is also easy for design and implementation even by non-experts in control theory, but it has the disadvantage of long computational time for multi-input systems due to the increased fuzzy rules.
Results The FL controller is integrated with the PD controller for enhanced performance of the 2-DOF robot. The PD-FL integrated controller is developed and tested to control the 2-DOF robot for point-to-point position control and also tip trajectory tracking (TTT) such as triangular TTT and rhombic TTT.
Conclusion The PD-FL integrated controller demonstrates enhanced performance compared to the conventional PD controller in both point-to-point position control and TTT. Furthermore, the PD-FL integrated controller has the advantage of less fuzzy rules which helps to overcome the computational time issue of the FL controller.

Keywords

2-DOF robot, SimMechanics model, PD-FL integrated controller, position control, tip trajectory tracking.

Corresponding author: Tian Soon Lee

Competing interests: No competing interests were disclosed.

Grant information: This research was supported by Multimedia University through MMU GRA Scheme (MMUI/180265).
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2021 Lee TS et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Lee TS, Alandoli EA and Vijayakumar V. 2-DOF robot modelling by SimMechanics and PD-FL integrated controller for position control and trajectory tracking [version 2; peer review: 1 approved, 1 approved with reservations]. F1000Research 2021, 10:1045 (https://doi.org/10.12688/f1000research.72912.2) First published: 15 Oct 2021, 10:1045 (https://doi.org/10.12688/f1000research.72912.1) Latest published: 17 Nov 2021, 10:1045 (https://doi.org/10.12688/f1000research.72912.2)

Revised Amendments from Version 1

The major improvement in this version is the adding the velocity and the acceleration of the proposed PD-FL integrated controller for the point-to-point position control and also the tip trajectory tracking.

See the authors' detailed response to the review by Xuan Bien Duong

Introduction

There is a wide use of planar robots in industries to achieve several required tasks, such as welding, handling, machining, polishing, pick and place, etc. Meanwhile, there is a high demand of fast and precise position control for such robots in industries¹. A dynamic model is required for several types of controllers in order to obtain the optimal parameters of a controller for satisfactory performance. There are many mathematical modelling methods, such as the kinematics method², Newtonian method³, Lagrange’s equation^4,5, and Hamilton's principle⁶. However, mathematical modelling is difficult and requires long calculations especially for nonlinear systems; critical and deep discussion of mathematical modelling methods is given in reference⁷. A numerical modelling method was used to obtain SimMechanics models of robots using Simulink and Simscape toolboxes from CAD assemblies^8–10. SimMechanics models are easily obtained and can be simulated and controlled, so they are preferable.

A proportional–derivative (PD) controller was tuned using root locus^11,12 and manually tuned^13,14 for position control of such robots. The manual tuning method helps to dispense about the mathematical model of a system which one of its advantages. However, the PD controller is not perfect for nonlinear and complex systems. A 2-DOF robot was controlled by a proportional–integral–derivative controller (PID) due to its simple structure, but it is not easy to obtain optimal PID parameters to give a satisfactory performance¹⁵. The linear quadratic regulator (LQR) is an optimal classical control technique and was utilized to control a planar robot with the necessity of a system mathematical model in order to calculate the controller gain^16,17. The fuzzy logic controller (FLC) is a common control technique in robotics and has continuous increasing interest due to its robustness performance for nonlinear systems and does not require a mathematical model to tune its membership functions and rules¹⁸. FLC has the disadvantage of computational time due to the fuzzy rules explosion for controlling multi-input systems^19,20.

Neural network (NN) is an intelligent control technique and can be developed with simple knowledge of the system behavior without a need for a dynamic model which assists to avert the complexity of the mathematical modelling²¹. NN was used to control a 2-DOF robot in terms of links’ position²². However, NN require many hidden layers in its network to provide an accurate position control which needs long time for training²³. Sliding mode controller (SMC) is a robust controller and was employed for position control of a 2-DOF robot^24,25. However, sliding mode controller has the chattering issue which is a serious disadvantage^26,27. Integrated controllers which consist of more than on control technique were also used for position control of 2-DOF robots such as FLC-SMC^28,29, FLC-PID³⁰, and FLC-NN³¹. There are many other control techniques were critically discussed in the literature³².

Based on the discussed previous studies, the mathematical modelling of robots is a serious problem faces researchers and control engineers either the difficulty of mathematical operations or the challenge of obtaining accurate models. Therefore, the first objective is to obtain the SimMechanics model of the 2-DOF robot from the CAD assembly design via SimMechanics environment in MATLAB (RRID:SCR_001622); an open access alternative is GNU Octave (RRID:SCR_014398). The second objective is to design the PD-FL integrated controller to control the 2-DOF robot in terms of point-to-point position control of the links, triangular TTT and rhombic TTT. The remaining sections of this paper are as follows: section 2 describes the system and the SimMechanics model. Section 3 explains the proposed controller design. Section 4 presents the results and discussion. Section 5 is the conclusion.

System and the SimMechanics model

A schematic diagram of the 2-DOF robot is shown in Figure 1 which consists of two links with 50-cm length of each link and a 4.5 cm² cross-sectional area. The links’ material is aluminum with the density of 2.7 g/cm³. The movement of this robot is only on the horizontal plane. The tip position of the robot is computed based on Equation 1.

[\begin{matrix} P_{x} \\ P_{y} \end{matrix}] = [\begin{matrix} \cos θ_{1} \\ \sin θ_{1} \end{matrix} \begin{matrix} \cos (θ_{1} + θ_{2}) \\ s in (θ_{1} + θ_{2}) \end{matrix}] [\begin{matrix} L_{1} \\ L_{2} \end{matrix}] (1)

Figure 1. Schematic diagram of the 2-DOF robot.

The CAD assembly of the 2-DOF is designed as shown in Figure 2. The CAD assembly is used to generate the SimMechanics model of the 2-DOF robot. The SimMechanics model is obtained starting by building the CAD assembly design of the robot and export the CAD assembly and save it in the format of ‘XML’ file. Then, the assembly ‘XML’ file is imported to the MATLAB SimMechanics toolbox using the ‘smimport’ function. The steps of generation the SimMechanics model is explained in detail in Figure 3. The SimMechanics model of the 2-DOF robot is presented in Figure 4. The SimMechanics model was generated and used in previous research such as in reference 9 and reference 10.

Figure 2. CAD assembly of the 2-DOF robot.

Figure 3. Steps of SimMechanics model generation.

Figure 4. SimMechanics model of the 2-DOF robot.

Control design

The 2-DOF robot is controlled by the PD-FL integrated controller. The PD controller is selected due to its simplicity of design and it is widely used. The PD parameters can be easily tuned based on trial and error^13,14, Equation 2 shown the PD control transfer function. Two PD controllers are designed as the PD controller is single input single output. The parameters of the two PD controllers are manually tuned and the better performance is achieved by the parameters tabulated in Table 1.

Table 1. Parameters of PD controllers.

Controller	K_P	K_D
PD 1	5	4.5
PD 2	16.2	1.5

G_{C} = K_{P} + K_{D} s (2)

FL controller is an intelligence control technique that depends on expressing the system behaviour. FL uses errors as its input variables and assigns the input into partial degrees of membership functions (MFs)³³. The MF amplitude varies between 0 and 1. The fuzzy rules are expressed in the form of IF-THEN to describe the relation between inputs and outputs depended on the MFs. The MFs are designed and tuned in terms of range, numbers, and shape as shown in Figure 5 for the two inputs and outputs, they are described by “positive big” (PB), “positive medium” (PM), “positive small” (PS), “zero” (ZE), “negative big” (NB), “negative medium” (NM), and “negative small” (NS). Then, the fuzzy rules are tuned to describe the system errors depended on the MFs and to decide what fuzzy output should be, Table 2 describes the fuzzy rule-base. Table 2 shows the fuzzy rules reduction from 49 rules to 25 rules. The fuzzy rules reduction improves the computational time and simplifies the FL controller design.

Figure 5. Membership function of FL controller for the 2-DOF robot.

Table 2. Fuzzy rules of FL controller for the 2-DOF robot based on error 1 (e₁), error 2 (e₂), output 1 (u₁), and output 2 (u₂).

e₁	PB		PM		PS		ZE		NS		NM		NB
e₂	u₁	u₂	u₁	u₂	u₁	u₂	u₁	u₂	u₁	u₂	u₁	u₂	u₁	u₂
PB	PB	PM	PB	PM	PB	PM	ZE	PM	NS	PM	Non-effective
PM	PB	PS	PB	PS	ZE	PS	ZE	PS	NS	PS
PS	PB	PS	PB	PS	PB	PS	ZE	PS	NS	PS
ZE	PB	ZE	PB	ZE	PB	ZE	ZE	ZE	NS	ZE
NS	PB	NS	PB	NS	PB	NS	ZE	NS	NS	NS
NM	Non-effective
NB	Non-effective

The 2-DOF robot model and proposed PD-FL controller is shown in Figure 6. The outputs of the two PD controllers are the fuzzy inputs, and the fuzzy outputs are the robot inputs. The first PD controller controls link 1 and the second PD controller control link 2. The two PD controllers initially control the robot and minimize the errors, which do not reach NM and NB regions. Thus, there is no effectiveness of the fuzzy rules for NM and NB of errors which helps to minimize the fuzzy rules number from 49 to 25. This fuzzy rules’ reduction solves the issue of the computational time and also simplifies the FL controller design. The proposed PD-FL integrated controller

Figure 6. SimMechanics model with PD-FL integrated controller.

Results and discussion

This section presents and discusses the results of point-to-point position control and the TTT.

Point-to-point position control

The performance of the PD-FL integrated controller and the conventional PD controller is shown in Figure 7 for the first link of the 2-DOF robot by the blue line and the red line, respectively. The PD-FL integrated controller demonstrated great improvement in terms of “rise time” (T_r), “settling time” (T_s), “overshoot” (OS), and “steady state error” (e_ss) compared with the PD controller alone as analyzed in Table 3.

Figure 7. Point-to-point position control of link 1.

Table 3. Performance analysis for position control of link 1.

Controller	T_r (ms)	T_s (s)	OS %	e_ss (rad)
PD-FL	129.471	0.196	0.505	0.00
PD	153.907	1.732	9.341	0.00

The PD controller has better performance for link 2 than link 1 as shown in Figure 8, this is because link 2 is a load to link 1 which makes the control of link 2 easier than control link 1 for the PD controller. However, the PD-FL integrated controller has better performance than the PD controller for link 2 as it has shorter rise time (T_r) and settling time (T_s), also it has less overshoot as described in Table 4. Based on the results of point-to-point position control of the 2-DOF robot, it is obvious that the PD-FL integrated controller is better than the conventional PD controller as it has shorter rise time (T_r), shorter settling time (T_s), and less overshoot for link 1 and link 2. Figure 9 (a) shows the velocity and Figure 9 (b) shows the acceleration of the links during the point-to-point position control by the PD-FL integrated controller.

Figure 8. Point-to-point position control of link 2.

Figure 9.

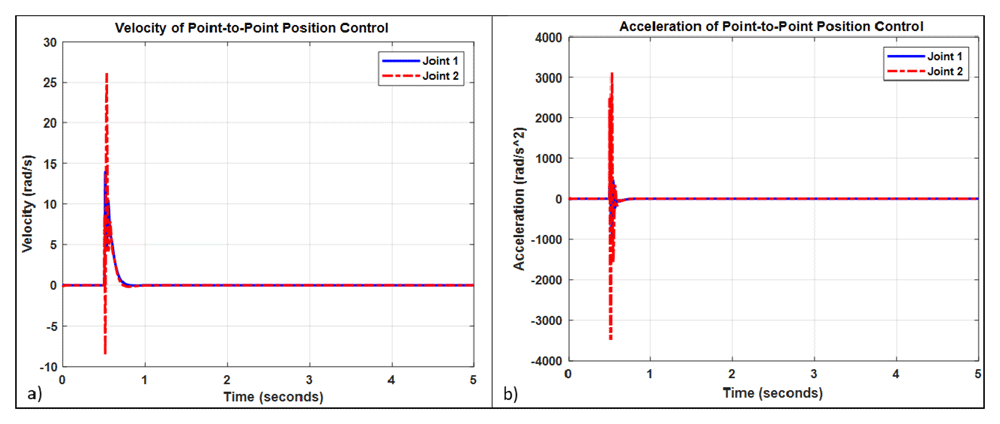
a) Velocity of the point-to-point position control, b) Acceleration of the point-to-point position control.

Table 4. Performance analysis for position control of link 2.

Controller	T_r (ms)	T_s (s)	OS %	e_ss (rad)
PD-FL	99.444	0.3011	2.577	0.00
PD	104.188	0.495	10.556	0.00

Tip trajectory tracking

The PD-FL integrated controller is tested for TTT of the 2-DOF robot for triangular TTT and rhombic TTT as follows.

Triangular tip trajectory tracking

The triangular TTT of the 2-DOF is shown in Figure 10 for the PD-FL controller and the PD controller, The triangular TTT starts and ends based on the following trajectory points (X,Y): (1.0,0.0), (0.9,−0.1), (0.9,0.1), (1.0,0.0). It can be seen that the TTT of the PD-FL controller trajectory is nearer to the reference than the TTT of the PD controller. Based on the X and Y errors of both controllers in Figure 11, the improvement of the PD-FL integrated controller for the triangular TTT is also noticeable. The maximum Y error of the PD-FL integrated controller is less than 6 millimeters, but it is more than 9 millimeters for the PD controller. The X error of the PD-FL integrated controller is also smaller than the X error of the PD controller as presented in Figure 11. The velocity and the acceleration of the links by the PD-FL integrated controller during the triangular TTT are shown in Figure 12 (a) and Figure 12 (b), respectively.

Figure 10. Triangular TTT performance of the 2-DOF robot.

Figure 11. X and Y error of the triangular TTT.

Figure 12.

a) Velocity of the triangular tip trajectory, b) Acceleration of the triangular tip trajectory.

Rhombic tip trajectory tracking

The rhombic TTT starts and ends based on the following trajectory points (X,Y): (1.0,0.0), (0.9,−0.1), (0.8,0.0), (0.9,0.1), (1.0,0.0). Figure 13 shows the rhombic TTT of the 2-DOF robot. It is clearly shown that the PD-FL integrated controller is better than the PD controller in tracking the tip of the 2-DOF robot as it is closer to the tip reference trajectory. Furthermore, the maximum Y error of the PD controller tracking is about 8 millimeters while the maximum Y error of the PD-FL controller is less than 4 millimeters as shown in Figure 14. The X error of the PD controller is also larger than the X error of the PD-FL integrated controller as presented in Figure 14. Thus, the PD-FL integrated controller performance for the rhombic TTT of the 2-DOF robot is better than the PD controller. Figure 15 (a) and Figure 15 (b) demonstrate the velocity and the acceleration of the links by the PD-FL integrated controller during the rhombic TTT, respectively.

Figure 13. Rhombic TTT performance of the 2-DOF robot.

Figure 14. X and Y error of the rhombic TTT.

Figure 15.

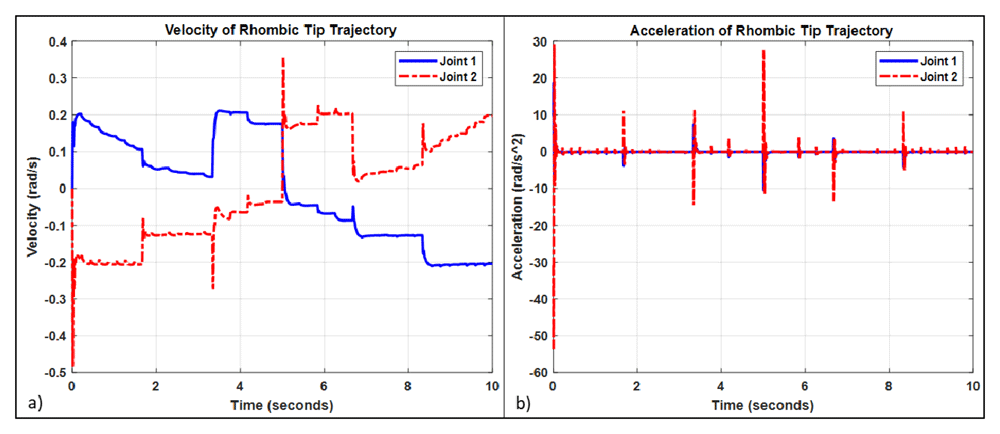
a) Velocity of the rhombic tip trajectory, b) Acceleration of the rhombic tip trajectory.

The discussed results of the point-to-point position control and the TTT demonstrate the improvement of the proposed controller in terms of fast response and accuracy. Normally, the faster response is the more overshoot and larger tip position error. However, the proposed PD-FL integrated controller has a faster response and reduces the overshoot and the tip position error of the 2-DOF robot. Furthermore, the proposed controller has the advantage of design simplicity compared with other integrated controllers.

Conclusion

The aim of this research was to obtain the SimMechanics model of the 2-DOF robot using MATLAB SimMechanics Toolbox from the CAD assembly design. Then, the PD-FL integrated controller was designed to control the 2-DOF robot in terms of point-to-point position control and TTT. This proposed integration technique of the PD controller and the FL controller improves the position control performance and reduces the fuzzy rules which results in avoiding the computational time drawback. The PD-FL integrated controller was used to control the 2-DOF robot for point-to-point position control which demonstrates enhanced performance compared with the conventional PD controller. Moreover, the 2-DOF robot was controlled for triangular TTT and rhombic TTT by the PD-FL integrated controller which has better performance than the PD controller.

Data availability

Figshare: Data are available under the term of the ‘2-DOF robot data of position control and tip trajectory tracking’ and has the following DOI: https://doi.org/10.6084/m9.figshare.16706458.

Figshare: The model of the 2-DOF robot and control is available under the term of the ‘2-DOF robot model’ and has the following DOI: https://doi.org/10.6084/m9.figshare.16714324.

Author contributions

All authors equally contributed to this research.

Faculty Opinions recommended

References

1. Chi J, Yu H, Yu J: Hybrid Tracking Control of 2-DOF SCARA Robot via Port-Controlled Hamiltonian and Backstepping. IEEE Access. 2018; 6: 17354–17360. Publisher Full Text
2. Zhang B, Wu J, Wang L, et al.: Accurate dynamic modeling and control parameters design of an industrial hybrid spray-painting robot. Robot Comput Integr Manuf. 2020; 63: 101923. Publisher Full Text
3. Lee SH, Kim J, Park FC, et al.: Newton-Type Algorithms for Dynamics-Based Robot Movement Optimization. IEEE Trans Robot. 2005; 21(4): 657–667. Publisher Full Text
4. Alandoli EA, Lee TS, My CA, et al.: Robust P-H∞ Integrated Controller for Flexible Link Manipulator System in the Presence of Disturbance. J Appl Comput Mech. 2021; 7(2): 646–654. Publisher Full Text
5. Amin ATM, Ab Rahim AH, Low CY: Adaptive controller algorithm for 2-DOF humanoid robot arm. Procedia Technol. 2014; 15: 765–774. Publisher Full Text
6. Cao F, Liu J: Optimal trajectory control for a two-link rigid-flexible manipulator with ODE-PDE model. Optim Control Appl Methods. 2018; 39(4): 1515–1529. Publisher Full Text
7. Lee TS, Alandoli EA: A critical review of modelling methods for flexible and rigid link manipulators. J Braz Soc Mech Sci Eng. 2020; 42(10): 508. Publisher Full Text
8. Boujnah F, Knani J: Motion simulation of a manipulator robot modeled by a CAD software. In: Proceedings of the 7th Int. Conf. Model. Identif. Control. 2015; 1–6. Publisher Full Text
9. West C, Montazeri A, Monk SD, et al.: A genetic algorithm approach for parameter optimization of a 7DOF robotic manipulator. IFAC-PapersOnLine. 2016; 49(12): 1261–1266. Publisher Full Text
10. Alandoli EA, Lee TS, Lin YJ, et al.: Dynamic model and intelligent optimal controller of flexible link manipulator system with payload uncertainty. Arab J Sci Eng. 2021; 46: 7423–7433. Publisher Full Text
11. Ali SA, Miskon MF, Shukor AZH, et al.: The Effect of Parameters Variation on Bilateral Controller. Int J Power Electron Drive Syst. 2018; 9(2): 648–659. Reference Source
12. Ali SA, Miskon MF, Shukor AZH, et al.: Single Link Bilateral Haptics Control with PD Controller and Geared DC-Motor in Robotic Rehabilitation Technology. Int J Mech Mechatronics Eng. 2019; 17(5): 148–155. Reference Source
13. Alandoli EA, Shah HNM, Sulaiman M, et al.: PD/H-∞ Integrated Controller for Position Tracking and Vibration Suppression of Flexible Link Manipulator System. Int J Mech Mechatronics Eng. 2018; 18(3): 54–61. Reference Source
14. Alandoli EA, Sulaiman M, Rashid MZA: Robustness and Disturbance Rejection of PD/H-∞ Integrated Controller for Flexible. J Eng Sci Technol Rev. 2019; 12(1): 27–36. Publisher Full Text
15. Bingül Z, Karahan O: A Fuzzy Logic Controller tuned with PSO for 2 DOF robot trajectory control. Expert Syst Appl. 2011; 38(1): 1017–1031. Publisher Full Text
16. Leines MT, Yang JS: LQR control of an under actuated planar biped robot. In: Proceedings of the 6th IEEE Conf. Ind. Electron. Appl. 2011; 1684–1689. Publisher Full Text
17. Ajwad SA, Iqbal J, Islam RU, et al.: Optimal and Robust Control of Multi DOF Robotic Manipulator: Design and Hardware Realization. Cybern Syst. 2018; 49(1): 77–93. Publisher Full Text
18. Kumar A, Kumar V: Hybridized ABC-GA optimized fractional order fuzzy pre-compensated FOPID Control design for 2-DOF robot manipulator. Int J Electron Commun. 2017; 79: 219–233. Publisher Full Text
19. Farah N, Talib MHN, Ibrahim Z, et al.: Self-Tuned Output Scaling Factor of Fuzzy Logic Speed Control of Induction Motor Drive. In: Proceedings of the 2017 7th IEEE International Conference on System Engineering and Technology (ICSET) 2017; 134–139. Publisher Full Text
20. Farah N, Talib MHN, Ibrahim Z, et al.: Self-tuning fuzzy logic control based on mras for induction motor drives. In: Proceedings of the 5th IET International Conference on Clean Energy and Technology (CEAT2018). 2018; 61–67. Publisher Full Text
21. Kiang CT, Spowage A, Yoong CK: Review of Control and Sensor System of Flexible Manipulator. J Intell Robot Syst Theory Appl. 2015; 77(1): 187–213. Publisher Full Text
22. He W, Chen Y, Yin Z: Adaptive Neural Network Control of an Uncertain Robot with Full-State Constraints. IEEE Trans Cybern. 2016; 46(3): 620–629. PubMed Abstract | Publisher Full Text
23. Tavoosi J, Jokandan AS, Daneshwar MA: A new method for position control of a 2-DOF robot arm using neuro-fuzzy controller. Indian J Sci Technol. 2012; 5(3): 1–5. Publisher Full Text
24. Islam S, Liu XP: Robust sliding mode control for robot manipulators. IEEE Trans Ind Electron. 2011; 58(6): 2444–2453. Publisher Full Text
25. Kuo TC, Huang YJ, Hong BW: Design of Adaptive Sliding Mode Controller for Robotic Manipulators Tracking Control. Int J Comput Electr Autom Control Inf Eng. 2011; 5(5): 453–457. Publisher Full Text
26. Piltan F, Sulaiman NB: Review of Sliding Mode Control of Robotic Manipulator. World Appl Sci J. 2012; 18(12): 1855–1869. Reference Source
27. Capisani LM, Ferrara A: Trajectory Planning and Second-Order Sliding Mode Motion/Interaction Control for Robot Manipulators in Unknown Environments. IEEE Trans Ind Electron. 2012; 59(8): 3189–3198. Publisher Full Text
28. Li THS, Huang YC: MIMO adaptive fuzzy terminal sliding-mode controller for robotic manipulators. Inf Sci. 2010; 180(23): 4641–4660. Publisher Full Text
29. Soltanpour MR, Khooban MH: A particle swarm optimization approach for fuzzy sliding mode control for tracking the robot manipulator. Nonlinear Dyn. 2013; 74(1): 467–478. Publisher Full Text
30. Sharma R, Rana KPS, Kumar V: Performance analysis of fractional order fuzzy PID controllers applied to a robotic manipulator. Expert Syst Appl. 2014; 41(9): 4274–4289. Publisher Full Text
31. Gierlak P, Muszyńska M, Żylski W: Neuro-fuzzy control of a robotic manipulator. Int J Appl Mech Eng. 2014; 19(3): 575–584. Publisher Full Text
32. Alandoli EA, Lee TS: A Critical Review of Control Techniques for Flexible and Rigid Link Manipulators. Robotica. 2020; 38(12): 2239–2265. Publisher Full Text
33. Farah N, Talib MHN, Shah NSM, et al.: A Novel Self-Tuning Fuzzy Logic Controller Based Induction Motor Drive System: An Experimental Approach. IEEE Access. 2019; 7: 68172–68184. Publisher Full Text

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 15 Oct 2021

Author details Author details

¹ Faculty of Engineering and Technology, Multimedia University, 75450 Ayer Keroh, Melaka, Malaysia
² Faculty of Computing and Informatics, Multimedia University, 63100 Cyberjaya, Selangor, Malaysia

Tian Soon Lee
Roles: Conceptualization, Formal Analysis, Funding Acquisition, Investigation, Methodology, Software, Supervision, Validation, Writing – Review & Editing

Esmail Ali Alandoli
Roles: Conceptualization, Formal Analysis, Investigation, Methodology, Software, Validation, Writing – Original Draft Preparation

V Vijayakumar
Roles: Conceptualization, Formal Analysis, Investigation, Methodology, Software, Supervision, Validation, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

This research was supported by Multimedia University through MMU GRA Scheme (MMUI/180265).
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (2)

version 2

Revised

Published: 17 Nov 2021, 10:1045

https://doi.org/10.12688/f1000research.72912.2

version 1

Published: 15 Oct 2021, 10:1045

https://doi.org/10.12688/f1000research.72912.1

© 2021 Lee TS et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

Lee TS, Alandoli EA and Vijayakumar V. 2-DOF robot modelling by SimMechanics and PD-FL integrated controller for position control and trajectory tracking [version 2; peer review: 1 approved, 1 approved with reservations]. F1000Research 2021, 10:1045 (https://doi.org/10.12688/f1000research.72912.2)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 2

VERSION 2

PUBLISHED 17 Nov 2021

Revised

Views

Reviewer Report 06 Aug 2024

Hassène Gritli, University of Carthage, Tunis, Tunisia

Approved with Reservations

https://doi.org/10.5256/f1000research.79499.r303666

This paper deals with the control of a two-degree-of-freedom manipulator robot using a CAD model. A PD plus fuzzy logic (FL) integrated controller was proposed, and which was applied to the CAD model.

Only the forward kinematic model of the robot is presented in the paper. Moreover, there is no condition on the two feedback gains of the PD part of the composite controller. Only trial works were realized to find the (best) gains.

To improve the paper, I suggest the following comments:
1- Add the canonical form of the dynamic model of the robot, the expression of the matrices in this model, and the corresponding values of the different parameters of the robot presented in these matrices.

2- you stated that the proposed controller is PD-FL integrated controller. It is not clear what you mean by integrated here in this controller. I suggest adding the controller's mathematical expression to be understood better.

3- Some related PD-based controllers can be found in the recent paper "JENHANİ S et.al. 2022 (ref 1)". I suggest comparing the proposed controller with some PD-based controllers proposed in that paper.

4- Generally, the same controller for trajectory tracking can be used for position control. However, the controller designed for the position control problem cannot be used for the motion control problem. So, the expression of the proposed PD-FL integrated controller should be given for the two problems.

5- In addition, you should add expressions of the desired trajectories used for the tracking.

6- I suggest adding external disturbances in the CAD model to show the efficiency and robustness of the proposed controller. You can consider some sinusoidal signals as external perturbations. in the two joints of the robot.

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Partly

References

1. JENHANİ S, GRİTLİ H, CARBONE P: Comparison Between Some Nonlinear Controllers for the Position Control of Lagrangian-type Robotic Systems. Chaos Theory and Applications. 2022; 4 (4): 179-196 Publisher Full Text

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Robotics, Control theory, Machine learning, Chaos theory

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Respond or Comment

Views

Reviewer Report 24 Nov 2021

Xuan Bien Duong, Advanced Technology Center, Le Quy Don Technical University, Hanoi, Vietnam

Approved

https://doi.org/10.5256/f1000research.79499.r100476

In my opinion, all of ... Continue reading

CITE

Report a concern

Respond or Comment

Version 1

VERSION 1

PUBLISHED 15 Oct 2021

Views

Reviewer Report 02 Nov 2021

Xuan Bien Duong, Advanced Technology Center, Le Quy Don Technical University, Hanoi, Vietnam

Approved with Reservations

https://doi.org/10.5256/f1000research.76525.r97077

Reviewer Comment for Authors
1. Comment No. 1

This paper implements modeling a planar two links robot with rotational joints based on 3D CAD model and SIMMECHANICS Toolbox in MATLAB software. This model retains the

Reviewer Comment for Authors
1. Comment No. 1

This paper implements modeling a planar two links robot with rotational joints based on 3D CAD model and SIMMECHANICS Toolbox in MATLAB software. This model retains the basic connections of the joints in the design environment. The PD-FL hybrid control system is designed to control the position and trajectory of the end-effector point. The control quality is compared with the traditional PD control system. The results show that the quality of the hybrid control system is much better than that of the PD system.

2. Comment No. 2

The article has not shown new points in terms of robot model because the 2DOF robot model is quite simple, common and not a model that is widely applied in industrial production.
Establishing and converting 3D models from CAD design environment to MATLAB environment is not prominent because this problem has been done for a long time and with more complex robot models, more degrees of freedom.

3. Comment No. 3

The concern point of the article is the position control and trajectory control problem of the end-effect point in the workspace, but it seems to only stop at the control for the kinematics model, not considering the factors dynamics, if any. The author should to add more information to the article.

4. Comment No. 4

The position control problem is presented quite clearly. However, the control trajectory problem needs to include more specific information, such as how the author describes the trajectory of the end-effector point in the workspace - the equation describing the trajectory should to be clearly shown.

5. Comment No. 5

The paper should to be further developed with consideration of the trajectory planning of the end-effector point in the workspace with more specific constraints on velocity and acceleration as well as the dynamic factors of the robot.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

Partly
Are all the source data underlying the results available to ensure full reproducibility?

Partly
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: CAD/CAM/CNC Technology, Robotics

CITE

Report a concern

Author Response 17 Nov 2021

tian lee, Faculty of Engineering and Technology, Multimedia University, 75450 Ayer Keroh, Malaysia

17 Nov 2021

Author Response

The following points are the comments from Dr. Xuan Bien Duong and the authors' responses.

Reviewer Comment No. 1
This paper implements modeling a planar two links robot with ... Continue reading The following points are the comments from Dr. Xuan Bien Duong and the authors' responses.

Reviewer Comment No. 1
This paper implements modeling a planar two links robot with rotational joints based on 3D CAD model and SIMMECHANICS Toolbox in MATLAB software. This model retains the basic connections of the joints in the design environment. The PD-FL hybrid control system is designed to control the position and trajectory of the end-effector point. The control quality is compared with the traditional PD control system. The results show that the quality of the hybrid control system is much better than that of the PD system.

Reviewer Comment No. 2
The article has not shown new points in terms of robot model because the 2DOF robot model is quite simple, common and not a model that is widely applied in industrial production.
Establishing and converting 3D models from CAD design environment to MATLAB environment is not prominent because this problem has been done for a long time and with more complex robot models, more degrees of freedom.

Authors’ response: The SimMechanics model can be obtained easier than the derivation of a mathematical model and might be more accurate to present the system. Thus, the SimMechanics model of the 2-DOF robot is obtained in this research in order to test the proposed PD-FL integrated controller in terms of position control and tip trajectory tracking. The main concern of this research is the PD-FL integrated controller design and it demonstrates significant enhancement in terms of the point-to-point position control of the links and the tip trajectory tracking.

Reviewer Comment No. 3
The concern point of the article is the position control and trajectory control problem of the end-effect point in the workspace, but it seems to only stop at the control for the kinematics model, not considering the factors dynamics, if any. The author should to add more information to the article.

Authors’ response: The SimMechanics model includes all the parameters of the 2-DOF robot which were identified in the CAD assembly design such as the material density, the weights, the cross-sectional area of the links, and the links’ lengths. In addition, the motion of the SimMechanics model is based on the torques actuation to the joints. Therefore, the position control of the 2-DOF robot is based on the dynamic motion. Such information is recently added to the article for more clarification of the model.

Reviewer Comment No. 4
The position control problem is presented quite clearly. However, the control trajectory problem needs to include more specific information, such as how the author describes the trajectory of the end-effector point in the workspace - the equation describing the trajectory should to be clearly shown.

Authors’ response: The tip trajectory of the 2-DOF robot is achieved by specific reference paths for the two joints simultaneously, the data of the joints’ references are available in the link provided in the “Data availability” section. The accurate position control of the joints related to the desired references will lead to an accurate tip trajectory of any demanded tip trajectory. From the position control output of the joints can obtain the tip position based on Equation 1 and compute the error.

Reviewer Comment No. 5
The paper should to be further developed with consideration of the trajectory planning of the end-effector point in the workspace with more specific constraints on velocity and acceleration as well as the dynamic factors of the robot.

Authors’ response: The velocity and acceleration for the position control response and the tip trajectory tracking are added to the article.
The following points are the comments from Dr. Xuan Bien Duong and the authors' responses.

Reviewer Comment No. 1
This paper implements modeling a planar two links robot with rotational joints based on 3D CAD model and SIMMECHANICS Toolbox in MATLAB software. This model retains the basic connections of the joints in the design environment. The PD-FL hybrid control system is designed to control the position and trajectory of the end-effector point. The control quality is compared with the traditional PD control system. The results show that the quality of the hybrid control system is much better than that of the PD system.

Reviewer Comment No. 2
The article has not shown new points in terms of robot model because the 2DOF robot model is quite simple, common and not a model that is widely applied in industrial production.
Establishing and converting 3D models from CAD design environment to MATLAB environment is not prominent because this problem has been done for a long time and with more complex robot models, more degrees of freedom.

Authors’ response: The SimMechanics model can be obtained easier than the derivation of a mathematical model and might be more accurate to present the system. Thus, the SimMechanics model of the 2-DOF robot is obtained in this research in order to test the proposed PD-FL integrated controller in terms of position control and tip trajectory tracking. The main concern of this research is the PD-FL integrated controller design and it demonstrates significant enhancement in terms of the point-to-point position control of the links and the tip trajectory tracking.

Reviewer Comment No. 3
The concern point of the article is the position control and trajectory control problem of the end-effect point in the workspace, but it seems to only stop at the control for the kinematics model, not considering the factors dynamics, if any. The author should to add more information to the article.

Authors’ response: The SimMechanics model includes all the parameters of the 2-DOF robot which were identified in the CAD assembly design such as the material density, the weights, the cross-sectional area of the links, and the links’ lengths. In addition, the motion of the SimMechanics model is based on the torques actuation to the joints. Therefore, the position control of the 2-DOF robot is based on the dynamic motion. Such information is recently added to the article for more clarification of the model.

Reviewer Comment No. 4
The position control problem is presented quite clearly. However, the control trajectory problem needs to include more specific information, such as how the author describes the trajectory of the end-effector point in the workspace - the equation describing the trajectory should to be clearly shown.

Authors’ response: The tip trajectory of the 2-DOF robot is achieved by specific reference paths for the two joints simultaneously, the data of the joints’ references are available in the link provided in the “Data availability” section. The accurate position control of the joints related to the desired references will lead to an accurate tip trajectory of any demanded tip trajectory. From the position control output of the joints can obtain the tip position based on Equation 1 and compute the error.

Reviewer Comment No. 5
The paper should to be further developed with consideration of the trajectory planning of the end-effector point in the workspace with more specific constraints on velocity and acceleration as well as the dynamic factors of the robot.

Authors’ response: The velocity and acceleration for the position control response and the tip trajectory tracking are added to the article.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 17 Nov 2021

tian lee, Faculty of Engineering and Technology, Multimedia University, 75450 Ayer Keroh, Malaysia

17 Nov 2021

Author Response

The following points are the comments from Dr. Xuan Bien Duong and the authors' responses.

Reviewer Comment No. 1
This paper implements modeling a planar two links robot with ... Continue reading The following points are the comments from Dr. Xuan Bien Duong and the authors' responses.

Reviewer Comment No. 1
This paper implements modeling a planar two links robot with rotational joints based on 3D CAD model and SIMMECHANICS Toolbox in MATLAB software. This model retains the basic connections of the joints in the design environment. The PD-FL hybrid control system is designed to control the position and trajectory of the end-effector point. The control quality is compared with the traditional PD control system. The results show that the quality of the hybrid control system is much better than that of the PD system.

Reviewer Comment No. 2
The article has not shown new points in terms of robot model because the 2DOF robot model is quite simple, common and not a model that is widely applied in industrial production.
Establishing and converting 3D models from CAD design environment to MATLAB environment is not prominent because this problem has been done for a long time and with more complex robot models, more degrees of freedom.

Authors’ response: The SimMechanics model can be obtained easier than the derivation of a mathematical model and might be more accurate to present the system. Thus, the SimMechanics model of the 2-DOF robot is obtained in this research in order to test the proposed PD-FL integrated controller in terms of position control and tip trajectory tracking. The main concern of this research is the PD-FL integrated controller design and it demonstrates significant enhancement in terms of the point-to-point position control of the links and the tip trajectory tracking.

Reviewer Comment No. 3
The concern point of the article is the position control and trajectory control problem of the end-effect point in the workspace, but it seems to only stop at the control for the kinematics model, not considering the factors dynamics, if any. The author should to add more information to the article.

Authors’ response: The SimMechanics model includes all the parameters of the 2-DOF robot which were identified in the CAD assembly design such as the material density, the weights, the cross-sectional area of the links, and the links’ lengths. In addition, the motion of the SimMechanics model is based on the torques actuation to the joints. Therefore, the position control of the 2-DOF robot is based on the dynamic motion. Such information is recently added to the article for more clarification of the model.

Reviewer Comment No. 4
The position control problem is presented quite clearly. However, the control trajectory problem needs to include more specific information, such as how the author describes the trajectory of the end-effector point in the workspace - the equation describing the trajectory should to be clearly shown.

Authors’ response: The tip trajectory of the 2-DOF robot is achieved by specific reference paths for the two joints simultaneously, the data of the joints’ references are available in the link provided in the “Data availability” section. The accurate position control of the joints related to the desired references will lead to an accurate tip trajectory of any demanded tip trajectory. From the position control output of the joints can obtain the tip position based on Equation 1 and compute the error.

Reviewer Comment No. 5
The paper should to be further developed with consideration of the trajectory planning of the end-effector point in the workspace with more specific constraints on velocity and acceleration as well as the dynamic factors of the robot.

Authors’ response: The velocity and acceleration for the position control response and the tip trajectory tracking are added to the article.
The following points are the comments from Dr. Xuan Bien Duong and the authors' responses.

Reviewer Comment No. 1
This paper implements modeling a planar two links robot with rotational joints based on 3D CAD model and SIMMECHANICS Toolbox in MATLAB software. This model retains the basic connections of the joints in the design environment. The PD-FL hybrid control system is designed to control the position and trajectory of the end-effector point. The control quality is compared with the traditional PD control system. The results show that the quality of the hybrid control system is much better than that of the PD system.

Reviewer Comment No. 2
The article has not shown new points in terms of robot model because the 2DOF robot model is quite simple, common and not a model that is widely applied in industrial production.
Establishing and converting 3D models from CAD design environment to MATLAB environment is not prominent because this problem has been done for a long time and with more complex robot models, more degrees of freedom.

Authors’ response: The SimMechanics model can be obtained easier than the derivation of a mathematical model and might be more accurate to present the system. Thus, the SimMechanics model of the 2-DOF robot is obtained in this research in order to test the proposed PD-FL integrated controller in terms of position control and tip trajectory tracking. The main concern of this research is the PD-FL integrated controller design and it demonstrates significant enhancement in terms of the point-to-point position control of the links and the tip trajectory tracking.

Reviewer Comment No. 3
The concern point of the article is the position control and trajectory control problem of the end-effect point in the workspace, but it seems to only stop at the control for the kinematics model, not considering the factors dynamics, if any. The author should to add more information to the article.

Authors’ response: The SimMechanics model includes all the parameters of the 2-DOF robot which were identified in the CAD assembly design such as the material density, the weights, the cross-sectional area of the links, and the links’ lengths. In addition, the motion of the SimMechanics model is based on the torques actuation to the joints. Therefore, the position control of the 2-DOF robot is based on the dynamic motion. Such information is recently added to the article for more clarification of the model.

Reviewer Comment No. 4
The position control problem is presented quite clearly. However, the control trajectory problem needs to include more specific information, such as how the author describes the trajectory of the end-effector point in the workspace - the equation describing the trajectory should to be clearly shown.

Authors’ response: The tip trajectory of the 2-DOF robot is achieved by specific reference paths for the two joints simultaneously, the data of the joints’ references are available in the link provided in the “Data availability” section. The accurate position control of the joints related to the desired references will lead to an accurate tip trajectory of any demanded tip trajectory. From the position control output of the joints can obtain the tip position based on Equation 1 and compute the error.

Reviewer Comment No. 5
The paper should to be further developed with consideration of the trajectory planning of the end-effector point in the workspace with more specific constraints on velocity and acceleration as well as the dynamic factors of the robot.

Authors’ response: The velocity and acceleration for the position control response and the tip trajectory tracking are added to the article.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 15 Oct 2021

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 2 (revision) 17 Nov 21	read	read
Version 1 15 Oct 21	read

Xuan Bien Duong, Le Quy Don Technical University, Hanoi, Vietnam
Hassène Gritli, University of Carthage, Tunis, Tunisia

Comments on this article

All Comments(0)

Add a comment

Browse by related subjects

Back to all reports

Reviewer Report

9 Views

06 Aug 2024 | for Version 2

Hassène Gritli, University of Carthage, Tunis, Tunisia

9 Views Cite this report Responses(0)

Approved With Reservations

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Partly

References

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Robotics, Control theory, Machine learning, Chaos theory

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

15 Views

24 Nov 2021 | for Version 2

Xuan Bien Duong, Advanced Technology Center, Le Quy Don Technical University, Hanoi, Vietnam

15 Views Cite this report Responses(0)

Approved

In my opinion, all of my comments are satisfactorily explained.

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

CAD/CAM/CNC Technology, Robotics

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

31 Views

02 Nov 2021 | for Version 1

Xuan Bien Duong, Advanced Technology Center, Le Quy Don Technical University, Hanoi, Vietnam

31 Views Cite this report Responses(1)

Approved With Reservations

Reviewer Comment for Authors
1. Comment No. 1

This paper implements modeling a planar two links robot with rotational joints based on 3D CAD model and SIMMECHANICS Toolbox in MATLAB software. This model retains the basic connections of the joints in the design environment. The PD-FL hybrid control system is designed to control the position and trajectory of the end-effector point. The control quality is compared with the traditional PD control system. The results show that the quality of the hybrid control system is much better than that of the PD system.

2. Comment No. 2

The article has not shown new points in terms of robot model because the 2DOF robot model is quite simple, common and not a model that is widely applied in industrial production.
Establishing and converting 3D models from CAD design environment to MATLAB environment is not prominent because this problem has been done for a long time and with more complex robot models, more degrees of freedom.

3. Comment No. 3

The concern point of the article is the position control and trajectory control problem of the end-effect point in the workspace, but it seems to only stop at the control for the kinematics model, not considering the factors dynamics, if any. The author should to add more information to the article.

4. Comment No. 4

The position control problem is presented quite clearly. However, the control trajectory problem needs to include more specific information, such as how the author describes the trajectory of the end-effector point in the workspace - the equation describing the trajectory should to be clearly shown.

5. Comment No. 5

The paper should to be further developed with consideration of the trajectory planning of the end-effector point in the workspace with more specific constraints on velocity and acceleration as well as the dynamic factors of the robot.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

Partly
Are all the source data underlying the results available to ensure full reproducibility?

Partly
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

CAD/CAM/CNC Technology, Robotics

Respond to this report

Responses (1)

Author Response

17 Nov 2021

tian lee, Faculty of Engineering and Technology, Multimedia University, 75450 Ayer Keroh, Malaysia

The following points are the comments from Dr. Xuan Bien Duong and the authors' responses.

Reviewer Comment No. 1
This paper implements modeling a planar two links robot with rotational joints based on 3D CAD model and SIMMECHANICS Toolbox in MATLAB software. This model retains the basic connections of the joints in the design environment. The PD-FL hybrid control system is designed to control the position and trajectory of the end-effector point. The control quality is compared with the traditional PD control system. The results show that the quality of the hybrid control system is much better than that of the PD system.

Reviewer Comment No. 2
The article has not shown new points in terms of robot model because the 2DOF robot model is quite simple, common and not a model that is widely applied in industrial production.
Establishing and converting 3D models from CAD design environment to MATLAB environment is not prominent because this problem has been done for a long time and with more complex robot models, more degrees of freedom.

Authors’ response: The SimMechanics model can be obtained easier than the derivation of a mathematical model and might be more accurate to present the system. Thus, the SimMechanics model of the 2-DOF robot is obtained in this research in order to test the proposed PD-FL integrated controller in terms of position control and tip trajectory tracking. The main concern of this research is the PD-FL integrated controller design and it demonstrates significant enhancement in terms of the point-to-point position control of the links and the tip trajectory tracking.

Reviewer Comment No. 3
The concern point of the article is the position control and trajectory control problem of the end-effect point in the workspace, but it seems to only stop at the control for the kinematics model, not considering the factors dynamics, if any. The author should to add more information to the article.

Authors’ response: The SimMechanics model includes all the parameters of the 2-DOF robot which were identified in the CAD assembly design such as the material density, the weights, the cross-sectional area of the links, and the links’ lengths. In addition, the motion of the SimMechanics model is based on the torques actuation to the joints. Therefore, the position control of the 2-DOF robot is based on the dynamic motion. Such information is recently added to the article for more clarification of the model.

Reviewer Comment No. 4
The position control problem is presented quite clearly. However, the control trajectory problem needs to include more specific information, such as how the author describes the trajectory of the end-effector point in the workspace - the equation describing the trajectory should to be clearly shown.

Authors’ response: The tip trajectory of the 2-DOF robot is achieved by specific reference paths for the two joints simultaneously, the data of the joints’ references are available in the link provided in the “Data availability” section. The accurate position control of the joints related to the desired references will lead to an accurate tip trajectory of any demanded tip trajectory. From the position control output of the joints can obtain the tip position based on Equation 1 and compute the error.

Reviewer Comment No. 5
The paper should to be further developed with consideration of the trajectory planning of the end-effector point in the workspace with more specific constraints on velocity and acceleration as well as the dynamic factors of the robot.

Authors’ response: The velocity and acceleration for the position control response and the tip trajectory tracking are added to the article.

View more View less

Competing Interests

No competing interests were disclosed.

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

[1] 1. Chi J, Yu H, Yu J: Hybrid Tracking Control of 2-DOF SCARA Robot via Port-Controlled Hamiltonian and Backstepping. IEEE Access. 2018; 6: 17354–17360. Publisher Full Text

[2] 2. Zhang B, Wu J, Wang L, et al.: Accurate dynamic modeling and control parameters design of an industrial hybrid spray-painting robot. Robot Comput Integr Manuf. 2020; 63: 101923. Publisher Full Text

[3] 3. Lee SH, Kim J, Park FC, et al.: Newton-Type Algorithms for Dynamics-Based Robot Movement Optimization. IEEE Trans Robot. 2005; 21(4): 657–667. Publisher Full Text

[4] 4. Alandoli EA, Lee TS, My CA, et al.: Robust P-H∞ Integrated Controller for Flexible Link Manipulator System in the Presence of Disturbance. J Appl Comput Mech. 2021; 7(2): 646–654. Publisher Full Text

[5] 5. Amin ATM, Ab Rahim AH, Low CY: Adaptive controller algorithm for 2-DOF humanoid robot arm. Procedia Technol. 2014; 15: 765–774. Publisher Full Text

[6] 6. Cao F, Liu J: Optimal trajectory control for a two-link rigid-flexible manipulator with ODE-PDE model. Optim Control Appl Methods. 2018; 39(4): 1515–1529. Publisher Full Text

[7] 7. Lee TS, Alandoli EA: A critical review of modelling methods for flexible and rigid link manipulators. J Braz Soc Mech Sci Eng. 2020; 42(10): 508. Publisher Full Text

[8] 8. Boujnah F, Knani J: Motion simulation of a manipulator robot modeled by a CAD software. In: Proceedings of the 7th Int. Conf. Model. Identif. Control. 2015; 1–6. Publisher Full Text

[9] 9. West C, Montazeri A, Monk SD, et al.: A genetic algorithm approach for parameter optimization of a 7DOF robotic manipulator. IFAC-PapersOnLine. 2016; 49(12): 1261–1266. Publisher Full Text

[10] 10. Alandoli EA, Lee TS, Lin YJ, et al.: Dynamic model and intelligent optimal controller of flexible link manipulator system with payload uncertainty. Arab J Sci Eng. 2021; 46: 7423–7433. Publisher Full Text

[11] 11. Ali SA, Miskon MF, Shukor AZH, et al.: The Effect of Parameters Variation on Bilateral Controller. Int J Power Electron Drive Syst. 2018; 9(2): 648–659. Reference Source

[12] 12. Ali SA, Miskon MF, Shukor AZH, et al.: Single Link Bilateral Haptics Control with PD Controller and Geared DC-Motor in Robotic Rehabilitation Technology. Int J Mech Mechatronics Eng. 2019; 17(5): 148–155. Reference Source

[13] 13. Alandoli EA, Shah HNM, Sulaiman M, et al.: PD/H-∞ Integrated Controller for Position Tracking and Vibration Suppression of Flexible Link Manipulator System. Int J Mech Mechatronics Eng. 2018; 18(3): 54–61. Reference Source

[14] 14. Alandoli EA, Sulaiman M, Rashid MZA: Robustness and Disturbance Rejection of PD/H-∞ Integrated Controller for Flexible. J Eng Sci Technol Rev. 2019; 12(1): 27–36. Publisher Full Text

[15] 15. Bingül Z, Karahan O: A Fuzzy Logic Controller tuned with PSO for 2 DOF robot trajectory control. Expert Syst Appl. 2011; 38(1): 1017–1031. Publisher Full Text

[16] 16. Leines MT, Yang JS: LQR control of an under actuated planar biped robot. In: Proceedings of the 6th IEEE Conf. Ind. Electron. Appl. 2011; 1684–1689. Publisher Full Text

[17] 17. Ajwad SA, Iqbal J, Islam RU, et al.: Optimal and Robust Control of Multi DOF Robotic Manipulator: Design and Hardware Realization. Cybern Syst. 2018; 49(1): 77–93. Publisher Full Text

[18] 18. Kumar A, Kumar V: Hybridized ABC-GA optimized fractional order fuzzy pre-compensated FOPID Control design for 2-DOF robot manipulator. Int J Electron Commun. 2017; 79: 219–233. Publisher Full Text

[19] 19. Farah N, Talib MHN, Ibrahim Z, et al.: Self-Tuned Output Scaling Factor of Fuzzy Logic Speed Control of Induction Motor Drive. In: Proceedings of the 2017 7th IEEE International Conference on System Engineering and Technology (ICSET) 2017; 134–139. Publisher Full Text

[20] 20. Farah N, Talib MHN, Ibrahim Z, et al.: Self-tuning fuzzy logic control based on mras for induction motor drives. In: Proceedings of the 5th IET International Conference on Clean Energy and Technology (CEAT2018). 2018; 61–67. Publisher Full Text

[21] 21. Kiang CT, Spowage A, Yoong CK: Review of Control and Sensor System of Flexible Manipulator. J Intell Robot Syst Theory Appl. 2015; 77(1): 187–213. Publisher Full Text

[22] 22. He W, Chen Y, Yin Z: Adaptive Neural Network Control of an Uncertain Robot with Full-State Constraints. IEEE Trans Cybern. 2016; 46(3): 620–629. PubMed Abstract | Publisher Full Text

[23] 23. Tavoosi J, Jokandan AS, Daneshwar MA: A new method for position control of a 2-DOF robot arm using neuro-fuzzy controller. Indian J Sci Technol. 2012; 5(3): 1–5. Publisher Full Text

[24] 24. Islam S, Liu XP: Robust sliding mode control for robot manipulators. IEEE Trans Ind Electron. 2011; 58(6): 2444–2453. Publisher Full Text

[25] 25. Kuo TC, Huang YJ, Hong BW: Design of Adaptive Sliding Mode Controller for Robotic Manipulators Tracking Control. Int J Comput Electr Autom Control Inf Eng. 2011; 5(5): 453–457. Publisher Full Text

[26] 26. Piltan F, Sulaiman NB: Review of Sliding Mode Control of Robotic Manipulator. World Appl Sci J. 2012; 18(12): 1855–1869. Reference Source

[27] 27. Capisani LM, Ferrara A: Trajectory Planning and Second-Order Sliding Mode Motion/Interaction Control for Robot Manipulators in Unknown Environments. IEEE Trans Ind Electron. 2012; 59(8): 3189–3198. Publisher Full Text

[28] 28. Li THS, Huang YC: MIMO adaptive fuzzy terminal sliding-mode controller for robotic manipulators. Inf Sci. 2010; 180(23): 4641–4660. Publisher Full Text

[29] 29. Soltanpour MR, Khooban MH: A particle swarm optimization approach for fuzzy sliding mode control for tracking the robot manipulator. Nonlinear Dyn. 2013; 74(1): 467–478. Publisher Full Text

[30] 30. Sharma R, Rana KPS, Kumar V: Performance analysis of fractional order fuzzy PID controllers applied to a robotic manipulator. Expert Syst Appl. 2014; 41(9): 4274–4289. Publisher Full Text

[31] 31. Gierlak P, Muszyńska M, Żylski W: Neuro-fuzzy control of a robotic manipulator. Int J Appl Mech Eng. 2014; 19(3): 575–584. Publisher Full Text

[32] 32. Alandoli EA, Lee TS: A Critical Review of Control Techniques for Flexible and Rigid Link Manipulators. Robotica. 2020; 38(12): 2239–2265. Publisher Full Text

[33] 33. Farah N, Talib MHN, Shah NSM, et al.: A Novel Self-Tuning Fuzzy Logic Controller Based Induction Motor Drive System: An Experimental Approach. IEEE Access. 2019; 7: 68172–68184. Publisher Full Text

2-DOF robot modelling by SimMechanics and PD-FL integrated controller for position control and trajectory tracking

Abstract

Keywords

Revised Amendments from Version 1

Introduction

System and the SimMechanics model

Figure 1. Schematic diagram of the 2-DOF robot.

Figure 2. CAD assembly of the 2-DOF robot.

Figure 3. Steps of SimMechanics model generation.

Figure 4. SimMechanics model of the 2-DOF robot.

Control design

Table 1. Parameters of PD controllers.

Figure 5. Membership function of FL controller for the 2-DOF robot.

Table 2. Fuzzy rules of FL controller for the 2-DOF robot based on error 1 (e1), error 2 (e2), output 1 (u1), and output 2 (u2).

Figure 6. SimMechanics model with PD-FL integrated controller.

Results and discussion

Point-to-point position control

Figure 7. Point-to-point position control of link 1.

Table 3. Performance analysis for position control of link 1.

Figure 8. Point-to-point position control of link 2.

Figure 9.

Table 4. Performance analysis for position control of link 2.

Tip trajectory tracking

Triangular tip trajectory tracking

Figure 10. Triangular TTT performance of the 2-DOF robot.

Figure 11. X and Y error of the triangular TTT.

Figure 12.

Rhombic tip trajectory tracking

Figure 13. Rhombic TTT performance of the 2-DOF robot.

Figure 14. X and Y error of the rhombic TTT.

Figure 15.

Conclusion

Data availability

Author contributions

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated

Table 2. Fuzzy rules of FL controller for the 2-DOF robot based on error 1 (e₁), error 2 (e₂), output 1 (u₁), and output 2 (u₂).