Substantial impact of post-vaccination contacts on cumulative infections during viral epidemics

Nash Rochman; Yuri I Wolf; Eugene V Koonin

doi:10.12688/f1000research.52341.2

Home Browse Substantial impact of post-vaccination contacts on cumulative infections...

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Revised

Substantial impact of post-vaccination contacts on cumulative infections during viral epidemics

[version 2; peer review: 2 approved]

Nash Rochman ¹, Yuri I Wolf¹, Eugene V Koonin ¹

PUBLISHED 26 Aug 2021

Author details Author details

¹ National Center for Biotechnology Information, NIH, Bethesda, MD, 20894, USA

Nash Rochman
Roles: Conceptualization, Formal Analysis, Investigation, Methodology, Writing – Original Draft Preparation, Writing – Review & Editing

Yuri I Wolf
Roles: Conceptualization, Investigation, Writing – Review & Editing

Eugene V Koonin
Roles: Conceptualization, Investigation, Supervision, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

Abstract

Background: The start of 2021 was marked by the initiation of a global vaccination campaign against the novel coronavirus SARS-CoV-2. Formulating an optimal distribution strategy under social and economic constraints is challenging. Optimal distribution is additionally constrained by the potential emergence of vaccine resistance. Analogous to chronic low-dose antibiotic exposure, recently inoculated individuals who are not yet immune play an outsized role in the emergence of resistance. Classical epidemiological modelling is well suited to explore how the behavior of the inoculated population impacts the total number of infections over the entirety of an epidemic.
Methods: A deterministic model of epidemic evolution is analyzed, with seven compartments defined by their relationship to the emergence of vaccine-resistant mutants and representing three susceptible populations, three infected populations, and one recovered population. This minimally computationally intensive design enables simulation of epidemics across a broad parameter space. The results are used to identify conditions minimizing the cumulative number of infections.
Results: When an escape variant is only modestly less infectious than the originating strain within a naïve population, the cumulative number of infections does not monotonically decrease with the rate of vaccine distribution. Analysis of the model also demonstrates that inoculated individuals play a major role in the mitigation or exacerbation of vaccine-resistant outbreaks. Modulating the rate of host–host contact for the inoculated population by less than an order of magnitude can alter the cumulative number of infections by more than 20%.
Conclusions: Mathematical modeling shows that limiting post-vaccination contacts can perceptibly affect the course of an epidemic. The consideration of limitations on post-vaccination contacts remains relevant for the entire duration of any vaccination campaign including the current status of SARS-CoV-2 vaccination.

Keywords

Virus infection; epidemics; vaccination; escape mutants; contact limitation

Corresponding authors: Nash Rochman, Eugene V Koonin

Competing interests: No competing interests were disclosed.

Grant information: U.S. Department of Health and Human Services. NDR, YIW, and EVK are supported by the Intramural Research Program of the National Institutes of Health (National Library of Medicine).
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2021 Rochman N et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. The author(s) is/are employees of the US Government and therefore domestic copyright protection in USA does not apply to this work. The work may be protected under the copyright laws of other jurisdictions when used in those jurisdictions.

How to cite: Rochman N, Wolf YI and Koonin EV. Substantial impact of post-vaccination contacts on cumulative infections during viral epidemics [version 2; peer review: 2 approved]. F1000Research 2021, 10:315 (https://doi.org/10.12688/f1000research.52341.2) First published: 23 Apr 2021, 10:315 (https://doi.org/10.12688/f1000research.52341.1) Latest published: 26 Aug 2021, 10:315 (https://doi.org/10.12688/f1000research.52341.2)

Revised Amendments from Version 1

In this version, additional details of the model have bene included in the main text, figure legends and the figures themselves, in response to the suggestions of the reviewers. Furthermore, as per the comments of reviewer 2, language has been added to emphasize the theoretical character of this work that cannot be used directly to make quantitative predictions on the course of any particular epidemic.

See the authors' detailed response to the review by Fyodor A. Kondrashov
See the authors' detailed response to the review by Sebastian Maximilian Schloer

Introduction

The emergence of the novel severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) responsible for the COVID-19 pandemic motivated dramatic public health intervention including recommendations for isolation and quarantine throughout most of 2020 and early 2021.¹ The beginning of 2021 was marked by widespread vaccine distribution which continues at an accelerating pace at the time of this writing. Optimizing distribution is challenging and subject to a myriad of social and economic constraints.²^–⁴ The potential emergence of vaccine-resistant variants of the virus⁵^,⁶ introduces additional complications. Vaccination applies new selective pressures which can lead to diverse intermediate outcomes even under conditions admitting eventual pathogen eradication.⁷^–¹³ The larger the size of the vaccinated population, the greater the pressure towards escape of vaccine-resistant variants.

Escape variants emerge within individual hosts after infection with the originating strain. Naïve, unvaccinated, hosts are more easily infected than vaccinated hosts but mutations conferring resistance are unlikely to provide a selective advantage in the naïve background. Thus, naïve hosts are likely to shed escape variants at low, likely, negligible rates. The reverse is true for vaccinated hosts. Recently vaccinated, inoculated, hosts that are not yet immune are a key population to consider. This population remains highly susceptible to infection with the originating strain, and in these hosts, mutations conferring resistance are more likely to provide a selective advantage. As a result, a substantial fraction or even most of the virus shed by such hosts will be resistant mutants. This situation is analogous to the administration of a low-dose antibiotic regime.¹⁴^,¹⁵ In both cases, the pathogen is introduced to a susceptible host and is subject to elevated selective pressure towards the emergence of resistant (escape) variants.

We sought to identify constraints on the reduction of the cumulative number of infections that might be imposed by vaccine escape and the role played by the small, but critical, population of inoculated hosts. To this end, we constructed an epidemiological compartment model to simulate vaccination campaigns over a broad parameter regime. This minimally computationally intensive approach enabled us to simulate many possible scenarios for epidemic evolution, in order to determine the optimal vaccination strategy for each condition.

Methods

We divided the population into seven compartments (Figure 1A). Three compartments are susceptible to infection by either the originating strain or escape mutants: naïve (N; unvaccinated and fully susceptible to the originating strain and escape mutants), inoculated (I; recently vaccinated and still partially susceptible to the originating strain, and fully susceptible to escape mutants), and vaccinated (V; minimally susceptible to the originating strain, but fully susceptible to escape mutants). Two compartments represent ongoing infection with the originating strain and are distinguished by the host’s previous compartment: infected–naïve (F, “Founder”) and infected–inoculated (M, “Mixed”). The third infected compartment represents infection by an escape variant, infected–escape (E). The remaining compartment, recovered (R), contains all hosts that were previously infected and are no longer infectious. Vaccination is represented by a reduction in susceptibility to infection with the originating strain. Naïve hosts are inoculated at rate k_V. Inoculated hosts do not immediately acquire immunity and mature into the vaccinated compartment at rate k_M. All infected hosts recover at rate k_R.

Figure 1. The model.

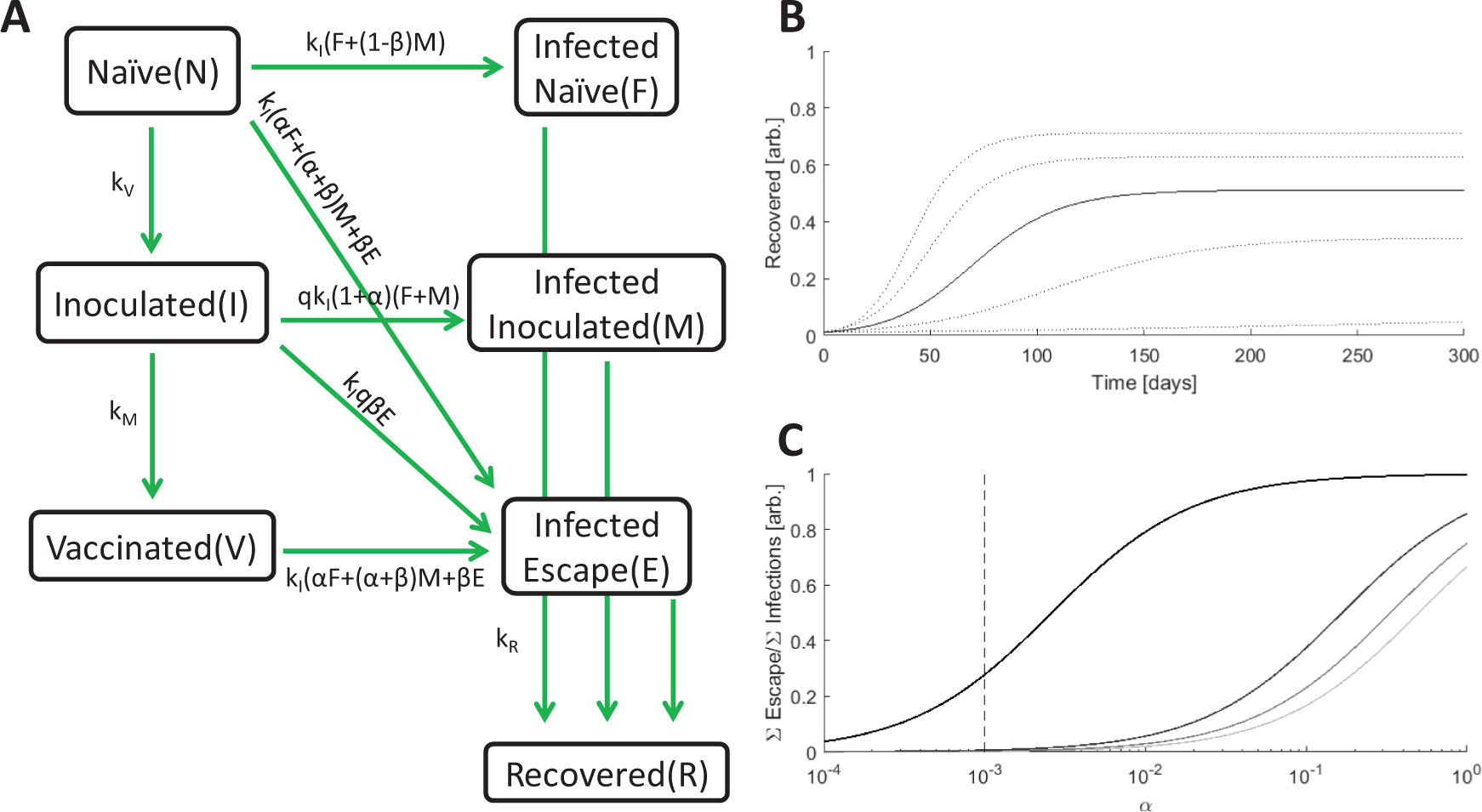
A. Schematic of the seven-compartment model with three susceptible, three infected, and one recovered compartments. Rates (divided by the state at the beginning of the arrow) are displayed. B. Simulated epidemics for k_I = [0.15,0.175,0.2 (solid line), 0.225,0.25], α = 0.001, β = 0.01. C. The ratio of cumulative escape infections to all cumulative infections for an epidemic over a range of α. β = [0.5,0.67,0.83,1], darker color indicates higher value, k_I = 0.2. The dotted line specifies the benchmark value of α = 0.001.

Within the timescale of the model, recovery is assumed to grant stable immunity, and any variation in population size due to birth/death is assumed to be negligible. It should be noted that, if recovery from the Infected-Naïve or Infected-Inoculated compartments does not confer immunity against escape infection, the key results in this work will have an even greater impact on the vaccination outcome. Hosts come into contact at rate k_C. For simplicity, we assume that contact with an escape-infected host can only produce an escape infection. Also, vaccine efficacy is assumed to be perfect such that vaccinated hosts cannot be infected with the originating strain. The inoculated–infected compartment is assumed to represent a symmetric composition of escape and originating infections such that the total probability of a naïve or inoculated host being infected after contact with a naïve–infected or inoculated–infected host is the same. Finally, we assume that the probability of escape infection is the same for naïve and vaccinated hosts across all three types of infected-susceptible host interactions. This construction yields the following transition probability matrices for naïve, inoculated, and vaccinated hosts:

k_{C} P_{N} = k_{I} [\begin{array}{c} 1 & 0 & α \\ 1 - β & 0 & α + β \\ 0 & 0 & β \end{array}]; k_{C} P_{I} = k_{I} [\begin{array}{c} 0 & 1 + α & 0 \\ 0 & 1 + α & 0 \\ 0 & 0 & β \end{array}]; k_{C} P_{V} = k_{I} [\begin{array}{c} 0 & 0 & α \\ 0 & 0 & α + β \\ 0 & 0 & β \end{array}]

where k_I represents the rate of infection for Naïve, Infected-Naïve host interactions which is determined both by the contact rate k_C and the infectivity of the originating strain. Rows represent interaction with each of the infected compartments (infected–naïve, infected–inoculated, and infected–escape). Columns represent transitions to each of the infected compartments.

An escape mutant can emerge in an infected–naïve or infected–inoculated host. The parameter α represents the infectivity of the escape variant relative to the originating strain when a naïve host interacts with an infected–naïve host. The parameter β represents the infectivity of an escape variant when a naïve host interacts with an infected–escape host relative to the infectivity of the originating strain when a naïve host interacts with an infected–naïve host. Informally, α reflects the ratio of escape variant to originating strain shed by infected–naïve hosts, whereas β reflects the fitness of an escape variant relative to the originating strain. Finally, we introduce the parameter q to represent the impact of varying the rate of host-host contact for Inoculated hosts relative to that for the other compartments. q>1 represents increased contact, and q < 1 corresponds to decreased contact. This completes the model description and structures the differential equations:

\begin{array}{c} N^{'} = - (k_{V} + k_{I} ((1 + α) (F + M) + βE)) N \\ I^{'} = k_{V} N - (k_{M} + {qk}_{I} ((1 + α) (F + M) + βE)) I \\ V^{'} = k_{M} I - k_{I} ((α + β) M + βE) V \\ F^{'} = k_{I} (NF + (1 - β) NM) - k_{R} F \\ M^{'} = {qk}_{I} (1 + α) (F + M) I - k_{R} M \\ E^{'} = k_{I} ((αF + (α + β) M + βE) (N + V) + qβEI) - k_{R} E \\ R^{'} = k_{R} (F + M + E) \end{array}

k_R = k_M = 1/7 are fixed across all simulations representing a time to recovery and time between inoculation and the acquisition of immunity of one week. Reducing k_I would prolong the epidemic and reducing k_M would increase the size of the inoculated compartment.

k_I is the principal determinant of epidemic magnitude and duration, with larger k_I leading to a greater cumulative number of infections over a shorter period of time (Figure 1B). However, feedback between the size of the infected population and the rate of host–host contact as well as spatial structure can decouple these variables. Throughout this work, k_I is set to a benchmark value of 0.2 resulting in 50% of the population being infected over a period of approximately 4 months.

The values of α and β impact the size of the infected–escape compartment. Even in the absence of vaccination, large α/β results in the emergence of would-be resistant variants (Figure 1C). In all analyses in this work, α is fixed at the benchmark value of 0.001 resulting in a modest number of would-be resistant infections for β close to 1 in the absence of vaccination. Although a larger α would result in a greater total number of escape infections, the fraction of those infections attributable to contact with inoculated hosts would be smaller.

The solutions of the ordinary differential equations (ODEs) were obtained using the MATLAB ode45 method.¹⁶ ode45 is based on the Dormand-Prince pair,¹⁷ an explicit Runge-Kutta formula which could be implemented in a variety of open-access alternatives. Epidemics are simulated until the size of the Recovery compartment at arbitrarily long times is approached. The principal quantity of interest is the cumulative number of infections. When k_V is selected to minimize this value, minima are found through explicit simulation over a range of rates. In the subsequent analysis, some values are expressed relative to the cumulative number of infections in the absence of vaccination, R_Null ~ 50%.

Results

In addition to the rate of vaccination, the outcome of a vaccination campaign depends on how far the epidemic has progressed before vaccination begins, which can be measured by the relative size of the recovered compartment. The results also depend on β, informally, the fitness of an escape variant relative to the originating strain. We considered two values for β (low: 0.01; high: 0.875) and varied both the start and the rate of vaccination. When β is low, that is, the escape mutant is much less fit than the originating strain (Figure 2A), vaccinating earlier and distributing the vaccine faster decreases the cumulative number of infections. If distribution is sufficiently prompt, the cumulative number of infections becomes negligible.

Figure 2. Optimal vaccine distribution.

A. The cumulative number of infections relative to no vaccination, R_Null, for a range of vaccine initiations and distribution rates. Here β is low, 0.01. B. The cumulative number of infections relative to no vaccination, R_Null, for a range of vaccine initiations and distribution rates and a large β (0.875). A/B. 3840 values were computed for each panel and 4× by 4× bilinearly interpolated points are displayed. Note that the color axis differs between A and B. C. The cumulative number of infections relative to no vaccination, R_Null, for β = [0.75 (dotted), 0.875 (dashed), 1 (solid)] and three relative contact rates, q = [0.2 (brown), 1 (black), 5 (gray)]. D. Simulated epidemics comparing a high fixed rate of vaccination, k_V = 0.03 (solid) representing the inoculation of 3% of naïve hosts per day, and the vaccination rate that minimizes the cumulative number of infections, MCI, each condition (dashed). β = 0.875 is fixed and q = [0.2 (brown), 1 (black), 5 (gray)]. E. Same as D. with a low fixed rate of vaccination, k_V = 0.01. C/D/E. The minima for the dashed lines in C correspond to the dashed lines in D/E.

However, the outcome substantially differs for high β (Figure 2B). In this case, the cumulative number of infections does not monotonically decrease with increasing vaccination rate due to the enhanced selective pressure for the emergence of escape variants, and the minimum cumulative number of infections is still substantial. In all subsequent analyses, the vaccination rate is varied but vaccination is fixed to begin when 1% of the population has recovered from infection.

Infections can be mitigated by reducing contacts among the hosts. We sought to determine how perturbing the contact rates for hosts in the inoculated compartment relative to that of all other compartments, q, affects the outcome. For β ranging between 0.75 and 1, we considered three relative contact rates, q = [0.2,1,5] (Figure 2C). Increasing the rate of host–host contact only within this compartment has a significant impact on the cumulative number of infections. The rate, at which the minimum cumulative number of infections, is achieved, is also perturbed. Furthermore, if k_V exceeds MCI, reducing q below 1 slows the accumulation of infections (Figure 2D). The converse is true for increasing q, and the landscape is similar when k_V is less than MCI (Figure 2E).

Having demonstrated how q perturbs MCI and how reducing q below 1 can mitigate or delay the accumulation of infections even if this rate is not met or, conversely, is exceeded, we sought to establish the impact of q on the cumulative number of infections across a wide range of β given k_V = MCI for each condition (Figure 3A). The cumulative number of infections is sensitive to q across the entire range of β. Varying q within an order of magnitude can substantially aid or hinder the vaccination campaign, and when q>>1, k_V = MCI = 0. Note that the maximum vaccination rate considered is k_V=0.03 representing the inoculation of 3% of naïve hosts per day. This rate is sufficiently high that the cumulative number of infections at this rate (Figure 3B) is similar or higher compared with the hypothetical case where the entire naïve population is immediately inoculated (Figure 3C). Some of these effects are not specific to the inoculated compartment. Increasing the rate of contact for any arbitrary subpopulation can increase the cumulative number of infections. We define the effective k_I, k_Ieff, such that the cumulative number of infections for k_I = k_Ieff and q = 1 is equal to the cumulative number of infections for k_I = 0.2 (the benchmark) and arbitrary q. Increasing q within an order of magnitude is equivalent to substantially increasing k_I for the entire population for the entirety of the epidemic (Figure 3D).

Figure 3. Post-vaccination contacts.

A. The cumulative number of infections relative to no vaccination, R_Null, for a range of β and q, where k_V = MCI minimizes the cumulative number of infections for each condition. B. Same as in A. for fixed k_V = 0.03 representing the inoculation of 3% of naïve hosts per day. C. Same as in A. for the case where all naïve hosts are immediately inoculated. D. Log of the effective k_I, k_Ieff, relative to k_I = 0.2, the benchmark, versus log of q for b = [0.5 (dotted line), 0.7 (dashed line), 1 (solid line)]. E. The cumulative number of infections relative to R_Null and q = 1 scaled by the fraction of infections due to vaccine escape, ∑Escape(q)/∑Infections(q)(∑Infections(q)-∑Infections (q = 1))/R_Null, for a range of β and q, where k_V = MCI for each condition. F. Same as in E for fixed k_V = 0.03. A-C/E/F. 961 values were computed for each panel and 4× by 4× bilinearly interpolated points are displayed.

We additionally consider the cumulative infections added or subtracted relative to the outcome corresponding to q = 1 and scaled by the fraction of infections due to vaccine escape (Figure 3E). Varying q within an order of magnitude alters the cumulative number of infections added or subtracted by more than 20% of the cumulative number of infections in the absence of vaccination, R_Null, again demonstrating the critical role played by inoculated hosts with respect to vaccine escape. The landscape is similar when then rate of vaccination is fixed (Figure 3F).

Discussion

Epidemics can be mitigated through the reduction of contact among the hosts via quarantines and other similar measures, and vaccination. A reduction in contact carries non-negligible social and economic burdens so that, when vaccination becomes possible, the continuation of such interventions might appear unnecessarily costly. Formulating the optimal public health response to balance these pressures is challenging and is further complicated by the possibility of vaccine escape. Escape variants emerging as a result of vaccination are likely to be less infectious than the originating strain. More infectious variants, which are also capable of vaccine escape, would likely already be in circulation. Indeed, multiple variants of SARS-CoV-2 capable of antibody evasion emerged prior to the onset of mass vaccination,¹⁸^–²³ indicating that this virus has a large mutational repertoire for evading antibodies while maintaining host receptor binding.

However, newly emergent variants after the onset of mass vaccination can still be substantially infectious and result in non-negligible disease incidence.²⁴^,²⁵ Here, we demonstrate that, even when escape variants are modestly less infectious than the originating strain, the cumulative number of infections does not monotonically decrease with the rate of vaccine distribution. This rate minimizing the cumulative number of infections, k_V = MCI, depends on the infectivity of the escape variants. To our knowledge this phenomenon, analogous to the evolution of antibiotic resistance, is not widely appreciated and, as such, seems to warrant consideration. However, minimizing the cumulative number of infections does not necessarily constitute the “optimal” vaccine distribution regime (see Limitations).

Of more practical concern is the role of inoculated hosts in the emergence of escape variants. Within low-dose antibiotic regimes,¹⁴^,¹⁵ hosts are susceptible to infection with the originating variant, and in such hosts, the pathogen is subjected to elevated selective pressures towards the emergence of resistance. Similarly, within inoculated hosts, the virus is subjected to gradually increasing selective pressures towards the emergence of resistance while the intra-host population remains sufficiently large to explore a substantial fraction of the mutation space. We demonstrate that moderately increasing or decreasing the host-host contact rates for inoculated hosts only can substantially aid or hinder the vaccination campaign. The time between vaccination and the acquisition of immunity can be readily approximated from clinical endpoints²⁶^,²⁷ and is likely to be short enough that the societal costs of limiting post-vaccination contact would be outweighed by these benefits.

Limitations

In this study, we leveraged classical modelling techniques to elucidate the factors that could substantially impact the outcome of any vaccination campaign; however the model presented here is not designed to forecast long-term outcome, a topic that has been thoroughly addressed for the case of SARS-Cov-2 and more generally.⁷^–¹³^,²⁸^–³⁰ Furthermore, it is important to emphasize that this is a theoretical analysis. Although we believe that our results highlight under appreciated aspects of vaccine distribution and that a thorough understanding of the features discussed here is critical for optimizing vaccine distribution, this work cannot be directly leveraged to make quantitative predictions about the ongoing SARS-CoV-2 pandemic.

Conclusions

The cumulative number of infections does not monotonically decrease with the rate of vaccine distribution. Contact rates for recently vaccinated and not yet fully immune (inoculated) hosts can have a substantial impact on the outcomes of vaccination campaigns. Even a brief and moderate limitation of contacts in this well-defined population can potentially mitigate epidemics.

The results presented here appear to be of immediate interest in relation to the vaccination campaign against SARS-CoV-2, which is ongoing at the time of this writing. Diversification of the virus is apparent³¹^–³³ and, as discussed above, antibody evasion had been investigated early on and demonstrated prior to mass vaccination.⁵^,⁶^,¹⁸^–²³^,³⁴^,³⁵ The existence of these variants indicates that evolution of the SARS-CoV-2 antigen is not subject to constraints that would prohibit reduction in antibody affinity to achieve immune evasion, while maintaining host receptor affinity sufficient for infection. In other words, the emergence of novel, infectious, vaccine-resistant variants remains possible if not probable for the duration of the ongoing vaccination campaign and beyond.

Obviously, virus evolution during a pandemic is a fast-moving target, so that some aspects of this analysis unavoidably will be outdated by the time of publication. In particular, vaccine efficiency is assumed to be perfect within this model, reflecting the expectation as of December 2020. As of March 2021, this is no longer the case. In this work, we emphasize the role played by individuals who recently received their vaccination. The selective environment within such a partially susceptible host in the days immediately following the administration of a perfect vaccine is not completely equivalent to that within a host that remains partially susceptible in the months following the administration of an imperfect vaccine. Nonetheless, we believe that this and related work³⁶^,³⁷ unequivocally demonstrates the continued importance of reducing host-host contact well after the onset of mass vaccination.

Author contributions

Conceptualization and Formal Analysis: NDR, YIW, and EVK

Writing – Original Draft Preparation: NDR and EVK

Writing – Review & Editing: NDR, YIW, and EVK

Data availability

Underlying data

No data are associated with this article.

Acknowledgements

The authors thank Koonin group members for helpful discussions.

References

1. CDC: Public Health Guidance for Potential COVID-19 Exposure Associated with Travel.2020.
2. Neumann-Böhme S, Varghese NE, Sabat I, et al.: Once we have it, will we use it? A European survey on willingness to be vaccinated against COVID-19. The European Journal of Health Economics. Springer; 2020.
3. Quinn SC, Kumar S, Freimuth VS, et al.: Public willingness to take a vaccine or drug under Emergency Use Authorization during the 2009 H1N1 pandemic. Biosecurity and Bioterrorism: Biodefense Strategy, Practice, and Science. 2009;7(3): 275–290. PubMed Abstract | Publisher Full Text | Free Full Text
4. Mills MC, Salisbury D: The challenges of distributing COVID-19 vaccinations. EClinicalMedicine. 2020. PubMed Abstract | Publisher Full Text | Free Full Text
5. Li Q, Wu J, Nie J, et al.: The impact of mutations in SARS-CoV-2 spike on viral infectivity and antigenicity. Cell 2020; 182(5): 1284–94. e9. Publisher Full Text
6. Kennedy DA, Read AF: Monitor for COVID-19 vaccine resistance evolution during clinical trials. PLoS Biol. 2020;18(11): e3001000. PubMed Abstract | Publisher Full Text | Free Full Text
7. Magpantay F, King A, Rohani P: Age-structure and transient dynamics in epidemiological systems. Journal of the Royal Society Interface. 2019;16(156): 20190151. PubMed Abstract | Publisher Full Text | Free Full Text
8. Restif O, Grenfell BT: Integrating life history and cross-immunity into the evolutionary dynamics of pathogens. Proceedings of the Royal Society B: Biological Sciences. 2006;273(1585): 409–416. PubMed Abstract | Publisher Full Text | Free Full Text
9. Rodrigues HS, Monteiro MTT, Torres DF: Vaccination models and optimal control strategies to dengue. Math Biosci. 2014;247: 1–12. PubMed Abstract | Publisher Full Text
10. Safan M, Kretzschmar M, Hadeler KP: Vaccination based control of infections in SIRS models with reinfection: special reference to pertussis. J Math Biol. 2013;67(5): 1083–1110. PubMed Abstract | Publisher Full Text
11. Scherer A, McLean A: Mathematical models of vaccination. British Medical Bulletin. 2002;62(1): 187–199. PubMed Abstract | Publisher Full Text
12. van Boven M, Mooi FR, Schellekens JF, de Melker HE , Kretzschmar M: Pathogen adaptation under imperfect vaccination: implications for pertussis. Proceedings of the Royal Society B: Biological Sciences 2005; 272(1572): 1617–1624. PubMed Abstract | Publisher Full Text | Free Full Text
13. Gandon S, Day T: The evolutionary epidemiology of vaccination. Journal of the Royal Society Interface. 2007;4(16): 803–817. PubMed Abstract | Publisher Full Text | Free Full Text
14. Livermore DM: Minimising antibiotic resistance. The Lancet Infectious Diseases. 2005;5(7): 450–459. PubMed Abstract | Publisher Full Text
15. Roberts JA, Kruger P, Paterson DL, et al.: Antibiotic resistance—what’s dosing got to do with it? Crit Care Med. 2008;36(8): 2433–2440. PubMed Abstract | Publisher Full Text
16. Shampine LF, Reichelt MW: The matlab ode suite. SIAM Journal on Scientific Computing. 1997;18(1): 1–22. Publisher Full Text
17. Dormand JR, Prince PJ: A family of embedded Runge-Kutta formulae. Journal of Computational and Applied Mathematics. 1980;6(1): 19–26. Publisher Full Text
18. Faria NR, Claro IM, Candido D, et al.: Genomic characterisation of an emergent SARS-CoV-2 lineage in Manaus: preliminary findings. Virological. Publisher Full Text
19. Tegally H, Wilkinson E, Giovanetti M, et al.: Emergence and rapid spread of a new severe acute respiratory syndrome-related coronavirus 2 (SARS-CoV-2) lineage with multiple spike mutations in South Africa. medRxiv. 2020. Publisher Full Text
20. Voloch CM, Ronaldo da Silva F, de Almeida LG , et al.: Genomic characterization of a novel SARS-CoV-2 lineage from Rio de Janeiro, Brazil. medRxiv 2020. PubMed Abstract | Publisher Full Text
21. Zhang W, Davis BD, Chen SS, et al.: Emergence of a Novel SARS-CoV-2 Variant in Southern California. JAMA. 2021. PubMed Abstract | Publisher Full Text | Free Full Text
22. England PH: Variants: distribution of cases data.
23. Brejová B, Hodorová V, Boršová K, et al.: B. 1.258_Delta, a SARS-CoV-2 variant with Delta_H69, Delta_V70 in the Spike protein circulating in the Czech Republic and Slovakia. arXiv preprint arXiv:210204689 2021.
24. Carman WF, Karayiannis P, Waters J, et al.: Vaccine-induced escape mutant of hepatitis B virus. The Lancet. 1990;336(8711): 325–329. PubMed Abstract | Publisher Full Text
25. Brueggemann AB, Pai R, Crook DW, et al.: Vaccine escape recombinants emerge after pneumococcal vaccination in the United States. PLoS Pathog. 2007;3(11): e168. PubMed Abstract | Publisher Full Text | Free Full Text
26. Polack FP, Thomas SJ, Kitchin N, et al.: Safety and efficacy of the BNT162b2 mRNA covid-19 vaccine. N Engl J Med. 2020. PubMed Abstract | Publisher Full Text | Free Full Text
27. Zhang Y, Zeng G, Pan H, et al.: Safety, tolerability, and immunogenicity of an inactivated SARS-CoV-2 vaccine in healthy adults aged 18–59 years: a randomised, double-blind, placebo-controlled, phase 1/2 clinical trial. The Lancet Infectious Diseases. 2020. PubMed Abstract | Publisher Full Text | Free Full Text
28. Saad-Roy CM, Wagner CE, Baker RE, et al.: Immune life history, vaccination, and the dynamics of SARS-CoV-2 over the next 5 years. Science. 2020;370(6518): 811–818. PubMed Abstract | Publisher Full Text | Free Full Text
29. Day T, Gandon S, Lion S, et al.: On the evolutionary epidemiology of SARS-CoV-2. Curr Biol. 2020. PubMed Abstract | Publisher Full Text | Free Full Text
30. Rochman ND, Wolf YI, Koonin EV: Evolution of Human Respiratory Virus Epidemics. medRxiv 2020. PubMed Abstract | Publisher Full Text | Free Full Text
31. Kumar S, Tao Q, Weaver S, et al.: An evolutionary portrait of the progenitor SARS-CoV-2 and its dominant offshoots in COVID-19 pandemic. bioRxiv 2020.
32. Rochman ND, Wolf YI, Faure G, Zhang F, Koonin EV: Ongoing Global and Regional Adaptive Evolution of SARS-CoV-2. bioRxiv 2020.
33. van Dorp L , Acman M, Richard D, et al.: Emergence of genomic diversity and recurrent mutations in SARS-CoV-2. Infection, Genetics, Evolution 2020; 104351. Publisher Full Text
34. Garrett ME, Galloway J, Chu HY, et al.: High resolution profiling of pathways of escape for SARS-CoV-2 spike-binding antibodies. bioRxiv 2020.
35. Starr TN, Greaney AJ, Hilton SK, et al.: Deep mutational scanning of SARS-CoV-2 receptor binding domain reveals constraints on folding and ACE2 binding. Cell 2020; 182(5): 1295–310. e20. Publisher Full Text
36. Makhoul M, Ayoub HH, Chemaitelly H, et al.: Epidemiological impact of SARS-CoV-2 vaccination: mathematical modeling analyses. Vaccines. 2020;8(4): 668. PubMed Abstract | Publisher Full Text | Free Full Text
37. Rella S, Kulikova Y, Dermitzakis E, Kondrashov F: SARS-CoV-2 transmission, vaccination rate and the fate of resistant strains. medRxiv 2021.

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 23 Apr 2021

Author details Author details

¹ National Center for Biotechnology Information, NIH, Bethesda, MD, 20894, USA

Nash Rochman
Roles: Conceptualization, Formal Analysis, Investigation, Methodology, Writing – Original Draft Preparation, Writing – Review & Editing

Yuri I Wolf
Roles: Conceptualization, Investigation, Writing – Review & Editing

Eugene V Koonin
Roles: Conceptualization, Investigation, Supervision, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

U.S. Department of Health and Human Services. NDR, YIW, and EVK are supported by the Intramural Research Program of the National Institutes of Health (National Library of Medicine).
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (2)

version 2

Revised

Published: 26 Aug 2021, 10:315

https://doi.org/10.12688/f1000research.52341.2

version 1

Published: 23 Apr 2021, 10:315

https://doi.org/10.12688/f1000research.52341.1

© 2021 Rochman N et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. The author(s) is/are employees of the US Government and therefore domestic copyright protection in USA does not apply to this work. The work may be protected under the copyright laws of other jurisdictions when used in those jurisdictions.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

Rochman N, Wolf YI and Koonin EV. Substantial impact of post-vaccination contacts on cumulative infections during viral epidemics [version 2; peer review: 2 approved]. F1000Research 2021, 10:315 (https://doi.org/10.12688/f1000research.52341.2)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 2

VERSION 2

PUBLISHED 26 Aug 2021

Revised

Views

Reviewer Report 26 Aug 2021

Sebastian Maximilian Schloer, Center for Molecular Biology of Inflammation, Institute of Medical Biochemistry, University of Muenster, Muenster, Germany

Approved

https://doi.org/10.5256/f1000research.76677.r92849

The authors have addressed all concerns adequately and improved the quality ... Continue reading

CITE

Report a concern

Respond or Comment

Views

Reviewer Report 26 Aug 2021

Fyodor A. Kondrashov, Institute of Science and Technology, Vienna, Austria

Approved

https://doi.org/10.5256/f1000research.76677.r92848

I thank the authors for addressing my ... Continue reading

CITE

Report a concern

Respond or Comment

Version 1

VERSION 1

PUBLISHED 23 Apr 2021

Views

Reviewer Report 12 Aug 2021

Fyodor A. Kondrashov, Institute of Science and Technology, Vienna, Austria

Approved with Reservations

https://doi.org/10.5256/f1000research.55607.r83821

The ongoing SARS-CoV-2 pandemic is driving the need to explore a new set of SIR models. One new feature that has not been considered previously is the impact of the state of individuals in the model that have just been vaccinated (inoculated) but have not yet achieved full immunity.

The authors took a classical SIR model and expanded it to include three new states: Infected with an Escape variant (E), Inoculated with the vaccine (I) and Inoculated but subsequently infected (M). The authors then explored the dynamics influenced by different parameters in this model. First, the higher contribution of Inoculated individuals to produce an Escaped variant. Second, a parameter that models limited interaction of inoculated hosts with others in the population. Third, the rate of vaccination.

In light of the ongoing debates on infection rate of those individuals that have been vaccinated with currently available vaccines against SARS-CoV-2, this study appears particularly timely and with potential to provide critical insight to contribution of the Inoculated but not fully vaccinated to the ongoing dynamics. However, some aspects of this model potentially reduce its applicability. Nevertheless, as a theoretical, rather than an empirical, model it does present an interesting view of the dynamics based on the model’s structure and assumptions, and even suggests a specific chokepoint of Escape variant evolution that may be controlled with simple policy solutions (the contact behavior of the Inoculated).

I have but two general criticisms, mostly related to presentation rather than design.

First, the presentation of the model made it challenging to understand the setup. Figure 1A could be more useful (for example, it could introduce the states I, F, M, etc), and it could even represent the transition parameters. The naming of the states departs from the SIR model, (so I is not Infected anymore, but Inoculated), which is fine, but added to the confusion. Finally, I was not a big fan of the equation representations. The authors have chosen to represent the equations in the shortest possible form. I prefer representation where each part of the equation reflects some transition state. To checkout the current equations I had to expand all of them and make my own determination of each transition state and how it fits to Figure 1A. Perhaps a more mathematically savvy reader would not have had to do it.

Second, as a theoretical model, it aims to describe some new understanding of interaction of parameters within the limitations of the model. A very successful example of this in the model is the analysis of the higher contribution of the Inoculated and Inoculated Infected states to dynamics and the introduction of another parameter, q, which limits the interaction of the Inoculated with other individuals. So, it explores the impact of the news states in the model and then introduces a specific way to mitigate their dangerous impact, which has important policy implications (granted that the underlying assumptions hold up). However, some aspects of the model cannot be applied directly to policy. Specifically, in several places of the manuscript the authors talk about the need for the determination of “optimal vaccination strategy”. While the model does explore vaccination rate as a parameter, I do not believe that their model is applicable to determination of a vaccine strategy at all. The reason for that is because a vaccine strategy considers some other parameters that are absent in the model. Specifically, an optimal vaccination strategy would consider, and probably prioritize, the short/medium term mortality rate and the hospital burden, something that is absent here.

The design of the model in the confines of the classical SIR structure (where the pandemic geos through the population without any negative feedback loops leading to waves) also makes it unrealistic in providing an optimization of policy. In sum, the conceptual description of the model, and the subsequent discussion, should avoid references to quantitative optimization of potential policy decisions that are likely to be influenced by parameters and outcomes that are not inherent in the model.

Minor issues:
Equation of V’ has a missing parenthesis.

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Partly

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Evolution

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Author Response (F1000Research Advisory Board Member) 26 Aug 2021

Eugene Koonin, National Center for Biotechnology Information, NIH, Bethesda, 20894, USA

26 Aug 2021

Author Response F1000Research Advisory Board Member

We thank the reviewer for their interest and constructive comments. The model presented has 7 compartments. There are two compartments which represent uninfected, vaccinated hosts: those recently inoculated (I) and ... Continue reading We thank the reviewer for their interest and constructive comments. The model presented has 7 compartments. There are two compartments which represent uninfected, vaccinated hosts: those recently inoculated (I) and those who have “matured” into the fully vaccinated compartment.

In light of the ongoing debates on infection rate of those individuals that have been vaccinated with currently available vaccines against SARS-CoV-2, this study appears particularly timely and with potential to provide critical insight to contribution of the Inoculated but not fully vaccinated to the ongoing dynamics. However, some aspects of this model potentially reduce its applicability. Nevertheless, as a theoretical, rather than an empirical, model it does present an interesting view of the dynamics based on the model’s structure and assumptions, and even suggests a specific chokepoint of Escape variant evolution that may be controlled with simple policy solutions (the contact behavior of the Inoculated).

We thank the reviewer again for their interest. This is precisely our motivation and we completely acknowledge the limitations of our model which is theoretical not empirical. As discussed below, we have modified the language in the text to emphasize this point.

I have but two general criticisms, mostly related to presentation rather than design.

First, the presentation of the model made it challenging to understand the setup. Figure 1A could be more useful (for example, it could introduce the states I, F, M, etc), and it could even represent the transition parameters. The naming of the states departs from the SIR model, (so I is not Infected anymore, but Inoculated), which is fine, but added to the confusion. Finally, I was not a big fan of the equation representations. The authors have chosen to represent the equations in the shortest possible form. I prefer representation where each part of the equation reflects some transition state. To checkout the current equations I had to expand all of them and make my own determination of each transition state and how it fits to Figure 1A. Perhaps a more mathematically savvy reader would not have had to do it.

We apologize for the confusion associated with the lack of detail in Figure 1A, which has been modified to include the state abbreviations (I,F,M, etc.) and the transition rates.

Second, as a theoretical model, it aims to describe some new understanding of interaction of parameters within the limitations of the model. A very successful example of this in the model is the analysis of the higher contribution of the Inoculated and Inoculated Infected states to dynamics and the introduction of another parameter, q, which limits the interaction of the Inoculated with other individuals. So, it explores the impact of the news states in the model and then introduces a specific way to mitigate their dangerous impact, which has important policy implications (granted that the underlying assumptions hold up). However, some aspects of the model cannot be applied directly to policy. Specifically, in several places of the manuscript the authors talk about the need for the determination of “optimal vaccination strategy”. While the model does explore vaccination rate as a parameter, I do not believe that their model is applicable to determination of a vaccine strategy at all. The reason for that is because a vaccine strategy considers some other parameters that are absent in the model. Specifically, an optimal vaccination strategy would consider, and probably prioritize, the short/medium term mortality rate and the hospital burden, something that is absent here.

We agree, and have modified the text accordingly, explicitly indicating that the model presented does not contain enough detail to define an optimal vaccination strategy. In many places in the revised version, we still refer to the “MCI”, which is the vaccination rate yielding the minimum cumulative number of infections for the given parameter set. We emphasize in the revised version that the MCI does not necessarily correspond to an “optimal” strategy given the many additional factors to consider.

The design of the model in the confines of the classical SIR structure (where the pandemic geos through the population without any negative feedback loops leading to waves) also makes it unrealistic in providing an optimization of policy.

We acknowledge this limitation and have briefly, but explicitly stated in the text that the reviewer’s work treats the impact of modeling cyclical transmission.

In sum, the conceptual description of the model, and the subsequent discussion, should avoid references to quantitative optimization of potential policy decisions that are likely to be influenced by parameters and outcomes that are not inherent in the model.

We have generally avoided language referring to optimization in the revised version.

Minor issues:
Equation of V’ has a missing parenthesis.

We apologize for the oversight and thank the reviewer for bringing this to our attention.
We thank the reviewer for their interest and constructive comments. The model presented has 7 compartments. There are two compartments which represent uninfected, vaccinated hosts: those recently inoculated (I) and those who have “matured” into the fully vaccinated compartment.

In light of the ongoing debates on infection rate of those individuals that have been vaccinated with currently available vaccines against SARS-CoV-2, this study appears particularly timely and with potential to provide critical insight to contribution of the Inoculated but not fully vaccinated to the ongoing dynamics. However, some aspects of this model potentially reduce its applicability. Nevertheless, as a theoretical, rather than an empirical, model it does present an interesting view of the dynamics based on the model’s structure and assumptions, and even suggests a specific chokepoint of Escape variant evolution that may be controlled with simple policy solutions (the contact behavior of the Inoculated).

We thank the reviewer again for their interest. This is precisely our motivation and we completely acknowledge the limitations of our model which is theoretical not empirical. As discussed below, we have modified the language in the text to emphasize this point.

I have but two general criticisms, mostly related to presentation rather than design.

First, the presentation of the model made it challenging to understand the setup. Figure 1A could be more useful (for example, it could introduce the states I, F, M, etc), and it could even represent the transition parameters. The naming of the states departs from the SIR model, (so I is not Infected anymore, but Inoculated), which is fine, but added to the confusion. Finally, I was not a big fan of the equation representations. The authors have chosen to represent the equations in the shortest possible form. I prefer representation where each part of the equation reflects some transition state. To checkout the current equations I had to expand all of them and make my own determination of each transition state and how it fits to Figure 1A. Perhaps a more mathematically savvy reader would not have had to do it.

We apologize for the confusion associated with the lack of detail in Figure 1A, which has been modified to include the state abbreviations (I,F,M, etc.) and the transition rates.

Second, as a theoretical model, it aims to describe some new understanding of interaction of parameters within the limitations of the model. A very successful example of this in the model is the analysis of the higher contribution of the Inoculated and Inoculated Infected states to dynamics and the introduction of another parameter, q, which limits the interaction of the Inoculated with other individuals. So, it explores the impact of the news states in the model and then introduces a specific way to mitigate their dangerous impact, which has important policy implications (granted that the underlying assumptions hold up). However, some aspects of the model cannot be applied directly to policy. Specifically, in several places of the manuscript the authors talk about the need for the determination of “optimal vaccination strategy”. While the model does explore vaccination rate as a parameter, I do not believe that their model is applicable to determination of a vaccine strategy at all. The reason for that is because a vaccine strategy considers some other parameters that are absent in the model. Specifically, an optimal vaccination strategy would consider, and probably prioritize, the short/medium term mortality rate and the hospital burden, something that is absent here.

We agree, and have modified the text accordingly, explicitly indicating that the model presented does not contain enough detail to define an optimal vaccination strategy. In many places in the revised version, we still refer to the “MCI”, which is the vaccination rate yielding the minimum cumulative number of infections for the given parameter set. We emphasize in the revised version that the MCI does not necessarily correspond to an “optimal” strategy given the many additional factors to consider.

The design of the model in the confines of the classical SIR structure (where the pandemic geos through the population without any negative feedback loops leading to waves) also makes it unrealistic in providing an optimization of policy.

We acknowledge this limitation and have briefly, but explicitly stated in the text that the reviewer’s work treats the impact of modeling cyclical transmission.

In sum, the conceptual description of the model, and the subsequent discussion, should avoid references to quantitative optimization of potential policy decisions that are likely to be influenced by parameters and outcomes that are not inherent in the model.

We have generally avoided language referring to optimization in the revised version.

Minor issues:
Equation of V’ has a missing parenthesis.

We apologize for the oversight and thank the reviewer for bringing this to our attention.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response (F1000Research Advisory Board Member) 26 Aug 2021

Eugene Koonin, National Center for Biotechnology Information, NIH, Bethesda, 20894, USA

26 Aug 2021

Author Response F1000Research Advisory Board Member

We thank the reviewer for their interest and constructive comments. The model presented has 7 compartments. There are two compartments which represent uninfected, vaccinated hosts: those recently inoculated (I) and ... Continue reading We thank the reviewer for their interest and constructive comments. The model presented has 7 compartments. There are two compartments which represent uninfected, vaccinated hosts: those recently inoculated (I) and those who have “matured” into the fully vaccinated compartment.

In light of the ongoing debates on infection rate of those individuals that have been vaccinated with currently available vaccines against SARS-CoV-2, this study appears particularly timely and with potential to provide critical insight to contribution of the Inoculated but not fully vaccinated to the ongoing dynamics. However, some aspects of this model potentially reduce its applicability. Nevertheless, as a theoretical, rather than an empirical, model it does present an interesting view of the dynamics based on the model’s structure and assumptions, and even suggests a specific chokepoint of Escape variant evolution that may be controlled with simple policy solutions (the contact behavior of the Inoculated).

We thank the reviewer again for their interest. This is precisely our motivation and we completely acknowledge the limitations of our model which is theoretical not empirical. As discussed below, we have modified the language in the text to emphasize this point.

I have but two general criticisms, mostly related to presentation rather than design.

First, the presentation of the model made it challenging to understand the setup. Figure 1A could be more useful (for example, it could introduce the states I, F, M, etc), and it could even represent the transition parameters. The naming of the states departs from the SIR model, (so I is not Infected anymore, but Inoculated), which is fine, but added to the confusion. Finally, I was not a big fan of the equation representations. The authors have chosen to represent the equations in the shortest possible form. I prefer representation where each part of the equation reflects some transition state. To checkout the current equations I had to expand all of them and make my own determination of each transition state and how it fits to Figure 1A. Perhaps a more mathematically savvy reader would not have had to do it.

We apologize for the confusion associated with the lack of detail in Figure 1A, which has been modified to include the state abbreviations (I,F,M, etc.) and the transition rates.

Second, as a theoretical model, it aims to describe some new understanding of interaction of parameters within the limitations of the model. A very successful example of this in the model is the analysis of the higher contribution of the Inoculated and Inoculated Infected states to dynamics and the introduction of another parameter, q, which limits the interaction of the Inoculated with other individuals. So, it explores the impact of the news states in the model and then introduces a specific way to mitigate their dangerous impact, which has important policy implications (granted that the underlying assumptions hold up). However, some aspects of the model cannot be applied directly to policy. Specifically, in several places of the manuscript the authors talk about the need for the determination of “optimal vaccination strategy”. While the model does explore vaccination rate as a parameter, I do not believe that their model is applicable to determination of a vaccine strategy at all. The reason for that is because a vaccine strategy considers some other parameters that are absent in the model. Specifically, an optimal vaccination strategy would consider, and probably prioritize, the short/medium term mortality rate and the hospital burden, something that is absent here.

We agree, and have modified the text accordingly, explicitly indicating that the model presented does not contain enough detail to define an optimal vaccination strategy. In many places in the revised version, we still refer to the “MCI”, which is the vaccination rate yielding the minimum cumulative number of infections for the given parameter set. We emphasize in the revised version that the MCI does not necessarily correspond to an “optimal” strategy given the many additional factors to consider.

The design of the model in the confines of the classical SIR structure (where the pandemic geos through the population without any negative feedback loops leading to waves) also makes it unrealistic in providing an optimization of policy.

We acknowledge this limitation and have briefly, but explicitly stated in the text that the reviewer’s work treats the impact of modeling cyclical transmission.

In sum, the conceptual description of the model, and the subsequent discussion, should avoid references to quantitative optimization of potential policy decisions that are likely to be influenced by parameters and outcomes that are not inherent in the model.

We have generally avoided language referring to optimization in the revised version.

Minor issues:
Equation of V’ has a missing parenthesis.

We apologize for the oversight and thank the reviewer for bringing this to our attention.
We thank the reviewer for their interest and constructive comments. The model presented has 7 compartments. There are two compartments which represent uninfected, vaccinated hosts: those recently inoculated (I) and those who have “matured” into the fully vaccinated compartment.

In light of the ongoing debates on infection rate of those individuals that have been vaccinated with currently available vaccines against SARS-CoV-2, this study appears particularly timely and with potential to provide critical insight to contribution of the Inoculated but not fully vaccinated to the ongoing dynamics. However, some aspects of this model potentially reduce its applicability. Nevertheless, as a theoretical, rather than an empirical, model it does present an interesting view of the dynamics based on the model’s structure and assumptions, and even suggests a specific chokepoint of Escape variant evolution that may be controlled with simple policy solutions (the contact behavior of the Inoculated).

We thank the reviewer again for their interest. This is precisely our motivation and we completely acknowledge the limitations of our model which is theoretical not empirical. As discussed below, we have modified the language in the text to emphasize this point.

I have but two general criticisms, mostly related to presentation rather than design.

First, the presentation of the model made it challenging to understand the setup. Figure 1A could be more useful (for example, it could introduce the states I, F, M, etc), and it could even represent the transition parameters. The naming of the states departs from the SIR model, (so I is not Infected anymore, but Inoculated), which is fine, but added to the confusion. Finally, I was not a big fan of the equation representations. The authors have chosen to represent the equations in the shortest possible form. I prefer representation where each part of the equation reflects some transition state. To checkout the current equations I had to expand all of them and make my own determination of each transition state and how it fits to Figure 1A. Perhaps a more mathematically savvy reader would not have had to do it.

We apologize for the confusion associated with the lack of detail in Figure 1A, which has been modified to include the state abbreviations (I,F,M, etc.) and the transition rates.

Second, as a theoretical model, it aims to describe some new understanding of interaction of parameters within the limitations of the model. A very successful example of this in the model is the analysis of the higher contribution of the Inoculated and Inoculated Infected states to dynamics and the introduction of another parameter, q, which limits the interaction of the Inoculated with other individuals. So, it explores the impact of the news states in the model and then introduces a specific way to mitigate their dangerous impact, which has important policy implications (granted that the underlying assumptions hold up). However, some aspects of the model cannot be applied directly to policy. Specifically, in several places of the manuscript the authors talk about the need for the determination of “optimal vaccination strategy”. While the model does explore vaccination rate as a parameter, I do not believe that their model is applicable to determination of a vaccine strategy at all. The reason for that is because a vaccine strategy considers some other parameters that are absent in the model. Specifically, an optimal vaccination strategy would consider, and probably prioritize, the short/medium term mortality rate and the hospital burden, something that is absent here.

We agree, and have modified the text accordingly, explicitly indicating that the model presented does not contain enough detail to define an optimal vaccination strategy. In many places in the revised version, we still refer to the “MCI”, which is the vaccination rate yielding the minimum cumulative number of infections for the given parameter set. We emphasize in the revised version that the MCI does not necessarily correspond to an “optimal” strategy given the many additional factors to consider.

The design of the model in the confines of the classical SIR structure (where the pandemic geos through the population without any negative feedback loops leading to waves) also makes it unrealistic in providing an optimization of policy.

We acknowledge this limitation and have briefly, but explicitly stated in the text that the reviewer’s work treats the impact of modeling cyclical transmission.

In sum, the conceptual description of the model, and the subsequent discussion, should avoid references to quantitative optimization of potential policy decisions that are likely to be influenced by parameters and outcomes that are not inherent in the model.

We have generally avoided language referring to optimization in the revised version.

Minor issues:
Equation of V’ has a missing parenthesis.

We apologize for the oversight and thank the reviewer for bringing this to our attention.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Views

Reviewer Report 16 Jul 2021

Sebastian Maximilian Schloer, Center for Molecular Biology of Inflammation, Institute of Medical Biochemistry, University of Muenster, Muenster, Germany

Approved with Reservations

https://doi.org/10.5256/f1000research.55607.r89322

In the manuscript entitled “Substantial impact of post-vaccination contacts on cumulative infections during viral epidemics”, the authors refer to the interaction between vaccination rate and limiting post-vaccination contacts for the course of an epidemic/pandemic.

Naturally, this is a very relevant issue that deserves the careful attention of researchers working in this field. By modeling the epidemic/pandemic spreading of zoonotic diseases considering the vaccination rate may provide new insights for the future management of COVID-19.

While study design and work are technically sound correct, the presentation of the results could be improved by adding figure legends (figure 2 C/D/E). To increase the readability of the data, it might be helpful to use a similar scale in figure 2 AB for easier comparison between the two different scenarios. The authors also assumed a very high vaccination rate for the calculation of epidemic/pandemic spreading, a lower vaccination rate (k_V=0.005 like observed in the USA) would be better at covering a realistic influence of vaccination and post-vaccination contacts for the course of the epidemic. Thus, the author should include data obtained with a lower daily vaccination rate to verify the relevance of the model and results for the management of future epidemics/pandemics.

The authors should also consider the pulsatile spreading and vaccination (that is normally, and currently observed in the SARS-CoV-2 pandemic) for zoonotic diseases and their management.

In sum, this is a relevant and timely topic. The manuscript is well-written and the comprehensive overview of vaccination rate and limiting post-vaccination contacts for the management of the ongoing COVID-19 pandemic is clearly presented. I hope that the authors can expand the section by adding the required changes and considerations.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

Partly
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: virology, pharmacology, zoonotic diseases

CITE

Report a concern

Author Response (F1000Research Advisory Board Member) 26 Aug 2021

Eugene Koonin, National Center for Biotechnology Information, NIH, Bethesda, 20894, USA

26 Aug 2021

Author Response F1000Research Advisory Board Member

We thank the reviewer for their kind and constructive remarks.

While study design and work are technically sound correct, the presentation of the results could be improved by adding ... Continue reading We thank the reviewer for their kind and constructive remarks.

While study design and work are technically sound correct, the presentation of the results could be improved by adding figure legends (figure 2 C/D/E).

Legends have been added.

To increase the readability of the data, it might be helpful to use a similar scale in figure 2 AB for easier comparison between the two different scenarios.

We appreciate the reviewer’s suggestion; however, we found if we set the color scale to run from 0 to 1 for both panels, the variation in Figure 2B is hard to see with the same colormap. We have elected to keep separate scales but have modified the Figure description to emphasize that the color scales are different.

The authors also assumed a very high vaccination rate for the calculation of epidemic/pandemic spreading, a lower vaccination rate (kV=0.005 like observed in the USA) would be better at covering a realistic influence of vaccination and post-vaccination contacts for the course of the epidemic. Thus, the author should include data obtained with a lower daily vaccination rate to verify the relevance of the model and results for the management of future epidemics/pandemics.

We apologize for any confusion. Figures 2A/B/C display results for a range of vaccination rates from 1e-5 to 3e-2. Figure 2D displays two fixed rates 0.01 and 0.03 in addition to the vaccination rate which yields the fewest cumulative number of infections which in some parameter regimes is approximately the rate suggested by the reviewer. Figure 3 displays both a fixed rate of 0.03 and the vaccination rate which yields the smallest cumulative number of infections. Regarding realism for the choice of fixed rates, we acknowledge and state in the text that 0.03 represents a high rate of vaccination; however, we also do not attempt (and have modified the language in the revised version to this effect) to make empirical projections which could be explicitly interpreted in the context of any specific epidemic. We do not model age structure, for example, which significantly affects both the natural history of SARS-CoV-2 as well as the vaccine rollout (administered to older individuals first). Our goal in selecting the range of rates displayed was to demonstrate that the dependence on the cumulative number of infections on vaccine distribution rate is nonmonotonic within a nontrivial parameter regime (the majority of the population is vaccinated over a period of months to a year).

The authors should also consider the pulsatile spreading and vaccination (that is normally, and currently observed in the SARS-CoV-2 pandemic) for zoonotic diseases and their management.

We appreciate the reviewer’s input. Incorporating pulsatile or periodic forcing into the model would require significant changes to be made which we feel are outside the scope of the current work. We do, however, cite Rella et al. (2021) and have modified the text to indicate that cyclical models are addressed in this reference.

In sum, this is a relevant and timely topic. The manuscript is well-written and the comprehensive overview of vaccination rate and limiting post-vaccination contacts for the management of the ongoing COVID-19 pandemic is clearly presented. I hope that the authors can expand the section by adding the required changes and considerations.

We thank the reviewer for their interest and hope they find the revised version satisfactory.
We thank the reviewer for their kind and constructive remarks.

While study design and work are technically sound correct, the presentation of the results could be improved by adding figure legends (figure 2 C/D/E).

Legends have been added.

To increase the readability of the data, it might be helpful to use a similar scale in figure 2 AB for easier comparison between the two different scenarios.

We appreciate the reviewer’s suggestion; however, we found if we set the color scale to run from 0 to 1 for both panels, the variation in Figure 2B is hard to see with the same colormap. We have elected to keep separate scales but have modified the Figure description to emphasize that the color scales are different.

The authors also assumed a very high vaccination rate for the calculation of epidemic/pandemic spreading, a lower vaccination rate (kV=0.005 like observed in the USA) would be better at covering a realistic influence of vaccination and post-vaccination contacts for the course of the epidemic. Thus, the author should include data obtained with a lower daily vaccination rate to verify the relevance of the model and results for the management of future epidemics/pandemics.

We apologize for any confusion. Figures 2A/B/C display results for a range of vaccination rates from 1e-5 to 3e-2. Figure 2D displays two fixed rates 0.01 and 0.03 in addition to the vaccination rate which yields the fewest cumulative number of infections which in some parameter regimes is approximately the rate suggested by the reviewer. Figure 3 displays both a fixed rate of 0.03 and the vaccination rate which yields the smallest cumulative number of infections. Regarding realism for the choice of fixed rates, we acknowledge and state in the text that 0.03 represents a high rate of vaccination; however, we also do not attempt (and have modified the language in the revised version to this effect) to make empirical projections which could be explicitly interpreted in the context of any specific epidemic. We do not model age structure, for example, which significantly affects both the natural history of SARS-CoV-2 as well as the vaccine rollout (administered to older individuals first). Our goal in selecting the range of rates displayed was to demonstrate that the dependence on the cumulative number of infections on vaccine distribution rate is nonmonotonic within a nontrivial parameter regime (the majority of the population is vaccinated over a period of months to a year).

The authors should also consider the pulsatile spreading and vaccination (that is normally, and currently observed in the SARS-CoV-2 pandemic) for zoonotic diseases and their management.

We appreciate the reviewer’s input. Incorporating pulsatile or periodic forcing into the model would require significant changes to be made which we feel are outside the scope of the current work. We do, however, cite Rella et al. (2021) and have modified the text to indicate that cyclical models are addressed in this reference.

In sum, this is a relevant and timely topic. The manuscript is well-written and the comprehensive overview of vaccination rate and limiting post-vaccination contacts for the management of the ongoing COVID-19 pandemic is clearly presented. I hope that the authors can expand the section by adding the required changes and considerations.

We thank the reviewer for their interest and hope they find the revised version satisfactory.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response (F1000Research Advisory Board Member) 26 Aug 2021

Eugene Koonin, National Center for Biotechnology Information, NIH, Bethesda, 20894, USA

26 Aug 2021

Author Response F1000Research Advisory Board Member

We thank the reviewer for their kind and constructive remarks.

While study design and work are technically sound correct, the presentation of the results could be improved by adding ... Continue reading We thank the reviewer for their kind and constructive remarks.

While study design and work are technically sound correct, the presentation of the results could be improved by adding figure legends (figure 2 C/D/E).

Legends have been added.

To increase the readability of the data, it might be helpful to use a similar scale in figure 2 AB for easier comparison between the two different scenarios.

We appreciate the reviewer’s suggestion; however, we found if we set the color scale to run from 0 to 1 for both panels, the variation in Figure 2B is hard to see with the same colormap. We have elected to keep separate scales but have modified the Figure description to emphasize that the color scales are different.

The authors also assumed a very high vaccination rate for the calculation of epidemic/pandemic spreading, a lower vaccination rate (kV=0.005 like observed in the USA) would be better at covering a realistic influence of vaccination and post-vaccination contacts for the course of the epidemic. Thus, the author should include data obtained with a lower daily vaccination rate to verify the relevance of the model and results for the management of future epidemics/pandemics.

We apologize for any confusion. Figures 2A/B/C display results for a range of vaccination rates from 1e-5 to 3e-2. Figure 2D displays two fixed rates 0.01 and 0.03 in addition to the vaccination rate which yields the fewest cumulative number of infections which in some parameter regimes is approximately the rate suggested by the reviewer. Figure 3 displays both a fixed rate of 0.03 and the vaccination rate which yields the smallest cumulative number of infections. Regarding realism for the choice of fixed rates, we acknowledge and state in the text that 0.03 represents a high rate of vaccination; however, we also do not attempt (and have modified the language in the revised version to this effect) to make empirical projections which could be explicitly interpreted in the context of any specific epidemic. We do not model age structure, for example, which significantly affects both the natural history of SARS-CoV-2 as well as the vaccine rollout (administered to older individuals first). Our goal in selecting the range of rates displayed was to demonstrate that the dependence on the cumulative number of infections on vaccine distribution rate is nonmonotonic within a nontrivial parameter regime (the majority of the population is vaccinated over a period of months to a year).

The authors should also consider the pulsatile spreading and vaccination (that is normally, and currently observed in the SARS-CoV-2 pandemic) for zoonotic diseases and their management.

We appreciate the reviewer’s input. Incorporating pulsatile or periodic forcing into the model would require significant changes to be made which we feel are outside the scope of the current work. We do, however, cite Rella et al. (2021) and have modified the text to indicate that cyclical models are addressed in this reference.

In sum, this is a relevant and timely topic. The manuscript is well-written and the comprehensive overview of vaccination rate and limiting post-vaccination contacts for the management of the ongoing COVID-19 pandemic is clearly presented. I hope that the authors can expand the section by adding the required changes and considerations.

We thank the reviewer for their interest and hope they find the revised version satisfactory.
We thank the reviewer for their kind and constructive remarks.

While study design and work are technically sound correct, the presentation of the results could be improved by adding figure legends (figure 2 C/D/E).

Legends have been added.

To increase the readability of the data, it might be helpful to use a similar scale in figure 2 AB for easier comparison between the two different scenarios.

We appreciate the reviewer’s suggestion; however, we found if we set the color scale to run from 0 to 1 for both panels, the variation in Figure 2B is hard to see with the same colormap. We have elected to keep separate scales but have modified the Figure description to emphasize that the color scales are different.

The authors also assumed a very high vaccination rate for the calculation of epidemic/pandemic spreading, a lower vaccination rate (kV=0.005 like observed in the USA) would be better at covering a realistic influence of vaccination and post-vaccination contacts for the course of the epidemic. Thus, the author should include data obtained with a lower daily vaccination rate to verify the relevance of the model and results for the management of future epidemics/pandemics.

We apologize for any confusion. Figures 2A/B/C display results for a range of vaccination rates from 1e-5 to 3e-2. Figure 2D displays two fixed rates 0.01 and 0.03 in addition to the vaccination rate which yields the fewest cumulative number of infections which in some parameter regimes is approximately the rate suggested by the reviewer. Figure 3 displays both a fixed rate of 0.03 and the vaccination rate which yields the smallest cumulative number of infections. Regarding realism for the choice of fixed rates, we acknowledge and state in the text that 0.03 represents a high rate of vaccination; however, we also do not attempt (and have modified the language in the revised version to this effect) to make empirical projections which could be explicitly interpreted in the context of any specific epidemic. We do not model age structure, for example, which significantly affects both the natural history of SARS-CoV-2 as well as the vaccine rollout (administered to older individuals first). Our goal in selecting the range of rates displayed was to demonstrate that the dependence on the cumulative number of infections on vaccine distribution rate is nonmonotonic within a nontrivial parameter regime (the majority of the population is vaccinated over a period of months to a year).

The authors should also consider the pulsatile spreading and vaccination (that is normally, and currently observed in the SARS-CoV-2 pandemic) for zoonotic diseases and their management.

We appreciate the reviewer’s input. Incorporating pulsatile or periodic forcing into the model would require significant changes to be made which we feel are outside the scope of the current work. We do, however, cite Rella et al. (2021) and have modified the text to indicate that cyclical models are addressed in this reference.

In sum, this is a relevant and timely topic. The manuscript is well-written and the comprehensive overview of vaccination rate and limiting post-vaccination contacts for the management of the ongoing COVID-19 pandemic is clearly presented. I hope that the authors can expand the section by adding the required changes and considerations.

We thank the reviewer for their interest and hope they find the revised version satisfactory.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 23 Apr 2021

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 2 (revision) 26 Aug 21	read	read
Version 1 23 Apr 21	read	read

Sebastian Maximilian Schloer, University of Muenster, Muenster, Germany
Fyodor A. Kondrashov, Institute of Science and Technology, Vienna, Austria

Comments on this article

All Comments(0)

Add a comment

Browse by related subjects

Back to all reports

Reviewer Report

11 Views

26 Aug 2021 | for Version 2

Sebastian Maximilian Schloer, Center for Molecular Biology of Inflammation, Institute of Medical Biochemistry, University of Muenster, Muenster, Germany

11 Views Cite this report Responses(0)

Approved

The authors have addressed all concerns adequately and improved the quality of the manuscript and its readability. I recommend the manuscript for indexing.

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Virology, pharmacology, zoonotic diseases

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

8 Views

26 Aug 2021 | for Version 2

Fyodor A. Kondrashov, Institute of Science and Technology, Vienna, Austria

8 Views Cite this report Responses(0)

Approved

I thank the authors for addressing my previous comments and have no further remarks.

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Evolution

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

10 Views

12 Aug 2021 | for Version 1

Fyodor A. Kondrashov, Institute of Science and Technology, Vienna, Austria

10 Views Cite this report Responses(1)

Approved With Reservations

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Partly

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Evolution

Respond to this report

Responses (1)

Author Response F1000Research Advisory Board Member

26 Aug 2021

Eugene Koonin, National Center for Biotechnology Information, NIH, Bethesda, 20894, USA

We thank the reviewer for their interest and constructive comments. The model presented has 7 compartments. There are two compartments which represent uninfected, vaccinated hosts: those recently inoculated (I) and those who have “matured” into the fully vaccinated compartment.

In light of the ongoing debates on infection rate of those individuals that have been vaccinated with currently available vaccines against SARS-CoV-2, this study appears particularly timely and with potential to provide critical insight to contribution of the Inoculated but not fully vaccinated to the ongoing dynamics. However, some aspects of this model potentially reduce its applicability. Nevertheless, as a theoretical, rather than an empirical, model it does present an interesting view of the dynamics based on the model’s structure and assumptions, and even suggests a specific chokepoint of Escape variant evolution that may be controlled with simple policy solutions (the contact behavior of the Inoculated).

We thank the reviewer again for their interest. This is precisely our motivation and we completely acknowledge the limitations of our model which is theoretical not empirical. As discussed below, we have modified the language in the text to emphasize this point.

I have but two general criticisms, mostly related to presentation rather than design.

First, the presentation of the model made it challenging to understand the setup. Figure 1A could be more useful (for example, it could introduce the states I, F, M, etc), and it could even represent the transition parameters. The naming of the states departs from the SIR model, (so I is not Infected anymore, but Inoculated), which is fine, but added to the confusion. Finally, I was not a big fan of the equation representations. The authors have chosen to represent the equations in the shortest possible form. I prefer representation where each part of the equation reflects some transition state. To checkout the current equations I had to expand all of them and make my own determination of each transition state and how it fits to Figure 1A. Perhaps a more mathematically savvy reader would not have had to do it.

We apologize for the confusion associated with the lack of detail in Figure 1A, which has been modified to include the state abbreviations (I,F,M, etc.) and the transition rates.

Second, as a theoretical model, it aims to describe some new understanding of interaction of parameters within the limitations of the model. A very successful example of this in the model is the analysis of the higher contribution of the Inoculated and Inoculated Infected states to dynamics and the introduction of another parameter, q, which limits the interaction of the Inoculated with other individuals. So, it explores the impact of the news states in the model and then introduces a specific way to mitigate their dangerous impact, which has important policy implications (granted that the underlying assumptions hold up). However, some aspects of the model cannot be applied directly to policy. Specifically, in several places of the manuscript the authors talk about the need for the determination of “optimal vaccination strategy”. While the model does explore vaccination rate as a parameter, I do not believe that their model is applicable to determination of a vaccine strategy at all. The reason for that is because a vaccine strategy considers some other parameters that are absent in the model. Specifically, an optimal vaccination strategy would consider, and probably prioritize, the short/medium term mortality rate and the hospital burden, something that is absent here.

We agree, and have modified the text accordingly, explicitly indicating that the model presented does not contain enough detail to define an optimal vaccination strategy. In many places in the revised version, we still refer to the “MCI”, which is the vaccination rate yielding the minimum cumulative number of infections for the given parameter set. We emphasize in the revised version that the MCI does not necessarily correspond to an “optimal” strategy given the many additional factors to consider.

The design of the model in the confines of the classical SIR structure (where the pandemic geos through the population without any negative feedback loops leading to waves) also makes it unrealistic in providing an optimization of policy.

We acknowledge this limitation and have briefly, but explicitly stated in the text that the reviewer’s work treats the impact of modeling cyclical transmission.

In sum, the conceptual description of the model, and the subsequent discussion, should avoid references to quantitative optimization of potential policy decisions that are likely to be influenced by parameters and outcomes that are not inherent in the model.

We have generally avoided language referring to optimization in the revised version.

Minor issues:
Equation of V’ has a missing parenthesis.

We apologize for the oversight and thank the reviewer for bringing this to our attention.

View more View less

Competing Interests

No competing interests were disclosed.

Back to all reports

Reviewer Report

21 Views

16 Jul 2021 | for Version 1

Sebastian Maximilian Schloer, Center for Molecular Biology of Inflammation, Institute of Medical Biochemistry, University of Muenster, Muenster, Germany

21 Views Cite this report Responses(1)

Approved With Reservations

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

Partly
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

virology, pharmacology, zoonotic diseases

Respond to this report

Responses (1)

Author Response F1000Research Advisory Board Member

26 Aug 2021

Eugene Koonin, National Center for Biotechnology Information, NIH, Bethesda, 20894, USA

We thank the reviewer for their kind and constructive remarks.

While study design and work are technically sound correct, the presentation of the results could be improved by adding figure legends (figure 2 C/D/E).

Legends have been added.

To increase the readability of the data, it might be helpful to use a similar scale in figure 2 AB for easier comparison between the two different scenarios.

We appreciate the reviewer’s suggestion; however, we found if we set the color scale to run from 0 to 1 for both panels, the variation in Figure 2B is hard to see with the same colormap. We have elected to keep separate scales but have modified the Figure description to emphasize that the color scales are different.

The authors also assumed a very high vaccination rate for the calculation of epidemic/pandemic spreading, a lower vaccination rate (kV=0.005 like observed in the USA) would be better at covering a realistic influence of vaccination and post-vaccination contacts for the course of the epidemic. Thus, the author should include data obtained with a lower daily vaccination rate to verify the relevance of the model and results for the management of future epidemics/pandemics.

We apologize for any confusion. Figures 2A/B/C display results for a range of vaccination rates from 1e-5 to 3e-2. Figure 2D displays two fixed rates 0.01 and 0.03 in addition to the vaccination rate which yields the fewest cumulative number of infections which in some parameter regimes is approximately the rate suggested by the reviewer. Figure 3 displays both a fixed rate of 0.03 and the vaccination rate which yields the smallest cumulative number of infections. Regarding realism for the choice of fixed rates, we acknowledge and state in the text that 0.03 represents a high rate of vaccination; however, we also do not attempt (and have modified the language in the revised version to this effect) to make empirical projections which could be explicitly interpreted in the context of any specific epidemic. We do not model age structure, for example, which significantly affects both the natural history of SARS-CoV-2 as well as the vaccine rollout (administered to older individuals first). Our goal in selecting the range of rates displayed was to demonstrate that the dependence on the cumulative number of infections on vaccine distribution rate is nonmonotonic within a nontrivial parameter regime (the majority of the population is vaccinated over a period of months to a year).

The authors should also consider the pulsatile spreading and vaccination (that is normally, and currently observed in the SARS-CoV-2 pandemic) for zoonotic diseases and their management.

We appreciate the reviewer’s input. Incorporating pulsatile or periodic forcing into the model would require significant changes to be made which we feel are outside the scope of the current work. We do, however, cite Rella et al. (2021) and have modified the text to indicate that cyclical models are addressed in this reference.

In sum, this is a relevant and timely topic. The manuscript is well-written and the comprehensive overview of vaccination rate and limiting post-vaccination contacts for the management of the ongoing COVID-19 pandemic is clearly presented. I hope that the authors can expand the section by adding the required changes and considerations.

We thank the reviewer for their interest and hope they find the revised version satisfactory.

View more View less

Competing Interests

No competing interests were disclosed.

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

[1] 1. CDC: Public Health Guidance for Potential COVID-19 Exposure Associated with Travel.2020.

[2] 2. Neumann-Böhme S, Varghese NE, Sabat I, et al.: Once we have it, will we use it? A European survey on willingness to be vaccinated against COVID-19. The European Journal of Health Economics. Springer; 2020.

[3] 3. Quinn SC, Kumar S, Freimuth VS, et al.: Public willingness to take a vaccine or drug under Emergency Use Authorization during the 2009 H1N1 pandemic. Biosecurity and Bioterrorism: Biodefense Strategy, Practice, and Science. 2009;7(3): 275–290. PubMed Abstract | Publisher Full Text | Free Full Text

[4] 4. Mills MC, Salisbury D: The challenges of distributing COVID-19 vaccinations. EClinicalMedicine. 2020. PubMed Abstract | Publisher Full Text | Free Full Text

[5] 5. Li Q, Wu J, Nie J, et al.: The impact of mutations in SARS-CoV-2 spike on viral infectivity and antigenicity. Cell 2020; 182(5): 1284–94. e9. Publisher Full Text

[6] 6. Kennedy DA, Read AF: Monitor for COVID-19 vaccine resistance evolution during clinical trials. PLoS Biol. 2020;18(11): e3001000. PubMed Abstract | Publisher Full Text | Free Full Text

[7] 7. Magpantay F, King A, Rohani P: Age-structure and transient dynamics in epidemiological systems. Journal of the Royal Society Interface. 2019;16(156): 20190151. PubMed Abstract | Publisher Full Text | Free Full Text

[8] 8. Restif O, Grenfell BT: Integrating life history and cross-immunity into the evolutionary dynamics of pathogens. Proceedings of the Royal Society B: Biological Sciences. 2006;273(1585): 409–416. PubMed Abstract | Publisher Full Text | Free Full Text

[9] 9. Rodrigues HS, Monteiro MTT, Torres DF: Vaccination models and optimal control strategies to dengue. Math Biosci. 2014;247: 1–12. PubMed Abstract | Publisher Full Text

[10] 10. Safan M, Kretzschmar M, Hadeler KP: Vaccination based control of infections in SIRS models with reinfection: special reference to pertussis. J Math Biol. 2013;67(5): 1083–1110. PubMed Abstract | Publisher Full Text

[11] 11. Scherer A, McLean A: Mathematical models of vaccination. British Medical Bulletin. 2002;62(1): 187–199. PubMed Abstract | Publisher Full Text

[12] 12. van Boven M, Mooi FR, Schellekens JF, de Melker HE , Kretzschmar M: Pathogen adaptation under imperfect vaccination: implications for pertussis. Proceedings of the Royal Society B: Biological Sciences 2005; 272(1572): 1617–1624. PubMed Abstract | Publisher Full Text | Free Full Text

[13] 13. Gandon S, Day T: The evolutionary epidemiology of vaccination. Journal of the Royal Society Interface. 2007;4(16): 803–817. PubMed Abstract | Publisher Full Text | Free Full Text

[14] 14. Livermore DM: Minimising antibiotic resistance. The Lancet Infectious Diseases. 2005;5(7): 450–459. PubMed Abstract | Publisher Full Text

[15] 15. Roberts JA, Kruger P, Paterson DL, et al.: Antibiotic resistance—what’s dosing got to do with it? Crit Care Med. 2008;36(8): 2433–2440. PubMed Abstract | Publisher Full Text

[16] 16. Shampine LF, Reichelt MW: The matlab ode suite. SIAM Journal on Scientific Computing. 1997;18(1): 1–22. Publisher Full Text

[17] 17. Dormand JR, Prince PJ: A family of embedded Runge-Kutta formulae. Journal of Computational and Applied Mathematics. 1980;6(1): 19–26. Publisher Full Text

[18] 18. Faria NR, Claro IM, Candido D, et al.: Genomic characterisation of an emergent SARS-CoV-2 lineage in Manaus: preliminary findings. Virological. Publisher Full Text

[19] 19. Tegally H, Wilkinson E, Giovanetti M, et al.: Emergence and rapid spread of a new severe acute respiratory syndrome-related coronavirus 2 (SARS-CoV-2) lineage with multiple spike mutations in South Africa. medRxiv. 2020. Publisher Full Text

[20] 20. Voloch CM, Ronaldo da Silva F, de Almeida LG , et al.: Genomic characterization of a novel SARS-CoV-2 lineage from Rio de Janeiro, Brazil. medRxiv 2020. PubMed Abstract | Publisher Full Text

[21] 21. Zhang W, Davis BD, Chen SS, et al.: Emergence of a Novel SARS-CoV-2 Variant in Southern California. JAMA. 2021. PubMed Abstract | Publisher Full Text | Free Full Text

[22] 22. England PH: Variants: distribution of cases data.

[23] 23. Brejová B, Hodorová V, Boršová K, et al.: B. 1.258_Delta, a SARS-CoV-2 variant with Delta_H69, Delta_V70 in the Spike protein circulating in the Czech Republic and Slovakia. arXiv preprint arXiv:210204689 2021.

[24] 24. Carman WF, Karayiannis P, Waters J, et al.: Vaccine-induced escape mutant of hepatitis B virus. The Lancet. 1990;336(8711): 325–329. PubMed Abstract | Publisher Full Text

[25] 25. Brueggemann AB, Pai R, Crook DW, et al.: Vaccine escape recombinants emerge after pneumococcal vaccination in the United States. PLoS Pathog. 2007;3(11): e168. PubMed Abstract | Publisher Full Text | Free Full Text

[26] 26. Polack FP, Thomas SJ, Kitchin N, et al.: Safety and efficacy of the BNT162b2 mRNA covid-19 vaccine. N Engl J Med. 2020. PubMed Abstract | Publisher Full Text | Free Full Text

[27] 27. Zhang Y, Zeng G, Pan H, et al.: Safety, tolerability, and immunogenicity of an inactivated SARS-CoV-2 vaccine in healthy adults aged 18–59 years: a randomised, double-blind, placebo-controlled, phase 1/2 clinical trial. The Lancet Infectious Diseases. 2020. PubMed Abstract | Publisher Full Text | Free Full Text

[28] 28. Saad-Roy CM, Wagner CE, Baker RE, et al.: Immune life history, vaccination, and the dynamics of SARS-CoV-2 over the next 5 years. Science. 2020;370(6518): 811–818. PubMed Abstract | Publisher Full Text | Free Full Text

[29] 29. Day T, Gandon S, Lion S, et al.: On the evolutionary epidemiology of SARS-CoV-2. Curr Biol. 2020. PubMed Abstract | Publisher Full Text | Free Full Text

[30] 30. Rochman ND, Wolf YI, Koonin EV: Evolution of Human Respiratory Virus Epidemics. medRxiv 2020. PubMed Abstract | Publisher Full Text | Free Full Text

[31] 31. Kumar S, Tao Q, Weaver S, et al.: An evolutionary portrait of the progenitor SARS-CoV-2 and its dominant offshoots in COVID-19 pandemic. bioRxiv 2020.

[32] 32. Rochman ND, Wolf YI, Faure G, Zhang F, Koonin EV: Ongoing Global and Regional Adaptive Evolution of SARS-CoV-2. bioRxiv 2020.

[33] 33. van Dorp L , Acman M, Richard D, et al.: Emergence of genomic diversity and recurrent mutations in SARS-CoV-2. Infection, Genetics, Evolution 2020; 104351. Publisher Full Text

[34] 34. Garrett ME, Galloway J, Chu HY, et al.: High resolution profiling of pathways of escape for SARS-CoV-2 spike-binding antibodies. bioRxiv 2020.

[35] 35. Starr TN, Greaney AJ, Hilton SK, et al.: Deep mutational scanning of SARS-CoV-2 receptor binding domain reveals constraints on folding and ACE2 binding. Cell 2020; 182(5): 1295–310. e20. Publisher Full Text

[36] 36. Makhoul M, Ayoub HH, Chemaitelly H, et al.: Epidemiological impact of SARS-CoV-2 vaccination: mathematical modeling analyses. Vaccines. 2020;8(4): 668. PubMed Abstract | Publisher Full Text | Free Full Text

[37] 37. Rella S, Kulikova Y, Dermitzakis E, Kondrashov F: SARS-CoV-2 transmission, vaccination rate and the fate of resistant strains. medRxiv 2021.

Substantial impact of post-vaccination contacts on cumulative infections during viral epidemics

Abstract

Keywords

Revised Amendments from Version 1

Introduction

Methods

Figure 1. The model.

Results

Figure 2. Optimal vaccine distribution.

Figure 3. Post-vaccination contacts.

Discussion

Limitations

Conclusions

Author contributions

Data availability

Underlying data

Acknowledgements

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated