Designing and developing an app to perform Hofstee cut-off calculations

Ken Masters; Nadia Al-Wardy

doi:10.12688/f1000research.53096.2

Home Browse Designing and developing an app to perform Hofstee cut-off calculations

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Software Tool Article

Revised

Designing and developing an app to perform Hofstee cut-off calculations

[version 2; peer review: 2 approved]

Ken Masters ¹, Nadia Al-Wardy²

PUBLISHED 05 Oct 2021

Author details Author details

¹ Medical Education and Informatics, Sultan Qaboos University, Al-Khoud, 0123, Oman
² Biochemistry, Sultan Qaboos University, Al-Khoud, 0123, Oman

Ken Masters
Roles: Conceptualization, Data Curation, Formal Analysis, Investigation, Methodology, Project Administration, Resources, Software, Supervision, Validation, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Nadia Al-Wardy
Roles: Conceptualization, Data Curation, Formal Analysis, Methodology, Validation, Visualization, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

This article is included in the Software and Hardware Engineering gateway.

Abstract

Determining a Hofstee cut-off point in medical education student assessment is problematic: traditional methods can be time-consuming, inaccurate, and inflexible. To counter this, we developed a simple Android app that receives raw, unsorted student assessment data in .csv format, allows for multiple judges’ inputs, mean or median inputs, calculates the Hofstee cut-off mathematically, and outputs the results with other guiding information. The app contains a detailed description of its functionality.

Keywords

Hofstee, Angoff, Assessment, Standard setting, Android, MARS

Corresponding author: Ken Masters

Competing interests: No competing interests were disclosed.

Grant information: The author(s) declared that no grants were involved in supporting this work.

Copyright: © 2021 Masters K and Al-Wardy N. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Masters K and Al-Wardy N. Designing and developing an app to perform Hofstee cut-off calculations [version 2; peer review: 2 approved]. F1000Research 2021, 10:450 (https://doi.org/10.12688/f1000research.53096.2) First published: 07 Jun 2021, 10:450 (https://doi.org/10.12688/f1000research.53096.1) Latest published: 05 Oct 2021, 10:450 (https://doi.org/10.12688/f1000research.53096.2)

Revised Amendments from Version 1

- The focus of the paper, and that it does not discuss the weaknesses of the Hofstee method, has been emphasised.
- Use of Angoff: as this is a debated issue, not central to the paper, the sentence has been removed.
- The caption of Figure 1 and the paragraph preceding Figure 3 have been corrected and amended to clarify that the final parameters used are the means or medians of all the judges’ parameters, and not an individual judge’s parameters.
- The sentence “An ‘Options’ screen allows…user’s needs” has been removed, as it is mostly a repetition of the preceding sentence.
- The comparison of accuracy and speed has been altered to reflect a comparison to manual methods only. In addition, the 2-decimal point precision of the app was verified with the AMBrSoft, (http://www.ambrsoft.com/MathCalc/Line/TwoLinesIntersection/TwoLinesIntersection.htm) website.

See the authors' detailed response to the review by Benedict Canny
See the authors' detailed response to the review by Adam E. Wyse

Introduction

Determining the pass/fail score in assessments

In medical education assessment, determining the student pass/fail mark is a contentious issue.¹ A range of methods can be used to determine this point and are covered in several other papers.²^–⁴ In summary, however, most methods fall into three categories: norm-referenced (determined by the performance of the student group), criterion-referenced (pre-determined as an absolute cut-off point) and compromise methods (a compromise between the previous two methods is found).⁴

Hofstee method

The Hofstee method⁴^–⁶ is a compromise method that follows four steps, and uses four variables or parameters (explained in more detail below) to determine the cut-off point. While there are weaknesses with the method, and they have been discussed elsewhere,⁶ this paper is focused on describing the method, and then describing an app that applies the method.

Step 1: Evaluation by judges

In Step 1, judges who are qualified to assess the test make an independent judgement about the values of the following four parameters:

• c_min: The minimum cut-off score (i.e. the score that the judge feels would be the lowest possible score that would be considered as a pass/fail score).
• c_max: The maximum cut-off score (i.e. the score that the judge feels would be the highest possible score that would be considered as a pass/fail score).
• f_min: The lowest percentage of students that the judge feels should fail this test.
• f_max: The highest percentage of students that the judge feels should fail this test.

The four parameters are often indicated with different abbreviations; in this paper, we use c_min, c_max, f_min and f_max as is used elsewhere.⁴

Step 2: Determining the arithmetic means

Based upon the independent judgements, the arithmetic mean of each parameter is calculated. (Some researchers, e.g. Norcini², have suggested that medians may also be used).

Step 3: Plot on a graph

After the test has been administered to the students, a graph (Figure 1) is then drawn, plotting the cumulative percentage of students against the scores obtained, and the means of the four parameters.

Figure 1.

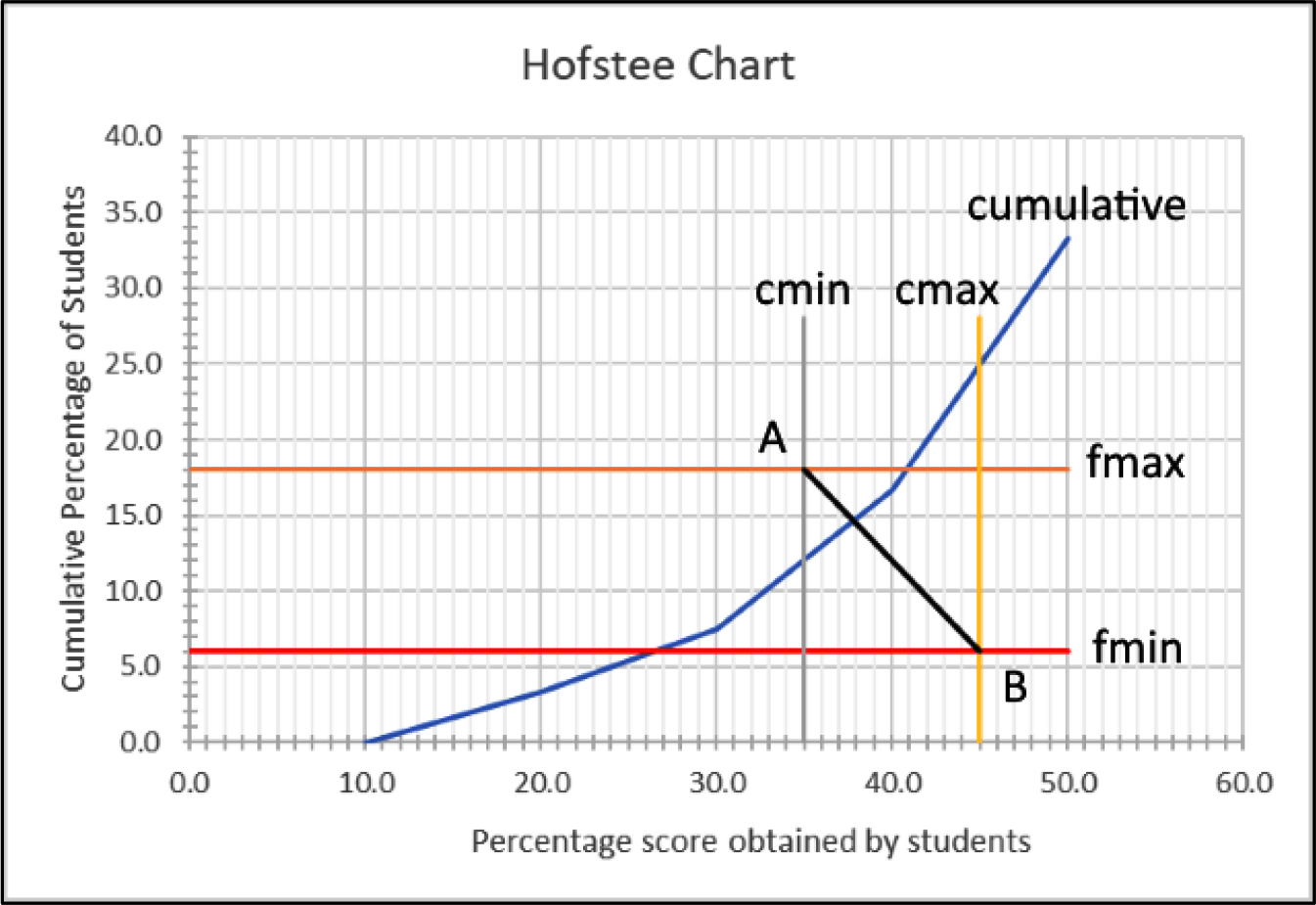
Hofstee chart showing cumulative scores, where c_min (minimum cut-off score) = 35, c_max (maximum cut-off score) = 45, f_min (the lowest percentage of students that the judges feel should fail) = 6, and f_max (the highest percentage of students that the judges feel should fail) = 18.

Step 4: Determining cut-off

The pass/fail cut-off point is then determined by drawing line AB and finding the intersect with the cumulative line. In the Figure 1 example, the cut-off is determined to be slightly less than 38%. A further 10 hand-drawn attempts by the lead author (KM) consistently placed the results between 37 and 38, with an overall estimation of 37.5.

Practical problems with using the Hofstee method

Apart from the fact that any cut-off method can be debated, there are practical problems associated with this method, and these include:

1. The time taken to accurately draw the chart, and all the associated lines.
2. Reading the cut-off point from an imperfect drawing, rather than determining it mathematically.
3. One might wish to allow for some flexibility, and test other values for the parameters. On a hand-drawn chart, this is time-consuming and untidy, to the point of being impossible.

Non-paper solutions

Hofstee produced a mathematical solution,⁷ but it requires sorting and frequency pre-calculation and data inspection, and the mathematics involved is not rudimentary (requiring several steps). Van Der Vleuten developed a useful one for SPSS,⁸ but it uses expensive licensed software.

An Excel template designed by one of the authors (KM) already exists, and plotting the chart on Excel is certainly an improvement over the hand-drawn chart. However, it still requires the data to be pre-sorted and also requires the generation of the cumulative data. In addition, although the chart is drawn more accurately than by hand, it still requires a manual reading of the intersection point.

An app

A search in both the Apple and Android app stores (conducted in January 2020 and again in March 2020) confirmed that there was no such app in either of the stores. To meet this need for a simple and accurate method of determining the Hofstee cut-off, we designed and developed a simple Android app. The app automatically sorts the data, draws the chart, and calculates the cut-off point algebraically. The result is a process that is faster and more accurate than the other methods that require manual drawing and/or reading of the graph.

For usability and evaluation, the app was designed according to the relevant principles laid out in the Mobile App Rating Scale (MARS).⁹ The overall MARS scale is broad, and so does have a few weaknesses when applied to this type of app (e.g. it rates the entertainment value of the app), but it is still a useful guide. In addition, the app is available free of charge, and with no advertisements.

Methods

Implementation

The app, HofsteeCalc, was developed using MIT App Inventor Version 2 (builds nb182 through to nb186a). MIT App Inventor uses its own visual, block-based programming interface to develop Android and iOS apps. In addition to the internal code, the app uses three external sets of libraries and routines for browsing to and selecting the data file,¹⁰ sorting the data,¹¹ and charting the data.¹² No user or device information is collected. The app is optimised for Android 2.1 and higher, API level 28, and requires permission to read from and store data to the device.

Operation

See Figure 2 for workflow chart.

Figure 2. App workflow.

The app automatically creates a data folder and has a test file that the user can use for testing before they insert their data.

The app allows each judge’s individual parameters to be entered (up to a maximum of 10 judges), and then calculates the means, standard deviations, and medians (Figure 3a). The parameters are automatically stored if required and are available the next times the app runs. When the user returns to the main screen (Figure 3b) the means or medians of all the judges’ parameters are automatically inserted into the text boxes. Alternately, if the final means or medians of the judges’ parameters have been calculated elsewhere, these means or medians can be entered directly into the main screen text boxes (Figure 3b).

Figure 3.

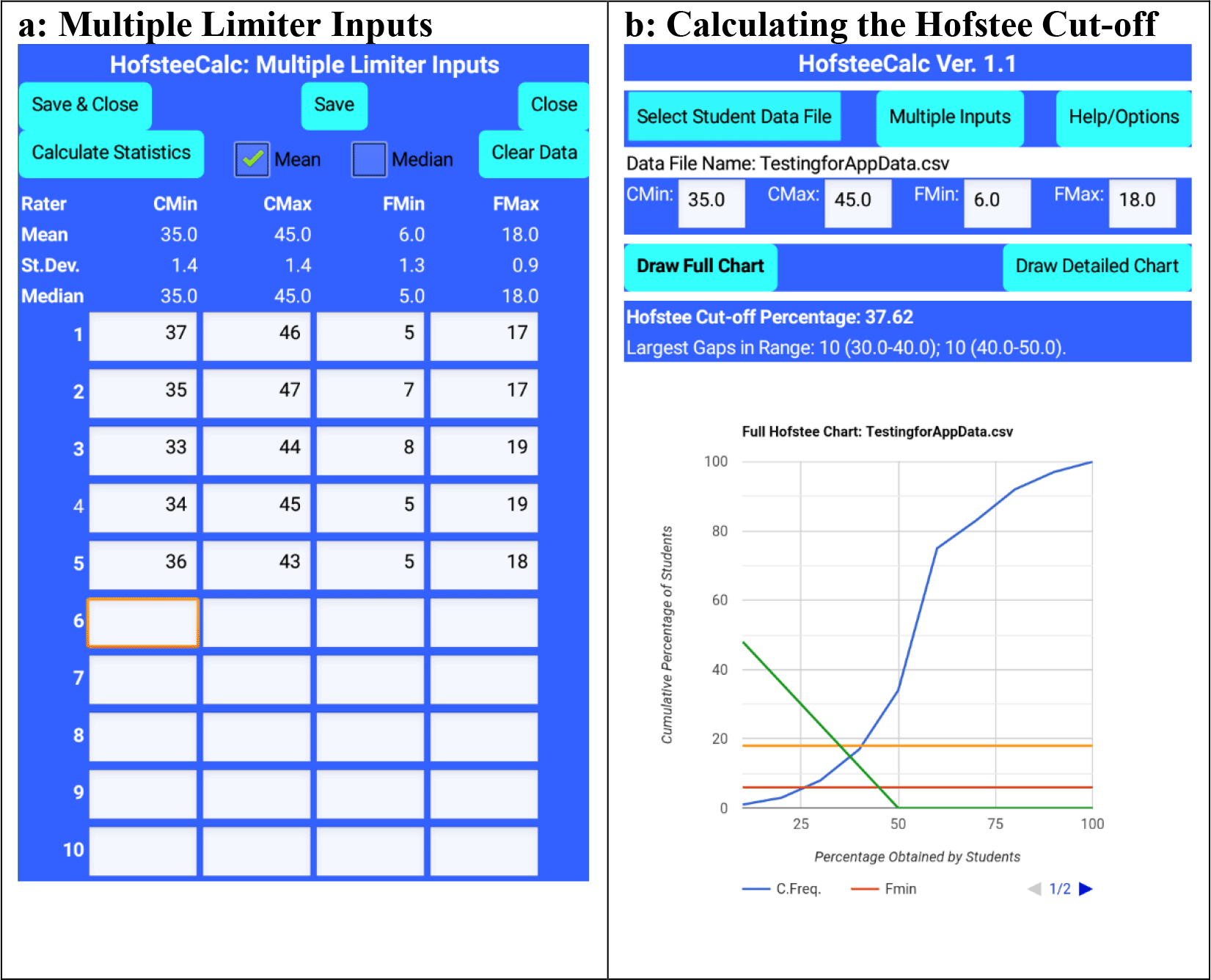
HofsteeCalc app: multiple judges’ parameters and output from Figure 1 data, where c_min is minimum cut-off score, c_max is maximum cut-off score, f_min is the lowest percentage of students that the judge feels should fail, and f_max is the highest percentage of students that the judge feels should fail.

For data input, the student data need to be in a single-column standard.csv file. If the.csv file contains more than one column of data, only the first column will be read. The app automatically sorts the data, so these do not have to be pre-sorted by the user.

When the charts are to be drawn, the user can view either the chart of the whole data set (see Figure 3b: Draw Full Chart), or a detailed section (covering data which is within and close to the range of the parameters (see Figure 3b: Draw Detailed Chart)). With pinching, users can zoom in and out of the charts.

As the focus of the app is a functional tool, it has a simple user interface, and includes a ‘Help’ screen that explains in detail how it is to be used. Although the app assumes a knowledge of the Hofstee method, it supplies additional references for the user. Allowing for personal preferences, it permits the user to change some user-interface colours to suit individual needs.

Central algorithm to algebraically determine the Hofstee cut-off

In the Hofstee chart, we know the x₁y₁ and x₂y₂ coordinates of line AB (Figure 1). However, because the cumulative score line does not have an algebraic formula, calculating the intersection between this straight line and the cumulative line is not possible (using ‘best fit’ or ‘nearest neighbour’ might be possible but will not give 100% accuracy). It is for this reason that current users of the Hofstee method read the point manually from hand-drawn charts.

The data, however, are x₁y₁ and x₂y₂ coordinates of straight lines, and these coordinates are stored in an array (or list). So, the algebraic algorithm for determining the cut-off can be expressed in the following pseudo-code:

For each straight line in the array of lines forming the cumulative line

Read the x₁y₁ and x₂y₂ coordinates of that line

Algebraically determine the intersection point (x_i) of this straight line and line AB

IF x₁ ≤ x_i ≤ x₂ [there is no need to test the y coordinate]

THEN x_i is the cut-off point

(If the cut-off (x_i) is a data point, then two lines would meet this condition, but that is no matter, as the point is identical.)

Readers may recognise that, because the cut-off point is determined algebraically, there is no need to draw the chart for the calculation. The chart, however, has been included in the app because most users are used to it, and also because they may wish to make manual adjustments to the parameters based on the visual reading of the data.

App completion

After various early test versions, Version 1.0 of the app was completed in February 2021, and uploaded into the Google Play Store at: https://play.google.com/store/apps/details?id=appinventor.ai_itmeded.HofsteeCalc. Since then, small updates have been performed, and the app is currently on Ver. 1.1.

App description and functionality

Conforming to the requirements laid out in the Introduction above, the app is available free of charge, with no advertisements. It does not require access to the internet, and it does not collect, store, or transmit any personal information about the user or the device.

Alpha testing

The app was alpha tested on various real and hypothetical, sorted and unsorted datasets (see Underlying data¹³), with up to 1,000 items, and consistently returned accurate results. For example, for the dataset used in Figure 1, the app calculated the cut-off at 37.62%, rather than “slightly less than 38%” (See Figure 3b). In addition, from the raw data, the coordinates of the two lines were manually determined (38,18; 45,6) and (40,17; 30,8), and the intersect between these two lines was arithmetically determined through the AmBrSoft site, and the result was found to be 37.62, which is the identical result from the app. This was confirmed with an enlarged manual graphing which also placed the result at slightly more than 37.6 (in real life, although this method would get similar accuracy to the app, it would extend the time by a further 10 minutes or so).

The time to draw the chart and determine the cut-off from a dataset of unsorted, 1,000 randomly-generated numbers (MS-Excel 2019 RANDBETWEEN(1,100)), was approximately 2 seconds (Samsung S8, Model SM-G955FD, Android Ver. 9, Build PPR1.180610.011.G955FXXS6DTA1).

Mobile App Rating Scale (MARS)

Using the Mobile App Rating Scale (MARS),⁹ both authors independently measured the app against the scale, and arrived at a score of 4.07 and 3.88, respectively. As detailed above, this less-than-ideal score was expected, as the MARS includes items not entirely appropriate to such an app.

Use case

For use cases, anonymised data sets are available in Underlying data.¹³

An example of a use case utilised the data in the sheet HofsteeCalcRealDataClass01.csv.

The data set has 181 items, and the item values range from 43 to 97. The data set is unsorted.

The input parameters were determined as shown in Table 1.

Table 1.

Use case input parameters for HofsteeCalcRealDataClass01.csv, where c_min is minimum cut-off score, c_max is maximum cut-off score, f_min is the lowest percentage of students that the judge feels should fail, and f_max is the highest percentage of students that the judge feels should fail.

Rater	c_min	c_max	f_min	f_max
1	50	60	1	4
2	44	56	3	8
3	41	52	4	8
4	45	54	5	8
5	45	53	2	7

Based on this use case, Figure 4a shows the input parameters. Figure 4b shows the resultant ‘Detailed chart’, the Hofstee cut-off percentage (53.80), and the largest data gaps in the vicinity of the Hofstee cut-off percentage. In addition, from the raw data, the coordinates of the two lines were manually determined (45,7; 55,3) and (53.5,3.31; 54.5,3.87), and the intersect between these two line was arithmetically determined through the AmBrSoft site, and the result was found to be 53.80, which is the identical result from the app.

Figure 4.

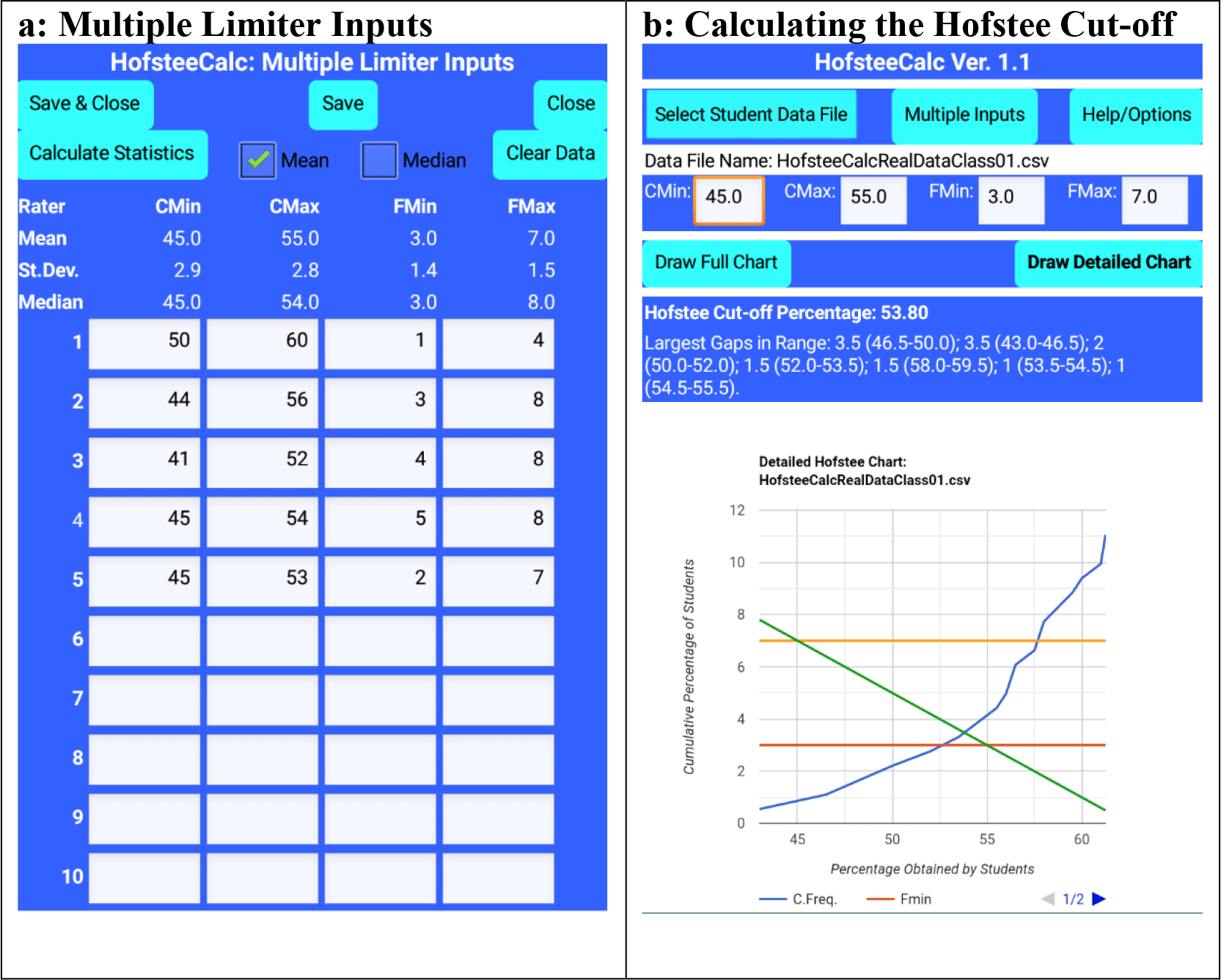
HofsteeCalc app: multiple judges’ parameters and output from HofsteeCalcRealDataClass01.csv, where c_min is minimum cut-off score, c_max is maximum cut-off score, f_min is the lowest percentage of students that the judge feels should fail, and f_max is the highest percentage of students that the judge feels should fail.

Comments

This paper has described the successful design and development of a free, advertisement-free, Android app to calculate the Hofstee cut-off. The app meets basic design principles as established in the MARS scale, and alpha- and beta- testing has shown the app to be accurate and fast. The app is available in the Google Play app store (see Software availability¹⁴).

Full usability and ease of use will be tested in the future through more rigorous, wide-spread testing among medical educators.

Conclusions

When educating future health professionals, determining fair pass/fail cut-off points is crucial. The time taken to perform such procedures, however, adds to medical educators’ already over-burdened schedules, and competes with a range of other demands in this schedule, so it is inevitable that short-cuts and errors will occur. This research has traced the design and development of a tool that can both save time and improve accuracy when determining the Hofstee cut-off.

Data availability

Underlying data

Zenodo: HofsteeCalcDataSets. https://doi.org/10.5281/zenodo.4699233.¹³

This project contains the following underlying data:

• RawDataForTesting.csv (data set that is built into the app’s assets).
• TestingForAppData.csv (data set used to generate Figure 1 and Figure 3b).
• HofsteeCalcRealDataClass01.csv (data set available for testing).
• HofsteeCalcRealDataClass02.csv (data set available for testing).
• HofsteeCalcRealDataClass03.csv (data set available for testing).
• HofsteeCalcRealDataClass04.csv (data set available for testing).

Data are available under the terms of the Creative Commons Attribution 4.0 International licenses (CC-BY 4.0).

Software availability

Software available from Google Play app store: https://play.google.com/store/apps/details?id=appinventor.ai_itmeded.HofsteeCalc

Archived source code at time of publication: https://doi.org/10.5281/zenodo.4633140.¹⁴

Licence: Creative Commons Attribution 4.0 International license (CC-BY 4.0).

Acknowledgments

The authors would like to acknowledge Prof. Cees van der Vleuten, Maastricht University, for sending us a copy of Hofstee 1997.⁷

References

1. Schauber SK, Hecht M: How sure can we be that a student really failed? On the measurement precision of individual pass-fail decisions from the perspective of Item Response Theory. Med Teach. 2020 Dec 1; 42(12): 1374–84. PubMed Abstract | Publisher Full Text
2. Norcini JJ: Standard setting on educational tests. Med Educ. 2003; 37(5): 464–9. PubMed Abstract | Publisher Full Text
3. Downing SM, Tekian A, Yudkowsky R: Procedures for establishing defensible absolute passing scores on performance examinations in health professions education. Teach Learn Med. 2006; 18(1): 50–7. PubMed Abstract | Publisher Full Text
4. Bandaranayake RC: Setting and maintaining standards in multiple choice examinations: AMEE Guide No. 37. Med Teach. 2008; 30(9–10): 836–45. PubMed Abstract | Publisher Full Text
5. Hofstee WKB: The case for compromise in educational selection and grading. In: Anderson SB, Helmick JS, editors. On Educational Testing . San Francisco: Jossey-Bass; 1983. p. 109–27.
6. Wyse AE, Babcock B: An investigation of undefined cut scores with the Hofstee Standard-Setting Method. Educ Meas Issues Pract. 2017; 36(4): 28–34. Publisher Full Text
7. Hofstee W: Cesuurprobleem opgelost [The standard setting problem resolved]. Onderz Van Onderwijs. 1977; 6: 6–7.
8. Van Der Vleuten C: Setting and maintaining standards in multiple choice examinations (AMEE Supplement 37.1). Med Teach. 2010; 32: 174–6. Publisher Full Text
9. Stoyanov SR, Hides L, Kavanagh DJ, et al.: Mobile App Rating Scale: A New Tool for Assessing the Quality of Health Mobile Apps. JMIR MHealth UHealth. 2015; 3(1): e27. PubMed Abstract | Publisher Full Text | Free Full Text
10. Pura Vida Apps: File Extension [Internet]. App Inventor Extensions . 2019 [cited 2020 Mar 1]. Reference Source
11. Pevest.com: QuickSort routine for your App Inventor Apps! [Internet].2017 [cited 2020 Mar 1]. Reference Source
12. Manning K, Kager E: ChartMaker [Internet].2017 [cited 2020 Mar 1]. Reference Source
13. Masters K: HofsteeCalcDataSets (Version Ver 1.1) [Data set]. Zenodo . 2021. Publisher Full Text
14. Masters K: HofsteeCalc (Version 1.1). Zenodo . 2021, March 24. Publisher Full Text

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 07 Jun 2021

Author details Author details

¹ Medical Education and Informatics, Sultan Qaboos University, Al-Khoud, 0123, Oman
² Biochemistry, Sultan Qaboos University, Al-Khoud, 0123, Oman

Nadia Al-Wardy
Roles: Conceptualization, Data Curation, Formal Analysis, Methodology, Validation, Visualization, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Article Versions (2)

version 2

Revised

Published: 05 Oct 2021, 10:450

https://doi.org/10.12688/f1000research.53096.2

version 1

Published: 07 Jun 2021, 10:450

https://doi.org/10.12688/f1000research.53096.1

© 2021 Masters K and Al-Wardy N. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

Masters K and Al-Wardy N. Designing and developing an app to perform Hofstee cut-off calculations [version 2; peer review: 2 approved]. F1000Research 2021, 10:450 (https://doi.org/10.12688/f1000research.53096.2)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 2

VERSION 2

PUBLISHED 05 Oct 2021

Revised

Views

Reviewer Report 01 Nov 2021

Adam E. Wyse, Renaissance, Arden Hills, MN, USA

Approved

https://doi.org/10.5256/f1000research.77792.r96239

I don’t have any additional feedback ... Continue reading

CITE

Report a concern

Author Response 02 Nov 2021

Ken Masters, Medical Education and Informatics, Sultan Qaboos University, Al-Khoud, 0123, Oman

02 Nov 2021

Author Response

Thank you for your comment and your approval. We trust that this paper makes a contribution to the field.
Competing Interests: No competing interests were disclosed.
Thank you for your comment and your approval. We trust that this paper makes a contribution to the field.
Thank you for your comment and your approval. We trust that this paper makes a contribution to the field.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 02 Nov 2021

Ken Masters, Medical Education and Informatics, Sultan Qaboos University, Al-Khoud, 0123, Oman

02 Nov 2021

Author Response

Thank you for your comment and your approval. We trust that this paper makes a contribution to the field.
Competing Interests: No competing interests were disclosed.
Thank you for your comment and your approval. We trust that this paper makes a contribution to the field.
Thank you for your comment and your approval. We trust that this paper makes a contribution to the field.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Views

Reviewer Report 07 Oct 2021

Benedict Canny, Adelaide Medical School, University of Adelaide, Adelaide, SA, Australia

Approved

https://doi.org/10.5256/f1000research.77792.r96240

The authors have addressed the ... Continue reading

CITE

Report a concern

Author Response 07 Oct 2021

Ken Masters, Medical Education and Informatics, Sultan Qaboos University, Al-Khoud, 0123, Oman

07 Oct 2021

Author Response

Thank you very much for taking the time to review our paper, and re-reading our 2nd version. Much appreciated.
Competing Interests: No competing interests were disclosed.
Thank you very much for taking the time to review our paper, and re-reading our 2nd version. Much appreciated.
Thank you very much for taking the time to review our paper, and re-reading our 2nd version. Much appreciated.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 07 Oct 2021

Ken Masters, Medical Education and Informatics, Sultan Qaboos University, Al-Khoud, 0123, Oman

07 Oct 2021

Author Response

Thank you very much for taking the time to review our paper, and re-reading our 2nd version. Much appreciated.
Competing Interests: No competing interests were disclosed.
Thank you very much for taking the time to review our paper, and re-reading our 2nd version. Much appreciated.
Thank you very much for taking the time to review our paper, and re-reading our 2nd version. Much appreciated.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Version 1

VERSION 1

PUBLISHED 07 Jun 2021

Views

Reviewer Report 11 Aug 2021

Benedict Canny, Adelaide Medical School, University of Adelaide, Adelaide, SA, Australia

Approved with Reservations

https://doi.org/10.5256/f1000research.56446.r90318

This paper describes the development and use of the an app to help with the use of the Hofstee method. I suspect it will be of considerable use to those who adopt this method. Importantly, the app only addresses the analysis of data, once the appropriate data have been generated, and users should fully acquaint themselves with strengths and weakness of the Hofstee standard setting method prior to use. Indeed, this advice could be applied to all standard setting approaches, as all have their pluses and minuses.

While aware of the Hofstee method, I have never used in practice, so I am unable to comment on the practicalities of this method when compared with performing this task long hand.

I am concerned about some of the terminology used in the paper. The authors use the words to "accurate" and "accuracy" in the Alpha Testing and Conclusions sections of the manuscript, and report cut scores to two significant decimal figures. I suspect that they mean the term "precision", as accuracy is a measure of the proximity of the estimated value to the "true" value, and would be best determined by comparing this method to another (e.g. van der Vleuten's method referred to in the paper), or a "gold" standard (making calculations long hand). The authors have not reported on the effect of the app on the "error rate" of using the method, and these additional data would be useful, if available.

Finally, the point is made in the conclusion that "determining fair pass/fail cut-off points is crucial". This method will only increase fairness if the error rate is reduced, and not the inherent "fairness" of Hofstee method, nor, indeed, any other standard setting method.

In conclusion, I suspect this app will be useful for those who use the Hofstee method. It would be nice to see an iOS version.

Is the rationale for developing the new software tool clearly explained?

Yes
Is the description of the software tool technically sound?

Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Yes
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Partly

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Education Research

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Author Response 06 Sep 2021

Ken Masters, Medical Education and Informatics, Sultan Qaboos University, Al-Khoud, 0123, Oman

06 Sep 2021

Author Response

We thank you for your comments. We shall take them into account and address them in more detail when we submit Version 2 of the paper.
Competing Interests: No competing interests were disclosed.
We thank you for your comments. We shall take them into account and address them in more detail when we submit Version 2 of the paper.
We thank you for your comments. We shall take them into account and address them in more detail when we submit Version 2 of the paper.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Author Response 05 Oct 2021

Ken Masters, Medical Education and Informatics, Sultan Qaboos University, Al-Khoud, 0123, Oman

05 Oct 2021

Author Response
We have now had the opportunity to respond in detail to this review. Below, we indicate the Reviewer’s comments and our response.

**Reviewer’s Comment
Approved With Reservations

**Authors’ ... Continue reading
We have now had the opportunity to respond in detail to this review. Below, we indicate the Reviewer’s comments and our response.

**Reviewer’s Comment
Approved With Reservations

**Authors’ Response
We thank the reviewer for their comments, and trust that our responses below and the changes to Version 1 of the paper will be to their satisfaction.

**Reviewer’s Comment
This paper describes the development and use of the an app to help with the use of the Hofstee method. I suspect it will be of considerable use to those who adopt this method. Importantly, the app only addresses the analysis of data, once the appropriate data have been generated, and users should fully acquaint themselves with strengths and weakness of the Hofstee standard setting method prior to use. Indeed, this advice could be applied to all standard setting approaches, as all have their pluses and minuses.

While aware of the Hofstee method, I have never used in practice, so I am unable to comment on the practicalities of this method when compared with performing this task long hand.

I am concerned about some of the terminology used in the paper. The authors use the words to "accurate" and "accuracy" in the Alpha Testing and Conclusions sections of the manuscript, and report cut scores to two significant decimal figures. I suspect that they mean the term "precision", as accuracy is a measure of the proximity of the estimated value to the "true" value, and would be best determined by comparing this method to another (e.g. van der Vleuten's method referred to in the paper), or a "gold" standard (making calculations long hand). The authors have not reported on the effect of the app on the "error rate" of using the method, and these additional data would be useful, if available.

**Authors’ Response
Thank you for this comment. Given that the final accurate answer is best determined by finding the intersect point of the two relevant lines in the chart, the final accurate result can be independently calculated with those known coordinates. (The main function of the app is to determine those two lines). So, for further verification, we have tested these coordinates using an online calculator (AMBrSoft, http://www.ambrsoft.com/MathCalc/Line/TwoLinesIntersection/TwoLinesIntersection.htm), and the app’s results are shown to be accurate to two decimal places. We also confirmed this with a enlarged hand-drawn calculation. Version 2 of the paper has been amended to reflect this, and the relevant coordinates have been placed in the paper, so that users can test these results independently.

The reviewer is correct, though, that this level of increased accuracy is only against the methods that require manual reading of the charts, so, we feel we can now claim that the app is more accurate than the standard manual process, which could not have the same level of accuracy, and we have amended the paper to reflect this.

**Reviewer’s Comment
Finally, the point is made in the conclusion that "determining fair pass/fail cut-off points is crucial". This method will only increase fairness if the error rate is reduced, and not the inherent "fairness" of Hofstee method, nor, indeed, any other standard setting method.

**Authors’ Response
Yes, we agree. Given that the accuracy of the app has been confirmed (and can easily be verified by readers), we feel that the general statement that “determining fair pass/fail cut-off points is crucial” is valid.

**Reviewer’s Comment
In conclusion, I suspect this app will be useful for those who use the Hofstee method. It would be nice to see an iOS version.

**Authors’ Response
Yes, it would. Although an iOS app is planned, it would be premature to develop the app (or even allude to it in the paper) until the Android version has been accepted by the academic community.

Is the rationale for developing the new software tool clearly explained?

Yes

Is the description of the software tool technically sound?

Yes

Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Yes

Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes

Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Partly

**Authors’ Response
We trust that our explanation and changes to the paper are to the reviewer’s satisfaction.
We have now had the opportunity to respond in detail to this review. Below, we indicate the Reviewer’s comments and our response.

**Reviewer’s Comment
Approved With Reservations

**Authors’ Response
We thank the reviewer for their comments, and trust that our responses below and the changes to Version 1 of the paper will be to their satisfaction.

**Reviewer’s Comment
This paper describes the development and use of the an app to help with the use of the Hofstee method. I suspect it will be of considerable use to those who adopt this method. Importantly, the app only addresses the analysis of data, once the appropriate data have been generated, and users should fully acquaint themselves with strengths and weakness of the Hofstee standard setting method prior to use. Indeed, this advice could be applied to all standard setting approaches, as all have their pluses and minuses.

While aware of the Hofstee method, I have never used in practice, so I am unable to comment on the practicalities of this method when compared with performing this task long hand.

I am concerned about some of the terminology used in the paper. The authors use the words to "accurate" and "accuracy" in the Alpha Testing and Conclusions sections of the manuscript, and report cut scores to two significant decimal figures. I suspect that they mean the term "precision", as accuracy is a measure of the proximity of the estimated value to the "true" value, and would be best determined by comparing this method to another (e.g. van der Vleuten's method referred to in the paper), or a "gold" standard (making calculations long hand). The authors have not reported on the effect of the app on the "error rate" of using the method, and these additional data would be useful, if available.

**Authors’ Response
Thank you for this comment. Given that the final accurate answer is best determined by finding the intersect point of the two relevant lines in the chart, the final accurate result can be independently calculated with those known coordinates. (The main function of the app is to determine those two lines). So, for further verification, we have tested these coordinates using an online calculator (AMBrSoft, http://www.ambrsoft.com/MathCalc/Line/TwoLinesIntersection/TwoLinesIntersection.htm), and the app’s results are shown to be accurate to two decimal places. We also confirmed this with a enlarged hand-drawn calculation. Version 2 of the paper has been amended to reflect this, and the relevant coordinates have been placed in the paper, so that users can test these results independently.

The reviewer is correct, though, that this level of increased accuracy is only against the methods that require manual reading of the charts, so, we feel we can now claim that the app is more accurate than the standard manual process, which could not have the same level of accuracy, and we have amended the paper to reflect this.

**Reviewer’s Comment
Finally, the point is made in the conclusion that "determining fair pass/fail cut-off points is crucial". This method will only increase fairness if the error rate is reduced, and not the inherent "fairness" of Hofstee method, nor, indeed, any other standard setting method.

**Authors’ Response
Yes, we agree. Given that the accuracy of the app has been confirmed (and can easily be verified by readers), we feel that the general statement that “determining fair pass/fail cut-off points is crucial” is valid.

**Reviewer’s Comment
In conclusion, I suspect this app will be useful for those who use the Hofstee method. It would be nice to see an iOS version.

**Authors’ Response
Yes, it would. Although an iOS app is planned, it would be premature to develop the app (or even allude to it in the paper) until the Android version has been accepted by the academic community.

Is the rationale for developing the new software tool clearly explained?

Yes

Is the description of the software tool technically sound?

Yes

Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Yes

Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes

Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Partly

**Authors’ Response
We trust that our explanation and changes to the paper are to the reviewer’s satisfaction.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 06 Sep 2021

Ken Masters, Medical Education and Informatics, Sultan Qaboos University, Al-Khoud, 0123, Oman

06 Sep 2021

Author Response

We thank you for your comments. We shall take them into account and address them in more detail when we submit Version 2 of the paper.
Competing Interests: No competing interests were disclosed.
We thank you for your comments. We shall take them into account and address them in more detail when we submit Version 2 of the paper.
We thank you for your comments. We shall take them into account and address them in more detail when we submit Version 2 of the paper.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Author Response 05 Oct 2021

Ken Masters, Medical Education and Informatics, Sultan Qaboos University, Al-Khoud, 0123, Oman

05 Oct 2021

Author Response
We have now had the opportunity to respond in detail to this review. Below, we indicate the Reviewer’s comments and our response.

**Reviewer’s Comment
Approved With Reservations

**Authors’ ... Continue reading
We have now had the opportunity to respond in detail to this review. Below, we indicate the Reviewer’s comments and our response.

**Reviewer’s Comment
Approved With Reservations

**Authors’ Response
We thank the reviewer for their comments, and trust that our responses below and the changes to Version 1 of the paper will be to their satisfaction.

**Reviewer’s Comment
This paper describes the development and use of the an app to help with the use of the Hofstee method. I suspect it will be of considerable use to those who adopt this method. Importantly, the app only addresses the analysis of data, once the appropriate data have been generated, and users should fully acquaint themselves with strengths and weakness of the Hofstee standard setting method prior to use. Indeed, this advice could be applied to all standard setting approaches, as all have their pluses and minuses.

While aware of the Hofstee method, I have never used in practice, so I am unable to comment on the practicalities of this method when compared with performing this task long hand.

I am concerned about some of the terminology used in the paper. The authors use the words to "accurate" and "accuracy" in the Alpha Testing and Conclusions sections of the manuscript, and report cut scores to two significant decimal figures. I suspect that they mean the term "precision", as accuracy is a measure of the proximity of the estimated value to the "true" value, and would be best determined by comparing this method to another (e.g. van der Vleuten's method referred to in the paper), or a "gold" standard (making calculations long hand). The authors have not reported on the effect of the app on the "error rate" of using the method, and these additional data would be useful, if available.

**Authors’ Response
Thank you for this comment. Given that the final accurate answer is best determined by finding the intersect point of the two relevant lines in the chart, the final accurate result can be independently calculated with those known coordinates. (The main function of the app is to determine those two lines). So, for further verification, we have tested these coordinates using an online calculator (AMBrSoft, http://www.ambrsoft.com/MathCalc/Line/TwoLinesIntersection/TwoLinesIntersection.htm), and the app’s results are shown to be accurate to two decimal places. We also confirmed this with a enlarged hand-drawn calculation. Version 2 of the paper has been amended to reflect this, and the relevant coordinates have been placed in the paper, so that users can test these results independently.

The reviewer is correct, though, that this level of increased accuracy is only against the methods that require manual reading of the charts, so, we feel we can now claim that the app is more accurate than the standard manual process, which could not have the same level of accuracy, and we have amended the paper to reflect this.

**Reviewer’s Comment
Finally, the point is made in the conclusion that "determining fair pass/fail cut-off points is crucial". This method will only increase fairness if the error rate is reduced, and not the inherent "fairness" of Hofstee method, nor, indeed, any other standard setting method.

**Authors’ Response
Yes, we agree. Given that the accuracy of the app has been confirmed (and can easily be verified by readers), we feel that the general statement that “determining fair pass/fail cut-off points is crucial” is valid.

**Reviewer’s Comment
In conclusion, I suspect this app will be useful for those who use the Hofstee method. It would be nice to see an iOS version.

**Authors’ Response
Yes, it would. Although an iOS app is planned, it would be premature to develop the app (or even allude to it in the paper) until the Android version has been accepted by the academic community.

Is the rationale for developing the new software tool clearly explained?

Yes

Is the description of the software tool technically sound?

Yes

Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Yes

Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes

Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Partly

**Authors’ Response
We trust that our explanation and changes to the paper are to the reviewer’s satisfaction.
We have now had the opportunity to respond in detail to this review. Below, we indicate the Reviewer’s comments and our response.

**Reviewer’s Comment
Approved With Reservations

**Authors’ Response
We thank the reviewer for their comments, and trust that our responses below and the changes to Version 1 of the paper will be to their satisfaction.

**Reviewer’s Comment
This paper describes the development and use of the an app to help with the use of the Hofstee method. I suspect it will be of considerable use to those who adopt this method. Importantly, the app only addresses the analysis of data, once the appropriate data have been generated, and users should fully acquaint themselves with strengths and weakness of the Hofstee standard setting method prior to use. Indeed, this advice could be applied to all standard setting approaches, as all have their pluses and minuses.

While aware of the Hofstee method, I have never used in practice, so I am unable to comment on the practicalities of this method when compared with performing this task long hand.

I am concerned about some of the terminology used in the paper. The authors use the words to "accurate" and "accuracy" in the Alpha Testing and Conclusions sections of the manuscript, and report cut scores to two significant decimal figures. I suspect that they mean the term "precision", as accuracy is a measure of the proximity of the estimated value to the "true" value, and would be best determined by comparing this method to another (e.g. van der Vleuten's method referred to in the paper), or a "gold" standard (making calculations long hand). The authors have not reported on the effect of the app on the "error rate" of using the method, and these additional data would be useful, if available.

**Authors’ Response
Thank you for this comment. Given that the final accurate answer is best determined by finding the intersect point of the two relevant lines in the chart, the final accurate result can be independently calculated with those known coordinates. (The main function of the app is to determine those two lines). So, for further verification, we have tested these coordinates using an online calculator (AMBrSoft, http://www.ambrsoft.com/MathCalc/Line/TwoLinesIntersection/TwoLinesIntersection.htm), and the app’s results are shown to be accurate to two decimal places. We also confirmed this with a enlarged hand-drawn calculation. Version 2 of the paper has been amended to reflect this, and the relevant coordinates have been placed in the paper, so that users can test these results independently.

The reviewer is correct, though, that this level of increased accuracy is only against the methods that require manual reading of the charts, so, we feel we can now claim that the app is more accurate than the standard manual process, which could not have the same level of accuracy, and we have amended the paper to reflect this.

**Reviewer’s Comment
Finally, the point is made in the conclusion that "determining fair pass/fail cut-off points is crucial". This method will only increase fairness if the error rate is reduced, and not the inherent "fairness" of Hofstee method, nor, indeed, any other standard setting method.

**Authors’ Response
Yes, we agree. Given that the accuracy of the app has been confirmed (and can easily be verified by readers), we feel that the general statement that “determining fair pass/fail cut-off points is crucial” is valid.

**Reviewer’s Comment
In conclusion, I suspect this app will be useful for those who use the Hofstee method. It would be nice to see an iOS version.

**Authors’ Response
Yes, it would. Although an iOS app is planned, it would be premature to develop the app (or even allude to it in the paper) until the Android version has been accepted by the academic community.

Is the rationale for developing the new software tool clearly explained?

Yes

Is the description of the software tool technically sound?

Yes

Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Yes

Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes

Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Partly

**Authors’ Response
We trust that our explanation and changes to the paper are to the reviewer’s satisfaction.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Views

Reviewer Report 14 Jul 2021

Adam E. Wyse, Renaissance, Arden Hills, MN, USA

Approved with Reservations

https://doi.org/10.5256/f1000research.56446.r86927

I appreciate the opportunity to review the article “Designing and developing an app to perform Hofstee cut-off calculations” by Ken Masters and Nadia Al-Wardy. I support the idea of developing simple software tools that people can use to perform standard setting. This is an area of definite need, especially in medical education contexts. I am unaware of a widely available software application to perform the Hofstee method. In most cases that I have seen the Hofstee method used, the people leading the standard setting use Excel or another statistical software package, such as R, to perform the calculations and figure out the cut score. In this sense, the app offered by Masters and Al-Wardy may be beneficial to people who want to perform the Hofstee method and do not have already developed software to perform the Hofstee method. I also liked how the authors provided screen shots of how the app works and several figures and examples throughout the article.

I do have several suggestions for changes to the article and app. First, the authors suggest in the section Step 1: Evaluation of Judges that “We should further note that judges will generally use the Angoff or similar method to determine these.” This statement is not completely accurate. Wyse (2020)¹ discusses several different methods for performing the Hofstee method. One strategy is to figure out the minimum and maximum cut scores from the panel of judges using the Angoff (1971)² method or another test-centered method, such as the Bookmark method (Lewis, Mitzel, & Green, 1996)³. However, this method is not the most common strategy I have seen used to collect these data. It is more common to directly ask panellists to answer four open-ended questions to solicit the data needed to estimate the Hofstee cut score. In addition, it should be noted that even if the Angoff method is used with the Hofstee method that the data on the lowest and high percentages of students that a judge feels should fail the test (which is sometimes alternatively phrased in terms of the highest and lowest students that should pass the test) need to be directly collected from individual judges.

It should also be clear that the description of using the Angoff method to provide data to calculate the cut scores appears to be inconsistent with how the app works in Figure 3. In Figure 3, the authors show a screen with input for each rater. It is not possible to use the Angoff method to provide the multiple limiter input data shown on this screen. The app could be improved if it allowed for data from an Angoff standard setting or other test-centered method to be input. This input could be either entering the minimum and maximum cut scores from a test-centered standard setting method or each judge’s cut score from such a standard setting. It would also be beneficial if the app allowed for an option to input the lowest and highest passing rates and a corresponding graph instead of failure rates. I have commonly seen the method used with passing rates instead of failure rates. Judges sometimes find it easier to conceptualize and use pass rates as many credentialing and licensing organizations as well as accrediting bodies use passing rates instead of failure rates. Finally, it appears that the app requires that cut scores needs to be expressed as a percentage correct. It would be useful if the app also allowed for raw scores to be input as an option as I have seen raw scores used in many different standard settings.

Another area for potential improvement is the example shown in Figure 1. The example shown in Figure 1 appears to be based on data from a single judge. While it is possible to determine the Hofstee cut score for each individual judge, this is rarely done as the authors note in Step 2: Determining the arithmetic mean. The figure would be more beneficial if it focused on data from a group of judges as this is how the method is typically implemented.

There is a fourth practical and very real problem that occurs with the Hofstee method that is not described by the authors. Wyse and Babcock (2017)⁴ illustrate that the Hofstee method can produce undefined cut scores where the Hofstee line segment does not intersect with the failure rate or pass rate curve. This problem is a more serious issue than the three issues described by the authors as it implies that a cut score cannot be estimated. This issue should be mentioned in this section. Wyse and Babcock (2017)⁴ offer a solution for how to simply solve this issue, which involves extending the Hofsee line segment so that it intersects with the pass rate or failure rate curve. The other three practical issues described by the authors are easy to solve with Excel or other statistical software for technical savvy standard setters.

It should also be pointed out that the way the authors describe calculating the Hofstee cut score is different than the way that I typically think about doing it. The authors description of their method based on arrays is not easy to understand and follow, especially for many educators who may use the app. Wyse and Babcock (2017)⁴ offer an easy way to determine the cut scores for the Hofstee method that guarantees a solution even if the Hofstee line segment does not intersect the pass rate or failure rate curve. The authors should consider implementing this method in their app and provide a corresponding description in the article. The strategy involves finding the equation for the line that passes through the two points represented by the means of the data collected from the standard-setting judges that was described in earlier section of the article by the authors. Then, one inputs range of possible scores on the exam to figure out the estimated pass rate or failure rate (depending on whether pass rate or failure rate data are collected from judges) for every possible score on the exam. The last step is to compare the estimated pass rates or failure rates to the observed pass rates or failure rates on the exam. The score with the smallest absolute difference between the observed and estimated pass rates or failure rates is the cut score.

In summary, I think having a simple software app to perform Hofstee calculations is useful. However, the current version of the app does not cover all possible ways that the Hofstee method may be implemented which may limit its utility. If the authors made several changes based on the suggestions in this review, I think the app and article would have more utility and be easier to make sense for users.

Is the rationale for developing the new software tool clearly explained?

Yes
Is the description of the software tool technically sound?

Partly
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Partly
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Partly

References

1. Wyse A: Comparing Cut Scores from the Angoff Method and Two Variations of the Hofstee and Beuk Methods. Applied Measurement in Education. 2020; 33 (2): 159-173 Publisher Full Text
2. Angoff WH: Scales, norms, and equivalent scores. In R. L. Thorndike (Ed.), Educational measurement (2nd ed.). American Council on Education. 1971. 508-597
3. Lewis DM, Mitzel HC, Green DR: Standard setting: A Bookmark approach. In D. R. Green (Chair), IRT-based standard setting procedures utilizing behavioral anchoring.Symposium presented at the Council of Chief State School Officers National Conference on Large-Scale Assessment. 1996.
4. Wyse A, Babcock B: An Investigation of Undefined Cut Scores With the Hofstee Standard-Setting Method. Educational Measurement: Issues and Practice. 2017; 36 (4): 28-34 Publisher Full Text

Competing Interests: I have published several papers on the Hofstee method. One of these papers is referenced by the authors. It is important to me that my work and some of the ideas presented in those papers are accurately reflected in the article.

Reviewer Expertise: Psychometrics; Standard Setting; Measurement; Item Response Theory; Assessment

CITE

Report a concern

Author Response 19 Jul 2021

Ken Masters, Medical Education and Informatics, Sultan Qaboos University, Al-Khoud, 0123, Oman

19 Jul 2021

Author Response

We thank you for your detailed comments. We shall take them into account and address them in more detail when we have received responses from other reviewers.
Competing Interests: No competing interests were disclosed.
We thank you for your detailed comments. We shall take them into account and address them in more detail when we have received responses from other reviewers.
We thank you for your detailed comments. We shall take them into account and address them in more detail when we have received responses from other reviewers.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Author Response 05 Oct 2021

Ken Masters, Medical Education and Informatics, Sultan Qaboos University, Al-Khoud, 0123, Oman

05 Oct 2021

Author Response
We have now had the opportunity to respond in detail to this review. Below, we indicate the Reviewer’s comments and our response.

**Reviewer’s Comment
Approved With Reservations

**Authors’ ... Continue reading
We have now had the opportunity to respond in detail to this review. Below, we indicate the Reviewer’s comments and our response.

**Reviewer’s Comment
Approved With Reservations

**Authors’ Response
We thank the reviewer for their very detailed comments, and trust that our responses below and the changes to Version 1 of the paper will be to their satisfaction.

**Reviewer’s Comment
I appreciate the opportunity to review the article “Designing and developing an app to perform Hofstee cut-off calculations” by Ken Masters and Nadia Al-Wardy. I support the idea of developing simple software tools that people can use to perform standard setting. This is an area of definite need, especially in medical education contexts. I am unaware of a widely available software application to perform the Hofstee method. In most cases that I have seen the Hofstee method used, the people leading the standard setting use Excel or another statistical software package, such as R, to perform the calculations and figure out the cut score. In this sense, the app offered by Masters and Al-Wardy may be beneficial to people who want to perform the Hofstee method and do not have already developed software to perform the Hofstee method. I also liked how the authors provided screen shots of how the app works and several figures and examples throughout the article.

**Authors’ Response
We thank the reviewer for their overall frank comments.

**Reviewer’s Comment
I do have several suggestions for changes to the article and app. First, the authors suggest in the section Step 1: Evaluation of Judges that “We should further note that judges will generally use the Angoff or similar method to determine these.” This statement is not completely accurate. Wyse (2020)¹ discusses several different methods for performing the Hofstee method. One strategy is to figure out the minimum and maximum cut scores from the panel of judges using the Angoff (1971)² method or another test-centered method, such as the Bookmark method (Lewis, Mitzel, & Green, 1996)³. However, this method is not the most common strategy I have seen used to collect these data. It is more common to directly ask panellists to answer four open-ended questions to solicit the data needed to estimate the Hofstee cut score. In addition, it should be noted that even if the Angoff method is used with the Hofstee method that the data on the lowest and high percentages of students that a judge feels should fail the test (which is sometimes alternatively phrased in terms of the highest and lowest students that should pass the test) need to be directly collected from individual judges.

**Authors’ Response
Thank you for this comment. The published texts that we were using (Bandaranayake 2008; Wyse and Babcock 2017) indicated that the Hofstee was frequently used in conjunction with the Angoff method and so we mentioned that. As this is not central to the paper, however, the sentence has been deleted.

**Reviewer’s Comment
It should also be clear that the description of using the Angoff method to provide data to calculate the cut scores appears to be inconsistent with how the app works in Figure 3. In Figure 3, the authors show a screen with input for each rater. It is not possible to use the Angoff method to provide the multiple limiter input data shown on this screen. The app could be improved if it allowed for data from an Angoff standard setting or other test-centered method to be input. This input could be either entering the minimum and maximum cut scores from a test-centered standard setting method or each judge’s cut score from such a standard setting. It would also be beneficial if the app allowed for an option to input the lowest and highest passing rates and a corresponding graph instead of failure rates. I have commonly seen the method used with passing rates instead of failure rates. Judges sometimes find it easier to conceptualize and use pass rates as many credentialing and licensing organizations as well as accrediting bodies use passing rates instead of failure rates.

**Authors’ Response
Thank you for this comment. We apologise for the misunderstanding about what is being portrayed in Figure 3, and we acknowledge that the misunderstanding is because the caption in Figure 1 (raised by the Reviewer below), and then the paragraph that immediately precedes Figure 3, which gives the impression that a single judge’s information has been input (in Figure 3b).

As a result, in addition to the corrections to the Figure 1 caption, we have altered the description in the paragraph preceding Figure 3 in order to clarify the process.

**Reviewer’s Comment
Finally, it appears that the app requires that cut scores needs to be expressed as a percentage correct. It would be useful if the app also allowed for raw scores to be input as an option as I have seen raw scores used in many different standard settings.

**Authors’ Response
Thank you for this comment. This may be an addition to Version 2 of the app, but the current literature (e.g. Bandaranayake 2008; Burr et al 2016) indicates percentage scores as the input, and so, it is prudent for Version 1 of the app to stick to the more common process as described in the dominant literature.

**Reviewer’s Comment
Another area for potential improvement is the example shown in Figure 1. The example shown in Figure 1 appears to be based on data from a single judge. While it is possible to determine the Hofstee cut score for each individual judge, this is rarely done as the authors note in Step 2: Determining the arithmetic mean. The figure would be more beneficial if it focused on data from a group of judges as this is how the method is typically implemented.

**Authors’ Response
Thank you for this point. Figure 1 is an illustrative example showing the chart after the arithmetic means of the parameters have been determined. As mentioned above, however, we acknowledge that the caption was erroneous, and it (and the sentence preceding it) have now been corrected.

**Reviewer’s Comment
There is a fourth practical and very real problem that occurs with the Hofstee method that is not described by the authors. Wyse and Babcock (2017)⁴ illustrate that the Hofstee method can produce undefined cut scores where the Hofstee line segment does not intersect with the failure rate or pass rate curve. This problem is a more serious issue than the three issues described by the authors as it implies that a cut score cannot be estimated. This issue should be mentioned in this section. Wyse and Babcock (2017)⁴ offer a solution for how to simply solve this issue, which involves extending the Hofsee line segment so that it intersects with the pass rate or failure rate curve. The other three practical issues described by the authors are easy to solve with Excel or other statistical software for technical savvy standard setters.

**Authors’ Response
We are reluctant to get into a discussion about the weaknesses of the Hofstee method or how to solve problems associated with it. To do so, and to do such a discussion justice (and view all arguments equally from all sides), is a paper by itself. In our discussion of the Hofstee Method, the aim is simply to explain it so that the functioning of the app is understood. Nevertheless, as readers may be expecting a discussion of the strengths and weaknesses of the Hofstee Method, we have inserted the sentence: “While there are weaknesses with the method, and they have been discussed elsewhere, this paper is focused on describing the method, and then describing an app that applies the method.” And the “elsewhere” in the sentence cites the Wyse & Babcock article mentioned by the reviewer.

**Reviewer’s Comment
It should also be pointed out that the way the authors describe calculating the Hofstee cut score is different than the way that I typically think about doing it. The authors description of their method based on arrays is not easy to understand and follow, especially for many educators who may use the app. Wyse and Babcock (2017)⁴ offer an easy way to determine the cut scores for the Hofstee method that guarantees a solution even if the Hofstee line segment does not intersect the pass rate or failure rate curve. The authors should consider implementing this method in their app and provide a corresponding description in the article. The strategy involves finding the equation for the line that passes through the two points represented by the means of the data collected from the standard-setting judges that was described in earlier section of the article by the authors. Then, one inputs range of possible scores on the exam to figure out the estimated pass rate or failure rate (depending on whether pass rate or failure rate data are collected from judges) for every possible score on the exam. The last step is to compare the estimated pass rates or failure rates to the observed pass rates or failure rates on the exam. The score with the smallest absolute difference between the observed and estimated pass rates or failure rates is the cut score.

**Authors’ Response
Thank you for your suggestion. The proposal for modification by Wyse and Babcock (2017) is, indeed, interesting. There are also others (e.g. Burr et al 2016).

The app (and, therefore, the article), however, is designed to determine the Hofstee cut-off as it is commonly practiced (e.g. Bandaranayake 2008). All proposed modifications cannot be implemented, and, if the app were to favour one modification over another, we would be open to criticisms of favouritism and of promoting and endorsing one modification over others. In this instance, the criticisms would be particularly sharp, because this modification has been proposed by one of the modification authors, who is also a reviewer of this paper. If we were to implement this modification (and not others), we would lay ourselves open to the accusation that we had made the modification to the app and the paper primarily to gain favour from the reviewer in the hopes of a more favourable review. As the reviewer can appreciate, both the authors and the journal would then be under pressure to retract such a paper (and remove the app from the app store).

That said, we could certainly envision a future version of the app that, based on a detailed literature review of all possible Hofstee variations and modification, would attempt to implement them all, allowing users to choose their favourite modification.

**Reviewer’s Comment
In summary, I think having a simple software app to perform Hofstee calculations is useful. However, the current version of the app does not cover all possible ways that the Hofstee method may be implemented which may limit its utility. If the authors made several changes based on the suggestions in this review, I think the app and article would have more utility and be easier to make sense for users.

**Authors’ Response
Thank you for your suggestion. We trust that our explanation and paper’s modifications detailed above satisfies the reviewer.

Is the rationale for developing the new software tool clearly explained?

Yes

Is the description of the software tool technically sound?

Partly

**Authors’ Response
We trust that our explanation and changes to the paper are to the reviewer’s satisfaction.

Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Partly

**Authors’ Response
We trust that our explanation and changes to the paper are to the reviewer’s satisfaction.

Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes

Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Partly

**Authors’ Response
We trust that our explanation and changes to the paper are to the reviewer’s satisfaction.
We have now had the opportunity to respond in detail to this review. Below, we indicate the Reviewer’s comments and our response.

**Reviewer’s Comment
Approved With Reservations

**Authors’ Response
We thank the reviewer for their very detailed comments, and trust that our responses below and the changes to Version 1 of the paper will be to their satisfaction.

**Reviewer’s Comment
I appreciate the opportunity to review the article “Designing and developing an app to perform Hofstee cut-off calculations” by Ken Masters and Nadia Al-Wardy. I support the idea of developing simple software tools that people can use to perform standard setting. This is an area of definite need, especially in medical education contexts. I am unaware of a widely available software application to perform the Hofstee method. In most cases that I have seen the Hofstee method used, the people leading the standard setting use Excel or another statistical software package, such as R, to perform the calculations and figure out the cut score. In this sense, the app offered by Masters and Al-Wardy may be beneficial to people who want to perform the Hofstee method and do not have already developed software to perform the Hofstee method. I also liked how the authors provided screen shots of how the app works and several figures and examples throughout the article.

**Authors’ Response
We thank the reviewer for their overall frank comments.

**Reviewer’s Comment
I do have several suggestions for changes to the article and app. First, the authors suggest in the section Step 1: Evaluation of Judges that “We should further note that judges will generally use the Angoff or similar method to determine these.” This statement is not completely accurate. Wyse (2020)¹ discusses several different methods for performing the Hofstee method. One strategy is to figure out the minimum and maximum cut scores from the panel of judges using the Angoff (1971)² method or another test-centered method, such as the Bookmark method (Lewis, Mitzel, & Green, 1996)³. However, this method is not the most common strategy I have seen used to collect these data. It is more common to directly ask panellists to answer four open-ended questions to solicit the data needed to estimate the Hofstee cut score. In addition, it should be noted that even if the Angoff method is used with the Hofstee method that the data on the lowest and high percentages of students that a judge feels should fail the test (which is sometimes alternatively phrased in terms of the highest and lowest students that should pass the test) need to be directly collected from individual judges.

**Authors’ Response
Thank you for this comment. The published texts that we were using (Bandaranayake 2008; Wyse and Babcock 2017) indicated that the Hofstee was frequently used in conjunction with the Angoff method and so we mentioned that. As this is not central to the paper, however, the sentence has been deleted.

**Reviewer’s Comment
It should also be clear that the description of using the Angoff method to provide data to calculate the cut scores appears to be inconsistent with how the app works in Figure 3. In Figure 3, the authors show a screen with input for each rater. It is not possible to use the Angoff method to provide the multiple limiter input data shown on this screen. The app could be improved if it allowed for data from an Angoff standard setting or other test-centered method to be input. This input could be either entering the minimum and maximum cut scores from a test-centered standard setting method or each judge’s cut score from such a standard setting. It would also be beneficial if the app allowed for an option to input the lowest and highest passing rates and a corresponding graph instead of failure rates. I have commonly seen the method used with passing rates instead of failure rates. Judges sometimes find it easier to conceptualize and use pass rates as many credentialing and licensing organizations as well as accrediting bodies use passing rates instead of failure rates.

**Authors’ Response
Thank you for this comment. We apologise for the misunderstanding about what is being portrayed in Figure 3, and we acknowledge that the misunderstanding is because the caption in Figure 1 (raised by the Reviewer below), and then the paragraph that immediately precedes Figure 3, which gives the impression that a single judge’s information has been input (in Figure 3b).

As a result, in addition to the corrections to the Figure 1 caption, we have altered the description in the paragraph preceding Figure 3 in order to clarify the process.

**Reviewer’s Comment
Finally, it appears that the app requires that cut scores needs to be expressed as a percentage correct. It would be useful if the app also allowed for raw scores to be input as an option as I have seen raw scores used in many different standard settings.

**Authors’ Response
Thank you for this comment. This may be an addition to Version 2 of the app, but the current literature (e.g. Bandaranayake 2008; Burr et al 2016) indicates percentage scores as the input, and so, it is prudent for Version 1 of the app to stick to the more common process as described in the dominant literature.

**Reviewer’s Comment
Another area for potential improvement is the example shown in Figure 1. The example shown in Figure 1 appears to be based on data from a single judge. While it is possible to determine the Hofstee cut score for each individual judge, this is rarely done as the authors note in Step 2: Determining the arithmetic mean. The figure would be more beneficial if it focused on data from a group of judges as this is how the method is typically implemented.

**Authors’ Response
Thank you for this point. Figure 1 is an illustrative example showing the chart after the arithmetic means of the parameters have been determined. As mentioned above, however, we acknowledge that the caption was erroneous, and it (and the sentence preceding it) have now been corrected.

**Reviewer’s Comment
There is a fourth practical and very real problem that occurs with the Hofstee method that is not described by the authors. Wyse and Babcock (2017)⁴ illustrate that the Hofstee method can produce undefined cut scores where the Hofstee line segment does not intersect with the failure rate or pass rate curve. This problem is a more serious issue than the three issues described by the authors as it implies that a cut score cannot be estimated. This issue should be mentioned in this section. Wyse and Babcock (2017)⁴ offer a solution for how to simply solve this issue, which involves extending the Hofsee line segment so that it intersects with the pass rate or failure rate curve. The other three practical issues described by the authors are easy to solve with Excel or other statistical software for technical savvy standard setters.

**Authors’ Response
We are reluctant to get into a discussion about the weaknesses of the Hofstee method or how to solve problems associated with it. To do so, and to do such a discussion justice (and view all arguments equally from all sides), is a paper by itself. In our discussion of the Hofstee Method, the aim is simply to explain it so that the functioning of the app is understood. Nevertheless, as readers may be expecting a discussion of the strengths and weaknesses of the Hofstee Method, we have inserted the sentence: “While there are weaknesses with the method, and they have been discussed elsewhere, this paper is focused on describing the method, and then describing an app that applies the method.” And the “elsewhere” in the sentence cites the Wyse & Babcock article mentioned by the reviewer.

**Reviewer’s Comment
It should also be pointed out that the way the authors describe calculating the Hofstee cut score is different than the way that I typically think about doing it. The authors description of their method based on arrays is not easy to understand and follow, especially for many educators who may use the app. Wyse and Babcock (2017)⁴ offer an easy way to determine the cut scores for the Hofstee method that guarantees a solution even if the Hofstee line segment does not intersect the pass rate or failure rate curve. The authors should consider implementing this method in their app and provide a corresponding description in the article. The strategy involves finding the equation for the line that passes through the two points represented by the means of the data collected from the standard-setting judges that was described in earlier section of the article by the authors. Then, one inputs range of possible scores on the exam to figure out the estimated pass rate or failure rate (depending on whether pass rate or failure rate data are collected from judges) for every possible score on the exam. The last step is to compare the estimated pass rates or failure rates to the observed pass rates or failure rates on the exam. The score with the smallest absolute difference between the observed and estimated pass rates or failure rates is the cut score.

**Authors’ Response
Thank you for your suggestion. The proposal for modification by Wyse and Babcock (2017) is, indeed, interesting. There are also others (e.g. Burr et al 2016).

The app (and, therefore, the article), however, is designed to determine the Hofstee cut-off as it is commonly practiced (e.g. Bandaranayake 2008). All proposed modifications cannot be implemented, and, if the app were to favour one modification over another, we would be open to criticisms of favouritism and of promoting and endorsing one modification over others. In this instance, the criticisms would be particularly sharp, because this modification has been proposed by one of the modification authors, who is also a reviewer of this paper. If we were to implement this modification (and not others), we would lay ourselves open to the accusation that we had made the modification to the app and the paper primarily to gain favour from the reviewer in the hopes of a more favourable review. As the reviewer can appreciate, both the authors and the journal would then be under pressure to retract such a paper (and remove the app from the app store).

That said, we could certainly envision a future version of the app that, based on a detailed literature review of all possible Hofstee variations and modification, would attempt to implement them all, allowing users to choose their favourite modification.

**Reviewer’s Comment
In summary, I think having a simple software app to perform Hofstee calculations is useful. However, the current version of the app does not cover all possible ways that the Hofstee method may be implemented which may limit its utility. If the authors made several changes based on the suggestions in this review, I think the app and article would have more utility and be easier to make sense for users.

**Authors’ Response
Thank you for your suggestion. We trust that our explanation and paper’s modifications detailed above satisfies the reviewer.

Is the rationale for developing the new software tool clearly explained?

Yes

Is the description of the software tool technically sound?

Partly

**Authors’ Response
We trust that our explanation and changes to the paper are to the reviewer’s satisfaction.

Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Partly

**Authors’ Response
We trust that our explanation and changes to the paper are to the reviewer’s satisfaction.

Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes

Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Partly

**Authors’ Response
We trust that our explanation and changes to the paper are to the reviewer’s satisfaction.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 19 Jul 2021

Ken Masters, Medical Education and Informatics, Sultan Qaboos University, Al-Khoud, 0123, Oman

19 Jul 2021

Author Response

We thank you for your detailed comments. We shall take them into account and address them in more detail when we have received responses from other reviewers.
Competing Interests: No competing interests were disclosed.
We thank you for your detailed comments. We shall take them into account and address them in more detail when we have received responses from other reviewers.
We thank you for your detailed comments. We shall take them into account and address them in more detail when we have received responses from other reviewers.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Author Response 05 Oct 2021

Ken Masters, Medical Education and Informatics, Sultan Qaboos University, Al-Khoud, 0123, Oman

05 Oct 2021

Author Response
We have now had the opportunity to respond in detail to this review. Below, we indicate the Reviewer’s comments and our response.

**Reviewer’s Comment
Approved With Reservations

**Authors’ ... Continue reading
We have now had the opportunity to respond in detail to this review. Below, we indicate the Reviewer’s comments and our response.

**Reviewer’s Comment
Approved With Reservations

**Authors’ Response
We thank the reviewer for their very detailed comments, and trust that our responses below and the changes to Version 1 of the paper will be to their satisfaction.

**Reviewer’s Comment
I appreciate the opportunity to review the article “Designing and developing an app to perform Hofstee cut-off calculations” by Ken Masters and Nadia Al-Wardy. I support the idea of developing simple software tools that people can use to perform standard setting. This is an area of definite need, especially in medical education contexts. I am unaware of a widely available software application to perform the Hofstee method. In most cases that I have seen the Hofstee method used, the people leading the standard setting use Excel or another statistical software package, such as R, to perform the calculations and figure out the cut score. In this sense, the app offered by Masters and Al-Wardy may be beneficial to people who want to perform the Hofstee method and do not have already developed software to perform the Hofstee method. I also liked how the authors provided screen shots of how the app works and several figures and examples throughout the article.

**Authors’ Response
We thank the reviewer for their overall frank comments.

**Reviewer’s Comment
I do have several suggestions for changes to the article and app. First, the authors suggest in the section Step 1: Evaluation of Judges that “We should further note that judges will generally use the Angoff or similar method to determine these.” This statement is not completely accurate. Wyse (2020)¹ discusses several different methods for performing the Hofstee method. One strategy is to figure out the minimum and maximum cut scores from the panel of judges using the Angoff (1971)² method or another test-centered method, such as the Bookmark method (Lewis, Mitzel, & Green, 1996)³. However, this method is not the most common strategy I have seen used to collect these data. It is more common to directly ask panellists to answer four open-ended questions to solicit the data needed to estimate the Hofstee cut score. In addition, it should be noted that even if the Angoff method is used with the Hofstee method that the data on the lowest and high percentages of students that a judge feels should fail the test (which is sometimes alternatively phrased in terms of the highest and lowest students that should pass the test) need to be directly collected from individual judges.

**Authors’ Response
Thank you for this comment. The published texts that we were using (Bandaranayake 2008; Wyse and Babcock 2017) indicated that the Hofstee was frequently used in conjunction with the Angoff method and so we mentioned that. As this is not central to the paper, however, the sentence has been deleted.

**Reviewer’s Comment
It should also be clear that the description of using the Angoff method to provide data to calculate the cut scores appears to be inconsistent with how the app works in Figure 3. In Figure 3, the authors show a screen with input for each rater. It is not possible to use the Angoff method to provide the multiple limiter input data shown on this screen. The app could be improved if it allowed for data from an Angoff standard setting or other test-centered method to be input. This input could be either entering the minimum and maximum cut scores from a test-centered standard setting method or each judge’s cut score from such a standard setting. It would also be beneficial if the app allowed for an option to input the lowest and highest passing rates and a corresponding graph instead of failure rates. I have commonly seen the method used with passing rates instead of failure rates. Judges sometimes find it easier to conceptualize and use pass rates as many credentialing and licensing organizations as well as accrediting bodies use passing rates instead of failure rates.

**Authors’ Response
Thank you for this comment. We apologise for the misunderstanding about what is being portrayed in Figure 3, and we acknowledge that the misunderstanding is because the caption in Figure 1 (raised by the Reviewer below), and then the paragraph that immediately precedes Figure 3, which gives the impression that a single judge’s information has been input (in Figure 3b).

As a result, in addition to the corrections to the Figure 1 caption, we have altered the description in the paragraph preceding Figure 3 in order to clarify the process.

**Reviewer’s Comment
Finally, it appears that the app requires that cut scores needs to be expressed as a percentage correct. It would be useful if the app also allowed for raw scores to be input as an option as I have seen raw scores used in many different standard settings.

**Authors’ Response
Thank you for this comment. This may be an addition to Version 2 of the app, but the current literature (e.g. Bandaranayake 2008; Burr et al 2016) indicates percentage scores as the input, and so, it is prudent for Version 1 of the app to stick to the more common process as described in the dominant literature.

**Reviewer’s Comment
Another area for potential improvement is the example shown in Figure 1. The example shown in Figure 1 appears to be based on data from a single judge. While it is possible to determine the Hofstee cut score for each individual judge, this is rarely done as the authors note in Step 2: Determining the arithmetic mean. The figure would be more beneficial if it focused on data from a group of judges as this is how the method is typically implemented.

**Authors’ Response
Thank you for this point. Figure 1 is an illustrative example showing the chart after the arithmetic means of the parameters have been determined. As mentioned above, however, we acknowledge that the caption was erroneous, and it (and the sentence preceding it) have now been corrected.

**Reviewer’s Comment
There is a fourth practical and very real problem that occurs with the Hofstee method that is not described by the authors. Wyse and Babcock (2017)⁴ illustrate that the Hofstee method can produce undefined cut scores where the Hofstee line segment does not intersect with the failure rate or pass rate curve. This problem is a more serious issue than the three issues described by the authors as it implies that a cut score cannot be estimated. This issue should be mentioned in this section. Wyse and Babcock (2017)⁴ offer a solution for how to simply solve this issue, which involves extending the Hofsee line segment so that it intersects with the pass rate or failure rate curve. The other three practical issues described by the authors are easy to solve with Excel or other statistical software for technical savvy standard setters.

**Authors’ Response
We are reluctant to get into a discussion about the weaknesses of the Hofstee method or how to solve problems associated with it. To do so, and to do such a discussion justice (and view all arguments equally from all sides), is a paper by itself. In our discussion of the Hofstee Method, the aim is simply to explain it so that the functioning of the app is understood. Nevertheless, as readers may be expecting a discussion of the strengths and weaknesses of the Hofstee Method, we have inserted the sentence: “While there are weaknesses with the method, and they have been discussed elsewhere, this paper is focused on describing the method, and then describing an app that applies the method.” And the “elsewhere” in the sentence cites the Wyse & Babcock article mentioned by the reviewer.

**Reviewer’s Comment
It should also be pointed out that the way the authors describe calculating the Hofstee cut score is different than the way that I typically think about doing it. The authors description of their method based on arrays is not easy to understand and follow, especially for many educators who may use the app. Wyse and Babcock (2017)⁴ offer an easy way to determine the cut scores for the Hofstee method that guarantees a solution even if the Hofstee line segment does not intersect the pass rate or failure rate curve. The authors should consider implementing this method in their app and provide a corresponding description in the article. The strategy involves finding the equation for the line that passes through the two points represented by the means of the data collected from the standard-setting judges that was described in earlier section of the article by the authors. Then, one inputs range of possible scores on the exam to figure out the estimated pass rate or failure rate (depending on whether pass rate or failure rate data are collected from judges) for every possible score on the exam. The last step is to compare the estimated pass rates or failure rates to the observed pass rates or failure rates on the exam. The score with the smallest absolute difference between the observed and estimated pass rates or failure rates is the cut score.

**Authors’ Response
Thank you for your suggestion. The proposal for modification by Wyse and Babcock (2017) is, indeed, interesting. There are also others (e.g. Burr et al 2016).

The app (and, therefore, the article), however, is designed to determine the Hofstee cut-off as it is commonly practiced (e.g. Bandaranayake 2008). All proposed modifications cannot be implemented, and, if the app were to favour one modification over another, we would be open to criticisms of favouritism and of promoting and endorsing one modification over others. In this instance, the criticisms would be particularly sharp, because this modification has been proposed by one of the modification authors, who is also a reviewer of this paper. If we were to implement this modification (and not others), we would lay ourselves open to the accusation that we had made the modification to the app and the paper primarily to gain favour from the reviewer in the hopes of a more favourable review. As the reviewer can appreciate, both the authors and the journal would then be under pressure to retract such a paper (and remove the app from the app store).

That said, we could certainly envision a future version of the app that, based on a detailed literature review of all possible Hofstee variations and modification, would attempt to implement them all, allowing users to choose their favourite modification.

**Reviewer’s Comment
In summary, I think having a simple software app to perform Hofstee calculations is useful. However, the current version of the app does not cover all possible ways that the Hofstee method may be implemented which may limit its utility. If the authors made several changes based on the suggestions in this review, I think the app and article would have more utility and be easier to make sense for users.

**Authors’ Response
Thank you for your suggestion. We trust that our explanation and paper’s modifications detailed above satisfies the reviewer.

Is the rationale for developing the new software tool clearly explained?

Yes

Is the description of the software tool technically sound?

Partly

**Authors’ Response
We trust that our explanation and changes to the paper are to the reviewer’s satisfaction.

Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Partly

**Authors’ Response
We trust that our explanation and changes to the paper are to the reviewer’s satisfaction.

Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes

Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Partly

**Authors’ Response
We trust that our explanation and changes to the paper are to the reviewer’s satisfaction.
We have now had the opportunity to respond in detail to this review. Below, we indicate the Reviewer’s comments and our response.

**Reviewer’s Comment
Approved With Reservations

**Authors’ Response
We thank the reviewer for their very detailed comments, and trust that our responses below and the changes to Version 1 of the paper will be to their satisfaction.

**Reviewer’s Comment
I appreciate the opportunity to review the article “Designing and developing an app to perform Hofstee cut-off calculations” by Ken Masters and Nadia Al-Wardy. I support the idea of developing simple software tools that people can use to perform standard setting. This is an area of definite need, especially in medical education contexts. I am unaware of a widely available software application to perform the Hofstee method. In most cases that I have seen the Hofstee method used, the people leading the standard setting use Excel or another statistical software package, such as R, to perform the calculations and figure out the cut score. In this sense, the app offered by Masters and Al-Wardy may be beneficial to people who want to perform the Hofstee method and do not have already developed software to perform the Hofstee method. I also liked how the authors provided screen shots of how the app works and several figures and examples throughout the article.

**Authors’ Response
We thank the reviewer for their overall frank comments.

**Reviewer’s Comment
I do have several suggestions for changes to the article and app. First, the authors suggest in the section Step 1: Evaluation of Judges that “We should further note that judges will generally use the Angoff or similar method to determine these.” This statement is not completely accurate. Wyse (2020)¹ discusses several different methods for performing the Hofstee method. One strategy is to figure out the minimum and maximum cut scores from the panel of judges using the Angoff (1971)² method or another test-centered method, such as the Bookmark method (Lewis, Mitzel, & Green, 1996)³. However, this method is not the most common strategy I have seen used to collect these data. It is more common to directly ask panellists to answer four open-ended questions to solicit the data needed to estimate the Hofstee cut score. In addition, it should be noted that even if the Angoff method is used with the Hofstee method that the data on the lowest and high percentages of students that a judge feels should fail the test (which is sometimes alternatively phrased in terms of the highest and lowest students that should pass the test) need to be directly collected from individual judges.

**Authors’ Response
Thank you for this comment. The published texts that we were using (Bandaranayake 2008; Wyse and Babcock 2017) indicated that the Hofstee was frequently used in conjunction with the Angoff method and so we mentioned that. As this is not central to the paper, however, the sentence has been deleted.

**Reviewer’s Comment
It should also be clear that the description of using the Angoff method to provide data to calculate the cut scores appears to be inconsistent with how the app works in Figure 3. In Figure 3, the authors show a screen with input for each rater. It is not possible to use the Angoff method to provide the multiple limiter input data shown on this screen. The app could be improved if it allowed for data from an Angoff standard setting or other test-centered method to be input. This input could be either entering the minimum and maximum cut scores from a test-centered standard setting method or each judge’s cut score from such a standard setting. It would also be beneficial if the app allowed for an option to input the lowest and highest passing rates and a corresponding graph instead of failure rates. I have commonly seen the method used with passing rates instead of failure rates. Judges sometimes find it easier to conceptualize and use pass rates as many credentialing and licensing organizations as well as accrediting bodies use passing rates instead of failure rates.

**Authors’ Response
Thank you for this comment. We apologise for the misunderstanding about what is being portrayed in Figure 3, and we acknowledge that the misunderstanding is because the caption in Figure 1 (raised by the Reviewer below), and then the paragraph that immediately precedes Figure 3, which gives the impression that a single judge’s information has been input (in Figure 3b).

As a result, in addition to the corrections to the Figure 1 caption, we have altered the description in the paragraph preceding Figure 3 in order to clarify the process.

**Reviewer’s Comment
Finally, it appears that the app requires that cut scores needs to be expressed as a percentage correct. It would be useful if the app also allowed for raw scores to be input as an option as I have seen raw scores used in many different standard settings.

**Authors’ Response
Thank you for this comment. This may be an addition to Version 2 of the app, but the current literature (e.g. Bandaranayake 2008; Burr et al 2016) indicates percentage scores as the input, and so, it is prudent for Version 1 of the app to stick to the more common process as described in the dominant literature.

**Reviewer’s Comment
Another area for potential improvement is the example shown in Figure 1. The example shown in Figure 1 appears to be based on data from a single judge. While it is possible to determine the Hofstee cut score for each individual judge, this is rarely done as the authors note in Step 2: Determining the arithmetic mean. The figure would be more beneficial if it focused on data from a group of judges as this is how the method is typically implemented.

**Authors’ Response
Thank you for this point. Figure 1 is an illustrative example showing the chart after the arithmetic means of the parameters have been determined. As mentioned above, however, we acknowledge that the caption was erroneous, and it (and the sentence preceding it) have now been corrected.

**Reviewer’s Comment
There is a fourth practical and very real problem that occurs with the Hofstee method that is not described by the authors. Wyse and Babcock (2017)⁴ illustrate that the Hofstee method can produce undefined cut scores where the Hofstee line segment does not intersect with the failure rate or pass rate curve. This problem is a more serious issue than the three issues described by the authors as it implies that a cut score cannot be estimated. This issue should be mentioned in this section. Wyse and Babcock (2017)⁴ offer a solution for how to simply solve this issue, which involves extending the Hofsee line segment so that it intersects with the pass rate or failure rate curve. The other three practical issues described by the authors are easy to solve with Excel or other statistical software for technical savvy standard setters.

**Authors’ Response
We are reluctant to get into a discussion about the weaknesses of the Hofstee method or how to solve problems associated with it. To do so, and to do such a discussion justice (and view all arguments equally from all sides), is a paper by itself. In our discussion of the Hofstee Method, the aim is simply to explain it so that the functioning of the app is understood. Nevertheless, as readers may be expecting a discussion of the strengths and weaknesses of the Hofstee Method, we have inserted the sentence: “While there are weaknesses with the method, and they have been discussed elsewhere, this paper is focused on describing the method, and then describing an app that applies the method.” And the “elsewhere” in the sentence cites the Wyse & Babcock article mentioned by the reviewer.

**Reviewer’s Comment
It should also be pointed out that the way the authors describe calculating the Hofstee cut score is different than the way that I typically think about doing it. The authors description of their method based on arrays is not easy to understand and follow, especially for many educators who may use the app. Wyse and Babcock (2017)⁴ offer an easy way to determine the cut scores for the Hofstee method that guarantees a solution even if the Hofstee line segment does not intersect the pass rate or failure rate curve. The authors should consider implementing this method in their app and provide a corresponding description in the article. The strategy involves finding the equation for the line that passes through the two points represented by the means of the data collected from the standard-setting judges that was described in earlier section of the article by the authors. Then, one inputs range of possible scores on the exam to figure out the estimated pass rate or failure rate (depending on whether pass rate or failure rate data are collected from judges) for every possible score on the exam. The last step is to compare the estimated pass rates or failure rates to the observed pass rates or failure rates on the exam. The score with the smallest absolute difference between the observed and estimated pass rates or failure rates is the cut score.

**Authors’ Response
Thank you for your suggestion. The proposal for modification by Wyse and Babcock (2017) is, indeed, interesting. There are also others (e.g. Burr et al 2016).

The app (and, therefore, the article), however, is designed to determine the Hofstee cut-off as it is commonly practiced (e.g. Bandaranayake 2008). All proposed modifications cannot be implemented, and, if the app were to favour one modification over another, we would be open to criticisms of favouritism and of promoting and endorsing one modification over others. In this instance, the criticisms would be particularly sharp, because this modification has been proposed by one of the modification authors, who is also a reviewer of this paper. If we were to implement this modification (and not others), we would lay ourselves open to the accusation that we had made the modification to the app and the paper primarily to gain favour from the reviewer in the hopes of a more favourable review. As the reviewer can appreciate, both the authors and the journal would then be under pressure to retract such a paper (and remove the app from the app store).

That said, we could certainly envision a future version of the app that, based on a detailed literature review of all possible Hofstee variations and modification, would attempt to implement them all, allowing users to choose their favourite modification.

**Reviewer’s Comment
In summary, I think having a simple software app to perform Hofstee calculations is useful. However, the current version of the app does not cover all possible ways that the Hofstee method may be implemented which may limit its utility. If the authors made several changes based on the suggestions in this review, I think the app and article would have more utility and be easier to make sense for users.

**Authors’ Response
Thank you for your suggestion. We trust that our explanation and paper’s modifications detailed above satisfies the reviewer.

Is the rationale for developing the new software tool clearly explained?

Yes

Is the description of the software tool technically sound?

Partly

**Authors’ Response
We trust that our explanation and changes to the paper are to the reviewer’s satisfaction.

Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Partly

**Authors’ Response
We trust that our explanation and changes to the paper are to the reviewer’s satisfaction.

Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes

Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Partly

**Authors’ Response
We trust that our explanation and changes to the paper are to the reviewer’s satisfaction.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 07 Jun 2021

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 2 (revision) 05 Oct 21	read	read
Version 1 07 Jun 21	read	read

Adam E. Wyse, Renaissance, Arden Hills, USA
Benedict Canny, University of Adelaide, Adelaide, Australia

Comments on this article

All Comments(0)

Add a comment

Browse by related subjects

Back to all reports

Reviewer Report

9 Views

01 Nov 2021 | for Version 2

Adam E. Wyse, Renaissance, Arden Hills, MN, USA

9 Views Cite this report Responses(1)

Approved

I don’t have any additional feedback or suggestions for the revised manuscript.

Competing Interests

I have published several papers on the Hofstee method. One of these papers is referenced by the authors. It is important to me that my work and some of the ideas presented in those papers are accurately reflected in the article.

Reviewer Expertise

Psychometrics; Standard Setting; Measurement; Item Response Theory; Assessment

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (1)

Back to all reports

Reviewer Report

12 Views

07 Oct 2021 | for Version 2

Benedict Canny, Adelaide Medical School, University of Adelaide, Adelaide, SA, Australia

12 Views Cite this report Responses(1)

Approved

The authors have addressed the concerns outlined in the original review.

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Education Research

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (1)

Back to all reports

Reviewer Report

12 Views

11 Aug 2021 | for Version 1

Benedict Canny, Adelaide Medical School, University of Adelaide, Adelaide, SA, Australia

12 Views Cite this report Responses(2)

Approved With Reservations

Is the rationale for developing the new software tool clearly explained?

Yes
Is the description of the software tool technically sound?

Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Yes
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Partly

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Education Research

Respond to this report

Responses (2)

Author Response

05 Oct 2021

Ken Masters, Medical Education and Informatics, Sultan Qaboos University, Al-Khoud, 0123, Oman

Is the rationale for developing the new software tool clearly explained?

Yes

Is the description of the software tool technically sound?

Yes

Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Yes

Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes

Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Partly

**Authors’ Response
We trust that our explanation and changes to the paper are to the reviewer’s satisfaction.

View more View less

Competing Interests

No competing interests were disclosed.

Back to all reports

Reviewer Report

30 Views

14 Jul 2021 | for Version 1

Adam E. Wyse, Renaissance, Arden Hills, MN, USA

30 Views Cite this report Responses(2)

Approved With Reservations

Is the rationale for developing the new software tool clearly explained?

Yes
Is the description of the software tool technically sound?

Partly
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Partly
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Partly

References

Competing Interests

Reviewer Expertise

Psychometrics; Standard Setting; Measurement; Item Response Theory; Assessment

Respond to this report

Responses (2)

Author Response

05 Oct 2021

Ken Masters, Medical Education and Informatics, Sultan Qaboos University, Al-Khoud, 0123, Oman

We have now had the opportunity to respond in detail to this review. Below, we indicate the Reviewer’s comments and our response.

**Reviewer’s Comment
Approved With Reservations

**Authors’ Response
We thank the reviewer for their very detailed comments, and trust that our responses below and the changes to Version 1 of the paper will be to their satisfaction.

**Reviewer’s Comment
I appreciate the opportunity to review the article “Designing and developing an app to perform Hofstee cut-off calculations” by Ken Masters and Nadia Al-Wardy. I support the idea of developing simple software tools that people can use to perform standard setting. This is an area of definite need, especially in medical education contexts. I am unaware of a widely available software application to perform the Hofstee method. In most cases that I have seen the Hofstee method used, the people leading the standard setting use Excel or another statistical software package, such as R, to perform the calculations and figure out the cut score. In this sense, the app offered by Masters and Al-Wardy may be beneficial to people who want to perform the Hofstee method and do not have already developed software to perform the Hofstee method. I also liked how the authors provided screen shots of how the app works and several figures and examples throughout the article.

**Authors’ Response
We thank the reviewer for their overall frank comments.

**Reviewer’s Comment
I do have several suggestions for changes to the article and app. First, the authors suggest in the section Step 1: Evaluation of Judges that “We should further note that judges will generally use the Angoff or similar method to determine these.” This statement is not completely accurate. Wyse (2020)¹ discusses several different methods for performing the Hofstee method. One strategy is to figure out the minimum and maximum cut scores from the panel of judges using the Angoff (1971)² method or another test-centered method, such as the Bookmark method (Lewis, Mitzel, & Green, 1996)³. However, this method is not the most common strategy I have seen used to collect these data. It is more common to directly ask panellists to answer four open-ended questions to solicit the data needed to estimate the Hofstee cut score. In addition, it should be noted that even if the Angoff method is used with the Hofstee method that the data on the lowest and high percentages of students that a judge feels should fail the test (which is sometimes alternatively phrased in terms of the highest and lowest students that should pass the test) need to be directly collected from individual judges.

**Authors’ Response
Thank you for this comment. The published texts that we were using (Bandaranayake 2008; Wyse and Babcock 2017) indicated that the Hofstee was frequently used in conjunction with the Angoff method and so we mentioned that. As this is not central to the paper, however, the sentence has been deleted.

**Reviewer’s Comment
It should also be clear that the description of using the Angoff method to provide data to calculate the cut scores appears to be inconsistent with how the app works in Figure 3. In Figure 3, the authors show a screen with input for each rater. It is not possible to use the Angoff method to provide the multiple limiter input data shown on this screen. The app could be improved if it allowed for data from an Angoff standard setting or other test-centered method to be input. This input could be either entering the minimum and maximum cut scores from a test-centered standard setting method or each judge’s cut score from such a standard setting. It would also be beneficial if the app allowed for an option to input the lowest and highest passing rates and a corresponding graph instead of failure rates. I have commonly seen the method used with passing rates instead of failure rates. Judges sometimes find it easier to conceptualize and use pass rates as many credentialing and licensing organizations as well as accrediting bodies use passing rates instead of failure rates.

**Authors’ Response
Thank you for this comment. We apologise for the misunderstanding about what is being portrayed in Figure 3, and we acknowledge that the misunderstanding is because the caption in Figure 1 (raised by the Reviewer below), and then the paragraph that immediately precedes Figure 3, which gives the impression that a single judge’s information has been input (in Figure 3b).

As a result, in addition to the corrections to the Figure 1 caption, we have altered the description in the paragraph preceding Figure 3 in order to clarify the process.

**Reviewer’s Comment
Finally, it appears that the app requires that cut scores needs to be expressed as a percentage correct. It would be useful if the app also allowed for raw scores to be input as an option as I have seen raw scores used in many different standard settings.

**Authors’ Response
Thank you for this comment. This may be an addition to Version 2 of the app, but the current literature (e.g. Bandaranayake 2008; Burr et al 2016) indicates percentage scores as the input, and so, it is prudent for Version 1 of the app to stick to the more common process as described in the dominant literature.

**Reviewer’s Comment
Another area for potential improvement is the example shown in Figure 1. The example shown in Figure 1 appears to be based on data from a single judge. While it is possible to determine the Hofstee cut score for each individual judge, this is rarely done as the authors note in Step 2: Determining the arithmetic mean. The figure would be more beneficial if it focused on data from a group of judges as this is how the method is typically implemented.

**Authors’ Response
Thank you for this point. Figure 1 is an illustrative example showing the chart after the arithmetic means of the parameters have been determined. As mentioned above, however, we acknowledge that the caption was erroneous, and it (and the sentence preceding it) have now been corrected.

**Reviewer’s Comment
There is a fourth practical and very real problem that occurs with the Hofstee method that is not described by the authors. Wyse and Babcock (2017)⁴ illustrate that the Hofstee method can produce undefined cut scores where the Hofstee line segment does not intersect with the failure rate or pass rate curve. This problem is a more serious issue than the three issues described by the authors as it implies that a cut score cannot be estimated. This issue should be mentioned in this section. Wyse and Babcock (2017)⁴ offer a solution for how to simply solve this issue, which involves extending the Hofsee line segment so that it intersects with the pass rate or failure rate curve. The other three practical issues described by the authors are easy to solve with Excel or other statistical software for technical savvy standard setters.

**Authors’ Response
We are reluctant to get into a discussion about the weaknesses of the Hofstee method or how to solve problems associated with it. To do so, and to do such a discussion justice (and view all arguments equally from all sides), is a paper by itself. In our discussion of the Hofstee Method, the aim is simply to explain it so that the functioning of the app is understood. Nevertheless, as readers may be expecting a discussion of the strengths and weaknesses of the Hofstee Method, we have inserted the sentence: “While there are weaknesses with the method, and they have been discussed elsewhere, this paper is focused on describing the method, and then describing an app that applies the method.” And the “elsewhere” in the sentence cites the Wyse & Babcock article mentioned by the reviewer.

**Reviewer’s Comment
It should also be pointed out that the way the authors describe calculating the Hofstee cut score is different than the way that I typically think about doing it. The authors description of their method based on arrays is not easy to understand and follow, especially for many educators who may use the app. Wyse and Babcock (2017)⁴ offer an easy way to determine the cut scores for the Hofstee method that guarantees a solution even if the Hofstee line segment does not intersect the pass rate or failure rate curve. The authors should consider implementing this method in their app and provide a corresponding description in the article. The strategy involves finding the equation for the line that passes through the two points represented by the means of the data collected from the standard-setting judges that was described in earlier section of the article by the authors. Then, one inputs range of possible scores on the exam to figure out the estimated pass rate or failure rate (depending on whether pass rate or failure rate data are collected from judges) for every possible score on the exam. The last step is to compare the estimated pass rates or failure rates to the observed pass rates or failure rates on the exam. The score with the smallest absolute difference between the observed and estimated pass rates or failure rates is the cut score.

**Authors’ Response
Thank you for your suggestion. The proposal for modification by Wyse and Babcock (2017) is, indeed, interesting. There are also others (e.g. Burr et al 2016).

The app (and, therefore, the article), however, is designed to determine the Hofstee cut-off as it is commonly practiced (e.g. Bandaranayake 2008). All proposed modifications cannot be implemented, and, if the app were to favour one modification over another, we would be open to criticisms of favouritism and of promoting and endorsing one modification over others. In this instance, the criticisms would be particularly sharp, because this modification has been proposed by one of the modification authors, who is also a reviewer of this paper. If we were to implement this modification (and not others), we would lay ourselves open to the accusation that we had made the modification to the app and the paper primarily to gain favour from the reviewer in the hopes of a more favourable review. As the reviewer can appreciate, both the authors and the journal would then be under pressure to retract such a paper (and remove the app from the app store).

That said, we could certainly envision a future version of the app that, based on a detailed literature review of all possible Hofstee variations and modification, would attempt to implement them all, allowing users to choose their favourite modification.

**Reviewer’s Comment
In summary, I think having a simple software app to perform Hofstee calculations is useful. However, the current version of the app does not cover all possible ways that the Hofstee method may be implemented which may limit its utility. If the authors made several changes based on the suggestions in this review, I think the app and article would have more utility and be easier to make sense for users.

**Authors’ Response
Thank you for your suggestion. We trust that our explanation and paper’s modifications detailed above satisfies the reviewer.

Is the rationale for developing the new software tool clearly explained?

Yes

Is the description of the software tool technically sound?

Partly

**Authors’ Response
We trust that our explanation and changes to the paper are to the reviewer’s satisfaction.

Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Partly

**Authors’ Response
We trust that our explanation and changes to the paper are to the reviewer’s satisfaction.

Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes

Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Partly

**Authors’ Response
We trust that our explanation and changes to the paper are to the reviewer’s satisfaction.

View more View less

Competing Interests

No competing interests were disclosed.

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

[1] 1. Schauber SK, Hecht M: How sure can we be that a student really failed? On the measurement precision of individual pass-fail decisions from the perspective of Item Response Theory. Med Teach. 2020 Dec 1; 42(12): 1374–84. PubMed Abstract | Publisher Full Text

[2] 2. Norcini JJ: Standard setting on educational tests. Med Educ. 2003; 37(5): 464–9. PubMed Abstract | Publisher Full Text

[3] 3. Downing SM, Tekian A, Yudkowsky R: Procedures for establishing defensible absolute passing scores on performance examinations in health professions education. Teach Learn Med. 2006; 18(1): 50–7. PubMed Abstract | Publisher Full Text

[4] 4. Bandaranayake RC: Setting and maintaining standards in multiple choice examinations: AMEE Guide No. 37. Med Teach. 2008; 30(9–10): 836–45. PubMed Abstract | Publisher Full Text

[5] 5. Hofstee WKB: The case for compromise in educational selection and grading. In: Anderson SB, Helmick JS, editors. On Educational Testing . San Francisco: Jossey-Bass; 1983. p. 109–27.

[6] 6. Wyse AE, Babcock B: An investigation of undefined cut scores with the Hofstee Standard-Setting Method. Educ Meas Issues Pract. 2017; 36(4): 28–34. Publisher Full Text

[7] 7. Hofstee W: Cesuurprobleem opgelost [The standard setting problem resolved]. Onderz Van Onderwijs. 1977; 6: 6–7.

[8] 8. Van Der Vleuten C: Setting and maintaining standards in multiple choice examinations (AMEE Supplement 37.1). Med Teach. 2010; 32: 174–6. Publisher Full Text

[9] 9. Stoyanov SR, Hides L, Kavanagh DJ, et al.: Mobile App Rating Scale: A New Tool for Assessing the Quality of Health Mobile Apps. JMIR MHealth UHealth. 2015; 3(1): e27. PubMed Abstract | Publisher Full Text | Free Full Text

[10] 10. Pura Vida Apps: File Extension [Internet]. App Inventor Extensions . 2019 [cited 2020 Mar 1]. Reference Source

[11] 11. Pevest.com: QuickSort routine for your App Inventor Apps! [Internet].2017 [cited 2020 Mar 1]. Reference Source

[12] 12. Manning K, Kager E: ChartMaker [Internet].2017 [cited 2020 Mar 1]. Reference Source

[13] 13. Masters K: HofsteeCalcDataSets (Version Ver 1.1) [Data set]. Zenodo . 2021. Publisher Full Text

[14] 14. Masters K: HofsteeCalc (Version 1.1). Zenodo . 2021, March 24. Publisher Full Text

Designing and developing an app to perform Hofstee cut-off calculations

Abstract

Keywords

Revised Amendments from Version 1

Introduction

Determining the pass/fail score in assessments

Hofstee method

Figure 1.

Practical problems with using the Hofstee method

Non-paper solutions

An app

Methods

Implementation

Operation

Figure 2. App workflow.

Figure 3.

Central algorithm to algebraically determine the Hofstee cut-off

App completion

App description and functionality

Alpha testing

Mobile App Rating Scale (MARS)

Use case

Table 1.

Figure 4.

Comments

Conclusions

Data availability

Underlying data

Software availability

Acknowledgments

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated