Keywords
Dendrites, computation, linearly non-separable, neuroscience
This article is included in the INCF gateway.
Dendrites, computation, linearly non-separable, neuroscience
We do not use a reduction in driving force to implement sublinear summation. We added a paragraph to the discussion to make this point crystal clear.
We updated the code and upgraded the figure to change time->episode. Fig.1C demonstrates what we mean by an episode. We added a reference to the figure in the result paragraph.
Finally we made slight changes to take into account all the minor comments from the reviewer.
See the author's detailed response to the review by Athanasia Papoutsi and Spyridon Chavlis
See the author's detailed response to the review by Balazs B Ujfalussy
We show here how dendrites can extend the computational capacity of all neurons, even the tiniest. We already knew that dendrites might extend the computational capacity of some pyramidal neurons. Their extended dendrites capable of dendritic spikes changed the way we saw them (see2 for one of the first articles presenting this idea). More recently a study suggested that we should model these neurons as a two layer neural networks.6 This theoretical model was further consolidated by experiments showing that we can see a pyramidal neuron as a collection of non-linear subunits.7 Certain non-linearities can even allow a dendrite to implement the exclusive or (XOR).9 Moreover, a similar kind of non-monotonic non-linearity was found in human pyramidal neurons.4 But what about other neurons with modest dendrites incapable of spiking?
Pyramidal neurons only represent a fraction of all neurons. For instance, the dendrites of cerebellar stellate cells cannot emit spikes, but they do saturate1 and they can be decomposed into multiple independent subunits - with independent membrane voltages - turning them into two-stage units like the pyramidal neuron.8 Previously we have shown that passive dendrites are sufficient to enable a neuron to perform linearly non-separable computations, for instance, the feature binding problem.3 We focus here on cells with a modest and passive dendritic tree. These cells form a single layer unit. In the present study, we demonstrate that these neurons can still implement a linearly non-separable computation. We use them as the simplest common denominator, as even spiking dendrites do saturate, and a 2 layer network can perform all the computation of a single layer architecture and more.
We started from a leaky integrate and fire (LIF). This model has a membrane V modelled by the following equation:
With τ = 20 ms the neuron time constant, v(t) the membrane voltage at time t and vE = −62 mV which sets the resting membrane voltage. R = 20 MΩ is the value of the resistance and Is(t) models the time varying synaptic inputs conductance.
This current depends on the difference between v(t) the neuron voltage, equal everywhere, and Es the synaptic reversal potential (0 mV) while is the synaptic conductance in dendrite i. Each is bounded between 0 and 10pS. Each jumps up instantaneously to its maximal value for each incoming input spike and decays exponentially with time constant τs = 1 ms. In a LIF all synaptic inputs are gathered into a single umbrella and i = 1. In the present study, we introduce the Dendrited Integrate and Fire (DIF) which includes at least two dendrites (i = 2). We cluster synaptic inputs into two groups, each targeting a dendrite (one green and one blue, see Figure 1). We used the Brian software version 2 to carry out our simulations, the code is freely available on the git repository attached with this report.10
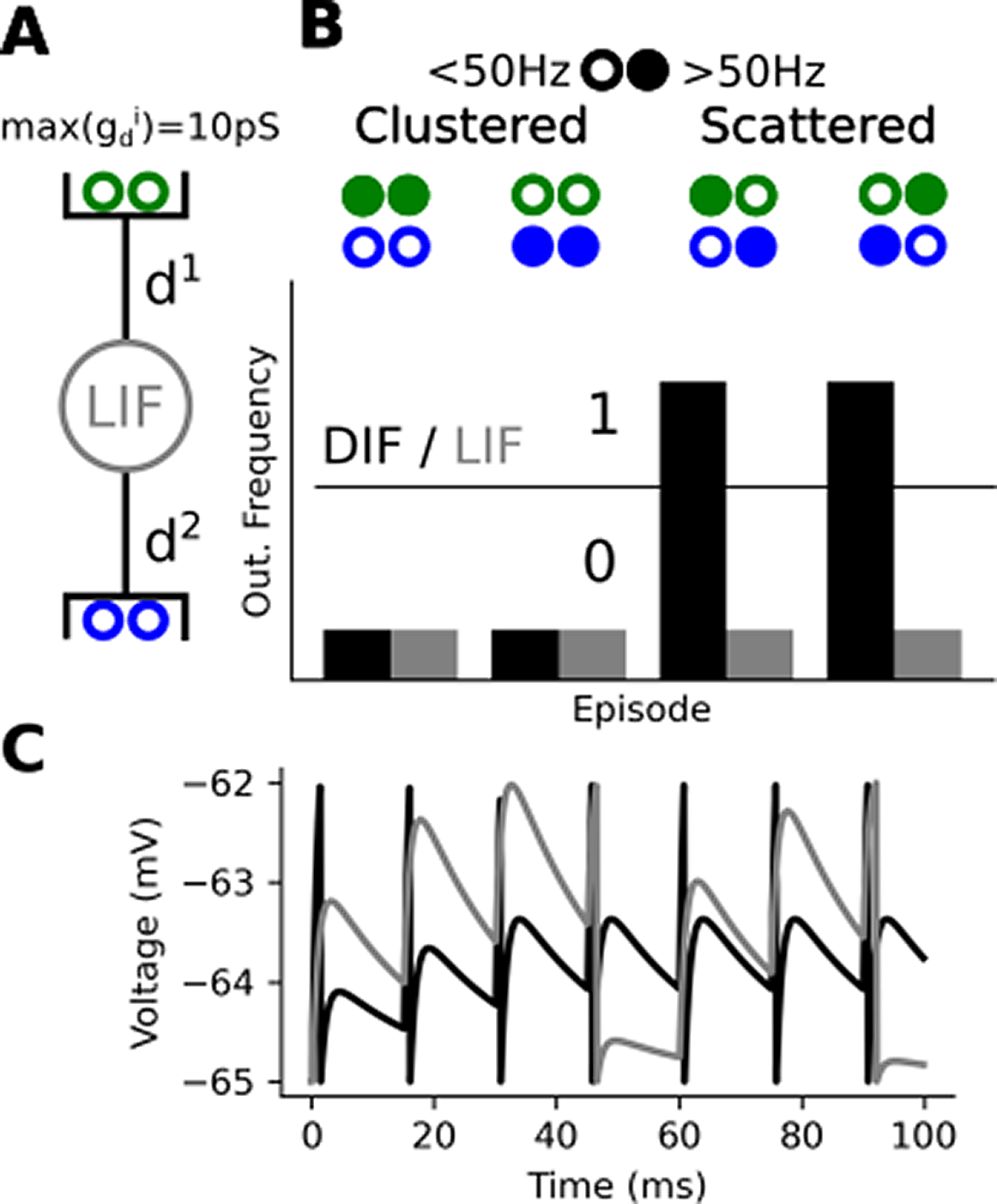
(A) A leaky integrate and fire (LIF) with two dendrites making it a dendrited integrate and fire (DIF), each half of the 4 synaptic inputs targets a distinct dendrite where g locally saturates at 10pS (B) Four stimulation episodes, filled circles stand for a >50 Hz input spike train while empty circles stand for >50 Hz input spike train. Below, we plotted the response of the DIF (black) and a LIF (grey) during the episode. We purposely removed the ticks label as the frequencies depend on the parameter of the model and input regularity. The parameters of the model can vary largely without affecting the observation. (C) Some voltage response during the 3rd episode. In the clustered case (grey), the neuron reach spike threshold three times whereas it reaches spike thresold seven times in the scattered case (black).5
First, let’s present Boolean functions:
Definition 1. A Boolean function of n variables is a function on {0,1}n into {0,1}, where n is a positive integer.
Importantly, we commonly assume that neurons can only implement linearly separable computations:
Definition 2. f is a linearly separable computation of n variables if and only if there exists at least one vector w ∈ and a threshold Θ ∈ such that:
where X ∈{0,1}n is the vector notation for the Boolean input variables.
In this section, we demonstrate a class of compact linearly inseparable (non-separable) computations that we are going to study. These computations are compact because they have four input/output lines.
We entirely specify an example in Table 1. This computation that we call the compact feature binding problem (cFBP) is linearly inseparable.
Proposition 1. The cFBP is linearly inseparable (non-separable)
Proof. The output must be 0 for two disjoint couples (1,2) and (3,4) of active inputs. It means that w1 + w2 ≤ Θ, and w3 + w4 ≤ Θ, and we can add these two inequalities to obtain w1 + w2 + w3 + w4 ≤ 2Θ. However, the output must be 1 for two other couples made of the same active inputs (1,3) and (2,4). It means that w1 + w3 > Θ, and w2 + w4 > Θ, and we can add these two inequalities to obtain w1 + w2 + w3 + w4 > 2Θ. This yield a contradiction proving that no weights set exists solving this set of inequalities.
The cFBP is simple in two ways:
• Four input/output relations define this computation - the same number as the famous XOR (exclusive or).
• Contrary to the XOR it can be implemented with excitatory inputs and a monotone transfer function.3
We can extend the cFBP by increasing the number of inputs. In this case we deal with tuples instead of couples. As such, the cFBP corresponds to an entire family of linearly inseparable computations, and a dendrited neuron can implement them using the strategy that we will present in the next section.
A LIF with its linear integration cannot implement such a computation. While a neuron with two saturating dendrites can easily implement it. We already proved how a ball-and-stick biophysical model can implement this computation in a previous study.3
We use two independently saturating conductances to implement the cFBP in a minimal extension of the LIF that we called the dendrited integrated and fire (DIF). The DIF has a single membrane voltage to account for its compactness so we might wonder how local saturation can arise in such a morphology. Saturation has two possible origins: (1) a reduction in driving force can cause saturation as in,1 but (2) it can also be due to the intrinsic limitations in conductance per unit of surface. This latter possibility makes saturation possible in an electrically compact neuron. Even in a neuron with a small dendritic tree, the conductance is going to reach an upper bound per unit of surface and the only possibility to increase excitation consists in stimulating a larger area. We are going to employ this local bounding of the conductance to implement the cFBP in a DIF.
To do that, we only need two dendrites as shown in Figure 1A. We can interpret the 0s and 1s in the truth table in at least two ways: (1) either the pre- or post-synaptic neurons activates (2) or they reach a given spike frequency. In the following section, we will use the latter interpretation. Consequently, we consider a pre-synaptic input active when it fires above 50 Hz regular spike-train and inactive if it fires below 50 Hz (this value is arbitrary and can largely vary to match a neuron working range). We stimulate our model in four distinct episodes to reproduce the truth table from the previous section. You can observe on Figure 1 that locally bounding g enables implement the of cFBP. When g has no bound, the membrane voltage always reaches the spiking threshold at the same speed (LIF case). When we locally bound conductances the membrane voltage takes more time (45 ms see Figure 1C) to reach threshold in the clustered case (total g = 10pS) than in the scattered case (total g = 20pS). All in all, a DIF will respond differently for the clustered and scattered case while a LIF won’t. This enables a DIF to implement the cFBP while a LIF can’t.
In this brief report, we introduced a small extension to the leaky integrate and fire neuron: a dendrited integrate and fire neuron which can implement linearly non-separable computations. This single layer model applied to cerebellar granule cells predicts that they can implement a linearly non-separable computation. These neurons have on average four dendrites, but we have shown here that two suffice. The DIF’s multiple distinctly bounded g underlie this ability. For example, we need a local saturation of to implement the cFBP.
Importantly, a reduction in driving force does not generate sublinear summation in a DIF. The implementation of a linearly inseparable computation would have been impossible in a single compartment neuron because of interaction via the unique membrane potential. The usage of locally bounded g is crucial to make our prediction possible.
The experiment demonstrating this prediction seems straightforward. One would need to stimulate four distinct groups of mossy fibres following our different scenarios. We could then record how a group of granule cell respond using optogenetics reporting (i.e. calcium imaging). We predict that a significant part of granule cells might implement the cFBP. This prediction could reveal the true potential of single neurons. The next step consists of looking at the network level as already done with spiking dendrites.5
• Source code available from: https://github.com/rcaze/21_03Ca/tree/1.
• Archived source code: https://doi.org/10.5281/zenodo.5355354.10
• License: MIT license.
This work was supported by the Centre National de la Recherche Scientifique [ANR-UWAKE].
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
I used “we” as science is a collective endeavour. Discussions on this topic had begun as early as 2013 with my former PhD Advisor and collaborators from Institut Pasteur Paris. I also want to acknowledge M. Humphries, F Zeldenrust, A. Foust for their valuable comments on the early draft and Ms Marini-Audouard for the proof-reading before submission. An earlier version of this article can be found on bioRxiv (doi: https://doi.org/10.1101/2021.04.02.438177).
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the work clearly and accurately presented and does it cite the current literature?
Partly
Is the study design appropriate and is the work technically sound?
Partly
Are sufficient details of methods and analysis provided to allow replication by others?
Yes
If applicable, is the statistical analysis and its interpretation appropriate?
Not applicable
Are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions drawn adequately supported by the results?
Yes
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Computational Neuroscience
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: computational neuroscience; dendritic computations
Is the work clearly and accurately presented and does it cite the current literature?
No
Is the study design appropriate and is the work technically sound?
Yes
Are sufficient details of methods and analysis provided to allow replication by others?
Yes
If applicable, is the statistical analysis and its interpretation appropriate?
Yes
Are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions drawn adequately supported by the results?
Yes
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: computational neuroscience; dendritic computations
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 3 (revision) 08 Jun 22 |
read | |
|
Version 2 (revision) 16 Sep 21 |
read | read |
|
Version 1 06 Jul 21 |
read | |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)