Keywords
fractal kinetics, COVID-19, airborne pandemics, herd immunity policy, SI model
This article is included in the Emerging Diseases and Outbreaks gateway.
This article is included in the HEAL1000 gateway.
This article is included in the Pathogens gateway.
This article is included in the Coronavirus (COVID-19) collection.
fractal kinetics, COVID-19, airborne pandemics, herd immunity policy, SI model
Recently, Jewell et al.1 criticized the predictive models of the COVID-19 pandemic. This rigorous analysis justifies the first portion of the famous quote by George Box2 “All models are wrong, some of them are useful”. All epidemiological models used in practice have a common origin, namely, the famous Kermack–McKendrick model.3 We argue in this work that their poor predictive power originates from the erroneous hypothesis of the “well-mixed” epidemiological system; this hypothesis is crucial for the validity of the differential equations, which describe the “reaction” between susceptible (S) and infected (I) subjects. We also argue that the violation of this hypothesis results in a wrong perception and definition of the basic reproductive number R04,5 of epidemiological models, which denotes the number of secondary infections produced by a single infection.
People worldwide are concerned about the uncontrolled “exponential” spread of a disease, yet it is not clear or justified if this description is correct. In fact, an alternative “power” model based on an adjustable exponent of time has been proposed.6 We expand this approach by first questioning the ‘well-mixed” hypothesis and introducing a “fractal kinetics’” approach7 which yields, as a special case, the “power” model. This model7 relies on fractal kinetics’ principles that are suitable for the study of reactions and diffusion processes in insufficiently mixed media.8,9 In the same vein, we explored all theoretical aspects of the fractal kinetics’ SI model and applied it for the description of the time evolution of the COVID-19 pandemic in several countries. Our results support that this “conceptual change” from classical to fractal kinetics principles offers a novel, useful approach for the analysis of airborne pandemics data and justifies the second portion of George Box2 quote above.
The “reaction” of susceptible-infected individuals under homogeneous conditions.
In the Kermack–McKendrick model,3 the studied population is divided into susceptible, S, infectious, I and recovered, R, sub-populations while the relevant terms SI and SIR model were coined a long time ago. For each one of the sub-populations, specific ordinary differential equations are written based on the principles of chemical kinetics. These equations rely on the law of mass action10 which states that the rate of the chemical reaction is directly proportional to the product of concentrations of the reactants. However, this law applies under the strict hypothesis that the studied chemical reaction takes place under well-stirred conditions. This dogma applies well in chemical systems and validates the use of time-independent reaction rate constants and molar concentrations of the reactants in the reaction rate expressions. Obviously, the well-mixed hypothesis cannot be applied to epidemiological models since individuals, unlike molecules in a stirred solution, do not mix homogeneously; this is particularly so when preventive measures are applied. This, in turn, makes the mathematical formalism used so far questionable and the derived estimates of the relevant parameters, e.g., R0, a very rough approximation of reality. In fact, R0 cannot capture time-dependent variations in the transmission potential; the time course of an epidemic can be partly described by the effective reproduction number, R(t), which is a time-dependent parameter defined11,12 as the actual average number of secondary cases per primary case at time t:
where S(t) and S(0) are the numbers of susceptible subjects at time t and zero, respectively. Eq. 1 shows that R(t) relies on an estimate of R0, which is usually derived from the early phase data of the pandemic. R0 is also crucial for the calculations of herd immunity.5
The current SIR models for the ongoing COVID-19 epidemic include additional features to the classical SIR model,3,5 namely, the probability of death in the vulnerable fraction of the population, infectious period, and a time from infection to death are included.13,14 The basic reproduction number, R0, and all variables and parameters of the model are expressed as Gaussian distributions around previously estimated means.2,4,14 However, R(t) is used extensively as a reliable measure of a pathogen’s transmissibility.15,16
The “reaction” of susceptible-infected individuals under heterogeneous conditions.
In 1988, Kopelman8 introduced the concept of fractal reaction kinetics for reactions taking place under topological constraints. Under these heterogeneous conditions, time-dependent coefficients k(t) and not rate constants govern the rate of the reaction process.8 Numerous disciplines9,17–28 study rate processes with this approach. It is also very appropriate in studying the “reaction” of susceptible-infected individuals under “real-life” conditions.
Consider two rooms of the same size shown in Figure 1 with the same “concentration” of 10 unmovable susceptible subjects and two COVID-19 infected subjects. The probability for SARS-CoV-2 transmission is much higher in the left-hand side room, because the distance for seven of the susceptible subjects from the two infected subjects is much smaller than the “critical distance” associated with the bimolecular reactions of fractal kinetics.8 On the contrary, only one of the susceptible subjects is within “critical distance” from infected subjects of the right-hand side room. The static picture depicts the equivalency of the social distancing (1.5 meters applied during the Covid-19 pandemic) with the “pair up” and “critical distance” concepts of fractal kinetics.8 Intuitively, if the subjects in the two rooms start moving, virus transmission will increase as a function of time and will be dependent on the trajectory of each individual. Obviously, continuous movement of the subjects in the two rooms sweeping the available space would result in the transmission of the disease to all susceptible subjects in accordance with the “well-mixed” hypothesis. This means that the “well-mixed” system is just a single limiting case of the myriad heterogeneous space/time configurations of the individuals in a population.
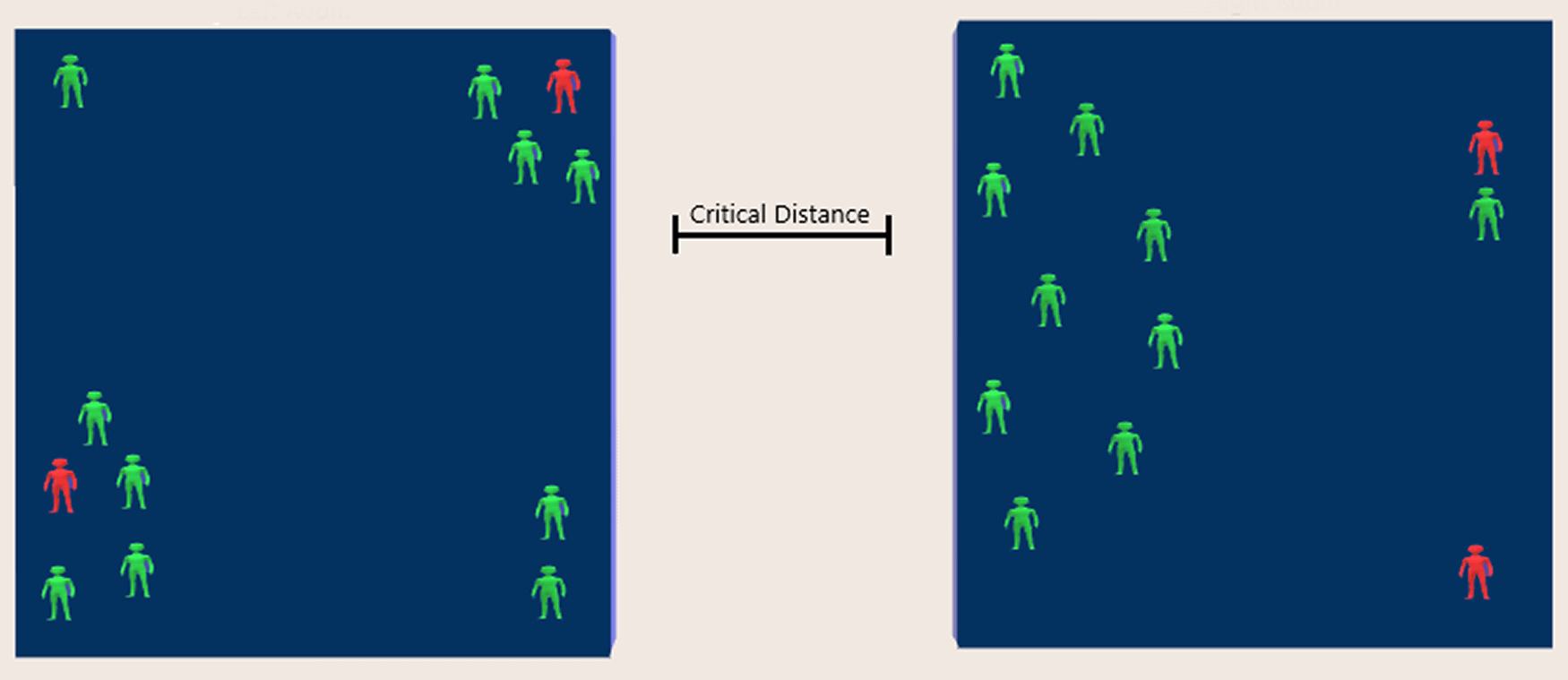
Although the number of infected (red) and susceptible subjects (green) is the same in both rooms, the instantaneous probability for virus transmission is 7/10 and 1/10 for the left- and right-hand side room, respectively.
These considerations lead us to the following very important conclusions relevant to airborne pandemics.
a. The time evolution of pandemics described by the classical SI and SIR models,5 which are based on the well-mixed hypothesis, are very crude approximations of reality.
b. The use of a fixed R0 value,4,5 is inadequate for capturing the transmission dynamics. The use of R(t) can capture time-dependent variations in the transmission potential,11,12,15,16 but is heavily dependent on the R0 estimate. In real-life conditions, the transmission of the disease is not only dependent on time, but also on the topology/movement associated with susceptible/infected individuals.
c. The importance of the “initial conditions” for fractal reaction kinetics has been delineated.8 In pandemics, the corresponding “initial conditions” are “patient zero” at the epicenter of the country of pathogen’s origin as well as “patient zeros” of the first humans infected in different countries. For the COVID-19 pandemic specifically, since most of the infected subjects are asymptomatic during the initial phase of the disease spreading, no precautions are taken. During this initial period, which lasts until social distancing measures are applied, disease spreading follows a “herd immunity”5 style, which we call “herd kinetics”. Similarly, we coin the term “fractal kinetics” for the disease spreading when containment measures are imposed.
The fractal kinetics’ SI model7 for epidemic spreading relies on the following equation:
where I(t) is the cumulative fraction of infected individuals at time t, β is a parameter proportional to the probability of an infected individual to infect a healthy one and h is the fractal dimensionless exponent associated with fractal kinetics.8 The core assumption of the model is that societies as complex systems will exhibit self-organization as a reaction to the emergence of a pandemic wave, enforcing preventive measures and increasing public awareness. Thus, instead of an infection rate constant, the fractal SI model uses a rate factor β/th decreasing of time. The solution of Eq. 2 gives I(t) as a function of time:7
where c is a parameter which determines the fraction of individuals that will become infected eventually.
By substituting we introduce parameter α of inverse time dimension,29 which changes Eq. 3 into 4, namely:
In the limit t → ∞ we find:7
The “well-mixed” model, described by Eq. 2 with h = 0, has a limiting value of I(t) equal to one as a result of a completely susceptible population. However, this is not a realistic feature for all pandemics that have appeared so far. Eq. 5 reveals that the plot of I(t) versus time for h > 1 reaches a plateau equal to 1/(1 + c) (see Figure 2), which is a reasonable feature for all pandemics. For the special case h = 1, Eq. 6 (also plotted in Figure 2) is derived which describes what we call “herd kinetics” not only because no precautions or measures are taken, but also because the rate of increase of infected subjects progressively diminishes in a similar fashion when a “herd immunity”5 policy is implemented:
A linearized form of Eq. 6 is as follows:
where the slope β is an “apparent” dimensionless transmissibility rate constant during the “herd kinetics” period; the term “apparent” is used to underline its proportional dependency to the probability of an infected individual to infect a healthy one (see Eq. 2). At t = 1, hence ln t = 0, we get:
Theoretically, the value of I(t = 1) corresponds to the “initial conditions”, i.e., the fraction of infected individuals at the first day of the pandemic; since the real “time zero” is unknown, c1 is proportional to the number of total (asymptomatic and symptomatic) infected cases from the real time zero to time t = 1 day, when the first case was confirmed. We use the notation c1 to distinguish it from c appearing in Eqs. 5, 6 and 7.
In all pandemics, a characteristic time is observed when the daily number of confirmed infected cases does not increase anymore and starts declining; this corresponds to the inflection point tip. When h > 1, an estimate for tip can be obtained by equating the second derivative of Eq. 4 to zero and solving the resulting equation for time. Lacking an analytical solution, this equation can only be solved numerically.
For the special case h = 0, tip, can be derived from Eq. 4:
The following t.ip can be derived from Eq. 2, under “herd kinetics” conditions (h = 1):
The inflection points for the three examples considered, h = 0, h = 1 and h = 2.5 are shown on the simulated curves of Figure 2. Inflection points denote when a curve changes from being convex (upwards) to concave (downwards), i.e., the confirmed infected new cases remain temporarily constant and then start to drop.
If the value of parameter c is low, all cases reach the asymptotic limit of 1. However, in real-life conditions the limiting value of the cumulative fraction of infected individuals, I(t) is always much smaller than 1. This epidemiological evidence (fact) can be explained only by the fractal kinetics SI model as shown in Figure 2. The curve of the example considered using h = 2.5 reaches the plateau value of 0.125, i.e., 12.5% of the population will be infected eventually.
For h > 1, the I(t) corresponding to the inflection time point, I (tip) can be derived from Eq. 4 using the tip estimate in the denominator of Eq. 4. The tip estimate is obtained by equating the second derivative of Eq. 4 to zero and solving numerically the resulting equation.
During the time course of the pandemics, an estimate for the time of the termination or close to the termination of the spreading is desperately needed as early as possible. An estimate for the time of 90% termination, t90% for h > 1, can be derived from Eq. 4 using I(t) = 0.90/(1 + c):
The best fits of Eqs. 4 and 6 to the data30 were obtained by maximizing the R2 of the two adjacent periods. By anchoring the date of each country’s lockdown decision (or any similar form of draconian measure) and moving forward in time, the Levenberg–Marquardt algorithm of least squares was implemented. The lockdown dates are close or very close to the transition from herd kinetics to fractal kinetics and vice versa. A minimum value of R2 = 0.985 was set as a criterion of goodness of fit and every value higher than that was accepted. The turning time data point at which the best R2 value began to diminish was rejected and its prior time data point was accepted. From that time segment and further on the consequent kinetic profile was fitted to the data points until the plateau of quasi-steady state was reached. The fitting discontinuities observed in the kinetics between the distinct periods (e.g., from second to third period for France) are associated with the fact that I(t) values at the boundary of the two periods were not equalized in our fitting methodology. Between the quasi-steady state and the beginning of the second herd period a 10% change of the number of cumulative infected cases at one week interval was sought in order to establish the commencement of a second viral wave and the reproduction of the according fitting procedure. Data acquisition, modelling and simulations were programmatically implemented with Python language31 and its respective libraries.
In our previous studies7,32 on COVID-19 data analysis, we applied the fractal kinetic SI model (Eq. 3) assuming that fractal kinetics commences at time zero. However, reconsideration of the topological characteristics of the virus transmission in the light of Eq. 4 led us to the realization that a “herd kinetics’” period precedes the “fractal kinetics’” period. Exponent β drives the kinetics during the “herd kinetics” stage and is the analogue of R0 for a not well-mixed system. But, unlike R0, β is not associated with the expected number of cases directly generated by one case in a population. During the “fractal kinetics” period, parameter α in Eq. 4 governs the rate of the disease, while the prevailing spatial conditions are reflected on the h value. During this period, a meaningful parameter for the rate of the process is the half-life, t½ = ln2/α.
Initially, virus transmission takes place under “herd kinetics’” conditions (Eq. 6, Figure 3A). This prevails until the first preventive measures are imposed; these can be followed by a lockdown decision. The preventive measures and the lockdown status induce a gradual reduction in the rate of the disease spread, i.e., “fractal kinetics” starts operating (Eq. 4, h>1, Figure 3B). The transition from herd kinetics (Eq. 6) to fractal kinetics (Eq. 4, h>1) can be gradual during this fuzzy period, with both equations operating concurrently. The prevalence of fractal kinetics during the lockdown period results in an asymptotic approach of I(t) to the steady state, i.e., I(t) = (1+c)-1 (see Eq. 5, Figure 3B); according to Eq. 4 the higher the value of the fractal exponent of time h, the more rapid is the approach of I(t) to the steady state. This pattern we call “Herd-Fuzzy-Fractal” (HFF) kinetic motif. When the confirmed new cases reach a steady state, governments relax lockdown rules. In theory, when such a decision is taken, the termination of the first wave of the pandemic has been accomplished. However, the relaxation of lockdown measures in conjunction with the large number of infected individuals at steady state can, after a while, initiate a second wave of the pandemic leading to the application of new preventive measures and new lockdown rules. Consequently, a second wave of the disease emerges (Figures 3C and 3D); hence, the (HFF)2 kinetic motif.

The gray line segments indicate fuzzy periods. A–D. Subplots correspond to the four distinct periods of the kinetic motif. Equations and parameter values used: A: Eq. 6, β = 8, c = 3 × 1016; B: Eq. 4, h = 4.5, α = 0.012 (time)−1, c = 240; C: Eq. 6, β = 1.18, c = 119350; D: Eq. 4, h = 8, α = 3.35 × 10−3(time)−1, c = 20.
We focused on the data30 of four model countries, namely, France, Greece, Italy, and Spain. Figure 4 shows for each one of the four countries, the fittings of Eqs. 6 and 4 to herd- and fractal-kinetics’ periods’ data, respectively. Parameter estimates derived are listed in Table 1. High R2 values listed in this Table indicate that the model of Eqs. 4 and 6, for all four countries, is in excellent agreement with the disease data except Italy’s fourth fractal kinetics’ period data.
Estimates of the secondary parameters tip, t90%, steady state infected fraction are also listed.
For the first herd kinetics’ period, the estimate for βherd 1 in Greece was found to be 2.38 ± 0.06, which is much smaller than for the other three countries. This is in agreement with the remarkably lower initial I(t) profile of Greece in Figure 4. We should emphasize the valid estimation of the parameter βherd1 for all countries studied. This is clear proof that the initial phase follows a power of time function (Eq. 6) which is contrary to the general belief that the initial phase increases exponentially. This subexponential increase has been observed in the early phase of COVID-19 spreading in different parts of China.6 During the first fractal kinetics’ period, the estimate for αfractal 2 in Greece was also higher, 0.02 ± 2 × 10−4 (days)−1 compared with 0.010–0.012 (days)-1 found for the other three countries. This leads to a shorter half-life of 42 days for Greece compared with an average of 63 days for the three other countries; this, coupled with the earlier lockdown rules imposed in Greece, explains the more rapid approach to the steady state (Figure 4). The fractal exponent hfractal 2 was smaller in Greece, 2.93 ± 0.06, while for France, Italy and Spain it was 4.71 ± 0.09, 4.39 ± 0.02, 5.14 ± 0.06, respectively (Table 1). On the contrary, the estimate for cfractal 2 in Greece 3227 ± 30.19 was roughly ten-times higher than in the other three countries, resulting in much lower I(t) steady-state value.
All countries remained in a slightly moving upwards quasi-steady state for 2–3 months (Figure 4). This period was followed by a gradually increasing phase in the number of confirmed infected cases. Relaxed rules led to higher population mobility. All countries re-entered a herd kinetics’ period (blue concaving upwards segment in Figure 4). The estimates for βherd 3 were found 1.17 ± 0.02, 3.56 ± 0.04, 3.80 ± 0.04, 5.08 ± 0.08 for Italy, Spain, Greece and France, respectively, in full agreement with the visually increasing “curvature” of the blue concaving upwards segment of the four countries. All countries imposed preventive measures and lockdown rules several times (Figure 4). For France, Greece and Spain a remarkably similar reliable estimate for αfractal 4, 0.003 (days)−1 was found; this is indicative of a slow process with a half-life of 231 days. However, different hfractal 4 estimates, 16.11 ± 0.54, 9.01 ± 0.42 and 6.28 ± 0.43 were found for France, Greece, and Spain, respectively. Assuming that the conditions will not change in the next time period, predictions, based on the parameter estimates of the fourth fractal kinetics period for the steady-state value and t90%, can be made for the three countries (Table 1). On the contrary, the fitting of Eq. 4 to Italy’s fourth fractal kinetics’ period data was not equally successful and reliable parameters estimates for hfractal 4, αfractal 4 and cfractal 4 were not derived (Table 1). This is due to the fact that the point of inflection has not been reached yet and therefore the fitting algorithm cannot converge to reliable parameters estimates.
The estimates for tip reported in Table 1 for France, Greece and Spain correspond to time (days) from the commencement of the fourth fractal kinetics’ period. These estimates were found to be in agreement with the observed values, which is an additional piece of evidence for the validity of the fractal model. An estimate for Italy’s tip was not obtained for reasons mentioned above. Besides, the fourth fractal kinetics period data were used to predict the t90% (expressed in days from the commencement of this period) and the final steady-state (1/(1+c)) for France, Greece and Spain (Table 1).
A large number of countries, besides the four analyzed, followed the (HFF)2 kinetic motif shown in Figure 4, e.g., Australia, China, Germany, Austria, United Kingdom.30 Yet, several countries did not exhibit the (HFF)2 motif, lacking a second wave and followed a “herd-fuzzy-fractal” (HFF) kinetic motif. Argentina and Brazil are examples of countries where strict/mild preventive measures were either not applied or did not work effectively. Both countries exhibit an (HFF) kinetic motif, Figure 5. Parameter values determined: Argentina, 1st stage: (h = 1), β = 1.929 ± 0.028; 2nd stage: h = 2.189 ± 0.043, α = (1.754 ± 0.067) × 10−3 (days)−1, c = 3.61 ± 0.38; Brazil, 1st stage: (h = 1), β = 4.633 ± 0.017; 2nd stage: h = 2.892 ± 0.023, α = (4.044 ± 0.017) × 10−3 (days)−1, c = 21.86 ± 0.24.
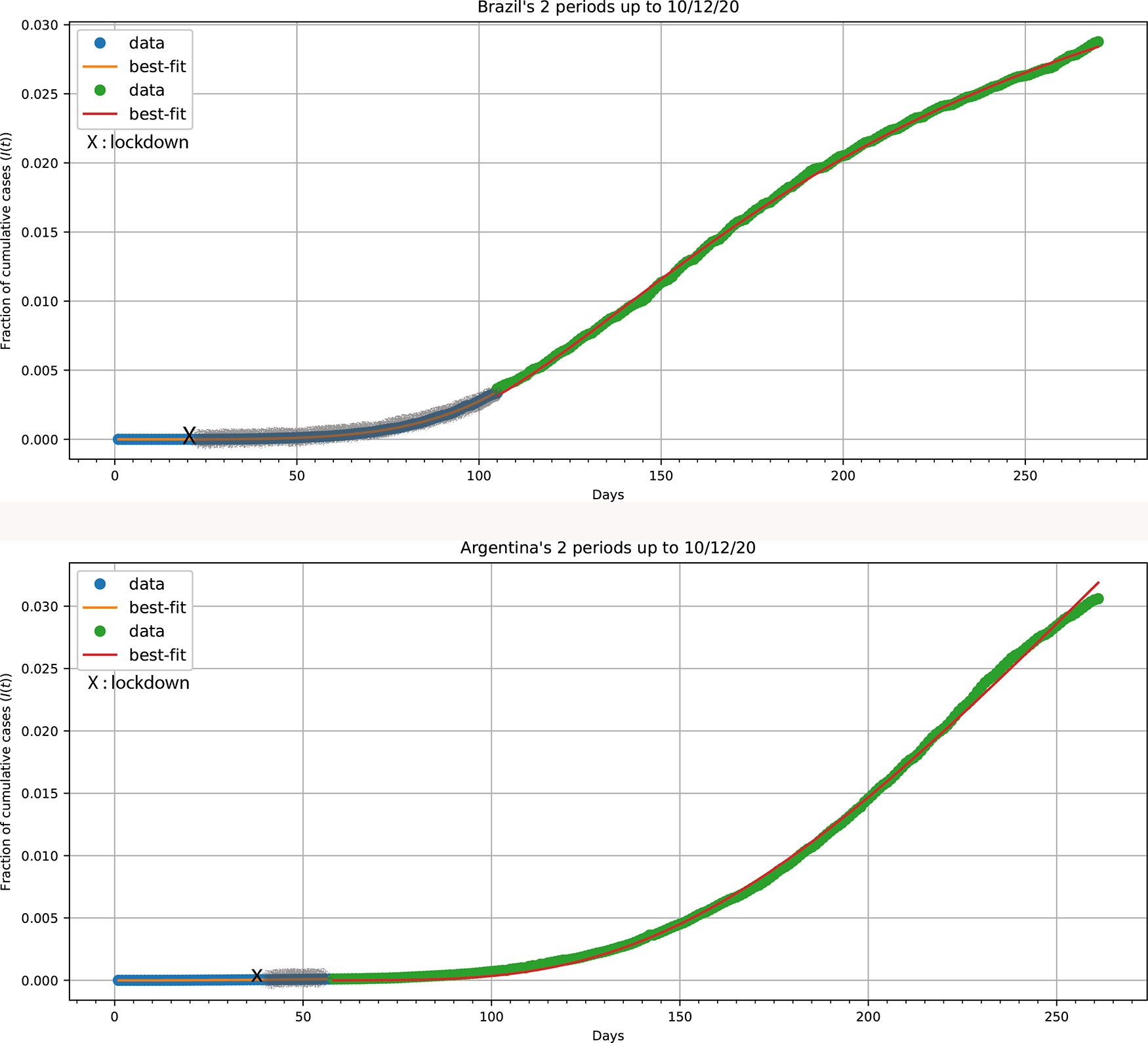
Xs mark the implementation of mild preventive measures. The gray lines indicate the fuzzy period after the X point.
On the other hand, some countries exhibited a more complex pattern, which deviates from the (HFF)2 and (HFF) motifs. Infection data for USA did not follow either the (HFF)2 or the (HFF) kinetic motif. The I(t) time profile never reached a steady state and the shape of the curve indicates a deformed three-wave like kinetic profile (Figure 6). Probably both types of kinetics (herd and fractal) run concurrently for most of the time throughout the course of the pandemic, with the contribution of each varying with time. This is most likely due to different COVID-19 policy containment measures followed in different states around the country. Sweden intentionally applied the herd immunity strategy30 during the COVID-19 pandemic. An initial herd-kinetics type continuous increase in the number of total infected cases reached a point of inflection around 20 July 2020, followed by a slower rate of increase of infected cases, (Figure 6). Since neither strict measures nor lockdown rules were applied at that time, the shape of the curve should be attributed to a fractal kinetics-like self-organization of the society. A rather sharp increase after 10 September 2020 can be attributed to the increased mobility of the individuals since no relaxation measures were taken close to this date.
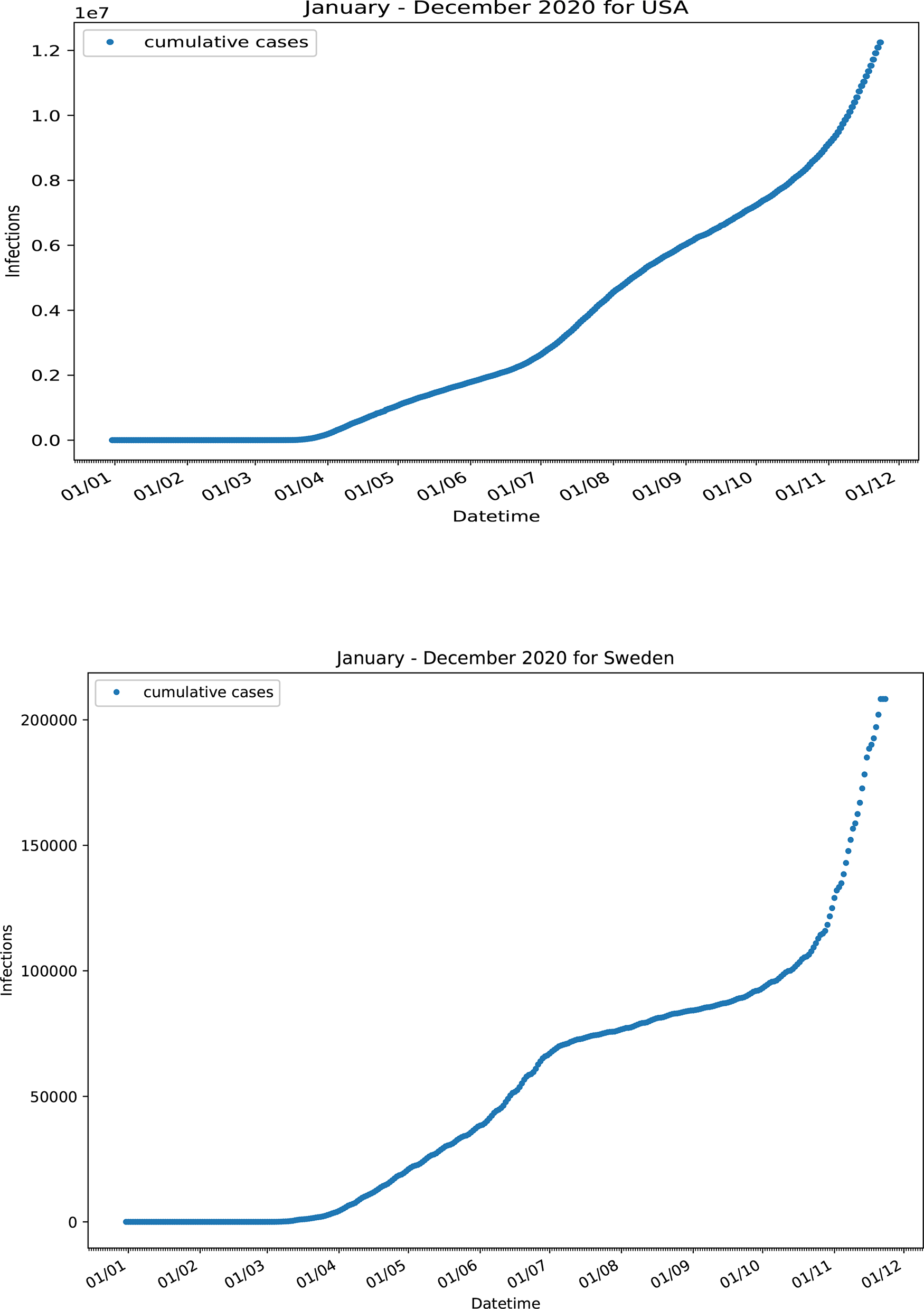
Confirmed infected cases for USA and Sweden.30
The above results (Figures 2, 3, Table 1) demonstrate that the fractal kinetics SI model is more akin to real life. Since the well-mixed hypothesis is the crux of the matter of the epidemiological models,5 the use of not well-mixed hypothesis has important implications, which can metamorphosize airborne pandemics; these implications are discussed and itemized (designated with italics) below.
The reproductive number, R0 is not needed for the initial growth of the disease4 being incompatible with the not well-mixed hypothesis, Figure 1. Limitations associated with the estimation of R0, can be found in numerous publications. Our results show that the time exponent β of Eq. 6 controls the time evolution of the disease throughout the initial herd kinetics’ period. In other words, β drives the initial phase of the disease spreading being the slope of Eq. 7, i.e. a linearized form of Eq. 6. The predominant role of β during the herd kinetics’ period can be also concluded from Eq. 12, which explicitly shows that the infected population fraction at the inflection point, I(t)ip is solely dependent on β. Although R0 and β are different, however, they can be used complementary to each other during the initial stages of the pandemics. Estimates for β derived from the analysis of herd kinetics’ period data at two time points from 100 countries are shown in Figure 7 and Table 2. The degree of uncertainty (standard deviation) for the estimates was found in most cases small; this was accompanied with high correlation coefficients (not shown). Overall, the estimates derived from the longer period of 35 days seem to be either similar or higher or significantly higher than these derived from the analysis of the shorter period (10 days) data. For some countries, the small number of confirmed infected cases in the first 10 days did not allow the estimation of β. In view of the diversity and variability of data presented in Figure 7, we quote the median values derived from the analysis of 100 countries, 2.44 (0.25–12.24) and 1.34 (0.20–6.13) for the β estimates corresponding to 35 and 10 days, respectively.
Data of 10 and 35 days, after the first reported case, were analyzed. Part of these results is shown in Figure 7. Blanks are due to fragmented data that prevented the fitting procedure to converge.
The classical phraseology “the exponential growth of the disease” used by medical doctors, scientists and laymen is questionable. This phrase is related to the approximate solution of the SIR model, which is an exponential function, when the parameter of the recovery rate is equal to zero.5 Based on our theoretical results and the good fittings of Eq. 6 to data of herd kinetics’ period (Figure 4), “the herd kinetics’ period seems to obey a power of time function”. According to Eq. 2, β drives the disease spreading when h = 1 and the rate of infection is inversely proportional to time. This is in agreement with the real-life conditions because of the continuous reduction of the probability of infection as a function of time (β/t). However, the resemblance of the I(t) profiles of the classical, h = 0 and the special case h = 1 in Figure 2 makes the discernment of the kinetics of the initial phase difficult.
Herd immunity
Herd immunity5 calculations rely on an estimate for R0 and syllogisms based on the relative magnitude, λ = R(t)/R0, which is the proportion of the population that is susceptible to catching the disease. If preventive measures are not applied, an estimate for the time needed to reach a certain level of the infected population fraction, e.g., I(t) = 0.6 ensuring herd immunity can be obtained from Eq. 7. Assuming an infected individual at time t=1, i.e., , where N is the population of the country, then, from Eq. 7, we get c = N − 1 ≈ N. Hence, the time thi needed to reach a certain level of herd immunity I (thi) under non preventive measures is
Figure 8 shows thi as a function of β and N assigning I (thi) = 0.6. It can be seen that population size has a mild effect, whereas the apparent transmissibility constant β severely reduces thi. Eq. 14 can be used at the initial stages of the pandemics and requires only a valid estimate for β. This will certainly provide valuable information for authorities, if coupled with estimates of the mortality rate and deaths, prior to a decision for a herd-immunity policy.33 Caution should be exercised with the use of Eq. 14, since it can be applied only under the strict assumption of herd kinetics operating throughout the entire period of the disease spreading. The example of Sweden (Figure 6) shows that societies can exhibit self-organization and move to a fractal kinetics’ mode.

A contour plot based on Eq. 14 showing the time required to reach herd immunity level I (thi) = 0.6 for various values of parameter β and population size N.
Deviation from the herd kinetic profile after the imposition of lockdown
Cumulative data of infected people from nine countries (Austria, Belgium, Denmark, France, Germany, Italy, Spain, Switzerland, United Kingdom) were gathered and analyzed under two different prisms. Analysis was broken down into two parts, before and after imposition of strict preventive measures (lockdown) (Figure 9). For the first period, the herd kinetic motif where h = 1 (Eq. 6) was found to be adequate, whereas after lockdown clearly fails. The latter period was also analyzed using the fractal kinetic motif of h > 1 with very persuasive goodness of fit (Figure 9). In all cases, R2 was greater than 0.98. This pictorial divergence shows that after implementing mobility restrictions the evolution of the pandemic could not be captured by a power law expression, but rather by a fractal kinetic one (Eq. 4) which eventually leads to a plateau of cumulative cases.
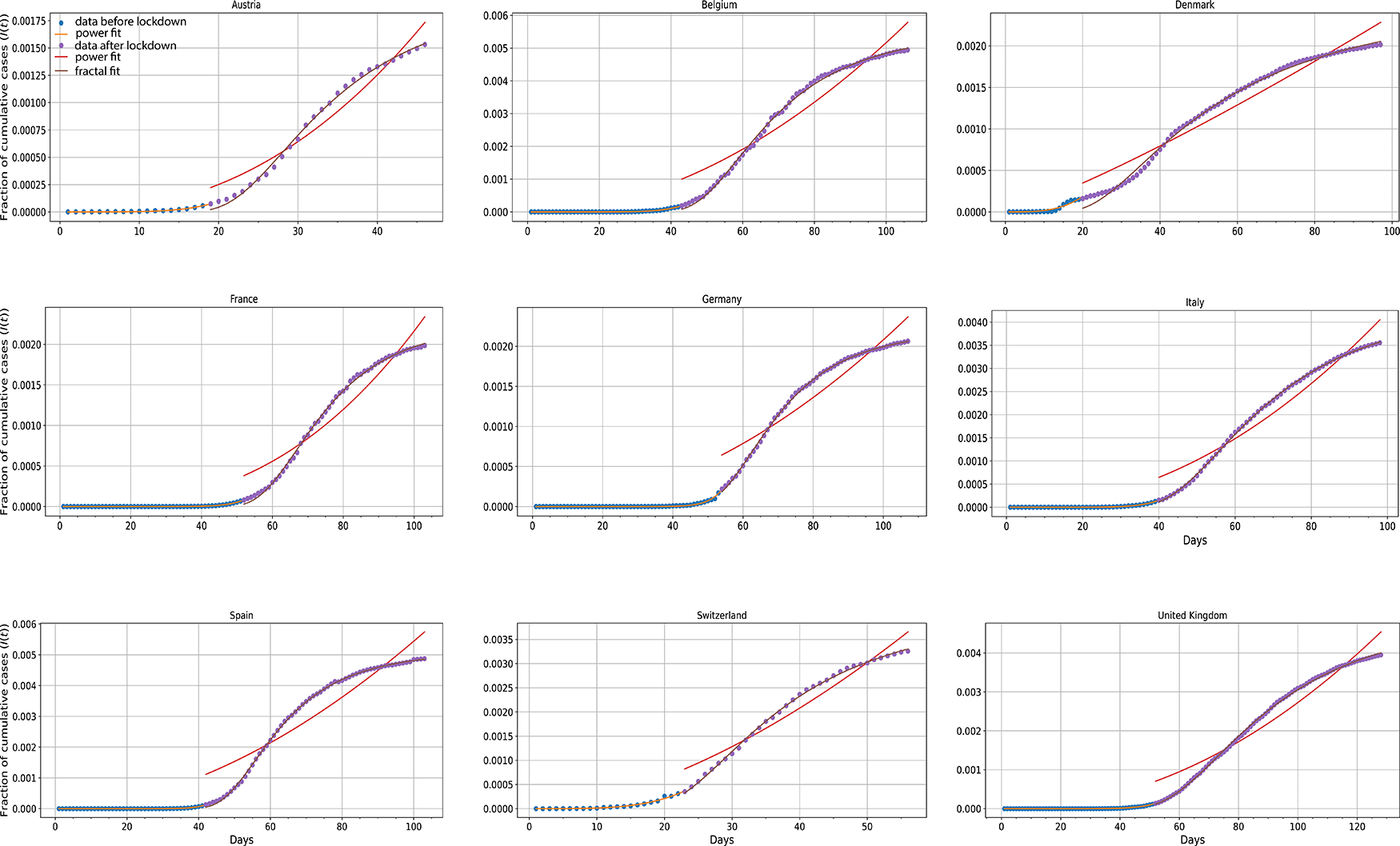
The blue dots represent cumulative infected cases up to lockdown datum points.16 The orange lines depict the power fit to these data. Purple dots represent data after lockdown imposition whereas the purple lines are their superimposed fractal fits. Red lines depict the hypothetical power fit to the aforementioned data points in the event that Covid-19 propagation followed a power law pattern. R2 values for all nine countries were measured higher than 0.98.
Model predictions
According to Jewell et al.,1 the ability of current models to predict is very poor. Our work demonstrates that the herd kinetics’ period is described by Eq. 6, while the kinetic motif “herd-fuzzy-fractal” should be taken into account in the modeling work. Apparently, these approaches have not been implemented so far. Roughly, predictions during the herd kinetics’ period can be based on a valid estimate for β, Eq. 6. Under preventive measures, valid estimates for the parameters of the model (Eq. 4, h>1) can be derived and used for predictive purposes provided that data beyond the point of inflection are available (see Table 1).
Since the early days of epidemics’ modeling,3 a great deal of work has been done and now there is a change of paradigm. Interestingly, the results of our work are in full agreement with the basic conclusion of the most recent, extensive and elegant COVID-19 study16 based on the effective reproduction number R(t), “… that major non-pharmaceutical interventions—and lockdowns in particular—have had a large effect on reducing transmission”. Our approach quantifies this large effect on the basis of Eq. 4, which captures the dynamics of the disease under “herd kinetics’” and “fractal kinetics’” conditions. In addition, our herd kinetics’ period results are in full agreement with the observations of the distinctive subexponential increase of confirmed cases during the early phase of the epidemic in China, contrasting an initial exponential growth expected for an unconstrained outbreak.6 The present fractal SI model can be extended to its SIR analogue, with the caveat that the corresponding differential equations require numerical solution. In conclusion, the fractal kinetics SI model with the kinetically established herd period as well as the (HFF)2 or (HFF) kinetic motifs opens up a new era in the field of epidemiological models for airborne pandemics.
This work is dedicated to physicians, nurses and paramedical personnel of the Greek public hospitals as well as to the elementary and high school teachers of public and private schools of Greece for their unceasing devotion and work commitment during the COVID-19 pandemic.
The underlying data are publicly available from https://www.ecdc.europa.eu/en/covid-19/data. 30
Archived source code available from: https://doi.org/10.5281/zenodo.4940276. 31
Data are available under the terms of the Creative Commons Attribution 4.0 International license (CC-BY 4.0).
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the work clearly and accurately presented and does it cite the current literature?
Partly
Is the study design appropriate and is the work technically sound?
Yes
Are sufficient details of methods and analysis provided to allow replication by others?
Yes
If applicable, is the statistical analysis and its interpretation appropriate?
Yes
Are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions drawn adequately supported by the results?
Yes
References
1. Ndaïrou F, Area I, Nieto JJ, Silva CJ, et al.: Fractional model of COVID-19 applied to Galicia, Spain and Portugal.Chaos Solitons Fractals. 2021; 144: 110652 PubMed Abstract | Publisher Full TextCompeting Interests: No competing interests were disclosed.
Reviewer Expertise: Pure and Applied Mathematics, Biomathematics
Is the work clearly and accurately presented and does it cite the current literature?
Yes
Is the study design appropriate and is the work technically sound?
Yes
Are sufficient details of methods and analysis provided to allow replication by others?
Yes
If applicable, is the statistical analysis and its interpretation appropriate?
I cannot comment. A qualified statistician is required.
Are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions drawn adequately supported by the results?
Yes
Competing Interests: No competing interests were disclosed.
Is the work clearly and accurately presented and does it cite the current literature?
Yes
Is the study design appropriate and is the work technically sound?
Yes
Are sufficient details of methods and analysis provided to allow replication by others?
Yes
If applicable, is the statistical analysis and its interpretation appropriate?
Yes
Are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions drawn adequately supported by the results?
Partly
Competing Interests: No competing interests were disclosed.
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | |||
|---|---|---|---|
| 1 | 2 | 3 | |
|
Version 1 20 Jul 21 |
read | read | read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)