Digital signature schemes with strong existential unforgeability

Jason Chia; Ji-Jian Chin; Sook-Chin Yip

doi:10.12688/f1000research.72910.1

Home Browse Digital signature schemes with strong existential unforgeability

ALL Metrics

-

Views

-

Downloads

Get PDF

Get XML

Export

▬

✚

Review

Digital signature schemes with strong existential unforgeability

[version 1; peer review: 2 approved]

Jason Chia ¹, Ji-Jian Chin², Sook-Chin Yip¹

PUBLISHED 16 Sep 2021

Author details Author details

¹ Faculty of Engineering, Multimedia University, Cyberjaya, Selangor, 63100, Malaysia
² Faculty of Computing and Informatics, Multimedia University, Cyberjaya, Selangor, 63100, Malaysia

Jason Chia
Roles: Conceptualization, Data Curation, Formal Analysis, Investigation, Methodology, Software, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Ji-Jian Chin
Roles: Conceptualization, Funding Acquisition, Methodology, Project Administration, Resources, Supervision, Validation, Writing – Review & Editing

Sook-Chin Yip
Roles: Methodology, Supervision, Validation, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

This article is included in the Research Synergy Foundation gateway.

Abstract

Digital signature schemes (DSS) are ubiquitously used for public authentication in the infrastructure of the internet, in addition to their use as a cryptographic tool to construct even more sophisticated schemes such as those that are identity-based. The security of DSS is analyzed through the existential unforgeability under chosen message attack (EUF-CMA) experiment which promises unforgeability of signatures on new messages even when the attacker has access to an arbitrary set of messages and their corresponding signatures. However, the EUF-CMA model does not account for attacks such as an attacker forging a different signature on an existing message, even though the attack could be devastating in the real world and constitutes a severe breach of the security system. Nonetheless, most of the DSS are not analyzed in this security model, which possibly makes them vulnerable to such an attack. In contrast, a better security notion known as strong EUF-CMA (sEUF-CMA) is designed to be resistant to such attacks. This review aims to identify DSS in the literature that are secure in the sEUF-CMA model. In addition, the article discusses the challenges and future directions of DSS. In our review, we consider the security of existing DSS that fit our criterion in the sEUF-CMA model; our criterion is simple as we only require the DSS to be at least secure against the minimum of existential forgery. Our findings are categorized into two classes: the direct and indirect classes of sEUF-CMA. The former is inherently sEUF-CMA without any modification while the latter requires some transformation. Our comprehensive review contributes to the security and cryptographic research community by discussing the efficiency and security of DSS that are sEUF-CMA, which aids in selecting robust DSS in future design considerations.

Keywords

Cryptography, Digital Signatures, Strong Existential Unforgeability

Corresponding authors: Jason Chia, Ji-Jian Chin, Sook-Chin Yip

Competing interests: No competing interests were disclosed.

Grant information: This research is supported by the Ministry of Higher Education of Malaysia through the Fundamental Research Grant Scheme under Grant FRGS/1/2019/ICT04/MMU/02/5 and in part by Multimedia University’s Research Management Fund.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2021 Chia J et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Chia J, Chin JJ and Yip SC. Digital signature schemes with strong existential unforgeability [version 1; peer review: 2 approved]. F1000Research 2021, 10:931 (https://doi.org/10.12688/f1000research.72910.1) First published: 16 Sep 2021, 10:931 (https://doi.org/10.12688/f1000research.72910.1) Latest published: 16 Sep 2021, 10:931 (https://doi.org/10.12688/f1000research.72910.1)

Introduction

The idea of a digital signature scheme (DSS) was proposed by Diffie and Hellman in 1976 as a necessity to design efficient authenticated electronic communications which can serve as legal evidence in the court of law.¹ Rivest, Shamir, and Adleman realized the idea in their seminal work known as the RSA cryptosystem,² the first of many. A DSS consists of three processes, as shown in Figure 1.

Figure 1. The three processes of a digital signature scheme and the relationship between the input/outputs.

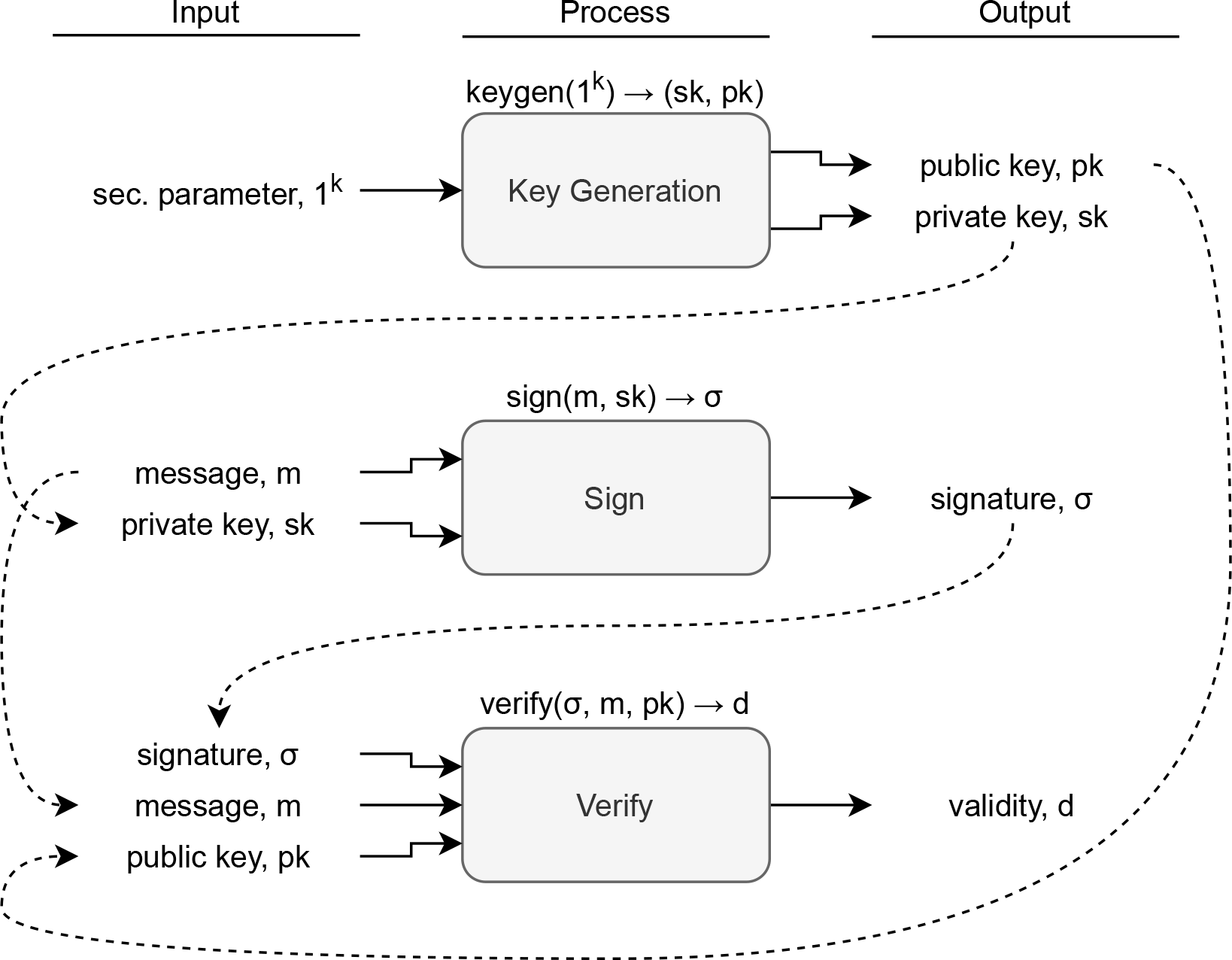
For every (sk,pk) ← keygen(1k) and every m, verify(sign(m,sk),m,pk) = 1 must hold. A σ on m is valid if verify(σ,m,pk) = 1. This is a standard (informal) definition of DSS.³ In the early 90s, a paradigm known as hash-then-sign forms the industry standard for issuing digital signatures.⁴ The idea is to sign on the hash of a message, $h \leftarrow H (m)$ instead of the m itself; this has a few benefits for h is constant size, which leads to efficient signing on speed and a constant sized signature. Verification would then require the verifiers to first validate the signed hash, then perform hashing $h^{'} \leftarrow H (m)$ before finally comparing h′ and h. Concrete examples of the hash-then-sign are discussed in.^5-15

Properties of DSS

The following properties are required by DSS³:

• Public verifiability: A signature σ generated from a private key sk can be verified using a public key pk. This property differentiates DSS from other integrity protection mechanisms, such as message authentication codes (MAC). A consequential result from this property is that signatures are also transferrable, meaning a party can copy σ and pk to use it to convince others that the message is authentic from the signer.
• Non repudiation: A signer cannot later deny that they have authenticated a message m once the signature of m, σ is generated and known. This is also another property that separates DSS from MAC, because the only entity that could have plausibly generated the signature in the case of DSS must possess the private key sk; whereas in a MAC scheme, the keys are shared. This property also implies that only the one in posession of sk can generate valid signatures, which disallows forgeries.

Message recovery

Notice that the verification process requires both the message and the signature as inputs, requiring the signer to transmit both. Alternatively, some DSS can support message recovery. DSS with message recovery (DSS-R) has a different sign and verification process, shown in Figure 2; the signer only needs to transmit a packed signature ρ, and the verifier would recover the message m successfully or abort ⊥ depending on signature validity. For practical purposes, |ρ|≤|σ| + |m|. Examples of DSS-R are found in previous literature.^16-23

Figure 2. Sign and verify process for a digital signature scheme with message recovery.

Security models

The security of DSS was first formalized by Goldwasser, Micali and Rivest in 1988.²⁴ Different security goals are used to model the different security guarantees of a DSS when faced with an adversary. The commonly accepted goal to model against is the goal of existential forgery (EUF), which is the easiest for attackers to achieve among other goals (e.g., selective forgery, total break). In addition,²⁴ defined the adversarial capabilities for a DSS, which aims to model what types of attacks can be carried out by an adversary when attempting to break the DSS. The strongest capability, known as adaptive chosen message (CMA) is the widely accepted adversarial capability that is the most used in the literature on DSS. Figure 3 shows the interactions of a challenger and an adversary in the EUF-CMA model. In step (1), the challenger sets up an empty set Q and gives the pk to the adversary. In step (2), the adversary may make oracle queries that model its chosen message attack capability. The queried messages are added to the set Q. In step (3), the adversary announces to the challenger the target message m* it wants to forge. m* must not be an element of Q, nor it can be queried to the oracle; this prevents trivial attacks which uses the oracle to break the security goal. Note, step (4) allows the adversary to use the signing oracle again, which models the adaptive nature of the attack. Finally, in step (5), the adversary outputs a forgery σ*. We say the adversary breaks the DSS if σ* on m* is valid. q_s quantifies the number message-signature pair made available to the adversary.

Figure 3. EUF-CMA security model.

Strong existential unforgeability (sEUF-CMA)

Consider the case for randomized signatures in the EUF-CMA model (e.g., DSA¹³ or PSS-R¹⁸). A randomized DSS allows multiple valid signatures for a single message, which has a subtle implication on the model: Suppose that the adversary queried for a message-signature pair (m,σ). Now, the adversary forges a different valid signature σ′ ≠ σ on the same message m. This is an easier security goal, but could be a critical vulnerability when the DSS is used in a scenario in which the designers assumed that no new signatures can be forged, because a different signature on an existing message is still new. In other words, EUF-CMA does not guarantee that if that an attacker knows (m,σ), it cannot forge (m,σ′) such that σ′ on m is valid. This gave rise to a stronger security model, known as strong existential unforgeability or sEUF-CMA.²⁵ Figure 4 shows the interactions of the adversary with the challenger in the sEUF-CMA model. The main difference is the constraint during the chosen message attacks and in the final step (5). Notably, the adversary can even query for signatures on the challenge message m*, but may not submit any of the signatures obtained from the sign oracle as forgeries. In contrast to EUF-CMA, sEUF-CMA ensures that an adversary cannot produce any new signatures at all; any valid signature must have originated from the signer.

Figure 4. sEUF-CMA security model.

Why does sEUF-CMA matter?

Let’s take a step back and consider why sEUF-CMA is even worth considering in the first place. DSS is very often used as a building block to construct other cryptographic schemes. For example, using the Fiat-Shamir transform,²⁶ a DSS can be turned into an identification protocol. DSS has also been used to create identity-based identification schemes,²⁷ signcryption schemes,²⁵ authenticated key exchanges,²⁸ and identity-based encryption schemes.²⁹ DSS with EUF-CMA security is found to be insufficient in some of the constructions, particularly to build non-malleable cryptographic schemes. In a nutshell, non-malleability refers to the impossibility of an adversary to generate a different ciphertext to some previously known ciphertext that decrypts to the same message, which is a desirable property in cryptographic schemes.³⁰ Thus, if a DSS is sEUF-CMA, it is much more versatile because it can be useful as a building block for many of the schemes which requires the property of non-malleability.

A simple attack for when a DSS is not sEUF-CMA

We show a toy example of a simple attack that can be achieved by an attacker if the DSS used for authentication is not sEUF-CMA. Figure 5 shows honest users Alice and Bob, as well as an attacker Mallory which has hijacked the channel. In step (1), Bob wants to authenticate that Alice is truly on the other end. Mallory launches a chosen message attack in step (2) and (3) on Alice and obtains the message m and signature σ. In step (4), Mallory forwards (m,σ) to Bob, which may initially convince them. After some time elapsed, Bob wants to re-authenticate Alice to ensure that they are still who they claim to be (5). Mallory forges a valid signature σ′ ≠ σ on m and forwards that to Bob (6). From Bob’s perspective, Alice generating a different signature ought to warrant some confidence that Alice is truly Alice. However, if the DSS is not sEUF, this is not the case, as Bob is obviously duped.

Figure 5. A simple problem on a digital signature schemes without sEUF-CMA.

Real life problems arising from signature malleability (non-sEUF)

We established sEUF-CMA is of theoretical interest. Here we briefly mention a few real-life needs for sEUF-CMA to emphasize the importance of it. Not too long ago, Stern et al. showed how to duplicate ECDSA signatures based on their malleability.³¹ A more recent example is the transaction malleability of the popular cryptocurrency, Bitcoin. When a transaction in Bitcoin is signed, the signature does not cover the entire transaction used for hashing; an attacker could perform strong forgery (i.e., maul the signature), then claim that the transaction has failed (because the hash is not valid). The sender would believe it because the signature is valid! This leads to the sender issuing a new transaction, without knowing that the original transaction is valid.^32,33 Decker and Wattenhofer pointed out that this subtle flaw could be responsible for a small portion of Bitcoins stolen during the 2014 MtGox attack.³⁴ They remarked that transaction malleability should be carefully considered when implementing Bitcoin clients. In another research, Jackson et al. found that signatures that are not sEUF-CMA may cause the strong session agreement of a well-known authenticated key exchange algorithm, the STS-ISO¹ to fail.³⁶ They analyzed STS-ISO using the Tamarin Prover and found that if sEUF is violated, attackers can force the parties in the session to accept message that do not originate from either of the honest parties.

DSS secure in sEUF-CMA

The notion of sEUF-CMA first appeared in the form of non-malleability of ciphertexts in the works of Dolev, Dwork and Naor³⁰ in 1991. The term sEUF-CMA was first introduced by An, Dodis and Rabin which presented it as requirement to construct signcryption schemes.²⁵ Boneh, Shen and Waters were the first DSS that is considered and proven in the sEUF-CMA model,³⁷ but mentions that DSS that are sEUF-CMA have existed earlier such as full domain hash (FDH)-RSA.¹⁸ FDH-RSA must be sEUF-CMA because the signatures generated are determined exactly by the message only. This means that FDH-RSA signatures are deterministic. For deterministic signatures, a strong forgery cannot occur without the message m′ being different from the original m, therefore, deterministic signatures are generally sEUF-CMA. We see that this is also the case for the widely used and popular EdDSA which had recently received a provable security treatment.³⁸ Boneh, Shen and Waters shows that non-deterministic signatures may also exhibit sEUF-CMA, such as the Micali-Reyzin signatures,³⁹ Goh-Jarecki signatures⁴⁰ and Boneh-Boyen signatures.¹¹ The reason for this is that if the forger manages to re-randomize a signature on the same message, the signature constitutes an existential forgery through clever binding of the messages. This is a recurring paradigm to design sEUF-CMA signature schemes.^11,41 Since the introduction of the sEUF-CMA model, existing EUF-CMA secure DSS are now re-considered in the sEUF-CMA model. An example of such work is by Fersch, Kiltz and Poettering on the well established DSA.¹³ DSA was shown to be secure under sEUF-CMA, while ECDSA was not².⁴³ More recently in 2021, Brendel et al. proved the IETF version of EdDSA to be sEUF-CMA secure.³⁸ Table 1 shows a list of DSS that are secure under sEUF-CMA.

Table 1. DSS that are directly sEUF-CMA.

Scheme	Req.	Sec. Assump	Sign Cost	Ver. Cost	Sig. len.	M.R.	Std.
Lamport⁴⁴	N/A	1-way functions	\|1k\| hash/0	\|1k\| hash	\|m\|×\|hash(⋅)\|	✗	✓
DSA^13,43	random oracle	DLP	0/ex	ex	2\| $ℤ_{q}$ \|	✗	✗
FDH-RSA¹⁸	random oracle	RSA	0/ex	ex	\| $ℤ_{n}$ \|	✗	✗
CS99⁴⁵	N/A	Strong RSA	0/4ex	4ex	3\| $ℤ_{n}$ \|	✗	✓
BLS01⁹	random oracle	GDH	0/ex	pair	$\| G \|$	✗	✗
BMS03⁴⁶	N/A	CDH	ex( ${log}_{2} n_{m}$ )/ex	(pair + ex)( ${log}_{2} n_{m}$ +1)	$({log}_{2} n_{m} + 1) \| G \|$	✗	✓
GJ03⁴⁷	random oracle	DDH	0/2ex	2ex	2\| $ℤ_{q}$ \|	✗	✗
KW03⁴⁷	random oracle	RSA	0/ex	ex	\| $ℤ_{n}$ \|	✗	✗
BB04¹¹	N/A	Strong DH	0/ex	pair	$\| G \| + \| ℤ_{q} \|$	✗	✓
mNR04^48,49	N/A	GGM	0/ex	2ex	2\| $ℤ_{q}$ \|	✓	✓
GJK +07-1⁵⁰	random oracle	CDH	0/3ex	2ex	— $G$ — + 2\| $ℤ_{q}$ \| + 1	✗	✗
GJK +07-2⁵⁰	random oracle	DDH	2ex/0	2ex	2\| $ℤ_{q}$ \|	✗	✗
TP09⁵¹	random oracle	RSA & DLP	0/2ex	3ex	2\| $ℤ_{n}$ \|	✗	✗
AGH +11⁵²	N/A	GGM	0/(2+kmn)ex	(kmn)pair	$3 \| G \|$	✗	✓
EdDSA^38,53	random oracle	ECDLP	0/2ex	2ex	$2 \| G \|$	✗	✗
NTC19⁵⁴	random oracle	1-way trapdoor sampleable relations	0/2ex	2ex	$\| G \| + 1$	✗	✗

Message recovery

From another perspective, we consider DSS with message recovery (DSS-R) candidates under sEUF-CMA. As pointed out by Ateniese and de Mediros, the modified Nyberg-Rueppel signature is sEUF-CMA secure.⁴⁹ While it is tempting to think that DSS-R must be sEUF-CMA, because modifying the signature will surely modify the message itself given that one can recover the message from the signature. However, we see that this is not the case as Ateniese and de Mediros found the original Nyberg-Rueppel signatures⁴⁹ to be insecure in sEUF-CMA.

Conversions to sEUF-CMA

Boneh, Shen and Waters opened a new field in the research of DSS under sEUF-CMA: Interest in sEUF-CMA conversion starts to accumulate with various works being published.^41,56-58 Instead of working on individual DSS, the line of research focuses on creating efficient conversions to enhance existing generic DSS with EUF-CMA into sEUF-CMA. Some transforms do not even need EUF-CMA security at minimum, only requiring EUF-GMA, which is a weaker notion than EUF-CMA.^59,60 Table 2 shows a list of conversion methods since 2006, including the use of DSS in leakage resilient settings.^61-64

Table 2.

Conversions that produces DSS with sEUF-CMA.

Scheme	DSS Req.	Add. Req.	Sec. Assump	Sign Cost	Ver. Cost	Sig. len.	Std.
MR00³⁹	factoring-based Fiat-Shamir	random oracle	integer fact.	0/2ex	2ex	2\| $ℤ_{q}$ \|	✗
BSW06³⁷	EUF-CMA, partitioned	randomized trapdoor	CDH + trapdoor	0/sg + ex + td	vf + ex + td	\|σ\| + \| $ℤ_{q}$ \|	✓
TOO06-1⁵⁶	EUF-CMA	random oracle	DLP	sg + ex/0	vf + ex	\|σ\| + \| $ℤ_{q}$ \|	✗
TOO06-2⁵⁶	EUF-CMA	collision resistant hash	DLP + collision resist	sg + ex/0	vf + ex	\|σ\| + 2\| $ℤ_{q}$ \|	✓
SPW07⁵⁷	EUF-CMA	strong randomized trapdoor	trapdoor	0/sg + 2td	vf + 2td	\|σ\| + \| $ℤ_{q}$ \|	✓
BS07⁴¹	EUF-CMA	2-tier DSS	EUF-CMA of 2-tier DSS	0/2sg + kg	2vf	2\|σ\| + \|pk\|	✓
Goldreich⁶⁵	EUF-CMA	1-time DSS	strong 1-time EUF DSS	sg( ${log}_{2} n_{m}$ )/sg	vf $({log}_{2} n_{m} + 1)$	$({log}_{2} n_{m}) (\| σ \| + \| p k \|)$	✓
HWZ07⁵⁸	EUF-CMA	1-time DSS	strong 1-time EUF DSS	sg + kg/sg	2vf	2\|σ\| + \|pk\|	✓
LKZ + 08-S⁵⁹	EUF-GMA, deterministic	N/A	N/A	sg + kg/sg	2vf	2\|σ\| + \|pk\|	✓
LKZ + 08-P⁵⁹	EUF-GMA, deterministic	N/A	N/A	sg/sg	2vf	2\|σ\| + \|1k\|	✓
LAS + 10⁶⁰	EUF-GMA/CMA	GTOW chameleon hash	one-wayness of GTOW hash	sg/td	vf + td	\|σ\| + \| $ℤ_{q}$ \|	✓
DSS with leakage resilience under sEUF-CMA
KV09-2.1⁶¹	Lamport DSS		1-time use 1-way functions	\|1k\| hash/0	\|1k\| hash	\|m\|×\|hash(⋅)\|	✓
WT14⁶²	EUF-FLR	strong randomized trapdoor	trapdoor leakage resilience	0/sig + 2td	vf + 2td	\|σ\| + \| $ℤ_{q}$ \|	✓
WT15⁶³	EUF-FLR	strong randomized trapdoor	trapdoor leakage resilience	0/sig + 2td + pair + ex	vf + 2td	$\| σ \| + \| ℤ_{q} \| + \| G \| + \| π \|$	✓
HHP16⁶⁴	EUF-FLR	1-time EUF-FLR DSS	strong 1-time EUF-FLR DSS	sg + kg/sig	2vf	2\|σ\| + \|pk\|	✓

DSS Req. - Requirement for DSS before using the conversion; Add. Req. - Additional requirements; EUF-GMA - Existential Unforgeability under Generic Chosen Message Attack; GTOW - Given Target One-Wayness (See⁶⁰); EUF-FLR - Existential Unforgeability with Full Leakage Resilience; sg - signature generation cost; td - trapdoor operation cost; kg - key generation cost; 1^k - security parameter; vf - signature verification cost; σ - underlying signature length; pk underlying signature public key length; π - Groth-Sahai proof statement (See⁶⁶).

Widely used DSS that have malleable signatures

Through our research, we investigated some of the most used DSS in the industry on their security in the sEUF-CMA model. The following are the popular DSS that are not sEUF-CMA secure.

1. RSA PKCS#1.5⁶⁷
2. ECDSA^31,43
3. Ed25519 (Original, not IETF RFC 8032)³⁸

Challenges and future direction

In recent work, there has been several post-quantum cryptographic DSS that incorporates the sEUF-CMA model during design.^68-71 DSS in various other contexts (e.g., privacy preserving computation, multiparty computation) such as a homomorphic DSS,⁷² group DSS,⁷³ and proxy DSS^74-76 are being considered in sEUF-CMA as well. In addition, DSS in even more complex cryptographic settings such as in certificateless and identity-based settings are also using sEUF-CMA as their standard model for security.^77-80 We see that the security goal post has been moved from EUF-CMA to sEUF-CMA in the span of a decade and believe this is the right direction forward as DSS is increasingly used in intricate security protocols, which cannot tolerate any design flaw that arises from as simple as malleable signatures.

Conclusion

In this work, we provided a comprehensive review on what is strong unforgeability in DSS, why is it needed, which of the DSS are secure under the model and how to obtain it if the DSS is only existentially unforgeable. We surveyed and analyzed existing DSS in literature which are secure under sEUF-CMA, and noted the requirements, computational and storage efficiency as well as the security assumptions of each DSS to provide an overview of DSS under the much more secure model.

Data availability

No data is associated with this article.

Acknowledgements

We would like to acknowledge our research funder: This research is supported by the Ministry of Higher Education of Malaysia through the Fundamental Research Grant Scheme under Grant FRGS/1/2019/ICT04/MMU/02/5 and in part by Multimedia University’s Research Management Fund.

References

1. Diffie W, Hellman M: New directions in cryptography. IEEE Trans. Inf. Theor. September 2006; 22(6): 644–654. 0018-9448. Publisher Full Text
2. Rivest RL, Shamir A, Adleman L: A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM February 1978; 21(2): 120–126. 0001-0782. Publisher Full Text
3. Katz J, Lindell Y: Introduction to Modern Cryptography (Chapman & Hall/Crc Cryptography and Network Security Series). Chapman & Hall/CRC; 2007. 1584885513.
4. Kaliski B: PKCS #1: RSA Encryption Version 1.5. RFC 2313, March 1998. Reference Source
5. Bellare M, Rogaway P: Random oracles are practical: A paradigm for designing efficient protocols. Proc 1st ACM Conf Computer Communications Security. , CCS ’93, New York, NY, USA: Association for Computing Machinery; 1993; page 62–73. 0897916298. Publisher Full Text
6. Gennaro R, Halevi S, Rabin T: Secure hash-and-sign signatures without the random oracle. In: Stern J, editor Advances in Cryptology — EUROCRYPT ’99. Berlin, Heidelberg: Springer Berlin Heidelberg; 1999; pages 123–139. 978-3-540-48910-8.
7. Cramer R, Shoup V: Signature schemes based on the strong rsa assumption. ACM Trans. Inf. Syst. Secur. August 2000; 3(3): 161–185. 1094-9224. Publisher Full Text
8. Kaliski B, Staddon J: PKCS #1: RSA Cryptography Specifications Version 2.0. RFC 2437. October 1998. Reference Source
9. Boneh D, Lynn B, Shacham H: Short signatures from the weil pairing. In: Boyd C, editor, Advances in Cryptology — ASIACRYPT 2001. Berlin, Heidelberg: Springer Berlin Heidelberg; 2001; pages 514–532. 978-3-540-45682-7.
10. Waters BR: Efficient identity-based encryption without random oracles. Cryptology ePrint Archive, Report 2004/180. 2004. Reference Source
11. Boneh D, Boyen X: Short signatures without random oracles. In: Cachin C, Camenisch JL, editors, Advances in Cryptology - EUROCRYPT 2004. Berlin, Heidelberg: Springer Berlin Heidelberg; 2004; pages 56–73. 978-3-540-24676-3.
12. Johnson D, Menezes A, Vanstone S: The elliptic curve digital signature algorithm (ECDSA). Int. J. Inf. Secur. August 2001; 1(1): 36–63. 1615-5262. Publisher Full Text
13. National Institute of Standards and Technology: Digital signature standard (DSS). Technical Report Federal Information Processing Standards Publications (FIPS PUBS) 186-4, Change Notice 4 July 19, 2013, U.S. Washington, D.C.: Department of Commerce; 2013.
14. Hofheinz D, Jager T, Kiltz E: Short signatures from weaker assumptions. In: Lee Dong Hoon, Wang X, editors, Advances in Cryptology – ASIACRYPT. Berlin, Heidelberg: Springer Berlin Heidelberg; 2011, pages 647–666. 978-3-642-25385-0.
15. Seo JH: Efficient digital signatures from rsa without random oracles. Info Sci. 2020; 512: 471–480. 0020-0255. Publisher Full Text Reference Source
16. Nyberg K, Rueppel Rainer A: Message recovery for signature schemes based on the discrete logarithm problem. In: De Santis A, editor, Advances in Cryptology — EUROCRYPT’94. Berlin, Heidelberg: Springer Berlin Heidelberg; 1995; pages 182–193. 978-3-540-44717-7.
17. Miyaji A: A message recovery signature scheme equivalent to dsa over elliptic curves.11 1996; 1163. Publisher Full Text
18. Bellare M, Rogaway P: The exact security of digital signatures-how to sign with rsa and rabin. In: Maurer U, editor, Advances in Cryptology — EUROCRYPT ’96. Berlin, Heidelberg: Springer Berlin Heidelberg; 1996; pages 399–416. 978-3-540-68339-1.
19. Abe M, Okamoto T: A signature scheme with message recovery as secure as discrete logarithm. In: Lam Kwok-Yan, Okamoto E, Xing C, editors, Advances in Cryptology - ASIACRYPT’99. Berlin, Heidelberg: Springer Berlin Heidelberg; 1999; pages 378–389. 978-3-540-48000-6.
20. Tzeng Shiang-Feng, Hwang Min-Shiang: Digital signature with message recovery and its variants based on elliptic curve discrete logarithm problem. Computer Standards & Interfaces. 2004; 26(2): 61–71. 0920-5489. Publisher Full Text Reference Source
21. Sekhar MR: Signature scheme with message recovery and its application. Int J Computer Mathematics. 2004; 81(3): 285–289. Publisher Full Text
22. Tahat N, Shaqboua R, Abdallah E, et al.: A new digital signature scheme with message recovery using hybrid problems. Int J Electrical Computer Eng (IJECE). 10 2019; 9: 3576. Publisher Full Text
23. Kazmirchuk S, Ilyenko A, Ilyenko S: Digital Signature Authentication Scheme with Message Recovery Based on the Use of Elliptic Curves. 01 2020; pages 279–288. 978-3-030-16620-5. Publisher Full Text
24. Goldwasser S, Micali S, Rivest Ronald L: A digital signature scheme secure against adaptive chosen-message attacks. SIAM J. Comput. April 1988; 17(2): 281–308. 0097-5397. Publisher Full Text
25. An JH, Dodis Y, Rabin T: On the security of joint signature and encryption. In: Knudsen LR, editor, Advances in Cryptology — EUROCRYPT 2002. Berlin, Heidelberg: Springer Berlin Heidelberg; 2002; pages 83–107. 978-3-540-46035-0.
26. Fiat A, Shamir A: How to prove yourself: Practical solutions to identification and signature problems. In: Odlyzko Andrew M, editor, Advances in Cryptology — CRYPTO’ 86. Berlin, Heidelberg: Springer Berlin Heidelberg; 1987; pages 186–194. 978-3-540-47721-1.
27. Kurosawa K, Heng S-H: From digital signature to id-based identification/signature. In: Bao F, Deng R, Zhou J, editors, Public Key Cryptography – PKC 2004. Berlin, Heidelberg: Springer Berlin Heidelberg; 2004; pages 248–261. 978-3-540-24632-9.
28. Katz J, Yung M: Scalable protocols for authenticated group key exchange. In: Boneh D, editor, Advances in Cryptology - CRYPTO 2003. Berlin, Heidelberg: Springer Berlin Heidelberg; 2003; pages 110–125. 978-3-540-45146-4.
29. Canetti R, Halevi S, Katz J: Chosen-ciphertext security from identity-based encryption. In: Cachin C, Camenisch JL, editors, Advances in Cryptology - EUROCRYPT 2004. Berlin, Heidelberg: Springer Berlin Heidelberg; 2004; pages 207–222. 978-3-540-24676-3.
30. Dolev D, Dwork C, Naor M: Non-malleable cryptography. SIAM J Computing. 03 1991; 30. Publisher Full Text
31. Stern J, Pointcheval D, Malone-Lee J, et al.: Flaws in applying proof methodologies to signature schemes. In: Yung M, editor, Advances in Cryptology — CRYPTO 2002. Berlin, Heidelberg: Springer Berlin Heidelberg; 2002; pages 93–110. 978-3-540-45708-4.
32. Bitcoin transaction malleability: 2017. Reference Source Accessed: 2021-06-03.
33. Transaction malleability: Bitcoin Wiki [Online].2018. Accessed: 2021-06-03.Reference Source
34. Decker C, Wattenhofer R: Bitcoin transaction malleability and mtgox. Lecture Notes in Computer Science. 2014; page 313–326. 1611-3349. Publisher Full Text
35. Diffie W, Van Oorschot PC, Wiener MJ: Authentication and authenticated key exchanges. Des. Codes Cryptography. June 1992; 2(2): 107–125. 0925-1022. Publisher Full Text
36. Jackson D, Cremers C, Cohn-Gordon K, et al.: Seems legit: Automated analysis of subtle attacks on protocols that use signatures. In Proc of the 2019 ACM SIGSAC Conference on Computer and Communications Security, CCS ’19. New York, NY, USA: Association for Computing Machinery; 2019; page 2165–2180. 9781450367479. Publisher Full Text
37. Boneh D, Shen E, Waters B: Strongly unforgeable signatures based on computational diffie-hellman. In: Yung M, Dodis Y, Kiayias A, et al., editors, Public Key Cryptography - PKC 2006. Berlin, Heidelberg: Springer Berlin Heidelberg; 2006; pages 229–240. 978-3-540-33852-9.
38. Brendel J, Cremers C, Jackson D, et al.: The provable security of ed25519: Theory and practice. 2021 2021 IEEE Symposium on Security and Privacy (SP). Los Alamitos, CA, USA: IEEE Computer Society; may 2021; pages 715–732. Publisher Full Text Reference Source
39. Micali S, Reyzin L: Improving the exact security of digital signature schemes. J. Cryptology. 03 2002; 15: 1–18. Publisher Full Text
40. Goh Eu-Jin, Jarecki Stanisław: A signature scheme as secure as the diffie-hellman problem. In: Biham E, editor, Advances in Cryptology — EUROCRYPT 2003. Berlin, Heidelberg: Springer Berlin Heidelberg; 2003; pages 401–415. 978-3-540-39200-2.
41. Bellare M, Shoup S: Two-tier signatures, strongly unforgeable signatures, and fiat-shamir without random oracles. In: Okamoto T, Wang X, editors, Public Key Cryptography – PKC 2007. Berlin, Heidelberg: Springer Berlin Heidelberg; 2007; pages 201–216. 978-3-540-71677-8.
42. Brown D: On the Provable Security of ECDSA, page 21–40. London Mathematical Society Lecture Note Series: Cambridge University Press; 2005. Publisher Full Text
43. Fersch M, Kiltz E, Poettering B: On the provable security of (ec)dsa signatures. Proc 2016 ACM SIGSAC Conference on Computer and Communications Security, CCS ’16. New York, NY, USA: Association for Computing Machinery; 2016; page 1651–1662. 9781450341394. Publisher Full Text
44. Lamport L: Constructing digital signatures from a one way function. Technical Report CSL-98. October 1979. Reference Source This paper was published by IEEE in the Proceedings of HICSS-43 in January, 2010.
45. Cramer R, Shoup V: Signature schemes based on the strong rsa assumption. Proc of the 6th ACM Conference on Computer and Communications Security, CCS ’99. New York, NY, USA: Association for Computing Machinery; 1999; page 46–51. 1581131488. Publisher Full Text
46. Boneh D, Mironov I, Shoup V: A secure signature scheme from bilinear maps. In: Joye M, editor, Topics in Cryptology — CT-RSA 2003. Berlin, Heidelberg: Springer Berlin Heidelberg; 2003; pages 98–110. 978-3-540-36563-1.
47. Katz J, Wang N: Efficiency improvements for signature schemes with tight security reductions. Proceedings of the 10th ACM Conference on Computer and Communications Security, CCS ’03. New York, NY, USA: Association for Computing Machinery; 2003; page 155–164. 1581137389. Publisher Full Text
48. Ateniese G, de Medeiros B: Efficient group signatures without trapdoors. In: Laih C-S, editor, Advances in Cryptology - ASIACRYPT 2003. Berlin, Heidelberg: Springer Berlin Heidelberg; 2003; pages 246–268. 978-3-540-40061-5.
49. Ateniese G, Medeiros BD: A provably secure nyberg-rueppel signature variant with applications. IACR Cryptol. ePrint Arch. 2004:93, 2004.
50. Goh E-J, Jarecki S, Katz J, et al.: Efficient signature schemes with tight reductions to the diffie-hellman problems. J. Cryptol. 2007; 20 (4): 493–514. Publisher Full Text
51. Tantikittipisut W, Premasathian N: Strongly unforgeable signature scheme without one-time key. 2009 Eighth IEEE/ACIS Int Conf Computer Information Sci. 2009; pages 313–316. Publisher Full Text
52. Abe M, Groth J, Haralambiev K, et al.: Optimal structure-preserving signatures in asymmetric bilinear groups. CRYPTO. 2011. Publisher Full Text
53. Josefsson S, Liusvaara I: Edwards-Curve Digital Signature Algorithm (EdDSA). RFC 8032. January 2017. Reference Source
54. Ng T-S, Tan S-Y, Chin J-J: Improving signature schemes with tight security reductions. In: Heng S-H, Lopez J: editors, Information Security Practice and Experience. Cham: Springer International Publishing; 2019; pages 273–292. ISBN 978-3-030-34339-2.
55. Rondepierre F: Revisiting atomic patterns for scalar multiplications on elliptic curves. Cryptology ePrint Archive, Report 2015/408. 2015. Reference Source
56. Teranishi I, Oyama T, Ogata W: General conversion for obtaining strongly existentially unforgeable signatures. In: Barua R, Lange T: editors, Progress in Cryptology - INDOCRYPT 2006. Berlin, Heidelberg: Springer Berlin Heidelberg; 2006; pages 191–205. 978-3-540-49769-1.
57. Steinfeld R, Pieprzyk J, Wang H: How to strengthen any weakly unforgeable signature into a strongly unforgeable signature. In: Abe M: editor, Topics in Cryptology – CT-RSA 2007. Berlin, Heidelberg: Springer Berlin Heidelberg; 2006; pages 357–371. 978-3-540-69328-4.
58. Huang Q, Wong DS, Zhao Y: Generic transformation to strongly unforgeable signatures. In: Katz J, Yung M: editors, Applied Cryptography and Network Security. Berlin, Heidelberg: Springer Berlin Heidelberg; 2007; pages 1–17. 978-3-540-72738-5.
59. Li J, Kim K, Zhang F, et al.: Generic security-amplifying methods of ordinary digital signatures. In: Bellovin SM, Gennaro R, Keromytis A, et al.: editors, Applied Cryptography and Network Security. Berlin, Heidelberg: Springer Berlin Heidelberg; 2008; pages 224–241. 978-3-540-68914-0.
60. Liu JK, Au MH, Susilo W, et al.: Short generic transformation to strongly unforgeable signature in the standard model. In: Gritzalis D, Preneel B, Theoharidou M: editors, Computer Security – ESORICS 2010. Berlin, Heidelberg: Springer Berlin Heidelberg; 2010; pages 168–181. 978-3-642-15497-3.
61. Katz J, Vaikuntanathan V: Signature schemes with bounded leakage resilience. In: Matsui M: editor, Advances in Cryptology – ASIACRYPT 2009. Berlin, Heidelberg: Springer Berlin Heidelberg; 2009; pages 703–720. 978-3-642-10366-7.
62. Wang Y, Tanaka K: Generic transformation to strongly existentially unforgeable signature schemes with leakage resiliency. In: Chow SSM, Liu JK, Hui LCK, et al.: editors, Provable Security. Cham: Springer International Publishing; 2014; pages 117–129. 978-3-319-12475-9.
63. Wang Y, Tanaka K: Generic transformation to strongly existentially unforgeable signature schemes with continuous leakage resiliency. In: Foo E, Stebila D: editors, Information Security and Privacy. Cham: Springer International Publishing; 2015; pages 213–229. 978-3-319-19962-7.
64. Huang J, Huang Q, Pan C: A black-box construction of strongly unforgeable signature schemes in the bounded leakage model. In: Chen L, Han J: editors, Provable Security. Cham: Springer International Publishing; 2016; pages 320–339. 978-3-319-47422-9.
65. Goldreich O: The foundations of cryptography - volume 2: Basic applications.2001.
66. Groth J, Sahai A: Efficient non-interactive proof systems for bilinear groups. Cryptology ePrint Archive, Report 2007/155. 2007. Reference Source
67. Moriarty K, Kaliski B, Jonsson J, et al.: PKCS #1: RSA Cryptography Specifications Version 2.2. RFC 8017.November 2016. Reference Source Section 9.2, Note 2.
68. Rückert M: Strongly unforgeable signatures and hierarchical identity-based signatures from lattices without random oracles. In: Sendrier N: editor, Post-Quantum Cryptography. Berlin, Heidelberg: Springer Berlin Heidelberg; 2010; pages 182–200. 978-3-642-12929-2.
69. Noh G, Chun JY, Jeong IR: Strongly unforgeable ring signature scheme from lattices in the standard model. J Appl Mathematics, 2014. 2014. 1110-757X. Publisher Full Text
70. Eaton E, Song F: Making existential-unforgeable signatures strongly unforgeable in the quantum random-oracle model. arXiv preprint arXiv:1509.02944. 2015.
71. Cremers C, Düzlü S, Fiedler R, et al.: Buffing signature schemes beyond unforgeability and the case of post-quantum signatures. Cryptology ePrint Archive, Report 2020/1525. 2020. Reference Source
72. Wang F, Wang K, Bao L, et al.: Leveled strongly-unforgeable identity-based fully homomorphic signatures. In: López J, Mitchell CJ: editors, Information Security - 18th International Conference, ISC 2015, Trondheim, Norway, September 9-11, 2015, Proceedings volume 9290 of Lecture Notes in Computer Science. Springer; 2015; pages 42–60. Publisher Full Text
73. Park H, Lim S, Yie I, et al.: Strong unforgeability in group signature schemes. Computer Standards Interfaces. 2009; 31(4): 856–862. 0920-5489. Publisher Full Text Reference Source
74. Sun Y, Xu C, Yu Y, et al.: Strongly unforgeable proxy signature scheme secure in the standard model. J Syst Soft. 2011; 84(9): 1471–1479. 0164-1212. Publisher Full Text Reference Source Selected papers from the 2009 Joint Working IEEE/IFIP Conference on Software Architecture & European Conference on Software Architecture (WICSA/ECSA 2009).
75. Yu Y, Yi M, Susilo W, et al.: Provably secure proxy signature scheme from factorization. Mathematical and Computer Modelling. 2012; 55(3): 1160–1168. 0895-7177. Publisher Full Text Reference Source
76. Pang L, Zhao H, Zhou X, et al.: Strongly unforgeable and efficient proxy signature scheme with fast revocation secure in the standard model. Int J Distributed Sensor Networks. 2016; 12 (1): 3205206. Publisher Full Text
77. Sato C, Okamoto T, Okamoto E: Strongly unforgeable id-based signatures without random oracles. In: Bao F, Li H, Wang G: editors, Information Security Practice and Experience. Berlin, Heidelberg: Springer Berlin Heidelberg; 2009: pages 35–46. 978-3-642-00843-6.
78. Zhang J, Liu X: An efficient strong id-based signature scheme with unforgeability. 2010 Fifth International Conference on Frontier of Computer Science and Technology. 2010; pages 239–245. Publisher Full Text
79. Yu Y, Yi M, Wang G, et al.: Improved certificateless signature scheme provably secure in the standard model. Information Security, IET. 06 2012; 6: 102–110. Publisher Full Text
80. Liu Z, Zhang X, Hu Y, et al.: Revocable and strongly unforgeable identity-based signature scheme in the standard model. Sec. and Commun. Netw. September 2016; 9(14): 2422–2433. 1939-0114. Publisher Full Text

Footnotes

1 STS stands for Station-to-Station and is an authenticated key exchange protocol due to Diffie et al.³⁵

2 Brown proved ECDSA to secure under sEUF-CMA,⁴² but this was refuted through a series of trivial attacks posed by.⁴³

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 16 Sep 2021

Author details Author details

¹ Faculty of Engineering, Multimedia University, Cyberjaya, Selangor, 63100, Malaysia
² Faculty of Computing and Informatics, Multimedia University, Cyberjaya, Selangor, 63100, Malaysia

Jason Chia
Roles: Conceptualization, Data Curation, Formal Analysis, Investigation, Methodology, Software, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Ji-Jian Chin
Roles: Conceptualization, Funding Acquisition, Methodology, Project Administration, Resources, Supervision, Validation, Writing – Review & Editing

Sook-Chin Yip
Roles: Methodology, Supervision, Validation, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

This research is supported by the Ministry of Higher Education of Malaysia through the Fundamental Research Grant Scheme under Grant FRGS/1/2019/ICT04/MMU/02/5 and in part by Multimedia University’s Research Management Fund.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (1)

version 1

Published: 16 Sep 2021, 10:931

https://doi.org/10.12688/f1000research.72910.1

Copyright

© 2021 Chia J et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

Chia J, Chin JJ and Yip SC. Digital signature schemes with strong existential unforgeability [version 1; peer review: 2 approved]. F1000Research 2021, 10:931 (https://doi.org/10.12688/f1000research.72910.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 1

VERSION 1

PUBLISHED 16 Sep 2021

Views

10

Reviewer Report 13 Feb 2023

Pin Shen Teh, Manchester Metropolitan University, Manchester, UK

Approved

https://doi.org/10.5256/f1000research.76522.r162696

The research objective was clear.
The concept of the work was straightforward.
The presentation style of the article was clear.
Grammar mistakes

The research objective was clear.
The concept of the work was straightforward.
The presentation style of the article was clear.
Grammar mistakes are noticeable. The sentence structure and choice of words used can be more concise and precise, some terms used were somewhat inconsistent, making reading and understanding the article quite challenging.
Further elaboration of why the three popular DSS that are not sEUF-CMA secure would be helpful.
Overall the depth of the work is sufficient for the calibre of this journal.

Is the topic of the review discussed comprehensively in the context of the current literature?

Yes
Are all factual statements correct and adequately supported by citations?

Yes
Is the review written in accessible language?

Yes
Are the conclusions drawn appropriate in the context of the current research literature?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Biometrics, Security, Machine Learning, Mobile Authentication

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Respond or Comment

Views

12

Reviewer Report 03 Nov 2021

Denis Chee-Keong Wong, Lee Kong Chian Faculty of Engineering and Science, Universiti Tunku Abdul Rahman, Kampar, Malaysia

Approved

https://doi.org/10.5256/f1000research.76522.r97082

The paper performs a review on existing DSS together with its properties, such as public verifiability, non-repudiation, and ability for message recovering. Furthermore, a detailed discussion on DSS security models are included, which are the EUF-CMA and sEUF-CMA. The differences ... Continue reading

The paper performs a review on existing DSS together with its properties, such as public verifiability, non-repudiation, and ability for message recovering. Furthermore, a detailed discussion on DSS security models are included, which are the EUF-CMA and sEUF-CMA. The differences between both security models are elaborated upon in detail. Finally, the authors provided comprehensive information on existing DSS in Table 1 for comparison purposes. As a survey paper, this work is comprehensive and suitable to be indexed. The authors need to re-check some of the entries in Table 1 to ensure the information stated is correct - please look at the "GJK +07-1", and please ensure the group G used is the same for all schemes with |G| in the column of "sig. len.".

Is the topic of the review discussed comprehensively in the context of the current literature?

Yes
Are all factual statements correct and adequately supported by citations?

Yes
Is the review written in accessible language?

Yes
Are the conclusions drawn appropriate in the context of the current research literature?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Algebraic cryptography, algebra

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Respond or Comment

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 16 Sep 2021

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 1 16 Sep 21	read	read

Denis Chee-Keong Wong, Universiti Tunku Abdul Rahman, Kampar, Malaysia
Pin Shen Teh, Manchester Metropolitan University, Manchester, UK

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

Back to all reports

Reviewer Report

10 Views

13 Feb 2023 | for Version 1

Pin Shen Teh, Manchester Metropolitan University, Manchester, UK

10 Views Cite this report Responses(0)

Approved

The research objective was clear.
The concept of the work was straightforward.
The presentation style of the article was clear.
Grammar mistakes are noticeable. The sentence structure and choice of words used can be more concise and precise, some terms used were somewhat inconsistent, making reading and understanding the article quite challenging.
Further elaboration of why the three popular DSS that are not sEUF-CMA secure would be helpful.
Overall the depth of the work is sufficient for the calibre of this journal.

Is the topic of the review discussed comprehensively in the context of the current literature?

Yes
Are all factual statements correct and adequately supported by citations?

Yes
Is the review written in accessible language?

Yes
Are the conclusions drawn appropriate in the context of the current research literature?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Biometrics, Security, Machine Learning, Mobile Authentication

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

12 Views

03 Nov 2021 | for Version 1

Denis Chee-Keong Wong, Lee Kong Chian Faculty of Engineering and Science, Universiti Tunku Abdul Rahman, Kampar, Malaysia

12 Views Cite this report Responses(0)

Approved

The paper performs a review on existing DSS together with its properties, such as public verifiability, non-repudiation, and ability for message recovering. Furthermore, a detailed discussion on DSS security models are included, which are the EUF-CMA and sEUF-CMA. The differences between both security models are elaborated upon in detail. Finally, the authors provided comprehensive information on existing DSS in Table 1 for comparison purposes. As a survey paper, this work is comprehensive and suitable to be indexed. The authors need to re-check some of the entries in Table 1 to ensure the information stated is correct - please look at the "GJK +07-1", and please ensure the group G used is the same for all schemes with |G| in the column of "sig. len.".

Is the topic of the review discussed comprehensively in the context of the current literature?

Yes
Are all factual statements correct and adequately supported by citations?

Yes
Is the review written in accessible language?

Yes
Are the conclusions drawn appropriate in the context of the current research literature?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Algebraic cryptography, algebra

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

[1] 1. Diffie W, Hellman M: New directions in cryptography. IEEE Trans. Inf. Theor. September 2006; 22(6): 644–654. 0018-9448. Publisher Full Text

[2] 2. Rivest RL, Shamir A, Adleman L: A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM February 1978; 21(2): 120–126. 0001-0782. Publisher Full Text

[3] 3. Katz J, Lindell Y: Introduction to Modern Cryptography (Chapman & Hall/Crc Cryptography and Network Security Series). Chapman & Hall/CRC; 2007. 1584885513.

[4] 4. Kaliski B: PKCS #1: RSA Encryption Version 1.5. RFC 2313, March 1998. Reference Source

[5] 5. Bellare M, Rogaway P: Random oracles are practical: A paradigm for designing efficient protocols. Proc 1st ACM Conf Computer Communications Security. , CCS ’93, New York, NY, USA: Association for Computing Machinery; 1993; page 62–73. 0897916298. Publisher Full Text

[6] 6. Gennaro R, Halevi S, Rabin T: Secure hash-and-sign signatures without the random oracle. In: Stern J, editor Advances in Cryptology — EUROCRYPT ’99. Berlin, Heidelberg: Springer Berlin Heidelberg; 1999; pages 123–139. 978-3-540-48910-8.

[7] 7. Cramer R, Shoup V: Signature schemes based on the strong rsa assumption. ACM Trans. Inf. Syst. Secur. August 2000; 3(3): 161–185. 1094-9224. Publisher Full Text

[8] 8. Kaliski B, Staddon J: PKCS #1: RSA Cryptography Specifications Version 2.0. RFC 2437. October 1998. Reference Source

[9] 9. Boneh D, Lynn B, Shacham H: Short signatures from the weil pairing. In: Boyd C, editor, Advances in Cryptology — ASIACRYPT 2001. Berlin, Heidelberg: Springer Berlin Heidelberg; 2001; pages 514–532. 978-3-540-45682-7.

[10] 10. Waters BR: Efficient identity-based encryption without random oracles. Cryptology ePrint Archive, Report 2004/180. 2004. Reference Source

[11] 11. Boneh D, Boyen X: Short signatures without random oracles. In: Cachin C, Camenisch JL, editors, Advances in Cryptology - EUROCRYPT 2004. Berlin, Heidelberg: Springer Berlin Heidelberg; 2004; pages 56–73. 978-3-540-24676-3.

[12] 12. Johnson D, Menezes A, Vanstone S: The elliptic curve digital signature algorithm (ECDSA). Int. J. Inf. Secur. August 2001; 1(1): 36–63. 1615-5262. Publisher Full Text

[13] 13. National Institute of Standards and Technology: Digital signature standard (DSS). Technical Report Federal Information Processing Standards Publications (FIPS PUBS) 186-4, Change Notice 4 July 19, 2013, U.S. Washington, D.C.: Department of Commerce; 2013.

[14] 14. Hofheinz D, Jager T, Kiltz E: Short signatures from weaker assumptions. In: Lee Dong Hoon, Wang X, editors, Advances in Cryptology – ASIACRYPT. Berlin, Heidelberg: Springer Berlin Heidelberg; 2011, pages 647–666. 978-3-642-25385-0.

[15] 15. Seo JH: Efficient digital signatures from rsa without random oracles. Info Sci. 2020; 512: 471–480. 0020-0255. Publisher Full Text Reference Source

[16] 16. Nyberg K, Rueppel Rainer A: Message recovery for signature schemes based on the discrete logarithm problem. In: De Santis A, editor, Advances in Cryptology — EUROCRYPT’94. Berlin, Heidelberg: Springer Berlin Heidelberg; 1995; pages 182–193. 978-3-540-44717-7.

[17] 17. Miyaji A: A message recovery signature scheme equivalent to dsa over elliptic curves.11 1996; 1163. Publisher Full Text

[18] 18. Bellare M, Rogaway P: The exact security of digital signatures-how to sign with rsa and rabin. In: Maurer U, editor, Advances in Cryptology — EUROCRYPT ’96. Berlin, Heidelberg: Springer Berlin Heidelberg; 1996; pages 399–416. 978-3-540-68339-1.

[19] 19. Abe M, Okamoto T: A signature scheme with message recovery as secure as discrete logarithm. In: Lam Kwok-Yan, Okamoto E, Xing C, editors, Advances in Cryptology - ASIACRYPT’99. Berlin, Heidelberg: Springer Berlin Heidelberg; 1999; pages 378–389. 978-3-540-48000-6.

[20] 20. Tzeng Shiang-Feng, Hwang Min-Shiang: Digital signature with message recovery and its variants based on elliptic curve discrete logarithm problem. Computer Standards & Interfaces. 2004; 26(2): 61–71. 0920-5489. Publisher Full Text Reference Source

[21] 21. Sekhar MR: Signature scheme with message recovery and its application. Int J Computer Mathematics. 2004; 81(3): 285–289. Publisher Full Text

[22] 22. Tahat N, Shaqboua R, Abdallah E, et al.: A new digital signature scheme with message recovery using hybrid problems. Int J Electrical Computer Eng (IJECE). 10 2019; 9: 3576. Publisher Full Text

[23] 23. Kazmirchuk S, Ilyenko A, Ilyenko S: Digital Signature Authentication Scheme with Message Recovery Based on the Use of Elliptic Curves. 01 2020; pages 279–288. 978-3-030-16620-5. Publisher Full Text

[24] 24. Goldwasser S, Micali S, Rivest Ronald L: A digital signature scheme secure against adaptive chosen-message attacks. SIAM J. Comput. April 1988; 17(2): 281–308. 0097-5397. Publisher Full Text

[25] 25. An JH, Dodis Y, Rabin T: On the security of joint signature and encryption. In: Knudsen LR, editor, Advances in Cryptology — EUROCRYPT 2002. Berlin, Heidelberg: Springer Berlin Heidelberg; 2002; pages 83–107. 978-3-540-46035-0.

[26] 26. Fiat A, Shamir A: How to prove yourself: Practical solutions to identification and signature problems. In: Odlyzko Andrew M, editor, Advances in Cryptology — CRYPTO’ 86. Berlin, Heidelberg: Springer Berlin Heidelberg; 1987; pages 186–194. 978-3-540-47721-1.

[27] 27. Kurosawa K, Heng S-H: From digital signature to id-based identification/signature. In: Bao F, Deng R, Zhou J, editors, Public Key Cryptography – PKC 2004. Berlin, Heidelberg: Springer Berlin Heidelberg; 2004; pages 248–261. 978-3-540-24632-9.

[28] 28. Katz J, Yung M: Scalable protocols for authenticated group key exchange. In: Boneh D, editor, Advances in Cryptology - CRYPTO 2003. Berlin, Heidelberg: Springer Berlin Heidelberg; 2003; pages 110–125. 978-3-540-45146-4.

[29] 29. Canetti R, Halevi S, Katz J: Chosen-ciphertext security from identity-based encryption. In: Cachin C, Camenisch JL, editors, Advances in Cryptology - EUROCRYPT 2004. Berlin, Heidelberg: Springer Berlin Heidelberg; 2004; pages 207–222. 978-3-540-24676-3.

[30] 30. Dolev D, Dwork C, Naor M: Non-malleable cryptography. SIAM J Computing. 03 1991; 30. Publisher Full Text

[31] 31. Stern J, Pointcheval D, Malone-Lee J, et al.: Flaws in applying proof methodologies to signature schemes. In: Yung M, editor, Advances in Cryptology — CRYPTO 2002. Berlin, Heidelberg: Springer Berlin Heidelberg; 2002; pages 93–110. 978-3-540-45708-4.

[32] 32. Bitcoin transaction malleability: 2017. Reference Source Accessed: 2021-06-03.

[33] 33. Transaction malleability: Bitcoin Wiki [Online].2018. Accessed: 2021-06-03.Reference Source

[34] 34. Decker C, Wattenhofer R: Bitcoin transaction malleability and mtgox. Lecture Notes in Computer Science. 2014; page 313–326. 1611-3349. Publisher Full Text

[35] 35. Diffie W, Van Oorschot PC, Wiener MJ: Authentication and authenticated key exchanges. Des. Codes Cryptography. June 1992; 2(2): 107–125. 0925-1022. Publisher Full Text

[36] 36. Jackson D, Cremers C, Cohn-Gordon K, et al.: Seems legit: Automated analysis of subtle attacks on protocols that use signatures. In Proc of the 2019 ACM SIGSAC Conference on Computer and Communications Security, CCS ’19. New York, NY, USA: Association for Computing Machinery; 2019; page 2165–2180. 9781450367479. Publisher Full Text

[37] 37. Boneh D, Shen E, Waters B: Strongly unforgeable signatures based on computational diffie-hellman. In: Yung M, Dodis Y, Kiayias A, et al., editors, Public Key Cryptography - PKC 2006. Berlin, Heidelberg: Springer Berlin Heidelberg; 2006; pages 229–240. 978-3-540-33852-9.

[38] 38. Brendel J, Cremers C, Jackson D, et al.: The provable security of ed25519: Theory and practice. 2021 2021 IEEE Symposium on Security and Privacy (SP). Los Alamitos, CA, USA: IEEE Computer Society; may 2021; pages 715–732. Publisher Full Text Reference Source

[39] 39. Micali S, Reyzin L: Improving the exact security of digital signature schemes. J. Cryptology. 03 2002; 15: 1–18. Publisher Full Text

[40] 40. Goh Eu-Jin, Jarecki Stanisław: A signature scheme as secure as the diffie-hellman problem. In: Biham E, editor, Advances in Cryptology — EUROCRYPT 2003. Berlin, Heidelberg: Springer Berlin Heidelberg; 2003; pages 401–415. 978-3-540-39200-2.

[41] 41. Bellare M, Shoup S: Two-tier signatures, strongly unforgeable signatures, and fiat-shamir without random oracles. In: Okamoto T, Wang X, editors, Public Key Cryptography – PKC 2007. Berlin, Heidelberg: Springer Berlin Heidelberg; 2007; pages 201–216. 978-3-540-71677-8.

[42] 42. Brown D: On the Provable Security of ECDSA, page 21–40. London Mathematical Society Lecture Note Series: Cambridge University Press; 2005. Publisher Full Text

[43] 43. Fersch M, Kiltz E, Poettering B: On the provable security of (ec)dsa signatures. Proc 2016 ACM SIGSAC Conference on Computer and Communications Security, CCS ’16. New York, NY, USA: Association for Computing Machinery; 2016; page 1651–1662. 9781450341394. Publisher Full Text

[44] 44. Lamport L: Constructing digital signatures from a one way function. Technical Report CSL-98. October 1979. Reference Source This paper was published by IEEE in the Proceedings of HICSS-43 in January, 2010.

[45] 45. Cramer R, Shoup V: Signature schemes based on the strong rsa assumption. Proc of the 6th ACM Conference on Computer and Communications Security, CCS ’99. New York, NY, USA: Association for Computing Machinery; 1999; page 46–51. 1581131488. Publisher Full Text

[46] 46. Boneh D, Mironov I, Shoup V: A secure signature scheme from bilinear maps. In: Joye M, editor, Topics in Cryptology — CT-RSA 2003. Berlin, Heidelberg: Springer Berlin Heidelberg; 2003; pages 98–110. 978-3-540-36563-1.

[47] 47. Katz J, Wang N: Efficiency improvements for signature schemes with tight security reductions. Proceedings of the 10th ACM Conference on Computer and Communications Security, CCS ’03. New York, NY, USA: Association for Computing Machinery; 2003; page 155–164. 1581137389. Publisher Full Text

[48] 48. Ateniese G, de Medeiros B: Efficient group signatures without trapdoors. In: Laih C-S, editor, Advances in Cryptology - ASIACRYPT 2003. Berlin, Heidelberg: Springer Berlin Heidelberg; 2003; pages 246–268. 978-3-540-40061-5.

[49] 49. Ateniese G, Medeiros BD: A provably secure nyberg-rueppel signature variant with applications. IACR Cryptol. ePrint Arch. 2004:93, 2004.

[50] 50. Goh E-J, Jarecki S, Katz J, et al.: Efficient signature schemes with tight reductions to the diffie-hellman problems. J. Cryptol. 2007; 20 (4): 493–514. Publisher Full Text

[51] 51. Tantikittipisut W, Premasathian N: Strongly unforgeable signature scheme without one-time key. 2009 Eighth IEEE/ACIS Int Conf Computer Information Sci. 2009; pages 313–316. Publisher Full Text

[52] 52. Abe M, Groth J, Haralambiev K, et al.: Optimal structure-preserving signatures in asymmetric bilinear groups. CRYPTO. 2011. Publisher Full Text

[53] 53. Josefsson S, Liusvaara I: Edwards-Curve Digital Signature Algorithm (EdDSA). RFC 8032. January 2017. Reference Source

[54] 54. Ng T-S, Tan S-Y, Chin J-J: Improving signature schemes with tight security reductions. In: Heng S-H, Lopez J: editors, Information Security Practice and Experience. Cham: Springer International Publishing; 2019; pages 273–292. ISBN 978-3-030-34339-2.

[55] 55. Rondepierre F: Revisiting atomic patterns for scalar multiplications on elliptic curves. Cryptology ePrint Archive, Report 2015/408. 2015. Reference Source

[56] 56. Teranishi I, Oyama T, Ogata W: General conversion for obtaining strongly existentially unforgeable signatures. In: Barua R, Lange T: editors, Progress in Cryptology - INDOCRYPT 2006. Berlin, Heidelberg: Springer Berlin Heidelberg; 2006; pages 191–205. 978-3-540-49769-1.

[57] 57. Steinfeld R, Pieprzyk J, Wang H: How to strengthen any weakly unforgeable signature into a strongly unforgeable signature. In: Abe M: editor, Topics in Cryptology – CT-RSA 2007. Berlin, Heidelberg: Springer Berlin Heidelberg; 2006; pages 357–371. 978-3-540-69328-4.

[58] 58. Huang Q, Wong DS, Zhao Y: Generic transformation to strongly unforgeable signatures. In: Katz J, Yung M: editors, Applied Cryptography and Network Security. Berlin, Heidelberg: Springer Berlin Heidelberg; 2007; pages 1–17. 978-3-540-72738-5.

[59] 59. Li J, Kim K, Zhang F, et al.: Generic security-amplifying methods of ordinary digital signatures. In: Bellovin SM, Gennaro R, Keromytis A, et al.: editors, Applied Cryptography and Network Security. Berlin, Heidelberg: Springer Berlin Heidelberg; 2008; pages 224–241. 978-3-540-68914-0.

[60] 60. Liu JK, Au MH, Susilo W, et al.: Short generic transformation to strongly unforgeable signature in the standard model. In: Gritzalis D, Preneel B, Theoharidou M: editors, Computer Security – ESORICS 2010. Berlin, Heidelberg: Springer Berlin Heidelberg; 2010; pages 168–181. 978-3-642-15497-3.

[61] 61. Katz J, Vaikuntanathan V: Signature schemes with bounded leakage resilience. In: Matsui M: editor, Advances in Cryptology – ASIACRYPT 2009. Berlin, Heidelberg: Springer Berlin Heidelberg; 2009; pages 703–720. 978-3-642-10366-7.

[62] 62. Wang Y, Tanaka K: Generic transformation to strongly existentially unforgeable signature schemes with leakage resiliency. In: Chow SSM, Liu JK, Hui LCK, et al.: editors, Provable Security. Cham: Springer International Publishing; 2014; pages 117–129. 978-3-319-12475-9.

[63] 63. Wang Y, Tanaka K: Generic transformation to strongly existentially unforgeable signature schemes with continuous leakage resiliency. In: Foo E, Stebila D: editors, Information Security and Privacy. Cham: Springer International Publishing; 2015; pages 213–229. 978-3-319-19962-7.

[64] 64. Huang J, Huang Q, Pan C: A black-box construction of strongly unforgeable signature schemes in the bounded leakage model. In: Chen L, Han J: editors, Provable Security. Cham: Springer International Publishing; 2016; pages 320–339. 978-3-319-47422-9.

[65] 65. Goldreich O: The foundations of cryptography - volume 2: Basic applications.2001.

[66] 66. Groth J, Sahai A: Efficient non-interactive proof systems for bilinear groups. Cryptology ePrint Archive, Report 2007/155. 2007. Reference Source

[67] 67. Moriarty K, Kaliski B, Jonsson J, et al.: PKCS #1: RSA Cryptography Specifications Version 2.2. RFC 8017.November 2016. Reference Source Section 9.2, Note 2.

[68] 68. Rückert M: Strongly unforgeable signatures and hierarchical identity-based signatures from lattices without random oracles. In: Sendrier N: editor, Post-Quantum Cryptography. Berlin, Heidelberg: Springer Berlin Heidelberg; 2010; pages 182–200. 978-3-642-12929-2.

[69] 69. Noh G, Chun JY, Jeong IR: Strongly unforgeable ring signature scheme from lattices in the standard model. J Appl Mathematics, 2014. 2014. 1110-757X. Publisher Full Text

[70] 70. Eaton E, Song F: Making existential-unforgeable signatures strongly unforgeable in the quantum random-oracle model. arXiv preprint arXiv:1509.02944. 2015.

[71] 71. Cremers C, Düzlü S, Fiedler R, et al.: Buffing signature schemes beyond unforgeability and the case of post-quantum signatures. Cryptology ePrint Archive, Report 2020/1525. 2020. Reference Source

[72] 72. Wang F, Wang K, Bao L, et al.: Leveled strongly-unforgeable identity-based fully homomorphic signatures. In: López J, Mitchell CJ: editors, Information Security - 18th International Conference, ISC 2015, Trondheim, Norway, September 9-11, 2015, Proceedings volume 9290 of Lecture Notes in Computer Science. Springer; 2015; pages 42–60. Publisher Full Text

[73] 73. Park H, Lim S, Yie I, et al.: Strong unforgeability in group signature schemes. Computer Standards Interfaces. 2009; 31(4): 856–862. 0920-5489. Publisher Full Text Reference Source

[74] 74. Sun Y, Xu C, Yu Y, et al.: Strongly unforgeable proxy signature scheme secure in the standard model. J Syst Soft. 2011; 84(9): 1471–1479. 0164-1212. Publisher Full Text Reference Source Selected papers from the 2009 Joint Working IEEE/IFIP Conference on Software Architecture & European Conference on Software Architecture (WICSA/ECSA 2009).

[75] 75. Yu Y, Yi M, Susilo W, et al.: Provably secure proxy signature scheme from factorization. Mathematical and Computer Modelling. 2012; 55(3): 1160–1168. 0895-7177. Publisher Full Text Reference Source

[76] 76. Pang L, Zhao H, Zhou X, et al.: Strongly unforgeable and efficient proxy signature scheme with fast revocation secure in the standard model. Int J Distributed Sensor Networks. 2016; 12 (1): 3205206. Publisher Full Text

[77] 77. Sato C, Okamoto T, Okamoto E: Strongly unforgeable id-based signatures without random oracles. In: Bao F, Li H, Wang G: editors, Information Security Practice and Experience. Berlin, Heidelberg: Springer Berlin Heidelberg; 2009: pages 35–46. 978-3-642-00843-6.

[78] 78. Zhang J, Liu X: An efficient strong id-based signature scheme with unforgeability. 2010 Fifth International Conference on Frontier of Computer Science and Technology. 2010; pages 239–245. Publisher Full Text

[79] 79. Yu Y, Yi M, Wang G, et al.: Improved certificateless signature scheme provably secure in the standard model. Information Security, IET. 06 2012; 6: 102–110. Publisher Full Text

[80] 80. Liu Z, Zhang X, Hu Y, et al.: Revocable and strongly unforgeable identity-based signature scheme in the standard model. Sec. and Commun. Netw. September 2016; 9(14): 2422–2433. 1939-0114. Publisher Full Text

Digital signature schemes with strong existential unforgeability

Abstract

Keywords

Introduction

Figure 1. The three processes of a digital signature scheme and the relationship between the input/outputs.

Properties of DSS

Message recovery

Figure 2. Sign and verify process for a digital signature scheme with message recovery.

Security models

Figure 3. EUF-CMA security model.

Strong existential unforgeability (sEUF-CMA)

Figure 4. sEUF-CMA security model.

Why does sEUF-CMA matter?

A simple attack for when a DSS is not sEUF-CMA

Figure 5. A simple problem on a digital signature schemes without sEUF-CMA.

Real life problems arising from signature malleability (non-sEUF)

DSS secure in sEUF-CMA

Table 1. DSS that are directly sEUF-CMA.

Message recovery

Conversions to sEUF-CMA

Table 2.

Widely used DSS that have malleable signatures

Challenges and future direction

Conclusion

Data availability

Acknowledgements

References

Footnotes

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated