Keywords
COVID-19, South Africa, Countermeasure, Agent-based Simulations, Public Health
This article is included in the Emerging Diseases and Outbreaks gateway.
This article is included in the Max Planck Society collection.
This article is included in the Coronavirus (COVID-19) collection.
COVID-19, South Africa, Countermeasure, Agent-based Simulations, Public Health
The first cases of the coronavirus disease COVID-19 were confirmed on December 29, 2019 in China1. Due to high contagiousness2, the disease has spread rapidly3,4 and by April 2020 the World Health Organization (WHO) had confirmed5 about 1.6 million cases worldwide. Consequently, the COVID-19 epidemic was declared a pandemic as it started to impact economies worldwide. However, epidemiological expertise lagged behind the exponential spread in this specific situation. In an attempt to contribute to the scientific assessment of the COVID-19 pandemic, we quickly derived first results and were able to make first predictions for the South African COVID-19 development. The significance of timely countermeasures could be seen in the development of infections in the United States, where cases surged from 1,678 to 307,318 between March 16, and April 6, 20206,7. Therefore, our research applied agent-based simulations to assess the effectiveness of countermeasures at an early stage of the COVID-19 pandemic and the following paper displays the state of literature and infection figures for the period of March and April 2020.
Most countries of the Global South were affected as well, often with reported case numbers just beginning to surge8. However, the reported low numbers in April, e.g. about 9000 cases in all of Africa, may be biased as only few individuals have been tested, see9 for the example of South Africa, and also10. Furthermore, such countries operate under vastly different socio-economic conditions, with larger social inequality, distinct transportation options and weaker health care systems compared to those of most countries in the global north11,12,13, such that core characteristics of potential COVID-19 spreading dynamics and thus the effectiveness of specific countermeasures remain largely unknown for countries of the Global South.
The transmission of COVID-19 is currently thought to occur through direct inter-person droplet-based infections through coughing and sneezing, with possible additional infection paths through aerosols and via contaminated surfaces. Symptoms often occur only after an incubation period of several days, with many infected responding entirely asymptomatic. Contagion may also occur via such symptom-free carriers, posing a challenge for tracing and estimating spreading patterns14. Transmission predominantly occurs through interactions while being at home, being at work, using shared transportation modes or during group-based leisure activities. In many countries of the Global South, most of these social activities occur under conditions drastically different from those in, for example, Europe or the U.S.. For instance, these countries feature, on average, more people per household, higher unemployment rates, more manual and lower payed work15,16 and much of publicly available transportation services used by the middle and low-income population are offered as paratransit shared-mobility services17,18. Moreover, public health care services are different and often less well equipped than in countries of the Global North13,19.
As a paradigmatic region offering large-scale data availability, we consider the Nelson Mandela Bay Municipality (NMBM) in South Africa to study scenarios of COVID-19 spreading dynamics and the impact of countermeasures. We combine socio-economic and travel survey data from more than 100,000 people20, about 10% of the local population, based on employment status, household size, age group and income level together with a detailed 24-hour travel diary component integrated into an agent-based traffic simulation (see Methods). The resulting contact network forms the basis for extended Susceptible-Infected-Recovered (SIR) model dynamics with parameters adapted to COVID-1921. Such agent-based simulations capture the inhomogeneity among the agents and are capable of modeling intricate nonlinear dynamic relationships between them, including a spreading rate that depends on the individual agent’s detailed activities, their modes of transportation used, and their distance to each other22.
To evaluate the impact of various policy measures on the course of the disease, we systematically compare several scenarios by varying simulation parameters accordingly (see Methods). First, a baseline scenario without any countermeasures; second, a default scenario in line with the current measures implemented in South Africa as of early April 202023. These include the shutdown of childcare and educational institutions, the prohibition of leisure activities of any kind and cutting shopping activity options by about 70%. Moreover, work related and “other” activities (for example trips to health care facilities and visits to public institutions) and travelling as passenger in a car are reduced by 80% and formal and informal public transport is reduced by 30%. Third, as a harsher variation of the lockdown that may be achievable in principle, we study the effect of a realistic lockdown scenario, increasing the restriction of activities related to work, shopping, leisure, and “other” by 90% while childcare, educational activities as well as formal and informal public transport are completely shut down. Finally, we consider a theoretical complete lockdown where all travel and outside activities are prohibited. All countermeasures come into effect 7 days after an initial infection of 100 people. We furthermore investigate additional simulations that start with the (currently enacted) default measures and introduce the realistic lockdown scenario after a number of days. Our results may inform and complement the ongoing discussion around tightening, loosening, introducing or repealing certain countermeasures.
For the transport simulation, we employ MATSim version 12.0-2019w48-SNAPSHOT24. The analysis relies on the population data file provided by Joubert20. It processes travel diaries from the 2004 Travel Survey to compute a synthetic population sample of the Nelson Mandela Bay Municipality (NMBM). Table 1 outlines the descriptive statistics of the synthetic agents and the modal split. It becomes apparent that the minibus taxis are the backbone of the region’s transport system. Private transport such as passenger cars play a rather marginal role. This difference underlines the interdependence of geographical, historical and economic characteristics of the region.
The 114,346 agents represent a 10% sample of the total population of NMBM. The trip distribution by transport mode shows the high prevalence of low cost transport modes (walk and minibus taxi) compared to private car usage. (Data from20,25).
We employ the Demand Responsive Transport (DRT) framework for MATSim26 to include the informal minibus taxi transit. In the underpinning MATSim, agents walk to a bus stop and request a DRT vehicle (in this case a minibus taxi). Their ride is pooled with rides of other agents with similar destinations. The simulated routing is more flexible than in reality, since the minibus taxis operate on a stop-based system with routes. Due to a lack of data, this mode is implemented based on a door-to-door based operating scheme and pick ups waiting passengers from the stops. Consequently on the one hand the vehicles are less frequented but on the other hand travel longer distances with passengers on board to pick up customers in the city. This reduces the likelihood of being on a minibus with an infected person, but increases the contact time if an infected person is actually on board. The formal bus transport services in NMBM are provided by Algoa Bus Company27. Currently, all formal bus operations are suspended in NMBM. It can therefore be assumed that customers are substituting regular bus services with minibus taxis. The MATSim population file is modified accordingly.
Due to the 10% population sample, the total capacity of the minibus taxis vehicles must be adapted to reflect the proportions in reality. In 2014, a total of 2,374 minibus taxis operated in NMBM with an average capacity of 15 persons25. As scaling the capacity of minibus taxis to 1.5 passengers would strongly underestimate the infections during minibus taxi trips, several test scenarios with different fleet sizes and passenger capacities were carried out.
Due to the operating scheme of door-to-door DRT a reduction either in fleet size and/or passenger capacity of the vehicles would lead to a high rejection rate and accordingly high infection numbers at home facilities that could bias the simulation results. For this reason, the number of vehicles is chosen with respect to the trade-off between capacity utilisation and the rejection rate. A fleet of 2,374 vehicles with a capacity of 15 optimises these criteria and is introduced into the model. The vehicles are placed randomly in the area at the beginning of the simulation, although in reality they wait for customers at designated places at the beginning of the day and start their tour when a certain degree of occupancy is reached.
Public minibus taxis are assumed to take an important role in the epidemic simulation, as both the probability and the intensity of contact are assumed to be high. Moreover, people with different places of work and residence mix up at this small space.
The model relies on the MATSim-based Episim-framework to simulate the epidemic spreading in the research area. The following briefly summarises both the functionality of the default Episim configuration and the parametric adaptions to the NMBN. It is important to note that the package is still in a early stage of development. For the following simulations, we used the latest version dated April 11, 2020 from the master branch (see https://github.com/matsim-org/matsim-episim/tree/85ca164a472b7f60117a51a365daed1eaf376199).
Episim is based on a traditional SIR model, which is a common model for the analysis of epidemics28 and has been continuously improved, e.g. by29,30,31. The basic mechanism is that people go through different stages during an epidemic, and have different characteristics with each transition. In short, initially all persons are susceptible for a disease and, over time, become infected with a given probability, partly influenced by individual characteristics. Later on, they recover. The states and transitions are usually extended to a more complex framework and include quarantine, seriously sick and critical patients in order to account for policy measures and the need for either hospital beds or ICUs.
The infection process is based on a probabilistic model and occurs in “containers”. These containers represent locations where several agents may interact, such as households, workplaces or transport vehicles, and are computed based on the information from NMBM MATSim simulation output event data. These chronicle all trajectories covered by agents during the day and the vehicles and facilities they visited and stayed at. Once a susceptible and a contagious agent stay in the same container, an infection occurs with a certain probability, which is described by equation 1 (see below).
At the beginning of the simulation, 10 randomly selected agents (corresponding to 100 people) are initially infected. After 7 days of uncontrolled spread, various countermeasures are implemented. We consider the dynamics until the countermeasures are in effect for 60 days.
In Episim, infected agents undergo several state transitions before their infection is terminated. Since not all humans suffer equally from COVID-19, the agents follow different paths from infection to recovery. In the beginning of the simulation, all agents except the ”Patients Zero” are initially healthy and thus susceptible. After an infection, an agent’s state changes to infected but not contagious, due to incubation time. With the beginning of the fourth day after an infection, the agent’s state changes to contagious. From this step on, the agent’s differ in their behaviour. In the default scenario, 20% of the agents put themselves into quarantine. The idea of the simulation model is that only a certain share of those suffering from COVID-19 notices symptoms. In addition, it is to be expected that some infected persons will go into public despite symptoms. The self-quarantine lasts 14 days and is assumed to mitigate social contacts completely, even within the household. 4.5% of all infected agents become seriously sick on day 10 and of these, 25% become critical the following day. In this way, a distinction is made between patients who require regular medical care and those who are dependent on ICUs. Contagious agents recover 16 days after infection, whereas the infection of patients with severe conditions terminates after 23 days.
In reality, an infection would end by recovery or death. For usability reasons, every infected agent recovers in Episim. As recovered agents are assumed to be immune and no longer contagious, omitting death does not bias the further course. The same mechanism is applied for self-quarantined, who remain mobile in the simulation but are neither contagious nor susceptible.
The probability of agent n becoming infected at time t when leaving a container is given by
Most of the contact intensities were left at their default since it is reasonable to assume that the contact intensities of most activities do not differ significantly from the values determined by21. The activities work, shopping, dropby and other were introduced so that the first two have the same contact intensity as leisure (5) and the other two take the values 7 and 3. It is assumed that due to the available space and seating arrangements in the minibus taxis, the contact between passengers in the minibus taxis is much higher than in formal public transport in Berlin. Since no reliable data on the contact intensity of passengers are available, we take the interaction intensity to be 20, compared to 10 in the default setting. Likewise, the contact intensity of being at home is doubled from 3 to 6 due to limited space, larger households and general living conditions.
The countermeasures in the default setting, realistic lockdown and complete lockdown are described by modifiers to the activity rates of the agents, describing the reduction in the frequency of the respective activity. Table 2 lists all parameters for the scenarios studied.
Allowed share per activity in four scenarios. Episim allows to prohibit or restrict the practice of certain activities in order to simulate social distancing. Four sets of restrictions were implemented in the simulations. While in the baseline scenarios no measures are in power, a complete lockdown does not allow the population to leave their homes. Between those extreme cases, two different partial lockdowns are set up.
| Scenario | Baseline | Default | Realistic | Lockdown |
|---|---|---|---|---|
| Home | 1 | 1 | 1 | 1 |
| Work | 1 | 0.2 | 0.1 | 0 |
| Minibus taxis | 1 | 0.7 | 0 | 0 |
| Leisure | 1 | 0 | 0.1 | 0 |
| KiGa and Prim. Educ. | 1 | 0 | 0 | 0 |
| Higher Education | 1 | 0 | 0 | 0 |
| Shopping | 1 | 0.3 | 0.1 | 0 |
| Dropby | 1 | 0 | 0 | 0 |
| Other | 1 | 0.2 | 0.1 | 0 |
Direct model simulations in the four scenarios (Figure 1) reveal that a large fraction of the population becomes infected, not only for the baseline scenario without countermeasures (as expected), but also with the default countermeasures active as of this writing (April 11 2020), see Figure panels 1A and 1B. Even if scenarios of harsh but realistically possible or complete lockdown were enacted only seven days after reaching 100 infected people, the outbreaks would still become macroscopic, with tens of thousands of infected people (Figure 1C and 1D) in the NMBM alone. Across all scenarios enacted, outbreak dynamics also causes overload of the approximately ICU beds estimated as baseline for NMBM (Figure 1E,F). As a precondition for successful containment, lockdown needs to be implemented sufficiently early on (in particular less than 7 days after the first 100 infected, not the first 100 confirmed infected).
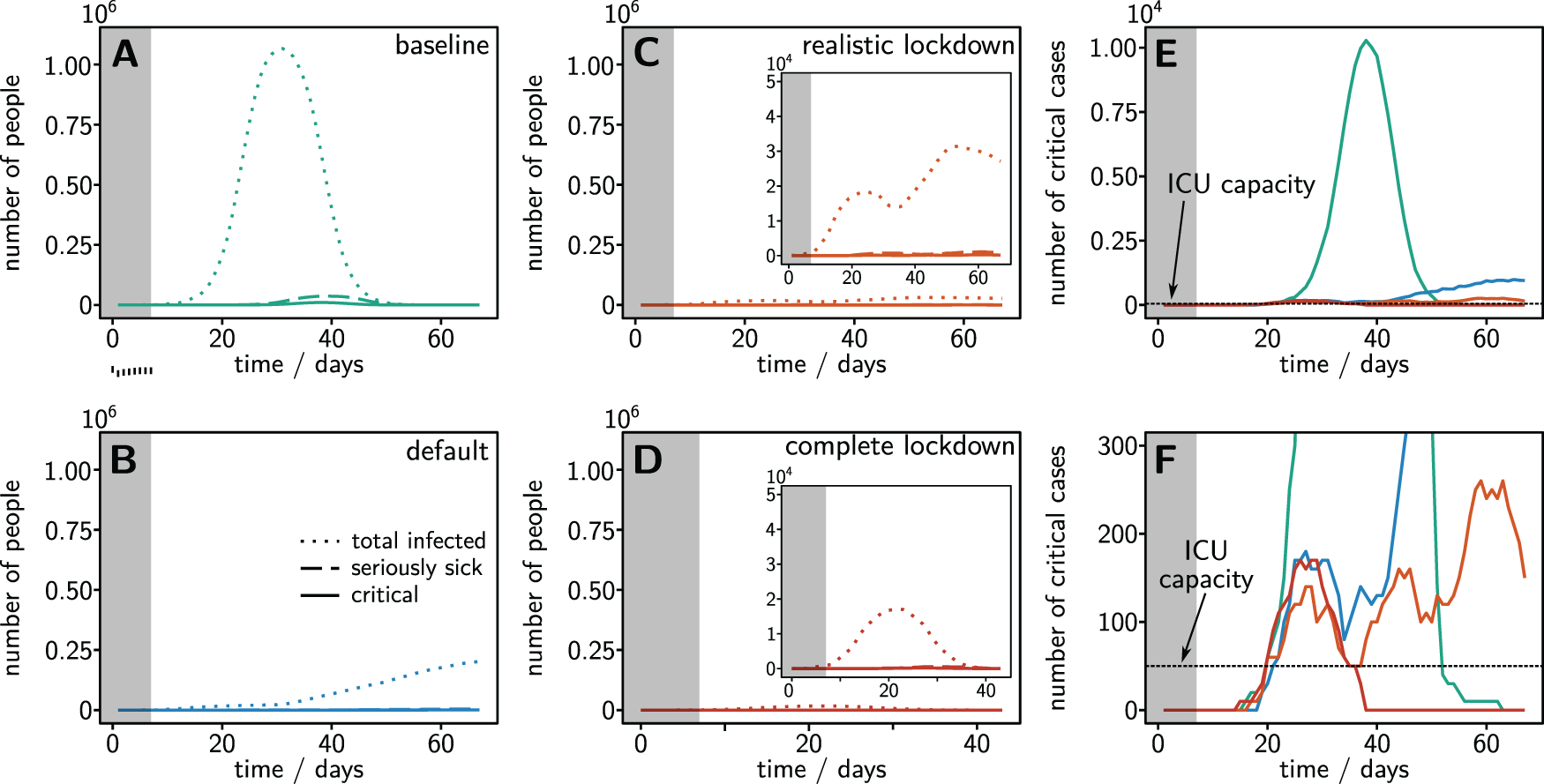
Dynamics for the Nelson Mandela Bay Municipality, Eastern Cape, South Africa, with a total population of 1.15 million people. (A-D) Evolution of the number of infected (dotted lines), seriously sick (dashed) and critical (solid) patients in four different scenarios: (A) baseline without any countermeasures, (B) with default countermeasures in line with current conditions in South Africa, (C) with harsh realistic countermeasures shutting down 90% of all activities, and (D) with complete lockdown prohibiting any movement and group activities (infections within a household are still possible, see Supplementary Material for details). All countermeasures are initiated 7 days (grey shading) after the an initial infection of 100 people. (E) and (F) Number of critical cases requiring intensive care compared to the available ICU capacity (horizontal dashed line) for all four countermeasure scenarios. None of the scenarios reduces the number of critical cases sufficiently to guarantee intensive care (ICU) treatment for all critical patients.
In all four scenarios, the outbreak strongly overloads the available intensive care unit (ICU) beds, with ten- to 100-fold overload in default and baseline scenario, respectively (see Figure 2A). Out of the total 267 ICU beds available in (public and private) hospitals in the whole Eastern Cape Province (data from 2008,32), only about 50 would be available for critical cases from the NMBM (scaled proportional to the relative population counts in 201133,34). We additionally quantify the sustained pressure on the health care system by computing the cumulative overload λ of the health system as the total number of person days critical patients go without intensive care (Figure 2B),
where Θ(⋅) denotes the Heaviside step function, Θ(x) = 1 for x ≥ 0 and Θ(x) = 0 otherwise, c(t) the number of critical cases at time t and cmax the available ICU capacity. The integral is taken over the entire time of simulation, 64 days after the 100 people are infected in NMBM. This cumulative measure λ thus quantifies the total long term overload of intensive care health services (and may be large even if the peak overload is small).The potential severity of the outbreak in NMBM even with strong countermeasures, is especially evident when compared to that of the United Kingdom (UK) (Figure 2C). In the UK, ICU capacity would be exceeded by a factor of about 35 without any countermeasures, by a factor of about 2 with social distancing (similar to default in our simulations) and not at all with measures currently enacted35. In our NMBM scenario simulations, ICU capacity would be exceeded by a factor of more than 200 without any countermeasures, by factor of about 20 with default measures, by a factor of 5 with realistic lockdown and still by a factor of 3 even with complete lockdown. These numbers underline the strong fragility of the health care services by example of the NMBM. We expect similar orders of magnitude of capacity exceedance throughout South Africa and in many countries of the Global South.
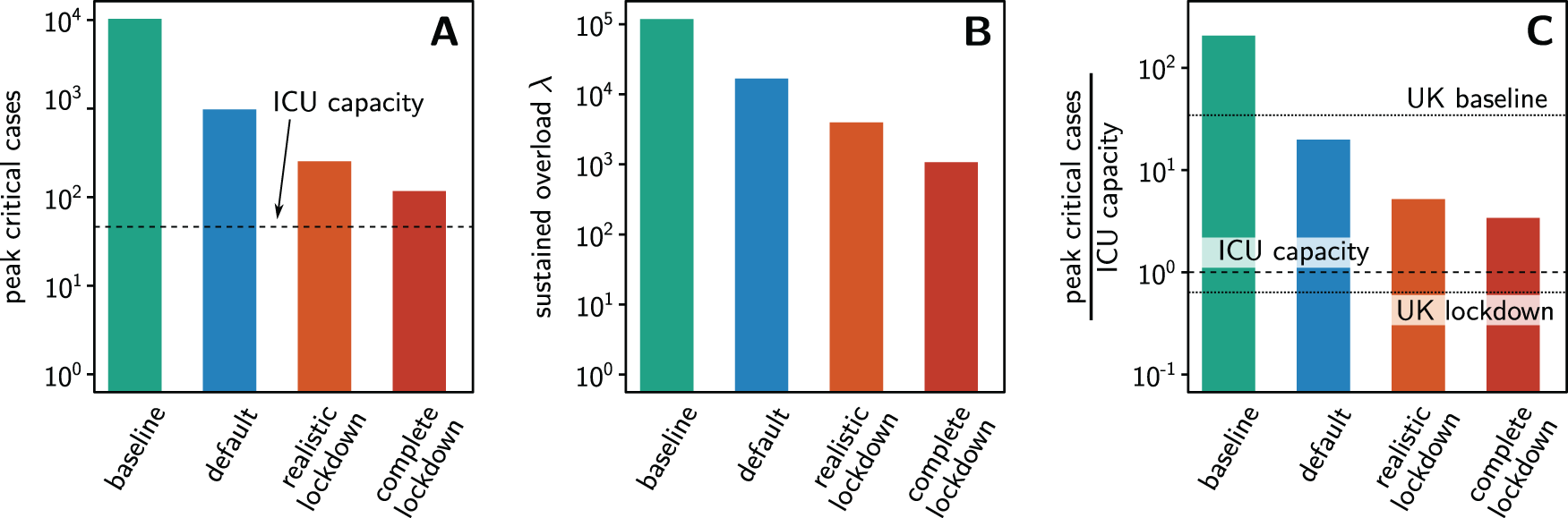
(A) Maximum number of concurrent critical patients during the peak of the outbreak. The available ICU capacity (dashed line) is widely exceeded in all scenarios. (B) The measure λ for the sustained overload, counting the total number of person days that critical patients are without intensive care. (C) Relative exceedance of the ICU capacity at the peak of the outbreak. The potential consequences of COVID-19 in countries of the Global South becomes clear from the comparison to UK estimates35 with about 35-fold overload without interventions (UK baseline, upper dotted line) and no overload with UK lockdown (lower dotted line) enforcing school and university closure, case isolation and general social distancing. Note the logarithmic vertical axes in all panels to make vast case number differences visible simultaneously with the capacity.
Therefore, all realistic scenarios, including the default scenario currently enacted in South Africa, hardly seem capable of containing the COVID-19 pandemic without substantially overloading ICU availability. Our results suggest that such overload could even be expected if all the 267 ICU beds in both private and public hospitals within the entire Eastern Cape Province would be exclusively available for critical COVID-19 patients in the Nelson Mandela Bay Municipality only.
Realistic or complete lockdown offer options of greatly reducing the pressure on the health care system if enacted rapidly enough. However, economic boundary conditions and in particular the large inequality in South Africa – and similarly in many other countries of the Global South – pose additional problems. Thus, in our opinion, in particular complete lockdown seems hardly enforceable and would appear unsustainable especially for a large share of people with lower income, as already weaker containment will likely lead to severe economic consequences in addition to disease related deaths36,37.
How can the number of critical cases be confined given that the default scenario is already enacted? On April 9th, 2020, the number of cases reported in NMBM was 3038. As the number of reported cases seem to systematically underestimate their actual number by at least a factor of three, as predicted for Austria on April 10, 202010, we estimate that on 9th of April, at least 100 cases existed in NMBM and take that as our initial condition. Starting simulations with the default scenario active, we find that critical cases are likely to vastly exceed the available ICU capacity (Figure 3A) within two months. In contrast, introducing the realistic lockdown scenario immediately, i.e. starting April 13th, might support a successful confinement of the number of critical COVID-19 patients in NMBM to manageable numbers (Figure 3B). In this scenario, the simulations suggest that there is about 80% likelihood that ICU capacity becomes overloaded at some time and that ,if overload occurs, it will be relatively mild (factor of 2-3 of the capacity, in contrast to factor of about 30 when keeping the default measures as they are).
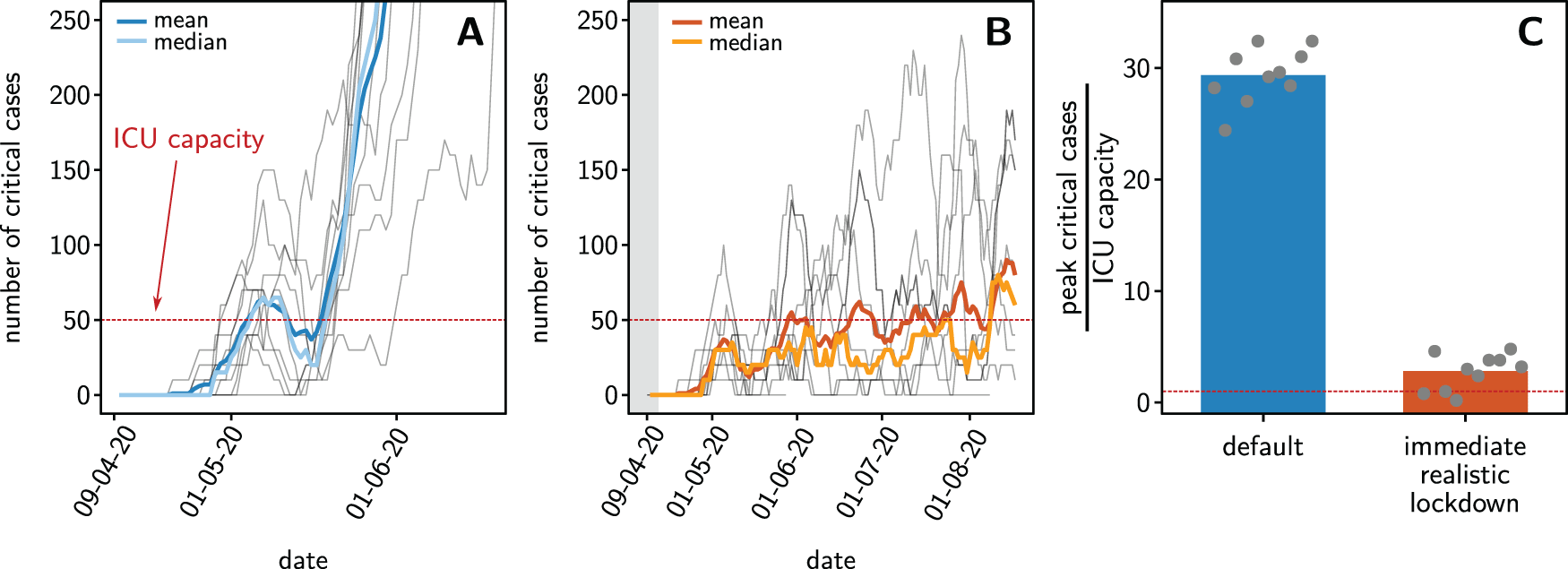
Ten stochastic realizations of agent-based simulations (gray lines in (A) and (B)) show increasing typical number of critical cases, quantified by the ensemble mean (dark) and median (light). (A) Stochastic dynamics of the number of critical cases when keeping the currently active default measures in NMBM. The ICU capacity is exceeded in almost all realizations within two months. (B) Switching from default (currently roughly enacted in South Africa) to the realistic lockdown scenario, limiting all activity by 90%, four days after crossing 100 infected people (estimated from 30 actually reported cases) in NMBM (that is on April 13, 2020), yields an exceeded ICU capacity in 80% of realizations, at most five times above the available capacity. (C) Relative exceedance of available ICU capacity in both scenarios. Keeping a default would cause roughly 3000% overload whereas enacting a stricter lockdown on April 13th substantially reduces expected overload to less than 300% and may completely avoid an overload in best cases.
We remark that the success of such lockdown countermeasures crucially relies on several restrictions and our simulations likely under- rather than overestimate future case numbers. First in our simulations, activities are immediately reduced to the set low values (complete shutdown of public transport, child care and educational facilities, 90% reduction of all other activities) and all inhabitants fully comply with these restrictions. Second, our simulations are based on estimated parameters that thereby come with uncertainties, and stochastic dynamics may create large deviations from the predicted values, in particular also earlier growth and larger total number of critical patients, not last due to an exponential growth of the outbreak in its initial phase without severe lockdown (compare39). Third, our estimates assume that all ICU beds would be available exclusively for COVID-19 patients during the entire time of the outbreak. Those and other constraints call for a more conservative, especially earlier introduction of realistic countermeasures.
We provide additional measures recorded from simulations on the location of infection events and exact values of the health care system overload in Tables 3 and 4, respectively.
Each event represents an initial infection of one out of 114.346 total agents. While most infections occur at home due to prolonged and close contact, paratransit in terms of minibus taxis is the second largest driver of the spreading process, accounting for approximately 15% of all infection events in the baseline scenario. These numbers decrease under countermeasures and almost disappear under complete lockdown, where only a few people are initially infected before all travel is stopped. A comparison to artificial settings where infections during minibus transit are neglected demonstrate the importance of the minibus taxi service as a driver for the spreading, in particular under partial lockdown.
During the first 6 days, the virus spreads uncontrolled. On day seven, countermeasures are initiated that restricts certain activities (see 2). The upper values result from simulations in which minibus taxis are possible locations of infection (presented in the main manuscript). The lower values are drawn from simulations, in which people could not become infected in minibus taxis (compare Table S3).
Across all scenarios studied, the results thus indicate that it may be hard to enact realistic, socially and economically feasible countermeasures without exceeding ICU capacity and that more drastic measures beyond the current default are rapidly needed. Finally, it seems reasonable to assume that the consequences of countermeasures would be qualitatively the same across South Africa as well as many countries of the Global South.
All data underlying the results are available as part of the article and no additional source data are required.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the work clearly and accurately presented and does it cite the current literature?
Partly
Is the study design appropriate and is the work technically sound?
Yes
Are sufficient details of methods and analysis provided to allow replication by others?
Partly
If applicable, is the statistical analysis and its interpretation appropriate?
Yes
Are all the source data underlying the results available to ensure full reproducibility?
Partly
Are the conclusions drawn adequately supported by the results?
Yes
References
1. Schröder M, Bossert A, Kersting M, Aeffner S, et al.: COVID-19 in South Africa: outbreak despite interventions. Scientific Reports. 2021; 11 (1). Publisher Full TextCompeting Interests: No competing interests were disclosed.
Reviewer Expertise: Infectious Diseases Immunology
Is the work clearly and accurately presented and does it cite the current literature?
No
Is the study design appropriate and is the work technically sound?
No
Are sufficient details of methods and analysis provided to allow replication by others?
No
If applicable, is the statistical analysis and its interpretation appropriate?
Not applicable
Are all the source data underlying the results available to ensure full reproducibility?
Partly
Are the conclusions drawn adequately supported by the results?
No
References
1. Kuehn B: Africa Succeeded Against COVID-19’s First Wave, but the Second Wave Brings New Challenges. JAMA. 2021; 325 (4). Publisher Full TextCompeting Interests: No competing interests were disclosed.
Reviewer Expertise: COVID-19, epidemiology, mathematical modeling
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 1 11 Feb 21 |
read | read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)