Chemical equilibrium model comprising calcaneus bone mineral density, low-density lipoprotein cholesterol, and physical work capacity in premenopausal women

Kazuto Mitsuhashi; Yasunori Imagawa; Yuta Kojima; Naokata Ishii; Yasushi Kishimoto

doi:10.12688/f1000research.126008.1

Home Browse Chemical equilibrium model comprising calcaneus bone mineral density,...

ALL Metrics

-

Views

-

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Chemical equilibrium model comprising calcaneus bone mineral density, low-density lipoprotein cholesterol, and physical work capacity in premenopausal women

[version 1; peer review: awaiting peer review]

Kazuto Mitsuhashi ^1,2, Yasunori Imagawa², Yuta Kojima³, Naokata Ishii¹, Yasushi Kishimoto⁴

Kazuto Mitsuhashi ^1,2, Yasunori Imagawa², [...] Yuta Kojima³, Naokata Ishii¹, Yasushi Kishimoto⁴

PUBLISHED 19 Oct 2022

Author details Author details

¹ Laboratory of Health Dynamics, Graduate School of Arts and Sciences, The University of Tokyo, Tokyo, 153-8902, Japan
² Yokohama Sports Medical Center, Yokohama, 222-0036, Japan
³ Faculty of Bioscience and Applied Chemistry, Hosei University, Tokyo, 184-8584, Japan
⁴ Laboratory of Physical Chemistry, Faculty of Pharma-Science, Teikyo University, Tokyo, 173-8605, Japan

Kazuto Mitsuhashi
Roles: Conceptualization, Data Curation, Formal Analysis, Investigation, Project Administration, Resources, Supervision, Writing – Original Draft Preparation, Writing – Review & Editing

Yasunori Imagawa
Roles: Data Curation, Methodology, Resources, Validation

Yuta Kojima
Roles: Investigation, Resources, Validation

Naokata Ishii
Roles: Funding Acquisition, Investigation, Project Administration, Resources, Supervision, Writing – Review & Editing

Yasushi Kishimoto
Roles: Data Curation, Formal Analysis, Funding Acquisition, Project Administration, Software, Supervision, Validation, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

OPEN PEER REVIEW

PEER REVIEW DISCONTINUED

Abstract

Background: During menopause, bone density decreases, and low-density lipoprotein cholesterol (LDL-C) rapidly increases; a decrease in the estrogen level is a common factor in these phenomena. Methods: In this study, we focused on the fact that menopause is a spontaneous process, and aimed to derive the conditions that mitigate the decline in the osteo sono-assessment index (OSI), an index of bone mineral density (BMD), using a chemical equilibrium model. We attempted to establish the relationship between variables related to female hormone secretion (OSI, LDL-C) and a variable related to work capacity (physical work capacity [PWC] at 75% of maximal heart rate) by analogy, using the fact that Gibbs free energy, a thermodynamic variable related to spontaneous change, is related by three variables. Results: Consequently, if linearity is established between PWC and OSI when LDL-C is used as the standard, then the analogy of chemical equilibrium can be established between the deviation values of these three variables, with equilibrium constant K. Finally, the theoretically determined equilibrium model with constant K was applied to data obtained from the Sports Program Service (SPS) of the Yokohama Sports Medical Center. Conclusions: The present study suggests that the decrease in bone density could be alleviated by promoting an increase in LDL-C or by mitigating the decrease in PWC. In discussing personal health, mitigating bone density loss and maintaining a high work capacity are important components, which should also take into account the appropriate levels of LDL-C.

Keywords

bone density; chemical equilibrium model; low-density lipoprotein cholesterol; menopause

Corresponding authors: Kazuto Mitsuhashi, Naokata Ishii

Competing interests: No competing interests were disclosed.

Grant information: This study was supported by the Grant-in-Aid for Scientific Research to
N.I. (grant number: 19H01085) and Y.K.(grant number : 22K06618 and 19K07337 ) from KAKENHI

The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2022 Mitsuhashi K et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Mitsuhashi K, Imagawa Y, Kojima Y et al. Chemical equilibrium model comprising calcaneus bone mineral density, low-density lipoprotein cholesterol, and physical work capacity in premenopausal women [version 1; peer review: awaiting peer review]. F1000Research 2022, 11:1196 (https://doi.org/10.12688/f1000research.126008.1) First published: 19 Oct 2022, 11:1196 (https://doi.org/10.12688/f1000research.126008.1) Latest published: 19 Oct 2022, 11:1196 (https://doi.org/10.12688/f1000research.126008.1)

Introduction

Women experience menopause between the ages of 45 and 55 years, as a normal part of the aging process.¹^,² Menopause is a period characterized by a decrease in bone mineral density (BMD) and a change in lipid metabolism due to a decrease in estrogen.³^,⁴ Thus, during menopause, bone density decreases and low-density lipoprotein cholesterol (LDL-C) rapidly increases. In postmenopausal life, women have about a 50% chance of developing osteoporotic fractures.⁵ In osteoporosis, there is an imbalance between bone formation and bone resorption, which starts during the menopausal transition period and intensifies after menopause. Genetic factors, endocrine status, nutrition, physical activity, and general health play critical roles in the occurrence of osteoporosis.⁶ Notably, high-impact exercise can reduce postmenopausal bone loss.⁷ In addition, dyslipidemia is one of the lifestyle-related diseases that often occur in women after menopause.⁸ It is known that estrogen deficiency associated with menopause affects lipid metabolism.⁹ Estrogen has various protective effects on the cardiovascular system; it is a vasorelaxant that improves lipid metabolism, and has antioxidant effects. In fact, premenopausal women have less ischemic cardiovascular disease due to atherosclerosis than men.¹⁰^–¹²

After menopause, the amount of estrogen in the body begins to decrease rapidly, with a loss of protective effects, and a rapid increase in the blood LDL-C. This is known to cause complications of arteriosclerotic diseases, such as cerebrovascular disorders and ischemic heart diseases.⁹ Although cholesterol is a source of estrogen, increasing LDL-C may increase the risk of atherosclerotic disease.¹³^,¹⁴ In the chemical equilibrium view, increased LDL-C should promote estrogen production and contribute to increased bone mass. However, studies on the relationship between LDL-C and BMD or the physical basis of athletic performance are inconclusive, and longitudinal data are lacking. The variables reflecting health and physical fitness factors are influenced by the prior lifestyle and exercise habits; thus, their effects on the maintenance of BMD after menopause are considered complicated. However, we believe that basic relationships between these variables can be clarified by defining the conditions that increase BMD in the premenopausal ages.

By paying attention to the phenomenon of a universal menopause process that does not depend on a bias in the data, we aimed to derive a chemical equilibrium model that holds among three variables, the calcaneus osteo-sono assessment index (OSI; an index of calcaneus BMD), LDL-C, and the physical work capacity at 75% of the maximum heart rate (PWC), and to derive the conditions that mitigate decreases in the OSI in premenopausal women (aged 20 to less than 45 years). Health factors (OSI, LDL-C) and physical fitness factors (PWC) should be mutually dependent variables, affected by other complex factors. In this paper, LDL-C is considered as a source of female hormones and OSI as an indicator of female hormones.¹⁵ Considering that high-density lipoprotein cholesterol (HDL-C) is a polymer of LDL-C, it is possible to consider that LDL-C is directly involved as a source of cholesterol, which is the raw material to produce female hormones. Therefore, we chose LDL-C instead of HDL-C as an indicator of the raw material for female hormones. Thus, we could capture the relationship between LDL-C and OSI from the perspective of female hormone production capacity. Next, we focused on the fact that the menopausal process is an irreversible change. Irreversible change is described as a decrease in Gibbs free energy. Gibbs free energy can then be related to work. Therefore, we considered female hormones and OSI, which spontaneously decrease in the menopausal process, as indicators of enthalpy; LDL-C, which increases in the menopausal process, as an indicator of entropy; and physical fitness factors (PWC) as an indicator of work. Hence, the menopausal process could be described by (LDL-C, PWC, and OSI), assuming an equilibrium state of these three variables in the premenopausal state. Thus, the aim of present study was to capture the properties of these three variables in a chemical equilibrium model.

Methods

Participants and data collection

The database used in this study comprised 1610 women aged 20 to 45 years who underwent the Sports Program Service (SPS) conducted by the Yokohama Sports Medical Center from April 1, 1998 to March 31, 2016. From this database, we selected only healthy women (n = 211) whose aspartate transaminase (AST), alanine aminotransferase (ALT), gamma-glutamyltransferase (γ-GTP), total protein, hemoglobin, triglyceride, hemoglobin A1C, and creatinine were within the normal range, based on the shared reference ranges established by the Japanese Committee for Clinical Laboratory Standards (2020).¹⁶ Subjects with a body mass index (BMI) outside the normal range (between 18.5 and 25 kg/m²) were also excluded.¹⁷ Medications, smoking history, drinking history, and menopausal status were confirmed in all participants. The SPS is intended to promote the health of Yokohama citizens. It is a paid service, in which women participate voluntarily. A feature of the SPS is that a medical examination and physical strength assessment were performed as a set, and included an exercise load test and various physical strength measurements.

This study was approved by the Ethics Committee of the Yokohama Sports Medical Center (approval number: K-2020-002). All participants provided written informed consent for the SPS and the potential use of their data for research purposes, including this study. All methods were performed in accordance with the Declaration of Helsinki, and the guidelines and regulations of the Research Ethics Committee of Yokohama Sports Medical Center.

Quantification of bone strength

The reproducibility and validity of the quantitative ultrasonic (QUS) calcaneal assessment have been previously established.¹⁸^–²² Calcaneal strength was measured by a QUS device, AOS-100NW (Hitachi ALOKA Medical, Ltd., Mitaka, Tokyo, Japan), which determined the speed of sound (SOS) as an index of bone density, and the bone structure of the dominant heel was inferred from the transmission index (TI). Calcaneus OSI provides information on bone stiffness. The OSI is highly correlated with BMD as assessed by dual X-ray absorptiometry. The OSI was calculated as TI × SOS².

Medical examination

Height and weight were measured using a height and weight scale (WB-510, Tanita Corporation, Tokyo, Japan), then BMI was calculated as weight (kilograms) divided by height squared (meters). Resting blood pressure was measured using the Riva-Roch-Korotkoff method (mercury sphygmomanometer) after participants had rested for 5 min. Blood was collected after a 12-hr fasting period, and LDL-C blood levels were measured using Cobas 6000 c501 (Roche Diagnostics K.K, Minato-ku, Tokyo). The blood concentration of AST, ALT, γ-GTP, total protein, hemoglobin, triglyceride, hemoglobin A1C, creatinine and LDL-C was measured by a dedicated laboratory technician at the Yokohama Sports Medical Center using the Roche INTEGRA 400 plus (Roche International Ltd., Basel, Switzerland) after a 12-hr fast. Self-report questionnaires were used to collect information on alcohol consumption (yes/no), smoking (yes/no), and medication for dyslipidemia (yes/no).

Physical exercise stress test

Physical work capacity at 75% of the maximum heart rate (PWC75% HR Max) was measured by a graded exercise test method on an electronic bicycle ergometer (The Multi Exercise Test System, ML-1800, Fukuda-Denshi, Tokyo, Japan),²³ which was used as an indicator of potential physical work capacity. During the graded exercise test, the rate of increase in load (10 – 60 watts/min), which is an individualized ramp protocol, was determined by a comprehensive judgment of researchers at Yokohama Sports Medical Center. The target heart rate was set at ≥75% of the estimated maximum heart rate (220 − age) and the test was stopped when the target heart rate was achieved. The test was stopped if an ECG abnormality (ST drop, frequent extrasystoles) was confirmed by a cardiologist at the Yokohama Sports Medical Center, or if the participant was unable to pedal at a constant rhythm (50 rpm) and complained of physical discomfort. Participants completed the exercise test in approximately 10 minutes.

Statistical analysis

The theoretical analysis of the relationships between the three variables in chemical equilibrium was the main focus of this research. We did not consider the confounding factors of each variable. All statistical analyses were performed with EZR (Saitama Medical Center, Jichi Medical University, Saitama, Japan), which is a graphical user interface for R (The R Foundation for Statistical Computing, Vienna, Austria). More precisely, it is a modified version of the R commander designed to add statistical functions frequently used in biostatistics.²⁴ The Turkey-Kramer test was used for multiple comparisons. If the null hypothesis could not be rejected in the multiple comparison test, a two-sided test was employed as a further equivalence test. The normality of the three variables was examined using the Kolmogorov-Smirnov test. A linear regression analysis was performed to describe the objective variable (dev.OSI-dev.PWC) as a linear function of the explanatory variable (dev.LDL-C-dev.PWC) and the objective variable (dev.OSI-dev.LDL-C) as a linear function of the explanatory variable (dev.PWC-dev.LDL-C). The difference was considered statistically significant when the P value was less than 0.05.

Results

Introducing deviation

In this study, the relationship between the three variables was first derived theoretically, and then its applicability to the clinical data of the Yokohama Sports Medical Center was assessed. For deriving the theoretical equation, the three variables of interest in this study were described by their deviation values in the sample population. We used the deviations as they have two main advantages over the absolute value of each variable or the rate of variation in each variable from its mean value. First, it is possible to treat the three variables in a standardized manner. Second, it is possible to express the bias of the equilibrium quantitatively. In this study, we use a new method to discuss the relationship between the three variables. In what follows, we use a case study to illustrate how to view the relationship between the other two variables when dev.LDL-C (prefix dev indicates deviation), is used as a reference.

Suppose that the deviations of the three variables of two persons (A and B) are described by the following:

A (dev . OSI, dev . PWC, dev . LDL-C) = (65, 65, 50)

B (dev . OSI, dev . PWC, dev . LDL-C) = (55, 55, 70)

The dev.OSI, dev.PWC based on dev.LDL-C is written in the following form:

A (dev . OSI-dev . LDL-C, dev . PWC-dev . LDL-C) = (+ 15, + 15)

B (dev . OSI-dev . LDL-C, dev . PWC-dev . LDL-C) = (- 15, - 15)

When viewed with respect to dev.LDL-C, the equilibrium in A is biased toward dev.OSI and dev.PWC, while in B, the equilibrium is biased toward dev.LDL-C.

Next, when the change in dev.OSI-dev.LDL-C from B to A is +30, the change in dev.PWC-dev.LDL-C is +30. In other words, when the equilibrium between dev.OSI and dev.LDL-C shifts toward dev.OSI, the equilibrium between dev.PWC and dev.LDL-C shifts toward dev.PWC.

Equilibrium migration hypothesis between LDL-C, OSI, and PWC

Figure 1 indicates the schematic representation of the chemical equilibrium model for LDL-C, OSI, and PWC. Focusing on the three variables, female hormones, OSI, and LDL-C, the following causal relationships, (1) and (2), occur in the menopausal process, which is a spontaneous change during aging.²⁵^–²⁷

Figure 1. Schematic representation of the chemical equilibrium model for LDL-C, OSI, and PWC.

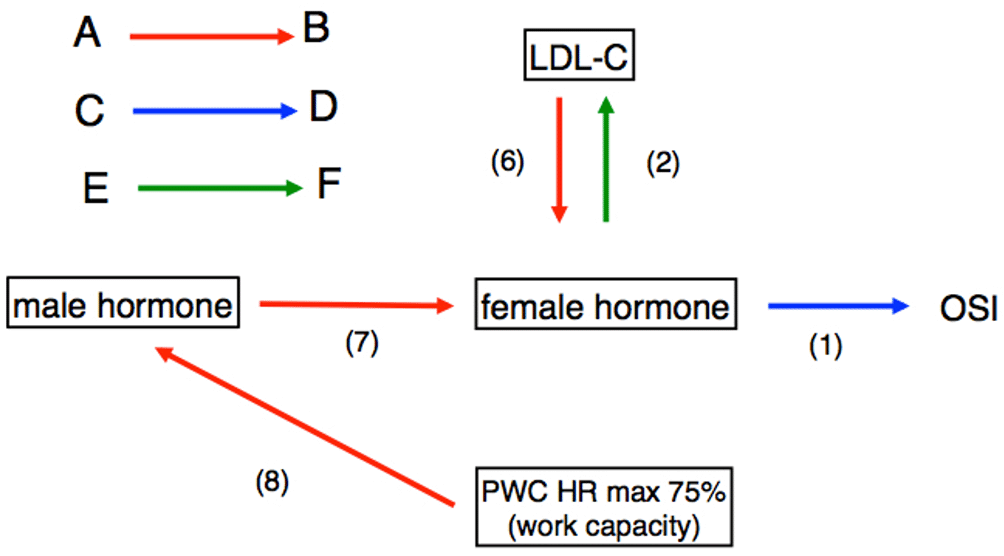
The relationship among each variable is schematically shown in the premenopausal generation.

There are two possible pathways for increasing OSI: one is the pathway in which activation of work capacity leads to activation of male hormones (8), which in turn leads to activation of female hormones, as derived from (7). The other pathway is the one by which elevated LDL-C leads to elevated female hormones (5, 6), which in turn leads to elevated OSI (1).

A red arrow (A → B) indicates that the increase of A induced the increase of B. A blue arrow (C→ D) indicates that the decrease of C induced the decrease of D. A green arrow (E → F) indicates that the decrease of E induced the increase of F.

Abbreviations: LDL-C, low-density lipoprotein cholesterol; OSI, osteo-sono assessment index; PWC, physical work capacity at 75% of the maximum heart rate.

(1)

Decrease in female hormones (cause) \to decrease in OSI (result) \dots

(2)

Decrease in female hormones (cause) \to increase in LDL-C (result) \dots

The rightward progression in relational expression (1) and (2) is generally not considered to be a desirable one.

If we take the counterpart of (1) and (2), we get the following relationships.

(3)

Increase in OSI \to increase in female hormone \dots

(4)

Decrease in LDL-C \to increase in female hormone \dots

From (2) and (4), we considered the menopausal process as a process in which the equilibrium state in (5) shifts to the left.

(5)

LDL - C ⇄ female hormone \dots

(Figure 1)

Using the deviation of the interval scale, dev.(female hormone)-dev.LDL-C expresses the rightward generative force of the response in (5).

Since LDL-C is a raw material for female hormones, the following cause-and-effect relationship can also be considered.

(6)

Increase in LDL-C (cause) \to increase in female hormone (result) \dots

(Figure 1)

Adapting Le Chatelier's principle to (5), (6) can be interpreted as a phenomenon in which the decrease in female hormones during menopause is alleviated by an increase in LDL-C.

The adrenal cortex produces male hormones (androstenedione), which are converted to female hormones by the enzyme aromatase, which is found in adipose tissue and muscle. Thus, male hormones are the only source of female hormones after menopause. Therefore, correlation (7) holds:

(7)

male hormone \to female hormone

(Figure 1)

Here, we introduce the parameter of PWC. As the PWC increases testosterone (quantity, activity),²⁸ correlation (8) holds.

(8)

Increase in PWC \to increase in male hormones \dots

(Figure 1)

In the premenopausal period, there are two possible pathways for increasing OSI: one is the pathway in which activation of work capacity leads to activation of male hormones, which in turn leads to activation of female hormones, as derived from (7) and (8). The other pathway is the one by which elevated LDL-C leads to elevated female hormones, which in turn leads to elevated OSI, according to (5). In other words, in the premenopausal phase, the relationship between each variable was considered to be as shown in Figure 1.

Relative relationship of the three variables with respect to one variable

By introducing a deviation value, the bias to the right in equilibrium shown in correlation (5) can be expressed as “dev. (female hormones) - dev.LDL-C”. In the same way, the level of OSI when viewed with respect to LDL-C can be described by dev.OSI-dev.LDL-C. If the increase in PWC, when viewed with respect to the LDL-C level, contributes to the increase in OSI, when viewed with respect to the LDL-C level, then the following equation should hold for both dev.PWC-dev.LDL-C and dev.OSI-dev.LDL-C.

α, β, γ, δ, m, and B used in equation (9) and thereafter are constants that are assumed to be statistically determined.

(9)

dev . OSI-dev . LDL-C = α \times (dev . PWC-dev . LDL-C) + β \dots

This equation means that the relative displacement of dev.OSI with respect to dev.LDL-C is in a linear relationship with the relative displacement of dev.PWC with respect to dev.LDL-C. Since there is generally an extremely high correlation between X-Y and X/Y, equation (9) could be rephrased in the following form (10).

(10)

dev . OSI / dev . LDL-C = γ \times dev . PWC / dev . LDL-C + δ \dots

Furthermore, in general, there is an extremely high correlation between X/Y and ln(X/Y). Therefore, the following equation could be derived.

(11)

ln (dev . OSI) - ln (dev . LDL-C) = m \times \{ln (dev . PWC) - ln (d e v . LDL-C)\} + B \dots

Equation (11) shows the relative relations among ln(dev.OSI) and ln(dev.PWC) with respect to ln(dev.LDL-C). By rearranging (11), the following formula was obtained.

(12)

ln (dev . OSI) - ln (dev . PWC) = (1 - m) \times \{ln (dev . LDL-C) - ln (dev . PWC)\} + B \dots

Equation (12) shows the relative relations among ln(dev.OSI) and ln(dev.LDL-C) with respect to ln(dev.PWC). From these equations, the following form can be derived.

(13)

K = \frac{dev . OSI}{{(dev . PWC)}^{m} {(dev . LDL-C)}^{1 - m}} \dots

Therefore, using equilibrium constant K, the relationship among the three variables can be explained by the following equilibrium equation, which is similar to that for a chemical equilibrium.

(14)

dev . OSI ⇌ dev . PWC + dev . LDL-C \dots The basic equilibrium equation .

Application of the theoretical equilibrium equation to real world data

Data regarding the OSI, LDL-C, and PWC in healthy women aged 20 to 45 years, collected by the SPS at Yokohama Sports Medical Center, are shown in Table 1. In addition, Table 1 shows the mean, variance and quartiles of age, height, weight, BMI, and various blood component parameters of the healthy female subjects recruited in the study. SPS features exercise stress tests and various physical fitness measurements that are not performed in general health checkups or physical examinations for the healthy person. Although the data visually appeared as close to following a normal distribution, statistical normality was not recognized (as assessed by the Kolmogorov-Smirnov test). Since the data were collected from a large sample population, each of the three variables had different and large variations.

Table 1. Summary of the SPS data analyzed in the present study.

	Mean	SD	25% percentile	50% percentile	75% percentile
OSI (10×10⁶)	2.92	0.38	2.67	2.88	3.11
LDL-C (mg/dL)	97.0	23.5	79.0	96.0	111.0
PWC (W)	102.9	32.2	84.5	98.0	111.0
Age (years)	31.5	7.7	25.0	31.0	38.0
Height (cm)	159.3	6.2	154.6	158.8	162.9
Weight (kg)	53.1	5.9	48.7	52.3	56.8
BMI (kg/m²)	20.9	1.8	19.4	20.4	22.0
Hemoglobin (g/dL)	12.8	0.7	12.3	12.9	13.2
Total protein (g/dL)	7.2	0.3	6.9	7.2	7.4
Total cholesterol (mg/dL)	186.9	26.7	168.0	185.0	203.0
TG (mg/dL)	57.0	20.8	40.0	51.0	67.5
GOT (U/L)	18.0	3.2	16.0	18.0	20.0
GPT (U/L)	13.3	3.4	11.0	13.0	15.0
γ-GPT (U/L)	14.0	4.6	11.0	13.0	16.0
HbA1C (%)	5.1	0.2	5.0	5.1	5.2
Creatinine (mg/dL)	0.6	0.1	0.6	0.6	0.7

Figure 2a shows the relationships between ln(dev.OSI) and ln(dev.PWC) with respect to ln(dev.LDL-C), indicating the following the regression curve.

(15)

ln (dev . OSI) - ln (dev . LDL-C) = - 0.000706 + 0.709 \times (ln (d e v . P W C) - ln (dev . LDL-C)) \dots

Figure 2. Relative relationships among ln (dev. OSI), ln (dev. PWC), and ln (dev. LDL-C) are shown.

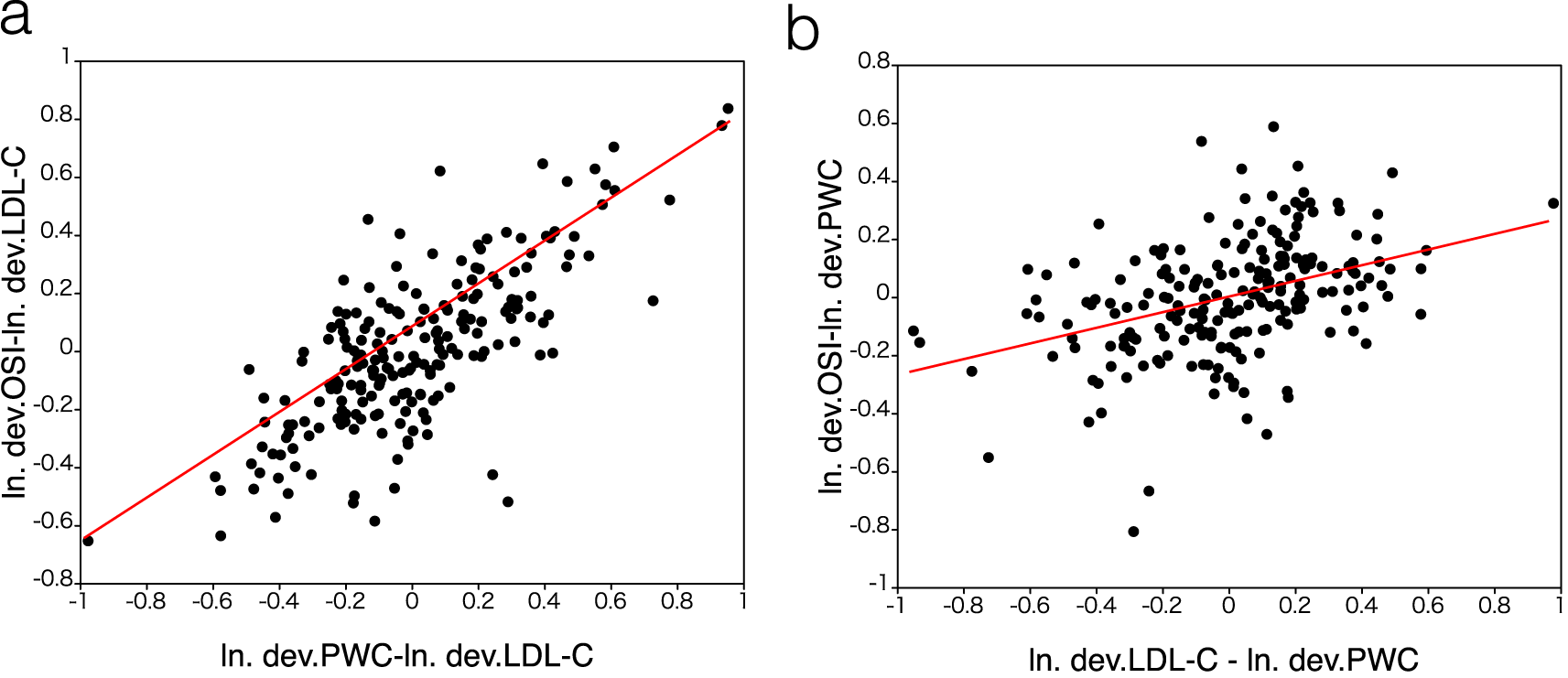
(a) Correlation between ln (dev. OSI) and ln (dev. PWC) with respect to ln (dev. LDL-C).

(b) Correlation between ln (dev. OSI) and ln (dev. LDL-C) with respect to ln (dev. PWC).

Abbreviations: LDL-C, low-density lipoprotein cholesterol; OSI, osteo-sono assessment index; PWC, physical work capacity at 75% of the maximum heart rate; ln, logarithmic; dev, deviation value.

A significant correlation was found, with a correlation coefficient of 0.753 (P<0.01).

Therefore, ln(dev.OSI) is an increasing function of ln(PWC) when ln(dev.LDL-C) is used as a reference. By rearranging (15), the following formula was obtained.

(16)

ln (dev . OSI) - ln (dev . PWC) = - 0.000706 + 0.291 \times (ln (dev . LDL-C) - ln (dev . PWC)) \dots

Figure 2b shows the relative relationships between ln(dev.OSI) and ln(dev.LDL-C) with respect to ln(dev.PWC), indicating the above regression curve. A significant correlation was found, with a correlation coefficient of 0.453 (P < 0.01). Therefore, ln(dev.OSI) is an increasing function of ln(dev.LDL- C) when ln(dev.PWC) is used as a reference.

According to (15) and (16), the equilibrium constant K is defined. K is a constant obtained by the below calculation.

(17)

K = \frac{dev . OSI}{{(dev . PWC)}^{0.709} {(dev . LDL-C)}^{0.291}} = 1 \dots

Equilibrium equation (17) is a necessary condition for equation (14) to be established. Since the deviation value was an interval measure, it was originally not suitable for multiplication and division. However, the variables were standardized by the deviation value; thus, it was possible to analogize the variables as concentrations. As indicated by the higher and smaller indices of dev.PWC and dev.LDL-C, respectively, in equation (17), the contribution to an increase in dev.OSI would be stronger for dev.PWC than for dev.LDL-C.

The robustness of the equilibrium constant K

Next, we investigated the range of each variable for which the equilibrium constant holds in order to identify the range of variation in the three variables for which homeostasis can be maintained. This property can be described as the robustness of the equilibrium constant K. Thus, we confirmed the robustness of the equilibrium constant K against fluctuations in dev.PWC, dev.LDL-C, and dev.OSI, respectively.

Robustness of the equilibrium constant K against fluctuations in PWC

One-way analysis of variance (ANOVA) followed by multiple comparison testing was performed on the PWC values of women aged 20 to 45 years, divided into quartiles (Q1 to Q4), with the natural logarithm of K as the objective variable (Figure 3a). There was a significant difference between Q1 and Q4 (Q1 - Q4), and between Q2 and Q4 (Q2 - Q4) (P < 0.01). There were no other significant differences between the quartile groups. Further equivalence testing showed statistically significant equivalence in all neighboring quartile ranges (Q1 - Q2), (Q2 - Q3), and (Q3 - Q4). When the K-value shows equivalence among the adjacent quartile groups, as in this case, the K-value can be considered robust. Therefore, the mechanism maintaining the equilibrium constant K stable against fluctuations in PWC is functioning throughout the entire quartile range.

Figure 3. Robustness of the equilibrium constant K against fluctuations in PWC, LDL-C, and OSI is shown.

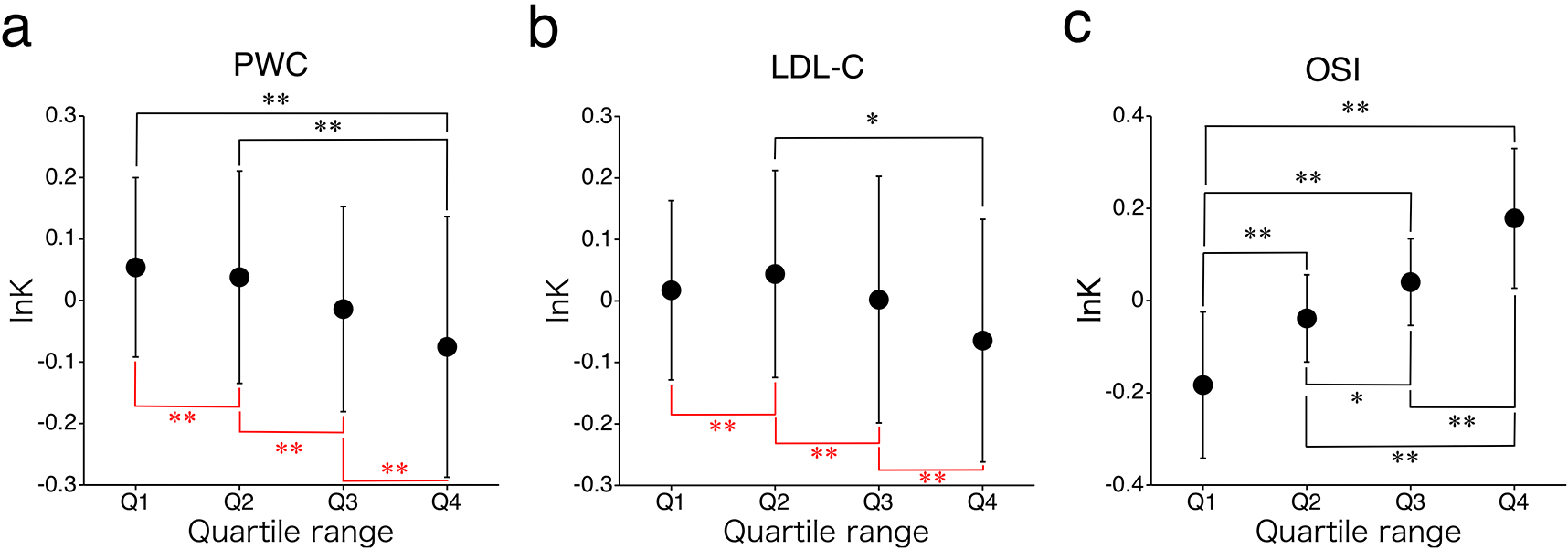
(a) Robustness of the equilibriums constant K for PWC is shown. Q1, Q2, Q3, and Q4 reflect the quartiles of the PWC between the ages of 20 and 45 years. The quartile range is as follows: Q1, under 84.5 W; Q2, 84.5–98 W; Q3, 98–111 W; and Q4, over 111 W. There is significant difference between Q1 and Q4 (P < 0.01). There is also a significant difference between Q2 and Q4 (P < 0.01). Importantly, equivalence is shown between Q1 and Q2, Q3 and Q4, and Q2 and Q4 with respect to the equilibrium constant K. In other words, the equilibrium constant K can be regarded as constant between all adjacent ranges.

(b) Robustness of the equilibrium constant K against fluctuations in LDL-C is shown. Q1, Q2, Q3, and Q4 reflect the quartiles of LDL-C between the ages of 20 and 45 years. The quartile range is as follows: Q1, under 79 mg/dL; Q2, 79–96 mg/dL; Q3, 96–111 mg/dL; and Q4, over 111 mg/dL. There is a significant difference between Q2 and Q4 (P < 0.01). The equivalence is ensured between all neighboring groups (between Q1 and Q2, Q2 and Q3, Q3 and Q4). This indicates that, as with the PWC, over a wide range of dev. LDL-C levels, the body can adapt to maintain a stable equilibrium constant K in response to dev. LDL-C fluctuations.

(c) Robustness of the equilibrium constant K against fluctuations in the OSI. Q1, Q2, Q3, and Q4 reflect the quartiles of OSI between the ages of 20 and 45 years. The quartile range is as follows: Q1, under 2.67×10⁶; Q2, 2.67–2.88×10⁶; Q3, 2.88–3.10×10⁶; and Q4, over 3.10×10⁶. There are significant differences between all pairwise combinations of Q1 to Q4 (P < 0.01). Thus, the equilibrium constant K is not robust for the quartile range of the OSI. Neither the LDL-C nor the PWC are responsive to large changes in the quartile range; thus, the fluctuation of dev. OSI to other quartile ranges is actually unrealistic. Even if such variation did occur, the mechanism for holding the equilibrium constant K does not work. This result suggests that dev. OSI is the result of a three-variable causal relationship, and not the cause, in the age range of 20 to 45 years.

Black asterisks (* or **) indicate a significant difference between groups (P < 0.05 or P < 0.01, respectively). In contrast, a red asterisk (**) indicates equivalence between groups (P < 0.01).

Abbreviations: LDL-C, low-density lipoprotein cholesterol; OSI, osteo-sono assessment index; PWC, physical work capacity at 75% of the maximum heart rate; dev, deviation value.

Robustness of the equilibrium constant K against fluctuations in LDL-C

Next, ANOVA followed by multiple comparison testing was performed on the LDL-C values of women aged 20 to 45 years, divided into quartile ranges, with the natural logarithm of K as the objective variable (Figure 3b). As a result, a statistically significant difference was found only in (Q2 - Q4) (P < 0.01). When equivalence tests were conducted for the other group combinations, significant equivalence was detected in all adjacent quartile groups (Q1 - Q2), (Q2 - Q3), and (Q3 - Q4), as with the PWC. Thus, the mechanism maintaining K constant against fluctuations in LDL-C is functioning throughout the entire quartile range.

Robustness of the equilibrium constant K against fluctuations in OSI

Finally, ANOVA followed by multiple comparison testing was performed again on the OSI values of women aged 20 to 45 years, divided into quartile ranges, with the natural logarithm of K as the objective variable (Figure 3c). There were significant differences between all pairwise combinations of Q1 to Q4 (P < 0.01). Thus, the mechanism maintaining the equilibrium constant K stable against fluctuations did not work for large fluctuations in OSI.

Discussion

In the present study, we developed a premenopausal chemical equilibrium model comprising three variables by focusing on the irreversible changes in the menopausal process, and deduced a basic relationship before menopause. Then the deduced results were applied to real-word data (i.e. SPS data) to check the robustness of the model. The study results show that the majority of women aged 20 to 45 years have a mechanism that reduces fluctuations in the equilibrium constant K against fluctuations in LDL-C and PWC in adjacent quartiles. This basic equilibrium works well for controllable fluctuations in PWC and LDL-C, but the equilibrium collapses in the case of large fluctuations in the OSI.

Life events such as pregnancy and menopause occur in women. Although a decrease in estrogen levels is natural and unavoidable, demonstrating the conditions that could mitigate the decline in BMD would be beneficial in improving the quality of life in women.

Muscle strength has been reported as an independent predictor of BMD in young women.²⁹ In addition, in the Nakanojo study, it was concluded that there is a positive correlation between the T-score and step count, and between the T-score and duration of physical activity >3 metabolic equivalents (METs; i.e., low to moderate intensity), in the elderly.³⁰^–³² Routine exercise of 7,000 steps or more and >15 minutes of exercise at >3 METs is recommended from the viewpoint of preventing osteoporosis.³² The PWC reflects both muscle mass and endurance.³³ Considering the results of these two studies together, an increase in PWC would contribute to an increase in OSI not only in the elderly, but also in young adult women.

While there are many reports supporting a positive correlation between PWC and OSI, there are differing conclusions regarding the correlation between OSI and LDL-C. A study in Korea found no significant correlation between LDL-C and BMD.¹¹ Thus, although LDL-C has been suggested to be involved in osteoporosis, its relationship with bone metabolism remains unclear.¹⁴ A recent epidemiological observational analysis showed a negative causal relationship between LDL-C and BMD.³⁴ This is apparently inconsistent with the results of our chemical equilibrium model. However, although the relationship between LDL-C and BMD has been examined in various studies, the results are often conflicting and inconclusive, with positive,³⁵^,³⁶ no,³⁷ and inverse³⁸^,³⁹ correlations reported. Indeed, Kuipers et al., found that in Afro-Caribbean men, lower LDL-C and higher HDL-C concentrations were associated with accelerated bone loss.³⁸ The reasons for these conflicting results regarding the relationship between serum lipids and bone metabolism are unclear, but further research is needed to better understand the mechanisms involved and the clinical implications of these findings.⁴⁰ However, all of these studies lack a consideration of the work capacity in association with both LDL-C and BMD.

There is no precedent for a study that comprehensively explains the relationship established among three variables that have the universal property of fluctuating during menopause, using a chemical equilibrium model. In the present study, we first focused on menopause, and then on the variation in three variables that did not depend on a data bias. Subsequently, we considered the changes in the three variables during the menopause period as an irreversible process, with the premenopausal state as a quasi-equilibrium state before reaching this irreversible process. In the present study, we reported on the relationship among three variables during the premenopausal stage (i.e. 20 to less than 45 year of age).

Changes in the three evaluated variables include both changes over time and variations within a particular age. Applying Le Chatelier's principle to the obtained equilibrium equation (14), it can be stated as follows: “increase in dev.PWC or increase in dev.LDL-C → increase in dev.OSI”. The conclusion of the basic equilibrium equation (14) is that at the premenopausal stage, with all other conditions being equal, an increase in dev.LDL-C will contribute to an increase in dev.OSI. As shown in the present study, it is important that the dev.PWC, dev.LDL-C, and dev.OSI in the premenopausal stage are controlled by the equilibrium constant K, and that the three variables are also mutually dependent variables.

The present study suggests that under restricted conditions, where the equilibrium constant K is kept at a constant value, the decrease in bone density could be alleviated by promoting an increase in LDL-C or by mitigating the decrease in PWC.

The spontaneous process of menopause is accompanied by changes in three variables: PWC, OSI, and LDL-C. Thus, they can be related to thermodynamic variables. If we view the progression of menopause as a spontaneous process, similar to a decrease in Gibbs free energy, OSI decreases and LDL-C increases, and we can compare OSI to enthalpy and LDL-C to entropy. This is an issue for future research.　

The existence of the equilibrium constant tells us that, for example, for the same value of PWC, the larger the LDL-C, the larger the OSI. In other words, for two people with the same level of work capacity, the equilibrium constant suggests that the person with higher LDL-C will have greater bone density. Therefore, it is not desirable to discuss good and bad health in terms of merely high and low LDL-C levels (not to mention that pathologically high LDL-C is undesirable). Instead, we should discuss the health status of an individual by simultaneously considering all the three variables, including work ability and bone density.

Conclusions

The present study suggests that the decrease in bone density could be alleviated by promoting an increase in LDL-C or by mitigating the decrease in PWC. The mitigation of bone density loss and maintenance of high work capacity are important factors when discussing an individual's health, and appropriate LDL-C levels may also need to be taken into account.

Data availability

This dataset was not generated nor is it owned by the authors of this article. Therefore, neither the authors nor F1000Research are responsible for the content of this dataset and cannot provide information about data collection. As this dataset contains potentially identifying images/information, caution is advised when using this dataset in future research. We note that only the results of data analysis may be used and published for research purposes, as stipulated by the ethics committee of the corresponding author's previous institution (Yokohama Sports Medical Center, Yokohama, Japan). Unfortunately, due to privacy and protocol issues, it is difficult at this time to grant the same access enjoyed by the authors to readers or reviewers. However, we believe that the data can be made available after this study is published. We provide you with the following information for the person in charge of the research institute that manages the data:

Those wishing to apply for access to the data should contact Shinji Nambu, Administrative Manager at the Yokohama Sports Medical Center Office (E-Mail:no01-nanbu@yspc.or.jp, +81-45-477-5050). When applying for access, interested parties must provide their affiliation, their background, and the purpose for which the data will be used in the body of the e-mail.

Acknowledgments

We thank the SPS participants and all staff members at the Yokohama Sports Medical Center. We express our gratitude to Haruhito Aoki, M.D., Ph.D. and Director of the Yokohama Sports Medical Center. K.M. is deeply grateful to Satoru Watanabe, Ph.D. and Shigeharu Saito, M.D., Ph.D. We would like to thank Editage (www.editage.com) for English language editing.

References

1. McKinlay S, Jefferys M, Thompson B: An investigation of the age at menopause. J. Biosoc. Sci. 1972; 4: 161–173. Publisher Full Text
2. Zhu D, Chung HF, Dobson AJ, et al.: Type of menopause, age of menopause and variations in the risk of incident cardiovascular disease: pooled analysis of individual data from 10 international studies. Hum. Reprod. 2020; 35: 1933–1943. PubMed Abstract | Publisher Full Text
3. Kalervo Väänänen HK, Härkönen PL: Estrogen and bone metabolism. Maturitas. 1996; 23(Suppl): S65–S69. Publisher Full Text
4. Ryu KJ, Park H, Kim YJ, et al.: Comparison of various menopausal symptoms and risk factor analysis in Korean women according to stage of menopause. Maturitas. 2020; 140: 41–48. PubMed Abstract | Publisher Full Text
5. Dobbs MB, Buckwalter J, Saltzman C: Osteoporosis: the increasing role of the orthopaedist. Iowa Orthop. J. 1999; 19: 43–52. PubMed Abstract
6. Pai MV: Osteoporosis prevention and management. J. Obstet. Gynaecol. India. 2017; 67: 237–242. PubMed Abstract | Publisher Full Text
7. Montgomery G, Abt G, Dobson C, et al.: The mechanical loading and muscle activation of four common exercises used in osteoporosis prevention for early postmenopausal women. J. Electromyogr. Kinesiol. 2019; 44: 124–131. PubMed Abstract | Publisher Full Text
8. Cífková R, Krajčoviechová A: Dyslipidemia and cardiovascular disease in women. Curr. Cardiol. Rep. 2015; 17: 609. Publisher Full Text
9. Knopp RH, Zhu X, Bonet B: Effects of estrogens on lipoprotein metabolism and cardiovascular disease in women. Atherosclerosis. 1994; 110(Suppl): S83–S91. Publisher Full Text
10. Barrett-Connor E: Menopause, atherosclerosis, and coronary artery disease. Curr. Opin. Pharmacol. 2013; 13: 186–191. PubMed Abstract | Publisher Full Text
11. Jeong IK, Cho SW, Kim SW, et al.: Lipid profiles and bone mineral density in pre- and postmenopausal women in Korea. Calcif. Tissue Int. 2010; 87: 507–512. PubMed Abstract | Publisher Full Text
12. Ko SH, Kim HS: Menopause-associated lipid metabolic disorders and foods beneficial for postmenopausal women. Nutrients. 2020; 12: 202. PubMed Abstract | Publisher Full Text
13. Andersen L, Ibarra J, Andersen R: Current familial hypercholesterolemia diagnostic criteria underdiagnose APOB mutations: lessons from the Amish community. J. Clin. Lipidol. 2016; 10: 443–444. PubMed Abstract | Publisher Full Text
14. Kemp JP, Morris JA, Medina-Gomez C, et al.: Identification of 153 new loci associated with heel bone mineral density and functional involvement of GPC6 in osteoporosis. Nat. Genet. 2017; 49: 1468–1475. PubMed Abstract | Publisher Full Text
15. Cui J, Shen Y, Li R: Estrogen synthesis and signaling pathways during aging: from periphery to brain. Trends Mol. Med. 2013; 19: 197–209. PubMed Abstract | Publisher Full Text
16. Japan Clinical Laboratory Standards Council: JCCLS Shared Reference Scope:2020.Reference Source
17. Kanazawa M, Yoshiike N, Osaka T, et al.: Criteria and classification of obesity in Japan and Asia-Oceania. World Rev. Nutr. Diet. 2005; 94: 1–12. PubMed Abstract | Publisher Full Text
18. Cheng S, Njeh CF, Fan B, et al.: Influence of region of interest and bone size on calcaneal BMD: implications for the accuracy of quantitative ultrasound assessments at the calcaneus. Br. J. Radiol. 2002; 75: 59–68. PubMed Abstract | Publisher Full Text
19. Greenspan SL, Bouxsein ML, Melton ME, et al.: Precision and discriminatory ability of calcaneal bone assessment technologies. J. Bone Miner. Res. 1997; 12: 1303–1313. PubMed Abstract | Publisher Full Text
20. Hans D, Dargent-Molina P, Schott AM, et al.: Ultrasonographic heel measurements to predict hip fracture in elderly women: the EPIDOS prospective study. Lancet. 1996; 348: 511–514. PubMed Abstract | Publisher Full Text
21. Sasaki M, Harata S, Kumazawa Y, et al.: Bone mineral density and osteo sono assessment index in adolescents. J. Orthop. Sci. 2000; 5: 185–191. PubMed Abstract | Publisher Full Text
22. Tsuda-Futami E, Hans D, Njeh CF, et al.: An evaluation of a new gel-coupled ultrasound device for the quantitative assessment of bone. Br. J. Radiol. 1999; 72: 691–700. PubMed Abstract | Publisher Full Text
23. Ohta T, Nagashima J, Sasai H, et al.: Relationship of cardiorespiratory fitness and body mass index with the incidence of dyslipidemia among Japanese women: a cohort study. Int. J. Environ. Res. Public Health. 2019; 16: 4647. PubMed Abstract | Publisher Full Text
24. Kanda Y: Investigation of the freely available easy-to-use software “EZR” for medical statistics. Bone Marrow Transplant. 2013; 48: 452–458. PubMed Abstract | Publisher Full Text
25. Kim CJ, Jang HC, Cho DH, et al.: Effects of hormone replacement therapy on lipoprotein(a) and lipids in postmenopausal women. Arterioscler. Thromb. 1994; 14: 275–281. Publisher Full Text
26. Mendelsohn ME, Karas RH: The protective effects of estrogen on the cardiovascular system. N. Engl. J. Med. 1999; 340: 1801–1811. Publisher Full Text
27. Yamaguchi T, Sugimoto T, Yano S, et al.: Plasma lipids and osteoporosis in postmenopausal women. Endocr. J. 2002; 49: 211–217. Publisher Full Text
28. Cook CJ, Crewther BT, Kilduff LP, et al.: Testosterone and dihydrotestosterone changes in male and female athletes relative to training status. Int. J. Sports Physiol. Perform. 2021; 16: 1700–1706. PubMed Abstract | Publisher Full Text
29. Snow-Harter C, Bouxsein M, Lewis B, et al.: Muscle strength as a predictor of bone mineral density in young women. J. Bone Miner. Res. 1990; 5: 589–595. PubMed Abstract | Publisher Full Text
30. Kumahara H, Schutz Y, Ayabe M, et al.: The use of uniaxial accelerometry for the assessment of physical-activity-related energy expenditure: a validation study against whole-body indirect calorimetry. Br. J. Nutr. 2004; 91: 235–243. Publisher Full Text
31. Licata AA: Diagnosing primary osteoporosis: it’s more than a T score. Cleve. Clin. J. Med. 2006; 73: 473–476. PubMed Abstract | Publisher Full Text
32. Park H, Togo F, Watanabe E, et al.: Relationship of bone health to yearlong physical activity in older Japanese adults: cross-sectional data from the Nakanojo study. Osteoporos. Int. 2007; 18: 285–293. PubMed Abstract | Publisher Full Text
33. Tanaka H, Monahan KD, Seals DR: Age-predicted maximal heart rate revisited. J. Am. Coll. Cardiol. 2001; 37: 153–156. PubMed Abstract | Publisher Full Text
34. Li GH, Cheung CL, Au PC, et al.: Positive effects of low LDL-C and statins on bone mineral density: an integrated epidemiological observation analysis and Mendelian randomization study. Int. J. Epidemiol. 2020; 49: 1221–1235. Publisher Full Text
35. Kuipers AL, Miljkovic I, Evans R, et al.: Optimal serum cholesterol concentrations are associated with accelerated bone loss in African ancestry men. Osteoporos. Int. 2016; 27: 1577–1584. PubMed Abstract | Publisher Full Text
36. Martín-González C, González-Reimers E, Quintero-Platt G, et al.: Lipid profile and bone mineral density in heavy alcoholics. Clin. Nutr. 2018; 37: 2137–2143. PubMed Abstract | Publisher Full Text
37. Li S, Guo H, Liu Y, et al.: Relationships of serum lipid profiles and bone mineral density in postmenopausal Chinese women. Clin. Endocrinol. 2015; 82: 53–58. PubMed Abstract | Publisher Full Text
38. Alay I, Kaya C, Cengiz H, et al.: The relation of body mass index, menopausal symptoms, and lipid profile with bone mineral density in postmenopausal women. Taiwan. J. Obstet. Gynecol. 2020; 59: 61–66. PubMed Abstract | Publisher Full Text
39. Garg MK, Marwaha RK, Tandon N, et al.: Relationship of lipid parameters with bone mineral density in Indian population. Indian J. Endocrinol. Metab. 2014; 18: 325–332. PubMed Abstract | Publisher Full Text
40. Keyhani D, Tartibian B, Dabiri A, et al.: Effect of high-intensity interval training versus moderate-intensity aerobic continuous training on galectin-3 gene expression in postmenopausal women: a randomized controlled trial. J. Aging Phys. Act. 2020; 1–9: 1–9. PubMed Abstract | Publisher Full Text

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 19 Oct 2022

Author details Author details

¹ Laboratory of Health Dynamics, Graduate School of Arts and Sciences, The University of Tokyo, Tokyo, 153-8902, Japan
² Yokohama Sports Medical Center, Yokohama, 222-0036, Japan
³ Faculty of Bioscience and Applied Chemistry, Hosei University, Tokyo, 184-8584, Japan
⁴ Laboratory of Physical Chemistry, Faculty of Pharma-Science, Teikyo University, Tokyo, 173-8605, Japan

Kazuto Mitsuhashi
Roles: Conceptualization, Data Curation, Formal Analysis, Investigation, Project Administration, Resources, Supervision, Writing – Original Draft Preparation, Writing – Review & Editing

Yasunori Imagawa
Roles: Data Curation, Methodology, Resources, Validation

Yuta Kojima
Roles: Investigation, Resources, Validation

Naokata Ishii
Roles: Funding Acquisition, Investigation, Project Administration, Resources, Supervision, Writing – Review & Editing

Yasushi Kishimoto
Roles: Data Curation, Formal Analysis, Funding Acquisition, Project Administration, Software, Supervision, Validation, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

This study was supported by the Grant-in-Aid for Scientific Research to
N.I. (grant number: 19H01085) and Y.K.(grant number : 22K06618 and 19K07337 ) from KAKENHI

The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (1)

version 1

Published: 19 Oct 2022, 11:1196

https://doi.org/10.12688/f1000research.126008.1

Copyright

© 2022 Mitsuhashi K et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

Mitsuhashi K, Imagawa Y, Kojima Y et al. Chemical equilibrium model comprising calcaneus bone mineral density, low-density lipoprotein cholesterol, and physical work capacity in premenopausal women [version 1; peer review: awaiting peer review]. F1000Research 2022, 11:1196 (https://doi.org/10.12688/f1000research.126008.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Peer review discontinued

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 19 Oct 2022

Peer review discontinued

At the request of the author(s), this article is no longer under peer review.

What does this mean?

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

[1] 1. McKinlay S, Jefferys M, Thompson B: An investigation of the age at menopause. J. Biosoc. Sci. 1972; 4: 161–173. Publisher Full Text

[2] 2. Zhu D, Chung HF, Dobson AJ, et al.: Type of menopause, age of menopause and variations in the risk of incident cardiovascular disease: pooled analysis of individual data from 10 international studies. Hum. Reprod. 2020; 35: 1933–1943. PubMed Abstract | Publisher Full Text

[3] 3. Kalervo Väänänen HK, Härkönen PL: Estrogen and bone metabolism. Maturitas. 1996; 23(Suppl): S65–S69. Publisher Full Text

[4] 4. Ryu KJ, Park H, Kim YJ, et al.: Comparison of various menopausal symptoms and risk factor analysis in Korean women according to stage of menopause. Maturitas. 2020; 140: 41–48. PubMed Abstract | Publisher Full Text

[5] 5. Dobbs MB, Buckwalter J, Saltzman C: Osteoporosis: the increasing role of the orthopaedist. Iowa Orthop. J. 1999; 19: 43–52. PubMed Abstract

[6] 6. Pai MV: Osteoporosis prevention and management. J. Obstet. Gynaecol. India. 2017; 67: 237–242. PubMed Abstract | Publisher Full Text

[7] 7. Montgomery G, Abt G, Dobson C, et al.: The mechanical loading and muscle activation of four common exercises used in osteoporosis prevention for early postmenopausal women. J. Electromyogr. Kinesiol. 2019; 44: 124–131. PubMed Abstract | Publisher Full Text

[8] 8. Cífková R, Krajčoviechová A: Dyslipidemia and cardiovascular disease in women. Curr. Cardiol. Rep. 2015; 17: 609. Publisher Full Text

[9] 9. Knopp RH, Zhu X, Bonet B: Effects of estrogens on lipoprotein metabolism and cardiovascular disease in women. Atherosclerosis. 1994; 110(Suppl): S83–S91. Publisher Full Text

[10] 10. Barrett-Connor E: Menopause, atherosclerosis, and coronary artery disease. Curr. Opin. Pharmacol. 2013; 13: 186–191. PubMed Abstract | Publisher Full Text

[11] 11. Jeong IK, Cho SW, Kim SW, et al.: Lipid profiles and bone mineral density in pre- and postmenopausal women in Korea. Calcif. Tissue Int. 2010; 87: 507–512. PubMed Abstract | Publisher Full Text

[12] 12. Ko SH, Kim HS: Menopause-associated lipid metabolic disorders and foods beneficial for postmenopausal women. Nutrients. 2020; 12: 202. PubMed Abstract | Publisher Full Text

[13] 13. Andersen L, Ibarra J, Andersen R: Current familial hypercholesterolemia diagnostic criteria underdiagnose APOB mutations: lessons from the Amish community. J. Clin. Lipidol. 2016; 10: 443–444. PubMed Abstract | Publisher Full Text

[14] 14. Kemp JP, Morris JA, Medina-Gomez C, et al.: Identification of 153 new loci associated with heel bone mineral density and functional involvement of GPC6 in osteoporosis. Nat. Genet. 2017; 49: 1468–1475. PubMed Abstract | Publisher Full Text

[15] 15. Cui J, Shen Y, Li R: Estrogen synthesis and signaling pathways during aging: from periphery to brain. Trends Mol. Med. 2013; 19: 197–209. PubMed Abstract | Publisher Full Text

[16] 16. Japan Clinical Laboratory Standards Council: JCCLS Shared Reference Scope:2020.Reference Source

[17] 17. Kanazawa M, Yoshiike N, Osaka T, et al.: Criteria and classification of obesity in Japan and Asia-Oceania. World Rev. Nutr. Diet. 2005; 94: 1–12. PubMed Abstract | Publisher Full Text

[18] 18. Cheng S, Njeh CF, Fan B, et al.: Influence of region of interest and bone size on calcaneal BMD: implications for the accuracy of quantitative ultrasound assessments at the calcaneus. Br. J. Radiol. 2002; 75: 59–68. PubMed Abstract | Publisher Full Text

[19] 19. Greenspan SL, Bouxsein ML, Melton ME, et al.: Precision and discriminatory ability of calcaneal bone assessment technologies. J. Bone Miner. Res. 1997; 12: 1303–1313. PubMed Abstract | Publisher Full Text

[20] 20. Hans D, Dargent-Molina P, Schott AM, et al.: Ultrasonographic heel measurements to predict hip fracture in elderly women: the EPIDOS prospective study. Lancet. 1996; 348: 511–514. PubMed Abstract | Publisher Full Text

[21] 21. Sasaki M, Harata S, Kumazawa Y, et al.: Bone mineral density and osteo sono assessment index in adolescents. J. Orthop. Sci. 2000; 5: 185–191. PubMed Abstract | Publisher Full Text

[22] 22. Tsuda-Futami E, Hans D, Njeh CF, et al.: An evaluation of a new gel-coupled ultrasound device for the quantitative assessment of bone. Br. J. Radiol. 1999; 72: 691–700. PubMed Abstract | Publisher Full Text

[23] 23. Ohta T, Nagashima J, Sasai H, et al.: Relationship of cardiorespiratory fitness and body mass index with the incidence of dyslipidemia among Japanese women: a cohort study. Int. J. Environ. Res. Public Health. 2019; 16: 4647. PubMed Abstract | Publisher Full Text

[24] 24. Kanda Y: Investigation of the freely available easy-to-use software “EZR” for medical statistics. Bone Marrow Transplant. 2013; 48: 452–458. PubMed Abstract | Publisher Full Text

[25] 25. Kim CJ, Jang HC, Cho DH, et al.: Effects of hormone replacement therapy on lipoprotein(a) and lipids in postmenopausal women. Arterioscler. Thromb. 1994; 14: 275–281. Publisher Full Text

[26] 26. Mendelsohn ME, Karas RH: The protective effects of estrogen on the cardiovascular system. N. Engl. J. Med. 1999; 340: 1801–1811. Publisher Full Text

[27] 27. Yamaguchi T, Sugimoto T, Yano S, et al.: Plasma lipids and osteoporosis in postmenopausal women. Endocr. J. 2002; 49: 211–217. Publisher Full Text

[28] 28. Cook CJ, Crewther BT, Kilduff LP, et al.: Testosterone and dihydrotestosterone changes in male and female athletes relative to training status. Int. J. Sports Physiol. Perform. 2021; 16: 1700–1706. PubMed Abstract | Publisher Full Text

[29] 29. Snow-Harter C, Bouxsein M, Lewis B, et al.: Muscle strength as a predictor of bone mineral density in young women. J. Bone Miner. Res. 1990; 5: 589–595. PubMed Abstract | Publisher Full Text

[30] 30. Kumahara H, Schutz Y, Ayabe M, et al.: The use of uniaxial accelerometry for the assessment of physical-activity-related energy expenditure: a validation study against whole-body indirect calorimetry. Br. J. Nutr. 2004; 91: 235–243. Publisher Full Text

[31] 31. Licata AA: Diagnosing primary osteoporosis: it’s more than a T score. Cleve. Clin. J. Med. 2006; 73: 473–476. PubMed Abstract | Publisher Full Text

[32] 32. Park H, Togo F, Watanabe E, et al.: Relationship of bone health to yearlong physical activity in older Japanese adults: cross-sectional data from the Nakanojo study. Osteoporos. Int. 2007; 18: 285–293. PubMed Abstract | Publisher Full Text

[33] 33. Tanaka H, Monahan KD, Seals DR: Age-predicted maximal heart rate revisited. J. Am. Coll. Cardiol. 2001; 37: 153–156. PubMed Abstract | Publisher Full Text

[34] 34. Li GH, Cheung CL, Au PC, et al.: Positive effects of low LDL-C and statins on bone mineral density: an integrated epidemiological observation analysis and Mendelian randomization study. Int. J. Epidemiol. 2020; 49: 1221–1235. Publisher Full Text

[35] 35. Kuipers AL, Miljkovic I, Evans R, et al.: Optimal serum cholesterol concentrations are associated with accelerated bone loss in African ancestry men. Osteoporos. Int. 2016; 27: 1577–1584. PubMed Abstract | Publisher Full Text

[36] 36. Martín-González C, González-Reimers E, Quintero-Platt G, et al.: Lipid profile and bone mineral density in heavy alcoholics. Clin. Nutr. 2018; 37: 2137–2143. PubMed Abstract | Publisher Full Text

[37] 37. Li S, Guo H, Liu Y, et al.: Relationships of serum lipid profiles and bone mineral density in postmenopausal Chinese women. Clin. Endocrinol. 2015; 82: 53–58. PubMed Abstract | Publisher Full Text

[38] 38. Alay I, Kaya C, Cengiz H, et al.: The relation of body mass index, menopausal symptoms, and lipid profile with bone mineral density in postmenopausal women. Taiwan. J. Obstet. Gynecol. 2020; 59: 61–66. PubMed Abstract | Publisher Full Text

[39] 39. Garg MK, Marwaha RK, Tandon N, et al.: Relationship of lipid parameters with bone mineral density in Indian population. Indian J. Endocrinol. Metab. 2014; 18: 325–332. PubMed Abstract | Publisher Full Text

[40] 40. Keyhani D, Tartibian B, Dabiri A, et al.: Effect of high-intensity interval training versus moderate-intensity aerobic continuous training on galectin-3 gene expression in postmenopausal women: a randomized controlled trial. J. Aging Phys. Act. 2020; 1–9: 1–9. PubMed Abstract | Publisher Full Text

Chemical equilibrium model comprising calcaneus bone mineral density, low-density lipoprotein cholesterol, and physical work capacity in premenopausal women

Abstract

Keywords

Introduction

Methods

Participants and data collection

Quantification of bone strength

Medical examination

Physical exercise stress test

Statistical analysis

Results

Introducing deviation

Equilibrium migration hypothesis between LDL-C, OSI, and PWC

Figure 1. Schematic representation of the chemical equilibrium model for LDL-C, OSI, and PWC.

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

Relative relationship of the three variables with respect to one variable

(9)

(10)

(11)

(12)

(13)

(14)

Application of the theoretical equilibrium equation to real world data

Table 1. Summary of the SPS data analyzed in the present study.

(15)

Figure 2. Relative relationships among ln (dev. OSI), ln (dev. PWC), and ln (dev. LDL-C) are shown.

(16)

(17)

The robustness of the equilibrium constant K

Robustness of the equilibrium constant K against fluctuations in PWC

Figure 3. Robustness of the equilibrium constant K against fluctuations in PWC, LDL-C, and OSI is shown.

Robustness of the equilibrium constant K against fluctuations in LDL-C

Robustness of the equilibrium constant K against fluctuations in OSI

Discussion

Conclusions

Data availability

Acknowledgments

References

Comments on this article Comments (0)

Peer review discontinued

Comments on this article Comments (0)

Peer review discontinued

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated