Keywords
grant scoring, multiple threshold model, grant quality, grant ranking
This article is included in the Research on Research, Policy & Culture gateway.
This article is included in the Meta-research and Peer Review collection.
grant scoring, multiple threshold model, grant quality, grant ranking
We have revised the manuscript taking helpful comments and suggestions from two reviewers into account, as detailed in our response to those reviewers, which can be found on the F1000 website. In particular:
(1). We have expanded the Introduction by including a new opening paragraph that places our study in context and cites relevant literature. We have also a new paragraph that states the motivation of our study. In total, we cite seven additional papers.
(2). We have made minor changes to the Methods section to explain how our parameterisation is related to single-rater reliability and to the Spearman-Brown equation for the reliability based upon multiple raters, and have specified how quantities of the normal distribution are computed in the statistical package R. We have defined the correlation on the underlying and observed scoring scales. We have clarified that for our theoretical calculations, the variance due to assessor (as a random effect) is also noise.
(3). We have added three new paragraphs in the Discussion about our assumptions of normality and how non-normally distributed scores, which are theoretically less tractable, could be investigated. We have added discussion on why assessors do not always score the same even if the category descriptors are well-defined and given examples. We have added a paragraph that the difference between Pearson and Spearman (rank) correlation will not change the conclusions from our study. We end with a take-home message concluding paragraph.
(4). We have updated our R script, added more comments to the code and expanded the Readme file. The github link remains unchanged but the updated version of the Zenodo link is available at https://doi.org/10.5281/zenodo.7519164
See the authors' detailed response to the review by Alejandra Recio-Saucedo
See the authors' detailed response to the review by Rachel Heyard
The peer review process for grant proposals is bureaucratic, costly and unreliable (Independent Review of Research Bureaucracy Interim Report, 2022; Guthrie et al., 2013, 2018). Empirical analyses on grant scoring shows that single-rater reliability is typically in the range of 0.2 to 0.5 (Marsh et al., 2008; Guthrie et al., 2018). For example, in a recent study of preliminary overall scores from 7,471 review on 2,566 grant applications from the National Institutes of Health (NIH), the authors used a mixed effects model to estimate fixed effects and variance components (Erosheva et al., 2020). From their results (model 1, Table 4), the proportion of total variance that is attributed to PI (Principal Investigator) was 0.27. This metric is also an estimate of the single-rater reliability and is consistent with the range reported in the literature (Marsh et al., 2008; Guthrie et al., 2018). Improvements in reliability of grant scoring are desirable because funding decisions are based upon the ranking of grant proposals.
Grant funding bodies use different ways to obtain a final ranking of grant proposals. The number of items that are scored can vary, as well as the scale on which each item is scored and the weighting scheme to combine the individual items scores into a single overall score. In attempts to decrease bureaucracy or increase efficiency and reliability, grant funding bodies can make changes to the peer review process (Guthrie et al., 2013). One such change is the way assessors score items or overall scores of individual grant proposals. In our study we address one particular element of grant scoring, which is the scale of scoring. Our motivation is that any change in the scale of scoring should be evidence-based and that changes to grant scores that are not evidence-based can increase bureaucracy without improving outcomes.
Scoring scales differ widely among grant funding bodies. For example, in Australia, the National Health and Medical Research Council (NHMRC) uses a scale of 1-7 whereas the Australian Research Council (ARC) uses 1-5 (A:E), and other funding bodies use scales such as 1-10. One question for the funding bodies, grant applicants and grant assessors is whether using a different scale would lead to more accurate outcomes. For example, if the NHMRC would allow half-scores (e.g., 5.5), expanding the scale to 13 categories (1, 1.5, …, 6.5, 7), or the ARC would expand to 1-10, then might that lead to a better ranking of grants? This is the question we address in this note. Specially, we address two questions that are relevant for grant scoring: (1) how much information is lost when scoring in discrete categories compared to scoring on a scale that is continuous; and (2) what is the effect of the scale of scoring on the accuracy of the ranking of grants?
To quantify the effect of grant scoring scale on scoring accuracy, a model of the unknown true distribution of grant quality has to be assumed, as well as the distribution of errors in scoring the quality of a grant. We assume a simple model where an unobserved underlying score (u) is continuous (so no discrete categories) and the error (e) is randomly distributed around the true quality (q) of the grant and that there is no correlation between the true quality of the grant and the error,
with ui the score of grant i on the underlying continuous scale, qi its quality value on that scale and ei a random deviation (error). Furthermore, we assume that q and e are normally distributed around zero and, without losing generality, that the variance of u is 1. Hence, σ2u = σ2q + σ2e = 1. We denote the signal-to-noise ratio as s = σ2q/ (σ2q + σ2e), which is a value between zero and one. This parameter is sometimes called the single-rater reliability (e.g., Marsh et al., 2008). Note that adding a mean to model and/or changing the total variance of u will not change subsequent results. This continuous scale is never observed unless the scoring system would allow full continuous scoring. A close approximation of this scale would be if the scoring scale were to be continuous in the range of, for example, 1-100. In summary, we propose a simple signal (q) + noise (e) model on an underlying scale which is continuous. Note that in principle this model could be extended by adding a random effect for assessor (e.g., Erosheva et al., 2020), but that for our model derivations and results the variance due to assessor would also appears as noise.We now define the way in which the grants are actually scored by assessors. Assume that there are k mutually exclusive categories (e.g., k = 7) which correspond to (k-1) fixed thresholds on the underlying scale and k discontinuities on the observed (Y) scale. We also assume that the scores on the Y-scale are linear and symmetrically distributed, so for an even number of categories, there will be a threshold on the u-scale located at zero (formally, if there are k categories then threshold tk/2 = 0). This is an example of a multiple threshold model. In the extreme case of k = 2 (assessors can only score 1 or 2), the threshold on the underlying u-scale is 0 and when u < 0 then the observed score Y = 1 and when u > 0 then the observed score Y = 2. The mean on the observed scale in this model is simply (k + 1)/2.
In summary, we assume that the actual observed score is a response in one of several mutually exclusive categories (1, 2, …, k), which arise from an unobserved underlying continuous scale. For a given number of categories (k), the (k-1) thresholds were determined numerically to maximise the correlation between the observed Y-scale and the unobserved continuous u-scale, while fixing the inter-threshold spacing on the u-scale to be constant. Per definition, this correlation is equal to cov(u,Y)/√(var(u)var(Y)), where both the covariance and the variance of Y depend on the position of the thresholds. Fixing the inter-threshold spacing ensures symmetry on the observed Y-scale and appears to be the optimal solution in that it gave identical results to a general optimisation of the thresholds (results not shown). Figure 1 gives a schematic for k = 5. To get the thresholds requires a numerical optimisation, which was done through a purpose-written program using the statistical software package R version 4.2.0 (see Software availability section). The question on the loss of information by using a finite versus continuous (infinite) scoring scale was addressed by calculating the correlation between Y (observed) and u (continuous) with increasing values of k from 1 to 100. For a given set of thresholds ti and assuming that the variance on the underlying scale (u) is 1, this correlation (Rk) was calculated as,
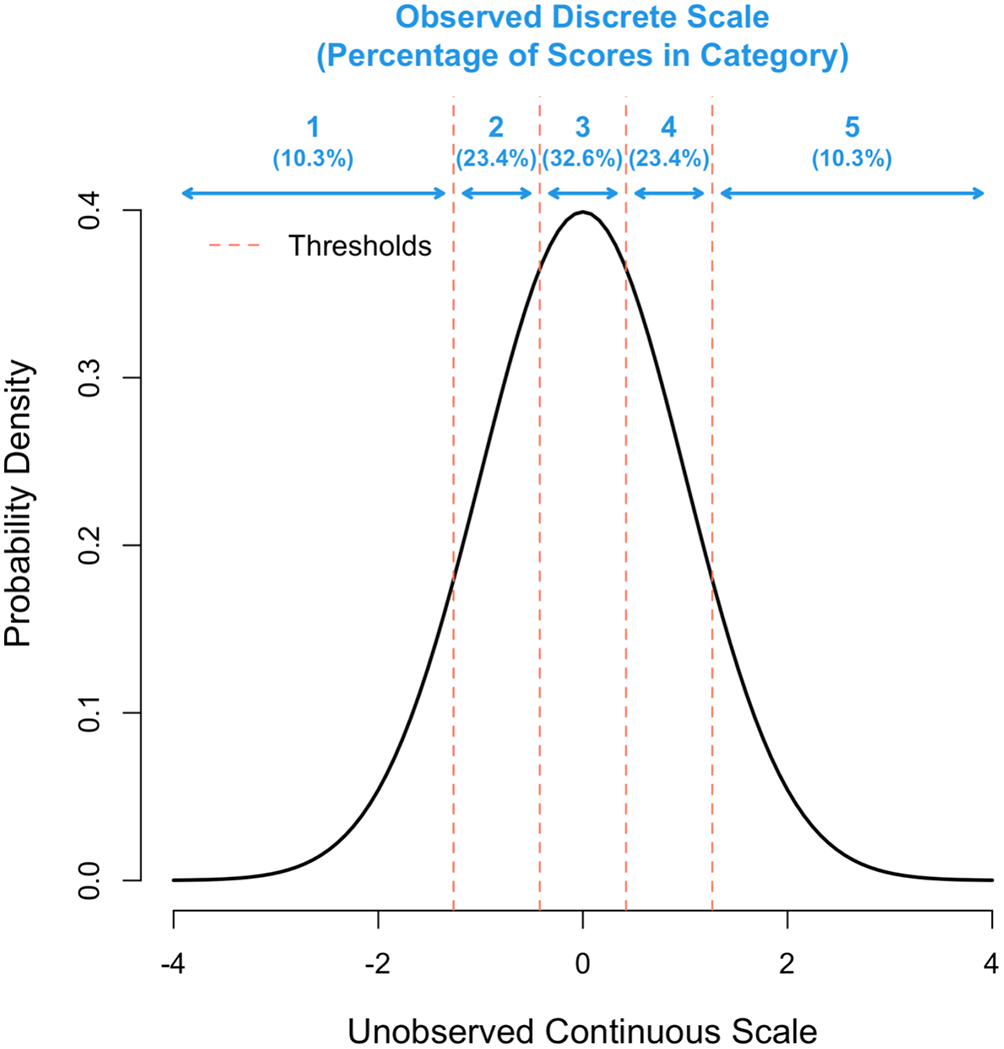
The x-axis shows the unobserved continuous scale in standard deviation units and the y-axis the density. The position of each of the 4 thresholds is shown as a vertical red line.
The expression for the correlation between the observed and underlying scale under the multiple threshold model is known from the genetics literature (Gianola, 1979). The square of the correlation in Equation [1] is the proportion of variation on the continuous scale that is captured by the discrete scale. For k = 2, t1 = 0, z1 = 0.3989, p1 = p2 = ½, Y1 = 1 and Y2 = 2, giving var(Y) = ¼ and R2 ~ √0.637 = 0.798. This is a known result for a threshold model with two equal categories, where the binary scale captures 63.7% of the variation on the continuous scale (Dempster and Lerner, 1950).
To address the question on the effect of scoring on the ranking of grants we need to estimate the signal-to-noise ratio of the Y-scale and u-scale. Thresholds models with two random effects on the underlying scale have been studied in the genetic literature (e.g., Dempster and Lerner, 1950; Gianola, 1979; Gianola and Norton, 1981). Gianola (1979) also deals with the case where the errors (e) are exponentially distributed, but this distribution was not considered here.
When the observed scores are 1, 2, …, k, Gianola (1979) showed that the ratio of signal-to-noise on the observed Y-scale and unobserved u-scale is Rk2, the square of the correlation in Equation [1]. Therefore, the ratio of signal-to-noise parameters (Rk2) does not depend on the signal-to-noise value on the underlying scale (s) itself. However, the effect of scaling on the ranking of grants does depend on the signal-to-ratio effects, and to address this question we need to also specify the number of assessors (m). Given m (e.g., m = 4, 5, 6), the correlation (Corr) between the true score of a grant (qi) and the mean score from m assessors on the u-scale or Y-scale can be shown to be,
On the continuous (u) scale, the square of this correlation is also known as the reliability of the mean rating from m raters (assessors) and can be calculated from the single-rater reliability using the equivalent Spearman-Brown equation (Marsh et al., 2008).
Finally, we can express the loss of information in ranking grants when m assessor score on the Y-scale instead of on the continuous scale as,
Equations [1] and [3] can also be used to compare different values for k against each other. For example k = 7 versus k = 13 can be compared by calculating R7/R13 and L(m,13,s)/L(m,7,s).
Grant assessors might not use the entire scale that is available to them or score too few grants in the extreme categories (categories 1 and k, respectively). The effect of such a scoring approach is to change the proportions in each of the k categories and thereby change the variance on the Y-scale and the covariance between the u and Y variables. These changes lead to a lower correlation between Y and u than given by Equation [1] and, consequently, reduce the ranking accuracy of grants. We simulated this scenario by using the same model as before, but now assuming that the proportions of scores in each category follow from a normal distribution with smaller variance (σ2us) than the variance of 1 which is assumed to be the true unobserved variance (when σ2us = σ2u = 1). When σ2us < 1, this model leads to more scores around the mean and fewer in the tails (the lowest and highest category).
We first quantify the correlation between the observed categorical score (Y) and the underlying continuous score (u), as a function of the number of categories. Figure 2 shows the results from Equation [1], for k = 2 to 100. It shows there is very little loss of information when the number of categories is five or more. For example, the correlation is 0.958, 0.976, 0.987 and 0.992, for k = 5, 7, 10 and 13, respectively. The association between the correlation and the number of categories can be approximated by the simple equation, R(k) ≈ 1 – 0.7k-1.7, which fits almost perfectly.
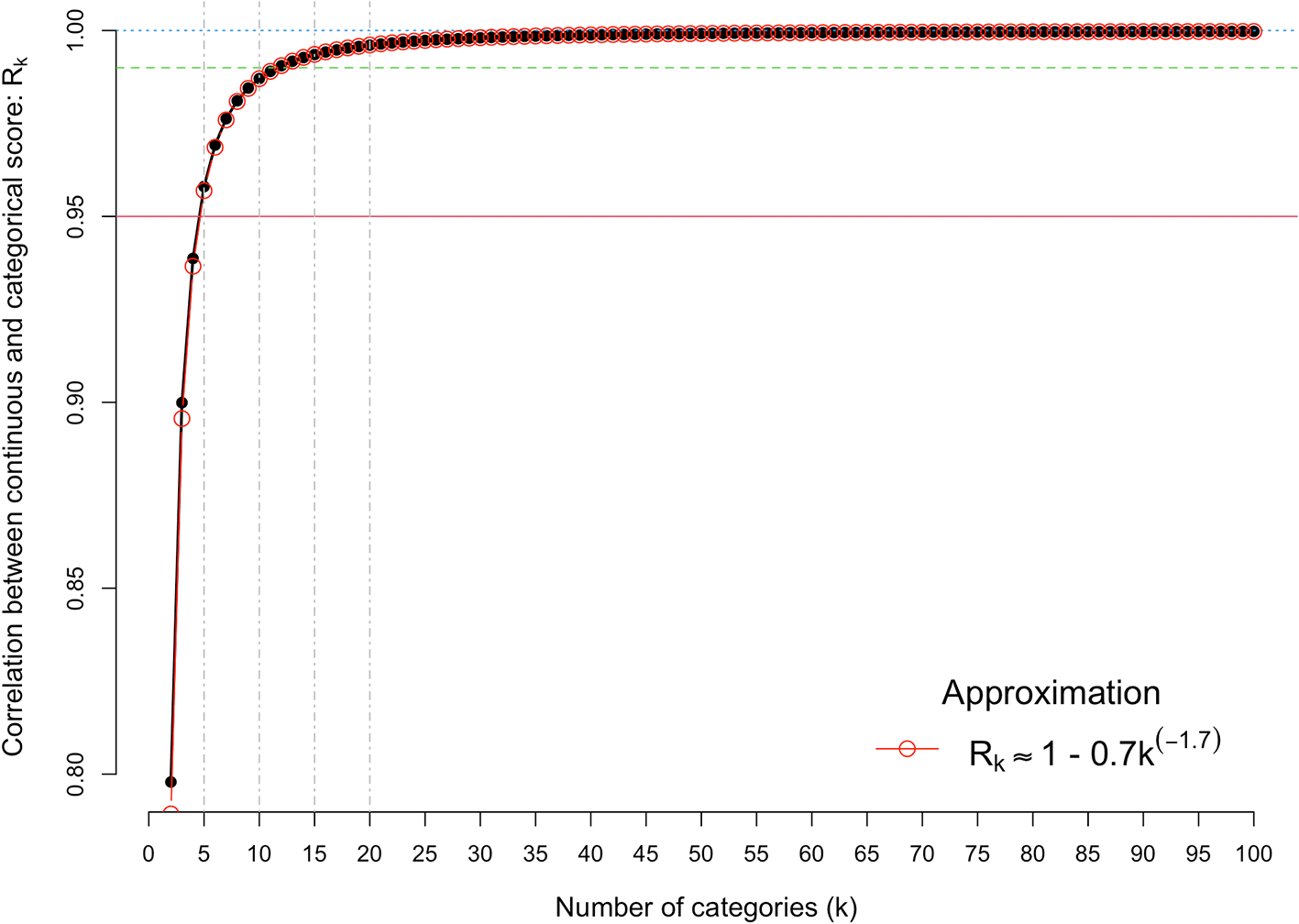
The x-axis is the number of discrete categorical scores (k) and the y-axis shows the correlation between the observed categorical score (Y) and the underlying continuous score (u). The red horizontal line denotes a correlation of 0.95.
Given the correlations in Figure 2 we calculated the correlation between the true quality of a grant (q) and the mean score on the categorical scale from m assessors. Figure 3 shows the results from Equation [3], for m = 3,4,5,6; k = 5,7,10,13; and s from 0.1 to 0.9. It shows that that loss of information on the correlation between true quality of the grant and its mean assessor score is very small – typically 2% or less.
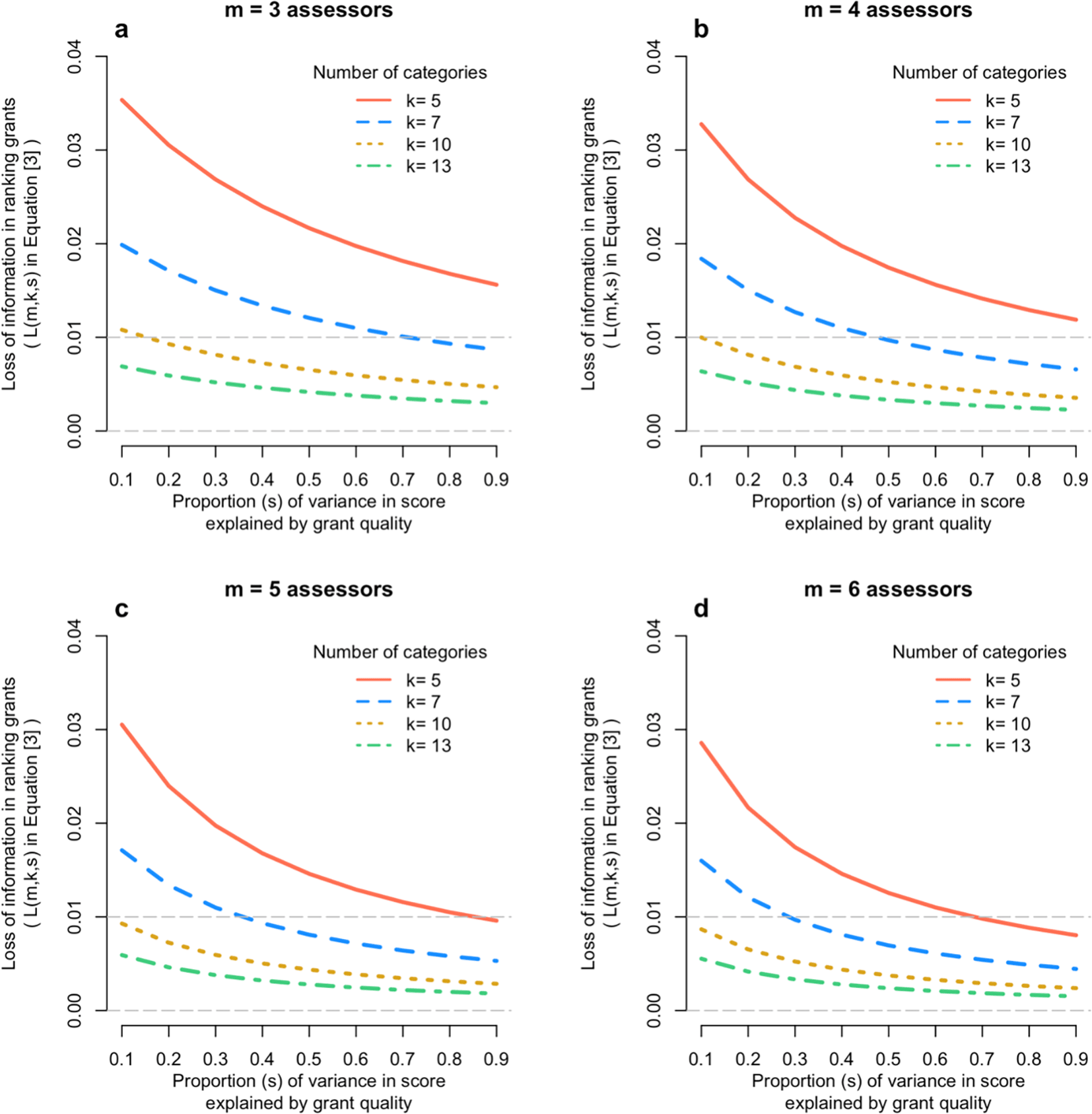
Each panel shows the loss of information (Equation [3]) when scoring a finite number of categories relative to the continuous score, as a function of the number of assessors (panels a to d) and the proportion of variation in scores due to the quality of the grant (x-axis).
We next explored the scenario where grant assessors do not sufficiently use the entire scale available to them, by simulating σ2us < 1, which leads to a deficiency of scores in the tails of the distribution. For example, the proportion of scores for k = 5 in categories 1-5 (Figure 1) are 10.3%, 23.4%, 32.6%, 23.4% and 10.3%, respectively, when the distribution underlying scores has a variance of σ2us = 1, but 3.7%, 23.9%, 44.8%, 23.9% and 3.7% when that variance is σ2us = 0.5. In this extreme scenario, the proportions in the tails are nearly 3-fold (10.3/3.7) lower than they should be yet decreasing σ2us from 1 to 0.5 induces only a small reduction of Rk from 0.958 to 0.944. Figure 4 shows Rk for a scoring scale with 2 to 10 categories when the variance of underlying distribution is σ2us = 0.5, 0.75 or 1.
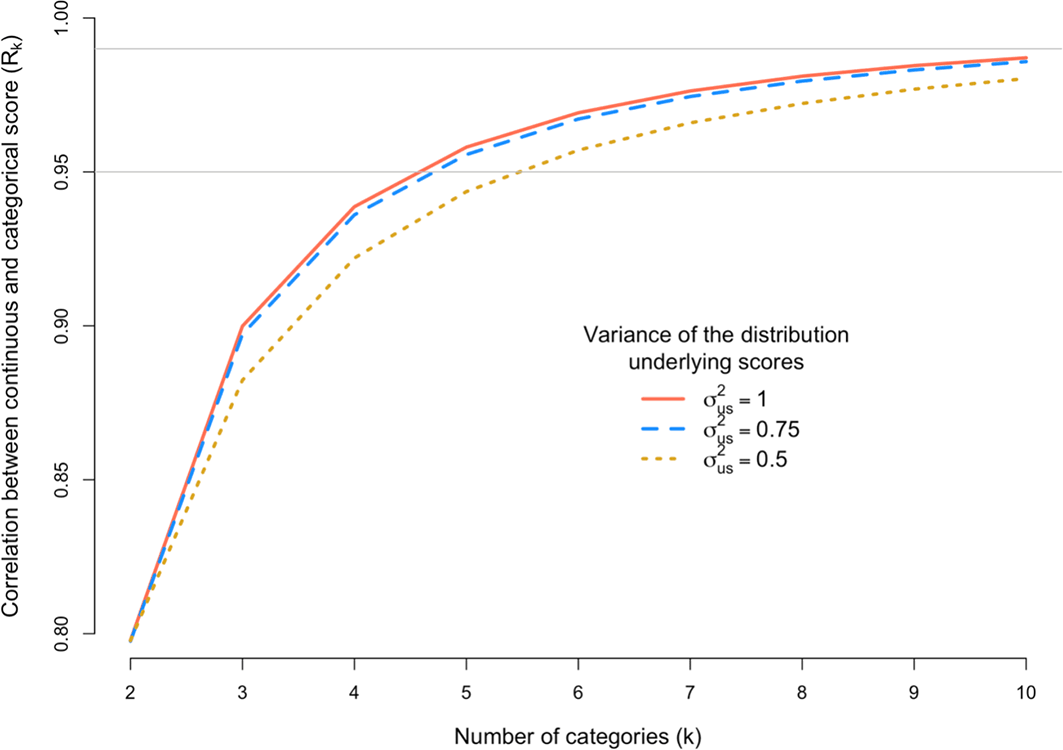
The x-axis is the number of discrete categorical scores (k) and the y-axis shows the correlation (Rk) between the observed categorical score (Y) and the underlying continuous score (u). The correlation Rk is calculated under three scenarios defined by the variance (σ2s) of the distribution of underlying scores. The grey horizontal line denotes a correlation of 0.95 or 0.99.
It is known from the grant peer review literature that scoring reliability is low (Marsh et al., 2008; Guthrie et al., 2018) and, therefore that the precision of estimating the “true” value of a grant proposal is low unless a very large number of assessors are used (Kaplan et al., 2008). Training researchers in scoring grants may improve accuracy (Sattler et al., 2015) but there will always be variation between assessors. For example, the Australian NHMRC has multiple pages of detailed category descriptors, yet assessors do not always agree. One source of variability is the discrete scale of scoring. If the true value of a grant proposal is, say, 5.5 on a 1-7 integer scale then some assessors may score a 5 while others may score a 6. Other sources of differences between assessors could involve genuine subjective differences in opinion about the “significance” and “innovation” of a proposal. To avoid the aforementioned hypothetical situation of the true value being midway between discrete scores one could change the scale.
Intuitively one might think that scoring with a broader scale is always better, but the results herein show that this can be misleading. Above k = 5 categories there is a very small gain in the signal-to-noise ratio compared to a fully continuous scale, and the effect on the accuracy of the ranking of grants is even smaller.
Comparing k = 5 with k = 10 categories and k = 7 with k = 13 categories shows a theoretical gain of 3% (0.987/0.958) and 1.6% (0.992/0.976) in the correlation between observed and continuous scales (Figure 2). These very small gains predicted by doubling the number of categories scored will have to be balanced with the cost of changing the grant scoring systems.
The effect of ranking grants on their quality is even smaller. Figure 3 shows that, for most existing Australian grant scoring schemes, the loss in accuracy of scoring a grant using discrete categories compared to a truly continuous scale is trivial – nearly always less than 1%. As shown in the methods section, the squared correlation between the true quality of a grant and the average score from m assessors is m/(m + λY), with λY = (1-Rk2s)/(Rk2s). Since Rk2 is close to 1 (Figure 2), the squared correlation is approximately equal to m/[m + (1-s)/s], which is the reliability based upon m assessors and equivalent to the Spearman-Brown equation. Therefore, even if the signal-to-noise ratio parameter s is as low as, say, 1/3, the squared correlation between the true quality and the mean assessor score is m/(m + 2), or 3/5, 2/3 and 5/7 for m = 3, 4 and 5, respectively, hence correlations ranging from 0.77 to 0.85.
The results in Figure 4 are to mimic a situation where assessors score too closely to the mean. As expected, Rk decreases when fewer grants are scored in the tails of the distribution of categories. However, the loss of information is generally very small. For example, for k = 7 and the most extreme case considered (σ2us = 0.5), Rk = 0.966, which is only slightly lower than 0.976, which is the correlation when the distribution of assessor scores is consistent with the underlying true distribution with variance of 1.
We have necessarily made a number of simplifying assumptions, but they could be relaxed in principle, for example different statistical distributions of the quality of the grant and the errors could be used, including distributions that are skewed. We have also assumed no systematic bias in scorers so that the true quality value of a grant on the observed scale is the mean value from a very large number of independent scorers. Departures from these assumptions will require additional assumptions and more parameters to model and will require extensive computer simulations because the results won’t be as theoretically tractable and generalisable as herein. However, assuming a multiple threshold model with normally distributed random effects on an underlying scale is simple and flexible and likely both robust and sufficient to address questions of the scale of grant scoring.
Throughout this study we have used the Pearson correlation to quantify the correlation between the score on the underlying and observed scales. We could also have used the Spearman rank correlation, but the conclusions would not change. In fact, the Spearman rank correlations are even larger than the Pearson correlations and they converge at k = 10 categories (results not shown).
The main take-home message from our study for grant funding agencies is to consider changing the scoring scale only when there is strong evidence to support it. Unnecessary changes will increase bureaucracy and cost. From the empirical literature it seems clear that the main source of variation in grant scoring is due to measurement error (noise) and that reliability is best improved by increasing the number of assessors.
The data underlying Figures 1-3 are generated automatically by the provided R scripts.
Source code available from: https://github.com/loic-yengo/GrantSCoring_Figures
Archived source code at the time of publication: https://doi.org/10.5281/zenodo.7519164
License: Creative Commons Attribution 4.0 International license (CC-BY 4.0).
The authors would like to thank Adrian Barnett for helpful discussions and for the prompt.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Statistics, Grant peer review, Research evaluation
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Research on Research; Health services delivery research
Is the rationale for developing the new method (or application) clearly explained?
Partly
Is the description of the method technically sound?
Yes
Are sufficient details provided to allow replication of the method development and its use by others?
Yes
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?
Yes
References
1. Kaplan D, Lacetera N, Kaplan C: Sample size and precision in NIH peer review.PLoS One. 2008; 3 (7): e2761 PubMed Abstract | Publisher Full TextCompeting Interests: No competing interests were disclosed.
Reviewer Expertise: Research on Research; Health services delivery research
Is the rationale for developing the new method (or application) clearly explained?
Partly
Is the description of the method technically sound?
Yes
Are sufficient details provided to allow replication of the method development and its use by others?
Partly
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?
Yes
References
1. Erosheva EA, Grant S, Chen MC, Lindner MD, et al.: NIH peer review: Criterion scores completely account for racial disparities in overall impact scores.Sci Adv. 6 (23): eaaz4868 PubMed Abstract | Publisher Full TextCompeting Interests: No competing interests were disclosed.
Reviewer Expertise: Statistics, Grant peer review, Research evaluation
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 2 (revision) 06 Feb 23 |
read | read |
|
Version 1 19 Oct 22 |
read | read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)