The odd log-logistic generalized exponential distribution: Application on survival times of chemotherapy patients data

Arnold K. Fulment; Srinivasa Rao Gadde; Josephat K. Peter

doi:10.12688/f1000research.127363.3

Home Browse The odd log-logistic generalized exponential distribution: Application...

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Revised

The odd log-logistic generalized exponential distribution: Application on survival times of chemotherapy patients data

[version 3; peer review: 2 approved]

Arnold K. Fulment¹, Srinivasa Rao Gadde ¹, Josephat K. Peter¹

PUBLISHED 21 Nov 2023

Author details Author details

¹ Mathematics and Statistics, The University of Dodoma, Dodoma, 338, Tanzania

Arnold K. Fulment
Roles: Data Curation, Methodology, Writing – Original Draft Preparation

Srinivasa Rao Gadde
Roles: Conceptualization, Software, Supervision

Josephat K. Peter
Roles: Methodology, Resources, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

Abstract

Background

The creation of developing new generalized classes of distributions has attracted applied and theoretical statisticians owing to their properties of flexibility. The development of generalized distribution aims to find distribution flexibility and suitability for available data. In this decade, most authors have developed classes of distributions that are new, to become valuable for applied researchers.

Methods

This study aims to develop the odd log-logistic generalized exponential distribution (OLLGED), one of the lifetime newly generated distributions in the field of statistics. The advantage of the newly generated distribution is the heavily tailed distributed lifetime data set. Most of the probabilistic properties are derived including generating functions, moments, and quantile and order statistics.

Results

Estimation of the model parameter is done by the maximum likelihood method. The performance of parametric estimation is studied through simulation. Application of OLLGED and its flexibilities is done using two data sets and while its performance is done on the randomly simulated data set.

Conclusions

The application and flexibility of the OLLGED are ensured through empirical observation using two sets of lifetime data, establishing that the proposed OLLGED can provide a better fit in comparison to existing rival models, such as odd generalized log-logistic, type-II generalized log-logistic, exponential distributions, odd exponential log-logistic, generalized exponential, and log-logistic.

Keywords

Odd log-logistic generalized exponential distribution, maximum-likelihood estimation, generating functions, moments, simulation and order statistics.

Corresponding author: Srinivasa Rao Gadde

Competing interests: No competing interests were disclosed.

Grant information: The author(s) declared that no grants were involved in supporting this work.

Copyright: © 2023 Fulment AK et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Fulment AK, Gadde SR and Peter JK. The odd log-logistic generalized exponential distribution: Application on survival times of chemotherapy patients data [version 3; peer review: 2 approved]. F1000Research 2023, 11:1444 (https://doi.org/10.12688/f1000research.127363.3) First published: 06 Dec 2022, 11:1444 (https://doi.org/10.12688/f1000research.127363.1) Latest published: 21 Nov 2023, 11:1444 (https://doi.org/10.12688/f1000research.127363.3)

Revised Amendments from Version 2

The revised manuscript version contains the following changes:
Introduction
We have provided some demerits of the distribution and some more explanation about Figure 1. The physical interpretation of shape parameter is also provided.
Data Analysis
Figures 7 and 8 are reconstructed by adding PP plots as suggested by the reviewer. Moreover, we have added some more explanation about real data applications.

See the authors' detailed response to the review by Boikanyo Makubate
See the authors' detailed response to the review by Sadaf Khan

1. Introduction

To cover the need for applied statistics in a field like economics, education, engineering, geology, health, and many others to mention, as well as in the area of development of models and analysis for lifetime data, some statistical probability distributions have been developed. However, these developed distributions have not been able to suffice the whole vacuum of data fit. As a result, room for the development of new distributions by researchers to model day-to-day lifetime data has always been there. The creation of developing new generalized classes of distributions has attracted applied and theoretical statisticians owing to their properties of flexibility. The development of generalized distribution aims to find distribution flexibility and suitability for available data. In this decade, most authors have developed classes of distributions that are new, to become valuable for applied researchers. Development methods for the new distribution are numerous in the literature. Generalization of probability distributions was initially introduced¹ where the authors generalized Weibull probability distribution, and the result was named exponential Weibull distribution which is common in modeling lifetime data.² Later, a modeling failure time data was developed³ by Lehmann-type alternatives named as an exponentiated form to base distribution. Later on, two parameters of generalized exponential distribution (GED) were developed,⁴ also called exponential distribution (ED). For more details on GED, refer to Refs. 5, 6. Due to its importance in statistical inference and reliability applications, numerous authors studied the various properties of this distribution.⁵^,⁷^–¹⁴ It is proved that the GED is an excellent substitute for gamma, log-Normal and Weibull distributions.

The motive for extending distributions for modeling lifetime data is the capacity to simulate both monotonically and non-monotonically growing, decreasing, and constant failure rates, or more critically with bathtub shaped failure rates, even if the baseline failure rate is monotonic. The fundamental justifications for implementing a new distribution model in practice are as follows: to create tail weight distributions for modeling various real data sets, to generate distributions with negative, positive, and symmetric skewness, to define special models with all varieties of hazard rate functions, to make the kurtosis more flexible than the baseline distribution, and to consistently produce better fits than other generated distributions with the same underlying model.

A random variable X is said to have the GED, hereafter referred to as baseline distribution with shape $(α)$ and scale $(λ)$ parameters if its probability density function (PDF) and cumulative density function (CDF) are given as respectively:

(1)

f (x) = αλ e^{- λx} {(1 - e^{- λx})}^{α - 1}; λ > 0, x \geq 0, α > 0

(2)

F (x) = {(1 - e^{- λx})}^{α} .

On the other hand, generalization was done in beta distribution under the name of generalized beta distribution; for more details refer to Ref. 15. They developed further generalized beta-generated (GBG) distribution, with a total of three parametric values.¹⁶ There are other many generalization methods in the literature depending on the nature of the distribution of data in hand.¹⁷ The researchers intend to introduce a new family of distribution which is named odd log-logistic generalized exponential distribution (OLLGED) to model heavy-tailed data set in daily-to-daily data set.¹⁸

The OLLGED is a generalization of exponential distribution with the addition of two parameters, which makes it have a total of three parametric values. The proposed distribution has a total of three parameters, lambda ( $λ$ ) as the only scale parameter, alpha ( $α$ ) and gamma ( $γ$ ), which are shape parameters introduced by generalization methods procedures, making it more flexible and thus, enabling the OLLGED to have an application to lifetime data and more extended to acceptance sampling plans and quality control charts.¹⁹^,²⁰

This paper is aimed at studying and defining a new lifetime paradigm namely OLLGED. Wide-ranging statistical properties and its applications through real data sets are given. More works on OLLGED have been presented.²¹^,²² The distribution proposed contains several lifetime distributions, such as GED.²³^–²⁵ OLLGED was introduced here for the reason:

1. It comprises a number above mentioned of well-known lifetime particular distributions;
2. The OLLGED demonstrates that shapes of hazard rates as monotonically decreasing, increasing, J, reversed-J, bathtub, and upside-down bathtub, which establishes that the recommended model has advanced to other lifetime distributions in hand;
3. To construct distribution to be used in special models that are capable of modeling skewed life time data and can also be used in a various areas of applications;
4. From the studies in section 2, the OLLGED would be considered with GED as baseline distribution⁶;
5. Asymmetric data that may not be well-fitted to other regular distributions may be fitted properly by the proposed model; and
6. The OLLGED beats numerous competitor distributions based on two real data illustrations.
7. The main drawback of this model or any model is while estimating parameters in simulation studies convergency creates a problem. Sometimes model validity is veridificult due more parameters in the model.

The class of distributions called the OLL-G family (generalized log-logistic-G family) by adding one more shape parameter was introduced.²² OLL-G family PDF and CDF are as follows:

(3)

g (x) = \frac{γf (x) {\{F (x) [1 - F (x)]\}}^{γ - 1}}{{\{F {(x)}^{γ} + {[1 - F (x)]}^{γ}\}}^{2}}

(4)

G (x) = \frac{F {(x)}^{γ}}{F {(x)}^{γ} + {[1 - F (x)]}^{γ}}

We note that

γ = \frac{log [\frac{G (x)}{\bar{G} (x)}]}{log [\frac{F (x)}{\bar{F} (x)}]} .

The next sections of this article are organized as follows; in Section 2, special models associated with OLLGED are explained. In Section 3, useful expansions and OLLGED properties are derived. Section 4 discussed the estimations of the parameters. The simulation study is carried out based on various parametric values of the proposed distribution in Section 5. Data analysis is done using two-lifetime data sets in Section 6, and in Section 7 of the article, discussion and conclusion are done.

2. The OLLGED and its special models

Using equations (1) and (2) in equations (3) and (4), we can develop the OLL-G family with baseline distribution as GED and it is named OLLGED. The PDF and CDF of OLLGED are given by

(5)

g (x) = \frac{γαλ e^{- λx} {(1 - e^{- λx})}^{α - 1} {\{{(1 - e^{- λx})}^{α} [1 - {(1 - e^{- λx})}^{α}]\}}^{γ - 1}}{{\{{(1 - e^{- λx})}^{α}^{γ} + {[1 - {(1 - e^{- λx})}^{α}]}^{γ}\}}^{2}}

(6)

G (x) = \frac{{(1 - e^{- λx})}^{α}^{γ}}{{(1 - e^{- λx})}^{α}^{γ} + {[1 - {(1 - e^{- λx})}^{α}]}^{γ}}; x > 0, λ > 0, α > 0, γ > 0 .

Here $γ$ and $α$ are shape parameters and $λ$ is a scale parameter of the distribution. Henceforth, if a random variable X follows to OLLGED with shape parameters $(γ, α)$ and scale parameter $λ$ , it is denoted as $X \sim OLLGED (γ, α, λ)$ .

The OLLGED is a more flexible distribution that provides several distributions by inter-changing parametric values. It contains the following models:

i) When $γ = 1$ , the resulting distribution becomes GED.⁶
ii) When $α = 1$ , the resulting distribution becomes an OLLGED.
iii) When $γ = 1$ and $α = 1$ , the resulting distribution becomes an ED.

Figure 1 is displayed for PDF and Figure 2 is displayed for CDF for various parametric values for OLLGED. Figures 1 and 2 reveal that the OLLGE family produces distributions with different shapes namely symmetrical, reversed-J and right-skewed. Figures 1 and 2 revealed that the OLLGED is more flexible with different shapes namely symmetrical, Reversed-J, and left and right-skewed. Figures 1 and 2 revealed that the OLLGED is more flexible with various parameter values considered which gives the property that it was suitable to use for lifetime data, for whichever data set distribution will fit its characteristics. More specifically, when $γ \leq 1$ and $α \leq 1$ the shape of the distribution is reversed-J. It shows that the shape parameter has more influence on the nature of the curve of the distribution. Specifically, for small values of shape parameters, there is a reverse J shape and for larger values of shape parameters, the nature of the curves is gradually increasing and then gradually decreasing.

Figure 1. Visual presentation of pdf plots of the OLLGED for various parameters.

Figure 2. Visual presentation of CDF plots of the OLLGED for various parameters.

The survival function and hazard rate, $s (x)$ and $h (x)$ respectively for OLLGED are respectively given below:

(7)

s (x) = \frac{{[1 - {(1 - e^{- λx})}^{α}]}^{γ}}{{(1 - e^{- λx})}^{α}^{γ} + {[1 - {(1 - e^{- λx})}^{α}]}^{γ}}

(8)

h (x) = \frac{γαλ e^{- λx} {(1 - e^{- λx})}^{αγ - 1} {\{1 - {(1 - e^{- λx})}^{α}\}}^{- 1}}{{(1 - e^{- λx})}^{α}^{γ} + {[1 - {(1 - e^{- λx})}^{α}]}^{γ}}

The visualization of survival functions and hazard rates of OLLGED for various parametric values are presented in Figures 3 and 4. Supplementary figures 3 and 4 disclose that this family can generate $h (x)$ shapes for instance increasing, reversed-J, decreasing, constant, and upside-down bathtubs. This shows that the OLLGE family could be extremely practical to fit data sets for diversified shapes.

Figure 3. Visual presentation of survival function plots of the OLLGED for various parameters.

Figure 4. Visual presentation of hazard rate plots of the OLLGED for various parameters.

3. Properties

3.1 Useful expansions

Using Taylor’s series specifically binomial series expansion for expansion of CDF and PDF for distribution as derived by OLLGED enables us to obtain the following functions as alternatives to the Equations given as PDF and CDF in equation (5) and (6) respectively. At this juncture, the CDF of OLLGED can be written using binomial expansion of its expressions as it was derived in Ref. 20 while expressing in much more simplified form parts of the CDF equations see in equation (9) and then substituted in the equation (6) to obtain the CDF see equation (10):

(9)

{[1 - e^{- λx}]}^{αγ} = \sum_{k = 0}^{\infty} a_{k} {[1 - e^{- λx}]}^{k} .

Whereas, $a_{k} = a_{k} (αγ) = \sum_{j = k}^{\infty} {(- 1)}^{k + 1} (\begin{matrix} αγ \\ j \end{matrix}) (\begin{matrix} j \\ k \end{matrix})$ .

The generalized binomial expansion is considered for $γ > 0$ :

(10)

{[1 - {(1 - e^{- λx})}^{α}]}^{γ} = \sum_{k = 0}^{\infty} a_{k}^{*} {[1 - e^{- λx}]}^{k}

Where $a_{k}^{*} = \sum_{i = 0}^{\infty} \sum_{j = k}^{\infty} {(- 1)}^{i + k + j} (\begin{matrix} γ \\ i \end{matrix}) (\begin{matrix} α \\ j \end{matrix}) (\begin{matrix} j \\ k \end{matrix})$ .

Thus, the CDFs of the OLLGED can be expressed as follows:

(11)

G (x) = \frac{\sum_{k = 0}^{\infty} a_{k} {[1 - e^{- λx}]}^{k}}{\sum_{k = 0}^{\infty} b_{k} {[1 - e^{- λx}]}^{k}} .

Where $b_{k} = a_{k} + a_{k}^{*}$ .

The following expression is for the ratio of the two-power series:

(12)

G (x) = \sum_{k = 0}^{\infty} c_{k} {[1 - e^{- λx}]}^{k}

Where $c_{0} = \frac{a_{0}}{b_{0}}$ and the coefficients of CK for $k \geq 1$ are determined from the recurrence generator which is given as:

(13)

c_{k} = b_{0}^{- 1} (a_{k} - b_{0}^{- 1} \sum_{r = 0}^{k} b_{r} c_{k - r}) .

Thus, PDF becomes

(14)

g (x) = \sum_{k = 0}^{\infty} c_{k + 1} λ e^{- λx} (k + 1) {(1 - e^{- λx})}^{k} .

3.2 Quantile function

The quantile function of the OLLGED is given by derivations while considering important theories.

Recalling the function for the quantile of the probability distribution to be given as:

G (X < x) = q

Insert equation (10) in equation (18), and solve for the variable x we get

(15)

x_{q} = \frac{- 1}{λ} ln [1 - {\{1 + {(q^{- 1} - 1)}^{\frac{1}{γ}}\}}^{\frac{- 1}{α}}] .

Upon substituting the appropriate value of quantile $q$ , we will be able to obtain its quantile value $(x_{q})$ .

3.3 Moments and generating functions

The $r^{th}$ moment for the OLLGED is given as:

(16)

μ_{r}^{'} = E (x^{r}) = \int_{0}^{\infty} x^{r} g (x) dx .

Since $g (x) = \sum_{k = 0}^{\infty} c_{k + 1} λ e^{- λx} (k + 1) {(1 - e^{- λx})}^{k}$

Thus, we get

(17)

\begin{matrix} μ_{r}^{'} = \int_{0}^{\infty} x^{r} \sum_{k = 0}^{\infty} c_{k + 1} λ e^{- λx} (k + 1) {(1 - e^{- λx})}^{k} dx \\ = \sum_{k = 0}^{\infty} (k + 1) λ c_{k + 1} \int_{0}^{\infty} x^{r} e^{- λx} {(1 - e^{- λx})}^{k} dx \end{matrix}

Now consider ${(1 - e^{- λx})}^{k} = \sum_{j = 0}^{\infty} {(- 1)}^{j} (\begin{matrix} k \\ j \end{matrix}) e^{- λkx}$ .

Then we obtain equation (17) as follows:

(18)

\begin{matrix} μ_{r}^{'} = \sum_{k = 0}^{\infty} (k + 1) λ c_{k + 1} \int_{0}^{\infty} x^{r} e^{- λx} \sum_{j = 0}^{\infty} {(- 1)}^{j} (\begin{matrix} k \\ j \end{matrix}) e^{- λkx} dx \\ = \sum_{k = 0}^{\infty} \sum_{j = 0}^{\infty} {(- 1)}^{j} (\begin{matrix} k \\ j \end{matrix}) (k + 1) λ c_{k + 1} \int_{0}^{\infty} x^{r} e^{- λx (1 + k)} dx \\ = λ \sum_{k = 0}^{\infty} \sum_{j = k}^{\infty} {(- 1)}^{j} (\begin{matrix} k \\ j \end{matrix}) (k + 1) c_{k + 1} \frac{Γ (r + 1)}{{[(1 + k) λ]}^{(r + 1)}} . \end{matrix}

Where $\int_{0}^{\infty} x^{r} e^{- λx (1 + k)} dx = \frac{Γ (r + 1)}{{[(1 + k) λ]}^{(r + 1)}}$

Therefore, mean is given by:

(19)

Mean = μ_{1}^{'} = \frac{1}{λ} \sum_{k = 0}^{\infty} \sum_{j = k}^{\infty} {(- 1)}^{j} (\begin{matrix} k \\ j \end{matrix}) (k + 1) c_{k + 1} \frac{1}{{[(1 + k)]}^{2}} .

μ_{2}^{'} = \frac{1}{λ^{2}} \sum_{k = 0}^{\infty} \sum_{j = 0}^{\infty} {(- 1)}^{j} (\begin{matrix} k \\ j \end{matrix}) (k + 1) c_{k + 1} \frac{2}{{(1 + k)}^{3}}

(20)

\begin{matrix} Variance μ_{2} = μ_{2}^{'} - {(μ_{1}^{'})}^{2} \\ = \frac{1}{λ^{2}} \{2 \sum_{k = 0}^{\infty} \sum_{j = k}^{\infty} {(- 1)}^{j} (\begin{matrix} k \\ j \end{matrix}) (k + 1) c_{k + 1} \frac{1}{{(1 + k)}^{3}} - {(\sum_{k = 0}^{\infty} \sum_{j = k}^{\infty} {(- 1)}^{j} (\begin{matrix} k \\ j \end{matrix}) (k + 1) c_{k + 1} \frac{1}{{(1 + k)}^{2}})}^{2}\} \end{matrix}

Moment generating function for the OLLGED is derived in the following manner:

(21)

\begin{array}{l} M_{x} (t) = E (e^{tx}) \\ = \int_{0}^{\infty} e^{tx} \sum_{k = 0}^{\infty} c_{k + 1} λ e^{- λx} (k + 1) {(1 - e^{- λx})}^{k} dx \\ = λ \sum_{k = 0}^{\infty} c_{k + 1} (k + 1) \int_{0}^{\infty} e^{tx} e^{- λx} {(1 - e^{- λx})}^{k} dx \\ = λ \sum_{k = 0}^{\infty} \sum_{j = k}^{\infty} {(- 1)}^{j} (\begin{matrix} k \\ j \end{matrix}) c_{k + 1} (k + 1) \int_{0}^{\infty} e^{tx} e^{- λx} e^{- λkx} dx \\ = λ \sum_{k = 0}^{\infty} \sum_{j = 0}^{\infty} {(- 1)}^{j} (\begin{matrix} k \\ j \end{matrix}) c_{k + 1} (k + 1) \frac{1}{(t - λ - λk)} . \end{array}

Where ${(1 - e^{- λx})}^{k} = \sum_{j = 0}^{\infty} {(- 1)}^{j} (\begin{matrix} k \\ j \end{matrix}) e^{- λkx}$ .

3.4 Skewness and Kurtosis

Since the moment cannot be obtained easily, in such a case, there are several methods for evaluating Skewness and Kurtosis in literature. Some of the famous methods are Galton's Skewness $(S_{k})$ and Moor’s Kurtosis $(M_{k})$ methods,²⁶ both of which utilize octile of the distribution.

Galton skewness of the distribution is given by considering octiles as follows:

(22)

S_{k} = \frac{Q (\frac{6}{8}) + Q (\frac{2}{8}) - 2 Q (\frac{4}{8})}{Q (\frac{6}{8}) - Q (\frac{2}{8})} .

Thus, based on varying values of distributional parameters, various values of skewness can be obtained and Figure 5 displayed the 3-dimensional plot of the skewness of the distribution. From Figure 5 it is evident that the skewness decreases as both $γ and α$ increase when $λ = 1$ .

Figure 5. Visual presentation for Skewness of the OLLGED.

While for kurtosis, Moor’s Kurtosis $(M_{k})$ method is used, which is based on octiles and it is given by:

(23)

M_{k} = \frac{Q (\frac{7}{8}) - Q (\frac{5}{8}) + Q (\frac{3}{8}) - Q (\frac{1}{8})}{Q (\frac{6}{8}) - Q (\frac{2}{8})} .

A 3-dimensional plot for varying values of distributional parameters is presented in Figure 6. From Figure 5 it is clear that the kurtosis decreases as both $γ and α$ increase when $λ = 1$ . The moments, skewness, and kurtosis for various parametric combinations are given in Table 1. When we fix the parameter λ, the skewness and kurtosis of OLLGED increases as α and γ increases. More specifically when parametric values are increases the skewness becomes negative and kurtosis becomes mesokurtic.

Figure 6. The Kurtosis of the OLLGED.

Table 1. The calculated moments, skewness, and kurtosis measures of the OLLGED for selected parameter values.

$λ$	$α$	$γ$	Mean	Variance	Skewness	Kurtosis
1.0	1.0	1.0	1.0000	1.0000	0.1918	1.2062
1.0	2.0	2.0	1.3079	0.3066	-0.0054	0.9772
1.1	1.1	1.1	0.9260	0.7008	0.1503	1.1137
1.2	1.2	1.2	0.8694	0.5073	0.1173	1.0327
1.3	1.3	1.3	0.8248	0.3772	0.0908	0.9619
1.4	1.4	1.4	0.7884	0.2868	0.0691	0.9001
1.5	1.5	1.5	0.7579	0.2223	0.0512	0.8460
1.6	1.6	1.6	0.7318	0.1752	0.0361	0.7985
1.6	2.6	2.6	0.9368	0.0760	-0.0387	0.7068
1.7	1.7	1.7	0.7090	0.1400	0.0233	0.7567
1.7	2.7	2.7	0.8991	0.0630	-0.0425	0.6767
1.8	1.8	1.8	0.6888	0.1133	0.0124	0.7196
1.8	2.8	2.8	0.8651	0.0527	-0.0459	0.6495
1.9	1.9	1.9	0.6705	0.0927	0.0029	0.6866
1.9	2.9	2.9	0.8344	0.0444	-0.0491	0.6249
2.0	2.0	2.0	0.6540	0.0766	-0.0054	0.6571
2.1	2.1	2.1	0.6387	0.0639	-0.0127	0.6306
2.2	2.2	2.2	0.6246	0.0538	-0.0191	0.6068
2.3	2.3	2.3	0.6114	0.0455	-0.0248	0.5852
2.4	2.4	2.4	0.5991	0.0388	-0.0299	0.5655
2.5	2.5	2.5	0.5875	0.0333	-0.0345	0.5476
2.6	2.6	2.6	0.5765	0.0288	-0.0387	0.5313
2.7	2.7	2.7	0.5661	0.0250	-0.0425	0.5163
2.8	2.8	2.8	0.5562	0.0218	-0.0459	0.5024
2.9	2.9	2.9	0.5467	0.0191	-0.0491	0.4897
3.0	3.0	3.0	0.5376	0.0168	-0.0520	0.4779
3.1	3.1	3.1	0.5290	0.0148	-0.0546	0.4669
3.2	3.2	3.2	0.5207	0.0131	-0.0571	0.4567
3.3	3.3	3.3	0.4467	0.0043	-0.0594	0.4472
3.4	3.4	3.4	0.5050	0.0104	-0.0615	0.4384
3.5	3.5	3.5	0.4976	0.0093	-0.0634	0.4301
3.6	3.6	3.6	0.4905	0.0084	-0.0653	0.4223
3.7	3.7	3.7	0.4836	0.0076	-0.0670	0.4150
3.8	3.8	3.8	0.4769	0.0068	-0.0686	0.4081
3.9	3.9	3.9	0.4705	0.0062	-0.0701	0.4016
4.0	4.0	4.0	0.4643	0.0056	-0.0715	0.3955
4.1	4.1	4.1	0.4582	0.0051	-0.0728	0.3897
4.2	4.2	4.2	0.4524	0.0047	-0.0741	0.3843
4.3	4.3	4.3	0.4467	0.0043	-0.0753	0.3791
4.4	4.4	4.4	0.4412	0.0039	-0.0764	0.3741
4.5	3.5	3.5	0.3870	0.0057	-0.0634	0.3798
4.5	4.5	4.5	0.4359	0.0036	-0.0775	0.3695
4.6	3.6	3.6	0.3839	0.0051	-0.0653	0.3746
4.6	4.6	4.6	0.4307	0.0033	-0.0785	0.3650
4.7	4.7	4.7	0.4256	0.0030	-0.0794	0.3608
4.8	4.8	4.8	0.4207	0.0028	-0.0804	0.3567
4.9	4.9	4.9	0.4159	0.0026	-0.0812	0.3529
5.0	5.0	5.0	0.4113	0.0024	-0.0821	0.3492

3.5 Residual and reversed residual life

For the residual life, $n^{th}$ moment is generally given as, $m_{n} (t) = E [{(X - t)}^{t}| X > t]$ , $n = 1, 2, 3, 4, \dots$ which is uniquely determined for the cumulative function $F (x)$ . Assuming X to be a random lifetime variable with $F (x)$ then the residual life $n^{th}$ moment is obtained as $m_{n} (t) = \frac{1}{R (t)} \int_{t}^{\infty} {(X - t)}^{n} dF (x)$ .

Many other functions are derived from the residual life $n^{th}$ moment such as mean residual life (MRLF) or life expectation at time t defined by:

$m_{1} (t) = E [(X - t)| X > t]$ , this presents the expected additional life length for a unit that is alive at time t.

The reversed residual life $n^{th}$ moment is generally defined as, $m_{n} (t) = E [{(X - t)}^{t}| X \leq t]$ only defined for $t > 0$ and $n = 1, 2, 3, 4, \dots$ , then, can be used to determine uniquely $F (x)$ .

Thus, the mean inactivity time (MIT) also referred to as mean waiting time (MWT) or mean reversed residual lifetime given by; $m_{1} (t) = E [(X - t)| X \leq t]$ , which is the waiting time, since the failure of an item on condition that the failure has occurred in (0, t).

3.6 Order statistics

In practice, most of the events occur randomly following a chronological order either ascending or descending. Thus, their probability distribution properties such as CDF and PDF can be written taking into consideration such criteria of their orders. The order statistics consider the order of occurrence of a random variable. Suppose that X₁, X₂ … X_n, is a random sample from the OLLGED, in the ascending values of the ordered random variables as $X_{1; n} \leq X_{2; n} \leq, \dots, \leq X_{n; n}$ , the PDF of the j^th order statistic, say X_j;n, is given in the next equation (24):

(24)

f_{j; n} (x) = \frac{g (x)}{B (j, n - j + 1)} \sum_{i = 0}^{n - j} {(- 1)}^{i} (\begin{matrix} n - j \\ i \end{matrix}) G^{i + j - 1} (x)

Whereas, $B (j, n - j + 1)$ is the beta function.

Upon substitution of equations (9) and (10) in equation (24) we get the following expression:

f_{j; n} (x) = \sum_{i = o}^{n - j} \sum_{r, k = 0}^{\infty} m_{i, r, k} h_{r + k + 1} (x)

Where $h_{r + k + 1} (x)$ denotes the probability density function for OLLGED having r+k+1 power parameter.

m_{i, r, k} = \frac{{(- 1)}^{i} (r + 1) c_{r + 1} f_{i + j - 1, k}}{B (j, n - j + 1) (r + k + 1)} .

Where, $c_{k} = b_{0}^{- 1} (a_{k} - b_{0}^{- 1} \sum_{r = 0}^{k} b_{r} c_{k - r})$ , hence the quantity $f_{i + j - 1, k}$ is obtained recursively by $f_{i + j - 1, 0} = c_{0}^{i + j - 1}$ and for values of $k \geq 1$ .

f_{i + j - 1, k} = {(k c_{0})}^{- 1} \sum_{m = 1}^{k} [m (i + j) - k] c_{m} f_{i + j - 1}, k - m .

Therefore, the density function of the OLLGED order statistics is a combination of GED. Based on $f_{i + j - 1, k}$ , it is noted that the properties of $X_{i; n}$ follow from the properties of $X_{r + k + 1}$ . Thus, the moment of $X_{i; n}$ can be expressed as:

(25)

E (X_{i; n}^{q}) = \sum_{j = 0}^{n - i} \sum_{r, k = 0}^{\infty} m_{j, r, k} E (X_{r + k + 1}^{q})

Consider moment in equation (25) for the derivation of explicit expression for L-moments of X as infinite weighted linear combinations of suitable OLLGED order statistics defined as a linear function as:

λ_{r} = \frac{1}{r} \sum_{d = 0}^{r - 1} {(- 1)}^{d} (\begin{matrix} r - 1 \\ d \end{matrix}) E (X_{r - d : r}), r \geq 1 .

4. Parametric estimation

The consideration of the unknown OLLGED model parameters from the complete samples is determined by using maximum likelihood estimations (MLE) as it is commonly used in the literature,²⁷ which for OLLGED parameters are $λ, α, and γ$ . Assuming $x_{1}, x_{2}, \dots, x_{n}$ be a random sample from OLLGED, the log-likelihood function is given by:

log L = nlog γ + \sum_{i = 0}^{n} log g (x) + (γ - 1) \sum_{i = 0}^{n} log G (x) + (γ - 1) \sum_{i = 0}^{n} log \bar{G} (x) - 2 (γ - 1) \sum_{i = 0}^{n} log \{G^{γ} (x) + {\bar{G}}^{γ} (x)\} .

Upon finding the second derivative, we obtain the following equations:

\frac{\partial^{2} log L}{\partial λ^{2}} = \sum_{i = 1}^{n} \frac{g^{(λλ)} (x_{i}) g (x_{i}) - {(g^{(λ)} (x_{i}))}^{2}}{g^{2} (x_{i})} + (γ - 1) \sum_{i = 1}^{n} \frac{G^{(λλ)} (x_{i}) G (x_{i}) - {(G^{(λ)} (x_{i}))}^{2}}{{(G (x_{i}))}^{2}} + (γ - 1) \sum_{i = 1}^{n} \frac{{(G^{(λ)} (x_{i}))}^{2} - G^{(λλ)} (x_{i}) \bar{G} (x_{i})}{{\bar{G}}^{2} (x_{i})} - 2 γ \sum_{i = 1}^{n} \{\begin{matrix} (γ - 1) \{\{G^{(λλ)} (x_{i}) G^{(λ)} (x_{i}) {(G (x_{i}))}^{γ - 2} - G^{(λλ)} (x_{i}) {(\bar{G} (x_{i}))}^{γ - 2} G^{(λ)} (x_{i})\} [{(G (x_{i}))}^{γ} + {(\bar{G} (x_{i}))}^{γ}]\} \\ - γ \{G^{(λ)} (x_{i}) {(G (x_{i}))}^{γ - 1} - {(\bar{G} (x_{i}))}^{γ - 1} G^{(λ)} (x_{i})\} [G^{(λ)} (x_{i}) {(G (x_{i}))}^{γ - 1} - G^{(λ)} (x_{i}) {(\bar{G} (x_{i}))}^{γ - 1}] \end{matrix}\} .

Similarly, second derivatives concerning parameters are obtained $(\frac{\partial^{2} log L}{\partial λ \partial α}, \frac{\partial^{2} log L}{\partial α^{2}}, \frac{\partial^{2} log L}{\partial λ \partial γ}, \frac{\partial^{2} log L}{\partial γ^{2}}$ and $\frac{\partial^{2} log L}{\partial α \partial γ})$

hence an information matrix is formed and given as:

I = [\begin{matrix} \frac{\partial^{2} log L}{\partial λ^{2}} & \frac{\partial^{2} log L}{\partial λ \partial α} & \frac{\partial^{2} log L}{\partial λ \partial γ} \\ \frac{\partial^{2} log L}{\partial λ \partial α} & \frac{\partial^{2} log L}{\partial α^{2}} & \frac{\partial^{2} log L}{\partial α \partial γ} \\ \frac{\partial^{2} log L}{\partial λ \partial γ} & \frac{\partial^{2} log L}{\partial α \partial γ} & \frac{\partial^{2} log L}{\partial γ^{2}} \end{matrix}] .

Since it seems not possible to solve the obtained MLE of parametric estimates analytically, then it is wise to solve these estimates using softwares such as R (an open source software for statistical computing and graphics) and SAS (an integrated software suite for advanced analytics, business intelligence, data management, and predictive analytics), we can find MLE for the OLLGED parameters or else find the solution to obtained non-linear likelihood equations. For the sake of this research work, the analysis is carried out using the R statistical software²⁸ to obtain parametric values for the MLE estimate of the suggested OLLGED.

5. Simulation study

This section deals with the behavior of the MLEs of the unknown parameters of the proposed OLLGED has been assessed through simulation. The simulation study is carried out for sample sizes n = 50, 100, 150, 200, 250, and 300 from OLLGED with 6 combinations of parameters. To evaluate the performance of the MLEs for the OLLGED model, the simulation study was performed as follows: Generate B = 3000 samples of size n from $OLLGED (λ, α, γ)$ , compute the MLE for the B samples, say $({\hat{λ}}_{j}, {\hat{α}}_{j}, {\hat{γ}}_{j}); j = 1, 2, \dots, B$ . Compute the biases and mean squared errors (MSE) based on B samples. We repeated these steps for n = 50, 100, 150, 200, 250, and 300 with different values of $(λ, α, γ)$ . To estimate the MLEs, the Broyden–Fletcher–Goldfarb–Shanno (BFGS) method in R software was used. Table 2 gives empirical results and its values reveal that the estimates are quite stable and, meaningfully, are near to the actual value of the parameters as the sample size increases for all parameters. The bias and mean square error (MSE) of both parameters decrease as the sample size increases as anticipated. The bias and MSE of the parameters are obtained as follows:

bias = \frac{1}{B} \sum_{i = 1}^{B} ({\hat{θ}}_{i} - θ)

Table 2. Average bias and MSE of OLLGED for various parametric combinations.

n	True values			Bias			MSE
n	$λ$	$α$	$γ$	$λ$	$α$	$γ$	$λ$	$α$	$γ$
50	1.5	1.5	0.2	0.2110	0.2793	0.0426	0.7762	0.9875	0.0311
100	1.5	1.5	0.2	0.1046	0.1317	0.0253	0.4006	0.4589	0.0142
150	1.5	1.5	0.2	0.0507	0.0682	0.0188	0.2507	0.2905	0.0083
200	1.5	1.5	0.2	0.0377	0.0491	0.0136	0.1839	0.2108	0.0055
250	1.5	1.5	0.2	0.0193	0.0269	0.0124	0.1452	0.1680	0.0042
300	1.5	1.5	0.2	0.0176	0.0230	0.0099	0.1168	0.1344	0.0033
50	0.2	0.2	1.5	0.4922	0.1680	-0.0593	2.2882	0.3726	0.4528
100	0.2	0.2	1.5	0.1647	0.0471	-0.0175	0.3980	0.0527	0.2235
150	0.2	0.2	1.5	0.0783	0.0199	-0.0117	0.0798	0.0102	0.1299
200	0.2	0.2	1.5	0.0511	0.0121	-0.0076	0.0285	0.0024	0.0916
250	0.2	0.2	1.5	0.0386	0.0093	-0.0061	0.0192	0.0017	0.0715
300	0.2	0.2	1.5	0.0313	0.0077	-0.0039	0.0150	0.0015	0.0604
50	0.2	0.2	1.0	0.2612	0.1174	-0.0375	0.6483	0.1617	0.1540
100	0.2	0.2	1.0	0.0826	0.0318	-0.0128	0.0861	0.0187	0.0688
150	0.2	0.2	1.0	0.0443	0.0168	-0.0070	0.0274	0.0060	0.0419
200	0.2	0.2	1.0	0.0295	0.0108	-0.0056	0.0115	0.0018	0.0292
250	0.2	0.2	1.0	0.0219	0.0082	-0.0027	0.0080	0.0013	0.0231
300	0.2	0.2	1.0	0.0186	0.0073	-0.0025	0.0065	0.0011	0.0194
50	1.0	0.2	1.0	1.2950	0.1185	-0.0353	16.0392	0.1693	0.1545
100	1.0	0.2	1.0	0.4037	0.0315	-0.0112	2.1329	0.0188	0.0685
150	1.0	0.2	1.0	0.2139	0.0164	-0.0054	0.6860	0.0062	0.0414
200	1.0	0.2	1.0	0.1409	0.0104	-0.0041	0.2811	0.0018	0.0289
250	1.0	0.2	1.0	0.1028	0.0078	-0.0009	0.1964	0.0013	0.0229
300	1.0	0.2	1.0	0.0871	0.0069	-0.0008	0.1578	0.0011	0.0193
50	0.2	1.5	0.2	0.0285	0.2780	0.0432	0.0139	0.9841	0.0313
100	0.2	1.5	0.2	0.0125	0.1184	0.0288	0.0073	0.4649	0.0154
150	0.2	1.5	0.2	0.0051	0.0530	0.0223	0.0047	0.3006	0.0092
200	0.2	1.5	0.2	0.0030	0.0309	0.0174	0.0035	0.2204	0.0063
250	0.2	1.5	0.2	0.0001	0.0058	0.0167	0.0029	0.1798	0.0050
300	0.2	1.5	0.2	-0.0002	0.0015	0.0140	0.0023	0.1444	0.0040
50	1.0	1.5	0.2	0.1403	0.2767	0.0424	0.3440	0.9796	0.0309
100	1.0	1.5	0.2	0.0674	0.1285	0.0258	0.1771	0.4563	0.0144
150	1.0	1.5	0.2	0.0330	0.0668	0.0191	0.1112	0.2903	0.0084
200	1.0	1.5	0.2	0.0242	0.0457	0.0139	0.0820	0.2075	0.0055
250	1.0	1.5	0.2	0.0129	0.0261	0.0126	0.0652	0.1679	0.0043
300	1.0	1.5	0.2	0.0115	0.0222	0.0099	0.0512	0.1313	0.0033

$MSE = \frac{1}{B} \sum_{i = 1}^{B} {({\hat{θ}}_{i} - θ)}^{2}$ . Where $θ = (λ, α, γ)$ .

6. Data analysis

The following two data sets were used to reveal the applications of OLLGED for showing the flexibility and importance of the proposed distribution. For the application of the OLLGED using the first data set for illustration, the data represent waiting times (in seconds) between 65 successive eruptions of water through a hole in the cliff at the coastal town of Kiama (New South Wales, Australia), known as the Blowhole; the data can be obtained from http://www.statsci.org/data/oz/kiama.html. This data set has already been used²⁹: DOI: http://dx.doi.org/10.15446/rce.v42n1.66205 as follows: 83, 51, 87, 60, 28, 95, 8, 27, 15, 10, 18, 16, 29, 54, 91, 8, 17, 55, 10, 35,47, 77, 36, 17, 21, 36, 18, 40, 10, 7, 34, 27, 28, 56, 8, 25, 68, 146, 89, 18, 73, 69, 9, 37, 10, 82, 29, 8, 60, 61, 61, 18, 169, 25, 8, 26, 11, 83, 11, 42, 17, 14, 9, 12.

The second data set used here was the survival times (given in years) of a group comprising 46 patients treated with chemotherapy alone. This data set was earlier reported¹⁸^,³⁰; doi: https://doi.org/10.1016/j.joems.2014.12.002, for ready reference, the survival times (years) are 0.047, 0.115, 0.121, 0.132, 0.164, 0.197, 0.203, 0.260, 0.282, 0.296, 0.334, 0.395, 0.458, 0.466, 0.501, 0.507,0.529,0.534,0.540, 0.641, 0.644, 0.696, 0.841, 0.863, 1.099, 1.219, 1.271, 1.326, 1.447, 1.485, 1.553, 1.581, 1.589, 2.178, 2.343, 2.416, 2.444, 2.825, 2.830, 3.578, 3.658, 3.743, 3.978, 4.003, 4.033.

Furthermore, the developed OLLGED fits were compared with other models like odd generalized exponential log-logistic distribution (OGELLD),³¹ Type-II generalized log-logistic distribution (ELLD),³² odd exponential log-logistic distribution (OELLD),³³ generalized exponential distribution (GED),⁶ exponential distribution (ED) and log-logistic distribution (LLD) studied by.²⁵^,³⁴ The competency of the proposed model with other models is examined based on goodness-of-fit criteria such as the maximized log-likelihood under the model ( $- 2 \hat{l}$ ), Akaike information criterion (AIC), Bayesian information criterion (BIC), Anderson-Darling (A^*), Cramer-von Mises (W^*) and Kolmogorov Smirnov (KS) statistic along with its p-value.

Tables 3 and 5 presented the MLEs of the model parameters respectively (of the fitted distribution) and their standard errors (SEs), KS, and p-value statistics for the distributions fitted OLLGED, OGELLD, OELLD, ELLD, LLD, GED, and ED models for the two data sets correspondingly. Tables 4 and 6 show the values of $- 2 \hat{l}$ , A^*, W^*, BIC, and AIC the for the two data sets separately. As shown in Tables 3-6, the OLLGED is the best among those distributions because it has the smallest value of (K-S), AIC, BIC, $- 2 \hat{l}$ , A* and W*. The histogram of the first data set, fitted PDFs of the best seven fitted OLLGED, OGELLD, OELLD, ELLD, LLD, GED, and ED, their CDF plots and PP-plot are demonstrated in Figure 7. The histogram of the second data set fitted PDFs of the best seven fitted OLLGED, OGELLD, OELLD, ELLD, LLD, GED, and ED, their CDF plots and PP-plot are displayed in Figure 8. From Figures 7 and 8, highlighted that the proposed OLLGED is best model as compared with rival existing distributions.

Table 3. Goodness-of-fit statistics for the waiting times' data.

Model	$- 2 \hat{l}$	AIC	BIC	W^*	A^*
OLLGED(γ,α,λ)	579.4480	585.4480	591.9247	0.0982	0.5837
OGELLD(α,λ,γ,σ)	587.9068	595.9068	604.5423	0.1198	0.8623
OELLD(α,λ,σ)	593.8000	598.8003	606.2791	0.1268	0.9163
ELLD(α,λ,σ)	598.5400	604.5390	611.0160	0.5723	2.9311
LLD(α,λ)	593.1488	597.1500	601.4700	0.1192	0.8909
GED(α,λ)	591.3320	595.3321	599.6498	0.1425	0.9606
ED(λ)	599.6254	601.6254	603.7843	0.1900	1.5899

Table 4. The estimates (SEs’), their p-value, and KS for waiting time data.

Model	Estimates (SEs)				KS	p-value
OLLGED(γ,α,λ)	0.2159 (0.0225)	41.5710 (1.1481)	0.1657 (0.0134)		0.0967	0.5867
OGELLD(α,λ,γ,σ)	32.7316 (89.1696)	0.3510 (0.2381)	0.6306 (1.6332)	2.1699 (15.6115)	0.0954	0.5604
OELLD(α,λ,σ)	1.2742 (0.1203)	5.4925 (42.2572)	11.3491 (68.5411)		0.1112	0.4072
ELLD(α,λ,σ)	0.0311 (0.0214)	24.2629 (16.0204)	7.5672 (0.3724)		0.1883	0.214
LLD(α,λ)	28.3417 (3.2940)	1.9650 (0.1985)			0.0999	0.5449
GED(α,λ)	1.7309 (0.3195)	0.0349 (0.0051)			0.1225	0.2917
ED(λ)	0.2510 (0.0310)				0.1664	0.0579

Table 5. Goodness-of-fit statistics for the survival time data.

Model	$- 2 \hat{l}$	AIC	BIC	W^*	A^*
OLLGED(γ,α,λ)	112.1880	118.1887	123.6081	0.0289	0.2410
OGELLD(α,λ,γ,σ)	116.0872	124.0872	131.3139	0.0719	0.4824
OELLD(α,λ,σ)	116.2474	122.2474	127.6674	0.0814	0.5363
ELLD(α,λ,σ)	118.2510	122.2511	127.6710	0.0812	0.5429
LLD(α,λ)	120.3712	124.3713	127.9846	0.0692	0.5028
GED(α,λ)	116.1897	120.1897	123.803	0.0827	0.5397
ED(λ)	116.4372	118.4372	124.2439	0.0589	0.4454

Table 6. The estimates (their SEs in parentheses), KS, and its p-value for survival time data.

Model	Estimates (SEs)				KS	p-value
OLLGED(γ,α,λ)	0.3193 (0.1349)	7.2769 (5.3527)	2.7667 (1.1212)		0.0594	0.9946
OGELLD(α,λ,γ,σ)	1.6103 (1.9739)	0.8079 (0.5274)	0.2539 (2.2143)	4.7280 (51.0672)	0.1004	0.7169
OELLD(α,λ,σ)	1.0531 (1.1238)	2.9579 (142.6629)	0.4892 (22.4021)		0.1094	0.6153
ELLD(α,λ,σ)	1261.1663 (2975.6993)	1.0505 (0.1224)	1224.1899 (2656.7019)		0.1090	0.6196
LLD(α,λ)	1.5075 (0.1832)	0.8332 (0.1460)			0.0849	0.8745
GED(α,λ)	1.1049 (1.2196)	1.7943 (1.1511)			0.1099	0.6093
ED(λ)	0.7455 (0.4111)				0.0908	0.8192

Figure 7. The densities fitted (left), CDF plots (middle) and PP-plot (right) for various models for waiting time data.

Figure 8. The densities fitted (left), CDF plots (middle) and PP-plot (right) for various models for survival time data.

7. Discussions and conclusion

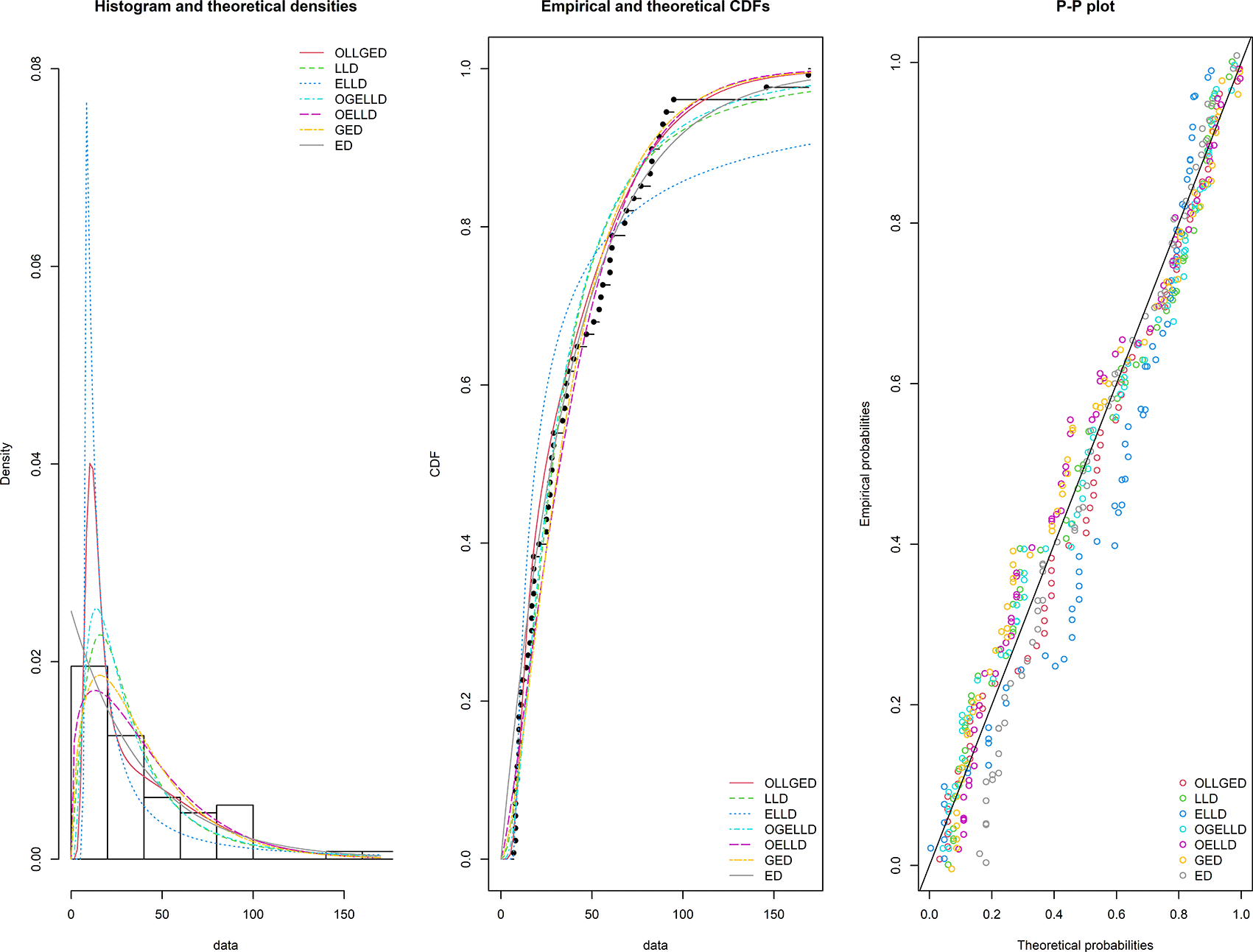
This article extends a new odd log-logistic generalized exponential distribution with three parameters to study the nature of the distribution in terms of kurtosis and skewness. The special models of the odd log-logistic generalized exponential family namely generalized exponential distribution, log-logistic distribution, and exponential distribution are presented. The common mathematical properties are obtained for the OLLGED. The parameters estimation is considered by the maximum-likelihood approach and simulation results are acquired to confirm the performance of these estimators. The application and flexibility of the OLLGED are ensured through empirical observation using two sets of lifetime data, establishing that the proposed OLLGED can provide a better fit in comparison to existing rival models, such as odd generalized log-logistic, type-II generalized log-logistic, exponential distributions, odd exponential log-logistic, generalized exponential, and log-logistic. The bias and mean square error of the parameters decrease as the sample size increases. The limitation of the proposed model is for very small values the bias and MSE are not stable. This model may not suitable for small samples and high peaked data.

Ethical considerations

This study was based on published data, so ethical approval was not required for published data.

Patient consent

Patient consent was not applicable as the study was based on published data.

Consent for publication

All authors agreed to publish this paper.

Data availability

Availability of data and material

The first data set related to waiting times (in seconds) between 65 successive eruptions of water through a hole in the cliff at the coastal town of Kiama obtained from http://www.statsci.org/data/oz/kiama.html. Used by Silva, R., Gomes-Silva, F., Ramos, M., Cordeiro, G., Marinho, P., & Andrade, T. A. N. D. (2019). The Exponentiated Kumaraswamy-G Class: General Properties and Application. Revista Colombiana de Estadística, 42, 1-33.

The second data set is drawn from Alizadeh, M., Tahir, M. H., Cordeiro, G. M., Mansoor, M., Zubair, M., & Hamedani, G. G. (2015). The Kumaraswamy Marshal-Olkin family of distributions. Journal of the Egyptian Mathematical Society, 23(3), 546-557. doi: https://doi.org/10.1016/j.joems.2014.12.002

Also, used by Bekker, A., Roux, J. J. J., & Mosteit, P. J. (2000). A generalization of the compound rayleigh distribution: using a bayesian method on cancer survival times. Communications in Statistics - Theory and Methods, 29(7), 1419-1433. doi: https://doi.org/10.1080/03610920008832554

Acknowledgements

The authors are deeply thankful to the editor and reviewers for their valuable suggestions to improve the quality of the paper. The authors would like to acknowledge the technical support received from the Office of the Deputy Vice Chancellor Academic, Research and Consultancy, The University of Dodoma, Tanzania.

References

1. Mudholkar G, Freimer M, Srivastava DK: The exponentiated weibull Family:a reanalysis of the bus-motorfailure-data. Technometrics. 1995; 436–445.
2. Martinez AS, Gonzal, Tercariol CAS: Generalized Probability Functions. Advances in Mathematical Physics. 2009; 1–13.
3. Gupta RC, Gupta PL, Gupta RD: Modeling failure time data by Lehmann alternatives. Commun. Stat. Theory Methods. 1998; 27(4): 887–904.
4. Gupta RD, Kundu D: Theory & Methods: Generalized exponential distributions. Aust. N. Z. J. Stat. 2002; 41(2).
5. Gupta RD, Kundu D: Generalized exponential distribution: different method of estimations. J. Stat. Comput. Simul. 2001; 69(4): 315–337. Publisher Full Text
6. Gupta RD, Kundu D: Generalized Exponential Distribution: Existing Methods and Some Recent Developments. J. Stat. Plan. Inference. 2007; 137(11): 3537–3547. Publisher Full Text
7. Gupta RD, Kundu D: Discriminating between Weibull and generalized exponential distributions. The Network Computational and Methodological Statistics (CMStatistics) and the International Association of Statistical Computing (IASC); 2003; 43(2).
8. Olapade A: On extended type I generalized logistic distribution. Intational Journal of Mathematics and Mathematical. Science. 2004; 57.
9. Raqab MZ, Ahsanullah M: Estimation of Location and Scale Parameters of Generalized Exponential Distribution Based on Order Statistics. J. Stat. Comput. Simul. 2001; 69.
10. Kundu D, Gupta RD: eneralized exponential distribution: Bayesian estimations. Comput. Stat. Data Anal. 2008; 52(4): 1873–1883. Publisher Full Text
11. Kundu S, Gupta AK: Analysis and Modeling of Fixed Bed Column Operations on As(V) Removal by Adsorption onto Iron Oxide-Coated Cement (IOCC). J. Colloid Interface Sci. 2005; 290(1): 52–60. PubMed Abstract | Publisher Full Text
12. Raqab MZ, Madi MT, Kundu D: Estimation of Probability of Y greater than X for the 3-parameter generalized exponential distribution. Commun. Stat. Theory Methods. 2008; 37(18): 2854–2864. Publisher Full Text
13. Dey S, Alzaatreh A, Zhang, et al.: A New Extension of Generalized Exponential Distribution with Application to Ozone Data. Ozone Sci. Eng. 2017; 39.
14. Nadarajah S, Kotz S: The Beta Exponential Distribution. Reliab. Eng. Syst. Saf. 2006; 91.
15. Cordeiro GM, Lemonte AJ: The β-Birnbaum–Saunders distribution: an improved distribution for fatigue life modeling. Comput. Stat. 2011; 1445–1461.
16. Alexander C, Cordeiro GM, Ortega, et al.: Generalized beta-generated distributions. Comput. Stat. Data Anal. 2012; 1880–1897.
17. Özyapıcı, Bilgehan B, Şensoy ZB: Generalized probability density function and applications to the experimental data in electrical circuits and systems. International Journal of Circuit Theory and Applications. 2020; 2266–2279.
18. Alizadeh, Ozel G, Altun, et al.: The Odd Log-Logistic Marshall-Olkin Lindley Model for Lifetime Data. J. Stat. Theory Appl. 2017; 16(3). Publisher Full Text
19. Karamikabir H, Afshari M, Alizadeh, et al.: The Odd Log-Logistic Burr-X Family of Distributions: Properties and Applications. J. Stat. Theory Appl. 2021; 20(2). Publisher Full Text
20. Eghwerido JT, Nzei LC, David IJ, et al.: The Gompertz extended generalized exponential distribution: properties and applications. Communications Faculty of Sciences University of Ankara Series A1: Mathematics and Statistics. 2020; 69(1): 739–753. Publisher Full Text
21. Gleaton U, Lynch JD: On the Distribution of the Breaking Strain of a Bundle of Brittle Elastic Fibers. Adv. Appl. Probab. 2003; 36(01).
22. Gleaton JU, Lynch JD: Properties of generalized log-logistic families of lifetime distributions. J. Probab. Stat. Sci. 2006; 04.
23. Gupta RD, Kundu D: Generalized exponential distribution: Existing results and some recent developments. J. Stat. Plan. Inference. 2007.
24. Ragab A, Green JR: On order statistics from thelog-logistic distribution and their properties. Communications in Statistics-theory and Methods. 1984; 13.
25. Kantam RRL, Rosaiah K, Rao GS: Acceptance sampling based on life tests: log-logistic models. J. Appl. Stat. 2001; 28.
26. Bleed O: New Exponential Cumulative Hazard Method for Generating Continuous Family Distributions. Journal of Alasmarya University: Basic and Applied Sciences. 2020; 5(1).
27. Coria VH, Maximov R-D, Melchor-Hernández CL: Perturbative method for maximum likelihood estimation of the Weibull distribution parameters. Springerplus. 2016; 5(5). Publisher Full Text
28. R Core Team: R: A Language and Environment for Statistical Computing.2020. Reference Source
29. Silva RV, Ramos MW, Silva FG, et al.: The Exponentiated Kumaraswamy-G Class: General Properties and Application. Revista Colombiana de Estadística. 2019; 1–33.
30. Bekker A, Roux JJJ, Mostert PJ: A Generalization of the Compound Rayleigh Distribution: Using a Bayesian Methods on Cancer Survival Times. Commun. Stat. Theory Methods. 2000; 29(7): 1419–1433. Publisher Full Text
31. Rosaiah K, Rao GS, Sivakumar D, et al.: The Odd Generalized Exponential Log Logistic Distribution. International Journal of Mathematics and Statistics Invention. 2016; 4(5).
32. Rosaiah, Kantam RRL, Prasad V, et al.: Reliability Estimation in Type-II Generalized Log-Logistic Distribution. Int. J. Agric. Stat. Sci.. 2008; 4(2).
33. Kanaparthi, Rao, Kalyani, et al.: Odds Exponential Log Logistic Distribution: Properties and Estimation. J. Math. Stat. 2017; 13(1): 14–23. Publisher Full Text
34. Ragab A, Green: On Order Statistics From the Log-Logistic Distribution and Their Properties. Commun. Stat. Theory Methods. 1984; 13(21): 2713–2724. Publisher Full Text

Comments on this article Comments (0)

Version 3

VERSION 3 PUBLISHED 06 Dec 2022

Author details Author details

¹ Mathematics and Statistics, The University of Dodoma, Dodoma, 338, Tanzania

Arnold K. Fulment
Roles: Data Curation, Methodology, Writing – Original Draft Preparation

Srinivasa Rao Gadde
Roles: Conceptualization, Software, Supervision

Josephat K. Peter
Roles: Methodology, Resources, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Article Versions (3)

version 3

Revised

Published: 21 Nov 2023, 11:1444

https://doi.org/10.12688/f1000research.127363.3

version 2

Revised

Published: 10 Aug 2023, 11:1444

https://doi.org/10.12688/f1000research.127363.2

version 1

Published: 06 Dec 2022, 11:1444

https://doi.org/10.12688/f1000research.127363.1

© 2023 Fulment AK et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

Fulment AK, Gadde SR and Peter JK. The odd log-logistic generalized exponential distribution: Application on survival times of chemotherapy patients data [version 3; peer review: 2 approved]. F1000Research 2023, 11:1444 (https://doi.org/10.12688/f1000research.127363.3)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 3

VERSION 3

PUBLISHED 21 Nov 2023

Revised

Views

Reviewer Report 31 May 2024

Sadaf Khan, The islamia university bahawalpur, Bahawalpur, Pakistan

Approved

https://doi.org/10.5256/f1000research.158863.r224409

CITE

Report a concern

Respond or Comment

Version 2

VERSION 2

PUBLISHED 10 Aug 2023

Revised

Views

Reviewer Report 10 Nov 2023

Sadaf Khan, The islamia university bahawalpur, Bahawalpur, Pakistan

Approved with Reservations

https://doi.org/10.5256/f1000research.153883.r195521

I did not find left skewness in Figure 1 of the proposed model.
... Continue reading

CITE

Report a concern

Author Response 21 Nov 2023

Srinivasa Rao Gadde, Mathematics and Statistics, The University of Dodoma, Dodoma, 338, Tanzania

21 Nov 2023

Author Response

Dear Editor-in-Chief and Reviewer:
Thank you very much for giving us the opportunity to revise our manuscript. We also appreciate the valuable input of anonymous reviewers. We are so happy ... Continue reading Dear Editor-in-Chief and Reviewer:
Thank you very much for giving us the opportunity to revise our manuscript. We also appreciate the valuable input of anonymous reviewers. We are so happy that all the reviewers have given positive feedback and encouraged the publication of our paper.
The suggestions made by all reviewers are incorporated, and changes are highlighted in the revised manuscript with RED color. Below are the responses regarding the comments made by the respected reviewer. We hope the revised manuscript will justify the higher standards of the journal.

Comments and Responses
Comment: I did not find left skewness in Figure 1 of the proposed model.
Response: Thank you for pointing out the mistake; we have deleted the word left skewed in the revised manuscript. We have tried many combinations of parameters, but unfortunately, the shapes are appearing in this manner.
Comment: The remarks 4,5,8,9 of review round 1 have not been addressed in a satisfactory manner.
Response: Respected sir, we are extremely sorry for the confusion and for not addressing those comments well.
Response to comment 4: The nature of distributions changes with the change in shape parameters. This was explained after drawing Figure 1, and now we have provided some more explanation on the nature of the distribution.
Response to comment 5: We have provided some disadvantages of our model.
Response to comment 8: Figures 7 and 8 are reconstructed by adding PP plots. In the literature review, numerous authors have displayed the figures (Figures 7 and 8) for comparing the various models. Due to this reason, we have displayed only pdf and CDF plots. As for your suggestion, we have added one more figure as a PP-plot. When we are fitting a single model for data, more researchers display it in pdf, cdf, pp, and qq plots. I hope the figures are now up to your expectations. Please refer to the following references: We have provided high-resolution figures.

Ishaq AI, Suleiman AA, Daud H, Singh NSS, Othman M, Sokkalingam R, Wiratchotisatian P,
Usman AG and Abba SI (2023) Log-Kumaraswamy distribution: its features and applications. Front. Appl. Math. Stat. 9:1258961. doi: 10.3389/fams.2023.1258961

Shah, S., Hazarika , P. J., Chakraborty , S., & Alizadeh, M. (2022). The Balakrishnan-Alpha-Beta-Skew-Laplace Distribution: Properties and Applications. Statistics, Optimization & Information Computing, 11(3), 755-772. https://doi.org/10.19139/soic-2310-5070-1247

Akarawak, E. E. E., Adeyeye, S. J., Khaleel, M. A., Adedotun, A. F., Ogunsanya, A. S., & Amalare, A. A. (2023). The inverted Gompertz-Fréchet distribution with applications. Scientific African, 21, e01769. doi: https://doi.org/10.1016/j.sciaf.2023.e01769

Shah, S., Hazarika, P. J., Chakraborty, S., & Ali, M. M. (2021). The Balakrishnan-Alpha-Beta-Skew-Normal Distribution: Properties and Applications. Pakistan Journal of Statistics and Operation Research, 17(2), 367-380. https://doi.org/10.18187/pjsor.v17i2.3731

Response to comment 9: Thank you for your suggestion; we have added some more explanation.
Dear Editor-in-Chief and Reviewer:
Thank you very much for giving us the opportunity to revise our manuscript. We also appreciate the valuable input of anonymous reviewers. We are so happy that all the reviewers have given positive feedback and encouraged the publication of our paper.
The suggestions made by all reviewers are incorporated, and changes are highlighted in the revised manuscript with RED color. Below are the responses regarding the comments made by the respected reviewer. We hope the revised manuscript will justify the higher standards of the journal.

Comments and Responses
Comment: I did not find left skewness in Figure 1 of the proposed model.
Response: Thank you for pointing out the mistake; we have deleted the word left skewed in the revised manuscript. We have tried many combinations of parameters, but unfortunately, the shapes are appearing in this manner.
Comment: The remarks 4,5,8,9 of review round 1 have not been addressed in a satisfactory manner.
Response: Respected sir, we are extremely sorry for the confusion and for not addressing those comments well.
Response to comment 4: The nature of distributions changes with the change in shape parameters. This was explained after drawing Figure 1, and now we have provided some more explanation on the nature of the distribution.
Response to comment 5: We have provided some disadvantages of our model.
Response to comment 8: Figures 7 and 8 are reconstructed by adding PP plots. In the literature review, numerous authors have displayed the figures (Figures 7 and 8) for comparing the various models. Due to this reason, we have displayed only pdf and CDF plots. As for your suggestion, we have added one more figure as a PP-plot. When we are fitting a single model for data, more researchers display it in pdf, cdf, pp, and qq plots. I hope the figures are now up to your expectations. Please refer to the following references: We have provided high-resolution figures.

Ishaq AI, Suleiman AA, Daud H, Singh NSS, Othman M, Sokkalingam R, Wiratchotisatian P,
Usman AG and Abba SI (2023) Log-Kumaraswamy distribution: its features and applications. Front. Appl. Math. Stat. 9:1258961. doi: 10.3389/fams.2023.1258961

Shah, S., Hazarika , P. J., Chakraborty , S., & Alizadeh, M. (2022). The Balakrishnan-Alpha-Beta-Skew-Laplace Distribution: Properties and Applications. Statistics, Optimization & Information Computing, 11(3), 755-772. https://doi.org/10.19139/soic-2310-5070-1247

Akarawak, E. E. E., Adeyeye, S. J., Khaleel, M. A., Adedotun, A. F., Ogunsanya, A. S., & Amalare, A. A. (2023). The inverted Gompertz-Fréchet distribution with applications. Scientific African, 21, e01769. doi: https://doi.org/10.1016/j.sciaf.2023.e01769

Shah, S., Hazarika, P. J., Chakraborty, S., & Ali, M. M. (2021). The Balakrishnan-Alpha-Beta-Skew-Normal Distribution: Properties and Applications. Pakistan Journal of Statistics and Operation Research, 17(2), 367-380. https://doi.org/10.18187/pjsor.v17i2.3731

Response to comment 9: Thank you for your suggestion; we have added some more explanation.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 21 Nov 2023

Srinivasa Rao Gadde, Mathematics and Statistics, The University of Dodoma, Dodoma, 338, Tanzania

21 Nov 2023

Author Response

Dear Editor-in-Chief and Reviewer:
Thank you very much for giving us the opportunity to revise our manuscript. We also appreciate the valuable input of anonymous reviewers. We are so happy ... Continue reading Dear Editor-in-Chief and Reviewer:
Thank you very much for giving us the opportunity to revise our manuscript. We also appreciate the valuable input of anonymous reviewers. We are so happy that all the reviewers have given positive feedback and encouraged the publication of our paper.
The suggestions made by all reviewers are incorporated, and changes are highlighted in the revised manuscript with RED color. Below are the responses regarding the comments made by the respected reviewer. We hope the revised manuscript will justify the higher standards of the journal.

Comments and Responses
Comment: I did not find left skewness in Figure 1 of the proposed model.
Response: Thank you for pointing out the mistake; we have deleted the word left skewed in the revised manuscript. We have tried many combinations of parameters, but unfortunately, the shapes are appearing in this manner.
Comment: The remarks 4,5,8,9 of review round 1 have not been addressed in a satisfactory manner.
Response: Respected sir, we are extremely sorry for the confusion and for not addressing those comments well.
Response to comment 4: The nature of distributions changes with the change in shape parameters. This was explained after drawing Figure 1, and now we have provided some more explanation on the nature of the distribution.
Response to comment 5: We have provided some disadvantages of our model.
Response to comment 8: Figures 7 and 8 are reconstructed by adding PP plots. In the literature review, numerous authors have displayed the figures (Figures 7 and 8) for comparing the various models. Due to this reason, we have displayed only pdf and CDF plots. As for your suggestion, we have added one more figure as a PP-plot. When we are fitting a single model for data, more researchers display it in pdf, cdf, pp, and qq plots. I hope the figures are now up to your expectations. Please refer to the following references: We have provided high-resolution figures.

Ishaq AI, Suleiman AA, Daud H, Singh NSS, Othman M, Sokkalingam R, Wiratchotisatian P,
Usman AG and Abba SI (2023) Log-Kumaraswamy distribution: its features and applications. Front. Appl. Math. Stat. 9:1258961. doi: 10.3389/fams.2023.1258961

Shah, S., Hazarika , P. J., Chakraborty , S., & Alizadeh, M. (2022). The Balakrishnan-Alpha-Beta-Skew-Laplace Distribution: Properties and Applications. Statistics, Optimization & Information Computing, 11(3), 755-772. https://doi.org/10.19139/soic-2310-5070-1247

Akarawak, E. E. E., Adeyeye, S. J., Khaleel, M. A., Adedotun, A. F., Ogunsanya, A. S., & Amalare, A. A. (2023). The inverted Gompertz-Fréchet distribution with applications. Scientific African, 21, e01769. doi: https://doi.org/10.1016/j.sciaf.2023.e01769

Shah, S., Hazarika, P. J., Chakraborty, S., & Ali, M. M. (2021). The Balakrishnan-Alpha-Beta-Skew-Normal Distribution: Properties and Applications. Pakistan Journal of Statistics and Operation Research, 17(2), 367-380. https://doi.org/10.18187/pjsor.v17i2.3731

Response to comment 9: Thank you for your suggestion; we have added some more explanation.
Dear Editor-in-Chief and Reviewer:
Thank you very much for giving us the opportunity to revise our manuscript. We also appreciate the valuable input of anonymous reviewers. We are so happy that all the reviewers have given positive feedback and encouraged the publication of our paper.
The suggestions made by all reviewers are incorporated, and changes are highlighted in the revised manuscript with RED color. Below are the responses regarding the comments made by the respected reviewer. We hope the revised manuscript will justify the higher standards of the journal.

Comments and Responses
Comment: I did not find left skewness in Figure 1 of the proposed model.
Response: Thank you for pointing out the mistake; we have deleted the word left skewed in the revised manuscript. We have tried many combinations of parameters, but unfortunately, the shapes are appearing in this manner.
Comment: The remarks 4,5,8,9 of review round 1 have not been addressed in a satisfactory manner.
Response: Respected sir, we are extremely sorry for the confusion and for not addressing those comments well.
Response to comment 4: The nature of distributions changes with the change in shape parameters. This was explained after drawing Figure 1, and now we have provided some more explanation on the nature of the distribution.
Response to comment 5: We have provided some disadvantages of our model.
Response to comment 8: Figures 7 and 8 are reconstructed by adding PP plots. In the literature review, numerous authors have displayed the figures (Figures 7 and 8) for comparing the various models. Due to this reason, we have displayed only pdf and CDF plots. As for your suggestion, we have added one more figure as a PP-plot. When we are fitting a single model for data, more researchers display it in pdf, cdf, pp, and qq plots. I hope the figures are now up to your expectations. Please refer to the following references: We have provided high-resolution figures.

Ishaq AI, Suleiman AA, Daud H, Singh NSS, Othman M, Sokkalingam R, Wiratchotisatian P,
Usman AG and Abba SI (2023) Log-Kumaraswamy distribution: its features and applications. Front. Appl. Math. Stat. 9:1258961. doi: 10.3389/fams.2023.1258961

Shah, S., Hazarika , P. J., Chakraborty , S., & Alizadeh, M. (2022). The Balakrishnan-Alpha-Beta-Skew-Laplace Distribution: Properties and Applications. Statistics, Optimization & Information Computing, 11(3), 755-772. https://doi.org/10.19139/soic-2310-5070-1247

Akarawak, E. E. E., Adeyeye, S. J., Khaleel, M. A., Adedotun, A. F., Ogunsanya, A. S., & Amalare, A. A. (2023). The inverted Gompertz-Fréchet distribution with applications. Scientific African, 21, e01769. doi: https://doi.org/10.1016/j.sciaf.2023.e01769

Shah, S., Hazarika, P. J., Chakraborty, S., & Ali, M. M. (2021). The Balakrishnan-Alpha-Beta-Skew-Normal Distribution: Properties and Applications. Pakistan Journal of Statistics and Operation Research, 17(2), 367-380. https://doi.org/10.18187/pjsor.v17i2.3731

Response to comment 9: Thank you for your suggestion; we have added some more explanation.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Views

Reviewer Report 17 Aug 2023

Boikanyo Makubate, Botswana International University of Science and Technology, Palapye, Central District, Botswana

Approved

https://doi.org/10.5256/f1000research.153883.r195520

The manuscript has improved. The manuscript is scientifically valid ... Continue reading

CITE

Report a concern

Respond or Comment

Version 1

VERSION 1

PUBLISHED 06 Dec 2022

Views

Reviewer Report 06 Jul 2023

Boikanyo Makubate, Botswana International University of Science and Technology, Palapye, Central District, Botswana

Not Approved

https://doi.org/10.5256/f1000research.139863.r171415

The comments on the above-mentioned manuscript are as follows:

Although some of the paper results seem correct, I have some doubts about whether there is enough innovation for a new publication, especially as many other related

The comments on the above-mentioned manuscript are as follows:

Although some of the paper results seem correct, I have some doubts about whether there is enough innovation for a new publication, especially as many other related papers have been published on this topic. Could you justify it more convincingly?
In addition the previous item, I would like to have read more tenable arguments about the need for a new distribution. Otherwise, you are left with just an analytical exercise of a new distribution that may never be used in practice. Would you be able to revise the text of the article in order to better justify it and thus make it more interesting?
Section 3.1 and hence 3.2 are incorrect.
I expected to see more discussion in the simulation study, real data analysis and conclusion.
I could not find detailed information about the software used for obtaining the results of simulation study and real data analysis.
Lastly, I also suggest reviewing the use of English carefully, and considerable rewording and pruning to make the paper more concise and precise.
Fig 1, the pdf plots, the researcher should include left skewed and symmetric shapes as they are explained in page 4.
Skewness plot on fig 5 is not well explained in relation to the pdf plots, especially the area of the graph in which we can observe symmetric, right or left skewness.
The kurtosis on Fig 6, is not interpreted especially in relation to leptokurtic, mesokurtic and platykurtic, and which area of the graph we can observe these.
On section 4, the researcher mentioned that they used the MLE parameter estimation technique as it is commonly used in the literature, the researcher should justify the method in relation to its efficiency, consistency, asymptotically normal and invariant property under transformation.
On section 6, the OLLGED has 3 parameters, LLD and GED have 2 parameters and the ED has a single parameter, therefore their comparison is nor fair based on the number of parameters. Suggested is to include at least 3 more 3 parameter comparative models. Interpretation of Fig 7 and 8 have to be incorporated
Finally, I do not recommend this article for indexing. It is poorly written and contains a lot of incorrect results.

Is the work clearly and accurately presented and does it cite the current literature?

No
Is the study design appropriate and is the work technically sound?

No
Are sufficient details of methods and analysis provided to allow replication by others?

No
If applicable, is the statistical analysis and its interpretation appropriate?

No
Are all the source data underlying the results available to ensure full reproducibility?

No
Are the conclusions drawn adequately supported by the results?

No

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Mathematical Statistics, Distributional theory, Applied Statistics, Medical statistics

I confirm that I have read this submission and believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

CITE

Report a concern

Author Response 10 Aug 2023

Srinivasa Rao Gadde, Mathematics and Statistics, The University of Dodoma, Dodoma, 338, Tanzania

10 Aug 2023

Author Response

1. Although some of the paper results seem correct, I have some doubts about whether there is enough innovation for a new publication, especially as many other related papers have been ... Continue reading 1. Although some of the paper results seem correct, I have some doubts about whether there is enough innovation for a new publication, especially as many other related papers have been published on this topic. Could you justify it more convincingly?

2. In addition, the previous item, I would like to have read more tenable arguments about the need for a new distribution. Otherwise, you are left with just an analytical exercise of a new distribution that may never be used in practice. Would you be able to revise the text of the article in order to better justify it and thus make it more interesting?

Response: The motive for extending distributions for modelling lifetime data is the capacity to simulate both monotonically and non-monotonically growing, decreasing, and constant failure rates, or more critically with bathtub-shaped failure rates, even if the baseline failure rate is monotonic. The fundamental justifications for implementing a new distribution model in practice are as follows: to create tail weight distributions for modelling various real data sets, to generate distributions with negative, positive, and symmetric skewness, to define special models with all varieties of hazard rate functions, to make the kurtosis more flexible than the baseline distribution, and to consistently produce better fits than other generated distributions with the same underlying model.

3. Section 3.1 and hence 3.2 are incorrect

Response: Some typographical errors were corrected

4. I could not find detailed information about the software used for obtaining the results of simulation study and real data analysis

Response: Explanation on the software used for various analytical activities in this paper is given in last part of section 4

5. I expected to see more discussion in the simulation study, real data analysis and conclusion

Response: More discussion on simulation is given in section 5 on the simulation and explanation of the so obtained results. Discussion on the real data used for the application is made in section 7.

6. On section 6, the OLLGED has 3 parameters, LLD and GED have 2 parameters and the ED has a single parameter, therefore their comparison is nor fair based on the number of parameters. Suggested is to include at least 3 more 3 parameter comparative models. Interpretation of Fig 7 and 8 have to be incorporated

Response: The suggested was compared with the commonly used distribution regardless of the number of parameters for there were distributions with four parameters see Table 3 proposed distribution proved to be more powerful over them, those with fewer distributions were used too to show that the proposed distribution would stand them too.

7. Lastly, I also suggest reviewing the use of English carefully, and considerable rewording and pruning to make the paper more concise and precise

Response: There manuscript was taken to the editor to structure it well the grammar

8. Fig 1, the pdf plots, the researcher should include left skewed and symmetric shapes as they are explained on page 4.

Response: The fourth part of Figure 1 shows the left-skewed and symmetric shapes.

9. The kurtosis on Fig 6, is not interpreted especially in relation to leptokurtic, mesokurtic and platykurtic, and which area of the graph we can observe these.

Response: When we fix the parameter λ, the skewness and kurtosis of OLLGED increases as α and γ increases. More specifically when parametric values are increased the skewness becomes negative and kurtosis becomes mesokurtic.

10. On section 4, the researcher mentioned that they used the MLE parameter estimation technique as it is commonly used in the literature, the researcher should justify the method in relation to its efficiency, consistency, asymptotically normal and invariant property under transformation.

Response: The justification is given for using MLE as suggested

11. On section 6, the OLLGED has 3 parameters, LLD and GED have 2 parameters and the ED has a single parameter, therefore their comparison is nor fair based on the number of parameters. Suggested is to include at least 3 more 3-parameter comparative models. Interpretation of Fig 7 and 8 have to be incorporated

Response: The suggested was compared with the commonly used distribution regardless of the number of parameters for there were distributions with four parameters see table 3 proposed distribution proved to be more powerful over them, those with fewer distributions were used too to show that the proposed distribution would stand them too.
1. Although some of the paper results seem correct, I have some doubts about whether there is enough innovation for a new publication, especially as many other related papers have been published on this topic. Could you justify it more convincingly?

2. In addition, the previous item, I would like to have read more tenable arguments about the need for a new distribution. Otherwise, you are left with just an analytical exercise of a new distribution that may never be used in practice. Would you be able to revise the text of the article in order to better justify it and thus make it more interesting?

Response: The motive for extending distributions for modelling lifetime data is the capacity to simulate both monotonically and non-monotonically growing, decreasing, and constant failure rates, or more critically with bathtub-shaped failure rates, even if the baseline failure rate is monotonic. The fundamental justifications for implementing a new distribution model in practice are as follows: to create tail weight distributions for modelling various real data sets, to generate distributions with negative, positive, and symmetric skewness, to define special models with all varieties of hazard rate functions, to make the kurtosis more flexible than the baseline distribution, and to consistently produce better fits than other generated distributions with the same underlying model.

3. Section 3.1 and hence 3.2 are incorrect

Response: Some typographical errors were corrected

4. I could not find detailed information about the software used for obtaining the results of simulation study and real data analysis

Response: Explanation on the software used for various analytical activities in this paper is given in last part of section 4

5. I expected to see more discussion in the simulation study, real data analysis and conclusion

Response: More discussion on simulation is given in section 5 on the simulation and explanation of the so obtained results. Discussion on the real data used for the application is made in section 7.

6. On section 6, the OLLGED has 3 parameters, LLD and GED have 2 parameters and the ED has a single parameter, therefore their comparison is nor fair based on the number of parameters. Suggested is to include at least 3 more 3 parameter comparative models. Interpretation of Fig 7 and 8 have to be incorporated

Response: The suggested was compared with the commonly used distribution regardless of the number of parameters for there were distributions with four parameters see Table 3 proposed distribution proved to be more powerful over them, those with fewer distributions were used too to show that the proposed distribution would stand them too.

7. Lastly, I also suggest reviewing the use of English carefully, and considerable rewording and pruning to make the paper more concise and precise

Response: There manuscript was taken to the editor to structure it well the grammar

8. Fig 1, the pdf plots, the researcher should include left skewed and symmetric shapes as they are explained on page 4.

Response: The fourth part of Figure 1 shows the left-skewed and symmetric shapes.

9. The kurtosis on Fig 6, is not interpreted especially in relation to leptokurtic, mesokurtic and platykurtic, and which area of the graph we can observe these.

Response: When we fix the parameter λ, the skewness and kurtosis of OLLGED increases as α and γ increases. More specifically when parametric values are increased the skewness becomes negative and kurtosis becomes mesokurtic.

10. On section 4, the researcher mentioned that they used the MLE parameter estimation technique as it is commonly used in the literature, the researcher should justify the method in relation to its efficiency, consistency, asymptotically normal and invariant property under transformation.

Response: The justification is given for using MLE as suggested

11. On section 6, the OLLGED has 3 parameters, LLD and GED have 2 parameters and the ED has a single parameter, therefore their comparison is nor fair based on the number of parameters. Suggested is to include at least 3 more 3-parameter comparative models. Interpretation of Fig 7 and 8 have to be incorporated

Response: The suggested was compared with the commonly used distribution regardless of the number of parameters for there were distributions with four parameters see table 3 proposed distribution proved to be more powerful over them, those with fewer distributions were used too to show that the proposed distribution would stand them too.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 10 Aug 2023

Srinivasa Rao Gadde, Mathematics and Statistics, The University of Dodoma, Dodoma, 338, Tanzania

10 Aug 2023

Author Response

1. Although some of the paper results seem correct, I have some doubts about whether there is enough innovation for a new publication, especially as many other related papers have been ... Continue reading 1. Although some of the paper results seem correct, I have some doubts about whether there is enough innovation for a new publication, especially as many other related papers have been published on this topic. Could you justify it more convincingly?

2. In addition, the previous item, I would like to have read more tenable arguments about the need for a new distribution. Otherwise, you are left with just an analytical exercise of a new distribution that may never be used in practice. Would you be able to revise the text of the article in order to better justify it and thus make it more interesting?

Response: The motive for extending distributions for modelling lifetime data is the capacity to simulate both monotonically and non-monotonically growing, decreasing, and constant failure rates, or more critically with bathtub-shaped failure rates, even if the baseline failure rate is monotonic. The fundamental justifications for implementing a new distribution model in practice are as follows: to create tail weight distributions for modelling various real data sets, to generate distributions with negative, positive, and symmetric skewness, to define special models with all varieties of hazard rate functions, to make the kurtosis more flexible than the baseline distribution, and to consistently produce better fits than other generated distributions with the same underlying model.

3. Section 3.1 and hence 3.2 are incorrect

Response: Some typographical errors were corrected

4. I could not find detailed information about the software used for obtaining the results of simulation study and real data analysis

Response: Explanation on the software used for various analytical activities in this paper is given in last part of section 4

5. I expected to see more discussion in the simulation study, real data analysis and conclusion

Response: More discussion on simulation is given in section 5 on the simulation and explanation of the so obtained results. Discussion on the real data used for the application is made in section 7.

6. On section 6, the OLLGED has 3 parameters, LLD and GED have 2 parameters and the ED has a single parameter, therefore their comparison is nor fair based on the number of parameters. Suggested is to include at least 3 more 3 parameter comparative models. Interpretation of Fig 7 and 8 have to be incorporated

Response: The suggested was compared with the commonly used distribution regardless of the number of parameters for there were distributions with four parameters see Table 3 proposed distribution proved to be more powerful over them, those with fewer distributions were used too to show that the proposed distribution would stand them too.

7. Lastly, I also suggest reviewing the use of English carefully, and considerable rewording and pruning to make the paper more concise and precise

Response: There manuscript was taken to the editor to structure it well the grammar

8. Fig 1, the pdf plots, the researcher should include left skewed and symmetric shapes as they are explained on page 4.

Response: The fourth part of Figure 1 shows the left-skewed and symmetric shapes.

9. The kurtosis on Fig 6, is not interpreted especially in relation to leptokurtic, mesokurtic and platykurtic, and which area of the graph we can observe these.

Response: When we fix the parameter λ, the skewness and kurtosis of OLLGED increases as α and γ increases. More specifically when parametric values are increased the skewness becomes negative and kurtosis becomes mesokurtic.

10. On section 4, the researcher mentioned that they used the MLE parameter estimation technique as it is commonly used in the literature, the researcher should justify the method in relation to its efficiency, consistency, asymptotically normal and invariant property under transformation.

Response: The justification is given for using MLE as suggested

11. On section 6, the OLLGED has 3 parameters, LLD and GED have 2 parameters and the ED has a single parameter, therefore their comparison is nor fair based on the number of parameters. Suggested is to include at least 3 more 3-parameter comparative models. Interpretation of Fig 7 and 8 have to be incorporated

Response: The suggested was compared with the commonly used distribution regardless of the number of parameters for there were distributions with four parameters see table 3 proposed distribution proved to be more powerful over them, those with fewer distributions were used too to show that the proposed distribution would stand them too.
1. Although some of the paper results seem correct, I have some doubts about whether there is enough innovation for a new publication, especially as many other related papers have been published on this topic. Could you justify it more convincingly?

2. In addition, the previous item, I would like to have read more tenable arguments about the need for a new distribution. Otherwise, you are left with just an analytical exercise of a new distribution that may never be used in practice. Would you be able to revise the text of the article in order to better justify it and thus make it more interesting?

Response: The motive for extending distributions for modelling lifetime data is the capacity to simulate both monotonically and non-monotonically growing, decreasing, and constant failure rates, or more critically with bathtub-shaped failure rates, even if the baseline failure rate is monotonic. The fundamental justifications for implementing a new distribution model in practice are as follows: to create tail weight distributions for modelling various real data sets, to generate distributions with negative, positive, and symmetric skewness, to define special models with all varieties of hazard rate functions, to make the kurtosis more flexible than the baseline distribution, and to consistently produce better fits than other generated distributions with the same underlying model.

3. Section 3.1 and hence 3.2 are incorrect

Response: Some typographical errors were corrected

4. I could not find detailed information about the software used for obtaining the results of simulation study and real data analysis

Response: Explanation on the software used for various analytical activities in this paper is given in last part of section 4

5. I expected to see more discussion in the simulation study, real data analysis and conclusion

Response: More discussion on simulation is given in section 5 on the simulation and explanation of the so obtained results. Discussion on the real data used for the application is made in section 7.

6. On section 6, the OLLGED has 3 parameters, LLD and GED have 2 parameters and the ED has a single parameter, therefore their comparison is nor fair based on the number of parameters. Suggested is to include at least 3 more 3 parameter comparative models. Interpretation of Fig 7 and 8 have to be incorporated

Response: The suggested was compared with the commonly used distribution regardless of the number of parameters for there were distributions with four parameters see Table 3 proposed distribution proved to be more powerful over them, those with fewer distributions were used too to show that the proposed distribution would stand them too.

7. Lastly, I also suggest reviewing the use of English carefully, and considerable rewording and pruning to make the paper more concise and precise

Response: There manuscript was taken to the editor to structure it well the grammar

8. Fig 1, the pdf plots, the researcher should include left skewed and symmetric shapes as they are explained on page 4.

Response: The fourth part of Figure 1 shows the left-skewed and symmetric shapes.

9. The kurtosis on Fig 6, is not interpreted especially in relation to leptokurtic, mesokurtic and platykurtic, and which area of the graph we can observe these.

Response: When we fix the parameter λ, the skewness and kurtosis of OLLGED increases as α and γ increases. More specifically when parametric values are increased the skewness becomes negative and kurtosis becomes mesokurtic.

10. On section 4, the researcher mentioned that they used the MLE parameter estimation technique as it is commonly used in the literature, the researcher should justify the method in relation to its efficiency, consistency, asymptotically normal and invariant property under transformation.

Response: The justification is given for using MLE as suggested

11. On section 6, the OLLGED has 3 parameters, LLD and GED have 2 parameters and the ED has a single parameter, therefore their comparison is nor fair based on the number of parameters. Suggested is to include at least 3 more 3-parameter comparative models. Interpretation of Fig 7 and 8 have to be incorporated

Response: The suggested was compared with the commonly used distribution regardless of the number of parameters for there were distributions with four parameters see table 3 proposed distribution proved to be more powerful over them, those with fewer distributions were used too to show that the proposed distribution would stand them too.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Views

Reviewer Report 06 Jul 2023

Sadaf Khan, The islamia university bahawalpur, Bahawalpur, Pakistan

Approved with Reservations

https://doi.org/10.5256/f1000research.139863.r181917

In this article, the odd log-logistic generalized exponential distribution (OLLGED) is proposed using Odd Log Logistic-G family, originally proposed by Gleaton and Lynch (2006). Various statistical properties including generating functions, moments, quantile and order statistics are dervied mathematically. The estimation of the model parameter is achieved by the maximum likelihood method and related inferences have been drawn. The convergence of the parameters estimates has been verified by Monte-Carlo simulation methods. The model is compared with 6 well established distributions by applying it on two real data sets.

Figure 1: bottom left and right are same.
Motivations are less convincing. There is no novelty in the proposed work. The authors need to justify why they chose generalize exponential distribution as baseline to OLL-G proposed by Gleaton and Lynch (2006)¹.
How do the authors justify the proposed distribution utility and scope in various scientific fields?
How come the authors justify the shape parameters’ physical interpretation?
What are some possible disadvantages of the model given in (5) and (6)?
In section 7, I would also recommend that the author comment more on the limitation of this distribution. How the distribution change when the size is large or too small, for example. Is it a critical point where the distribution does not apply anymore?
In section 7, the authors did not show how to interpret model parameters and their practical meanings in real data. How does OLLGED perform in comparison to OLL-Gamma, OLL-Weibull or OLL-LogNormal distribution?
Figure 7 and Figure 8 are difficult to read. Also add other graphical measures such as PP-Plots, QQ-Plots, estimated hazard rate etc.
Comment on the behavior of the datasets being employed.
What are future directives one can extract from the proposed model?

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Partly

References

1. Gleaton JU, Lynch JD: Properties of generalized log-logistic families of lifetime distributions.J Probab Statist Sci.2006; 4 (1): 51-64

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Distribution theory, applied statistics, mathematical modelling.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Author Response 10 Aug 2023

Srinivasa Rao Gadde, Mathematics and Statistics, The University of Dodoma, Dodoma, 338, Tanzania

10 Aug 2023

Author Response

Reviewer Report 1

1 Figure 1: bottom left and right are same

Response: The two figures are not the same see the shape parameter sigma which made the change ... Continue reading Reviewer Report 1

1 Figure 1: bottom left and right are same

Response: The two figures are not the same see the shape parameter sigma which made the change in the figures

2. Motivations are less convincing. There is no novelty in the proposed work. The authors need to justify why they chose generalize exponential distribution as baseline to OLL-G proposed by Gleaton and Lynch (2006)1.

Response: More justification for the selection of GED as baseline over others distributions in existence including OLL-G as proposed by Gleaton and Lynch (2006)

3 How do the authors justify the proposed distribution utility and scope in various scientific fields?

Response: A number (6) of justification for the proposed distribution are given

4. How come the authors justify the shape parameters’ physical interpretation?

Response: We have explained the various physical appearances of our model in Figure 1

5. What are some possible disadvantages of the model given in (5) and (6)?

Response: They are very flexible and change into other distributions as the parameters change

6. In section 7, I would also recommend that the author comment more on the limitation of this distribution. How the distribution change when the size is large or too small, for example? Is it a critical point where the distribution does not apply anymore?

Response: The bias and mean square error of the parameters decrease as the sample size increases. The limitation of the proposed model is for very small values the bias and MSE are not stable. This model may not suitable for small samples and high peaked data.

7. In section 7, the authors did not show how to interpret model parameters and their practical meanings in real data. How does OLLGED perform in comparison to OLL-Gamma, OLL-Weibull or OLL-Log Normal distribution?

Response: The part was added to give more practical meaning and comparison of suggested OLLGED to other existing distributions.

8. Figure 7 and Figure 8 are difficult to read. Also add other graphical measures such as PP-Plots, QQ-Plots, estimated hazard rate etc.

Response: Now figures can be ready and pp and qq are displayed in Figure 9 and Figure 10

9. Comment on the behavior of the datasets being employed.

Response: Table 3 and Table 6 have been added to describe data sets

10. What are future directives one can extract from the proposed model?

Response: The proposed OLLGED is among the best in dealing with heavy-tailed data sets and right-skewed data
Reviewer Report 1

1 Figure 1: bottom left and right are same

Response: The two figures are not the same see the shape parameter sigma which made the change in the figures

2. Motivations are less convincing. There is no novelty in the proposed work. The authors need to justify why they chose generalize exponential distribution as baseline to OLL-G proposed by Gleaton and Lynch (2006)1.

Response: More justification for the selection of GED as baseline over others distributions in existence including OLL-G as proposed by Gleaton and Lynch (2006)

3 How do the authors justify the proposed distribution utility and scope in various scientific fields?

Response: A number (6) of justification for the proposed distribution are given

4. How come the authors justify the shape parameters’ physical interpretation?

Response: We have explained the various physical appearances of our model in Figure 1

5. What are some possible disadvantages of the model given in (5) and (6)?

Response: They are very flexible and change into other distributions as the parameters change

6. In section 7, I would also recommend that the author comment more on the limitation of this distribution. How the distribution change when the size is large or too small, for example? Is it a critical point where the distribution does not apply anymore?

Response: The bias and mean square error of the parameters decrease as the sample size increases. The limitation of the proposed model is for very small values the bias and MSE are not stable. This model may not suitable for small samples and high peaked data.

7. In section 7, the authors did not show how to interpret model parameters and their practical meanings in real data. How does OLLGED perform in comparison to OLL-Gamma, OLL-Weibull or OLL-Log Normal distribution?

Response: The part was added to give more practical meaning and comparison of suggested OLLGED to other existing distributions.

8. Figure 7 and Figure 8 are difficult to read. Also add other graphical measures such as PP-Plots, QQ-Plots, estimated hazard rate etc.

Response: Now figures can be ready and pp and qq are displayed in Figure 9 and Figure 10

9. Comment on the behavior of the datasets being employed.

Response: Table 3 and Table 6 have been added to describe data sets

10. What are future directives one can extract from the proposed model?

Response: The proposed OLLGED is among the best in dealing with heavy-tailed data sets and right-skewed data
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 10 Aug 2023

Srinivasa Rao Gadde, Mathematics and Statistics, The University of Dodoma, Dodoma, 338, Tanzania

10 Aug 2023

Author Response

Reviewer Report 1

1 Figure 1: bottom left and right are same

Response: The two figures are not the same see the shape parameter sigma which made the change ... Continue reading Reviewer Report 1

1 Figure 1: bottom left and right are same

Response: The two figures are not the same see the shape parameter sigma which made the change in the figures

2. Motivations are less convincing. There is no novelty in the proposed work. The authors need to justify why they chose generalize exponential distribution as baseline to OLL-G proposed by Gleaton and Lynch (2006)1.

Response: More justification for the selection of GED as baseline over others distributions in existence including OLL-G as proposed by Gleaton and Lynch (2006)

3 How do the authors justify the proposed distribution utility and scope in various scientific fields?

Response: A number (6) of justification for the proposed distribution are given

4. How come the authors justify the shape parameters’ physical interpretation?

Response: We have explained the various physical appearances of our model in Figure 1

5. What are some possible disadvantages of the model given in (5) and (6)?

Response: They are very flexible and change into other distributions as the parameters change

6. In section 7, I would also recommend that the author comment more on the limitation of this distribution. How the distribution change when the size is large or too small, for example? Is it a critical point where the distribution does not apply anymore?

Response: The bias and mean square error of the parameters decrease as the sample size increases. The limitation of the proposed model is for very small values the bias and MSE are not stable. This model may not suitable for small samples and high peaked data.

7. In section 7, the authors did not show how to interpret model parameters and their practical meanings in real data. How does OLLGED perform in comparison to OLL-Gamma, OLL-Weibull or OLL-Log Normal distribution?

Response: The part was added to give more practical meaning and comparison of suggested OLLGED to other existing distributions.

8. Figure 7 and Figure 8 are difficult to read. Also add other graphical measures such as PP-Plots, QQ-Plots, estimated hazard rate etc.

Response: Now figures can be ready and pp and qq are displayed in Figure 9 and Figure 10

9. Comment on the behavior of the datasets being employed.

Response: Table 3 and Table 6 have been added to describe data sets

10. What are future directives one can extract from the proposed model?

Response: The proposed OLLGED is among the best in dealing with heavy-tailed data sets and right-skewed data
Reviewer Report 1

1 Figure 1: bottom left and right are same

Response: The two figures are not the same see the shape parameter sigma which made the change in the figures

2. Motivations are less convincing. There is no novelty in the proposed work. The authors need to justify why they chose generalize exponential distribution as baseline to OLL-G proposed by Gleaton and Lynch (2006)1.

Response: More justification for the selection of GED as baseline over others distributions in existence including OLL-G as proposed by Gleaton and Lynch (2006)

3 How do the authors justify the proposed distribution utility and scope in various scientific fields?

Response: A number (6) of justification for the proposed distribution are given

4. How come the authors justify the shape parameters’ physical interpretation?

Response: We have explained the various physical appearances of our model in Figure 1

5. What are some possible disadvantages of the model given in (5) and (6)?

Response: They are very flexible and change into other distributions as the parameters change

6. In section 7, I would also recommend that the author comment more on the limitation of this distribution. How the distribution change when the size is large or too small, for example? Is it a critical point where the distribution does not apply anymore?

Response: The bias and mean square error of the parameters decrease as the sample size increases. The limitation of the proposed model is for very small values the bias and MSE are not stable. This model may not suitable for small samples and high peaked data.

7. In section 7, the authors did not show how to interpret model parameters and their practical meanings in real data. How does OLLGED perform in comparison to OLL-Gamma, OLL-Weibull or OLL-Log Normal distribution?

Response: The part was added to give more practical meaning and comparison of suggested OLLGED to other existing distributions.

8. Figure 7 and Figure 8 are difficult to read. Also add other graphical measures such as PP-Plots, QQ-Plots, estimated hazard rate etc.

Response: Now figures can be ready and pp and qq are displayed in Figure 9 and Figure 10

9. Comment on the behavior of the datasets being employed.

Response: Table 3 and Table 6 have been added to describe data sets

10. What are future directives one can extract from the proposed model?

Response: The proposed OLLGED is among the best in dealing with heavy-tailed data sets and right-skewed data
Competing Interests: No competing interests were disclosed. Close
Report a concern

Comments on this article Comments (0)

Version 3

VERSION 3 PUBLISHED 06 Dec 2022

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 3 (revision) 21 Nov 23	read
Version 2 (revision) 10 Aug 23	read	read
Version 1 06 Dec 22	read	read

Sadaf Khan, The islamia university bahawalpur, Bahawalpur, Pakistan
Boikanyo Makubate, Botswana International University of Science and Technology, Palapye, Botswana

Comments on this article

All Comments(0)

Add a comment

Browse by related subjects

Back to all reports

Reviewer Report

2 Views

31 May 2024 | for Version 3

Sadaf Khan, The islamia university bahawalpur, Bahawalpur, Pakistan

2 Views Cite this report Responses(0)

Approved

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Distribution theory, applied statistics, mathematical modelling.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

13 Views

10 Nov 2023 | for Version 2

Sadaf Khan, The islamia university bahawalpur, Bahawalpur, Pakistan

13 Views Cite this report Responses(1)

Approved With Reservations

I did not find left skewness in Figure 1 of the proposed model.

The remarks 4,5,8,9 of review round1 have not been addressed in a satisfactory manner.

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Distribution theory, applied statistics, mathematical modelling.

Respond to this report

Responses (1)

Author Response

21 Nov 2023

Srinivasa Rao Gadde, Mathematics and Statistics, The University of Dodoma, Dodoma, 338, Tanzania

Dear Editor-in-Chief and Reviewer:
Thank you very much for giving us the opportunity to revise our manuscript. We also appreciate the valuable input of anonymous reviewers. We are so happy that all the reviewers have given positive feedback and encouraged the publication of our paper.
The suggestions made by all reviewers are incorporated, and changes are highlighted in the revised manuscript with RED color. Below are the responses regarding the comments made by the respected reviewer. We hope the revised manuscript will justify the higher standards of the journal.

Comments and Responses
Comment: I did not find left skewness in Figure 1 of the proposed model.
Response: Thank you for pointing out the mistake; we have deleted the word left skewed in the revised manuscript. We have tried many combinations of parameters, but unfortunately, the shapes are appearing in this manner.
Comment: The remarks 4,5,8,9 of review round 1 have not been addressed in a satisfactory manner.
Response: Respected sir, we are extremely sorry for the confusion and for not addressing those comments well.
Response to comment 4: The nature of distributions changes with the change in shape parameters. This was explained after drawing Figure 1, and now we have provided some more explanation on the nature of the distribution.
Response to comment 5: We have provided some disadvantages of our model.
Response to comment 8: Figures 7 and 8 are reconstructed by adding PP plots. In the literature review, numerous authors have displayed the figures (Figures 7 and 8) for comparing the various models. Due to this reason, we have displayed only pdf and CDF plots. As for your suggestion, we have added one more figure as a PP-plot. When we are fitting a single model for data, more researchers display it in pdf, cdf, pp, and qq plots. I hope the figures are now up to your expectations. Please refer to the following references: We have provided high-resolution figures.

Ishaq AI, Suleiman AA, Daud H, Singh NSS, Othman M, Sokkalingam R, Wiratchotisatian P,
Usman AG and Abba SI (2023) Log-Kumaraswamy distribution: its features and applications. Front. Appl. Math. Stat. 9:1258961. doi: 10.3389/fams.2023.1258961

Shah, S., Hazarika , P. J., Chakraborty , S., & Alizadeh, M. (2022). The Balakrishnan-Alpha-Beta-Skew-Laplace Distribution: Properties and Applications. Statistics, Optimization & Information Computing, 11(3), 755-772. https://doi.org/10.19139/soic-2310-5070-1247

Akarawak, E. E. E., Adeyeye, S. J., Khaleel, M. A., Adedotun, A. F., Ogunsanya, A. S., & Amalare, A. A. (2023). The inverted Gompertz-Fréchet distribution with applications. Scientific African, 21, e01769. doi: https://doi.org/10.1016/j.sciaf.2023.e01769

Shah, S., Hazarika, P. J., Chakraborty, S., & Ali, M. M. (2021). The Balakrishnan-Alpha-Beta-Skew-Normal Distribution: Properties and Applications. Pakistan Journal of Statistics and Operation Research, 17(2), 367-380. https://doi.org/10.18187/pjsor.v17i2.3731

Response to comment 9: Thank you for your suggestion; we have added some more explanation.

View more View less

Competing Interests

No competing interests were disclosed.

Back to all reports

Reviewer Report

6 Views

17 Aug 2023 | for Version 2

Boikanyo Makubate, Botswana International University of Science and Technology, Palapye, Central District, Botswana

6 Views Cite this report Responses(0)

Approved

The manuscript has improved. The manuscript is scientifically valid in its current form. I recommend the manuscript for indexing.

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Mathematical Statistics, Distributional theory, Applied Statistics, Medical statistics

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

18 Views

06 Jul 2023 | for Version 1

Boikanyo Makubate, Botswana International University of Science and Technology, Palapye, Central District, Botswana

18 Views Cite this report Responses(1)

Not Approved

The comments on the above-mentioned manuscript are as follows:

Although some of the paper results seem correct, I have some doubts about whether there is enough innovation for a new publication, especially as many other related papers have been published on this topic. Could you justify it more convincingly?
In addition the previous item, I would like to have read more tenable arguments about the need for a new distribution. Otherwise, you are left with just an analytical exercise of a new distribution that may never be used in practice. Would you be able to revise the text of the article in order to better justify it and thus make it more interesting?
Section 3.1 and hence 3.2 are incorrect.
I expected to see more discussion in the simulation study, real data analysis and conclusion.
I could not find detailed information about the software used for obtaining the results of simulation study and real data analysis.
Lastly, I also suggest reviewing the use of English carefully, and considerable rewording and pruning to make the paper more concise and precise.
Fig 1, the pdf plots, the researcher should include left skewed and symmetric shapes as they are explained in page 4.
Skewness plot on fig 5 is not well explained in relation to the pdf plots, especially the area of the graph in which we can observe symmetric, right or left skewness.
The kurtosis on Fig 6, is not interpreted especially in relation to leptokurtic, mesokurtic and platykurtic, and which area of the graph we can observe these.
On section 4, the researcher mentioned that they used the MLE parameter estimation technique as it is commonly used in the literature, the researcher should justify the method in relation to its efficiency, consistency, asymptotically normal and invariant property under transformation.
On section 6, the OLLGED has 3 parameters, LLD and GED have 2 parameters and the ED has a single parameter, therefore their comparison is nor fair based on the number of parameters. Suggested is to include at least 3 more 3 parameter comparative models. Interpretation of Fig 7 and 8 have to be incorporated
Finally, I do not recommend this article for indexing. It is poorly written and contains a lot of incorrect results.

Is the work clearly and accurately presented and does it cite the current literature?

No
Is the study design appropriate and is the work technically sound?

No
Are sufficient details of methods and analysis provided to allow replication by others?

No
If applicable, is the statistical analysis and its interpretation appropriate?

No
Are all the source data underlying the results available to ensure full reproducibility?

No
Are the conclusions drawn adequately supported by the results?

No

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Mathematical Statistics, Distributional theory, Applied Statistics, Medical statistics

Respond to this report

Responses (1)

Author Response

10 Aug 2023

Srinivasa Rao Gadde, Mathematics and Statistics, The University of Dodoma, Dodoma, 338, Tanzania

1. Although some of the paper results seem correct, I have some doubts about whether there is enough innovation for a new publication, especially as many other related papers have been published on this topic. Could you justify it more convincingly?

2. In addition, the previous item, I would like to have read more tenable arguments about the need for a new distribution. Otherwise, you are left with just an analytical exercise of a new distribution that may never be used in practice. Would you be able to revise the text of the article in order to better justify it and thus make it more interesting?

Response: The motive for extending distributions for modelling lifetime data is the capacity to simulate both monotonically and non-monotonically growing, decreasing, and constant failure rates, or more critically with bathtub-shaped failure rates, even if the baseline failure rate is monotonic. The fundamental justifications for implementing a new distribution model in practice are as follows: to create tail weight distributions for modelling various real data sets, to generate distributions with negative, positive, and symmetric skewness, to define special models with all varieties of hazard rate functions, to make the kurtosis more flexible than the baseline distribution, and to consistently produce better fits than other generated distributions with the same underlying model.

3. Section 3.1 and hence 3.2 are incorrect

Response: Some typographical errors were corrected

4. I could not find detailed information about the software used for obtaining the results of simulation study and real data analysis

Response: Explanation on the software used for various analytical activities in this paper is given in last part of section 4

5. I expected to see more discussion in the simulation study, real data analysis and conclusion

Response: More discussion on simulation is given in section 5 on the simulation and explanation of the so obtained results. Discussion on the real data used for the application is made in section 7.

6. On section 6, the OLLGED has 3 parameters, LLD and GED have 2 parameters and the ED has a single parameter, therefore their comparison is nor fair based on the number of parameters. Suggested is to include at least 3 more 3 parameter comparative models. Interpretation of Fig 7 and 8 have to be incorporated

Response: The suggested was compared with the commonly used distribution regardless of the number of parameters for there were distributions with four parameters see Table 3 proposed distribution proved to be more powerful over them, those with fewer distributions were used too to show that the proposed distribution would stand them too.

7. Lastly, I also suggest reviewing the use of English carefully, and considerable rewording and pruning to make the paper more concise and precise

Response: There manuscript was taken to the editor to structure it well the grammar

8. Fig 1, the pdf plots, the researcher should include left skewed and symmetric shapes as they are explained on page 4.

Response: The fourth part of Figure 1 shows the left-skewed and symmetric shapes.

9. The kurtosis on Fig 6, is not interpreted especially in relation to leptokurtic, mesokurtic and platykurtic, and which area of the graph we can observe these.

Response: When we fix the parameter λ

, the skewness and kurtosis of OLLGED increases as α

and γ

increases. More specifically when parametric values are increased the skewness becomes negative and kurtosis becomes mesokurtic.

10. On section 4, the researcher mentioned that they used the MLE parameter estimation technique as it is commonly used in the literature, the researcher should justify the method in relation to its efficiency, consistency, asymptotically normal and invariant property under transformation.

Response: The justification is given for using MLE as suggested

11. On section 6, the OLLGED has 3 parameters, LLD and GED have 2 parameters and the ED has a single parameter, therefore their comparison is nor fair based on the number of parameters. Suggested is to include at least 3 more 3-parameter comparative models. Interpretation of Fig 7 and 8 have to be incorporated

Response: The suggested was compared with the commonly used distribution regardless of the number of parameters for there were distributions with four parameters see table 3 proposed distribution proved to be more powerful over them, those with fewer distributions were used too to show that the proposed distribution would stand them too.

View more View less

Competing Interests

No competing interests were disclosed.

Back to all reports

Reviewer Report

15 Views

06 Jul 2023 | for Version 1

Sadaf Khan, The islamia university bahawalpur, Bahawalpur, Pakistan

15 Views Cite this report Responses(1)

Approved With Reservations

Figure 1: bottom left and right are same.
Motivations are less convincing. There is no novelty in the proposed work. The authors need to justify why they chose generalize exponential distribution as baseline to OLL-G proposed by Gleaton and Lynch (2006)¹.
How do the authors justify the proposed distribution utility and scope in various scientific fields?
How come the authors justify the shape parameters’ physical interpretation?
What are some possible disadvantages of the model given in (5) and (6)?
In section 7, I would also recommend that the author comment more on the limitation of this distribution. How the distribution change when the size is large or too small, for example. Is it a critical point where the distribution does not apply anymore?
In section 7, the authors did not show how to interpret model parameters and their practical meanings in real data. How does OLLGED perform in comparison to OLL-Gamma, OLL-Weibull or OLL-LogNormal distribution?
Figure 7 and Figure 8 are difficult to read. Also add other graphical measures such as PP-Plots, QQ-Plots, estimated hazard rate etc.
Comment on the behavior of the datasets being employed.
What are future directives one can extract from the proposed model?

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Partly

References

1. Gleaton JU, Lynch JD: Properties of generalized log-logistic families of lifetime distributions.J Probab Statist Sci.2006; 4 (1): 51-64

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Distribution theory, applied statistics, mathematical modelling.

Respond to this report

Responses (1)

Author Response

10 Aug 2023

Srinivasa Rao Gadde, Mathematics and Statistics, The University of Dodoma, Dodoma, 338, Tanzania

Reviewer Report 1

1 Figure 1: bottom left and right are same

Response: The two figures are not the same see the shape parameter sigma which made the change in the figures

2. Motivations are less convincing. There is no novelty in the proposed work. The authors need to justify why they chose generalize exponential distribution as baseline to OLL-G proposed by Gleaton and Lynch (2006)1.

Response: More justification for the selection of GED as baseline over others distributions in existence including OLL-G as proposed by Gleaton and Lynch (2006)

3 How do the authors justify the proposed distribution utility and scope in various scientific fields?

Response: A number (6) of justification for the proposed distribution are given

4. How come the authors justify the shape parameters’ physical interpretation?

Response: We have explained the various physical appearances of our model in Figure 1

5. What are some possible disadvantages of the model given in (5) and (6)?

Response: They are very flexible and change into other distributions as the parameters change

6. In section 7, I would also recommend that the author comment more on the limitation of this distribution. How the distribution change when the size is large or too small, for example? Is it a critical point where the distribution does not apply anymore?

Response: The bias and mean square error of the parameters decrease as the sample size increases. The limitation of the proposed model is for very small values the bias and MSE are not stable. This model may not suitable for small samples and high peaked data.

7. In section 7, the authors did not show how to interpret model parameters and their practical meanings in real data. How does OLLGED perform in comparison to OLL-Gamma, OLL-Weibull or OLL-Log Normal distribution?

Response: The part was added to give more practical meaning and comparison of suggested OLLGED to other existing distributions.

8. Figure 7 and Figure 8 are difficult to read. Also add other graphical measures such as PP-Plots, QQ-Plots, estimated hazard rate etc.

Response: Now figures can be ready and pp and qq are displayed in Figure 9 and Figure 10

9. Comment on the behavior of the datasets being employed.

Response: Table 3 and Table 6 have been added to describe data sets

10. What are future directives one can extract from the proposed model?

Response: The proposed OLLGED is among the best in dealing with heavy-tailed data sets and right-skewed data

View more View less

Competing Interests

No competing interests were disclosed.

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

[1] 1. Mudholkar G, Freimer M, Srivastava DK: The exponentiated weibull Family:a reanalysis of the bus-motorfailure-data. Technometrics. 1995; 436–445.

[2] 2. Martinez AS, Gonzal, Tercariol CAS: Generalized Probability Functions. Advances in Mathematical Physics. 2009; 1–13.

[3] 3. Gupta RC, Gupta PL, Gupta RD: Modeling failure time data by Lehmann alternatives. Commun. Stat. Theory Methods. 1998; 27(4): 887–904.

[4] 4. Gupta RD, Kundu D: Theory & Methods: Generalized exponential distributions. Aust. N. Z. J. Stat. 2002; 41(2).

[5] 5. Gupta RD, Kundu D: Generalized exponential distribution: different method of estimations. J. Stat. Comput. Simul. 2001; 69(4): 315–337. Publisher Full Text

[6] 6. Gupta RD, Kundu D: Generalized Exponential Distribution: Existing Methods and Some Recent Developments. J. Stat. Plan. Inference. 2007; 137(11): 3537–3547. Publisher Full Text

[7] 7. Gupta RD, Kundu D: Discriminating between Weibull and generalized exponential distributions. The Network Computational and Methodological Statistics (CMStatistics) and the International Association of Statistical Computing (IASC); 2003; 43(2).

[8] 8. Olapade A: On extended type I generalized logistic distribution. Intational Journal of Mathematics and Mathematical. Science. 2004; 57.

[9] 9. Raqab MZ, Ahsanullah M: Estimation of Location and Scale Parameters of Generalized Exponential Distribution Based on Order Statistics. J. Stat. Comput. Simul. 2001; 69.

[10] 10. Kundu D, Gupta RD: eneralized exponential distribution: Bayesian estimations. Comput. Stat. Data Anal. 2008; 52(4): 1873–1883. Publisher Full Text

[11] 11. Kundu S, Gupta AK: Analysis and Modeling of Fixed Bed Column Operations on As(V) Removal by Adsorption onto Iron Oxide-Coated Cement (IOCC). J. Colloid Interface Sci. 2005; 290(1): 52–60. PubMed Abstract | Publisher Full Text

[12] 12. Raqab MZ, Madi MT, Kundu D: Estimation of Probability of Y greater than X for the 3-parameter generalized exponential distribution. Commun. Stat. Theory Methods. 2008; 37(18): 2854–2864. Publisher Full Text

[13] 13. Dey S, Alzaatreh A, Zhang, et al.: A New Extension of Generalized Exponential Distribution with Application to Ozone Data. Ozone Sci. Eng. 2017; 39.

[14] 14. Nadarajah S, Kotz S: The Beta Exponential Distribution. Reliab. Eng. Syst. Saf. 2006; 91.

[15] 15. Cordeiro GM, Lemonte AJ: The β-Birnbaum–Saunders distribution: an improved distribution for fatigue life modeling. Comput. Stat. 2011; 1445–1461.

[16] 16. Alexander C, Cordeiro GM, Ortega, et al.: Generalized beta-generated distributions. Comput. Stat. Data Anal. 2012; 1880–1897.

[17] 17. Özyapıcı, Bilgehan B, Şensoy ZB: Generalized probability density function and applications to the experimental data in electrical circuits and systems. International Journal of Circuit Theory and Applications. 2020; 2266–2279.

[18] 18. Alizadeh, Ozel G, Altun, et al.: The Odd Log-Logistic Marshall-Olkin Lindley Model for Lifetime Data. J. Stat. Theory Appl. 2017; 16(3). Publisher Full Text

[19] 19. Karamikabir H, Afshari M, Alizadeh, et al.: The Odd Log-Logistic Burr-X Family of Distributions: Properties and Applications. J. Stat. Theory Appl. 2021; 20(2). Publisher Full Text

[20] 20. Eghwerido JT, Nzei LC, David IJ, et al.: The Gompertz extended generalized exponential distribution: properties and applications. Communications Faculty of Sciences University of Ankara Series A1: Mathematics and Statistics. 2020; 69(1): 739–753. Publisher Full Text

[21] 21. Gleaton U, Lynch JD: On the Distribution of the Breaking Strain of a Bundle of Brittle Elastic Fibers. Adv. Appl. Probab. 2003; 36(01).

[22] 22. Gleaton JU, Lynch JD: Properties of generalized log-logistic families of lifetime distributions. J. Probab. Stat. Sci. 2006; 04.

[23] 23. Gupta RD, Kundu D: Generalized exponential distribution: Existing results and some recent developments. J. Stat. Plan. Inference. 2007.

[24] 24. Ragab A, Green JR: On order statistics from thelog-logistic distribution and their properties. Communications in Statistics-theory and Methods. 1984; 13.

[25] 25. Kantam RRL, Rosaiah K, Rao GS: Acceptance sampling based on life tests: log-logistic models. J. Appl. Stat. 2001; 28.

[26] 26. Bleed O: New Exponential Cumulative Hazard Method for Generating Continuous Family Distributions. Journal of Alasmarya University: Basic and Applied Sciences. 2020; 5(1).

[27] 27. Coria VH, Maximov R-D, Melchor-Hernández CL: Perturbative method for maximum likelihood estimation of the Weibull distribution parameters. Springerplus. 2016; 5(5). Publisher Full Text

[28] 28. R Core Team: R: A Language and Environment for Statistical Computing.2020. Reference Source

[29] 29. Silva RV, Ramos MW, Silva FG, et al.: The Exponentiated Kumaraswamy-G Class: General Properties and Application. Revista Colombiana de Estadística. 2019; 1–33.

[30] 30. Bekker A, Roux JJJ, Mostert PJ: A Generalization of the Compound Rayleigh Distribution: Using a Bayesian Methods on Cancer Survival Times. Commun. Stat. Theory Methods. 2000; 29(7): 1419–1433. Publisher Full Text

[31] 31. Rosaiah K, Rao GS, Sivakumar D, et al.: The Odd Generalized Exponential Log Logistic Distribution. International Journal of Mathematics and Statistics Invention. 2016; 4(5).

[32] 32. Rosaiah, Kantam RRL, Prasad V, et al.: Reliability Estimation in Type-II Generalized Log-Logistic Distribution. Int. J. Agric. Stat. Sci.. 2008; 4(2).

[33] 33. Kanaparthi, Rao, Kalyani, et al.: Odds Exponential Log Logistic Distribution: Properties and Estimation. J. Math. Stat. 2017; 13(1): 14–23. Publisher Full Text

[34] 34. Ragab A, Green: On Order Statistics From the Log-Logistic Distribution and Their Properties. Commun. Stat. Theory Methods. 1984; 13(21): 2713–2724. Publisher Full Text

The odd log-logistic generalized exponential distribution: Application on survival times of chemotherapy patients data

Abstract

Background

Methods

Results

Conclusions

Keywords

Revised Amendments from Version 2

1. Introduction

(1)

(2)

(3)

(4)

2. The OLLGED and its special models

(5)

(6)

Figure 1. Visual presentation of pdf plots of the OLLGED for various parameters.

Figure 2. Visual presentation of CDF plots of the OLLGED for various parameters.

(7)

(8)

Figure 3. Visual presentation of survival function plots of the OLLGED for various parameters.

Figure 4. Visual presentation of hazard rate plots of the OLLGED for various parameters.

3. Properties

3.1 Useful expansions

(9)

(10)

(11)

(12)

(13)

(14)

3.2 Quantile function

(15)

3.3 Moments and generating functions

(16)

(17)

(18)

(19)

(20)

(21)

3.4 Skewness and Kurtosis

(22)

Figure 5. Visual presentation for Skewness of the OLLGED.

(23)

Figure 6. The Kurtosis of the OLLGED.

Table 1. The calculated moments, skewness, and kurtosis measures of the OLLGED for selected parameter values.

3.5 Residual and reversed residual life

3.6 Order statistics

(24)

(25)

4. Parametric estimation

5. Simulation study

Table 2. Average bias and MSE of OLLGED for various parametric combinations.

6. Data analysis

Table 3. Goodness-of-fit statistics for the waiting times' data.

Table 4. The estimates (SEs’), their p-value, and KS for waiting time data.

Table 5. Goodness-of-fit statistics for the survival time data.

Table 6. The estimates (their SEs in parentheses), KS, and its p-value for survival time data.

Figure 7. The densities fitted (left), CDF plots (middle) and PP-plot (right) for various models for waiting time data.

Figure 8. The densities fitted (left), CDF plots (middle) and PP-plot (right) for various models for survival time data.

7. Discussions and conclusion

Ethical considerations

Patient consent

Consent for publication

Data availability

Availability of data and material

Acknowledgements

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated