Keywords
Investment Activity, Investment Project, Financial Risk, Financial Markets
Investment Activity, Investment Project, Financial Risk, Financial Markets
Mathematical models designed to forecast the dynamics of investment projects with risky returns are necessary for socially responsible activities.1 The considered activities aimed at maintaining or improving the quality of life of the population. This applies, primarily to certain groups of society such as the elderly, and others in need of social protection, youth, women, and minors.2,3
Long-term planning distinguishes the operation of such institutional investors like pension funds. These financial players differ in their incomparably longer business cycles from other market participants such as the manufacturing sector, trade in goods and services to the population.2 In addition, being socially oriented subjects and the tasks of making a profit, they consider the sustainability of development of the society and maintenance of the quality of life to be the most critical priority.1–3 Such institutional investors in the world have a significant impact on the business climate due to the scale of their activities.4 Over the following decades, they are among the top participants in NYSE (The New York Stock Exchange), SSE (Shanghai Stock Exchange), and LSE (London Stock Exchange) securities markets and stand out on the Tokyo Stock Exchange. This research outlines the methods and results aimed at the digital transformation of methods for forecasting long-term institutional investments.1–3 The considered global institutional investors could include such as BlackRock Vanguard Asset Management, State Street Global Advisors, BNY (Bank of New York) Mellon Investment Management EMEA (Europe, the Middle East and Africa) Limited, J.P. Morgan Asset Management, PIMCO (Pacific Investment Management Company), Capital Group, Prudential Financial, Inc., Goldman Sachs Asset, Management International, Amundi Asset Management etc.
The most significant benefit to the study is brought by mathematical modeling with the use of computer calculations. This is because it becomes possible to replicate the results and implement the obtained algorithms as part of expert systems and automated software systems for consulting specialists and helping in making decisions. Regardless of their activity area, the sustainability calculation must assume that the life cycle of citizens providing contributions is limited. Also, from statistical reports regularly maintained by governmental organizations, the parameters of the distribution of the duration of the accumulation phase over the array of people and the time of life in the subsequent period are known.4 The authors are trying to show that the point of the maximum value of profit is one of the reference indicators. The considered indicator makes the great impact on the relevant investment decision.
When developing a mathematical description of the activities of institutional investors, it is necessary to consider the fundamental factor related to the business planning horizon. The basis of mathematical formalisms in this paper is the dynamic analysis of projects classified as the high yield investment program (HYIP).
The main similarity in digital transformation is noticeable in such criteria as the global use of Internet platforms using Web 4.0 technologies.5 An additional driver was transferring the services online during the pandemic and the resulting new opportunities to attract the broad masses of citizens to the activities of institutional investors. Also, the development of such projects is facilitated by the widespread introduction of online money transfer systems, anonymous payment systems, cryptocurrency technologies, and the availability of investment programs of the leading banks.6–8
The next feature of the operation conditions of an institutional financial player is the significant values of dispersion when calculating the distribution function of the time of reaching the threshold for payments to investors of HYIP projects. Consequently, a part of the assets must have high liquidity. But on the other hand, institutional participants use the second feature, which is the most extended activity horizon in terms of time, and can use low liquidity instruments due to the low probability of occurrence of circumstances forcing them to sell ahead of schedule. Combining these factors increases sustainability through risk diversification. The authors assume that a significant number of investors needs the assessment of the risks of entering the project. The authors are trying to show that the point of the maximum value of profit is one of the reference indicators. Meanwhile, the investor’s choice depends on this indicator.
For our mathematical modeling, we will divide the players by the time they have been present on the market. A very high percentage of profitability distinguishes the so-called fast HYIPs, but the duration of their activity is minimal. This puts them in the category of risky investments, more like gambling. More common is the long-term HYIP type with a meager interest rate and terms of deferred payment.9
We define the arguments of the mathematical model as:
is the regular rate of return; means the sequence number of the payment period, meets the condition ; is the volume of investment; is the number of participants making contributions to the project; is the total amount of the project; is the amount of project funds available during the period of activity with the sequence number ; means the overall planning horizon of the project. In this presentation, the indicator is not the traditional annual interest rate but the widely varying interest rate for the period specified by the investment conditions adopted in HYIP calculations. If it is necessary to compare the requirements provided by different projects, we use the calculation of the practical value according to the nominal value by the following formula that returns the effective annual interest rate:
where indicates the period of compounding interest in days in the 360 days year using the American NASD method (National Association of Securities Dealers).10
Let’s calculate the variant of the linear dependence number of participants , while the number of investors involved in the project on an accrual basis is equal to , then the following expression for the total amount is true:
Since the break-even operation is necessary, (because it is necessary to avoid losses with a negative ratio of attracted and paid funds) it follows the restriction that the inequality is satisfied. We take the integer part of this result to calculate the project's duration because the calculation needs an integer: .11 This is the break-even time of the project. Accordingly, it is possible to calculate the maximum possible total amount of money at the project's disposal . To do this, we use the well-known formula for calculating an arithmetic progression for the considered sum.12–14
where means summation index.Since this progression is equal to: , then using the available duration , as a result we get the value of maximum possible total amount of money :
The distinctive features distinguishing the fast and long term HYIPs are immediately visible.15 Indeed, when decreases, the income increases. But on the other hand, the attractiveness of such projects is decreasing, limiting the possibility of lowering the rate.13,14
For an ordinary participant, an unprepared investor, a methodology for assessing the risks of entering such projects is necessary.16–18 For this, a mathematical model of the dynamics of HYIP programs is proposed. For illustration purposes, Figure 1 shows the calculation of in the case of linear modeling of number of investors (participants) for a quantity of participants below 20 000. Cash receipts line reflects the difference between the income of the investors’ sums and the amounts payable to investors.
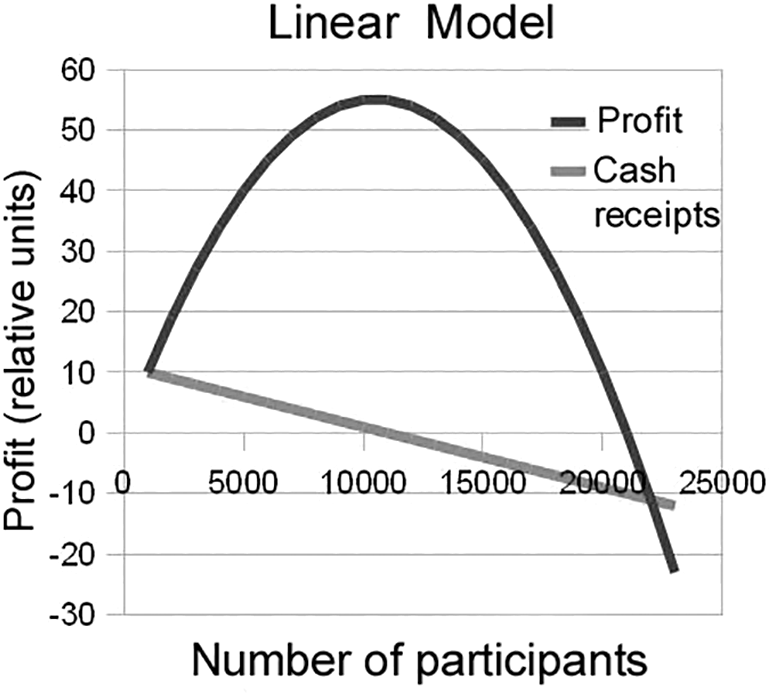
Such a simple approximate calculation gives a general idea of the process dynamics and allows to estimate the period of profit zeroing. This point of the maximum value of profit calculated either by taking the first derivative, or on a computer, is essential for decision-making and risk assessment.19–21 For long periods of project operation, it is recommended to use other calculation conditions. For example, the Verhulst method is standard in economic calculations.22,23
We then carried out the analysis with two types of dependency of changes in the number of investors of the following type:
1. growth in geometric progression, the denominator of which is equal to ()
2. by Verhulst’s S-dependency where ( is the starting pool of participants, reflects the equivalent of the value , which allows comparing two types of processes, is the potential volume of the pool of investors).
The calculation results are shown in Figure 2 and show that these two types of dependencies show similar dynamics at the initial stage (both curves could look similar). The calculation was carried out using a computer for a geometric progression and for Verhulst's S-dependency.
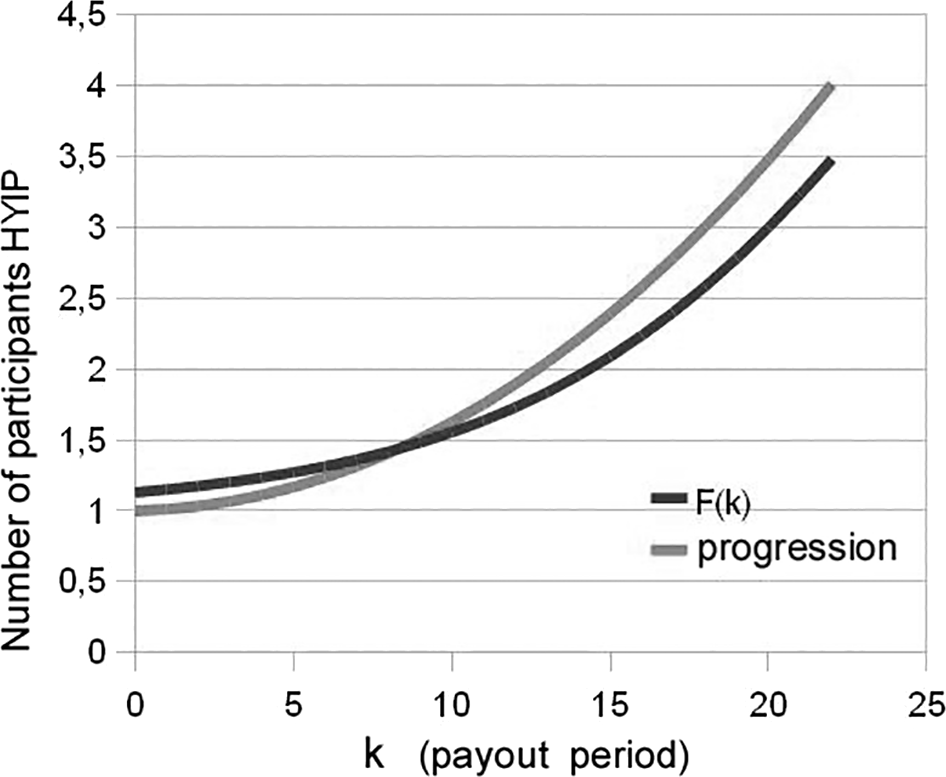
So, the obtained result allows one to carry out the calculation using a geometric progression and present the formulas in an analytical form. The analysis begins with determining the volume of funds in the amount of raised during the period . Next, we determine the payments in the period to the project participants.24,25 Their number for the previous periods is calculated22,23 using the well-known formula for geometric progression: . Profitability condition is formulated as:
For a significant number of investors, it is necessary to be able to assess the risks of entering the project. One of the reference indicators is the point of the maximum value of profit. Knowing this indicator makes it possible to take a balanced approach to choosing the investment direction. For determination, the following calculation method can be used.
Calculating the sum of the progression in the equation by using the well-known formula for geometric progression:
Then we can formulate the break-even condition:
Additionally, from the conditions and , it follows that: .
Hence, it is clear that the left side of equation (2) is always greater than zero. Let’s carry out the transformation and analysis of its right side.26–29
In case if the relation is fulfilled: , or, which is the same: , the break-even indicators are always met. In reality, this corresponds to an increase in money that exceeds the amount of interest paid. The sum increases as long as the relation is fulfilled: .
On the other hand, the number of investors, especially those interested in a particular project, is limited. This condition is met only at the initial stage.30–32
In the case , for a sufficiently large , inequality2 is no longer fulfilled due to the growth of the summand included in the denominator. The solution of equation (2) concerning an unknown argument leads to the following calculations:
from this expression, carrying out a conversion of type:
we obtain: .By an algebraic substitution, we have the following condition: .
This makes it possible to calculate the break-even parameters by solving the inequality:
Calculation by formula (3) gives the desired value of the considered point of the maximum value.
The article outlines the methods and results aimed at the digital transformation of methods for forecasting long-term institutional investments. The mathematical formalisms1–3 are of great practical importance. To restore the dynamics of HYIP projects, it is enough to get several slices of economic indicators. This can be implemented in software in the form of a decision-making system. The advanced planning algorithm can be immediately applied since payments are made online and using the digital trail in most high-yield projects. On the one hand, this will reduce the risks for investors.
On the other hand, carrying out such analysis regarding its sustainability will enable project organizers to conduct business more confidently. Since this segment of economic relations affects a significant proportion of the population, the confident operation also has a severe social effect. It belongs to the system of life quality indicators.
Sergey Evgenievich Barykin; Orignal draft, conceptualization, methods; Sergey Mikhailovich Sergeev: Formal analysis, investigation; Irina Vasilievna Kapustina: validation, visualization; Elena de la Poza: Data curation, reviews, editing, formal analysis; Larisa Nikolaevna Borisoglebskaya: Resources, supervision, visualization; Daria Varlamova: Resources, software; Marianna Serezhaevna Ovakimyan: Data curation, formal analysis, software; Anna Evgenievna Karmanova: software, validation, formal analysis. All author agreed to the published version of the manuscript.
figshare: Barykin, Sergey (2022): Figures (Linear & Non-linear).xlsx. https://doi.org/10.6084/m9.figshare.20407509.v1. 33
This project contains the following underlying data:
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the work clearly and accurately presented and does it cite the current literature?
Partly
Is the study design appropriate and is the work technically sound?
Partly
Are sufficient details of methods and analysis provided to allow replication by others?
Partly
If applicable, is the statistical analysis and its interpretation appropriate?
Partly
Are all the source data underlying the results available to ensure full reproducibility?
Partly
Are the conclusions drawn adequately supported by the results?
Partly
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: NA
Is the work clearly and accurately presented and does it cite the current literature?
Yes
Is the study design appropriate and is the work technically sound?
Yes
Are sufficient details of methods and analysis provided to allow replication by others?
Yes
If applicable, is the statistical analysis and its interpretation appropriate?
Yes
Are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions drawn adequately supported by the results?
Yes
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: AI, ML, Business Rules Management (Finance Domains).
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 1 07 Dec 22 |
read | read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)