Introduction
Radiomics is the science of high-throughput mining of quantitative image information from medical images to reveal a spectrum of characteristics and information content in form of features that are not appreciable by the human eyes.1–7 Many studies have shown that medical images contain abundant information about shape, intensity, and texture of the volume of interest that can reveal characterization of underlying pathology.1,2,5–19 In modern medicine, such information can play an important role in detection of image-based biomarkers/signatures to enhance the predictive power of diagnostic and prognostic tools. Radiomics information constitutes a part of multi-omics,20 which typically consists of ample of features extracted from different information modalities. Radiomics features show promise toward serving as biomarkers of outcome of cancer and other human pathology.1–20
In the recent years, as many complex multi-omics datasets have been applied in different fields of healthcare, the importance of feature engineering process with capability of feature interpretation has increased.21 Nowadays, feature engineering plays a key role in the field of multi-omics. Feature engineering enables mining of associations between input variables and relevant outcomes, including underlying pathology, to reveal feature- predictive biomarkers among different multi-omics data.21
Feature engineering or multivariable feature analysis refers to the process of recruiting comprehensive statistical methods and domain knowledge to reveal the most relevant subset of features from the raw feature sets to be used in supervised or unsupervised predictive analytics processes.22–28 Such analyses can be either performed in the spatial-domain (image feature space), or the frequency-domain to highlight specific information and reveal the most relevant and explanatory features towards the application of interest. The focus of the frequency-based feature engineering techniques is to decompose the raw information into different frequency bandwidths or information components in the frequency-domain which can be compared among different samples/cases and used for model development.29–33 Multiresolution and filter-based radiomics analyses such as wavelet transform,29,30,34,35 Fourier-based adaptive filter or transform,36–39 Discrete Orthonormal Stock-well Transform (DOST),40,41 Law’s textural information,31,42 and Gabor filter banks32,33 are examples of such frequency-based analysis approaches.
Wavelet decomposition (WD) techniques43,44 form a more recent addition to the collection of multispectral signal analysis techniques. Unlike other frequency-based analysis methods such as Discrete Fourier Transform analysis,38,39,45–48 Laplacian pyramids49 and etc., WD techniques provide a complete image representation by performing a full decomposition of the data according to scale and orientation, which are considered essential properties of feature description in the feature engineering process.
Our research group50–53 among others29,30,34,35,54–66 have shown that the frequency and wavelet analysis of multi-spectral features in the frequency domain can reveal more structured and relevant information details pertinent to the outcome of interest compared to the spatial domain.29,30,36,48,67 We have recently demonstrated that radiomic features extracted from primary tumor gross tumor volumes (GTVs) delineated on contrast-enhanced (CE) CT images of oropharyngeal squamous cell carcinoma (OPSCC) patients can be used to construct a highly sensitive and specific classifier for characterization and prediction of human papilloma virus (HPV).53,68,69 In a related study, we have also shown36,50–52 that frequency analysis of these images can provide valuable information to enhance the predictive power of the radiomics-based model for classification of HPV+/- in OPSCC patients.
In this pilot study, we investigated the potential predictive value and interpretability of the three-dimensional (3D) Discrete Wavelet Decomposition (3D-WD) analysis for HPV characterization of GTVs of OPSCC patients. The primary objective of this research was to characterize and identify the spatial frequency sub-bands and their respective regions of primary tumor most likely responsible for characterization of HPV.
Methods
Ethical approval
In this study, CT images and HPV status information of 128 OPSCC patients treated at our institution were retrospectively retrieved from our institutional head and neck databases. All the datasets were de-identified and used in this research according to a retrospective protocol approved by our institutional review board of Henry Ford Health System. The IRB approval number was 8751 and there was no requirement for patients to provide written informed consent for this study.
Patient population, Imaging specifications, and HPV detection
One hundred twenty-eight OPSCC patients with known HPV-status (60 HPV+ and 68 HPV-) from our institutional head and neck database were retrospectively studied. The retrospective protocol for this research was approved by our institutional review board (IRB#: 8751). All patients had tumor biopsies to evaluate HPV status using immunohistochemistry P16 protein (IHC) testing (70% nuclear and cytoplasmic staining cutoff) as a surrogate with PCR and ISH tests used only in equivocal cases.70–73 We excluded all cases with non-squamous cell carcinoma, those with no/equivocal P16 protein testing as well as P16+ve cases located in oral cavity or larynx. HPV+ve neck lymph nodes with no oropharyngeal primary were also excluded. All cases underwent diagnostic intravenous contrast enhanced Computed Tomography (CE-CT) scans of the head and neck region within eight weeks of radiotherapy planning or staging surgery. Primary GTV’s were delineated by a radiation oncologist based on enhancing lesions on diagnostic CE-CT guided by FDG-PET CT whenever available. Contouring was performed using the Eclipse v15.5 treatment planning system (TPS, Varian Medical Systems/Siemens Healthineers, Palo Alto CA). CE-CT images were acquired using a Philips Brilliance Big bore scanner (Philips HealthCare, Best, Netherlands) with 199-441 mA at 120 kVp, FOV = 23-26 cm, matrix size = 512 × 512, in-plane resolution: 0.041 to 0.055 cm, with thickness of 0.9 to 3.5 mm with 75-140 ml of contrast agent injected at a rate of 2-3 ml-sec-1, followed by scanning after a 35 second delay.
Image pre-processing
Data quantization, and image re-segmentation74,75 were performed according to the recommendations provided by the image biomarker standardization initiative (IBSI)75,76 using our in-house-developed software system (ROdiomiX77,78) as follows: Effects of variable voxel sizes (Signal to Noise Ratio, SNR inconsistency) from CE-CT images were minimized by resampling the image voxels isotropically (1 mm3/voxel) using trilinear interpolation technique.74,75 GTV intensities were then quantized and uniformly resampled into 64 intensity levels using a Fixed Bin Number (FBN74,75) and volume re-segmentation was also performed to exclude any ‘out of range’ voxels (due to partial volume effect of resampling and FBN quantization).74,75
Three-dimensional discrete wavelet decomposition analysis and feature extraction
Discrete wavelet decomposition analysis refers to a discrete multiresolution representation of a signal based on the theory of the wavelets,79 using a finite set of resolutions namely the powers of two. A Discrete Wavelet Transform (DWT) of a signal is computed by applying a quadrature mirror filter (QMF) on the signal.80,81 QMF filter bank is one of the key components in the design of frequency-based signal processing systems with a wide range of applications in the fields of Electrical engineering and Biomedical signal processing.82 The main structure of a two-channel QMF bank consists of analysis and synthesis components (see subfigure 1A). In the analysis component, the input signal is divided into two segments using a low-pass filter and a high-pass filter followed by decimators. At the receiving end, the output of the decimators is given to the interpolators, followed by a low-pass filter and a high-pass filter in the synthesis components. The outputs of both filters are then combined to obtain the reconstructed signal. As shown in subfigure 1A and the following equations (1)-(3), the analysis and synthesis filters must meet the following criteria in the filter space (z):
(1)
(2)
(3)
where
and
are the analysis filters, while
and
are the synthesis filters. In QMF filter bank,
is defined as the prototype filter and
and
are derived from this prototype filter.
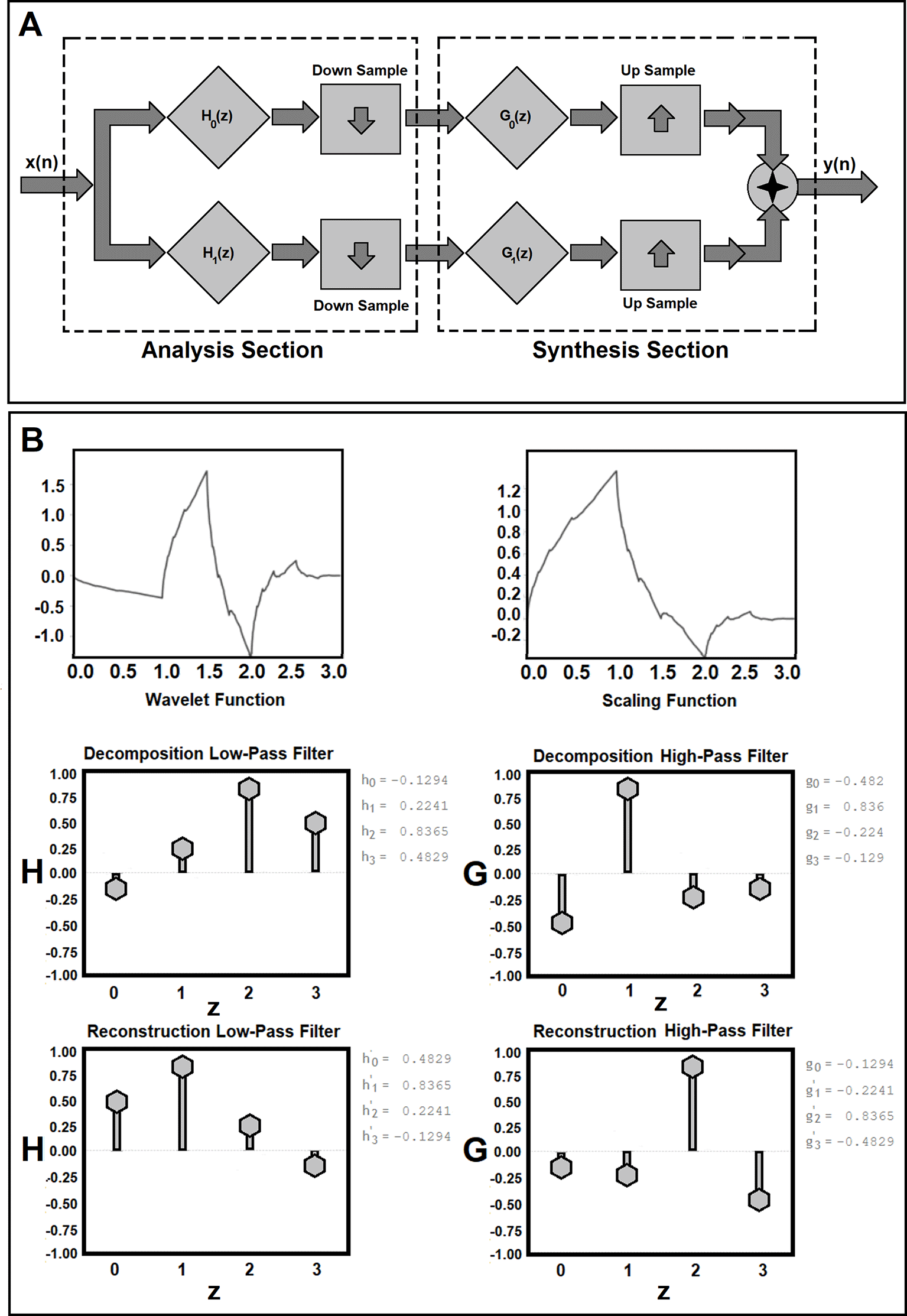
Figure 1. Workflow for Quadrature Mirror Filter (QMF) bank for analysis and synthesis components of the discrete wavelet decomposition and reconstruction is shown in subfigure 1A. Subfigure 1B shows the mother wavelet (ψ) and its scaling functions (father wavelet, φ) in the time domain along with their four corresponding discrete analysis (H(z)), z is the discrete normalized frequency number) and synthesis filters (G(z)) generated for a Symlets function with two momentums.
As shown in subfigure 1B, the Symlets function is nearly symmetric and meet the orthogonality, and biorthogonality properties.
In this study, similar to the conventional digital signal processing, the magnitude of the QMF79,83 was chosen as the mirror image around π/2 of that of another filter. The filter responses in the filter space are also symmetric around and meet the following criteria:
(4)
where Ω refers to the frequency,
H0 is the prototype filter, and the sampling rate is normalized to 2π. During the analysis process of the original signal, the resulting high-pass and low-pass signals were reduced by a factor of two, giving a critically sampled two-channel representation of the original signal. Finally, in addition to meeting the standard QMF properties, the analysis filters also met the following criteria:
(5)
The main idea was to split the higher half and the lower half of the signal spectrum by means of a second order band-pass filter and a low pass filter, to subsample the signal corresponding to the lower half of the spectrum and to iterate the process. This is roughly equivalent to dividing the spectrum of the signal in successive bands and extracting the signal details corresponding to each of these bands independently.79,83 A modified version of Daubechies wavelets, called Symlets (with two vanishing momentums), nearly symmetrical, which met the orthogonality and biorthogonality conditions, was used as the ‘mother’ (ψ) and ‘father' (scaling function, φ) wavelets in the time domain84–86 (see the first two rows of subfigure 1B).
Before decomposing the tumor information, to make the spatial resolution of the GTV on the CE-CT information consistent and comparable, the largest GTV (among all patient GTV’s) encompassing a rectangular prism were identified and selected as the reference dimensions. All segmented GTVs were three-dimensionally zero-padded using the reference dimensions and a 3D Discrete WD analysis was performed on the CE-CT images of patients’ GTVs to decompose their tumor information (see subfigure 2A for one level of decomposition) into three decomposition levels (corresponding to 22 3D Wavelet Coefficient matrices). These were modeled by series of bi-orthonormal high-pass and low-pass wavelet coefficients. Then, the following equation (Eq. 6), the Log Energy Entropy (LEE) of the 3D wavelet coefficients was calculated as the radiomics features for all the decomposition levels:
(6)
where
refers to the 3D discrete wavelet coefficient at decomposition level
L (
L = 1, 2, and 3), with
dimensions at the decomposition level of
L.
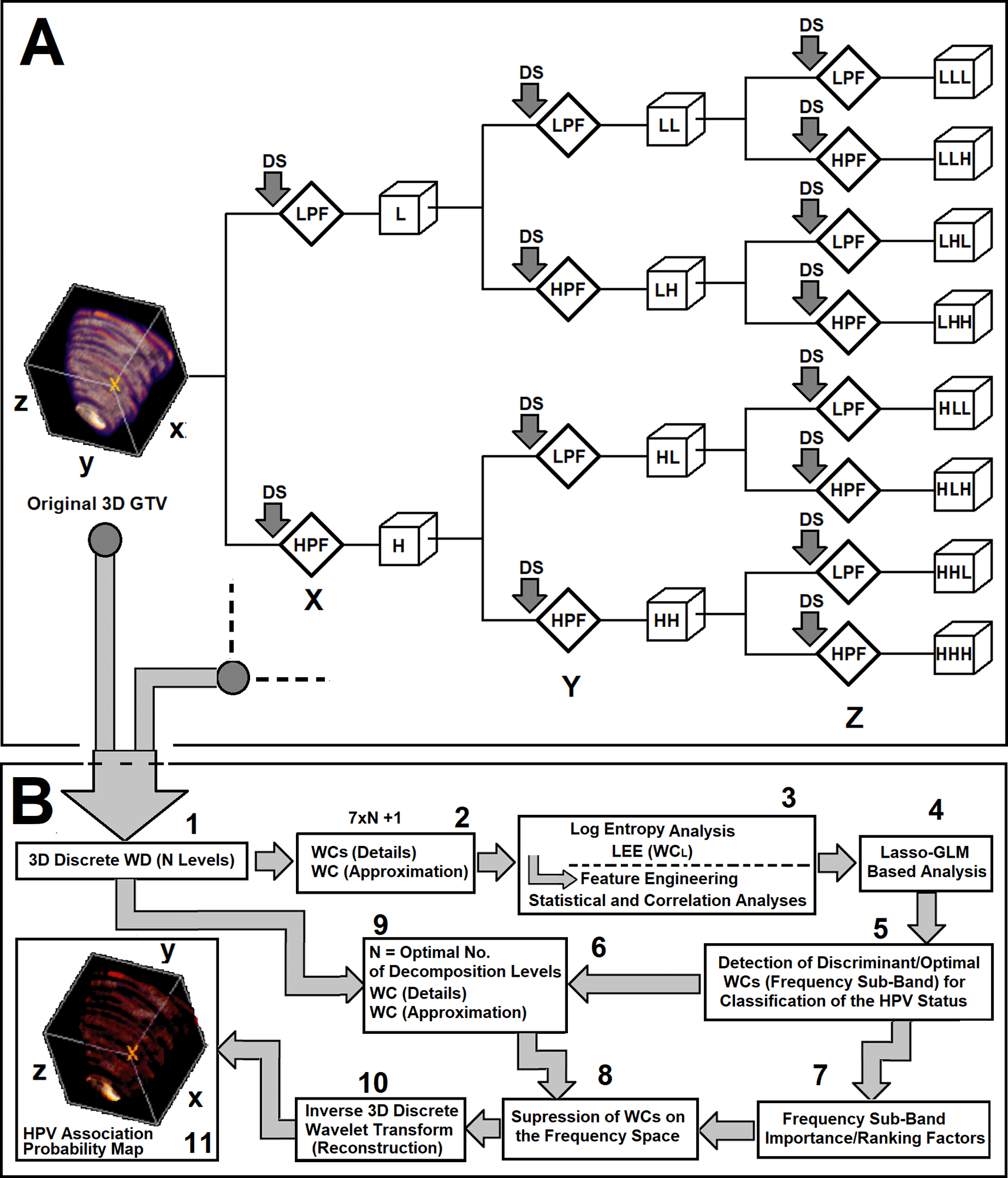
Figure 2. Subfigure 2A shows one level of decomposition for 3D wavelet decomposition technique. As shown in this figure, the GTV information is decomposed based on the basic block of two-channel filter bank (QMF) and for each decomposition level, seven Wavelet Coefficients (WCs, details) plus one approximation are generated. As Shown in this subfigure, the 3D data is decomposed into a series of frequency-based details and approximation coefficients. The first filtering operation, LLL, contains the lowpass component (approximation) at the level of the decomposition. The rest of the filtering operations, ‘HLL’, ‘LHL’, ‘HHL’, ‘LLH’, ‘HLH’, ‘LHH’, and ‘HHH’ refer to the detail coefficients. The sequence of letters gives the order in which the separable filtering operations are applied from left to right. For example, ‘LHH’ means that the low-pass (scaling) filter with down-sampling is applied to the rows of X of the GTV, followed by the high-pass (wavelet) filter with down-sampling applied to the columns of Y of the GTV. Finally, the high-pass filter with down-sampling is applied to the 3rd dimension, Z, of the GTV. Subfigure 2B demonstrate the workflow and processing stages of the 3D-WD analysis, feature extraction, feature engineering, model development, and frequency-domain interpretation analyses of the study.
Feature screening and correlation analysis
For each patient cohort (with known HPV status), a series of LEE features were computed from different WCL. A total of 22 features were computed for each patient. The Levene’s test87 was performed on the mean values of the computed LEEs of the two patient cohorts (HPV- and HPV+) to test for homogeneity of the variance between the two groups. For each individual feature corresponding to a specific frequency sub-band, at each decomposition level, based on the results of the Levene’s test, either the Welch’s test88 or analysis of variance (ANOVA) was used (CI=95%) as a measure of statistically significant differences between the two groups. The test results were used to select the discriminant WC features at different decomposition levels between the two frequency sub-bands of the two groups. Biserial correlation (BSC)89 between HPV status and the values of each LEE feature set was also calculated and used as a threshold (|BSC|> 0.20,89) for further screening of the discriminant features. Afterwards, the Belsley collinearity diagnostics test90 was also applied on the discriminant LEE features for assessing the strength of multicollinearity among different LEE features. This process removes the features of different frequency sub-bands (at different decomposition level, L) with high multicollinearity (with condition index larger than the default tolerance, 30, and variance-decomposition proportions exceeding the default tolerance, 0.50)90 from the feature space. These feature engineering analyses were used to identify statistically dominant and discriminant frequency sub-bands contributing towards the prediction of HPV+/- status.
Lasso-based feature selection, feature ranking, classification performance, and generalization error: After removing the correlated features and identifying the discriminant features, a Generalized Linear Model (GLM)91 combined with a Least Absolute Shrinkage Selection Operator (Lasso,92,93) method for regularization and optimization of model coefficients (Lasso-GLM) was used to evaluate and select the most significant frequency sub-band features among the engineered features for the prediction of HPV status. Lasso imposes a penalty on the GLM coefficients to perform variable selection by setting certain coefficients to zero and shrinking remaining coefficients. A Lasso-GLM with k-fold (k=10) cross validation technique (Lasso-GLM-KFCV)91–93 was used to perform L1-Regularization, where a parameter, λ was tuned to produce the optimal coefficient values in the entropy-based Wavelet coefficient feature space. For each tuning parameter value, λ, a deviance value was computed, representing the average error (mean square error, MSE) over all 10 sub cohorts (cross-validation91–93) of the full dataset (128 cases). The optimal λ, value of λ at minimum deviance plus one Standard Error (1 SE), was selected for the Lasso-GLM for all possible cross validation (CV) folds91–93 for feature selection and ranking.
The generalization error and performance of the sub-band features in the prediction of HPV status were estimated using a 10-fold Nested Cross-Validation (Nested-CV) technique.94 As shown in Figure 3A, the full dataset was split into 10 non-overlapping folds and two independent loops (outer and inner loops) were defined. In the outer loop, for each trial, the data was split into two folds (training + validation fold and test fold), and for the inner loop, only the validation + training fold was used to select and tune the model parameters via a k-fold cross-validation technique. This process was repeated 10 times (see subfigure 3A, outer loop) and each time an independent test set was held out for the estimation of the generalization error and performance of the tuned model (in the inner loop). Finally, a non-parametric adjusted Receiver-Operating-Characteristic (ROC) method was employed to calculate the average values of the Area-Under ROC (AUC), Positive predictive values (PPV’s) and Negative Predictive Values (PPV’s) for all holdout test sets as the estimate of the generalization error and performance of the classifiers. Then, an optimal Lasso-GLM model was constructed based on the most frequent features selected by the Lasso-GLM analysis for different folds and evaluated based on the average value of the L1-regularization, λ plus 1SE.
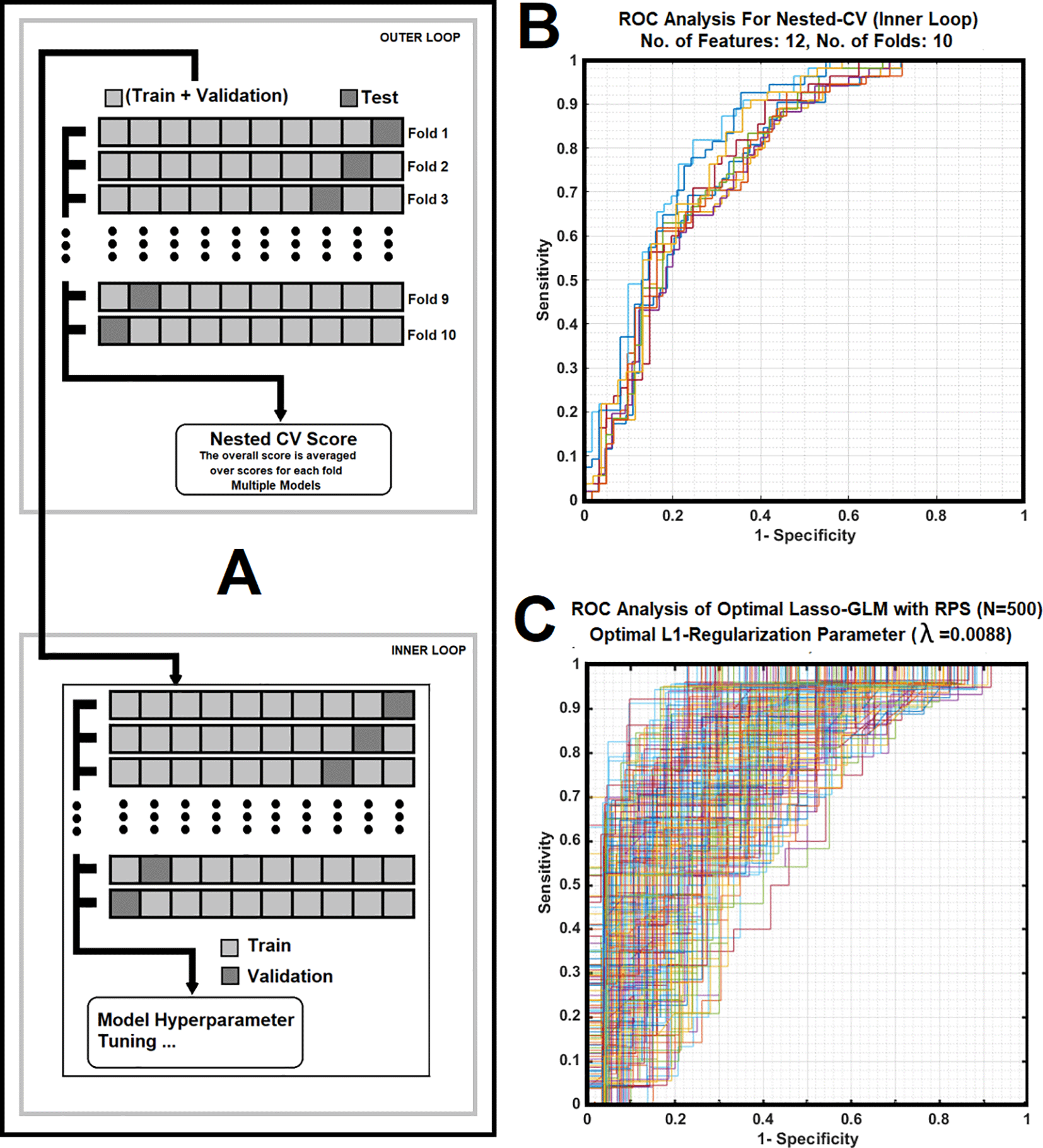
Figure 3. Subfigure 3A shows a 10-fold nested cross validation with its inner and outer loop cores that was used in the study. Subfigure 3B illustrates average of Receiver operating characteristic (ROC) curves corresponding to 10 folds nested CV for the inner loop, with each iteration related to a different division of the training plus validation sub-cohort for the Lasso-GLM analysis. Subfigure 3C demonstrates ROC curves of the optimal classifier corresponding to 500 iterations (RPS), with each iteration related to a different division of training for the K-fold CV (optimal λ = 0.0088).
Frequency and time-domain based interpretation analyses
Ultimately, the optimal set of Wavelet Coefficients (WC) selected by the Lasso analysis of LEE and their corresponding importance factors were used to weight (enhance/suppress) the wavelet sub-bands of each decomposed GTV followed by a 3D Inverse Discrete Wavelet Transform (3D-IDWT) for reconstructing (see steps 7 to 11 of the Subfigure 2B) the tumor zones with highest information towards characterizing HPV.
Results
Workflow for Quadrature Mirror Filter (QMF) bank for analysis and synthesis components of the discrete WD decomposition and reconstruction is shown in subfigure 1A. Subfigure 1A shows the main structure of a two-channel QMF bank which consists of analysis and synthesis components. Subfigure 1B shows the ‘mother’ wavelet (ψ) and its scaling functions (‘father’ wavelet, φ) in the time domain along with their four corresponding discrete analysis filters (H(z)) and synthesis filters (G(z)) generated for a Symlet function with two vanishing momentums. As shown in subfigure 1B, the Symlet function (with two momentums) is nearly symmetric and meets the orthogonality and biorthogonality properties.
Subfigure 2A shows one level of decomposition for the 3D discrete wavelet decomposition analysis used in this work. As shown in subfigures 2A and B, the 3D GTV information is successively decomposed using the basic operator block, the two-channel filter bank (QMF, see Subfigure 1A). At each decomposition level, seven Wavelet Coefficients (WCs, details) plus one approximation Wavelet Coefficient were generated.
The GTVs of the patients were decomposed at three levels. As shown in subfigure 2A and B, the 3D data is decomposed into a series of frequency-based details and approximation coefficients (corresponding to 22 WCs, 21 details plus one approximation). The first filtering operation at the end of each decomposition level, LLL, contains the low-pass component (highest approximation of the information) at that particular decomposition level. The rest of the filtering operations, ‘HLL’, ‘LHL’, ‘HHL’, ‘LLH’, ‘HLH’, ‘LHH’, and ‘HHH’ refer to the detailed coefficients (higher frequency sub-bands). The sequence of letters in each filtering operation gives the order in which the separable filtering operations are applied from left to right. For instance, ‘LHH’ means that the low-pass filter (scaling) with down-sampling (order of two) is applied to the rows (X dimension) of the GTV data, followed by the high-pass filter (wavelet) with down-sampling (order two) applied to the columns (Y dimension) of the GTV data. Finally, the high-pass filter with down-sampling (order of two) is applied to the 3rd dimension (Z) of the GTV information. Subfigure 2B demonstrates the workflow and processing stages of the 3D-WD analysis, feature extraction, feature engineering, model development, and frequency-domain interpretation analysis used in the study. Among 22 LEE feature set corresponding to 22 different frequency sub-bands from three decomposition levels, only 13 LEE features showed high predictive power and were discriminant between the two patient cohorts (HPV- and HPV+).
Subfigure 3A shows a 10-fold nested cross validation with its inner and outer loop cores that was used in the model development and validation parts of the study. During each iteration, in the inner loop, 116 subjects were used as the training plus validation set, while 12 cases were used as the test set. Subfigure 3B illustrates average of the Receiver operating characteristic (ROC) curves corresponding to 10 folds nested CV for the inner loop, with each iteration related to a different division of the training plus validation sub-cohort for the Lasso-GLM analysis. Subfigure 3C demonstrates Receiver operating characteristic (ROC) curves corresponding to 500 iterations (using RPS), with each iteration related to a different division of training and testing for the optimal (λ=0.0088) Lasso-GLM classifier.
Table 1 illustrates the average values for AUC, PPV, NPV, and their corresponding values at 95% Confidence Intervals as well as their standard deviations and standard errors for the outer loop of the nested cross validation (NCV, N=10) process.
Table 1. This table illustrates the average values for AUC, precision, accuracy, PPV, NPV, and their corresponding values at 95% CIs, as well as their standard deviations and standard errors for the outer loop of the nested cross validation (N=10) process.
| NCV (Outer Loop, K=10, Metric) | AUC | PPV | NPV |
|---|
| Mean Value | 0.800 | 0.800 | 0.910 |
| Confidence Interval | [0.719, 0.880] | [0.702, 0.897] | [0.840, 0.981] |
| Standard Deviation | 0.113 | 0.137 | 0.098 |
| Standard Error | 0.036 | 0.043 | 0.031 |
Subfigure 4A shows cross-validation analysis (K=10) results for finding the optimal L1-regularization parameter (λ at one standard error, Lambda 1SE). As shown in this figure, the average value of the λ at 1SE over ten different folds was 0.009. Subfigure 4B illustrates the Lasso-GLM feature ranking of the selected sub-band features in the Wavelet feature space at the optimal L1-regularization (λ=0.009). Subfigure 4C shows the trace plot of Lasso-GLM selected coefficients for the LEE based Wavelet features after L1-regularization. Trace plots with negative and positive coefficients are associated with HPV- and + classes respectively. As shown in this figure, the LEEs of the two WCs (HHL1 and HLL1 corresponding to details information) at decomposition level of one were associated with positive Lasso coefficients (shown in yellow and purple colors respectively, corresponding to HPV+ cohorts). Similarly, the LEEs of the two WCs (one approximation, LLL3, and one detail information, LHL3) at decomposition level of three were associated with negative Lasso coefficients (in blue, and brown colors respectively, corresponding to HPV- cohorts).
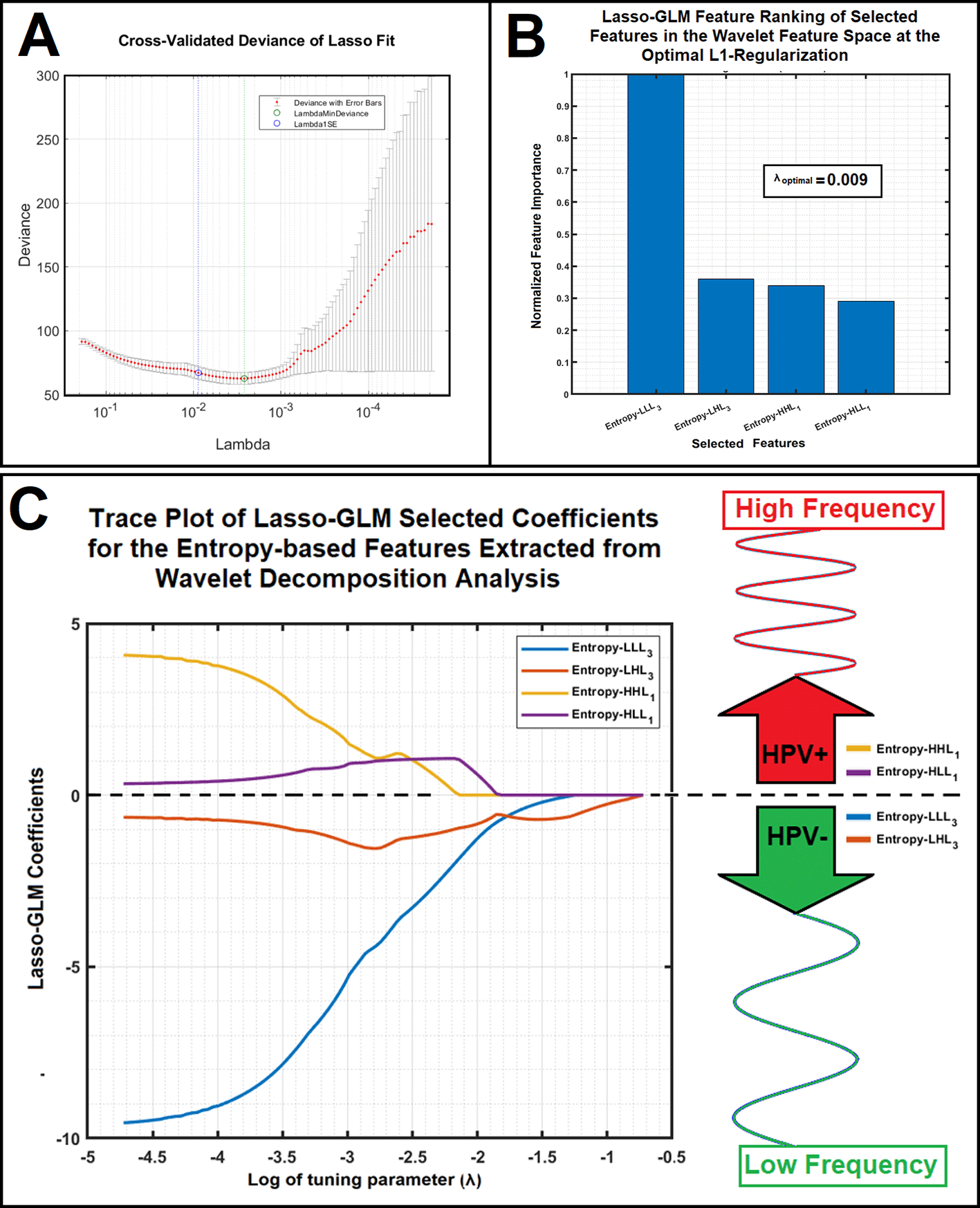
Figure 4. Subfigure 4A shows cross-validation analysis (K=10) results for finding the optimal L1 regularization parameter: Lambda at one standard error (Lambda 1SE). Subfigure 4B illustrates the Lasso-GLM feature ranking of the selected sub-band features in the Wavelet feature space for the optimal L1-regularization (λ=0.009). Subfigure 4C shows the trace plot of Lasso-GLM selected coefficients for the LEE based Wavelet features after L1-regularization. Trace plots with negative and positive coefficients are associated with HPV- and + classes respectively.
As shown in this figure, Entropy of HHL1 and Entropy of HLL1 features have positive Lasso coefficients (shown in yellow and purple colors respectively) and Entropy of LLL3 and Entropy of LHL3 features have negative Lasso coefficients (in blue, and brown colors respectively).
Figure 5 demonstrates normalized contrast enhanced CT images (first and third columns) after isotropic resampling, quantization, and re-segmentation of the data along with respective HPV probability maps (second and forth columns) for the segmented GTV cross sections of 10 example patients reconstructed by the inverse 3D-discrete WD analysis (see steps 7 to 11 of the Subfigure 2B).
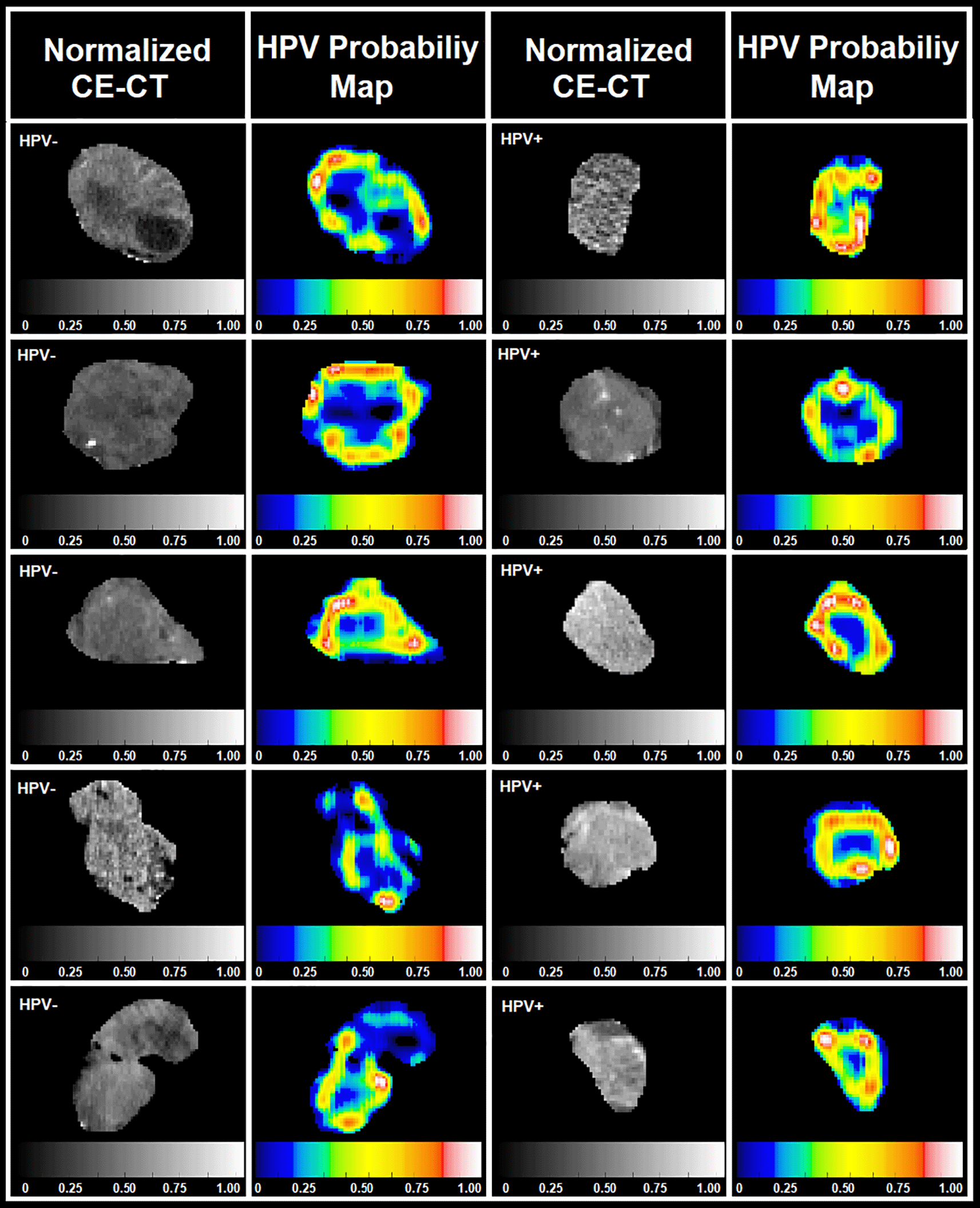
Figure 5. This figure shows normalized contrast enhanced CT images (first and third columns) and their respective HPV association probability maps (second and forth columns) for GTV cross sections of 10 patients reconstructed by the inverse 3D-WD analysis.
As shown in Table 1, the NCV-based performance of the Lasso-GLM classifier for the prediction of HPV status was: 0.800, 0.800, and 0.910 for AUC, PPV, and NPV, respectively. The CV-based evaluation (with 500 RPS) of the optimal Lasso-GLM (with average L1 regularization parameter) performance were: AUC/PPV/NPV= 0.798/0.745/0.823.
Discussion
A frequency-based spectral analysis was introduced to decompose the intensity and textural information of the tumor into different frequency sub-bands to reveal the frequency-based information most associated with characteristics of HPV. Figure 4B and 4C demonstrate spatial frequency sub-bands most associated with the characterization of HPV. Inclusion of such spatial frequency information in the development of radiomics-based models for prediction of HPV is likely to enhance model performance. Our group, among others36,95–98 have studied the recruitment of spatial frequency-based information to extract image characteristics relevant to the target/outcome of interest. We have shown that frequency-based data can contain more relevant information compared to real-domain data. For instance, Martinez et al.67 utilized the Fourier frequency-spectral analysis method to evaluate different machine learning systems for automatic categorization of ovarian tumors on ultrasound images. Lofstedt et al.95 investigated GLCM textural analysis for generating textural features that are invariant from image pre-processing steps (e.g. image quantization).
Other groups95–98 have also recruited Fourier spectral analyses to find the optimal scale selection method for refinement of the GLCM textural analysis as well as for other tasks in image-based classification.
Despite the promise of the applications of radiomics analysis in the therapeutic and diagnosis fields for stratification and predictive modeling, many unanswered questions remain, as elaborated previously by the IBSI.6,76 IBSI’s protocols for data processing are considered an important step toward standardization of algorithms used for extraction of radiomics features from medical images. These procedures will ensure that consistency and reproducibility are achieved among radiomics implementations at different institutions. The next step involves association between radiomics features with known patient outcomes such that reliable connections can be developed between significant radiomic features and outcomes for use in clinical modeling. These factors are considered key elements in the field of radiomics and much further investigation is needed to move this field forward.75,76 This research provides an important step toward understanding of frequency-based parameters of the radiomics feature extractor cores based on the available information content and frequency spectra of image structures. Frequency-based features have the potential to improve association between radiomics features and outcomes by minimizing the chance of under/over-sampling of the image dataset during the feature extraction phase.
The conventional feature engineering processes along with multicollinearity analysis significantly reduced the number of correlated features from 22 to 13, suggesting a benefit of statistical-based feature engineering analysis prior to modeling to remove correlated features. Indeed, the feature engineering analysis results confirmed that suppression of the multicollinearity effects among different spatial frequencies prior to the Lasso analysis can improve model performance and enable more robust L1 regularization in the frequency-based feature space. We used L1 regularization to control the overfitting problem by penalizing the model coefficients in Lasso optimization. However, the Lasso technique is limited. For instance, in a group of variables where pairwise correlations are high (or where variables have high level of multicollinearity) Lasso will tend to select only arbitrarily and randomly one feature as the representative of the entire group of features. To address this limitation, we utilized the Belsley collinearity diagnostics test90 to remove the frequency-based features with high level of multicollinearity. This decreases the feature dimensionality, which improves model accuracy and generalizability. However, the Belsley test can still be limited in the small sample size setting which is the case in this study (N = 128).
In addition to the multicollinearity effect, the Lasso-GLM classifier may be prone to overfitting due to the small sample size (N = 128). The Lasso method is also sensitive to the chosen value of the tuning parameter (penalty term) which constrains the magnitude of the estimated coefficients.91–93 The tuning parameter controls the amount of regularization, and selecting the optimal value is an important step since each parameter value corresponds to a different fitted model.91–93 To address this issue, we utilized K-fold Cross validation (KFCV) in the inner loop of the NCV with collective deviance.91–93 To minimize the effects of potential feature non-uniformities from different patient sub cohorts/folds, we used a higher number of folds (K = 10) in the KFCV and NCV analyses compared to the default number (K=5) recommended by the literature.91–93
As shown in Figure 3C and Table 1, the high variance of the prediction performance in the ROC analysis of the optimal Lasso-GLM classifier illustrates the contributions of different frequency bandwidths with insignificant information at an average L1-regularization toward characterization of HPV. The ROC family curves (corresponding to 10 folds) show a tight spread (see Figure 3B) suggests higher generalizability of the Lasso-GLM from contribution of distinct frequency bands at different L1-regularization levels. Such a tight spread implies that the dominant frequency features used to develop the model are sparse and less sensitive to tumor heterogeneity across different patients.
Model development, validation, and testing without nested CV uses the same data to train the classifier parameters and evaluate model performance. This could lead to information leakage from the training cohort into the testing cohort resulting in overfitting of the model. The overfitting magnitude is primarily dependent on the size of the dataset and the complexity of the model. To minimize this problem, we implemented a nested CV technique94 with a conventional KFCV in its inner loop, in which the testing dataset is held-out during the training and validation phases at each of multiple folds.
Prior to the wavelet analysis, the time-domain spectral information of the GTVs was interpolated to the reference dimensions. Such interpolation can increase the chance of additional up-sampling of the tumor information/resolution, adding uncertainty to the dominant frequency sub-bands identified as the discriminant features for the characterization of HPV. Finding an optimal interpolation technique with minimal effect on the tumor resolution/information is a challenging task and requires further investigation.99
Image artifacts have potential to impact on the wavelet analysis results and consequently impact the detection of the dominant frequency sub-bands. We inspected CT images of all 128 patients for identification of streaking artifacts impacting the visibility of the GTV’s. Given that the number of CT slices with dental filling artifacts was less than about 1% of the total number of 2D-CT cuts utilized (N=3596), we elected not to split the dataset into separate cohorts (with and without CT artifacts) for separate wavelet analyses and relevant modeling.
The wavelet decomposition technique is a mathematical transformation which decomposes a signal into multiple lower resolution levels by controlling the scaling and shifting factors of a single wavelet function (‘mother’ wavelet). Unlike the discrete Fourier transform (DFT), the wavelet analysis refers not just to a single transform, but rather a set of transforms, each with a different set of wavelet basis functions. Robustness and efficiency of different frequency-based methods are highly dependent on the properties of their transformation kernels. Here, a Symlet wavelet function (with two momentums) which was nearly symmetrical, orthogonal, and biorthogonal was used as the ‘mother’ wavelet of the analysis. The symlets are nearly symmetrical wavelets proposed by Daubechies as modifications to the Daubechies wavelet family.84–86
Nonsymmetrical filters can cause a shift variance on the frequency spectrum which can introduce a biasing effect on the analysis results. It has been shown100,101 that the Symlet functions which belongs to the orthogonal wavelet family are compactly supported wavelets with minimal asymmetry and a maximum number of vanishing moments for a given support length.100,101 One of the main advantages of using bi-orthogonal wavelet (such as Symlets) compared to orthogonal wavelet is their ability to filter phase information linearly. This means that the phase response of the filter is a linear function of the frequency which ensures preservation of energy of the signal during the transformation.
Indeed, in addition to the Symlets, there are many other ‘mother’ wavelet functions (such as Haar, Daubechies, Coiflets, Morlet, Mexican Hat, Meyer, and other real and complex wavelets) which can be used in the wavelet analysis. However, each of these basis functions has different properties and can produce different results when they are applied on the same dataset. Thus, the “mother’ wavelet function and its properties (such as supporting length, number of vanishing momentums, etc.) can be selected and fine-tuned according to the image specifications and the goals of the study. Thus, for a more accurate analysis of different image resolutions, these parameters should be carefully selected and optimized accordingly. For instance, the wavelet kernel with the shortest possible support length of one (such as the Haar wavelet) can capture more detailed information enabling a more precise linear transformation to generate the high-pass coefficients. Thus, it might be more beneficial to use an asymmetrical frequency-based ‘mother’ wavelet for the analysis of images in which axial sampling pitch (i.e. slice thickness, intra slice distance) is much larger than in-plane sampling pitch (inter-slice distance), as it is often the case with CT and MR modalities. Of note, in our analyses, we used a nearly symmetrical ‘mother’ wavelet because the wavelet analysis was performed on a volumetric dataset which was isotropically resampled to 1 mm3/voxel.
The results (see Figure 5) of this pilot study confirm that compared to the central-zones of tumors, peritumoral-regions have more information for characterization of HPV. The 3D-wavelet analysis of GTVs in these patients not only provided adequate information for building an HPV classifier, but also revealed important spatial frequency-based tumor information which can be used as the most representative features for HPV classification. The HPV association probability maps can be susceptible to the radiomics feature Log Energy Entropy (LEE) which was used to evaluate the importance of the wavelet coefficients as well as the properties of the ‘mother’ wavelet function. The number of vanishing moments, shape (symmetric or asymmetric), scaling function, minimum supporting length, orthogonality or biorthogonality conditions, etc. can impact on the reconstruction error of the inverse wavelet analysis, directly affecting the identified tumor zones associated with the HPV. Further investigation in this area of research is warranted.
The frequency decomposition analysis results revealed that any spatial frequency information of the tumor with up-sampling level higher than three (2L with L = 3, equivalent to eight times of the image resolution, 8 mm) does not add any significant HPV-related information to the extracted features set. Results also imply that tumor zones with smaller image structures or components corresponding to higher details or higher spatial frequencies (components ~<2 mm corresponding to one decomposition level) contain important radiomics information for characterization of HPV+ patients. On the other hand, tumor zones with larger image structures or components corresponding to lower spatial frequencies (components ~>8 mm, corresponding to three decomposition levels) contain more information for classification of HPV- cases.
Our group and others53,102–106 have previously shown that in OPSCC patients, as the mean breadth value (proportional to tumor size) of the tumor increases the chance the tumor for being classified as HPV negative increases. Interestingly, in this study, the LLL3 frequency sub-band (spatial frequency information approximation with three levels of up-sampling being more related to the overall structure of tumor) being identified as a discriminant feature associated with the HPV negativity agrees with this finding.
Further investigation, including adaptive filtering analysis (designing ‘mother’ wavelet filters according to the image specifications), using different radiomics features and related impact on reconstruction errors in images with different levels of frequency information are warranted.
The findings of this pilot study and similar studies can be beneficial toward establishing the role of filter-based radiomic analysis in studying the underlying imaging characteristics of clinical relevance. The main aim of this study was to apply a series of feature engineering processes in the frequency domain to suppress the frequency bandwidth information of the tumor less relevant to HPV characterization while enhancing the tumor frequency bandwidths information descriptive towards prediction of HPV.
Another limitation of this work pertains to the use of p-16 immunohistochemistry (IHC) testing for determining the HPV status of the OPSCC patients. Although it has become a standard-of-care method for HPV testing of OPSCC, the p-16 IHC testing method does have limitations which can impact the accuracy of HPV test results.107–110 Recent systematic reviews of the diagnostic accuracy of p16-IHC in OPSCCs analyzed 24 and 31 different studies and concluded that p16-IHC has a high sensitivity (90.5%), but modest specificity (83.3%) to classify HPV status when used as a single test.109,111,112 Such variations in the performance of the p16-IHC testing can directly affect the source of truth, which was used for the feature engineering and model development parts of the study. This would also add a degree of uncertainty to the model accuracy. Despite this limitation, the radiomics findings here agree with those of other studies and with radiological findings of tumor characteristics of HPV+/- patients with OPSCC’s.113
Conclusion
We developed a frequency-based wavelet analysis to characterize and identify the spatial frequency sub-bands and regions of primary tumor responsible for the characterization of HPV in patients with OPSCC. The overall findings of this study, albeit subject to confirmation in a larger patient population, demonstrated encouraging results in support of frequency analysis of CT images toward tumor zone-based interpretation, characterization, radiomics-based modeling of HPV and differentiation between HPV+/- cohorts in this patient cohort.
Data and Software availability
This project contains the following underlying data which can be directly downloaded from GITHUB using the following link:
https://github.com/Ebadian-HFHS/F1000-DATASETS
1- HPVClass_128_Cases.txt: The tumor biopsies immunohistochemistry P16 protein (IHC) testing results for all128 OPSCC patients.
2- MAIN-LEE-WCS.txt: The Log Energy Entropy (LEE) features of the 3D wavelet coefficients calculated as the radiomics features for all the three decomposition levels (21 detail information plus one approximation).
3- MAIN-LEE-WCS-FEATURE-NAMES: Names of different Wavelet Coefficients for three different decomposition levels corresponding to the computed features listed in MAIN-LEE-WCS.txt.
4- FEATURE_ENGINEERING.txt: Feature Engineering analysis results including: Levene’s test, the Welch’s test or analysis of variance (ANOVA) between the two HPV cohorts, the Biserial correlation (BSC) analysis for further screening of the discriminant features, and the Belsley collinearity diagnostics test results.
5- FEATURE_ENGINEERING-NAMES: Names of different Wavelet Coefficients for three different decomposition levels selected by the feature engineering analysis corresponding to the computed features listed in FEATURE_ENGINEERING.txt.
6- Details of the repository where your data are hosted, a description of the data files and the license under which they are held should be included.
Software availability
Pre-processing stages of the project can be replicated using the ROdiomiX software. ROdiomX is an IBSI validated software for radiomics analysis of medical images in radiation oncology. ROdiomX is a free research software that can be shared and redistributed amongst different research users. This software is shared and distributed among research communities to accelerate radiomic analysis as well as supporting the goal of radiomic feature standardization based on the IBSI guidelines.
URL: https://github.com/Ebadian-HFHS/ROdiomiX
Bagher-Ebadian H, Chetty IJ. Technical Note: ROdiomiX: A validated software for radiomics analysis of medical images in radiation oncology [published online ahead of print 2020/11/11]. Med Phys. 2020;48(1):354-365.Copyright (C) 2020. Authors: Drs. Hassan Bagher-Ebadian & Indrin J. Chetty, Location: Department of Radiation Oncology, Henry Ford Health System, Detroit, MI 48202, USA.
The ROdiomiX is a publicly shared software that meets the criteria requested by the F1000Research.





Comments on this article Comments (0)