Keywords
Cosmology, large-scale structure of universe, relativistic processes.
The success of the theories of special and general relativity in describing localised phenomena, such as objects undergoing high speed motion or located in gravitational fields, needs no further elaboration. However, when applied to the evolution of the universe several problems arise which can require an additional model, e.g., inflation during the early expansion, and adjustments to parameters to account for phenomena such as the late-time acceleration of the universe.
Focusing on the difference between the ways in which space and time are measured, this paper shows that there are two paths which allow the equations of special relativity to be produced from the same basic postulates.
Both the standard theory and the energy/momentum, or dynamic model, utilise the Minkowski metric, but with different coordinate systems. The dynamic model transforms Cartesian coordinates into an Euclidean form by multiplying the coordinates by functions of γ (= (1– ν 2/c 2)-1/2). When utilising these coordinates, the relativistic equations are unchanged for local phenomena such as the Lorentz coordinate transformation and the energy/momentum equation for high-velocity objects.
However, the derived coordinates alter the perceived overall structure of the universe in a manner that, for the simplest model under this system, allows the reproduction of observed cosmological features, such as the intrinsic flatness of the universe and the apparent late-time acceleration of its expansion, without the need of additional models or changes in parameter values.
Cosmology, large-scale structure of universe, relativistic processes.
This version tightens up the definitions of the coordinate systems, the transformations between them and the circumstances in which coordinate systems can be directly observed and when they have to be inferred. It attempts greater clarification of the relationships between the dynamic coordinates, the Minkowski metric and how they fit into the simple dynamic model of the universe. In turn this attempts to show how the dynamic coordinate system, by possessing a continually changing present, can be transformed into the standard Cartesian coordinates which only occupy time-like world lines. The paper emphasises there is no relationship between the dynamic models of the universe's behaviour and the FLRW standard models. However, comparisons of the results from the dynamic model with those from FLRW show a good fit, and presumably in turn are a good fit to astronomical data that support FLRW.
See the author's detailed response to the review by Boudewijn F. Roukema
See the author's detailed response to the review by Jackson Levi Said
The success of the current theories of special (SR) and general relativity (GR) in describing localised phenomena, such as objects undergoing high speed motion, located in local gravitational fields or generating gravitational waves, needs no further elaboration. However, when applied to the evolution of the universe several problems arise which require either an additional model, e.g., inflation to account for the flatness or the horizon problems, or adjustments to coefficients and/or parameters to account for phenomena such as the universe’s late-time acceleration and the lack of observable mass to match the universe’s expansion1.
In exploring an approach which attempts to answer at least some of these problems, while still satisfying the basic postulates of relativity, it will be shown that it is possible to utilise the same Minkowski space-time metric to construct a set of coordinates that produce an alternative overall structure of the universe. Any modification of the current theory must still conform to both the observation that the speed of light (c) is a constant in all inertial frames, and to the principle that the laws of nature are the same in all inertial frames. It also must conform to the principle of consistency, i.e., any new theory has to account for the successful predictions of the Newtonian and relativistic theories that it attempts to modify.
When carrying out such modifications care must be taken over the definitions of what is directly observable and what can only be inferred. Changes in coordinates that occur in the observer’s present can be defined as direct observations. When transforming these changes into a dimension, we can define the resulting coordinates as being directly observed if they can be revisited and are able to have different actions carried out at their location. Inferred coordinates are those that are based on a location which can only be visited once. The former can be associated with spatial dimensions while the latter is associated with time. Any temporal dimension must be constructed from indirect observations such as the reliance on memory or artificial aids such as film. Current theories rely on such a construction to complete a four-dimensional space-time, which has been very successful but has some problems on a universal scale such as those outlined above. An alternative approach is discussed which assumes, for reasons explained below, that it is the energy and momentum of objects that are fundamental to their behaviour, and from which the time element of a four-dimensional space-time coordinate system can be inferred, rather than starting from a four-dimensional coordinate system against which the energy and momentum of objects can be measured. Such an approach using the Minkowski metric allows Cartesian coordinates to be transformed into an Euclidean form (see Equation (7)–Equation (11) below). The changes between coordinate systems will be discussed, and the consequences of such changes are explored.
It will be shown that the simplest model of the universe that can be constructed using this dynamic set of coordinates consists of a surface resulting from the loci of all inertial frames of reference which have a single point of origin (the Big Bang). This surface is assumed to move radially outwards from this point in four spatial dimensions, but direct observations can only be obtained from a single viewpoint, i.e. from within each frame of reference where this surface is observed as consisting of three spatial dimensions, while the fourth spatial dimension, along which the radial motion is assumed to take place, is not directly observed but the motion is experienced as a changing present. This link between time (albeit changing) and spatial dimension results from the differences between Cartesian and dynamic coordinate systems, as discussed in the SR sections of the paper. Consequently, what is effectively a temporal dimension can be constructed to replace this fourth spatial dimension, as discussed in the Cosmology Section, but only relates to the frame containing the observer under consideration. The surface is assumed flat in the three directly observed spatial dimensions but curved in the fourth. This results in changes in orientation between the dimensions of various frames, which in turn results in frame A able to directly observe a component of frame B’s radial motion as a relative spatial motion within A’s 3D space, while the remaining component in A’s temporal dimension is directly observed as a changing time – albeit changing at a reduced rate when compared to A’s clock. The spatial component is transformed into a velocity relative to A by comparing it to the changes in time observed by A within his own frame of reference (see the sections on SR).
Every frame has the same view which, due to the surface curvature (Figure 3), has a boundary frame (now labelled frame B) which apparently travels at the velocity of light relative to the observer’s frame (frame A) and, from A’s viewpoint, B is frozen in time. Since all frames are considered equivalent then B must directly observe A as having the same conditions. This leads to the postulation that from within a frame (A) a changing present is equivalent to the changes in the spatial position of A seen from outside this frame by B - with both phenomena resulting from direct observations. In the limit since only spatial changes are seen at A by B, and only time changes are seen within A of himself, then the assumption is made that the two phenomena are equivalent. It should be noted that this is due to the space-time expanding radially in the dynamic model and so it is the universe’s space-time surface (in which all observers are located) that is apparently able to travel at the velocity of light, but only along the inferred time axis (i.e. radially) within each observer’s frame, e.g. A or B. When the boundary frame B is observed by A, B’s time axis lies completely in A’s spatial direction due to the universe’s curvature, i.e. again it is the expansion of the universe’s surface that is seen and B, in this simple model has no motion along the 3D spatial surface that is local to B’s frame and orthogonal to B’s radial motion. This radial direction is time-like in Cartesian coordinates (see SR Section) in terms of the trajectories it generates (Figure 1), while the 3D spatial surface orthogonal to this is, unsurprisingly, space-like. Frames that have no motion along the spatial surface are entirely time-like (i.e. where the observations are made of phenomena within the frame) while frames that have a real spatial motion relative to an outside observer (such as those local to A that are discussed in the SR section) are still time-like but with components in A’s spatial dimensions. However, they cannot exceed or, unless they are objects such as photons, even equal the velocity of light along the surface that is orthogonal to the local radial direction (see Figure 1b and Figure 3).

Cartesian coordinates follow the blue lines (hyperbolae) while dynamic coordinates follow the time-like axes OA, OB, OF etc. Note the time-like hyperbolae are also the locus of all time axes for inertial frames with an origin at O. As shown in Figure 1b, there are no dynamic locations on the space-like hyperbolae because in Equation (3), Equation (4), DxNNN = 0, while only DxNNM ≠ 0.
In the dynamic theory no one observer can directly observe both A and B’s views simultaneously. Hence in the Cosmology Section the labelling of views from a single frame are both direct observations and local (i.e. centred on A), while consideration of the entire surface (i.e. every inertial frame) is non-local and hence inferred.
It should be emphasised that in the transformation of the dynamic view into Cartesian space-time (see below) no object can either be inferred or directly observed in this theory as moving along spacelike world lines where they would have velocities exceeding that of light along the 3D spatial surface (see above and SR section).
In this theory all gravitational effects that we can directly observe take place along the three dimensional spatial surface. Consequently, since this dynamic model also approximates the mass distribution, both along this surface and at any given time during the surface’s expansion, as being uniform, the gravitational potential along the surface (which is normal to its expansion) is zero. This approximation allows the surface behaviour to be calculated using only special relativity (SR) and without recourse to general relativity (GR) - as will be shown in the Cosmology sections. Obviously more detailed analyses using realistic mass distributions would require GR to take a role, but the current approach shows that even in its most basic form this model provides very good predictions of the universe’s expansion (Cosmology Section).
Since the resulting model of the universe does not account for gravity, it is not related to the standard Friedmann-Lemaître-Robertson-Walker (FLRW) models. However, its results can be compared to those from the FLRW Standard Cosmology Model (Figure 5) and the combined Friedmann equations (Figure 8), which are assumed to currently give the best fits to astronomical observations. Consequently, the fact that the dynamic theory gives a good fit to such models implies it also gives a good fit to the corresponding astronomical data without the paper being sidetracked into extensive explanations and attributions of this data.
As already stated, a possible area that could lead to more than one approach arises with the inclusion of time as the equivalent of a spatial dimension. This paper leaves aside any philosophical questions about what space and time “really” are and just concentrates on the phenomena that humans consider as providing realistic analogues of such phenomena, i.e., as discussed below, changes in energy are considered to be analogues of changes in time (clocks) while a spatial dimension can be considered as corresponding to a distribution in mass (rulers). It is these analogues that are used to provide quantifiable tests of relativistic theories. They also illustrate the problems of mixing time and space to form the space-time of standard, or indeed any, theory of relativity.
Basically, relativistic effects are measured with a clock and a ruler. To state the obvious a ruler is composed of a distribution of matter which is taken to define a spatial dimension. For the purposes of relativistic measurements, the ruler is unchanging for an observer in the same inertial frame, i.e. the coordinates it provides along a spatial dimension are static within an inertial frame and any position on this ruler can be revisited at will (albeit at different times). In contrast a clock gives a continuous (and regular) conversion of potential into kinetic energy, which is able to do work on its surroundings, e.g. the release in energy from a clock spring to continuously move the clock’s hands, or the decay of radioactive material to activate a counter. This is intended to correspond to what an observer experiences as time, i.e. he is always trapped in the current moment in the sense that he can only influence or be influenced by events which happen in his present (memories of past events may be said to influence him, but can only do so in his present), but this moment is always changing*. Since the observer is always in his present, past events can only be accessed by memory or aids such as film. This access is of a different order to the interactions granted to events in the present. An observer can visit a spatial location many times and interact with what is happening at that location. The ability to physically interact with an event in time is restricted by the fact that a temporal location can only be visited once. Since the observer only exists in his changing present, temporal coordinates can only be inferred by integrating experiences of the changing present using memories or other recording devices. The ever-changing present has no real coordinate that can be directly observed in the sense of spatial coordinates, there are only directly observed changes in time - see above definitions. Hence from within an inertial frame no dimension can be directly observed in what can be assumed as the time direction. The experience of time is analogous to a piece of cardboard with a vertical slit cut in it being placed over a train window. There is an ever-changing view of a segment of the landscape seen through the slit, but you cannot see what is coming and you need either a good memory or some recording apparatus to build a complete picture of where you have been. The whole directly observable view of the world is the ever-changing view through the slit.
Changes in time in this view appear to facilitate changes in the energy state - objects appear, grow, change or vanish as they pass the slit - while space provides a framework which can facilitate a distribution of objects. Consequently, there are two routes that can be taken when attempting to mix space and time. The coordinate route of the standard theory keeps the spatial dimension unchanged while integrating the changing temporal view to give a fourth dimension which is analogous to space. The dynamic view keeps time as an ever-changing entity but requires this to be linked to objects (including other observers) which have an ever-changing spatial position. Hence the dynamic view is based on energy and momentum while the coordinate view is based on dimensions.
Since the integral of the dynamic view will give space-time coordinates (albeit artificially constructed), and since it has already been stated that, at least locally, the standard and dynamic theories must match for the dynamic view to have any validity, the next two sections show where the two theories coincide, where they diverge and the derivation of the dynamic metric.
To clarify which theory is being referred to in the following, the derivatives in the standard theory result from infinitesimal changes in the dimensional coordinates and can be used to construct trajectories. In this paper such changes are denoted by d(). In the dynamic theory D() are infinitesimal changes in coordinates which are derived from the magnitude of the change in energy experienced in the present (located in what can be constructed as the time direction - i.e., orthogonal to the spatial directions), and the momentum of objects in the spatial dimensions. These are changes along trajectories. Subscripts N and M denote any inertial frame, in contrast to A and B which usually have specified conditions such as which frame contains the observer and which the observed.
In the standard theory a single subscript is used to denote the frame in which the coordinates are located, e.g. dtA, dxB, see Equation (1) below. In the dynamic theory more than one subscript is used to describe the direct observation within a single frame (A in what follows) of how other frames appear relative to A’s measuring apparatus, e.g. two subscripts are used for time, DtAB, where the first subscript is the frame containing the observer and the second the frame from which the object being observed originates. For space there are three subscripts, e.g. DxACB where the first and third subscripts are as in the description for time, while the middle subscript is the frame in which the ruler is located against which the spatial motion is measured. In this example A is the observer, B is the object being observed relative to A’s space and C is the frame containing the ruler against which A measures B’s motion and again is relative to A’s space. Coordinates are transformed between dynamic and Cartesian descriptions within a given frame by Equation (7), while both dynamic and Cartesian coordinates are transformed between different frames by Lorentz transforms. The dynamic transform is given in Table 1 and the Cartesian in Table 2 below.
| Column 1: A’s view of B’s coordinates. | Column 2: B’s view of A’s coordinates. |
|---|---|
| DxBBG = γ(DxAAG – νDtAA): | DxAAG = γ(DxBBG + νDtBB) |
| DtBB = γ(DtAA – vDxAAG⁄c2): | DtAA = γ(DtBB + νDxBBG⁄c2). |
| Column 1 | Column 2 |
|---|---|
| dxB = γ(dxA – νdtA): | dxA = γ(dxB + νdtB) |
| dtB = γ(dtA – νdxA⁄c2): | dtA = γ(dtB + νdxB⁄c2). |
Both theories must satisfy the condition that the speed of light is the same in all inertial frames.
For the standard dimensional coordinate theory, this leads to the Minkowski metric which provides the following Cartesian relationship between space and time
where A and B are inertial frames of reference, and dτ is defined as the proper time interval, i.e. it is time recorded by a clock which moves with the object of interest and is an invariant quantity. In this paper, for brevity - but without any loss of generality – the total component of spatial motion is usually assumed to be lying along the x axis. For photons dτ = 0.
In the dynamic theory several points must be considered.
The view of all inertial frames is always done from the present of an observer, and since both theories agree that there is no such thing as a universal present, the continuous changes are seen from a single viewpoint.
The dynamic theory deals with energy and momentum, i.e. the constant change in time (where coordinates must be inferred) and space (real coordinates). For brevity, these phenomena will sometimes be referred to as “motion”. As already outlined, this motion will be denoted by DtNM for time – where M is the frame in which the clock resides, and N is the frame containing the observer – while DxNNM refers to spatial motion where M is the frame in motion relative to both a ruler (middle subscript) and observer (first subscript) located in N.
The key point in dynamic SR is that the theory assumes that the fundamental parameters are the energy/momentum (motions) of objects (which includes observers) which are used to construct a 4-vector coordinate system, and not a 4-vector coordinate system that the motion is measured against. Consequently, for the dynamic theory the above equation has to be written as
to preserve both the existence and equivalence of two unique viewpoints - A sees B as B sees A - as well as the constant value of the speed of light from both viewpoints, i.e. if B is a photon then DtAB = 0 and vice versa. However, as will now be shown, the grouping of the parameters and the general invariance of the time term will be different.
Concentrating on A as the observer with the single viewpoint, then in an inertial frame the only motion that he can directly experience is that of his clock (DtAA). He does not experience any spatial motion (DxAAA = 0), and any such motion that could be seen from outside the frame will, from A’s view, be added to the spatial motion of B. This motion A sees as being relative to A’s own ruler (DxAAB). However, A is able to see (for this illustration and accounting for relativistic Doppler effects) B’s clock (DtAB). Consequently, grouping the motion that A can see of himself, and the motion that A sees of B on separate sides of the above equation gives the infinitesimal changes in dynamic coordinates (which should be compared to the changes in standard coordinates in Equation (1)) as
The same view can be seen from B with the appropriate change in subscripts, i.e.
The first thing to note is that the invariant is now DtNN as this is the only changing parameter that N can experience of itself, and one of the main principles of SR is that nature’s laws must be the same when seen from inside an inertial frame. Since a lot of these laws are time-dependent, then if DtAA ≠ DtBB there should be an effect seen from outside the frame which cannot be ascribed to either relative velocity or gravity. No such effect has ever been reliably reported so it is a safe postulate that DtAA ≡ DtBB.
The second thing is that the only coordinates that A can directly observe are spatial. Hence the three subscripts for Dx – where the middle one relates to a ruler - compared to the two subscripts for Dt. However, as already mentioned, a time coordinate can be inferred by simply integrating Dt between two recorded events. If there is to be any overlap between the dynamic and coordinate theories, we need to find the relationship between the inferred and standard coordinates and, consequently, the relationship between their differentials.
In the standard coordinate theory, it is dτ that is the invariant between inertial frames, i.e. when we look for where the two coordinate systems overlap, we are looking for specific conditions where dτ = DtNN. This will be shown to be along the time-like hyperbola in Figure 1a where dτ is an invariant for all possible inertial frames that have their origin at O, i.e. OA= OB= OG= cdτ.
Since the dynamic theory has an ever-changing present, this is equivalent in Cartesian coordinates to mapping out a trajectory such as OB in Figure 1a.
In Figure 1a, A is the observer, and the condition dτ = DtNN can only occur where the observer and the event or object being observed lie entirely on their respective time axes, e.g. along OA, OB, OF and OG in Figure 1a. This condition corresponds to dxN = 0 in Equation (1), and DxNNM = DxNNN = 0 in Equation (3) and Equation (4). The four sets of inertial axes (A, B, F and G) in this figure are shown from A’s viewpoint. All frames have a common initial location at O. These positions are consistent with the dynamic hypothesis that from within any inertial frame, the only features of the frame that changes are those entirely connected with changes in time (i.e. DtNN).
The divisions shown on the axes in the figure are arbitrary.
In the Figure it can be seen that all inertial time axes with a common origin (O) must intersect the hyperbola, and so this hyperbola can be considered as the locus of intersections of all the time axes of objects undergoing different inertial spatial motions as seen from A.
Consequently, for these conditions to be met, the dynamic equivalence of the Cartesian coordinate viewpoint requires that every object (and hence every observer) must be located on its own time axis, even though such an axis can only be inferred by such an observer. This corresponds to the initial definitions that were given about the dynamic condition. Every point on the above hyperbola coincides with a time axis of an object which has a given relative velocity to A, and whose velocity is different to every other point on the curve. The location of an object on its own time axis means that DtAA = DtNN . However, since this occurs at every point along this curve, in general terms, DtNN and dτ are both invariant along this hyperbola.
Hence, from the above along the time-like hyperbola
And since
c2 = c2dτ2 then from Equation (1) & Equation (3),
Also, since dxN/cdtN = DxNNM/cDtNN = v/c,
then from this and Equation (6) we can, after some manipulation, derive the following relationships between dynamic and Cartesian coordinates within a given frame (N) as
Where γN = (1–v2/c2)–1/2, and γN is constant for a given inertial frame.
Hence
Consequently, we can rewrite the dynamic portion of Equation (6) in terms of Cartesian coordinates to give
To express the Cartesian and dynamic coordinates in more familiar nomenclature, let
μ,v = 0 to 3. Then cdtN = dx0; dxN = dx1; dyN = dx2; dzN = dx3.
The Minkowski metric is
Where in Cartesian coordinates
While the dynamic coordinates are
From the above it is straightforward to show the dynamic theory gives the same 4-momentum vector as the standard theory, i.e.
let U0 = dx0/dτ = γN cDtNN/dτ = cγN; and U1 = dx1/dτ = γN DxNNM/DtNN = vxγN, etc.
Then Uμ = γN(c,V) where V is the complete spatial vector, and by multiplying by the mass (m) of the object under investigation in frame M, we get
which is the 4-momentum of the standard theory. The main difference between the theories is that one corresponds to an Eulerian form while the other does not. This gives rise to the following relationship between spatial motion and a changing present.
The equivalent dynamic diagram to Figure 1a is, from A’s viewpoint, given in Figure 2. However, from this Figure when B moves relative to A in the dynamic theory, it appears to A that B’s time is partly at a reduced time rate and partly as a motion against A’s spatial dimensions. In the limit a photon would appear to A as only having a spatial motion and with no time element present. Although to an imaginary observer within the photon’s frame of reference, according to the requirement of nature’s laws having to be constant, the photon’s time would appear to proceed at DtNN while A would only have a motion along the photon’s spatial dimension during which A’s clock would appear frozen. Hence in this limit of possible frame rotations, what appears to be time from within the frame is seen from the outside as a motion through space against the background of the outside observer’s spatial dimensions. To an observer within a frame there is no observation (as distinct from inference) of any dimension of any sort - temporal or spatial - in the time direction and so it appears that the space against which this motion takes place does not exist, i.e. it has collapsed to a point on the time axis where it corresponds to the ever-changing, dimensionless present. However, the summation of all the views from every possible frame indicates the overall framework within which any individual observation is made is of four orthogonal spatial dimensions. It is just that the individual observer can only see three of them plus a changing present (see Cosmology Section).
Time dilation. In Equation (3) it should be noted that all the observations can be made by A, so the dynamics are A’s clock as seen by A (cDtAA), equated to B’s spatial motion (DxAAB) and clock (cDtAB). Dividing through by and noting v = DxAAB/DtAA, gives DtAB = DtAA, where γA = (1–v2/c2)–1/2.
Hence for the Cartesian coordinates where dtA ≠ dτ
i.e. the dynamic is the same as the standard coordinate time dilation relationship. Substituting the equivalent standard coordinates for the dynamic ones in Figure 2 (see Equation (7)) would give the same Euclidean diagram but with cdtA being kept constant and cdτ changing as the velocity of B is increased.
Length contraction. The key element when dealing with spatial dimensions in the dynamic theory is that no spatial dimension can be seen to exist by an observer in his own time direction. However, there will be items that have unchanging spatial coordinates within an inertial frame, and which can also be seen outside of that frame. Take frames A and B as being stationary relative to each other at some point in time. Both are equipped with rods of equal length along the x axis. The frames are then given a relative velocity of v, and A then compares B’s rod with his own. The dynamic equations given above can be represented by a simple axis rotation equal to ζ = sin–1(v/c), and by the acknowledgement that the spatial x coordinates lie in the same direction as Dx.
For the dynamic theory let any coordinate terms be represented (e.g. the rod length) by δx, δy etc. Being a coordinate within an inertial frame, this is unchanging in time, in contrast to Dx which we have defined as constantly changing to match the ever-changing present. The subscript convention is the same as for Dx, e.g. δxABC where A is the observer, B the frame containing the ruler and C is the frame containing an object that A wishes to measure, and which lies in A’s x direction. For a complete four-dimensional Euclidean-type coordinate transform, A would see δxBBB as having a component δxBBB cos ζ in A’s spatial direction and δxBBB sin ζ along A’s time axis. However, since there is no spatial dimension that can be seen by A along his own time axis, the length of B’s rod which is present in A’s inertial frame is seen by A to only be
This is the same length contraction result as for the standard theory, and this length contraction is independent of time since we are using δx. The apparent contraction in coordinate space for B (seen from A), is also seen (by A) to occur in the spatial motion of frames relative to B, since the motion takes place in a space that appears to have contracted by a factor of . Since only space is involved when considering just δ, and A’s clock is unaffected, then in turn the motion arising from this contraction can be assumed to occur for all times between inertial frames. This includes observations by both A and B due to the postulation of the equivalence of viewpoints in inertial frames in SR.
Both the time and space effects in special relativity are apparent effects. The word "apparent" is used as the changes in the parameters are brought about by changes in perspective rather than any fundamental change of the value of the parameter, e.g. in the length contraction discussed above, the same contraction is seen by B in A’s rod. Fundamental changes may be assumed to only occur once gravitation (or acceleration according to Einstein’s equivalence principle) is considered, but this is beyond the scope of the present paper.
It should also be noted that in the dynamic theory while DxNNN and DxNMM are always zero (the frame cannot move relative to its own ruler), δxNNN and δxNMM can have non-zero values.
Lorentz transformation. This is the transformation of the same type of coordinate (dynamic or Cartesian) between different frames, in contrast to Equation (7) where the transformation is between coordinate systems in the same frame.
An additional spatial motion must be used by the dynamic theory to obtain the Lorentz transformation, as DxNNN is zero. For all spatial motions taking place along A’s x direction, the transformation can be derived as follows.
Take frame G moving relative to both A and B, where the spatial motion of G relative to the ruler in B is observed by B to be DxBBG, and the spatial motion relative to a ruler in A (observed by A) is DxAAG. The velocity of B (observed by A) is given by v = DxAAB/DtAA; the velocity of G relative to B (observed by B) is w = DxBBG/DtBB and the velocity of G relative to A (observed by A) is u = DxAAG/DtAA.
Let
γ1 = (1–v2/c2)–1/2; γ2 = (1–u2/c2)–1/2 and γ3 = (1–w2/c2)–1/2
Where in Table 1, γ= (γ1 γ2)⁄γ3 for Column 1, and γ= (γ1 γ3)⁄γ2 for Column 2.
Dividing the top row by the bottom in Column 1 gives
while dividing the top row by the bottom in Column 2 gives
When comparing these equations with the Cartesian coordinate version of the Lorentz transformation, they give both the same velocity-addition relationships and, as will be shown, the same coordinate transforms.
In Table 1 multiply both sides of each equation by γ and substituting the appropriate d() term from Equation (7). This gives substitute Table 2 in standard Cartesian coordinates which corresponds to the standard transformation.
The 4-vector, energy and momentum. As already shown the dynamic theory gives the same 4-momentum relationship as the coordinate theory, but this results in a change of interpretation of the role of rest mass energy (E0). This result can be obtained geometrically for the dynamic theory by taking the top right-hand quadrant of Figure 2, but omitting the G axis. In the following, the terms OA, OB, OE and EB are those used in Figure 2.
Note that γ = γ1 in the rest of the text. Let each of the sides of the triangle OBE in this figure be divided by cDtAB and denote them by a dashed superscript, which then gives OB′ = OB/cDtAB; OE′ = OE/cDtAB. Hence triangles OBE and OB′E′ are similar which gives
OB′ = OA′ = cDtBB/cDtAB = cDtAA/cDtAB = γ;
E′B′ = DxAAB/cDtAB = γv/c;
OE′ = 1.
The energy/momentum vectors can then be obtained by multiplying each of the sides by B’s rest mass energy (E0 = mc2) where m is B’s mass. In turn this gives
OE′ = E0.
OB′ = γE0 = E.
E′B′ = γmvc2/c = pc,
where p is momentum, i.e. p = γmv.
From Figure 2, OB2 = OE2 + EB2. Hence (OB′)2 = (OE′)2 + (E′ B′)2, and so
as in the Cartesian coordinate theory.
It should be noted that the rest mass energy lies in A’s time direction and so appears to be linked to the continually changing time, i.e. it is a kinetic rather than a static phenomenon.
Let κ = E/cDtAA = E/cDtBB where the mass term m in E = γmc2 is still B’s mass. From this, κ is also equal to E0/cDtAB. Substituting κ into Equation (15) leads to the general conclusions that DtNN is proportional to E; DtNM is proportional to E0 and hence
This is consistent with the basic hypothesis made in the dynamic theory that the measurement of time, which underpins SR, is based on the observed expenditure of the energy of objects.
In describing the universe, the standard theory has evidence of an expanding space-time which started from a singularity and was impelled outwards by the Big Bang some 13.8 billion years ago. In the simplest model the mass of the universe is assumed to be uniformly distributed and the expanding 4D space-time is taken as analogous to the surface of an expanding balloon in which all views and expansions are along the surface. Nothing is assumed to exist outside of this surface so what can be taken in an ordinary balloon as an expansion which is normal to its surface, is only seen in the standard model as a stretching surface. There are a number of problems with this model1 which can be summarised as
The need for an inflation model. This postulates that at very early times the universe underwent a very rapid expansion which was abruptly switched on and then off and has never been seen since. There currently appears no solid physical explanation for this model1,3 and the reason for adopting it is that it provides an explanation of some of the following observational conundrums.
The flatness problem. From observation the universe is very close to its critical mass density which means the curvature of space-time is near zero4. Since the universe is thought to start from a point, the inflation model is needed to suddenly expand to a surface whose curvature is locally insignificant.
The isotropic or horizon problem. The microwave background radiation is very uniform in all directions. Either we are somehow at a unique place in the cosmos, or all parts of the universe were in contact at the earliest times after the Big Bang. However, the areas that needed to be in contact exist along a line of sight that precludes even the speed of light to be fast enough to provide a connection. Again, the inflation theory can be used to provide an initial expansion that was far faster than the speed of light and so allowed such connections to exist at early times.
The existence of quantum fluctuations needed to provide the seeds of the current galaxies. The origin of such fluctuations requires the formation of virtual particles that are separated by space-time expanding too fast for them to recombine. An inflation-type model is needed for this expansion.
And some items which cannot be explained by inflation.
Dark matter. There is a lack of observable mass in the universe needed to account for its expansion using the standard general relativity theory. There also appears to be too little mass to account for the rotation of galaxies. The shortfall is sometimes postulated as being due to a so-far unobserved particle and is often referred to as dark mass. To account for the dynamics of the universe’s expansion using the standard theory, this dark mass would have to consist of about 25% of the matter in the universe.
Dark energy. It has recently been found5,6 that the expansion of the universe appears to be accelerating, rather than decaying as would be expected if the expansion were only controlled by gravitational effects (or at least, effects due to the standard theory of gravitation**). This energy would be equivalent to about 70% of the matter needed to model the universe using the standard theory.
The dynamic theory will attempt to answer all of the above points based on the different structure of the universe generated by the differences between Cartesian and dynamic relativistic models. In the dynamic theory no further models, such as inflation, will be needed. The next segment will construct the simplest model of the universe that is consistent with the dynamic theory. The last segment will compare quantitative predictions from this theory with FLRW fits to observations. The reasons for this approach have been outlined at the start of this paper.
In the simplest model the dynamic theory assumes the universe started from a singularity embedded in four spatial (not space-time) dimensions at, what we consider, the time of the Big Bang. This provides a uniform radial expansion in the four dimensions if we assume that mass is uniformly distributed throughout the history of the expansion. This is assumed to be analogous to the expanding shell of a 3D sphere, where the mass can be taken as lying at the centre of the sphere, despite all the material being located in the shell, and there is no gravitational potential along the shell normal to the radial expansion vector.
Time comes into being as soon as the expansion starts. This is the radial expansion vector which is related to the velocity of light (see above). In effect the model is the opposite of the standard theory. There nothing exists apart from a 4D surface and expansion, gravitation etc. takes place along this surface. In the dynamic theory, assuming uniform mass, the expansion only occurs radially into a 4D space. From the model outlined in the first few Sections, in our local surroundings 3D beings such as ourselves see this radial expansion as time acting on 3D space, but with no observation of a fourth spatial dimension.
Quite when this expansion transforms to a Minkowski space-time is not clear other than it is assumed by the dynamic theory to occur soon after the Big Bang. Also, like the standard theory, quantum effects should be important in these very early stages but are not considered in this paper. Equally speculation on what exists in the space outside the expanding surface is again outside the scope of the current paper.
Because this is a radial expansion, an observer (A) sees a non-local galaxy (such as B) as having a spatial motion away from him as the radial expansion occurs at an angle to A’s time direction. This is very similar to the behaviour of inertial frames in special relativity section. To reiterate, the motion and the curvature are assumed to be normal to a three-dimensional spatial surface. This 3D spatial surface is assumed to be flat, i.e., there is zero intrinsic curvature along this surface while there is extrinsic curvature in the fourth dimension which is locally seen as time, and non-locally seen as providing an increasing velocity of the 3D surface in relation to A, so providing a stretching surface. However, it should be emphasised that the curvature is only in the fourth dimension (see Figure 3).
The trajectories of all objects are assumed in this simple model to be constant and are seen from outside their frames of reference to obey R = cT, R being the dynamic spatial coordinate of the surface at time cT, and T is the dynamic time coordinate relative to the Big Bang, i.e. which is the integral of DtNN along N’s trajectory as inferred by an observer located within N’s frame of reference. and is the position of a photon in frame P, emitted at the Big Bang, in N’s spatial axes while (see above for nomenclature). All inferred surfaces (see Figure 4) are the loci of all such trajectories originating from the Big Bang.
There are some points which have to be attached to the simple 4D picture of the dynamic universe (see also Figure 3):-
There is no significant motion along the surface normal to the radial expansion otherwise matter will tend to clump, and the uniform mass model will be invalid. Obviously this does happen to an extent in the real universe as galaxies etc. exist. But in this model we are taking the simplest possible mass distribution where in spatial terms it is assumed that most of the universe can be treated as having a uniformly smooth matter distribution.
There is then no overall gravitational potential along the 3D surface as it is assumed analogous to a uniform shell of material which forms the surface of a 3D sphere in Newtonian space, where the potential gradient lies along the radius but is zero along the surface normal to this radius. Locally the same comment about non-uniformity applies as in the previous bullet.
As a consequence of the previous points General Relativistic effects can, to a first approximation, be ignored when considering the observed overall motion of this surface, in contrast to the standard theory where they dominate due to all forces having to lie along a 4D surface***.
In the standard theory the redshift in B, as seen by A, could be generated by either a receding velocity or a gravitational redshift (or a combination of both). From the previous bullets, in the dynamic theory it is assumed that to fit the simple theory the redshift is overwhelmingly provided by a receding velocity, which in turn results from the angle the radial velocity at any location makes with an observer. Hence, to reiterate previous bullets, it is assumed that there is little matter (compared to the mass of the universe) that is trapped in intense local gravitational fields (in a black hole or around stars) or moving at high speeds along the 3D surface.
The expansion velocity of the universe would be inferred to be constant (and equal to the velocity of light) once the perspective effects due to curvature have been subtracted, despite the overall expansion probably decreasing. This apparently contradictory situation results from there being no direct way for 3D observers to measure changes in the actual 4D radial expansion rate from within the universe. Any real change in radial motion will be equally seen in both the passage of time and the expansion of space (see Figure 3), so that a phenomenon such as velocity remains unchanged.
Although the time dimension does not exist when observed from within a given reference frame, the remaining analysis requires the construction of a “time dimension” in order to situate the relative position of bodies and events, e.g. such as where and when A locates galaxy B, or where events are located relative to the Big Bang. This is an inferred dimension and, as indicated above, is carried out by integrating the radial motion to provide a dimensional construct in which events lie relative to A.
There are three types of time shown in the following diagram (Figure 4). Solid blue lines are inferred surfaces which consist of the locus of 4D trajectories from the Big Bang to the present. Each trajectory is locally constructed, e.g. OA and OB in the Figure. The present is the surface constructed from the termination of these trajectories such as at A and B. This surface is where the 4D sphere lies but is not observable other than locally since information about B can only arrive at A in B’s past.
The second type (solid red line) is the directly observed surface. Observer A sees time dilation effects in B because of the galaxy’s recessional velocity, and these, plus the time delay for photons from B to reach A (vertical lines such as CF in the figure), only allows A to see B in B’s past. This is the only directly observable surface due to observations of the Doppler effect, and as such its position is linked to the change in scale factor with time (see below for a more detailed analysis of the scale factors relating to the universe). Such observations always occur in A’s continually changing present (which is equivalent in Cartesian terms of laying down a time-like trajectory) since this is the only location at which A can interact with events or phenomena such as photons. However, that the observation is of B’s past allows A to construct B as a point on A’s own time axis, e.g. OF in Figure 4.
The third type (broken red line) is also inferred and results from the correction needed for A to obtain the location of the observed surface in terms of B’s “proper” time relative to the Big Bang, i.e. the removal of the time dilation term and the assumption that the change in time along trajectories such as OB will proceed at the same rate as occurs along OA while keeping the observed scale factor the same. The removal of the time dilation term removes the link with recessional velocity, and thus the curve’s position is linked to the scale factor rather than its time derivative. For this to happen OF would be located at OD on B’s trajectory (surface FDJ is at constant s) and in turn OD would be located at OG on A’s trajectory. This broken red line will be referred to as the corrected surface and is always relative to the observer. This observer is A in Figure 4, but the same diagram can be applied to an observer located on any other trajectory.
To quantify the simple dynamic model we can draw the Figure 4 from the assumptions previously discussed, i.e. that each part of the universe’s surface is expanding radially outwards at a function of the velocity of light and that the trajectories of OA and OB since the Big Bang are straight. These straight lines result from the unchanged velocity (see above) of objects seen by an observer to be moving with this surface. Note that in this simple model the only observable movement on a universal scale is due to the expansion of this surface, high velocity objects along the surface are ignored. From the viewpoint of these observers the surface resulting from the locus of the endpoints of these trajectories is located at cT0 (T0 is the integral of DtNN over the period from the Big Bang to the present - see above). Note that the value of T0 is frozen for this analysis, and changes along the trajectories are indicated by d( ) rather than D( ) under these conditions despite still referring to dynamic coordinates. The principal observer is located in the present at position A, although the same figure will be obtained if we swap to B being the principal observer.
The details of Figure 4 are summarised in the following bullet points.
A’s view of the universe originates from the directly observed surface (solid red line) and whose observed and inferred surfaces can be calculated as described below.
The inferred surface moves radially out from the Big Bang. All observers are located on the “present” surface (although they will only have the same restricted view as A of the rest of the universe), and the past is located at previous positions of the present surface as it expanded out from the Big Bang. These are the concentric surfaces represented by EC and FD on A’s time axis. Note that T = 0 is the location of the Big Bang while T = T0 is the present. Also R = 0 is the Big Bang location in what A sees as a spatial axis, while R = cT0 is the inferred spatial position of the present surface.
It should be re-emphasised that from A’s viewpoint his time axis is an imaginary construct where the observable surface is seen in A’s present and consists of a single view of all other trajectories where the time dilated surface (solid red line), the object’s trajectory (e.g. OB) and the photon trajectory (e.g. CF) intersect. From the photon trajectory A calculates B as apparently appearing at a location OF in time relative to the Big Bang. Although the result of every intersection is seen at A, he has (in the current theory) artificially spread out these locations along an imaginary dimension (OA). The method by which the events are separated is discussed below.
A cannot see surface ABL, he can only see surface ACO which he knows will contain clocks that are time dilated due to Doppler effects (see below). However, he assumes they are time dilated relative to ACO and not ABL. Consequently, to correct for this time dilation he will correct the observed times onto the broken red line, ADO. Hence we have the inferred present surface ABL, the observed surface ACO and the inferred corrected surface ADO.
Also note that temporal simultaneity occurs along the inferred surfaces such as ABL and ECK, and not along the vertical lines which connect different times such as OF and OC between the observed surface and the observer.
Let us assume that A and B had clocks travelling with them that were set to zero at the Big Bang and have been accumulating time ever since. Because of the fourth-dimension curvature, A sees B moving at velocity v/c along A’s spatial axis. Because B has a straight radial trajectory, this velocity has not changed over time.
We are only dealing with special relativity so that A’s observation of B is from C where OC/OB = OE /OA = (1 − v2/c2)1/2, i.e. to A the galaxy at B has not travelled as far along OB as it should due to the time dilation factor of the apparent velocity.
The geometric construction of the surfaces can be obtained by remembering we are only dealing with concentric circles and straight lines, and by letting cT0 = OB; cTG = OG; cTF = OF; cTE = OE; X = CF and X0 = BE in Figure 4. Then
The inferred present surface ABL is given by
The time-dilated observed surface (solid red line) relative to A is
The inferred corrected surface (broken red line) is
The links between these construction surfaces and the dynamic theory are explored below.
The evolution of the universe is calculated in terms of the scale factor s of the universe at time T after the Big Bang, which can be expressed as
Since a dynamic coordinate is being used (e.g. T or R) it should be emphasized that this is along a given trajectory (e.g. OA or OB), but inferred surfaces (e.g. FDJ in Figure 4) link constant values of s. This parameter can measure the amount of stretch in the surface between then (T) and now (T0), and is often used when comparing experiment and theory The connection between the observed and inferred surfaces, and the scale factor is given by the three phenomena discussed below :-
The relativistic Doppler redshift.
The only scale factor that can be directly seen by A is the value of s given by the Doppler redshift, and corresponds to the frequency of light emitted at any point along the trajectory OB (fe) since B’s velocity along this trajectory is, from A’s viewpoint, a constant. The frequency observed at A by at locations such as F and G is f0, where 1 + z = fe/f0 and s is assumed as equal to 1/(1 + z).
The Doppler redshift is then related to the recessional velocity by the standard relativistic relationship
1/s = 1 + z = ((1 + v/c)/(1 – v/c))1/2 or on rearranging
In dynamic coordinates sinζ = v/c, and so cosζ = (1 – v2/c2)1/2. From this and Equation (21) we then have
which provides the link between construction geometry and observation, and which is further explored below.
The trajectory reduction.
As already mentioned, A will see B’s trajectory foreshortened due to the space-time dilation effects of B’s relative velocity. B will have only apparently travelled to OC rather than OB where OC/OB = (1 – v2/c2)1/2 = cosζ.
The photon travel.
Photons travel vertically in dynamic coordinates and so while time dilation places B at OC on B’s trajectory, B appears at OF on A’s trajectory. Hence from A’s viewpoint s = OF/OA and it should be noted that since simultaneity occurs along inferred surfaces, s will be constant along arc FDJ, and consequently s = OD/OB.
From geometry OF/OC = cosζ. It is then straightforward to show that for arc ECK s1/2 = a constant = OC/OB = OE/OA. These values of s are from observations within a given trajectory.
Between trajectories,
However, since OA=OB then we can write that from within A’s trajectory B’s position appears as
Consequently
Let H(T) be the Hubble parameter at time T after the Big Bang and H0 is the present value of the parameter. Then H0 = 1/T0 and along a trajectory that is frozen at R0, T0 ≡ RL, TA we have H(T) = s–1 ds/dT. From A’s viewpoint H(T) varies along the time axis (OA) and at a point along this axis RJ/TF = dRJ/dTF = c, the velocity of light. The observed surface on which A sees B is at RJ = cTF. Since s = RJ/R0 then ds/dT = dRJ/dT and so
H(TF) = s–1 ds/dTF = dRJ/dTF = c/RJ = 1/TF. Hence H(TF) = 1/TF. So
Let H(T) be designated as H. In the standard coordinate theory
where ΩM is the current normalised density of matter (the Standard Cosmology Model (SCM) value quoted in 9 is 0.32); ΩR is the normalised density of radiation (5×10−5 and so is ignored for what follows); and the SCM value for ΩΛ (the normalised dark energy coefficient) is 0.68.
Figure 5 shows a comparison of the two theories (Equation (26) and Equation (27)).
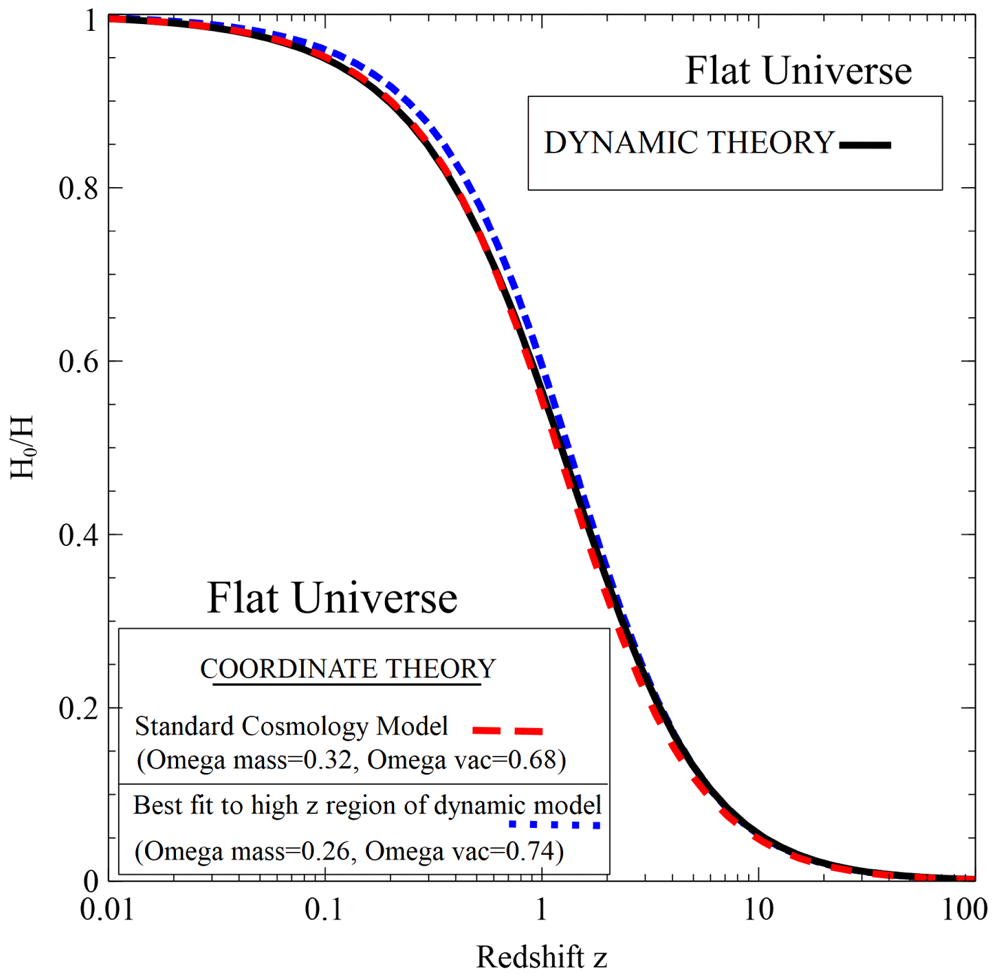
Considering the simplicity of the model used in the dynamic theory, it is remarkably close overall to the SCM coordinate theory’s values for the coefficients (red dashed line, in the Figure). A rather better fit to the higher z values is given by the blue line (coefficients given in the Figure) as will be explored below and in Figure 6 when the relationships are differentiated.

At the high z values a good fit is obtained to the dynamic theory by the SCM’s coefficients when the curve is reduced by 10%. This is shown in Figure 7 (green curve). Consequently, to fit to the dynamic curve over the complete range of z two SCM curves are needed (see Figure 7), the high z curve needing a value of H0 which is 10% lower than its value obtained from nearby (low z) cosmological data. This would allow the dynamic theory to explain the current “tension” between values of H0 obtained from the cosmic microwave background (high z) and from more recent (low z) cosmological feature (e.g. 10).
It should be noted from Figure 6 that when the dynamic curve is divided by T0 - the current age of the universe for an observer - the shape of the curve (i.e. the late time acceleration) is independent of the epoch in which the observation is made.
The differential ds/dT of A’s observation of B in both the standard and dynamic theories is given by H0/H = s(ds/dT)–1. Hence for the dynamic theory, substituting this into Equation (26) gives
In the standard theory a similar substitution in Equation (27) gives
These equations are shown in terms of redshift (z) in Figure 6 and (za) in Table 3 below.
| za | Comments | Reference |
|---|---|---|
| 0.732 | Shape independent of T0. | Dynamic Theory |
| 0.619 | Value at current epoch. | SCM9 |
| 0.752 +/-0.041 | Astronomical data | 4 |
| 0.72 +/-0.05 to 0.84 +/-0.03 | 5 models plus 38 measurements of H(z) | 11 |
The match between the theories means that it is possible that dark energy (the accelerating universe represented by ΩΛ) could be just a feature of perspective. This follows from the differential of the observable surface that shows the universe slowing down at large redshifts - as would be expected in the Standard theory from the effects of gravity - and then in the relatively recent past beginning to accelerate. This is shown above (Figure 5 & Figure 6), along with the position, in terms of redshift, where the dynamic theory predicts the acceleration to start. Comparisons of this acceleration start (za) with results from various models based on both the Standard theory and observational astronomy are given in Table 3 below.
For A to adjust B’s times to a non-time dilated system to get comparative absolute times for s for both A and B relative to the Big Bang, it should be noted that s occurs on the same inferred surface (FDJ) when considered from within the appropriate trajectory, i.e. it is located at F on trajectory OA, and at D for trajectory OB. Consequently, in Figure 4, A’s adjusted estimate, i.e. from the inferred corrected surface containing B’s absolute location, would be at G.
By a similar reasoning that led to Equation (26), OG/OA = OD/OB = s cosζ, or
The standard curves can be obtained from any text on cosmology and can be summarised as follows; comparisons with dynamic theory are given in Figure 8.
Radiation-only model; s = (T/T0)1/2.
Einstein-de Sitter (matter-only); s = (T/T0)2/3.
Dark energy only; s = eH0(T–T0).
Combined Friedmann equations; s = (ΩM/ΩΛ)1/3 sinh2/3(T/TΛ).
where TΛ = (4/3Λc2)1/2 and Λ ≈ 10–35 secs–2.
The key elements in the dynamic theory are: -
Very much like in special relativity A’s view of B is due to perspective rather than any real relationship. B’s view of A will be identical.
The match between the dynamic and coordinate theories in describing the universe’s evolution means that if there is any merit in the dynamic solution, there is no need to consider that the overwhelming proportion of dark mass (represented by ΩM in the coordinate theory) exists. However, some must be present (or some currently unknown physical phenomenon must apply) as the rotation of galaxies requires more mass than is observable.
The match can also mean that dark energy (the accelerating universe represented by ΩΛ) is also just a feature of perspective. This follows from the differential of the observable surface that shows the universe slowing down at large redshifts - as would be expected in the coordinate theory from the effects of gravity - and then in the relatively recent past beginning to accelerate. This is shown in Figure 6, along with the position, in terms of redshift, where the dynamic theory predicts the acceleration to start. Comparisons of this acceleration start (za) with results from various models based on both the coordinate theory and observational astronomy are given in Table 3.
The following current cosmological problems have possible dynamic solutions
The flatness problem. In the dynamic theory the curvature is always caused by the radial velocity. In turn this is always in the time direction for human observers - a direction in which locally they cannot see any sort of dimension. This is illustrated in qualitative terms by Figure 3 in which it is assumed that A can see the current (according to both A’s and B’s clocks) position of B with no account taken of time dilations or delays. See previous Sections for a more quantitatively precise description of A’s view of B in the dynamic theory. In Figure 3, A is again the main observer and B a distant galaxy. The real (i.e., total) motion of B lies along B’s time axis, which is orthogonal to the 4D surface. A directly sees only the spatial component of B’s real motion as a velocity lying parallel to A’s spatial dimension, and hence, from A’s viewpoint, projected onto it. In the Figure, a photon would have its time direction aligned with A’s spatial axis and its space direction along A’s time axis.
The dynamic universe has an extrinsic curvature, the curvature being confined to the fourth dimension. However, to any observer on this 4D surface one of these dimensions is missing (it is in the time direction) and the three remaining spatial dimensions having no intrinsic curvature appear flat.
Consequently, it is possible for this 3D space to appear flat from the viewpoint of any observer located on the 4D surface (B and A can be interchanged in terms of what each sees of the other). The only view an observer such as A has of this curvature is the projection of the radial velocity onto his 3D space by distant objects.
The horizon problem. This is simply solved in the dynamic theory because all elements of the universe are in contact in the 4D space at the location of the Big Bang. While the coordinate theory must deal with connections between various parts of the universe within an expanding surface when trying to explain the isotropic nature of the microwave radiation, the dynamic theory postulates that all parts were initially in contact and expanded radially outwards.
Dark mass and dark energy. The dark energy needed to explain the late-time acceleration of the universe in the coordinate theory, appears in the dynamic theory to be due to the perspective created by the presence of a directly observed surface (see above), i.e. in the dynamic theory there is no requirement for it to exist.
A lot of the dark mass also appears to be due to problems with the perspective and can be explained away as not required in the dynamic theory. However, this may not be true for all of it as there remains some unanswered questions about the rotation of galaxies for instance.
Inflation-type behaviour. Working through the various relationships obtained previously shows that Equation (28) tends to infinity for values of R close to zero at T = 0. Hence the inflation-type behaviour is implicit in the model without resorting to a separate phenomenon.
The basis of this paper results from a paradox. The way we measure space and time show that they are two very different entities. And yet it has also been shown beyond doubt that they need to be fused into space-time to accurately describe our universe. One may argue that “real” space and time are far removed from the way we define them, and this could well be the case. However, at its most basic construction these two entities have been defined by the ruler and the clock, and on this has been erected one of the most successful theories in science. However, it is a theory which on a cosmic scale has produced conundrums. It has been argued in this paper that such conundrums have arisen because there is more than one way that this fusion of space and time can be achieved.
The use of a dynamic theory to create such a fusion utilises the Minkowski metric, but where the standard Cartesian coordinates have been transformed into an Eulerian configuration (the dynamic coordinates) by multiplying them by a function of γ (see Equation 7–Equation 11) within a given inertial frame. The resulting two sets of coordinates (standard Cartesian and dynamic) give the same local descriptions of motion for special relativity (SR), but has these motions occurring against the background of a different universal structures. The dynamic theory arises from the following summary of the chain of arguments:-
There is no directly observable dimension in time when seen from within an inertial frame, and changes in time are the only dynamic property of the frame that can be experienced by an observer from within this frame. However, both spatial and temporal changes relating to that frame can be seen from other frames.
Only spatial coordinates are present in all the observed frames. A spatial position can physically be visited many times, a temporal event can only be physically visited once.
Spatial coordinates can be directly observed but temporal coordinates must be constructed from second-hand experiences, such as memory or films, coupled with the calculation of the integral of the change in time displayed by clocks.
It is argued that the changes in the present are measured by changes in energy, and so it is possible to choose energy and momentum to construct a space-time coordinate system rather than assume a coordinate system exists against which energy and momentum can be measured.
The consequences of these assumptions are
That time from a viewpoint within a frame is a constant motion along a fourth space dimension from a viewpoint outside that frame. When converted to Cartesian coordinates this motion lies along a time-like trajectory (see Figure 1 and Equation (7)–Equation (11)).
In the limit this spatial motion is equivalent to the velocity of light, while the space along which this motion takes place is rolled up into a point for an observer inside the frame who experiences this phenomenon as time (i.e. there is no observable dimension in one’s own time).
This indicates a universe of four spatial dimensions, which are always seen as three spatial dimensions and a continuously changing present.
In this theory, relative velocity is obtained from differences in the spatial direction of the motion in the fourth dimension, and not by changing its real magnitude.
Consequently SR phenomena such as time dilation result from a change of perspective, not a change in magnitude. Consequently, while frame A sees frame B as having a slower clock than his own, frame B has exactly the same view of A.
Both theories give the same form of the Lorentz transformation (Table 1 and Table 2) between different inertial frames.
Both theories give the same relativistic 4-momentum equation (Equation 10b).
Counter-intuitively GR does not play a role in the simplest dynamic cosmology model outlined in the next segment. The reason is that GR is important in local phenomena such as the space-time surrounding massive objects, but on the cosmological scale in the dynamic theory, observations such as the Hubble redshift can be treated as geometric-based phenomena which arise from the presence of a fourth spatial dimension, as discussed above.
The extra spatial dimension along which objects are in motion, that is derived from the SR model in the dynamic theory, allows a simple description of the universe:-
In the simplest model that can be constructed, the dynamic theory assumes the universe started from a singularity embedded in four spatial (not space-time) dimensions at - what we consider to be- the time of the Big Bang.
This provides a uniform radial expansion in the four dimensions if it is assumed that mass is uniformly distributed throughout the expansion.
Time comes into being as soon as the expansion starts. This is the radial expansion vector which is related to the speed of light. In this configuration the transition to a Minkowski space-time occurs at some unknown point which is assumed to be soon after the Big Bang. Quantum effects in the early expansion are ignored. In the simple dynamic model, assuming uniform mass and negligible motion along the universe’s surface, the expansion only occurs radially into a 4D space. See Figure 3 and the accompanying section for how the radial expansion is experienced locally as time, and from a distance as a spatial velocity.
Equally, for such a model, there is assumed to be no overall gravitational potential along the 3D surface. It is assumed to be analogous to a uniform shell of material which forms the surface of a 3D sphere in Newtonian space, where the potential gradient lies along the radius but is zero along the surface.
In the standard theory the redshift in a distant galaxy, as seen from Earth, could be generated by either a receding velocity or a gravitational redshift (or a combination of both). From the previous two bullets, in the dynamic theory it is assumed that to fit the simple theory the redshift is overwhelmingly provided by a receding velocity, which in turn results from the angle the radial velocity at any location makes with an observer (Figure 3). Hence, it is also assumed that there is little matter (compared to the mass of the universe) that is trapped in intense local gravitational fields (in a black hole or around stars) or moving at high speeds along the 3D surface.
In effect the model is the opposite of the standard theory. There nothing exists apart from a 4D surface, and expansion, gravitation etc. takes place along this surface. From the model outlined above, in our local surroundings 3D beings such as us see this radial expansion as time acting on 3D space, but with no observation of a fourth spatial dimension. The universe, from some outside perspective, is a 3D surface located in a 4D space into which it is expanding.
The quantitative version of the model is derived in the cosmology sections. The results can be summarised as follows:-
There is excellent agreement between the dynamic theory and the best observations of the evolving universe (Figure 5, Figure 6 and Table 3). Consequently, if there is any merit in the dynamic theory the implications can be summarised by the following bullets.
Very much like in special relativity Earth’s view of a distant galaxy’s motion (i.e. the redshift) is due to perspective. The galaxy’s view of Earth will be identical.
The match between the dynamic and coordinate theories in describing the universe’s evolution means that there is no need to consider that the overwhelming proportion of dark mass exists. However, some must be present (or some currently unknown physical phenomenon must apply) as the rotation of galaxies requires more mass than is observable.
The match means that dark energy is just a feature of perspective and not real, or at least cannot be determined by current direct observations. (One drawback of the dynamic theory is that there is no direct way for 3D observers to measure changes in the actual 4D radial expansion rate from within the universe. Any real change in radial motion will be equally seen in both the passage of time and the expansion of space, so that a phenomenon such as velocity remains unchanged.)
Comparisons of the theory’s start of the universe’s late time acceleration (za) with results from various models based on both the coordinate theory and observational astronomy show good agreement.
It should be noted from Figure 6 that when the universe’s acceleration curve is normalised to the current age of the universe, the shape of the curve (i.e., the late time acceleration) is independent of the epoch in which the observation is made.
The inflation model is not needed to account for the flatness and horizon problems, although it is implicit in the dynamic model. Near the time of the Big Bang the expansion tends to infinite velocity to an observer at any point on the current 3D surface of the simple universe. Consequently, it can be deduced to have the right conditions to supply the quantum fluctuations needed to provide the seeds of the current galaxies. The origin of such fluctuations requires the formation of virtual particles that are separated by space-time expanding too fast for them to recombine, but see above comment that detailed models of this era lie outside the purview of this paper.
When comparing the fit of the standard and dynamic models to the history of the universe in terms of its acceleration and deceleration (Figure 7), the single dynamic curve must be fitted by two SCM curves over the complete range of z. The two SCM curves differ by a factor of 10% in the value of H0 between fitting the high z and low z regimes. This difference is also observed when fitting the standard theory to cosmological data and is currently described as the Hubble tension10. This is not present in the dynamic formulation which has a single value of H0.
To sum up, this paper attempts to show that it is possible to have an alternative view of space-time which agrees with the standard theory for local phenomena but provides a different view of the overall structure of the universe. This in turn provides some possible answers to some of the current problems faced in cosmology. It is far from the complete answer to every conundrum, but it is hoped that it may provide some alternative pathways to explore in the future.
Professor John Curtis confirms that the author has an appropriate level of expertise to conduct this research, and confirms that the submission is of an acceptable scientific standard. Professor John Curtis declares they have no competing interests. Affiliation: Atomic Weapons Establishment; Visiting Professor UCL Mathematics Department.
The author wished to thank those who initiated invaluable discussions and gave advice during the early stages of the production of this paper.
*This view has a long history, e.g. Heraclitus of Ephesus (c.535-c.475BC) has an ever-present change being a fundamental essence of the universe2
**There are theories which postulate non-standard gravitational behaviours and a large number of alternative theories exist to explain the apparent effect of dark energy. See a summary and references in 7
***See, however8, for example where an eleven dimensional space is discussed.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the work clearly and accurately presented and does it cite the current literature?
No
Is the study design appropriate and is the work technically sound?
No
Are sufficient details of methods and analysis provided to allow replication by others?
No
If applicable, is the statistical analysis and its interpretation appropriate?
No
Are all the source data underlying the results available to ensure full reproducibility?
Partly
Are the conclusions drawn adequately supported by the results?
No
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: I am a cosmologist working on the theoretical development of models to resolve open issues in observational cosmology.
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Observational cosmology; galaxy formation; large-scale structure; cosmic topology; inhomogeneous cosmology
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Observational cosmology; galaxy formation; large-scale structure; cosmic topology; inhomogeneous cosmology.
Is the work clearly and accurately presented and does it cite the current literature?
Partly
Is the study design appropriate and is the work technically sound?
No
Are sufficient details of methods and analysis provided to allow replication by others?
No
If applicable, is the statistical analysis and its interpretation appropriate?
Not applicable
Are all the source data underlying the results available to ensure full reproducibility?
No source data required
Are the conclusions drawn adequately supported by the results?
No
References
1. Taylor E, Wheeler J, Bowen J: Spacetime Physics: Introduction to Special Relativity, 2nd ed.American Journal of Physics. 1993; 61 (3). Publisher Full TextCompeting Interests: No competing interests were disclosed.
Reviewer Expertise: Observational cosmology; galaxy formation; large-scale structure; cosmic topology; inhomogeneous cosmology.
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 5 (revision) 18 Dec 25 |
||
|
Version 4 (revision) 27 Jan 25 |
read | |
|
Version 3 (revision) 30 Sep 24 |
read | |
|
Version 2 (revision) 30 Jan 23 |
read | |
|
Version 1 21 Mar 22 |
read | |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)